Piles et récursivités

1. Introduction

Ce document introduit la structure de données pile et les algorithmes récursifs, qui peuvent être implémentés en utilisant des appels de fonction récursifs. On verra un exemple d'algorithme récursif qui peut être implémenté au moyen d'une pile.

2. Pile

2.a. Définition

La pile est une structure de données qui ne permet que deux opérations :

empiler un élément, qui consiste à ajouter un élément en haut de la pile;
dépiler un élément, qui consiste à retirer le dernier élément empilé et à lire son contenu.

Une pile est une structure de données de type Last In First Out (LIFO) puisque le dernier élément ajouté est le premier enlevé.

Pour représenter l'état de la pile, on la considère comme une liste. Le sommet de la pile est le dernier élément ajouté. Nous allons représenter les piles horizontalement, le sommet étant par convention à droite.

Voici une pile contenant 5 éléments. Les éléments peuvent être des nombres, des chaînes de caractères, ou plus généralement des objets de type quelconque.

\begin{matrix} e_{0} & e_{1} & e_{2} & e_{3} & e_{4} \end{matrix}

Les éléments sont repérés par un indice. Si n est la taille de la pile, l'indice du dernier élément ajouté est n-1. La notion d'indice n'intervient pas dans l'utilisation d'une pile (en principe) car on ne fait pas d'accès aléatoire aux éléments. Par exemple, il n'est pas possible en principe d'accéder à l'élément e₂ de cette pile. e₀ est le premier élément ajouté à la pile, e₁ le deuxième, etc. Si l'on empile un élément e₅, l'état de la pile devient :

\begin{matrix} e_{0} & e_{1} & e_{2} & e_{3} & e_{4} & e_{5} \end{matrix}

Si l'on dépile, on enlève ce dernier élément et on revient à l'état antérieur de la pile.

Dans python, les piles sont réalisées avec le type List (qui sert aussi à faire des listes et d'autres types de structures comme les files, les arbres, etc.). Voici comment créer une pile vide et ajouter un premier élément (ici un nombre) :

pile = []
pile.append(5)

La fonction attachée à la pile qui permet d'empiler un élément est append. Ajoutons trois autres éléments :

pile.append(2)
pile.append(0)
pile.append(10)

print(pile)
--> [5, 2, 0, 10]

La pile permet d'ajouter des éléments sans se préoccuper du nombre d'éléments déjà présents, et sans savoir a priori combien d'éléments on va finalement ajouter. En principe, la pile n'a pas de taille maximale.

Pour dépiler un élément, on utilise la fonction pop, qui enlève le dernier élément ajouté et le renvoie :

a = pile.pop()

print(a)
--> 10

print(pile)
--> [5, 2, 0]

Dans python, les piles sont aussi des listes. Il est donc possible de faire un accès aléatoire à ses éléments, par exemple :

print(pile[1])
--> 2

En toute rigueur, cette opération n'est pas une opération de pile (ce qui n'empêche pas de l'utiliser).

Dans les langages pour compilateur (par ex. C/C++), les piles sont généralement des structures de données optimisées pour les opérations d'empilement et de dépilement et ne sont pas prévues pour un accès aléatoire afficace. Si l'on souhaite faire des accès aléatoires avec un temps d'accès indépendant de la position, il faut utiliser une structure de type tableaux.

Il est fréquent qu'on ait besoin d'une liste tout en utilisant la fonction append. Par exemple, supposons que l'on ait à lire des données dans un fichier de manière séquentielle. Comme il n'est pas possible de connaître à l'avance le nombre d'éléments dans le fichier, on utilise la fonction append pour remplir la liste.

contenu = []
f = open('fichier.txt')
for ligne in f:
    contenu.append(ligne.rstrip())
f.close()

print(contenu)
--> ['Ligne 1', 'Ligne 2', 'Ligne 3', 'Ligne 4', 'Ligne 5', 'Ligne 6', 'Ligne 7']

Pour lire le contenu du fichier ainsi stocké dans la pile, on peut utiliser la pile comme une liste et accéder à ses éléments avec leur indice, en commençant par le premier. Si l'on veut une pile dans laquelle les lignes du fichiers sont rangés dans l'ordre inverse, on peut l'obtenir comme ceci :

inverse = []
while len(contenu)>0:
    inverse.append(contenu.pop())

print(inverse)
--> ['Ligne 7', 'Ligne 6', 'Ligne 5', 'Ligne 4', 'Ligne 3', 'Ligne 2', 'Ligne 1']

La fonction pop déclenche une erreur lorsqu'on l'applique sur une liste vide, c'est pourquoi on doit tester la longueur de la pile.

2.b. Exercice

Écrire un script qui permet à l'utilisateur d'entrer une liste de points du plan, chacun sous la forme x,y. Il doit avoir trois possibilités :

Entrer un point sous la forme x,y.
Entrer le caractère e pour effacer le dernier point saisi.
Entrer le caractère f pour finir la boucle de saisie et tracer un graphique représentant les points.

Pour effectuer la saisie au clavier, utiliser la fonction input, qui s'utilise de la manière suivante :

reponse = input("texte ")

La chaîne de caractères fournie en paramètre et affichée et le programme se met en attente d'une saisie au clavier. Lorsque l'utilisateur appuie sur Entrée, la fonction renvoie la chaîne de caractères saisie par l'utilisateur.

On utilisera aussi la fonction split, qui permet de séparer une chaîne de caractères à partir d'un caractère :

liste = chaine.split(",")

Réponse : saisieListePoints.py

3. Récursivité

3.a. Récursivité simple

Dans un algorithme récursif, la tâche accomplie se scinde en une ou plusieurs tâches secondaires similaires à la tâche principale.

Un exemple très simple d'algorithme récursif est le calcul du produit factoriel d'un entier fact(n)=n(n-1)(n-2)...2. En effet fact(n)=n fact(n-1). Pour calculer le produit factoriel de n, on fait appel au produit factoriel de n-1. Voici une première manière de calculer le produit factoriel :

def fact(n):
    produit = n
    while n > 2:
        n -= 1
        produit *= n
    return produit

print(fact(6))
--> 720

On a fait ici une implémentation itérative de l'algorithme récursif, en itérant sur l'entier qui apparaît dans le produit. Il y a une autre manière de procéder, qui utilise une possibilité du langage python appelée la récursivité (que la plupart des langages possèdent). Il s'agit de la possibilité, au sein d'une fonction, de faire un appel à cette même fonction. Voici une implémentation qui utilise la récursivité :

def fact_recursif(n):
    if n > 1:
        produit =  n*fact_recursif(n-1)
        print(produit)
        return produit
    else:
        return 1

L'appel récursif se fait à condition que n>1. Dans une implémentation récursive, il y a toujours une condition qui permet de stopper la récursion : ici cette condition est n<=1. Le niveau de récursion atteint est le nombre d'appels récursifs.

La ligne print(produit) a été ajoutée pour suivre le déroulement des appels récursifs. Cette ligne est exécutée juste après le calcul du produit de la ligne précédente.

p = fact_recursif(6)

print(p)
--> 720

Il faut remarquer l'ordre d'exécution des produits, qui est différent de l'ordre dans la fonction fact (mais ce dernier est facile à inverser). Le calcul des produits ne commence que lorsque le dernier appel a été fait (fact_recursif(1)). La séquence des opérations effectuées comporte deux parties : dans la première partie, les appels de la fonction s'enchaînent. Dans la seconde partie, les produits sont calculés. Voici la séquence des opérations :

appel de fact_recursif(6)
appel de fact_recursif(5)
appel de fact_recursif(4)
appel de fact_recursif(3)
appel de fact_recursif(2)
appel de fact_recursif(1)
renvoie de 1 (fin de fact_recursif(1))
calcul de 2*1 -> renvoie de 2 (fin de fact_recursif(2))
calcul de 3*2 -> renvoie de 6 (fin de fact_recursif(3))
calcul de 4*6 -> renvoie de 24 (fin de fact_recursif(4))
calcul de 5*24 -> renvoie de 120 (fin de fact_recursif(5))
calcul de 6*120 -> renvoie de 720 (fin de fact_recursif(6))

L'implémentation de la récursivité nécessite l'utilisation d'une pile. À chaque appel récursif, il faut en effet mémoriser les valeurs des variables locales de la fonction. Voici ce qu'il se passe lorsque la ligne produit=n*fact_recursif(n-1) est exécutée :

analyse syntaxique de la ligne n*fact_recursif(n-1) : un appel récursif est détecté
sauvegarde des valeurs des variables locales (ici n) dans une pile
appel de fact_recursif(n-1)
valeur de retour mise dans une variable provisoire (retour)
calcul de n*retour et stockage de la valeur dans produit

La pile nécessaire au stockage des valeurs des variables locales a une taille par défaut de 1000. Si l'on souhaite faire plus de 1000 appels récursifs, il faut modifier la limite de la manière suivante :

import sys
sys.setrecursionlimit(10000)

Le temps d'exécution de ces deux implémentations (itérative et récursive) est similaire, dans le sens où il est dans les deux cas proportionnel à l'entier n (le nombre de multiplications est le même dans les deux cas). L'appel récursif peut conduire à une légère surchage de travail comparé à la boucle itérative, c'est pourquoi la seconde option est probablement moins rapide que la première (d'un facteur constant indépendant de n). Par ailleurs, l'implémentation récursive utilise plus de mémoire (à cause de la pile).

Dans cet exemple simple, il n'y pas donc pas d'intérêt à choisir l'implémentation récursive. Dans des cas plus complexes, l'implémentation récursive est rarement indispensable mais elle peut faciliter grandement le travail du programmeur.

Voyons un exemple plus intéressant : la méthode de dichotomie pour calculer la racine d'une fonction. Soit une fonction f: $R \to R$ continue, dont on sait qu'elle a une racine et une seule sur un intervalle [a,b]. On cherche une valeur approchée de cette racine. La figure suivante montre le principe de la dichotomie :

Figure pleine page

Soit c=(a+b)/2, qui divise l'intervalle initial en deux parties égales. On calcule f(c) et on compare son signe à f(a) et f(b). La racine est nécessairement dans le sous-intervalle aux bornes duquel la fonction f prend deux valeurs de signes opposés (ou éventuellement nulles toutes les deux). On est donc conduit à répéter la recherche sur l'intervalle [a,c], qui est similaire au premier, d'où le caractère récursif de cet algorithme. La récursion doit être stoppée lorsque la valeur |f(c)| est inférieure à une tolérance ε que l'on fixe en fonction de la précision souhaitée.

Voici une implémentation qui utilise la récursivité :

def dichotomie_recursive(fonction,a,b,epsilon):
    c = (a+b)*0.5 
    fc = fonction(c)
    if abs(fc) < epsilon:
        return c
    else:
        if fc*fonction(a) <= 0:
            return dichotomie_recursive(fonction,a,c,epsilon)
        else:
            return dichotomie_recursive(fonction,c,b,epsilon)

Voici un exemple d'utilisation :

def f(x):
    return x**2-2.0

print(dichotomie_recursive(f,0.0,2.0,1e-3))
--> 1.4140625

Cette fonction a un léger défaut : la valeur f(a) est évaluée alors qu'elle est certainement déjà disponible. Voici le remède :

def dichotomie_recursive(fonction,a,b,fa,fb,epsilon):
    c = (a+b)*0.5 
    fc = fonction(c)
    if abs(fc) < epsilon:
        return c
    else:
        if fc*fa <= 0:
            return dichotomie_recursive(fonction,a,c,fa,fc,epsilon)
        else:
            return dichotomie_recursive(fonction,c,b,fc,fb,epsilon)

Dans ce cas, la fonction appelée récursivement utilise des données que l'utilisateur n'a pas besoin de fournir. On écrit alors une fonction pour démarrer la récursion :

def demarrage_dichotomie_recursive(fonction,a,b,epsilon):
    return dichotomie_recursive(fonction,a,b,fonction(a),fonction(b),epsilon)

print(demarrage_dichotomie_recursive(f,0.0,2.0,1e-3))
--> 1.4140625

Il est tout à fait possible de faire une implémentation itérative de la dichotomie :

def dichotomie(fonction,a,b,epsilon):
    c = (a+b)*0.5
    fa = fonction(a)
    fb = fonction(b)
    fc = fonction(c)
    while abs(fc) > epsilon:
        if fc*fa <=0:
            b = c
            fb = fc 
        else:
            a = c
            fa = fc
        c = (a+b)*0.5
        fc = fonction(c) 
    return c

print(dichotomie(f,0.0,2.0,1e-3))
--> 1.4140625

Les deux fonctions ont la même efficacité mais l'implémentation récursive est plus facile à écrire et à déboguer.

3.b. Exercice

Soit un tableau contenant des nombres entiers triés par ordre croissant :

import numpy.random
import numpy

N = 50
L = numpy.random.randint(0,200,N)
L = numpy.sort(L)

Écrire une fonction qui permet d'insérer un nombre entier x dans cette liste. La recherche de l'emplacement d'insertion doit se faire par dichotomie. Pour faire l'insertion juste avant l'élément d'indice i :

L1 = numpy.insert(L,i,x)

Cela renvoie un nouveau tableau avec l'élément inséré.

Réponse : insertionListe.py

3.c. Récursivité double

Nous allons développer un exemple dans lequel la tâche se scinde en deux tâches similaires, et non pas seulement une seule comme dans les exemples précédents.

On considère la surface délimitée par un triangle, que l'on souhaite trianguler, c'est-à-dire diviser en triangles plus petits. La figure suivante montre le principe de la triangulation récursive :

Figure pleine page

Pour trianguler le triangle P₀P₁P₂, on déterminer le point P₃, milieu du segment [P₁P₂]. Cela permet d'obtenir deux triangles P₃P₂P₀ et P₃P₀P₁ qui peuvent à leur tour être divisés selon la même procédure.

Il faut adopter une condition pour stopper la récursion. On choisit de définir la taille d'un triangle comme la somme de la longueur de ses côtés et d'arrêter la récursion lorsque la taille du triangle est inférieure à une taille minimale.

Les points sont représentés par leurs coordonnées sous forme d'une liste [x,y]. La fonction suivante divise un triangle (une liste de trois points) et fournit les deux sous-triangles :

import math
import numpy
from matplotlib.pyplot import *
from matplotlib.patches import Polygon
from matplotlib.collections import PatchCollection
                   
def division_triangle(triangle):
    P0 = triangle[0]
    P1 = triangle[1]
    P2 = triangle[2]
    P3 = [(P1[0]+P2[0])*0.5,(P1[1]+P2[1])*0.5]
    return ([P3,P2,P0],[P3,P0,P1])

Les deux fonctions suivantes permettent de calculer la taille d'un triangle :

def longueur_segment(P0,P1):
    x = P1[0]-P0[0]
    y = P1[1]-P0[1]
    return math.sqrt(x*x+y*y)

def taille_triangle(triangle):
    P0 = triangle[0]
    P1 = triangle[1]
    P2 = triangle[2]
    return longueur_segment(P0,P1)+longueur_segment(P1,P2)+longueur_segment(P2,P0)

Voici l'implémentation qui utilise la récursivité :

def triangulation_recursive(triangle,taille_minimale,liste_triangles):
    (triangle_1,triangle_2)=division_triangle(triangle)
    if taille_triangle(triangle_1) > taille_minimale:
        triangulation_recursive(triangle_1,taille_minimale,liste_triangles)
    else:
        liste_triangles.append(triangle_1)
    if taille_triangle(triangle_2) > taille_minimale:
        triangulation_recursive(triangle_2,taille_minimale,liste_triangles)
    else:
        liste_triangles.append(triangle_2)

Chaque sous triangle est lui-même transmis à la fonction de triangulation si sa taille n'est pas assez petite. Sinon, il est ajouté à la liste des triangles. Voici la fonction qui démarre la récursion :

def demarrage_triangulation_recursive(triangle,taille_minimale):
    liste_triangles = []
    triangulation_recursive(triangle,taille_minimale,liste_triangles)
    return liste_triangles

La fonction suivante permet de colorier les triangles avec une couleur liée à la position dans la liste :

def draw_liste_triangles(liste_triangles):
    fig,ax = subplots(figsize=(8,8))
    patches = []
    for triangle in liste_triangles:
        patches.append(Polygon(triangle))
    p = PatchCollection(patches, cmap=matplotlib.cm.jet, alpha=0.5, edgecolors='k')
    p.set_array(numpy.arange(len(patches)))
    ax.add_collection(p)

Voici un exemple :

triangle=[[0,0],[1,0],[0.7,1]]
taille_minimale = 0.3
liste_triangles = demarrage_triangulation_recursive(triangle,taille_minimale)
draw_liste_triangles(liste_triangles)
axis([0,1,0,1])

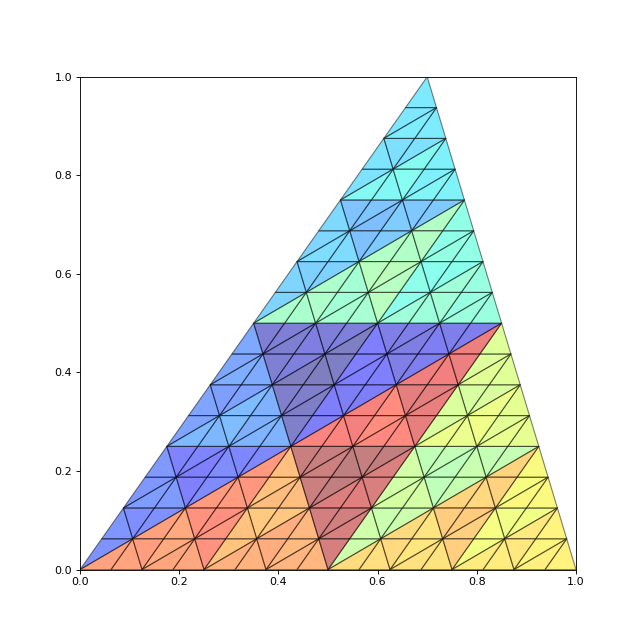figA.pdf

Voyons à présent comment faire une implémentation itérative en utilisant une pile. La pile sert à mémoriser les triangles qui doivent être divisés en deux. À chaque itération, on enlève le triangle situé au sommet de la pile pour le diviser en deux.

def triangulation_pile(triangle,taille_minimale):
    pile_triangles = [triangle]
    liste_triangles = []
    while len(pile_triangles) > 0:
        T = pile_triangles.pop()
        (triangle_1,triangle_2)=division_triangle(T)
        if taille_triangle(triangle_1) > taille_minimale:
            pile_triangles.append(triangle_1)
        else:
            liste_triangles.append(triangle_1)
        if taille_triangle(triangle_2) > taille_minimale:
            pile_triangles.append(triangle_2)
        else:
            liste_triangles.append(triangle_2)
        
    return liste_triangles

liste_triangles = triangulation_pile(triangle,taille_minimale)
draw_liste_triangles(liste_triangles)
axis([0,1,0,1])

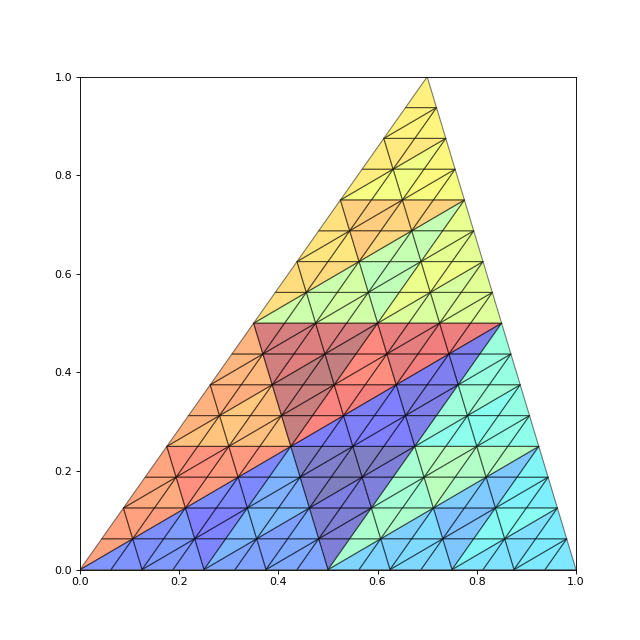figB.pdf

Voici pour finir une petite application : la triangulation d'un polygone régulier à n côté :

def triangulation_polygone_regulier(n,taille_minimale):
    d_angle = numpy.pi*2.0/n
    liste_triangles = []
    P0 = [0,0]
    for i in range(n):
        angle = i*d_angle
        P1 = [numpy.cos(angle),numpy.sin(angle)]
        angle += d_angle
        P2 = [numpy.cos(angle),numpy.sin(angle)]
        triangulation_recursive([P0,P1,P2],taille_minimale,liste_triangles)
    return liste_triangles

liste_triangles = triangulation_polygone_regulier(8,0.3)
draw_liste_triangles(liste_triangles)
axis([-1,1,-1,1])

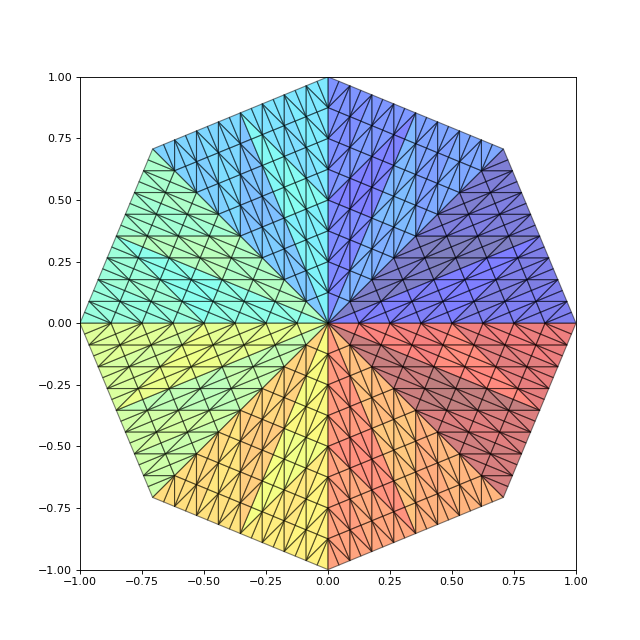figC.pdf