Équation de diffusion : méthode des différences finies

1. Introduction

Ce document montre comment résoudre numériquement l'équation de diffusion en géométrie unidirectionnelle, par la méthode des différences finies avec un schéma explicite.

Ce document est une copie du notebook

cours/diffusion/diffusion-explicite.ipynb

2. Définition du problème

On considère l'équation de diffusion (par exemple diffusion thermique) pour un problème unidirectionnel. La fonction $T(x,t)$ obéit à l'équation aux dérivées partielles suivante :

$$\frac{\partial T}{\partial t}=D\frac{{\partial }^{2}T}{\partial x^2}\text{(1)}$$ La résolution se fait pour $x\in[a,b]$. La condition initiale est supposée donnée par la fonction $T(x,0)$ pour $x\in[a,b]$. On considère le cas où les conditions limites en $x=a$ et $x=b$ consistent à imposer les valeurs de $T$ aux bornes : $$\begin{array}{cc}\hfill & T(a,t)=T_a,\forall t\ge 0\hfill \\ \hfill & T(b,t)=T_b,\forall t\ge 0\hfill \end{array}$$

3. Variables réduites

Pour faire la résolution numérique de l'équation de diffusion, il est intéressant d'introduire des variables réduites, c'est-à-dire des variables sans dimensions. Posons tout d'abord

$$x\text{'}=\frac{x-a}{b-a}$$

$x'$ est une abscisse sans dimensions, appartenant à l'intervalle $[0,1]$. On a :

$$\begin{array}{cc}\hfill & \frac{\partial T}{\partial x}=\frac{\partial T}{\partial x\text{'}}\frac{\partial x\text{'}}{\partial x}=\frac{\partial T}{\partial x\text{'}}\frac{1}{b-a}\hfill \\ \hfill & \frac{{\partial }^{2}T}{\partial x^2}=\frac{{\partial }^{2}T}{\partial x{\text{'}}^2}\frac{1}{{(b-a)}^2}\hfill \end{array}$$

Soit le temps $\tau$ défini par :

$$\tau =\frac{{(b-a)}^2}{D}$$

Introduisons le temps sans dimension :

$$t\text{'}=\frac{t}{\tau }$$

On a :

$$\frac{\partial T}{\partial t}=\frac{\partial T}{\partial t\text{'}}\frac{\partial t\text{'}}{\partial t}=\frac{\partial T}{\partial t\text{'}}\frac{1}{\tau }$$

En reportant ces expressions des dérivées partielles dans l'équation de diffusion, on obtient l'équation de diffusion exprimée avec les variables sans dimensions $x'$ et $t'$, pour la fonction $T(x',t')$ :

$$\frac{\partial T}{\partial t\text{'}}=\frac{{\partial }^{2}T}{\partial x{\text{'}}^2}$$

La condition initiale est donnée par la fonction $T(x',0)$ pour $x'\in[0,1]$. Les conditions limites s'écrivent :

$$\begin{array}{cc}\hfill & T(0,t\text{'})=T_a,\forall t\text{'}\ge 0\hfill \\ \hfill & T(1,t\text{'})=T_b,\forall t\text{'}\ge 0\hfill \end{array}$$

4. Différences finies

L'équation de diffusion est :

$$\frac{\partial T}{\partial t}=D\frac{{\partial }^{2}T}{\partial x^2}\text{(2)}$$

Si les variables $x$ et $t$ sont les variables sans dimensions $x'$ et $t'$ définies ci-dessus, on posera $D=1$.

On doit commencer par discrétiser les variables $x$ et $t$. La discrétisation de $x$ consiste à poser :

$$\begin{array}{cc}\hfill & \Delta x=\frac{1}{N-1}\hfill \\ \hfill & x_n=n\Delta xpourn=0,1,\dots N-1\hfill \end{array}$$

$\Delta x$ est le pas d'espace.

La discrétisation du temps consiste à poser :

$$t_k=k\Delta tpourk=0,1,2,\dots$$

$\Delta t$ est le pas de temps.

L'indice $n$ est donc un nombre entier (compris entre $0$ et $N-1$) représentant la variable d'espace alors que $k$ est un nombre entier positif ou nul représentant le temps.

Une résolution numérique de l'équation de diffusion consiste à rechercher une approximation de $T(x_n,t_k)$ pour tout $n$ compris entre $0$ et $N-1$ et pour $k=0,1,\ldots$. Notons $T_{n,k}$ cette approximation.

Considérons le développement de Taylor par rapport à la variable $t$ :

$$T(x_n,t_k+\Delta t)=T(x_n,t_k)+\frac{\partial T}{\partial t}(x_n,t_k)\Delta t+O\left({\left(\Delta t\right)}^2\right)$$

La notation $O((\Delta t)^2)$ désigne un terme dont la valeur absolue est inférieure à $K(\Delta t)^2$ si $\Delta t$ est assez petit (où $K$ est une constante).

On déduit de cette relation :

$$\frac{\partial T}{\partial t}(x_n,t_k)=\frac{T(x_n,t_k+\Delta t)-T(x_n,t_k)}{\Delta t}+O\left(\Delta t\right)$$

Il s'en suit qu'une approximation de la dérivée partielle par rapport au temps est donnée par :

$$\frac{\partial T}{\partial t}(x_n,t_k)\approx \frac{T_{n,k+1}-T_{n,k}}{\Delta t}$$

et que l'erreur de cette approximation (erreur de troncature) est $O(\Delta t)$. On sait donc que, si $\Delta t$ est assez petit, il existe une constante $K$ telle que l'erreur de troncature est inférieure à $K\Delta t$ (en valeur absolue).

Dans cette expression, la dérivée est remplacée par une différence finie.

Afin d'obtenir une différence finie pour la dérivée seconde par rapport à $x$, considérons les développement de Taylor suivants :

$$\begin{array}{cc}\hfill & T(x_n+\Delta x,t_k)=T(x_n,t_k)+\frac{\partial T}{\partial x}(x_n,t_k)\Delta x+\frac{{\partial }^{2}T}{\partial x^2}(x_n,t_k)\frac{{\left(\Delta x\right)}^2}{2}+\frac{{\partial }^{3}T}{\partial x^3}(x_n,t_k)\frac{{\left(\Delta x\right)}^3}{6}+O\left({\left(\Delta x\right)}^4\right)\hfill \\ \hfill & T(x_n-\Delta x,t_k)=T(x_n,t_k)-\frac{\partial T}{\partial x}(x_n,t_k)\Delta x+\frac{{\partial }^{2}T}{\partial x^2}(x_n,t_k)\frac{{\left(\Delta x\right)}^2}{2}-\frac{{\partial }^{3}T}{\partial x^3}(x_n,t_k)\frac{{\left(\Delta x\right)}^3}{6}+O\left({\left(\Delta x\right)}^4\right)\hfill \end{array}$$

La différence de ces deux relations conduit à :

$$\frac{{\partial }^{2}T}{\partial x^2}(x_n,t_k)=\frac{T(x_n+\Delta x,t_k)-2T(x_n,t_k)+T(x_n-\Delta x,t_k)}{{\left(\Delta x\right)}^2}+O\left({\left(\Delta x\right)}^2\right)$$

Une expression de la dérivée seconde sous forme de différence finie est donc :

$$\frac{{\partial }^{2}T}{\partial x^2}(x_n,t_k)\approx \frac{T_{n+1,k}-2T_{n,k}+T_{n-1,k}}{\left(\Delta x\right)}$$

L'erreur de troncature de cette approximation est $O((\Delta x)^2)$.

On dispose ainsi d'une expression de chaque dérivée partielle sous la forme d'une différence finie, que l'on reporte dans l'équation de diffusion :

$$\frac{T_{n,k+1}-T_{n,k}}{\Delta t}=D\frac{T_{n+1,k}-2T_{n,k}+T_{n-1,k}}{{\left(\Delta x\right)}^2}\text{(3)}$$

5. Schéma numérique explicite

Un schéma numérique est une relation qui permet de calculer les valeurs de $T_{n,k}$ en partant de $k=0$ (instant $t=0$).

La relation $\mathrm{(3)}$ fournit immédiatement un moyen de calculer les $T_{n,k+1}$ (pour $n=0,\ldots N-1$) explicitement si les $T_{n,k}$ sont connus :

$$T_{n,k+1}=T_{n,k}+\frac{D\Delta t}{{\left(\Delta x\right)}^2}(T_{n+1,k}-2T_{n,k}+T_{n-1,k})$$

Soit le coefficient sans dimensions :

$$\alpha =\frac{D\Delta t}{{\left(\Delta x\right)}^2}\text{(4)}$$

Le schéma explicite s'écrit :

Cette relation de récurrence est valable pour tout $k\ge 0$ et pour $n=1,2,\dots N-2$.

La condition initiale consiste en la donnée de $T_{n,0}$ pour $n=0,1,\ldots N-1$. Les deux conditions limites sont :

$$\begin{array}{cc}\hfill & T_{0,k}=T_a,\forall k\ge 0\hfill \\ \hfill & T_{N-1,k}=T_b,\forall k\ge 0\hfill \end{array}$$

Le schéma explicite et les conditions limites permettent de calculer $T_{n,1}$ pour $n=0,1,\cdots N-1$, puis $T_{n,2}$, etc.

Le schéma explicite est stable à condition que :

$$\alpha <\frac{1}{2}\text{(6)}$$

Pour un pas d'espace $\Delta x$ donné, le pas de temps devra donc vérifier :

$$\Delta t<\frac{{\left(\Delta x\right)}^2}{2D}$$

6. Implémentation

            
import numpy as np
from matplotlib.pyplot import * 
rcParams['figure.figsize'] = [13, 6]
            
            

Les $T_{n,k}$ (instant $k$) sont stockés dans un tableau à $N$ éléments ($n=0,1,\ldots N-1$). L'itération consiste à calculer le tableau des $T_{n,k+1}$ (instant $k+1$) à partir du tableau des $T_{n,k}$ et à appliquer les conditions limites. Il est nécessaire de créer un nouveau tableau pour faire ce calcul. La fonction iteration effectue ce calcul et renvoie le nouveau tableau.

def iteration(T,N,alpha,Ta,Tb):
    # tableau contenant T(n,k) pour n=0,1,.. N-1
    # N : taille du tableau
    # alpha
    # Ta,Tb : températures aux frontières
    T1 = np.zeros(N)
    T1[0] = Ta
    T1[N-1] = Tb
    for n in range(1,N-1):
        T1[n] = T[n] +alpha*(T[n+1]-2*T[n]+T[n-1])
    return T1           
            

Il n'est pas nécessaire de garder en mémoire les $T_{n,k}$ pour tout $k$. La fonction calcul effectue les itérations pour $t$ variant de $t_i$ à $t_f$. La variable $t$ n'apparaît pas explicitement dans ce calcul mais elle pourrait apparaître dans un problème où les conditions limites seraient variables. La fonction renvoie l'instant final (qui peut être différent de $t_f$), le tableau des $T_{n,k}$ pour cet instant et le nombre d'itérations.

def calcul(T,N,ti,tf,delta_t,alpha,Ta,Tb):
    t = ti
    niter = 0
    while t<tf:
        T = iteration(T,N,alpha,Ta,Tb)
        t += delta_t
        niter += 1
    return (t,T,niter)            
            

Voici un exemple où $x\in[0,1]$ désigne $x'$ (abscisse sans dimension) et $t$ désigne $t'$ (temps sans dimensions). La condition initiale est $T(x,0)=0$ pour $x\in[0,1]$. Les conditions limites sont $T(0,t)=1$ et $T(1,t)=0$. Le choix de $\Delta x$ dépend de la pente maximale de la fonction $x\rightarrow T(x,t)$ sur l'intervalle $[0,1]$. Plus cette pente maximale est grande, plus $\Delta x$ doit être petit. Dans le problème de diffusion étudié ici, la pente est très forte au voisinage de $x=0$ pour les instants petits. Le pas de temps est choisi à $90\,\%$ de sa valeur maximale. Essayons avec $N=2^{10}$ :

N=2**10
delta_x = 1/(N-1)
x = np.arange(N)*delta_x
T = np.zeros(N)
Ta = 1
Tb = 0
D = 1
delta_t_max = delta_x**2/(2*D) # valeur maximale pour garantir la stabilité
delta_t = 0.9*delta_t_max
alpha = D*delta_t/delta_x**2        
        

Faisons un premier calcul de l'instant $t'=0$ à $t'=10^{-4}$ puis traçons la courbe de $x'\rightarrow T(x',t')$ :

(t1,T1,niter1) = calcul(T,N,0,1e-4,delta_t,alpha,Ta,Tb)

figure()
plot(x,T1)
xlabel("x'")
ylabel('T')
grid()
xlim(0,1)      
        

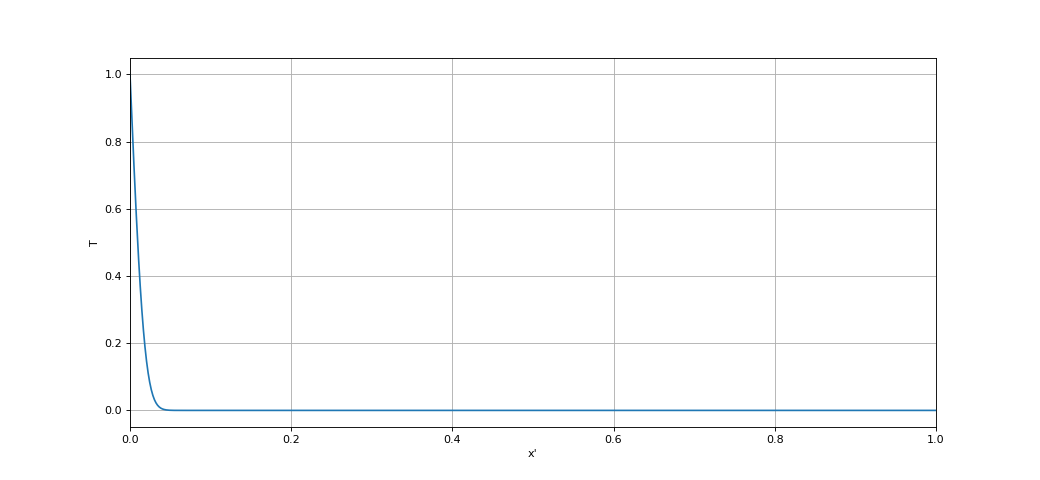fig1.pdf

Voici le pas de temps qui a été utilisé pour ce calcul et le nombre d'itérations

print((delta_t,niter1))
--> (4.2999286211848885e-07, 233)

L'évolution du profil de température est rapide lorsque $t$ est petit puis devient de plus en plus lente. Nous cherchons à présent à calculer l'évolution de $t'=10^{-4}$ à $t'=10^{-3}$. Si $\Delta x$ reste inchangé, la valeur de $\Delta t$ ne peut pas être augmentée car elle a été choisie à $90\,\%$ de la limite de stabilité. Or l'intervalle de temps du calcul de $t'=10^{-4}$ à $t'=10^{-3}$ est environ 10 fois plus grand que le précédent. Il y aura donc 10 fois plus de calculs.

(t2,T2,niter2) = calcul(T1,N,1e-4,1e-3,delta_t,alpha,Ta,Tb)

figure()
plot(x,T2)
xlabel("x'")
ylabel('T')
grid()
xlim(0,1)       
        

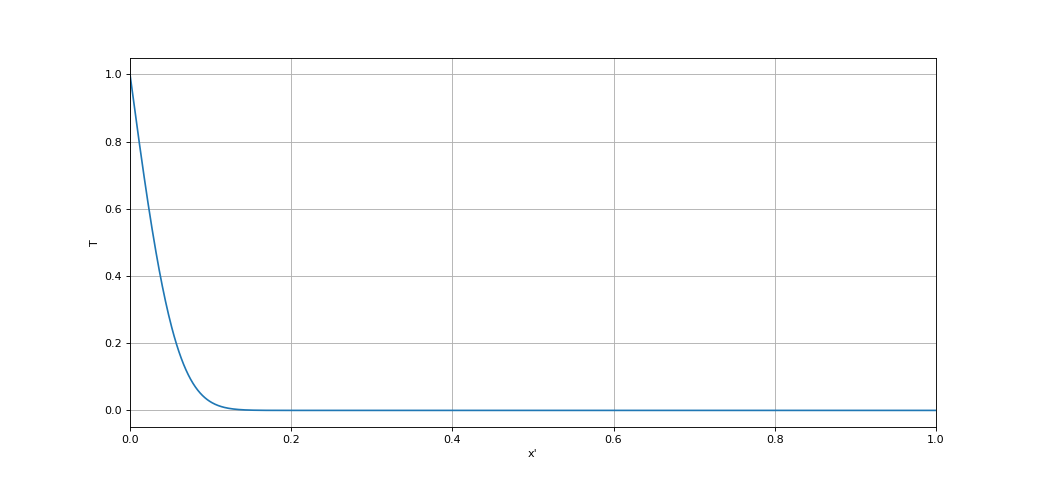fig2.pdf

print(niter2)
--> 2094

Le temps de calcul est encore acceptable. L'étape suivante consiste à calculer de $t'=10^{-3}$ à $t'=10^{-2}$. Si on ne change pas $\Delta x$, le nombre d'itérations sera 10 fois plus grand que le précédent. On remarque que la pente maximale de la courbe est plus faible que pour $t'=10^{-4}$. Il devrait donc être possible d'augmenter $\Delta x$ afin d'augmenter $\Delta t$, donc de réduire le nombre d'itérations. Nous avons défini $N$ comme une puissance de $2$. Il est donc facile de réduire la valeur de $N$ en le divisant pas 4, ce qui aura pour effet de réduire le nombre d'itérations d'un facteur $16$.

N_1 = N//4
T2_1 = T2[0::4]
x_1 = x[0::4]
figure()
plot(x_1,T2_1)
xlabel("x'")
ylabel('T')
grid()
xlim(0,1)
        

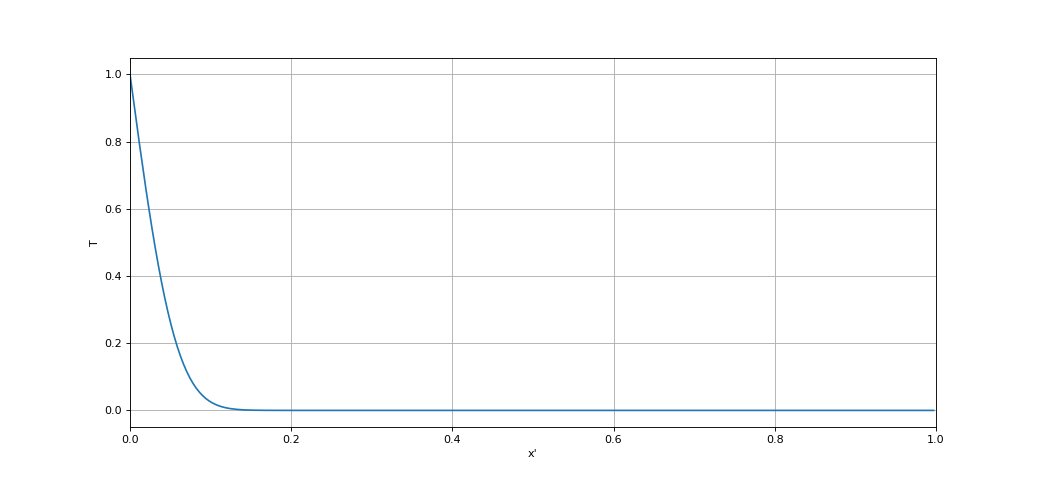fig3.pdf

Comme on le voit sur cette figure, l'augmentation de $\Delta x$ est sans conséquence sur la bonne représentation de la fonction $x'\rightarrow T(x',t')$. Calculons les nouveaux paramètres du calcul :

delta_x_1 = 1/(N_1-1)
delta_t_max_1 = delta_x_1**2/(2*D) # valeur maximale pour garantir la stabilité
delta_t_1 = 0.9*delta_t_max_1
alpha_1 = D*delta_t_1/delta_x_1**2       
        

Voici le calcul de $t'=10^{-3}$ à $t'=10^{-2}$ :

(t3,T3_1,niter3) = calcul(T2_1,N_1,1e-3,1e-2,delta_t_1,alpha_1,Ta,Tb)
figure()
plot(x_1,T3_1)
xlabel("x'")
ylabel('T')
grid()
xlim(0,1)     
        

fig4.pdf

print(niter3)
--> 1301

Pour le calcul de $t'=10^{-2}$ à $t'=10^{-1}$, on peut garder le même $\Delta x$ car le nombre d'itérations sera encore acceptable (10 fois plus que le précédent).

(t4,T4_1,niter4) = calcul(T3_1,N_1,1e-2,1e-1,delta_t_1,alpha_1,Ta,Tb)

figure()
plot(x_1,T4_1)
xlabel("x'")
ylabel('T')
grid()
xlim(0,1)      
        

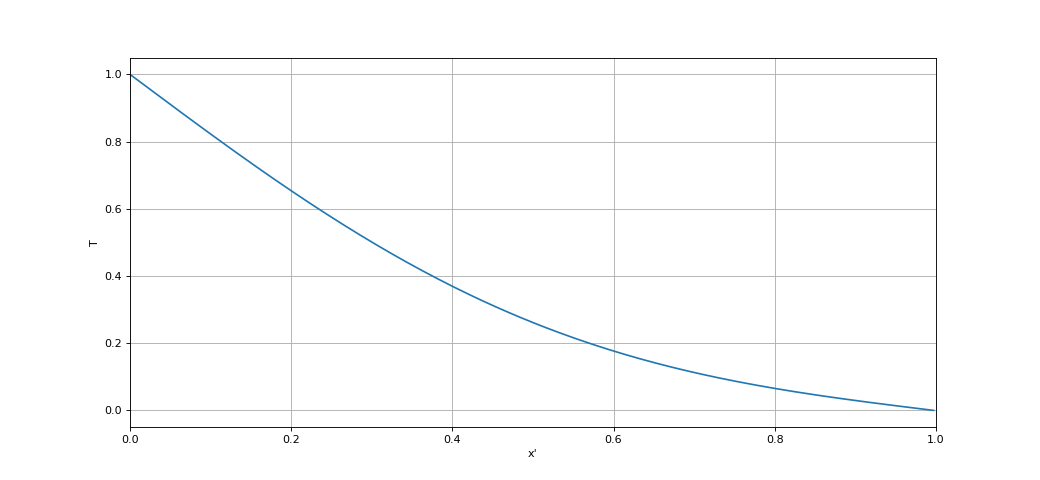fig5.pdf

print(niter4)
--> 13005

Le régime stationnaire n'est pas encore atteint. Il faut encore calculer de $t'=10^{-1}$ à $t'=1$, ce qui demanderait 10 fois plus d'itérations si on ne change pas $\Delta x$. Il est donc judicieux de procéder à nouveau à une division de $N$ d'un facteur $4$ :

N_2 = N_1//4
T4_2 = T4_1[0::4]
x_2 = x_1[0::4]
figure()
plot(x_2,T4_2)
xlabel("x'")
ylabel('T')
grid()
xlim(0,1)       
        

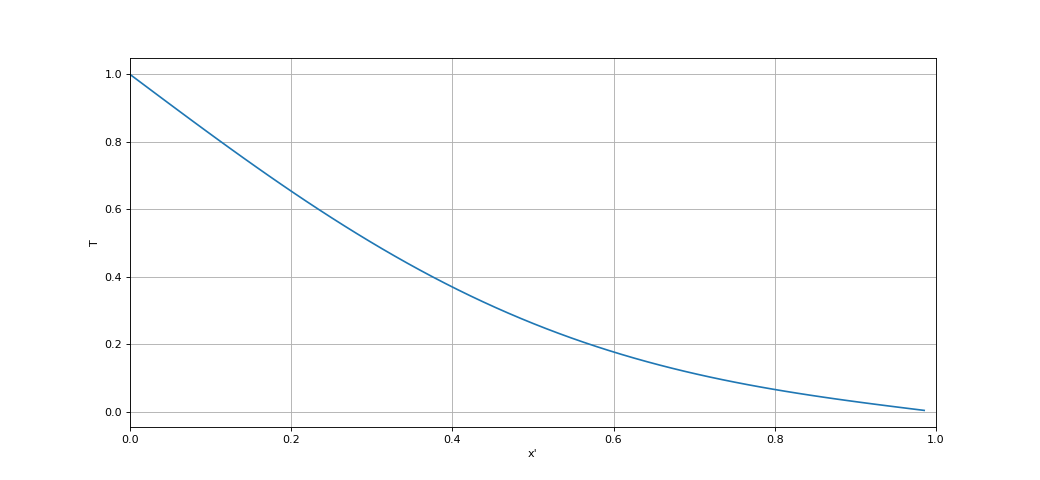fig6.pdf

delta_x_2 = 1/(N_2-1)
delta_t_max_2 = delta_x_2**2/(2*D) # valeur maximale pour garantir la stabilité
delta_t_2 = 0.9*delta_t_max_2
alpha_2 = D*delta_t_2/delta_x_2**2
(t5,T5_2,niter5) = calcul(T4_2,N_2,1e-1,1,delta_t_2,alpha_2,Ta,Tb)

figure()
plot(x_2,T5_2)
xlabel("x'")
ylabel('T')
grid()
xlim(0,1)
        

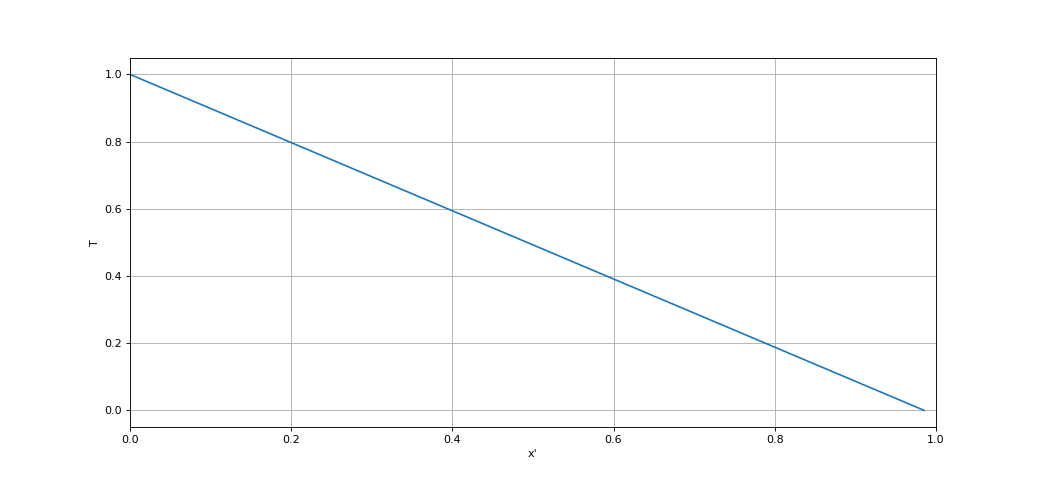fig7.pdf

print(niter5)
--> 7939

Le régime stationnaire est bien atteint à $t'=1$ (un examen plus détaillé montre qu'il est atteint pratiquement pour $t'=0{,}2$). On voit ici l'intérêt d'avoir défini des variables $x'$ et $t'$ sans dimensions. Le temps $t'$ qu'il faut pour atteindre le régime stationnaire est de l'ordre de $1$. La durée réelle correspondante est $\tau$. Pour finir, on trace les courbes de $x'\rightarrow T(x',t')$ obtenues pour les différents instants :

figure()
plot(x,T1,label="t'=%0.2g"%t1)
plot(x,T2,label="t'=%0.2g"%t2)
plot(x_1,T3_1,label="t'=%0.2g"%t3)
plot(x_1,T4_1,label="t'=%0.2g"%t4)
plot(x_2,T5_2,label="t'=%0.2g"%t5)
xlabel("x'")
ylabel('T')
grid()
xlim(0,1)
legend(loc='upper right')       
        

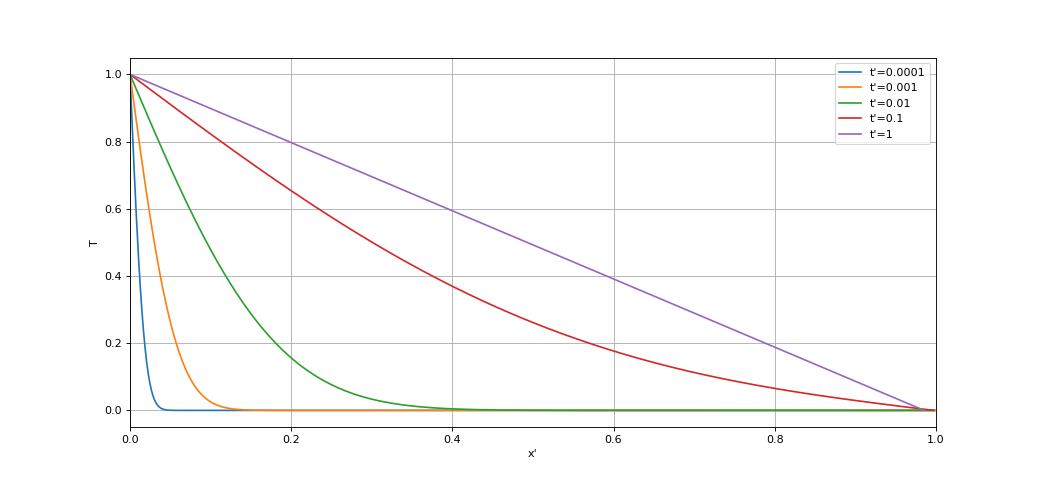fig8.pdf