Équation de Poisson 2D : méthode des éléments finis

2.a. Formulation variationnelle

Pour une fonction $f:\Omega \to ℝ$ de classe C¹, on a :

$${\int }_{\Omega }\frac{\partial f}{\partial x}d\sigma ={\int }_{\partial \Omega }f\overrightarrow{n}\cdot \overrightarrow{u_x}d\ell \text{(5)}$$

où $\overrightarrow{n}$ désigne le vecteur unitaire orthogonal à $\partial \Omega$ et dirigé dans le sens sortant par rapport à $\Omega$. La même égalité est évidemment valable pour la coordonnée y. Appliquons ce théorème à :

$$f=va\frac{\partial u}{\partial x}\text{(6)}$$

On obtient :

$${\int }_{\Omega }a\frac{\partial u}{\partial x}\frac{\partial v}{\partial x}d\sigma +{\int }_{\Omega }v\frac{\partial }{\partial x}\left(a\frac{\partial u}{\partial x}\right)d\sigma ={\int }_{\partial \Omega }va\frac{\partial u}{\partial x}\overrightarrow{n}\cdot \overrightarrow{u_x}d\ell \text{(7)}$$

et de même :

$${\int }_{\Omega }a\frac{\partial u}{\partial y}\frac{\partial v}{\partial y}d\sigma +{\int }_{\Omega }v\frac{\partial }{\partial x}\left(a\frac{\partial u}{\partial y}\right)d\sigma ={\int }_{\partial \Omega }va\frac{\partial u}{\partial y}\overrightarrow{n}\cdot \overrightarrow{u_y}d\ell \text{(8)}$$

La somme de ces deux égalités conduit à :

$${\int }_{\Omega }a\left(\overrightarrow{grad}u\right)\cdot \left(\overrightarrow{grad}v\right)d\sigma +{\int }_{\Omega }vdiv\left(a\overrightarrow{grad}u\right)d\sigma ={\int }_{\partial \Omega }va\left(\overrightarrow{grad}u\right)\cdot \overrightarrow{n}d\ell \text{(9)}$$

qui devient, en utilisant l'équation $\mathrm{(1)}$ :

$${\int }_{\Omega }a\left(\overrightarrow{grad}u\right)\cdot \left(\overrightarrow{grad}v\right)d\sigma ={\int }_{\Omega }vsd\sigma +{\int }_{\partial \Omega }va\left(\overrightarrow{grad}u\right)\cdot \overrightarrow{n}d\ell \text{(10)}$$

Cette égalité est écrite dans le cas bidimensionnel, où $\Omega$ est une surface plane et $\partial \Omega$ le contour de cette surface. $d\sigma$ est donc l'élément de surface et $d\ell$ l'élément du contour. Le même résultat est bien sûr valable en tridimensionnel ($\Omega$ est alors un volume et $\partial \Omega$ la surface qui le délimite).

Soit V l'ensemble des fonctions $\Omega :\to ℝ$ de carré sommable et dont le gradient est aussi de carré sommable sur $\Omega$.

La formulation variationnelle du problème (la recherche de u) s'énonce ainsi [1] : on recherche une fonction $u\in V$ telle que pour toute fonction $v\in V$ on ait l'égalité $\mathrm{(10)}$. Cet énoncé est souvent appelé forme faible du problème de Poisson car les exigences sur la fonction u sont moindres que pour l'équation $\mathrm{(1)}$ (elle n'est plus nécessairement deux fois dérivable).

2.b. Conditions limites

Séparons la frontière du domaine en deux parties : la partie $\partial {\Omega }_d$ sur laquelle une condition limite de Dirichlet est imposée, la partie $\partial {\Omega }_n$ sur laquelle une condition limite de Neumann est imposée. L'égalité $\mathrm{(10)}$ s'écrit :

$${\int }_{\Omega }a\left(\overrightarrow{grad}u\right)\cdot \left(\overrightarrow{grad}v\right)d\sigma ={\int }_{\Omega }vsd\sigma +{\int }_{\partial {\Omega }_d}va\left(\overrightarrow{grad}u\right)\cdot \overrightarrow{n}d\ell +{\int }_{\partial {\Omega }_n}va\left(\overrightarrow{grad}u\right)\cdot \overrightarrow{n}d\ell \text{(11)}$$

Comme il est montré dans Équation de Poisson 1D : méthode des éléments finis, la formulation variationnelle doit être modifiée en considérant les fonctions de V qui s'annulent sur $\partial {\Omega }_d$. Notons V₀ l'ensemble de ces fonctions. La formulation variationnelle devient : obtenir une fonction u telle que pour toute fonction $v\in V_0$ :

$${\int }_{\Omega }a\left(\overrightarrow{grad}u\right)\cdot \left(\overrightarrow{grad}v\right)d\sigma ={\int }_{\Omega }vsd\sigma +{\int }_{\partial {\Omega }_n}va\left(\overrightarrow{grad}u\right)\cdot \overrightarrow{n}d\ell \text{(12)}$$

La condition de Neumann consiste à fixer la valeur de $\left(\overrightarrow{grad}u\right)\cdot \overrightarrow{n}$ sur $\partial {\Omega }_n$. Une variante de la condition de Neumann est la condition de Robin, qui consiste à écrire sur la frontière :

$$\left(\overrightarrow{grad}u\right)\cdot \overrightarrow{n}=K_0(u-u_0)+g_0\text{(13)}$$

où K₀, u₀ et g₀ sont des constantes. Pour K₀=0, on retrouve la condition de Neumann avec g₀ la composante normale du gradient sur la frontière. Plus généralement, ces trois constantes peuvent dépendre du point de la frontière (auquel cas il ne s'agit plus de constantes). Dans ce document, on nommera condition de Neumann la condition définie par l'équation $\mathrm{(13)}$.

Finalement, l'égalité de la formulation variationnelle s'écrit :

$${\int }_{\Omega }a\left(\overrightarrow{grad}u\right)\cdot \left(\overrightarrow{grad}v\right)d\sigma ={\int }_{\Omega }vsd\sigma +{\int }_{\partial {\Omega }_n}va(K_0(u-u_0)+g_0)d\ell \text{(14)}$$

2.c. Maillage triangulaire - Fonctions affines par morceaux

Le domaine $\Omega$ est subdivisé en triangles : chaque maille est un triangle et comporte donc trois nœuds. Une maille partage avec une maille voisine deux nœuds. La figure suivante montre un maillage triangulaire très simple pour un domaine rectangulaire (celui que nous utiliserons pour les tests) :

Figure pleine page

Le maillage comporte P nœuds. Le nœud N_i a pour coordonnées (x_i,y_i). En général, les nœuds ne sont évidemment pas disposés sur une grille.

Les fonctions u et v du problème variationnel sont considérées dans l'ensemble, noté V_h, des fonctions continues et affines par morceaux sur le maillage (l'indice h désigne le maillage). Pour $u_h\in V_h$ on a sur chaque maille : $u_h(x,y)=c_{0}x+c_{1}y+c_2$. Si les mailles sont assez petites, les valeurs de u_h aux nœuds sont censées être de bonnes approximations de u, la solution de l'équation $\mathrm{(1)}$ avec les conditions limites. La fonction u_h est une solution du problème variationnel mais elle n'est évidemment pas une solution de $\mathrm{(1)}$.

Si l'on note $c_0,c_1,c_2$ et $c{\text{'}}_0,c{\text{'}}_1,c{\text{'}}_2$ les coefficients de u_h pour deux mailles voisines, on a sur le côté commun à ces deux mailles, par continuité :

$$c_{0}x+c_{1}y+c_2=c{\text{'}}_{0}x+c{\text{'}}_{1}y+c{\text{'}}_2\text{(15)}$$

ce qui est l'équation de la droite passant par les deux nœuds communs. On a bien évidemment :

$$u_h\left(N_i\right)=c_0{x}_i+c_1{y}_i+c_2\text{(16)}$$

où $c_0,c_1,c_2$ sont les coefficients d'un des trois triangles qui partagent le nœud N_i.

On définit les fonctions affines par morceaux suivantes, pour $i=1,\dots P$ :

$$\begin{array}{ccc}\hfill & {\varphi }_i\left(N_j\right)=1,j=i\hfill & \hfill \text{(17)}\\ \hfill & {\varphi }_i\left(N_j\right)=0,j\ne i\hfill & \hfill \text{(18)}\end{array}$$

Autrement dit, la fonction ${\varphi }_i$ vaut 1 sur le nœud N_i et 0 sur tous les autres nœuds. Ces fonctions constituent une base V_h. Pour toute fonction $u_h\in V_h$, on a en effet :

$$u_h=\sum _{i=1}^P{u}_h\left(N_i\right){\varphi }_i\text{(19)}$$

Le support de ${\varphi }_i$ est constitué des triangles qui ont le nœud N_i en commun. La figure suivante montre le support de ${\varphi }_{13}$ et de ${\varphi }_1$ :

Figure pleine page

Pour un noeud N_i, la fonction ${\varphi }_i$ s'annule sur le côté opposé de chaque triangle auxquels ce nœud appartient.

Considérons un nœud N_i et ses nœuds voisins. Le support de ${\varphi }_i$ est constitué des triangles définis avec le nœud N_i et ces voisins. La figure suivante montre ces triangles :

Figure pleine page

Considérons un de ces triangles, dont les sommets sont notés 1,2,3, le sommet 1 étant le nœud N_i. Les coefficients $c_0,c_1,c_2$ de ${\varphi }_i$ sur ce triangle sont solutions des trois équations suivantes :

$$\begin{array}{cc}\hfill & c_0{x}_1+c_1{y}_1+c_2=1\hfill \\ \hfill & c_0{x}_2+c_1{y}_2+c_2=0\hfill \\ \hfill & c_0{x}_3+c_1{y}_3+c_2=0\hfill \end{array}$$

Si detT désigne le déterminant de ce système, il est facile de démontrer que, si les sommets N₁,N₂,N₃ sont ordonnés dans le sens direct, l'aire du triangle s'écrit :

$$S_T=\frac{1}{2}\left(\overrightarrow{N_1{N}_2}\wedge \overrightarrow{N_1{N}_3}\right)\cdot \overrightarrow{u_z}=\frac{1}{2}detT\text{(20)}$$

Si les trois points ne sont pas alignés, ce système a un déterminant non nul. L'unique solulion peut être obtenue sans difficulté avec les règles de Cramer :

$$c_0=\frac{y_2-y_3}{detT},c_1=\frac{x_3-x_2}{detT},c_2=\frac{x_2{y}_3-x_3{y}_2}{detT}\text{(21)}$$

Soit V_h,0 l'ensemble des fonctions affines par morceaux sur le maillage et qui s'annulent sur les nœuds qui appartiennent à la frontière $\partial {\Omega }_d$ (la partie de la frontière où une condition de Dirichlet est appliquée). Notons $Nint$ les indices de tous les nœuds à l'exception de ces nœuds (indices des nœuds intérieurs). Pour toute fonction $v\in V_{h,0}$ on a :

$$v=\sum _{i\in Nint}v\left(N_i\right){\varphi }_i\text{(22)}$$

La formulation variationnelle s'énonce comme suit. Trouver une fonction $u_h\in V_h$ telle que pour toute fonction $v\in V_{h,0}$ on ait :

$${\int }_{\Omega }a\left(\overrightarrow{grad}{u}_h\right)\cdot \left(\overrightarrow{grad}v\right)d\sigma ={\int }_{\Omega }vsd\sigma +{\int }_{\partial {\Omega }_n}va(K_0(u_h-u_0)+g_0)d\ell \text{(23)}$$

Un énoncé équivalent est : trouver une fonction $u_h\in V_h$ telle que :

$${\int }_{\Omega }a\left(\overrightarrow{grad}{u}_h\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)d\sigma ={\int }_{\Omega }{\varphi }_{i}sd\sigma +{\int }_{\partial {\Omega }_n}{\varphi }_{i}a(K_0(u_h-u_0)+g_0)d\ell ,i\in Nint\text{(24)}$$

2.d. Équations algébriques

Introduisons les composantes de u_h sur la base :

$$u_h=\sum _{j=1}^P{\xi }_j{\varphi }_j\text{(25)}$$

Les ${\xi }_i$ sont les valeurs de u_h aux nœuds, autrement dit les approximations de la solution u. Le report de cette décomposition dans $\mathrm{(23)}$ conduit à un système d'équations linéaires pour les composantes ${\xi }_i$ :

$$\sum _{j=1}^P{\xi }_j{\int }_{\Omega }a\left(\overrightarrow{grad}{\varphi }_j\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)d\sigma ={\int }_{\Omega }{\varphi }_{i}sd\sigma +\sum _{j=1}^P{\int }_{\partial {\Omega }_n}{\varphi }_{i}a{K}_0{\xi }_j{\varphi }_{j}d\ell +{\int }_{\partial {\Omega }_n}{\varphi }_i(a{g}_0-K_0{u}_0)d\ell ,i\in Nint\text{(26)}$$

Ce système comporte plus d'inconnues que d'équations : le nombre d'équations est égal aux nombres de nœuds à l'exception de ceux de la frontière où une condition de Dirichlet est appliquée alors que le nombre d'inconnues est égal aux nombre total de nœuds. Il faut donc enlever du système les ${\xi }_i$ des nœuds qui sont sur $\partial {\Omega }_d$. Pour cela, on écrit u_h comme la somme d'une fonction de V_h,0 (qui s'annule sur la frontière de Dirichlet) et d'une fonction de V_h,d, l'ensemble des fonctions affines par morceaux qui vérifient précisément la condition de Dirichlet choisie :

$$u_h=u_{h,0}+u_{h,d}\text{(27)}$$

Il peut être démontré que u_h est indépendant du choix de u_h,d [1]. On choisit donc la fonction la plus simple : celle qui s'annule sur tous les nœuds à l'exception de ceux où la condition de Dirichlet est appliquée. Notons Nd les indices des nœuds où une condition de Dirichlet est appliquée. On a :

$$u_h=\sum _{j\in Nint}{\xi }_j{\varphi }_j+\sum _{k\in Nd}{\xi }_k{\varphi }_k\text{(28)}$$

Les ${\xi }_k$ dans la seconde somme sont connues puisqu'il s'agit des valeurs de u sur les nœuds appartenant à la frontière où une condition de Dirichlet est appliquée.

On obtient un système d'équations pour les inconnues ${\xi }_j,j\in Nint$ :

$$\begin{array}{cc}\hfill & \sum _{j\in Nint}{\xi }_j{\int }_{\Omega }a\left(\overrightarrow{grad}{\varphi }_j\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)d\sigma +\sum _{k\in Nd}{\xi }_k{\int }_{\Omega }a\left(\overrightarrow{grad}{\varphi }_k\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)d\sigma \hfill \\ \hfill & ={\int }_{\Omega }{\varphi }_{i}sd\sigma +\sum _{j\in Nint}{\int }_{\partial {\Omega }_n}{\varphi }_{i}a{K}_0{\xi }_j{\varphi }_{j}d\ell +\sum _{k\in Nd}{\int }_{\partial {\Omega }_n}{\varphi }_{i}a{K}_0{\xi }_k{\varphi }_{k}d\ell +{\int }_{\partial {\Omega }_n}{\varphi }_{i}a(g_0-K_0{u}_0)d\ell ,i\in Nint\hfill \end{array}$$

Réécrivons ces équations en mettant à gauche la combinaison linéaire des inconnues :

$$\begin{array}{cc}\hfill & \sum _{j\in Nint}{\xi }_j{\int }_{\Omega }a\left(\overrightarrow{grad}{\varphi }_j\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)d\sigma -\sum _{j\in Nint}{\xi }_j{\int }_{\partial {\Omega }_n}{\varphi }_{i}a{K}_0{\varphi }_{j}d\ell \hfill \\ \hfill & =-\sum _{k\in Nd}{\xi }_k{\int }_{\Omega }a\left(\overrightarrow{grad}{\varphi }_k\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)d\sigma +{\int }_{\Omega }{\varphi }_{i}sd\sigma +\sum _{k\in Nd}{\int }_{\partial {\Omega }_n}{\varphi }_{i}a{K}_0{\xi }_k{\varphi }_{k}d\ell +{\int }_{\partial {\Omega }_n}{\varphi }_{i}a(g_0-K_0{u}_0)d\ell ,i\in Nint\hfill \end{array}$$

Posons :

$$\begin{array}{ccc}\hfill & A_{ij}={\int }_{\Omega }a\left(\overrightarrow{grad}{\varphi }_j\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)d\sigma ,(i,j)\in Nint\hfill & \hfill \text{(29)}\\ \hfill & R_{ij}=-{\int }_{\partial {\Omega }_n}a{K}_0{\varphi }_i{\varphi }_{j}d\ell ,(i,j)\in Nint\hfill & \hfill \text{(30)}\\ \hfill & B_i=-\sum _{k\in Nd}{\xi }_k{\int }_{\Omega }a\left(\overrightarrow{grad}{\varphi }_k\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)d\sigma +{\int }_{\Omega }{\varphi }_{i}sd\sigma +\sum _{k\in Nd}{\xi }_k{\int }_{\partial {\Omega }_n}{\varphi }_{i}a{K}_0{\varphi }_{k}d\ell +{\int }_{\partial {\Omega }_n}{\varphi }_{i}a(g_0-K_0{u}_0)d\ell ,i\in Nint\hfill & \hfill \text{(31)}\end{array}$$

Le système d'équations linéaires s'écrit :

$$\sum _{j\in Nint}{A}_{ij}{\xi }_j+\sum _{j\in Nint}{R}_{ij}{\xi }_j=B_i,i\in Nint\text{(32)}$$

2.e. Matrice du système

La matrice du système d'équations est M=A+R. La matrice A est indépendante des conditions limites. La matrice R est non nulle seulement si une condition de Robin ($K_0\ne 0$) est appliquée sur une partie de la frontière $\partial {\Omega }_n$.

Pour $i\ne j$, le coefficient A_ij est non nul si les nœuds i et j ont une partie de leur support en commun, autrement dit si ce sont deux nœuds voisins (rappelons que les nœuds où une condition de Dirichlet est appliquée sont exclus). Pour évaluer approximativement l'intégrale sur un triangle T dont les sommets sont N₁,N₂,N₃, on utilise la formule de quadrature du barycentre :

$${\int }_{T}fd\sigma \approx f\left(\frac{N_1+N_2+N_3}{3}\right)S_T\text{(33)}$$

où S_T est l'aire du triangle. Considérons $A_{ij}^T$, l'intégrale sur un des deux triangles dont un côté est constitué des nœuds i et j, le troisième étant noté N_k. Soient $c_{i0},c_{i1},c_{i2}$ les coefficients qui définissent ${\varphi }_i$ sur ce triangle et $c_{j0},c_{j1},c_{j2}$ les coefficients qui définissent ${\varphi }_j$ sur le même triangle.

Figure pleine page

On a :

$$\left(\overrightarrow{grad}{\varphi }_j\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)=c_{j0}{c}_{i0}+c_{j1}{c}_{i1}\text{(34)}$$

La formule du barycentre donne :

$$A_{ij}^T=a\left(\frac{N_i+N_j+N_k}{3}\right)(c_{j0}{c}_{i0}+c_{j1}{c}_{i1})S_T\text{(35)}$$

En pratique, il sera plus simple d'attribuer une valeur de a à chaque nœud et on écrira donc :

$$A_{ij}^T=\frac{1}{3}(a_i+a_j+a_k)(c_{j0}{c}_{i0}+c_{j1}{c}_{i1})S_T\text{(36)}$$

Il faut aussi déterminer le coefficient sur la diagonale :

$$A_{ii}={\int }_{\Omega }a{\left(\overrightarrow{grad}{\varphi }_i\right)}^{2}d\sigma \text{(37)}$$

Le support de la fonction à intégrer est constitué des triangles auquel le nœud N_i appartient. Pour un de ces triangles, l'intégrale vaut approximativement :

$$A_{ii}^T=\frac{1}{3}(a_i+a_j+a_k)(c_{i0}^2+c_{i1}^2)S_T\text{(38)}$$

Le remplissage de la matrice A se fait en parcourant tous les triangles du maillage. Pour chaque triangle :

• Pour chaque nœud du triangle n'appartenant pas à $\partial {\Omega }_d$, on ajoute A_ii^T à M_ii.
• Pour chaque paire de nœuds du triangle n'appartenant pas à $\partial {\Omega }_d$, on ajoute A_ij^T à M_ij et à M_ji.

Pour $i\ne j$, R_ij est non nul si les deux nœuds N_i et N_j sont voisins et s'ils appartiennent à une frontière où une condition de Robin est appliquée.

Figure pleine page

Le produit ${\varphi }_i{\varphi }_j$ est non nul sur le triangle constitué de ces deux nœuds et du nœud N_k. R_ij est l'intégrale sur le segment N_iN_j de $f=-a{K}_0{\varphi }_i{\varphi }_j$. Les coefficients a et K₀ seront dans la plupart des cas constants sur le segment ou peuvent être considérés comme tel. Si $\ell$ est l'abscisse sur le segment, on a :

$$f\left(\ell \right)=-a{K}_0\frac{\ell (d-\ell )}{d_{ij}^2}\text{(39)}$$

où d_ij est la distance entre les deux nœuds. On a donc :

$$R_{ij}=-\frac{a{K}_0}{d_{ij}^2}{\int }_0^{d_{ij}}\ell (d_{ij}-\ell )d\ell =-\frac{a{K}_0{d}_{ij}}{6}\text{(40)}$$

aK₀ est la moyenne des valeurs sur le côté. Une valeur de K₀ est attribuée au côté et la valeur moyenne de a est évaluée à partir des valeurs sur les deux nœuds. On a donc :

$$R_{ij}=-\frac{1}{12}(a_i+a_j)K_{0,ij}{d}_{ij}\text{(41)}$$

Il faut aussi déterminer le coefficient sur la diagonale :

$$R_{ii}=-{\int }_{\partial {\Omega }_n}a{K}_0{\varphi }_i^{2}d\ell \text{(42)}$$

La fonction à intégrer est non nulle sur les deux segments (notés 1 et 2) de la frontière auquel le nœud N_i appartient :

Figure pleine page

Notons a₁,K₁ et a₂,K₂ les valeurs des coefficients aux milieux des segments 1 et 2. On a :

$$R_{ii}\approx -a_1{K}_1{\int }_0^{d_1}\frac{{\ell }^2}{d_1^2}d\ell -a_2{K}_2{\int }_0^{d_2}\frac{{\ell }^2}{d_2^2}d\ell =-\frac{1}{3}{a}_1{K}_1{d}_1-\frac{1}{3}{a}_2{K}_2{d}_2\text{(43)}$$

Pour un triangle donné, le terme à considérer est une intégrale sur le côté du triangle situé sur la frontière :

$$R_{ii}^T=-\frac{1}{6}(a_i+a_j)K_{0,ij}{d}_{ij}\text{(44)}$$

Le remplissage de la matrice R se fait en parcourant tous les triangles du maillage. Pour chaque triangle :

• Pour chaque paires de nœuds du triangle appartenant à $\partial {\Omega }_n$, on ajoute R_ij à M_ij et à M_ji.
• Pour chaque nœuds des paires de nœuds du triangle appartenant à $\partial {\Omega }_n$, on ajoute R_ii^T à M_ii.

Les matrices A et R sont symétriques. La ligne i de la matrice A comporte un coefficient diagonal et des coefficients non diagonaux correspondant aux nœuds voisins du nœud N_i. La ligne i de la matrice R comporte un coefficient diagonal et des coefficients non diagonaux correspondant aux nœuds voisins de N_i situés sur le bord $\partial {\Omega }_n$.

Rappelons que tous les nœuds qui interviennent dans le calcul de ces deux matrices sont des nœuds intérieurs, c'est-à-dire qu'il faut exclure les nœuds où une condition de Dirichlet et appliquée.

2.f. Matrice colonne

Il faut expliciter les coefficients de la matrice colonne B. Le premier terme de B_i est :

$$B_{1,i}=-\sum _{k\in Nd}{\xi }_k{\int }_{\Omega }a\left(\overrightarrow{grad}{\varphi }_k\right)\cdot \left(\overrightarrow{grad}{\varphi }_i\right)d\sigma ,i\in Nint\text{(45)}$$

Pour $i\in Nint$ (nœud n'appartenant pas à $\partial {\Omega }_d$), il faut considérer les nœuds N_k appartenant à $\partial {\Omega }_d$ tels que le support de ${\varphi }_k$ ait une partie commune avec celui de ${\varphi }_i$. $B_{1,i}$ est non nul si et seulement si N_i est voisin d'un nœud de la frontière de Dirichlet. La figure suivante montre un nœud de ce type et les triangles qui constituent la partie commune des supports.

Figure pleine page

Pour chaque triangle du maillage, on recherche les paires de nœuds contituées d'un nœud N_i n'appartenant pas à $\partial {\Omega }_d$ et d'un nœud N_k appartenant à $\partial {\Omega }_d$. La contribution de cette paire à B_1,i est :

$$B_{1,i}^p=-{\xi }_k\frac{1}{3}(a_i+a_j+a_k)(c_{i0}{c}_{k0}+c_{i1}{c}_{k1})S_T\text{(46)}$$

Le deuxième terme de B_i est :

$$B_{2,i}={\int }_{\Omega }{\varphi }_{i}sd\sigma ,i\in Nint\text{(47)}$$

Il s'agit du terme qui contient la source de l'équation de Poisson. Pour $i\in Nint$, il faut évaluer l'intégrale sur le support de ${\varphi }_i$, qui est constitué des triangles auxquels ce nœud appartient. Pour un de ces triangles, dont les sommets sont N₁,N₂,N₃, la formule de quadrature du barycentre donne :

$$B_{2,i}\approx s\left(\frac{N_1+N_2+N_3}{3}\right){\varphi }_i\left(\frac{N_1+N_2+N_3}{3}\right)S_T\text{(48)}$$

La fonction ${\varphi }_i$ vaut 1/3 au barycentre. Pour la source, on considère plutôt la moyenne des valeurs aux sommets du triangle :

$$B_{2,i}\approx \frac{s_1+s_2+s_3}{3}\frac{1}{3}{S}_T\text{(49)}$$

Pour chaque triangle du maillage et pour chaque nœuds du triangle (d'indice i) n'appartenant pas à $\partial {\Omega }_d$, on ajoute B_2,i à B_i.

Le troisième terme de B_i est :

$$B_{3,i}=\sum _{k\in Nd}{\xi }_k{\int }_{\partial {\Omega }_n}a{K}_0{\varphi }_i{\varphi }_{k}d\ell ,i\in Nint\text{(50)}$$

Ce coefficient peut être non nul s'il existe un nœud N_k de la frontière de Dirichlet tel que ${\varphi }_k$ soit non nul sur au moins un segment de la frontière de Neumann. Cela ne peut se rencontrer qu'à la jonction entre ces deux frontières, comme le montre la figure suivante :

Figure pleine page

L'intégrale se fait sur le segment N_kN_i. Le calcul est similaire à celui du coefficient R_ij. On obtient :

$$B_{3,i}={\xi }_k\frac{1}{2}(a_i+a_k)K_{0,ik}\frac{d}{6}\text{(51)}$$

où d est la distance N_kN_i.

Le quatrième terme de B_i est :

$$B_{4,i}={\int }_{\partial {\Omega }_n}{\varphi }_{i}a(g_0-K_0{u}_0)d\ell ,i\in Nint\text{(52)}$$

Ce terme contient la condition de Neumann (gradient g₀) et le terme constant de la condition de Robin. Il est non nul si et seulement si le nœud N_i appartient à la frontière $\partial {\Omega }_n$. Pour chaque triangle du maillage et pour chaque paire de nœuds de ce triangle appartenant à $\partial {\Omega }_n$, la contribution de cette paire est, pour chacun des deux nœuds :

$$B_{4,i}^p=\frac{1}{2}(a_i+a_j)(g_{0,ij}-K_{0,ij}{u}_{0,ij})\frac{1}{2}{d}_{ij}\text{(53)}$$

où $g_{0ij}$ est la composante normale du gradient sur la frontière définie par les nœuds N_i et son voisin N_j, $K_{0,ij}$ et $u_{0,ij}$ les coefficients relatifs à la condition de Robin sur la même frontière.

4.a. Exemple A

On considère le domaine carré $\Omega :[0,1]\times [0,1]$. La source est nulle (s=0) et le coefficient a est uniforme (le même partout). En x=0 et x=1 on applique des conditions limites de Dirichlet, avec respectivement les valeurs 0 et 1. En y=0 et y=1 on applique des conditions de Neumann avec g₀=0. La solution est : u(x,y)=x (il s'agit en fait d'un problème unidimensionnel).

La structure du maillage est montré sur la figure suivante :

Figure pleine page

Les 4 nœuds des coins sont affectés de la condition de Dirichlet. Chaque nœud non situé sur un bord a 6 nœuds voisins.

On commence par définir les noeuds :

N = 50
x = np.linspace(0,1,N)
y = np.linspace(0,1,N)
noeuds = []
a = 1
s = 0
for j in range(N):
    for i in range(N):
        if i!=0 and i!=N-1 and j!=0 and j!=N-1:
            n = Noeud(x[i],y[j],a,s)
        else:  
            if i==0:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
            elif i==N-1:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=1)
            if j==0 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
            elif j==N-1 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
        noeuds.append(n)
        

puis les triangles :

triangles = []
for j in range(N-1):
    for i in range(N-1):
        k = i+j*N
        bords = [False,False,False]
        if i==N-2 :
            bords=[False,True,False]
            g = [0,0,0]
        if j==0:
            bords=[True,False,False]
            g = [0,0,0]
        if j==0 and i==N-2:
            bords=[True,True,False]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+1],noeuds[k+1+N],bords=bords,g=g))
        bords = [False,False,False]
        if i==0:
            bords = [False,False,True]
            g = [0,0,0]
        if j==N-2 :
            bords = [False,True,False]
            g = [0,0,0]
        if i==0 and j==N-2:
            bords = [False,True,True]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+N+1],noeuds[k+N],bords=bords,g=g))
        

Pour le maillage considéré, il est aisé de tracer u(x,y) car les nœuds sont disposés sur une grille. Dans le cas général, il faudra procéder à une interpolation dans les triangles (par la fonction affine par morceaux) pour obtenir les valeurs de u sur une grille.

elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
U = np.zeros((N,N),dtype=np.float64)
indice = 0
for j in range(N):
    for i in range(N):
        n = noeuds[indice]
        U[j,i] = n.ksi
        indice+= 1
from matplotlib.pyplot import *
figure()
contour(U,10,extent=(0,1,0,1))

                     

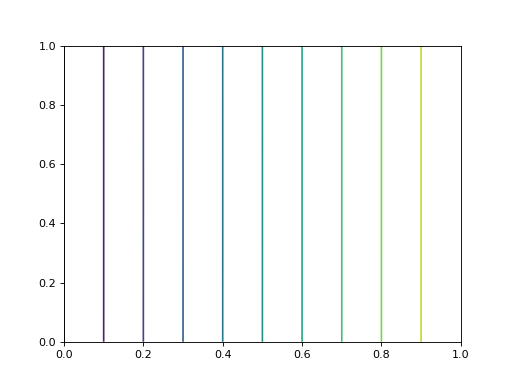fig1.pdf

figure()
plot(x,U[N//2,:])
grid()
                     

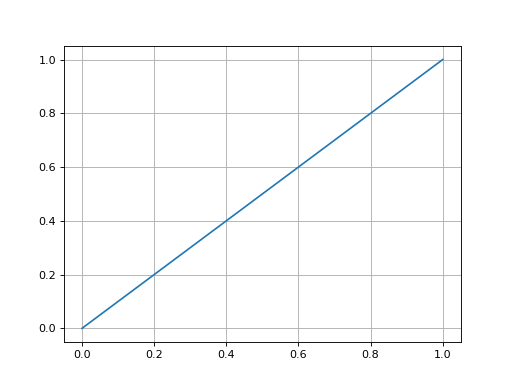fig2.pdf

La même solution peut être obtenue en remplaçant la condition de Dirichlet en x=1 par la condition de Neumann u'(1)=1 :

N = 51
x = np.linspace(0,1,N)
y = np.linspace(0,1,N)
noeuds = []
a = 1
s = 0
for j in range(N):
    for i in range(N):
        if i!=0 and i!=N-1 and j!=0 and j!=N-1:
            n = Noeud(x[i],y[j],a,s)
        else:  
            if i==0:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
            elif i==N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
            if j==0 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
            elif j==N-1 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
        noeuds.append(n)
        

triangles = []
for j in range(N-1):
    for i in range(N-1):
        k = i+j*N
        bords = [False,False,False]
        if i==N-2 :
            bords=[False,True,False]
            g = [0,1,0]
        if j==0:
            bords=[True,False,False]
            g = [0,0,0]
        if j==0 and i==N-2:
            bords=[True,True,False]
            g = [0,1,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+1],noeuds[k+1+N],bords=bords,g=g))
        bords = [False,False,False]
        if i==0:
            bords = [False,False,True]
            g = [0,0,0]
        if j==N-2 :
            bords = [False,True,False]
            g = [0,0,0]
        if i==0 and j==N-2:
            bords = [False,True,True]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+N+1],noeuds[k+N],bords=bords,g=g))
        

elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
U = np.zeros((N,N),dtype=np.float64)
indice = 0
for j in range(N):
    for i in range(N):
        n = noeuds[indice]
        U[j,i] = n.ksi
        indice+= 1
from matplotlib.pyplot import *
figure()
contour(U,10,extent=(0,1,0,1))

                     

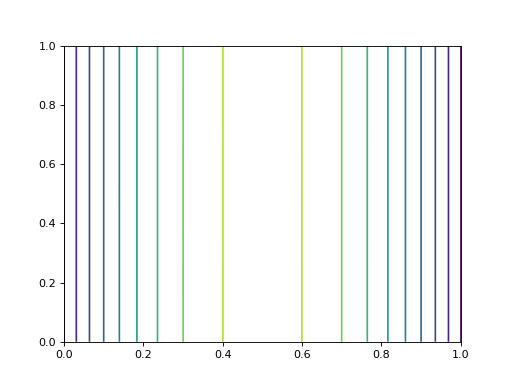fig3.pdf

figure()
plot(x,U[N//2,:])
grid()
                     

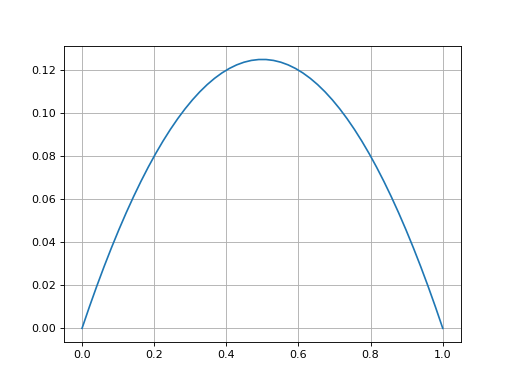fig4.pdf

4.b. Exemple B

On reprend l'exemple A avec une source uniforme et des conditions de Dirichlet nulle en x=0 et x=1. La solution est $u(x,y)=\frac{s}{2}(x-x^2)$.

N = 50
x = np.linspace(0,1,N)
y = np.linspace(0,1,N)
noeuds = []
a = 1
s = 1
for j in range(N):
    for i in range(N):
        if i!=0 and i!=N-1 and j!=0 and j!=N-1:
            n = Noeud(x[i],y[j],a,s)
        else:  
            if i==0:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
            elif i==N-1:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
            if j==0 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
            elif j==N-1 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
        noeuds.append(n)
        

triangles = []
for j in range(N-1):
    for i in range(N-1):
        k = i+j*N
        bords = [False,False,False]
        if i==N-2 :
            bords=[False,True,False]
            g = [0,0,0]
        if j==0:
            bords=[True,False,False]
            g = [0,0,0]
        if j==0 and i==N-2:
            bords=[True,True,False]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+1],noeuds[k+1+N],bords=bords,g=g))
        bords = [False,False,False]
        if i==0:
            bords = [False,False,True]
            g = [0,0,0]
        if j==N-2 :
            bords = [False,True,False]
            g = [0,0,0]
        if i==0 and j==N-2:
            bords = [False,True,True]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+N+1],noeuds[k+N],bords=bords,g=g))
        

elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
U = np.zeros((N,N),dtype=np.float64)
indice = 0
for j in range(N):
    for i in range(N):
        n = noeuds[indice]
        U[j,i] = n.ksi
        indice+= 1
from matplotlib.pyplot import *
figure()
contour(U,10,extent=(0,1,0,1))

                     

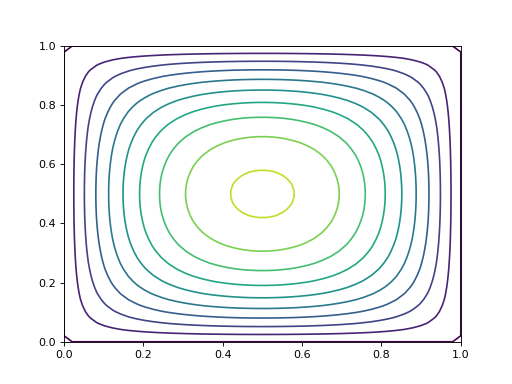fig5.pdf

figure()
plot(x,U[N//2,:])
plot(x,s/2*(x-x*x),"k--")
grid()
                     

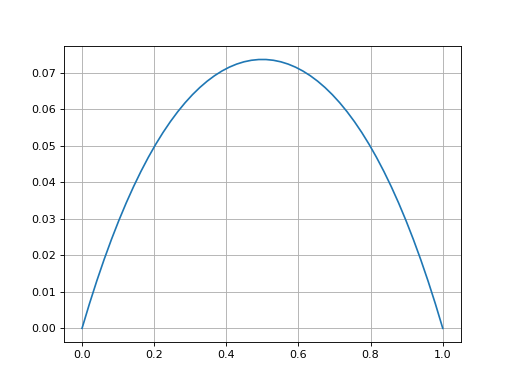fig6.pdf

4.c. Exemple C

On reprend l'exemple A avec une source uniforme et des conditions de Dirichlet nulle sur les quatre bords :

N = 50
x = np.linspace(0,1,N)
y = np.linspace(0,1,N)
noeuds = []
a = 1
s = 1
for j in range(N):
    for i in range(N):
        if i!=0 and i!=N-1 and j!=0 and j!=N-1:
            n = Noeud(x[i],y[j],a,s)
        else:  
            if i==0:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
            elif i==N-1:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
            if j==0 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
            elif j==N-1 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
        noeuds.append(n)
        

triangles = []
for j in range(N-1):
    for i in range(N-1):
        k = i+j*N
        bords = [False,False,False]
        if i==N-2 :
            bords=[False,True,False]
            g = [0,0,0]
        if j==0:
            bords=[True,False,False]
            g = [0,0,0]
        if j==0 and i==N-2:
            bords=[True,True,False]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+1],noeuds[k+1+N],bords=bords,g=g))
        bords = [False,False,False]
        if i==0:
            bords = [False,False,True]
            g = [0,0,0]
        if j==N-2 :
            bords = [False,True,False]
            g = [0,0,0]
        if i==0 and j==N-2:
            bords = [False,True,True]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+N+1],noeuds[k+N],bords=bords,g=g))
        

elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
U = np.zeros((N,N),dtype=np.float64)
indice = 0
for j in range(N):
    for i in range(N):
        n = noeuds[indice]
        U[j,i] = n.ksi
        indice+= 1
from matplotlib.pyplot import *
figure()
contour(U,10,extent=(0,1,0,1))

                     

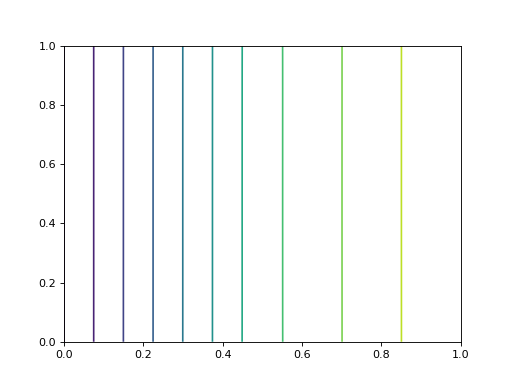fig7.pdf

figure()
plot(x,U[N//2,:])
grid()
                     

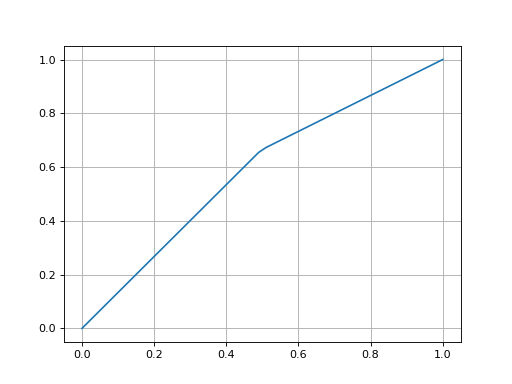fig8.pdf

4.d. Exemple D

On reprend l'exemple A avec deux milieux différents : la moitié à droite du domaine a une valeur de a deux fois plus grande.

N = 50
x = np.linspace(0,1,N)
y = np.linspace(0,1,N)
noeuds = []
a = 1
s = 0
a1 = 1
a2 = 2
for j in range(N):
    for i in range(N):
        if i < N//2 : a=a1
        else : a=a2
        if i!=0 and i!=N-1 and j!=0 and j!=N-1:
            n = Noeud(x[i],y[j],a,s)
        else:  
            if i==0:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
            elif i==N-1:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=1)
            if j==0 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
            elif j==N-1 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
        noeuds.append(n)
        

triangles = []
for j in range(N-1):
    for i in range(N-1):
        k = i+j*N
        bords = [False,False,False]
        if i==N-2 :
            bords=[False,True,False]
            g = [0,0,0]
        if j==0:
            bords=[True,False,False]
            g = [0,0,0]
        if j==0 and i==N-2:
            bords=[True,True,False]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+1],noeuds[k+1+N],bords=bords,g=g))
        bords = [False,False,False]
        if i==0:
            bords = [False,False,True]
            g = [0,0,0]
        if j==N-2 :
            bords = [False,True,False]
            g = [0,0,0]
        if i==0 and j==N-2:
            bords = [False,True,True]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+N+1],noeuds[k+N],bords=bords,g=g))
        

elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
U = np.zeros((N,N),dtype=np.float64)
indice = 0
for j in range(N):
    for i in range(N):
        n = noeuds[indice]
        U[j,i] = n.ksi
        indice+= 1
from matplotlib.pyplot import *
figure()
contour(U,10,extent=(0,1,0,1))

                     

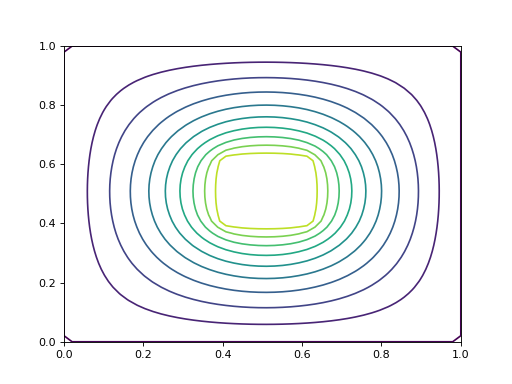fig9.pdf

figure()
plot(x,U[N//2,:])
grid()
                     

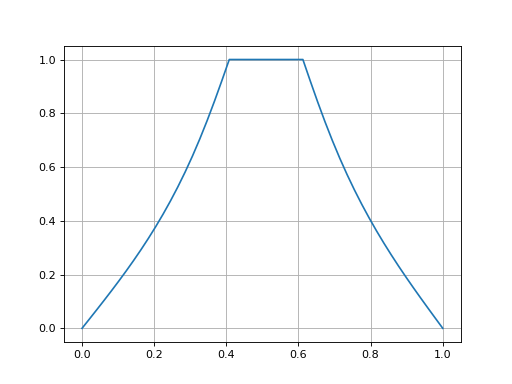fig10.pdf

4.e. Exemple E

Un objet de forme carrée est introduit dans le domaine, avec une condition de Dirichlet sur ses bords. Les quatres bords du domaine ont une condition de Dirichlet. La figure suivante montre comment l'objet est défini :

Figure pleine page

N = 50
x = np.linspace(0,1,N)
y = np.linspace(0,1,N)
noeuds = []
a = 1
s = 0
# bords de l'objet
e = 5
i1 = N//2-e 
i2 = N//2+e 
j1 = N//2-e 
j2 = N//2+e
for j in range(N):
    for i in range(N):
        if (i==i1 and j1<=j<=j2) or (i==i2 and j1<=j<=j2) or (j==j1 and i1<=i<=i2) or (j==j2 and i1<=i<=i2):
            n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=1)
        else:
            if i!=0 and i!=N-1 and j!=0 and j!=N-1:
                n = Noeud(x[i],y[j],a,s)
            else:  
                if i==0:
                    n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
                elif i==N-1:
                    n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
                if j==0 and i!=0 and i!=N-1:
                    n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
                elif j==N-1 and i!=0 and i!=N-1:
                    n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
        noeuds.append(n)
        

triangles = []
for j in range(N-1):
    for i in range(N-1):
        k = i+j*N
        bords = [False,False,False]
        if i==N-2 :
            bords=[False,True,False]
            g = [0,0,0]
        if j==0:
            bords=[True,False,False]
            g = [0,0,0]
        if j==0 and i==N-2:
            bords=[True,True,False]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+1],noeuds[k+1+N],bords=bords,g=g))
        bords = [False,False,False]
        if i==0:
            bords = [False,False,True]
            g = [0,0,0]
        if j==N-2 :
            bords = [False,True,False]
            g = [0,0,0]
        if i==0 and j==N-2:
            bords = [False,True,True]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+N+1],noeuds[k+N],bords=bords,g=g))
        

elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
U = np.zeros((N,N),dtype=np.float64)
indice = 0
for j in range(N):
    for i in range(N):
        n = noeuds[indice]
        U[j,i] = n.ksi
        indice+= 1
from matplotlib.pyplot import *
figure()
contour(U,10,extent=(0,1,0,1))

                     

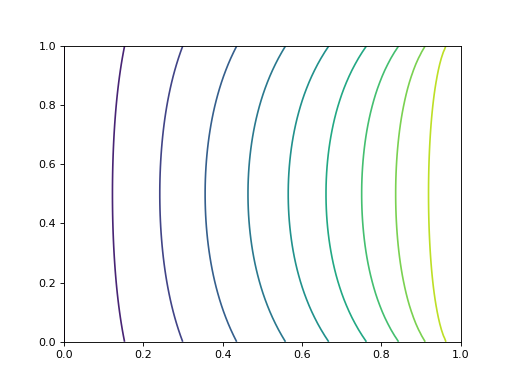fig11.pdf

figure()
plot(x,U[N//2,:])
grid()
                     

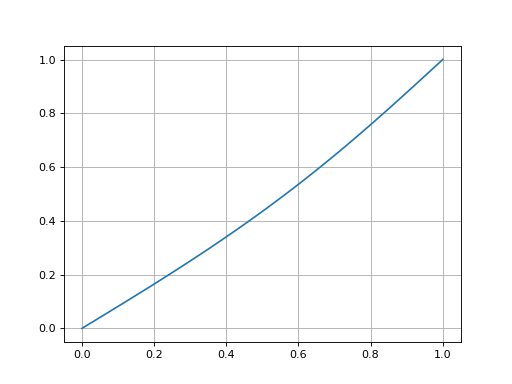fig12.pdf

4.f. Exemple F

On reprend l'exemple A mais avec une condition de Robin sur les bords en y=0 et y=1 :

N = 50
x = np.linspace(0,1,N)
y = np.linspace(0,1,N)
noeuds = []
a = 1
s = 0
for j in range(N):
    for i in range(N):
        if i!=0 and i!=N-1 and j!=0 and j!=N-1:
            n = Noeud(x[i],y[j],a,s)
        else:  
            if i==0:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=0)
            elif i==N-1:
                n = Noeud(x[i],y[j],a,s,lim=DIR,ksi=1)
            if j==0 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
            elif j==N-1 and i!=0 and i!=N-1:
                n = Noeud(x[i],y[j],a,s,lim=NEU)
        
        noeuds.append(n)
        

triangles = []
for j in range(N-1):
    for i in range(N-1):
        k = i+j*N
        bords = [False,False,False]
        K0 = [0,0,0]
        u0 = [0,0,0]
        if i==N-2 :
            bords=[False,True,False]
            g = [0,0,0]
        if j==0:
            bords=[True,False,False]
            g = [0,0,0]
            K0 = [-2,0,0]
        if j==0 and i==N-2:
            bords=[True,True,False]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+1],noeuds[k+1+N],bords=bords,g=g,K0=K0,u0=u0))
        bords = [False,False,False]
        K0 = [0,0,0]
        u0 = [0,0,0]
        if i==0:
            bords = [False,False,True]
            g = [0,0,0]
        if j==N-2 :
            bords = [False,True,False]
            g = [0,0,0]
            K0 = [0,-2,0]
        if i==0 and j==N-2:
            bords = [False,True,True]
            g = [0,0,0]
        triangles.append(Triangle(noeuds[k],noeuds[k+N+1],noeuds[k+N],bords=bords,g=g,K0=K0,u0=u0))
        

elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
U = np.zeros((N,N),dtype=np.float64)
indice = 0
for j in range(N):
    for i in range(N):
        n = noeuds[indice]
        U[j,i] = n.ksi
        indice+= 1
from matplotlib.pyplot import *
figure()
contour(U,10,extent=(0,1,0,1))

                     

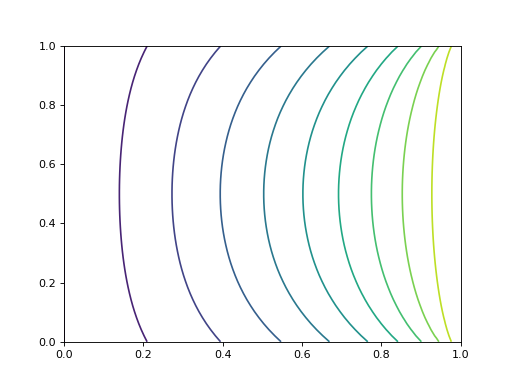fig13.pdf

figure()
plot(x,U[N//2,:])
grid()
                     

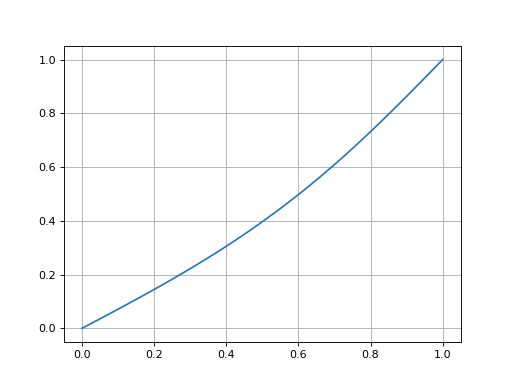fig14.pdf

5.a. Principe

Pour un ensemble de points, il existe au moins une triangulation, appelée triangulation de Delaunay, qui vérifie la propriété suivante : pour chaque triangle, le disque ouvert défini par le cercle qui passe par les trois sommets ne contient aucun point de l'ensemble. La triangulation de Delaunay est unique si l'ensemble ne contient pas quatre points situés sur un même cercle. Il existe un algorithme qui permet d'obtenir une triangulation de Delaunay. La fonction scipy.spatial.Delaunay implémente cet algorithme.

Une méthode simple de triangulation consiste à définir des points sur le domaine $\Omega$, avec en particulier des points sur les frontières du domaine et sur les frontières des objets à l'intérieur du domaine. Ces points devront être espacés convenablement afin que les triangles obtenus par triangulation de Delaunay n'aient pas des angles trop petits (idéalement supérieurs à 30 degrés).

On traite comme exemple un domaine circulaire avec une objet de forme carré au milieu :

from scipy.spatial import Delaunay                       
theta = np.linspace(0,2*np.pi,20)
points = [[0,0]]
for R in [10,8,6]:
    for i in range(len(theta)):
        points.append([R*np.cos(theta[i]),R*np.sin(theta[i])])
a = 3
N = 5
xx = np.linspace(-a,a,N)
yy = np.linspace(-a,a,N)
for x in xx:
    points.append([x,-a])
    points.append([x,a])
for y in yy:
    points.append([-a,y])
    points.append([a,y])

points = np.array(points)
tri = Delaunay(points)
figure(figsize=(8,8))
triplot(points[:,0], points[:,1], tri.simplices)

            

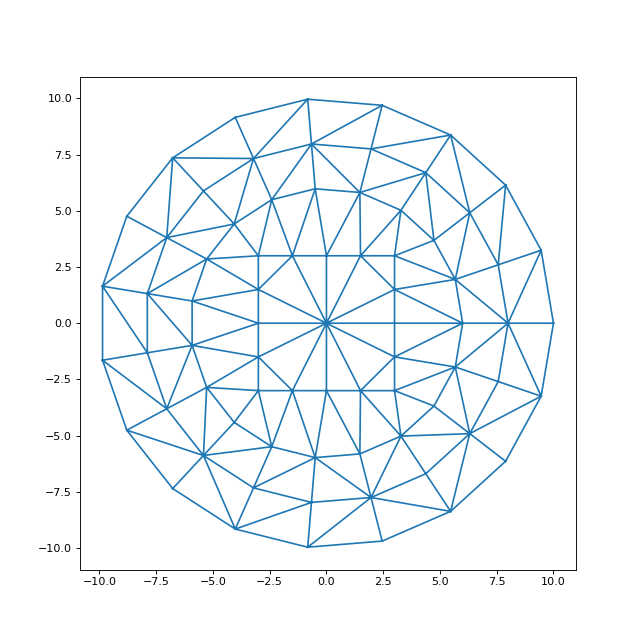fig15.pdf

Les triangles sont donnés par tri.simplices, dont voici un échantillon :

print(tri.simplices[0:10])
--> array([[74, 59, 41],
       [63, 65,  0],
       [66, 45, 46],
       [42, 78, 41],
       [47, 48, 79],
       [48, 49, 79],
       [47, 64, 46],
       [64, 66, 46],
       [64, 47, 79],
       [66, 64,  0]], dtype=int32)

Chaque triangle est défini par les trois indices de ses sommets dans la liste des points. Nous pouvons facilement définir un objet de la classe Noeud pour chaque point. Un objet de la classe Triangle doit être défini pour chaque triangle. Il y a cependant une difficulté : il faut identifier les triangles dont au moins un côté se trouve sur une frontière et attribuer la condition limite de Neumann s'il s'agit de $\partial {\Omega }_n$. Pour la condition de Dirichlet, il n'y a aucune difficulté puisque celle-ci est définie sur chaque nœud de $\partial {\Omega }_d$.

Les nœuds situés sur une frontière $\partial {\Omega }_n$ sont facilement identifiables puisque l'appartenance à cette frontière est définie dès le début, mais il faut en plus définir les segments de $\partial {\Omega }_n$. Considérons le cas du contour du domaine $\Omega$ et supposons qu'une condition de Neumann soit adoptée sur ce contour. Afin de repérer les points de ce contour dans les triangles, il suffit d'ajouter dans la classe Noeud un objet indiquant la frontière auquel le nœud appartient et l'indice du nœud dans cette frontière, les nœuds étant numérotés dans l'ordre de parcours de la frontière. Au moment de la création d'un triangle, on doit repérer les points du triangle qui appartiennent à chaque frontière et, pour une frontière donnée, repérer ceux qui sont consécutifs sur cet frontière. Ces deux points constituent un côté du triangle situé sur la frontière.

5.b. Implémentation

On définit une classe pour représenter une frontière de Neumann :

class Frontiere:
    def __init__(self,nom,g0,K0,u0):
        self.nom = nom
        self.g0 = g0
        self.K0 = K0 
        self.u0 = u0
        self.nbpoints = 0
    def nombrePoints(self,n):
        self.nbpoints = n
                    

Voici la nouvelle définition de la classe Noeud :

class Noeud:
    def __init__(self,x,y,a,s,lim=0,ksi=0,frontiere=None,indiceFrontiere=0):
        self.xy = np.array([x,y])
        self.x = x 
        self.y = y
        self.a = a
        self.s = s
        self.lim = lim
        self.ksi = ksi
        self.indice = 0 # indice dans le maillage
        self.frontiere = frontiere
        self.indiceFrontiere = indiceFrontiere
        

Lorsque lim==NEU, il faudra attribuer au nœud un objet de la classe Frontiere et l'indice du nœud sur cette frontière.

La fonction suivante permet de savoir si deux nœuds sont les deux sommets d'un segment appartenant à une frontière donnée :

def segment(n1,n2,frontiere):
    if n1.lim==NEU and n1.frontiere.nom == frontiere.nom and n2.lim==NEU and n2.frontiere.nom == frontiere.nom:
        if abs(n1.indiceFrontiere-n2.indiceFrontiere)==1:
            return (frontiere.g0,frontiere.K0,frontiere.u0)
        if abs(n1.indiceFrontiere-n2.indiceFrontiere)==frontiere.nbpoints-1:
            return (frontiere.g0,frontiere.K0,frontiere.u0)
    return None
         

La fonction suivante génère les triangles à partir de la liste tri.simplices :

def creerTriangles(noeuds,simplices,frontieres):
    # noeuds : liste de noeuds
    # simplices : liste de triangles 
    # frontieres : liste de frontieres
    triangles = []
    for t in simplices:
        n1 = noeuds[t[0]]
        n2 = noeuds[t[1]]
        n3 = noeuds[t[2]]
        f1 = f2 = f3 = (0,0,0)
        b1 = b2 = b3 = False
        for front in frontieres:
            s1 = segment(n1,n2,front)
            if s1!=None: 
                f1 = s1
                b1 = True
            s2 = segment(n2,n3,front)
            if s2!=None: 
                f2 = s2
                b2 = True
            s3 = segment(n3,n1,front)
            if s3!=None: 
                f3 = s3
                b3 = True
        
        tr = Triangle(n1,n2,n3,bords=[b1,b2,b3],g=[f1[0],f2[0],f3[0]],K0=[f1[1],f2[1],f3[1]],u0=[f1[2],f2[2],f3[2]])
        triangles.append(tr)
    return triangles
                
         

Lorsque la résolution est terminée, il peut être nécessaire de déterminer les valeurs de u sur une grille rectangulaire. Pour cela, on parcourt les triangles et, pour chacun, on repère les points de la grille qui sont dans ce triangle. La valeur de u sur chacun de ces points est calculée au moyen des trois fonctions ${\varphi }_i$ relatives aux trois sommets du triangle (fonction interpol de la classe Triangle).

La figure suivante montre un triangle et une grille rectangulaire :

Figure pleine page

Le rectangle représenté en trait pointillé est le plus petit rectangle (de côtés parallèles aux axes de la grille) qui contient le triangle. On commence par identifier les points de la grille qui sont dans ce rectangle. La grille est définie par les points suivants :

$$\begin{array}{cc}\hfill & x_p=x_0+p\Delta x,p=0,1\dots N_x-1\hfill \\ \hfill & y_q=y_0+p\Delta y,q=0,1,\dots N_y-1\hfill \end{array}$$

Les indices des points de la grille contenus dans le rectangle sont définis par :

$$\begin{array}{cc}\hfill & E\left(\frac{x_{min}-x_0}{\Delta x}\right)\le p\le E\left(\frac{x_{max}-x_0}{\Delta x}\right)+1\hfill \\ \hfill & E\left(\frac{y_{min}-y_0}{\Delta y}\right)\le q\le E\left(\frac{y_{max}-y_0}{\Delta y}\right)+1\hfill \end{array}$$

Pour savoir si un point P de la grille est dans le triangle, on doit déterminer de quel côté il se trouve par rapport à chaque droite définie par deux sommets. Les sommets du triangle sont ordonnés dans le sens direct. Pour la droite N_iN_j, le point P se trouve à gauche de la droite parcourue dans le sens N_i vers N_j si :

$$\left(\overrightarrow{N_i{N}_j}\wedge \overrightarrow{N_{i}P}\right)\cdot \overrightarrow{u_z}>0\text{(54)}$$

Le point P est à l'intérieur du triangle si et seulement si cette condition est vérifiée pour les trois côtés du triangle. La fonction contientPoint de la classe Triangle effectue ce test. Le rectangle contenant le triangle est donné par la fonction rectangle, sous la forme [x_min,x_max,y_min,y_max].

La fonction suivante effectue l'interpolation sur une grille :

def interpolGrille(triangles,x0,x1,y0,y1,Nx,Ny):
    U = np.zeros((Nx,Ny),dtype=np.float64)
    Delta_x = (x1-x0)/(Nx-1)
    Delta_y = (y1-y0)/(Ny-1)
    for tr in triangles:
        rect = tr.rectangle()
        pmin = np.floor((rect[0]-x0)/Delta_x)
        pmax = np.floor((rect[1]-x0)/Delta_x)+1
        qmin = np.floor((rect[2]-y0)/Delta_y)
        qmax = np.floor((rect[3]-y0)/Delta_y)+1
        if pmin<pmax and qmin<qmax:
            for p in range(int(pmin),int(pmax)+1):
                for q in range(int(qmin),int(qmax)+1):
                    x = x0+p*Delta_x
                    y = y0+q*Delta_y
                    if tr.contientPoint(x,y):
                        U[q,p] = tr.interpol(x,y)
                        
    return U
            

5.c. Exemple A

Une source uniforme est présente sur tout le domaine et une condition de Dirichlet avec une valeur nulle est appliquée sur le contour. La liste des objets de la classe Noeud est générée en même temps que la liste des points.

points = [[0,0]]
noeuds = []
s = 1
a = 1
noeuds.append(Noeud(0,0,a,s))
theta = np.linspace(0,2*np.pi,40)
R = 10
for i in range(len(theta)-1):
        x = R*np.cos(theta[i])
        y = R*np.sin(theta[i])
        points.append([x,y])
        noeuds.append(Noeud(x,y,a,s,lim=DIR,ksi=0))
for R in [9,8,7,6,5,4,2,1]:
    for i in range(len(theta)-1):
        x = R*np.cos(theta[i])
        y = R*np.sin(theta[i])
        points.append([x,y])
        noeuds.append(Noeud(x,y,a,s))
L = 3
N = 10
xx = np.linspace(-L,L,N)
yy = np.linspace(-L,L,N)
for x in xx:
    points.append([x,-L])
    noeuds.append(Noeud(x,-L,a,s))
    points.append([x,L])
    noeuds.append(Noeud(x,L,a,s))
for y in yy:
    points.append([-L,y])
    noeuds.append(Noeud(-L,y,a,s))
    points.append([L,y])
    noeuds.append(Noeud(L,y,a,s))

points = np.array(points)
tri = Delaunay(points)

figure(figsize=(8,8))
triplot(points[:,0], points[:,1], tri.simplices)
   
                    

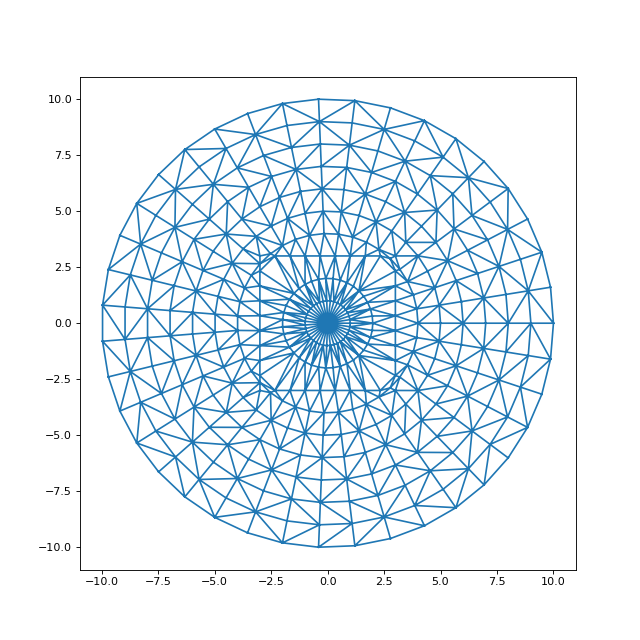fig16.pdf

Voici le calcul puis le tracé des lignes d'isovaleurs de u au moyen de la fonction matplotlib.pyplot.tricontour :

triangles = creerTriangles(noeuds,tri.simplices,[])
elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
figure(figsize=(8,8))
U = np.zeros(len(noeuds))
for i in range(len(noeuds)):
    U[i] = noeuds[i].ksi
    
figure(figsize=(8,8))
tricontour(points[:,0], points[:,1], tri.simplices,U,levels=10)

                     

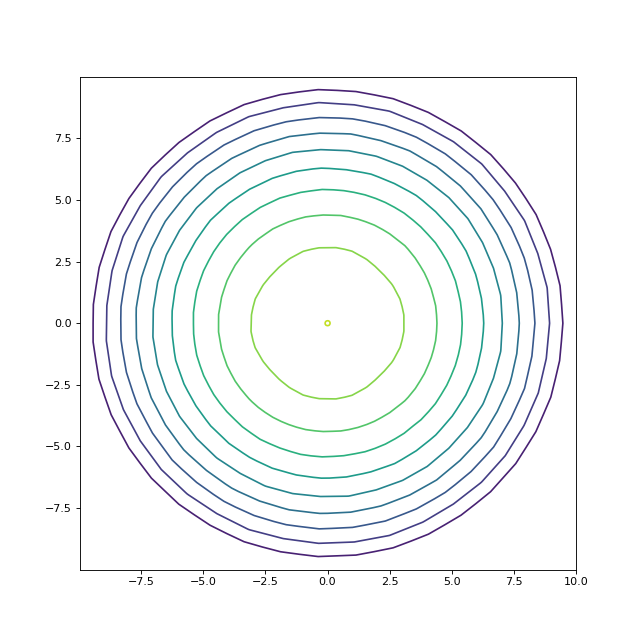fig17.pdf

Voici l'utilisation de la fonction interpolGrille :

Nx,Ny = 100,100
x0,y0 = -10,-10
x1,y1 = 10,10 
U = interpolGrille(triangles,x0,x1,y0,y1,Nx,Ny)
figure(figsize=(8,8))
contour(U,levels=10,extent=(-10,10,-10,10))
                      

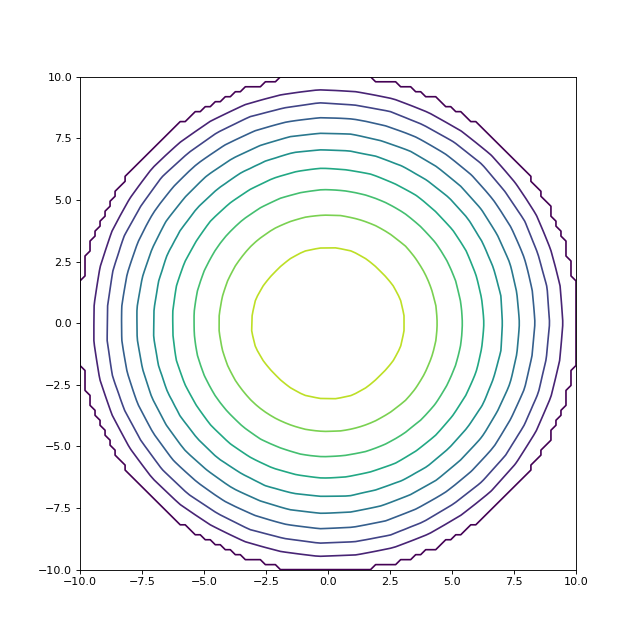fig18.pdf

Le fait de disposer des valeurs dur une grille permet de tracer un profil sur une droite parallèle à un des axes :

figure()
plot(np.linspace(-10,10,Nx),U[Ny//2,:])
xlabel("x")
ylabel("u(x,0)")
                      

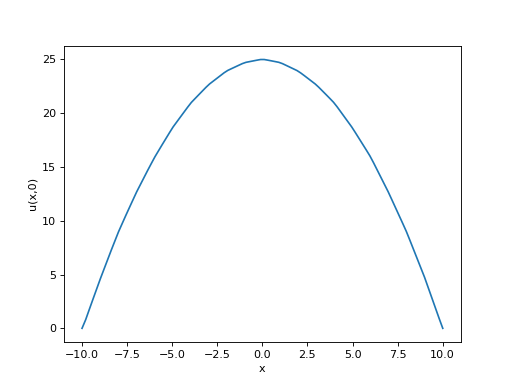fig19.pdf

5.d. Exemple B

La source est nulle mais une condition de Dirichlet de valeur 1 est mise sur l'objet carré situé au centre :

points = [[0,0]]
noeuds = []
s = 0
a = 1
noeuds.append(Noeud(0,0,a,s))
theta = np.linspace(0,2*np.pi,30)
R = 10
for i in range(len(theta)-1):
        x = R*np.cos(theta[i])
        y = R*np.sin(theta[i])
        points.append([x,y])
        noeuds.append(Noeud(x,y,a,s,lim=DIR,ksi=0))
for R in [9,8,7,6,5,4,2,1]:
    for i in range(len(theta)-1):
        x = R*np.cos(theta[i])
        y = R*np.sin(theta[i])
        points.append([x,y])
        noeuds.append(Noeud(x,y,a,s))
L = 3
N = 10
xx = np.linspace(-L,L,N)
yy = np.linspace(-L,L,N)
for x in xx:
    points.append([x,-L])
    noeuds.append(Noeud(x,-L,a,s,lim=DIR,ksi=1))
    points.append([x,L])
    noeuds.append(Noeud(x,L,a,s,lim=DIR,ksi=1))
for y in yy:
    points.append([-L,y])
    noeuds.append(Noeud(-L,y,a,s,lim=DIR,ksi=1))
    points.append([L,y])
    noeuds.append(Noeud(L,y,a,s,lim=DIR,ksi=1))

points = np.array(points)
tri = Delaunay(points) 
                    
triangles = creerTriangles(noeuds,tri.simplices,[])
elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
figure(figsize=(8,8))
U = np.zeros(len(noeuds))
for i in range(len(noeuds)):
    U[i] = noeuds[i].ksi
figure(figsize=(8,8))
tricontour(points[:,0], points[:,1], tri.simplices,U,levels=10)

                     

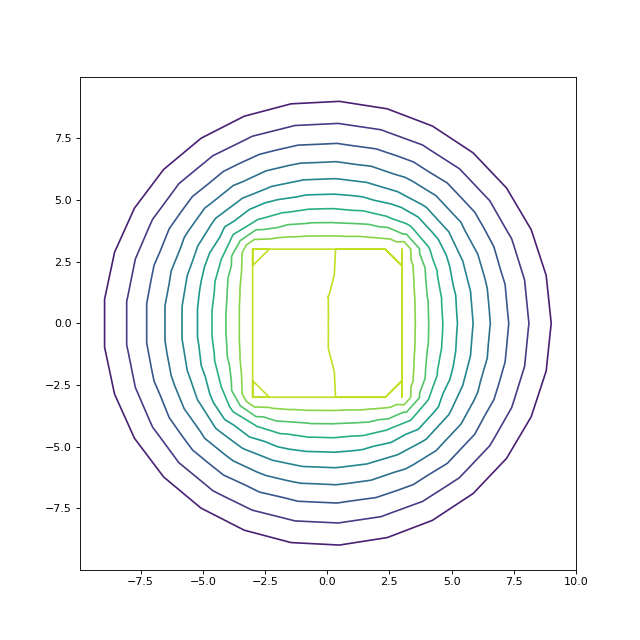fig20.pdf

5.e. Exemple C

Une condition de Neumann avec un gradient -1 est placée sur le contour. Une condition de Dirichlet de valeur 1 est mise sur l'objet carré situé au centre.

bord = Frontiere("bord",-1,0,0)
frontieres = [bord]
points = [[0,0]]
noeuds = []
s = 0
a = 1
noeuds.append(Noeud(0,0,a,s))
theta = np.linspace(0,2*np.pi,30)
R = 10
for i in range(len(theta)-1):
        x = R*np.cos(theta[i])
        y = R*np.sin(theta[i])
        points.append([x,y])
        noeuds.append(Noeud(x,y,a,s,lim=NEU,frontiere=bord,indiceFrontiere=i))
bord.nombrePoints(len(theta)-1)
for R in [9,8,7,6,5,4,2,1]:
    for i in range(len(theta)-1):
        x = R*np.cos(theta[i])
        y = R*np.sin(theta[i])
        points.append([x,y])
        noeuds.append(Noeud(x,y,a,s))
L = 3
N = 10
xx = np.linspace(-L,L,N)
yy = np.linspace(-L,L,N)
for x in xx:
    points.append([x,-L])
    noeuds.append(Noeud(x,-L,a,s,lim=DIR,ksi=1))
    points.append([x,L])
    noeuds.append(Noeud(x,L,a,s,lim=DIR,ksi=1))
for y in yy:
    points.append([-L,y])
    noeuds.append(Noeud(-L,y,a,s,lim=DIR,ksi=1))
    points.append([L,y])
    noeuds.append(Noeud(L,y,a,s,lim=DIR,ksi=1))

points = np.array(points)
tri = Delaunay(points) 

triangles = creerTriangles(noeuds,tri.simplices,frontieres)
elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
figure(figsize=(8,8))
U = np.zeros(len(noeuds))
for i in range(len(noeuds)):
    U[i] = noeuds[i].ksi
figure(figsize=(8,8))
tricontour(points[:,0], points[:,1], tri.simplices,U,levels=10)

                     

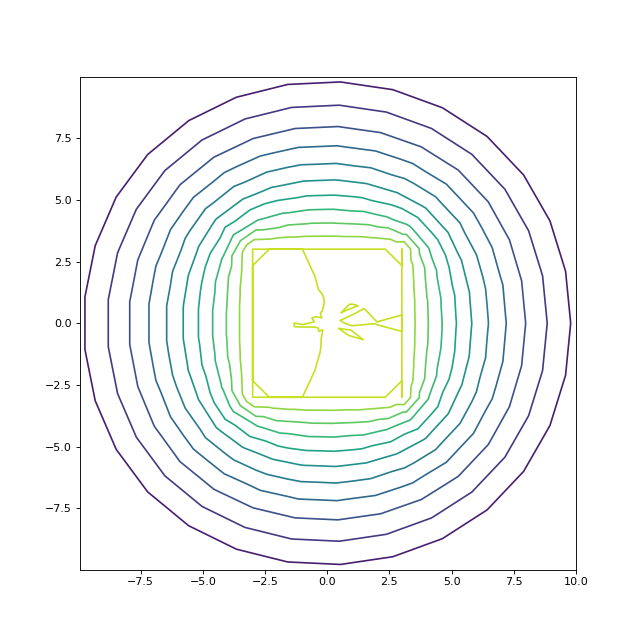fig21.pdf

Voici l'utilisation de la fonction interpolGrille :

Nx,Ny = 100,100
x0,y0 = -10,-10
x1,y1 = 10,10 
U = interpolGrille(triangles,x0,x1,y0,y1,Nx,Ny)
figure(figsize=(8,8))
contour(U,levels=10,extent=(-10,10,-10,10))
                      

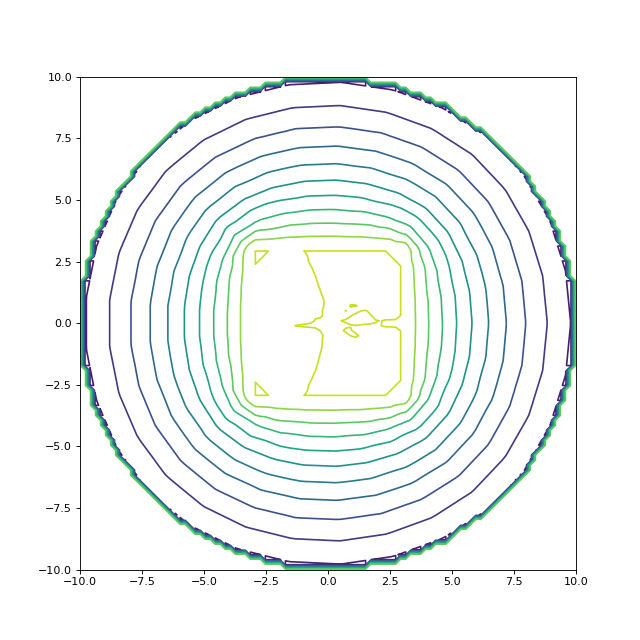fig22.pdf

figure()
plot(np.linspace(-10,10,Nx),U[Ny//2,:],".")
xlabel("x")
ylabel("u(x,0)")
                      

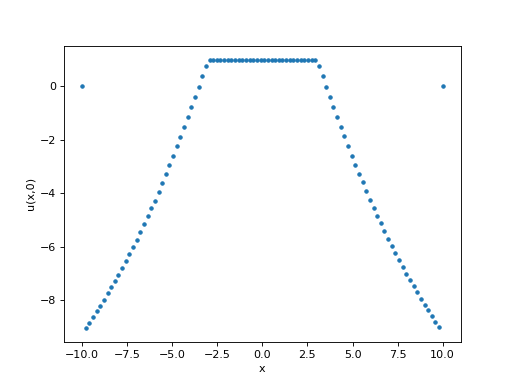fig23.pdf

figure()
plot(np.linspace(-10,10,Ny),U[:,Nx//2],".")
xlabel("y")
ylabel("u(0,y)")
                      

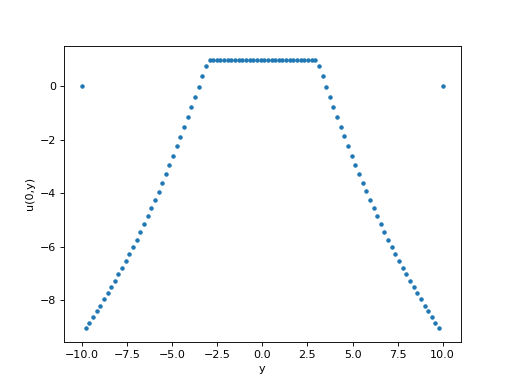fig24.pdf

La valeur sur le bord du domaine n'est pas nulle mais elle reste évidemment nulle dans les parties de la grille hors du maillage. Pour les deux courbes ci-dessus, les deux points extrêmes ne sont pas dans le maillage.

5.f. Exemple D

Le domaine est rectangulaire et les points sont disposés sur un grille. Deux objets circulaires sont placés avec une condition de Dirichlet sur chacun d'eux. Une condition de Dirichlet est appliquée sur les bords. Il s'agit du problème d'électrostatique comportant deux conducteurs cylindriques parallèles avec une différence de potentiel entre eux.

points = []
noeuds = []
s = 0
a = 1
x1,y1 = 0,3
x2,y2 = 0,-3
R1 = 1
N = 51
xx = np.linspace(-10,10,N)
yy = np.linspace(-10,10,N)
for i in range(N):
    for j in range(N):
        x = xx[i]
        y = yy[j]
        points.append([x,y])
        if i!=0 and i!=N-1 and j!=0 and j!=N-1:
            noeuds.append(Noeud(x,y,a,s))
        else:
            noeuds.append(Noeud(x,y,a,s,lim=DIR,ksi=0))


theta = np.linspace(0,2*np.pi,20)
for i in range(len(theta)-1):
    x = x1+R1*np.cos(theta[i])
    y = y1+R1*np.sin(theta[i])
    points.append([x,y])
    noeuds.append(Noeud(x,y,a,s,lim=DIR,ksi=1))
    
for i in range(len(theta)-1):
    x = x2+R1*np.cos(theta[i])
    y = y2+R1*np.sin(theta[i])
    points.append([x,y])
    noeuds.append(Noeud(x,y,a,s,lim=DIR,ksi=-1))
        
points = np.array(points)
tri = Delaunay(points)
figure(figsize=(8,8))
triplot(points[:,0], points[:,1], tri.simplices)    
                    

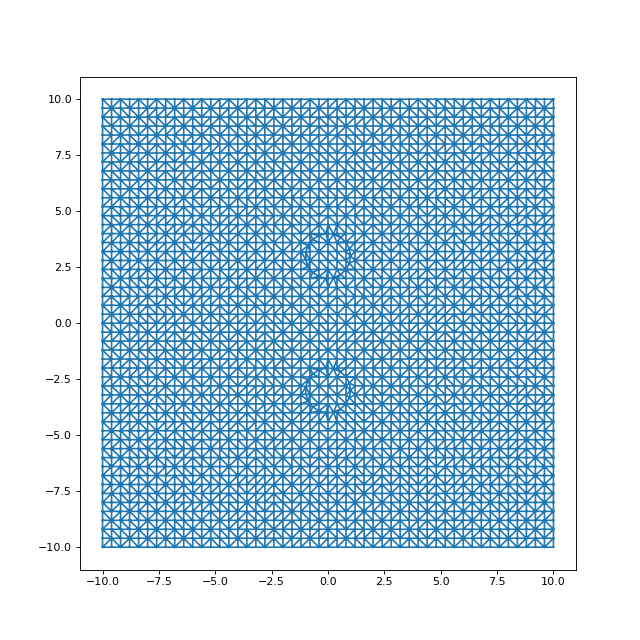fig25.pdf

triangles = creerTriangles(noeuds,tri.simplices,frontieres)
elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
figure(figsize=(8,8))
U = np.zeros(len(noeuds))
for i in range(len(noeuds)):
    U[i] = noeuds[i].ksi
figure(figsize=(8,8))
tricontour(points[:,0], points[:,1], tri.simplices,U,levels=10)             
                     

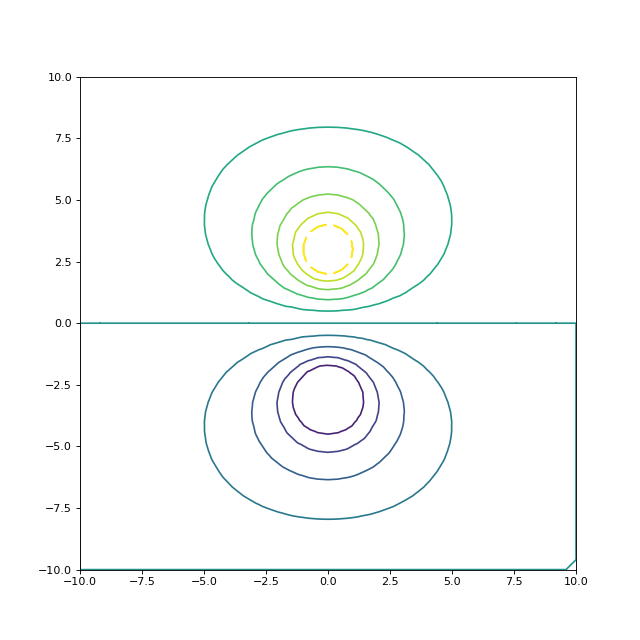fig26.pdf

Nx,Ny = 100,100
x0,y0 = -10,-10
x1,y1 = 10,10 
U = interpolGrille(triangles,x0,x1,y0,y1,Nx,Ny)
figure(figsize=(8,8))
contour(U,levels=10,extent=(-10,10,-10,10))
                      

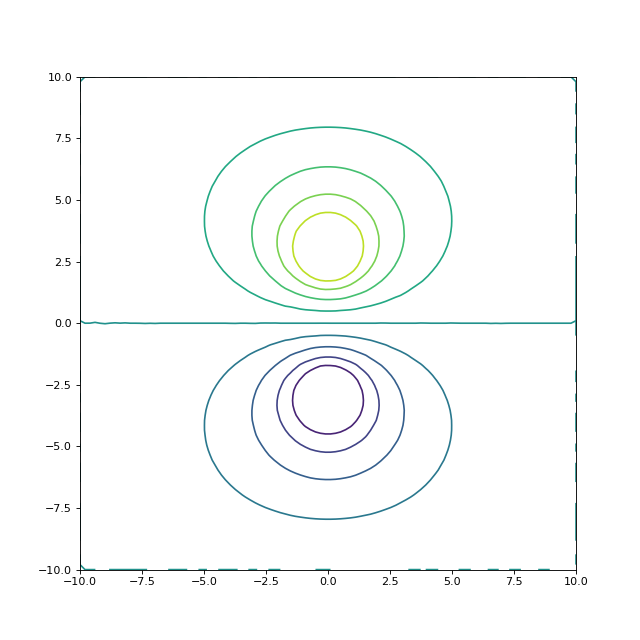fig27.pdf

figure()
plot(np.linspace(-10,10,Ny),U[:,Nx//2])
xlabel("y")
ylabel("u(0,y)")
                      

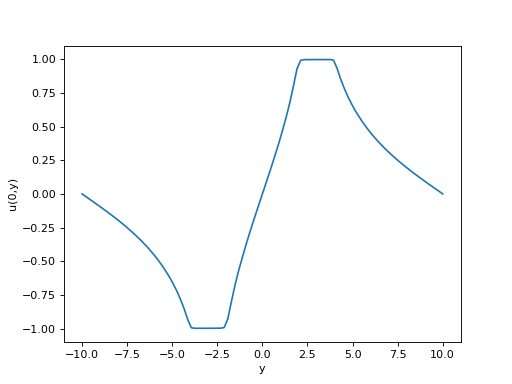fig28.pdf

Le maillage n'est pas optimal : certains triangles au voisinage des cercles ont un angle trop petit. Pourtant, le résultat semble satisfaisant.

Si l'on réduit la distance entre les deux cercles, il faut aussi réduire la grille principale car la variation de u entre les deux cercles augmente :

points = []
noeuds = []
s = 0
a = 1
x1,y1 = 0,1.5
x2,y2 = 0,-1.5
R1 = 1
N = 71
xx = np.linspace(-10,10,N)
yy = np.linspace(-10,10,N)
for i in range(N):
    for j in range(N):
        x = xx[i]
        y = yy[j]
        points.append([x,y])
        if i!=0 and i!=N-1 and j!=0 and j!=N-1:
            noeuds.append(Noeud(x,y,a,s))
        else:
            noeuds.append(Noeud(x,y,a,s,lim=DIR,ksi=0))


theta = np.linspace(0,2*np.pi,20)
for i in range(len(theta)-1):
    x = x1+R1*np.cos(theta[i])
    y = y1+R1*np.sin(theta[i])
    points.append([x,y])
    noeuds.append(Noeud(x,y,a,s,lim=DIR,ksi=1))
    
for i in range(len(theta)-1):
    x = x2+R1*np.cos(theta[i])
    y = y2+R1*np.sin(theta[i])
    points.append([x,y])
    noeuds.append(Noeud(x,y,a,s,lim=DIR,ksi=-1))
        
points = np.array(points)
tri = Delaunay(points)

figure(figsize=(8,8))
triplot(points[:,0], points[:,1], tri.simplices)    
                    

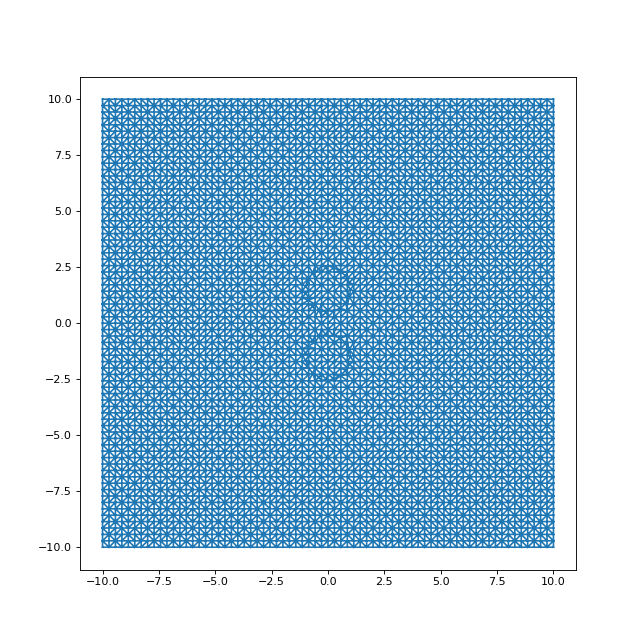fig29.pdf

triangles = creerTriangles(noeuds,tri.simplices,frontieres)
elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
figure(figsize=(8,8))
U = np.zeros(len(noeuds))
for i in range(len(noeuds)):
    U[i] = noeuds[i].ksi
figure(figsize=(8,8))
tricontour(points[:,0], points[:,1], tri.simplices,U,levels=10)             
                     

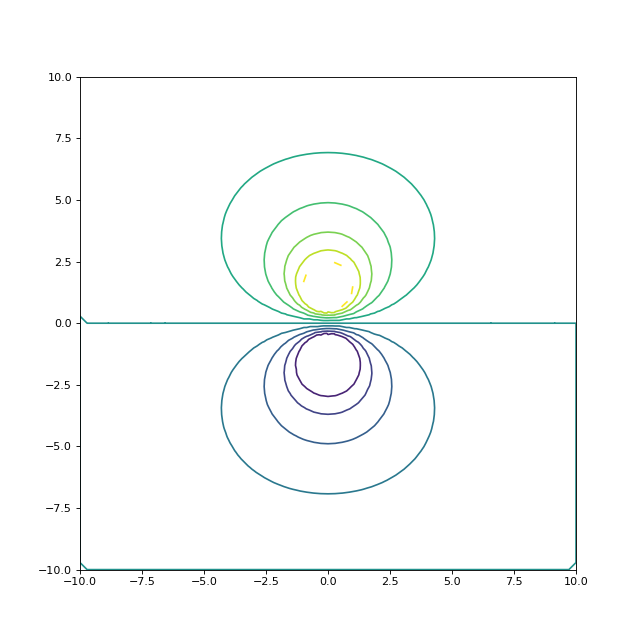fig30.pdf

Nx,Ny = 100,100
x0,y0 = -10,-10
x1,y1 = 10,10 
U = interpolGrille(triangles,x0,x1,y0,y1,Nx,Ny)
figure(figsize=(8,8))
contour(U,levels=10,extent=(-10,10,-10,10))
                      

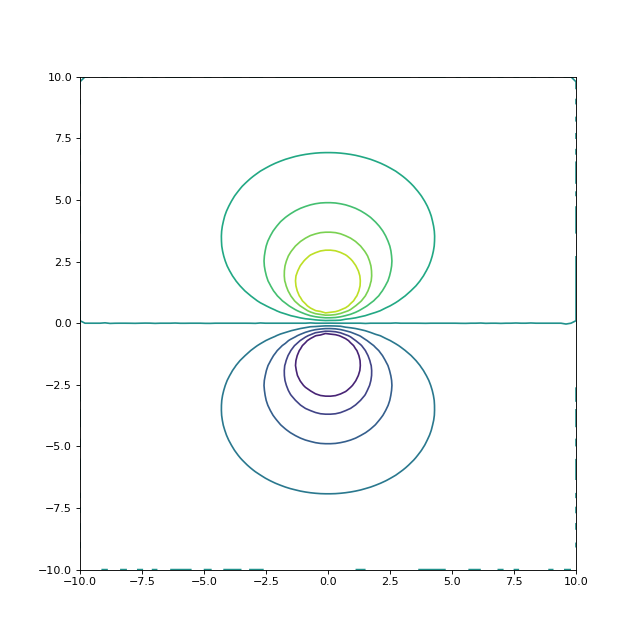fig31.pdf

figure()
plot(np.linspace(-10,10,Ny),U[:,Nx//2])
xlabel("y")
ylabel("u(0,y)")
                      

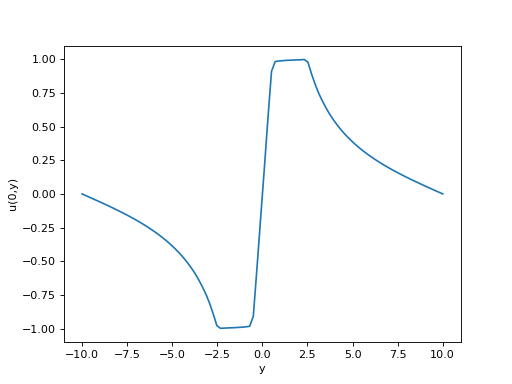fig32.pdf

5.g. Exemple E

On reprend la configuration précédente mais avec une condition de Neumann sur chaque cercle. Pour un problème d'électrostatique, cela correspond à deux corps isolants cylindriques avec une densité de charge uniforme sur leur surface.

cercle1 = Frontiere("cercle1",-1,0,0)
cercle2 = Frontiere("cercle2",1,0,0)
frontieres = [cercle1,cercle2]
points = []
noeuds = []
s = 0
a = 1
x1,y1 = 0,3
x2,y2 = 0,-3
R1 = 1
N = 51
xx = np.linspace(-10,10,N)
yy = np.linspace(-10,10,N)
for i in range(N):
    for j in range(N):
        x = xx[i]
        y = yy[j]
        points.append([x,y])
        if i!=0 and i!=N-1 and j!=0 and j!=N-1:
            noeuds.append(Noeud(x,y,a,s))
        else:
            noeuds.append(Noeud(x,y,a,s,lim=DIR,ksi=0))


theta = np.linspace(0,2*np.pi,20)
for i in range(len(theta)-1):
    x = x1+R1*np.cos(theta[i])
    y = y1+R1*np.sin(theta[i])
    points.append([x,y])
    noeuds.append(Noeud(x,y,a,s,lim=NEU,frontiere=cercle1,indiceFrontiere=i))
cercle1.nombrePoints(len(theta)-1)
for i in range(len(theta)-1):
    x = x2+R1*np.cos(theta[i])
    y = y2+R1*np.sin(theta[i])
    points.append([x,y])
    noeuds.append(Noeud(x,y,a,s,lim=NEU,frontiere=cercle2,indiceFrontiere=i))
cercle2.nombrePoints(len(theta)-1)  
points = np.array(points)
tri = Delaunay(points)
triangles = creerTriangles(noeuds,tri.simplices,frontieres)

elem = ElementsFinis2D(noeuds,triangles)
elem.solve()
figure(figsize=(8,8))
U = np.zeros(len(noeuds))
for i in range(len(noeuds)):
    U[i] = noeuds[i].ksi

Nx,Ny = 100,100
x0,y0 = -10,-10
x1,y1 = 10,10 
U = interpolGrille(triangles,x0,x1,y0,y1,Nx,Ny)
figure(figsize=(8,8))
contour(U,levels=10,extent=(-10,10,-10,10))
                      

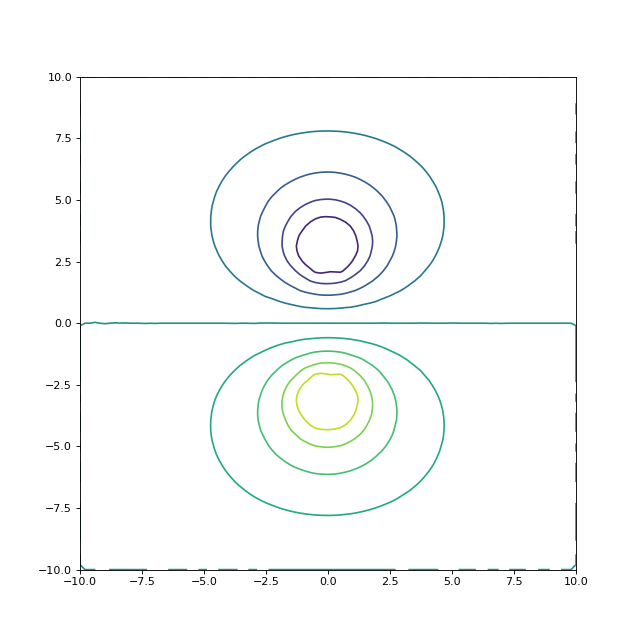fig33.pdf

figure()
plot(np.linspace(-10,10,Ny),U[:,Nx//2])
xlabel("y")
ylabel("u(0,y)")
                      

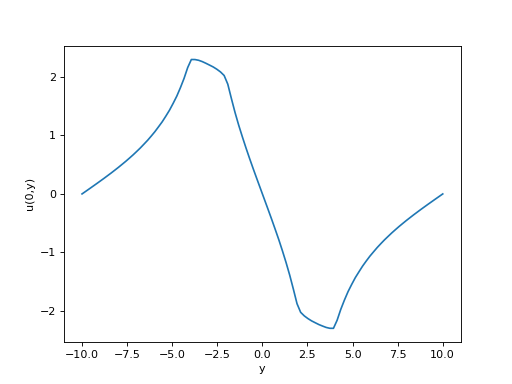fig34.pdf