Mesure de déphasage
1. Introduction
Ce document montre comment mesurer le déphasage entre deux signaux sinusoïdaux échantillonnés.
Nous utilisons deux méthodes différentes :
- Méthode du cosinus, consistant à obtenir le cosinus du déphasage par la moyenne du produit des signaux.
- Méthode d'analyse temporelle par détection des passages pas zéro.
La première méthode ne fournit que le cosinus du déphasage. Elle permet d'obtenir le déphasage dans la mesure où son signe est connu a priori ou peut être obtenu par simple observation des signaux. Il est possible d'obtenir simultanément le cosinus et le sinus mais la méthode est plus complexe car elle fait appel à une interpolation des signaux par transformée de Fourier (voir Mesure de déphasage et Diagramme de Bode).
Nous faisons dans un premier temps une étude et une comparaison de ces deux méthodes au moyen d'une simulation de Monte-Carlo. Dans un second temps nous verrons une étude expérimentale au moyen de centrale Sysam SP5 et de l'Analog Discovery 2.
On considère deux signaux de forme sinusoïdale et . Les signaux échantillonnés à la fréquence d'échantillonnage fe sont notés en et sn. Il s'agit de déterminer le déphasage . On adoptera la convention d'un déphasage dans l'intervalle [-π,π].
2. Méthodes de mesure du déphasage.
2.a. Méthode du cosinus
Cette méthode repose sur le résultat suivant :
Les valeurs efficaces sont définies par :
L'intégrale est évaluée à partir des signaux échantillonnés comme étant la moyenne de ensn sur la totalité de l'enregistrement, qui en général s'étend sur un grand nombre de cycles. Les valeurs efficaces sont les écart-types de en et sn.
Ces calculs conduisent donc à la valeur de . La fonction arccos fournit le déphasage mais cette méthode ne permet pas de savoir s'il est dans l'intervalle [0,π] ou dans l'intervalle [-π,0]. Elle est cependant intéressante si l'on connaît a priori le signe du déphasage, c'est-à-dire si s(t) est en avance ou en retard sur e(t).
L'avantage de cette méthode est qu'elle ne nécessite pas de connaître la fréquence du signal et que l'agorithme de calcul est extrêmement simple. En revanche, elle nécessite de disposer d'un signal échantillonné sur une durée couvrant un grand nombre de cycles (au moins une centaine). Bien évidemment, cette méthode n'a de sens que si le déphasage entre les deux signaux est constant, ce qui est le cas en principe lorsqu'on étudie le déphasage entre deux grandeurs dans un circuit alimenté par une seule source sinusoïdale.
2.b. Méthode d'analyse temporelle
Cette méthode consiste à parcourir les valeurs sn par indice n croissant et à détecter un passage par zéro par valeur croissante. On procède ensuite à la même recherche pour en. Le décalage temporel entre les deux passages par zéro par valeur croissante donne accès au décalage temporel entre les deux signaux puis au déphasage à condition de connaître la période (que l'on connaît par configuration du générateur). La recherche est répétée sur la totalité du signal échantillonné afin de calculer une moyenne des décalages temporels. Cette méthode a l'avantage de s'appliquer aussi aux signaux périodiques non sinusoïdaux, en particulier les signaux carrés.
Cette méthode a l'avantage de permettre une détermination du déphasage cycle par cycle, ce qui est important par exemple pour l'étude d'une boucle à verrouillage de phase. Par aillleurs, la fréquence d'échantillonnage doit être très grande par rapport à la fréquence des signaux (au moins un facteur 1000).
2.c. Algorithmes et simulation
import numpy as np
from numpy.random import normal,uniform
from matplotlib.pyplot import *
RAD2DEG = 180/np.pi
DEG2RAD = np.pi/180
La fonction suivante calcule le déphasage par la méthode du cosinus (le déphasage est supposé positif) :
def dephasageCos(u1,u2):
U1_eff = np.sqrt(np.mean(u1*u1))
U2_eff = np.sqrt(np.mean(u2*u2))
cos = np.mean(u1*u2)/(U1_eff*U2_eff)
return np.arccos(cos)*RAD2DEG
La fonction suivante génère deux signaux échantillonnés, avec une fréquence égale à 1 par convention. Le déphasage est donné en degrés. On introduit un décalage aléatoire de l'origine du temps et un bruit gaussien.
def signaux(phi,fechant,N,bruit):
t = np.arange(N)*1/fechant
t0 = uniform(0,1,1)
u1 = np.sin(2*np.pi*(t+t0))+normal(0,bruit,N)
u2 = np.sin(2*np.pi*(t+t0)+phi*DEG2RAD)+normal(0,bruit,N)
return t,u1,u2
Voici une première simulation avec une fréquence d'échantillonnage égale à 100 fois celle du signal et une analyse sur 10 cycles, en l'absence de bruit. On trace l'erreur sur le déphasage déterminé par la méthode du cosinus :
phi = np.linspace(1,179,500)
fechant = 100
N = 1000 # 10 cycles
phi_mesure = np.zeros(len(phi))
bruit = 0
for i in range(len(phi)):
t,u1,u2 = signaux(phi[i],fechant,N,bruit)
phi_mesure[i] = dephasageCos(u1,u2)
figure(figsize=(12,6))
plot(phi,phi_mesure-phi,"r-")
grid()
xlabel(r"$\phi\ (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi\ (\rm deg)$",fontsize=18)
ylim(-1,1)
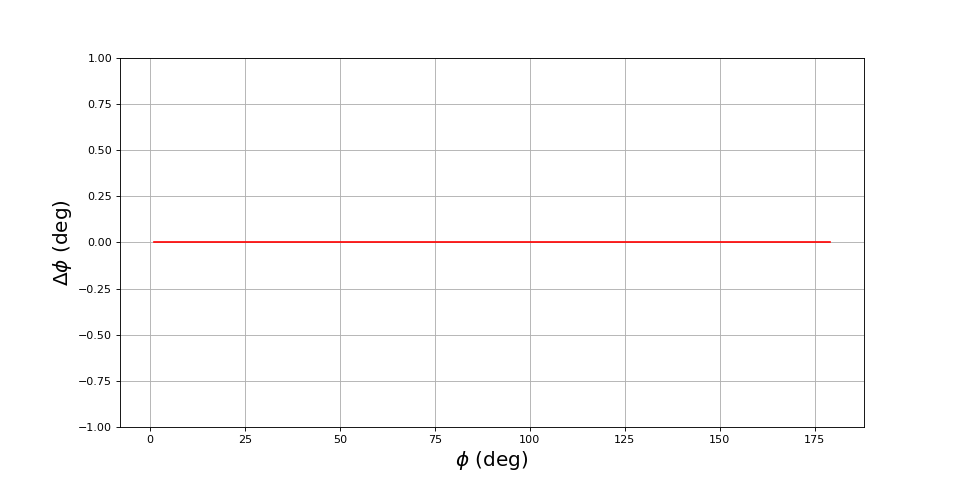 fig1.pdf
fig1.pdf
Voici une simulation avec les mêmes paramètres mais un bruit d'écart-type 0.01 (un centième de l'amplitude) :
bruit = 0.01
for i in range(len(phi)):
t,u1,u2 = signaux(phi[i],fechant,N,bruit)
phi_mesure[i] = dephasageCos(u1,u2)
figure(figsize=(12,6))
plot(phi,phi_mesure-phi,"r-")
grid()
xlabel(r"$\phi\ (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi\ (\rm deg)$",fontsize=18)
ylim(-1,1)
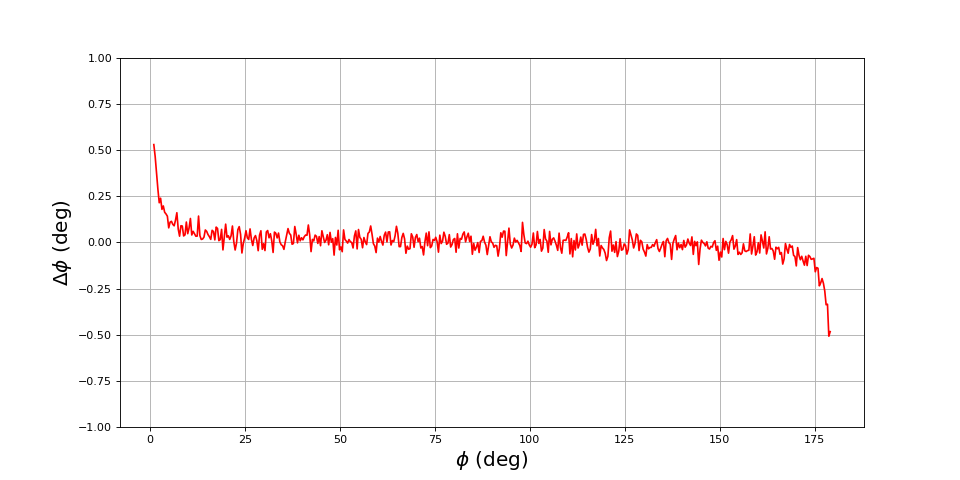 fig2.pdf
fig2.pdf
Les fluctations de l'erreur relative d'un angle au suivant donne une idée de l'incertitude (nous ferons le calcul de l'écart-type plus loin). Lorsque l'angle est petit ou proche de 180 degrés (c'est-à-dire lorsque le cosinus est proche de 1 ou -1), l'erreur relative augmente mais avec un signe déterminé. Par exemple pour les angles petits, la valeur mesurée est systématiquement plus grande que la valeur réelle mais il ne semble pas y avoir d'augmentation de l'écart-type. Ce résultat est étonnant et contraire à l'idée que l'on peut se faire en général de l'influence d'un paramètre aléatoire. Dans le cas présent et lorsque la valeur absolue du cosinus est proche de 1, l'effet principal du bruit est l'introduction d'une erreur systématique. Ce phénomène peut se comprendre de manière générale de la manière suivante : si x est une variable aléatoire d'espérance nulle et f une fonction alors f(x) est une variable aléatoire d'espérance nulle si la fonction est paire mais elle ne l'est pas en général. Le problème posé par cette erreur systématique est qu'elle est indétectable par une analyse statistique d'un grand nombre de mesures.
Voyons l'effet d'une augmentation du nombre de cycles analysés, pour un bruit de faible intensité (écart-type 0.01) :
N=10000
bruit = 0.01
for i in range(len(phi)):
t,u1,u2 = signaux(phi[i],fechant,N,bruit)
phi_mesure[i] = dephasageCos(u1,u2)
figure(figsize=(12,6))
plot(phi,phi_mesure-phi,"r-")
grid()
xlabel(r"$\phi\ (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi\ (\rm deg)$",fontsize=18)
ylim(-1,1)
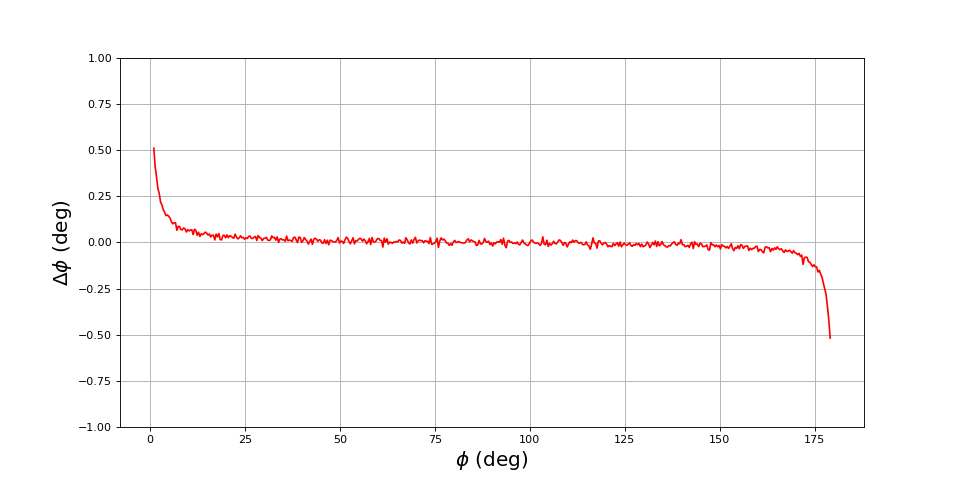 fig3.pdf
fig3.pdf
Faire passer le nombre de cycles de 10 à 100 apporte une amélioration de la précision (l'écart-type se réduit) mais ne change rien à l'erreur systématique aui apparaît lorsque le cosinus est proche de 1 ou -1.
Voici une simulation avec un bruit 3 fois plus intense :
bruit = 0.03
for i in range(len(phi)):
t,u1,u2 = signaux(phi[i],fechant,N,bruit)
phi_mesure[i] = dephasageCos(u1,u2)
figure(figsize=(12,6))
plot(phi,phi_mesure-phi,"r-")
grid()
xlabel(r"$\phi\ (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi\ (\rm deg)$",fontsize=18)
ylim(-1,1)
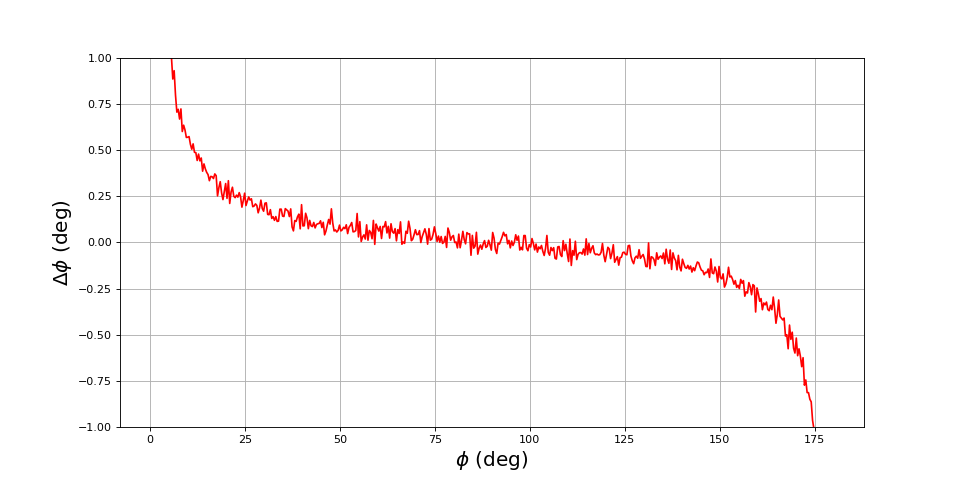 fig4.pdf
fig4.pdf
Les fluctuations augmentent et l'augmentation systématique est beaucoup plus importante. Par exemple pour un déphasage de 25 degrés, on a une valeur moyenne proche de 0,25 degrés, largement plus grande que l'amplitude des fluctuations.
Revenons à un bruit d'écart-type 0.01 et divisons par 10 la fréquence d'échantillonnage :
freq = 10
N = 1000
bruit = 0.01
for i in range(len(phi)):
t,u1,u2 = signaux(phi[i],fechant,N,bruit)
phi_mesure[i] = dephasageCos(u1,u2)
figure(figsize=(12,6))
plot(phi,phi_mesure-phi,"r-")
grid()
xlabel(r"$\phi\ (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi\ (\rm deg)$",fontsize=18)
ylim(-1,1)
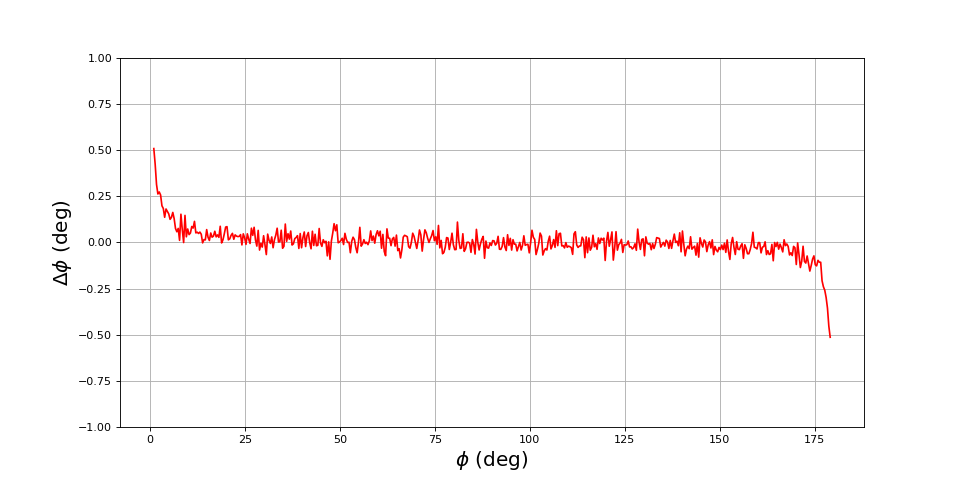 fig5.pdf
fig5.pdf
Diviser par 10 la fréquence d'échantillonnage semble avoir le même effet que diviser par dix le nombre de cycles.
Pour implémenter la seconde méthode, il faut tout d'abord écrire une fonction qui détermine les instants de passage par zéro d'une fonction (par valeur croissante). Le comparateur à hysérésis consiste à utiliser un seuil de détection de changement de signe -ε lorsque le signal est positif et un seuil +ε lorsque le signal est négatif. La fonction renvoie les instants de passage par zéro et les intervalles de temps entre un passage par zéro et le suivant (période) :
def passageZeros(t,u,eps=0):
instants = []
if u[0] > 0 :
signe1 = 1
else:
signe1 = -1
for i in range(1,len(t)):
if signe1>0 and u[i]<-eps:
signe1 = -1
elif signe1<0 and u[i]>eps:
signe1 = 1
instants.append(t[i])
Np = len(instants)-1
period = np.zeros(Np)
for i in range(1,len(instants)):
period[i-1] = instants[i]-instants[i-1]
return np.array(instants),np.array(period)
Pour tester cette fonction, nous traçons deux signaux bruités en reportant les instants détectés :
fechant = 100
N = 100000
bruit = 0.01
eps = 0.0
phi = 50
t,u1,u2 = signaux(phi,fechant,N,bruit)
Z1,T1 = passageZeros(t,u1,eps)
Z2,T2 = passageZeros(t,u2,eps)
figure(figsize=(16,6))
plot(t,u1,'r-')
for i in range(len(Z1)):
tz = Z1[i]
plot([tz,tz],[0,1],'r--')
plot(t,u2,'b-')
for i in range(len(Z2)):
tz = Z2[i]
plot([tz,tz],[0,1],'b--')
grid()
xlabel("t",fontsize=18)
xlim(0,10)
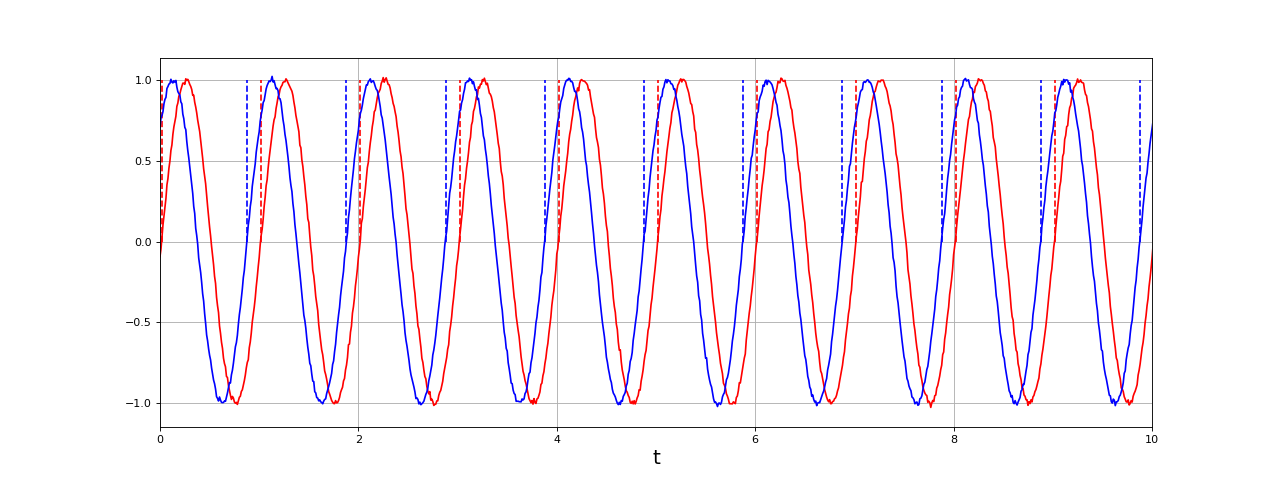 fig6.pdf
fig6.pdf
Voici les intervalles de temps entre deux passages par zéro successifs (en théorie égaux à 1) :
figure(figsize=(12,6))
plot(T1,"r.",label="T1")
plot(T2,"b.",label="T2")
legend(loc='upper right')
grid()
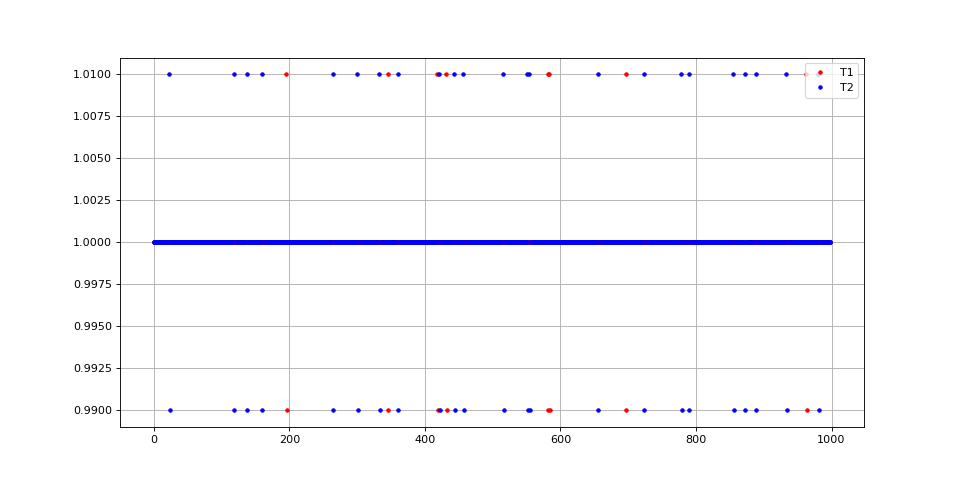 fig7.pdf
fig7.pdf
À ce niveau de bruit relativement faible, il ne semble pas nécessaire d'appliquer un hystérésis sur le seuil de détection puisque les intervalles restent proches de 1. Voyons un exemple avec un bruit plus intense :
fechant = 100
N = 100000
bruit = 0.03
eps = 0.0
phi = 50
t,u1,u2 = signaux(phi,fechant,N,bruit)
Z1,T1 = passageZeros(t,u1,eps)
Z2,T2 = passageZeros(t,u2,eps)
figure(figsize=(16,6))
plot(t,u1,'r-')
for i in range(len(Z1)):
tz = Z1[i]
plot([tz,tz],[0,1],'r--')
plot(t,u2,'b-')
for i in range(len(Z2)):
tz = Z2[i]
plot([tz,tz],[0,1],'b--')
grid()
xlabel("t",fontsize=18)
xlim(0,10)
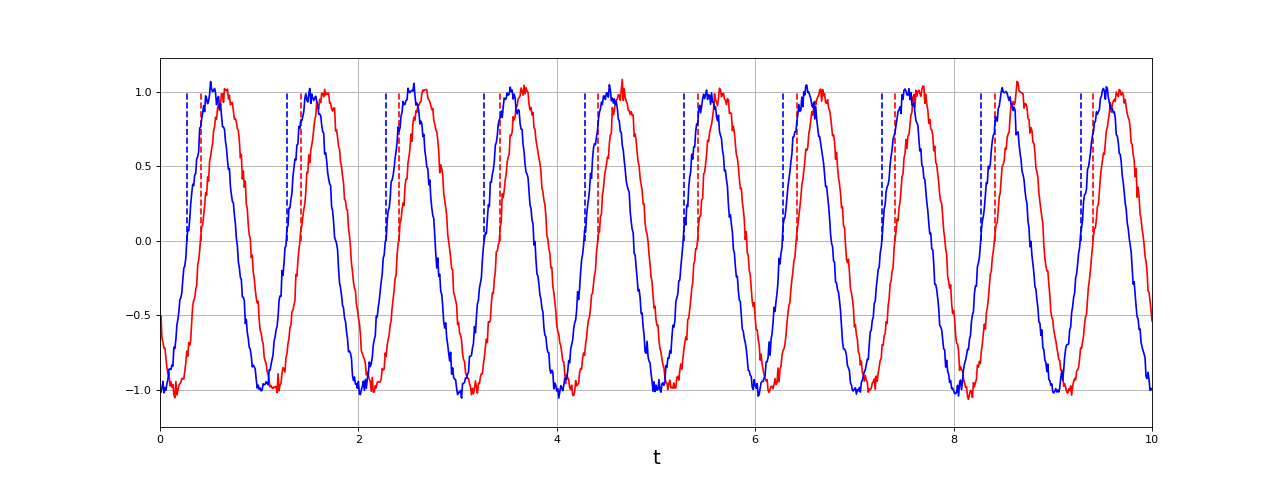 fig8.pdf
fig8.pdf
figure(figsize=(12,6))
plot(T1,"r.",label="T1")
plot(T2,"b.",label="T2")
legend(loc='upper right')
grid()
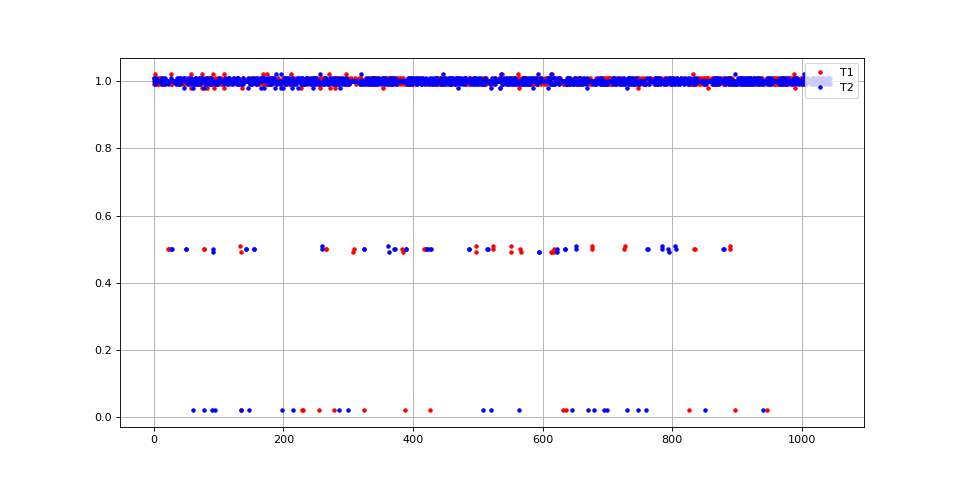 fig9.pdf
fig9.pdf
Dans ce cas, il y des intervalles faux (0.5 et proche de 0) qu'il convient d'éliminer au moyen de l'hystéréris :
fechant = 100
N = 100000
bruit = 0.03
eps = 0.05
phi = 50
t,u1,u2 = signaux(phi,fechant,N,bruit)
Z1,T1 = passageZeros(t,u1,eps)
Z2,T2 = passageZeros(t,u2,eps)
figure(figsize=(16,6))
plot(t,u1,'r-')
for i in range(len(Z1)):
tz = Z1[i]
plot([tz,tz],[0,1],'r--')
plot(t,u2,'b-')
for i in range(len(Z2)):
tz = Z2[i]
plot([tz,tz],[0,1],'b--')
grid()
xlabel("t",fontsize=18)
xlim(0,10)
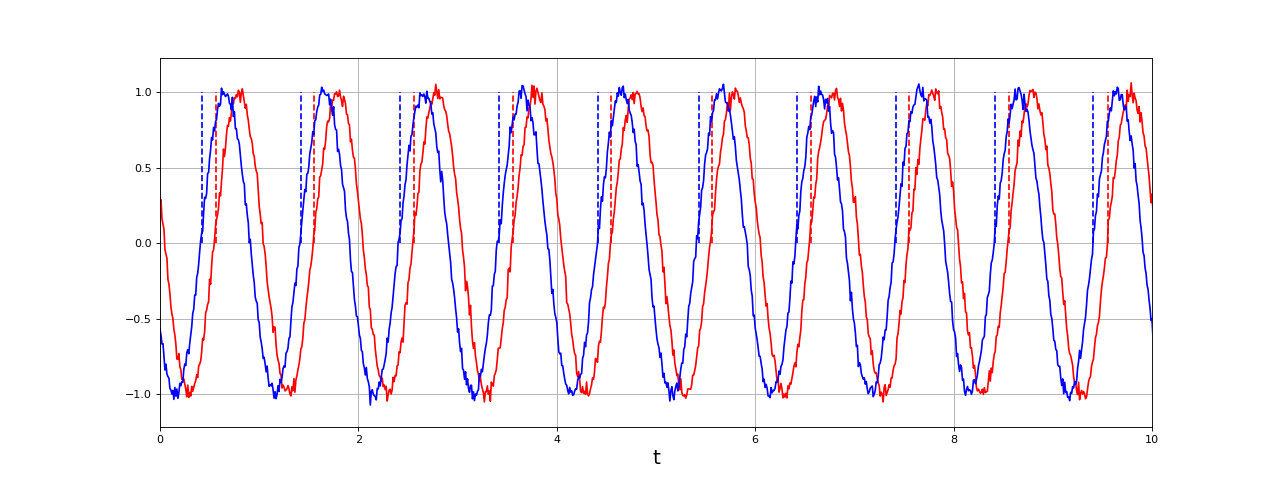 fig10.pdf
fig10.pdf
figure(figsize=(12,6))
plot(T1,"r.",label="T1")
plot(T2,"b.",label="T2")
legend(loc='upper right')
grid()
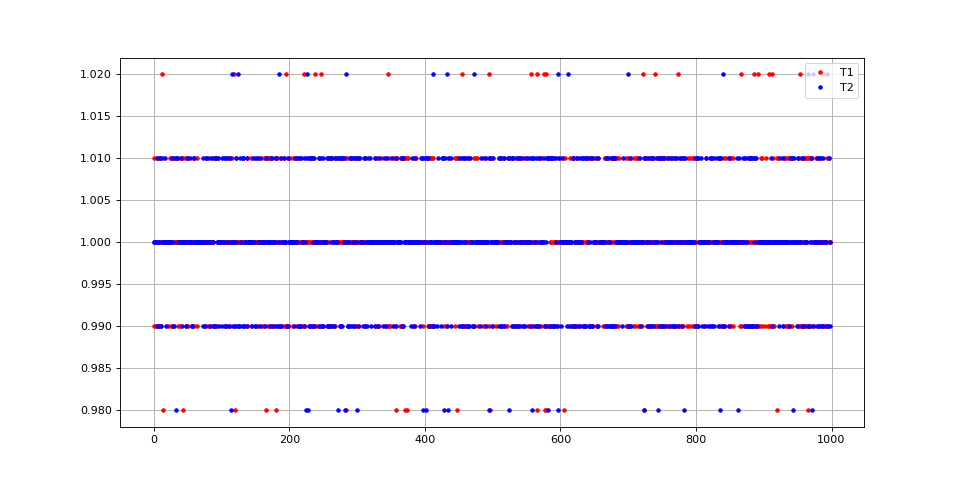 fig11.pdf
fig11.pdf
En pratique, l'évaluation de la dispersion des intervalles de temps obtenus pourra être un bon moyen de savoir si la valeur de ε est assez grande.
Voyons à présent le calcul du décalage temporel entre le passage par zéro des deux signaux :
def decalageZeros(freq,Z1,Z2):
decal = []
dec = Z1[0]-Z2[0]
if abs(dec) > 1/(2*freq):
i0 = 1
else:
i0 = 0
N = min(len(Z1),len(Z2))
for i in range(N-i0):
decal.append(Z1[i+i0]-Z2[i])
return np.array(decal)
freq = 1
tau = decalageZeros(freq,Z1,Z2)
dephas = tau.mean()*360 % 180 # déphasage de 2 par rapport à 1
print(dephas) --> 50.09759999999886
Pour finir, nous pouvons écrire une fonction qui calcule le déphasage :
def dephasageTemp(freq,t,u1,u2,eps):
Z1,T1 = passageZeros(t,u1,eps)
Z2,T2 = passageZeros(t,u2,eps)
tau = decalageZeros(freq,Z1,Z2)
return tau.mean()*freq*360 % 180
Voici une simulation de mesures, avec une fréquence d'échantillonnage de 100 et 100 cycles analysés :
phi = np.linspace(1,179,500)
fechant = 100
N = 1000 # 10 cycles
phi_mesure = np.zeros(len(phi))
bruit = 0.01
eps = 0.0
for i in range(len(phi)):
t,u1,u2 = signaux(phi[i],fechant,N,bruit)
phi_mesure[i] = dephasageTemp(1,t,u1,u2,eps)
figure(figsize=(12,6))
plot(phi,phi_mesure-phi,"r-")
grid()
xlabel(r"$\phi\ (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi\ (\rm deg)$",fontsize=18)
ylim(-10,10)
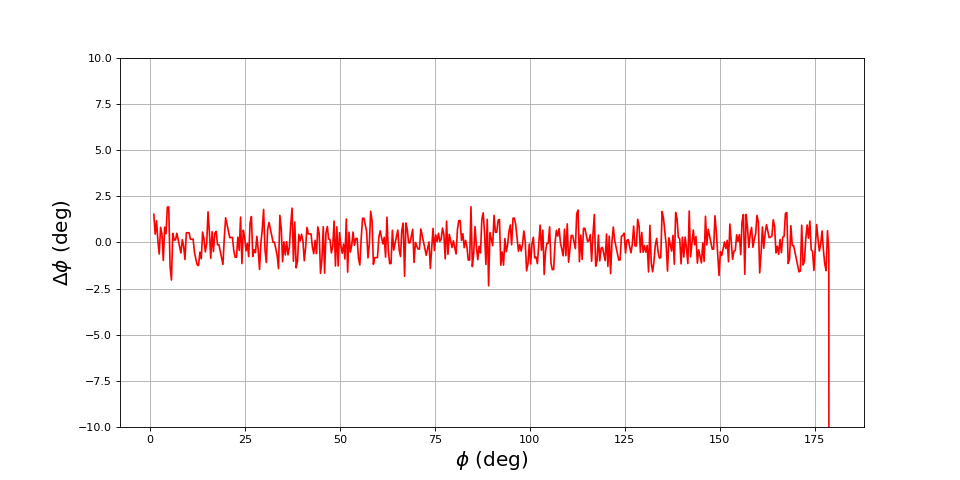 fig12.pdf
fig12.pdf
Ce graphique montre que la méthode d'analyse temporelle est beaucoup moins précise que la méthode du cosinus (pour un échantillonnage de 100 par cycle). En revanche, elle ne souffre pas d'une augmentation de l'erreur lorsque le déphasage est proche de 0 ou 180 degrés. Pour améliorer la précision, il faut évidemment augmenter la fréquence d'échantillonnage, ce qui nous faisons sans changer le nombre d'échantillons. Nous devons aussi augmenter l'hystérésis de détection car l'augmentation de la fréquence d'échantillonnage augmente l'effet du bruit :
phi = np.linspace(1,179,500)
fechant = 1000
N = 10000 # 10 cycles
phi_mesure = np.zeros(len(phi))
bruit = 0.01
eps = 0.05
for i in range(len(phi)):
t,u1,u2 = signaux(phi[i],fechant,N,bruit)
phi_mesure[i] = dephasageTemp(1,t,u1,u2,eps)
figure(figsize=(12,6))
plot(phi,phi_mesure-phi,"r-")
grid()
xlabel(r"$\phi\ (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi\ (\rm deg)$",fontsize=18)
ylim(-10,10)
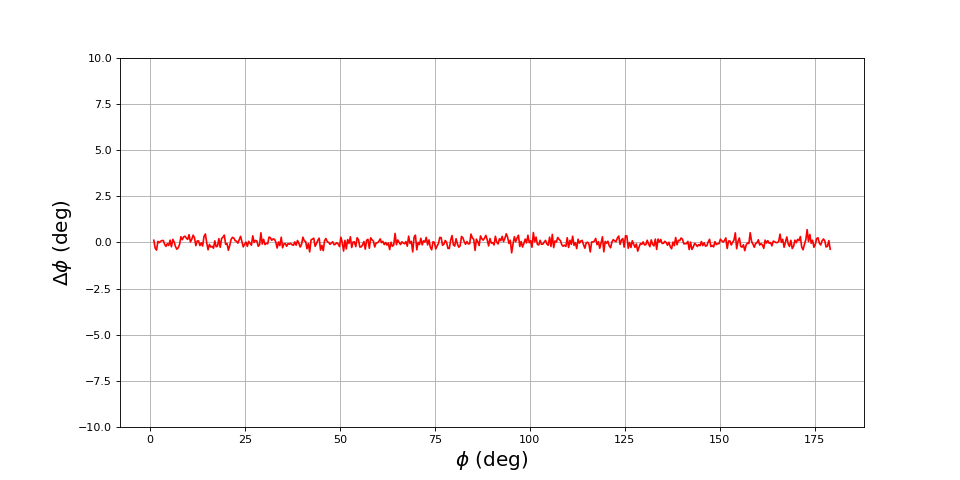 fig13.pdf
fig13.pdf
Les fonctions suivantes effectuent le calcul de l'incertitude-type pour un déphasage donné :
def incertitudeCos(phi,fechant,N,bruit,Nt=1000):
phi_mes = np.zeros(Nt)
for k in range(1000):
t,u1,u2 = signaux(phi,fechant,N,bruit)
phi_mes[k] = dephasageCos(u1,u2)
return phi_mes.std()
def incertitudeTemp(freq,phi,fechant,N,bruit,eps,Nt=1000):
phi_mes = np.zeros(Nt)
for k in range(1000):
t,u1,u2 = signaux(phi,fechant,N,bruit)
phi_mes[k] = dephasageTemp(freq,t,u1,u2,eps)
return phi_mes.std()
L'utilisation de ces fonctions dans un contexte expérimental nécessite la connaissance de l'écart-type du bruit (paramètre bruit). Dans le cas d'un signal analogique de très faible bruit, il s'agit de l'écart-type du bruit de quantification (situation courante dans un oscilloscope 8 bits). Voici des exemples de calcul de l'incertitude :
incert = incertitudeCos(40,100,10000,0.01)
print(incert) --> 0.011873164182895718
incert = incertitudeCos(1,100,10000,0.01)
print(incert) --> 0.009810818633654099
Ces deux résutats pour la méthode du cosinus confirment que l'augmentation de l'erreur lorsque l'angle diminue n'a pas d'effet sur l'écart-type.
incert = incertitudeTemp(1,40,1000,10000,0.01,0.05)
print(incert) --> 0.20521141390283482
incert = incertitudeTemp(1,1,1000,10000,0.01,0.05)
print(incert) --> 0.20483776960317115
Même avec une fréquence d'échantillonnage de 1000 par cycle, la méthode d'analyse temporelle conduit à une incertitude-type beaucoup plus grande que la méthode du cosinus. En revanche, cette méthode ne comporte pas d'apparition d'une erreur systématique lorsque l'angle est proche de 0 ou de 180 degrés.
Conclusion : à l'exception des mesures de déphasages proches de 0 ou 180 degrés, la méthode du cosinus est nettement plus précise que la méthode d'analyse temporelle. Lorsque l'angle est proche de 0 ou 180, une erreur systématique apparaît. Dans ce cas, il peut être intéressant d'utiliser la méthode d'analyse temporelle mais celle-ci nécessite une fréquence d'échantillonnage très élevée (au moins 1000 par cycle).
3. Étude expérimentale
3.a. Génération des signaux
Nous utilisons le générateur numérique intégré à l'Analog Discovery 2 (AD2). Les deux sorties W1 et W2 peuvent se programmer avec le logiciel Waveforms fourni avec l'AD2 (excellent logiciel) mais nous utilisons pour cela l'interface Python décrite dans Interface Python pour Analog Discovery. Nous verrons d'ailleurs plus loin comment faire la mesure du déphasage avec l'AD2 lui-même.
Le script suivant permet de générer deux sinusoïdes avec un déphasage donné :
from analog_0_1 import Device,AnalogOutput
device = Device(-1)
device.open()
output = AnalogOutput(device)
freq = 100
amp = 2.0
while True:
phi = float(input("Déphasage (deg) ?"))
output.function(0,'sine',freq,amp,phase=0)
output.function(1,'sine',freq,amp,phase=phi)
output.setMaster(1,0)
output.start(0)
device.close()
3.b. Numérisation 12 bits
La centrale Sysam SP5 permet de numériser les signaux avec 12 bits de précision.
import pycanum.main as pycan
import matplotlib.pyplot as plt
import numpy as np
RAD2DEG = 180/np.pi
DEG2RAD = np.pi/180
def passageZeros(t,u,eps=0):
instants = []
if u[0] > 0 :
signe1 = 1
else:
signe1 = -1
for i in range(1,len(t)):
if signe1>0 and u[i]<-eps:
signe1 = -1
elif signe1<0 and u[i]>eps:
signe1 = 1
instants.append(t[i])
Np = len(instants)-1
period = np.zeros(Np)
for i in range(1,len(instants)):
period[i-1] = instants[i]-instants[i-1]
return np.array(instants),np.array(period)
def decalageZeros(freq,Z1,Z2):
decal = []
dec = Z1[0]-Z2[0]
if abs(dec) > 1/(2*freq):
i0 = 1
else:
i0 = 0
N = min(len(Z1),len(Z2))
for i in range(N-i0):
decal.append(Z1[i+i0]-Z2[i])
return np.array(decal)
def dephasageCos(u1,u2):
U1_eff = np.sqrt(np.mean(u1*u1))
U2_eff = np.sqrt(np.mean(u2*u2))
cos = np.mean(u1*u2)/(U1_eff*U2_eff)
return np.arccos(cos)*RAD2DEG
def dephasageTemp(freq,t,u1,u2,eps):
Z1,T1 = passageZeros(t,u1,eps)
Z2,T2 = passageZeros(t,u2,eps)
tau = decalageZeros(freq,Z1,Z2)
return tau.mean()*freq*360 % 180
sys = pycan.Sysam("SP5")
sys.config_quantification(12)
sys.config_entrees([0,1],[5,5])
freq = 100
fe = 1000*freq
te = 1/fe
Ne = 100000
sys.config_echantillon(te*10**6,Ne)
eps = 0.05
list_phi = []
list_phi_cos = []
list_phi_temp = []
while True:
phi = input("Déphasage (deg) (q pour quitter) ?")
if phi=="q": break
phi = float(phi)
list_phi.append(phi)
sys.acquerir()
t=sys.temps()
u=sys.entrees()
u0 = u[0]
u1 = u[1]
temps = t[0]
phi_cos = dephasageCos(u0,u1)
phi_temp = dephasageTemp(freq,temps,u0,u1,eps)
list_phi_cos.append(phi_cos)
list_phi_temp.append(phi_temp)
print(phi_cos,phi_temp)
sys.fermer()
data = np.array([list_phi,list_phi_cos,list_phi_temp]).T
np.savetxt("dephasage.txt",data)
plt.figure()
plt.plot(list_phi,list_phi_cos,"ro",label="Cosinus")
plt.plot(list_phi,list_phi_temp,"bo",label="Temporel")
plt.grid()
plt.xlabel(r"$\phi (deg)$",fontsize=18)
plt.show()
Voici les résultats pour une fréquence de 100 Hz. La fréquence d'échantillonnage est de 100 kHz, soit 1000 échantillons par cycle (minimum nécessaire pour la méthode d'analyse temporelle). L'enregistrement comporte 100000 échantillons (100 cycles). On trace l'écart entre la valeur mesurée et la valeur configurée dans l'AD2.
[phi,phi_cos,phi_temp] = np.loadtxt("dephasage-0.txt",unpack=True)
figure(figsize=(12,6))
plot(phi,phi_cos-phi,"ro",label="Cosinus")
plot(phi,phi_temp-phi,"bo",label="Temporel")
grid()
ylim(-1,1)
legend(loc='upper right')
xlabel(r"$\phi (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi (\rm deg)$",fontsize=18)
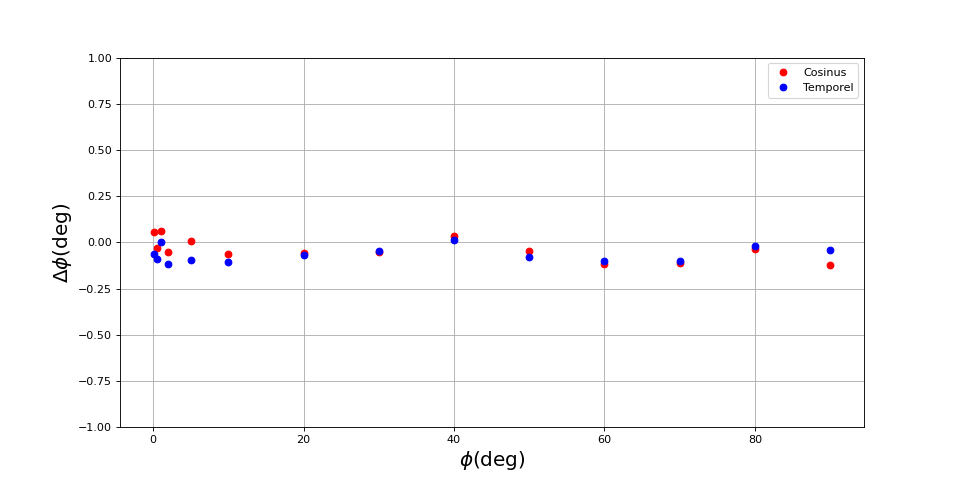 fig14.pdf
fig14.pdf
La valeur mesurée est presque toujours inférieure à la valeur programmée sur le générateur mais l'écart de dépasse pas 0,25 degrés. Il semble y avoir une erreur systématique mais on ne peut pas savoir son origine : elle peut venir de la numérisation ou bien du générateur. En tout cas, elle ne peut pas venir de la méthode de mesure (d'après les simulations précédentes).
Voici les résultats avec les mêmes paramètres mais une quantification de 8 bits :
[phi,phi_cos,phi_temp] = np.loadtxt("dephasage-2.txt",unpack=True)
figure(figsize=(12,6))
plot(phi,phi_cos-phi,"ro",label="Cosinus")
plot(phi,phi_temp-phi,"bo",label="Temporel")
grid()
ylim(-1,1)
legend(loc='upper right')
xlabel(r"$\phi (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi (\rm deg)$",fontsize=18)
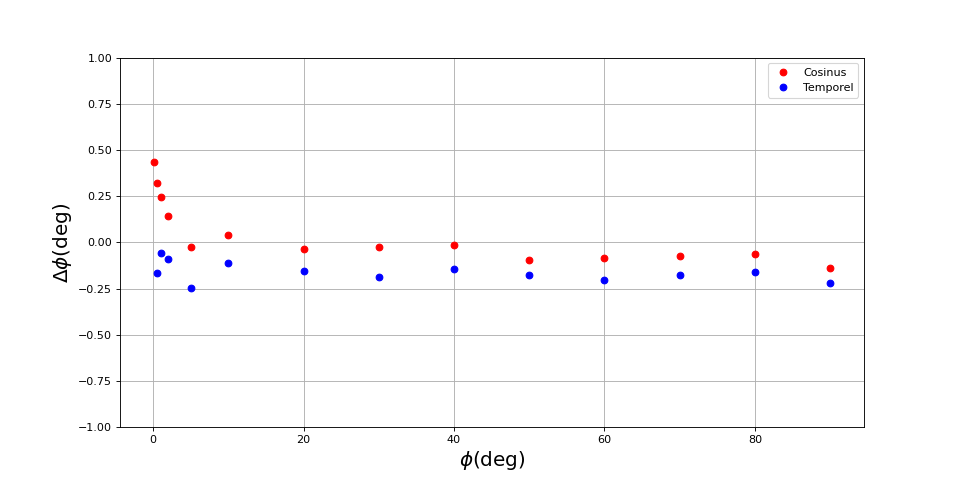 fig15.pdf
fig15.pdf
L'effet de la réduction de la précision de la numérisation (passage de 12 bits à 8 bits) peut se voir comme l'effet de l'augmentation du bruit dans le signal numérique (bruit de quantification). La méthode du cosinus est très affectée par cette augmentation pour les déphasages petits. L'apparition d'une erreur systématique positive pour les petites angles est bien prévue par la simulation montrée plus haut.
Voici les résultats pour une fréquence de 1000 Hz (1000 échantillons par cycle, 100000 échantillons et numérisation 12 bits) :
[phi,phi_cos,phi_temp] = np.loadtxt("dephasage-3.txt",unpack=True)
figure(figsize=(12,6))
plot(phi,phi_cos-phi,"ro",label="Cosinus")
plot(phi,phi_temp-phi,"bo",label="Temporel")
grid()
ylim(-1,1)
legend(loc='upper right')
xlabel(r"$\phi (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi (\rm deg)$",fontsize=18)
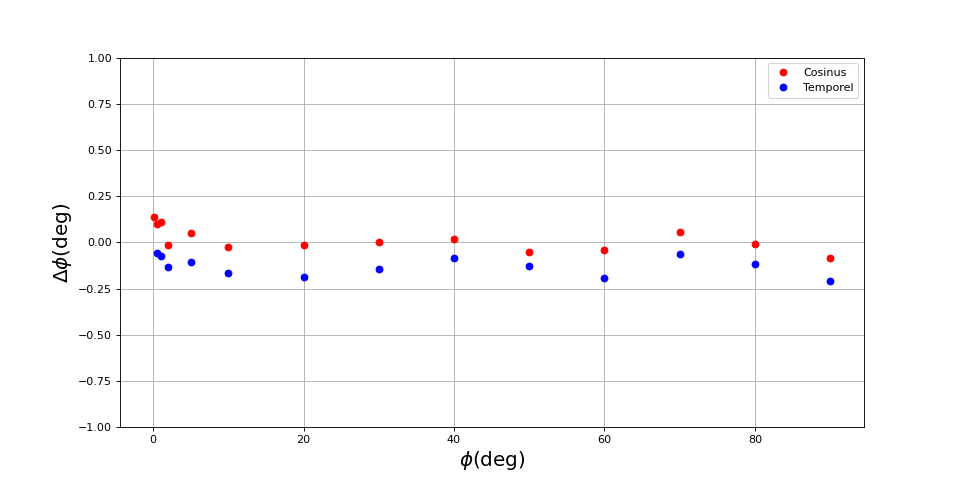 fig16.pdf
fig16.pdf
3.c. Numérisation 14 bits
L'analog discovery 2 (AD2) permet de numériser deux voies avec une précision de 14 bits. Le même script est utilisé pour programmer la génération des signaux et leur numérisation, ce qui permet d'automatiser le balayage du déphasage.
from analog_0_1 import Device,AnalogOutput,AnalogInput
import matplotlib.pyplot as plt
import numpy as np
RAD2DEG = 180/np.pi
DEG2RAD = np.pi/180
def passageZeros(t,u,eps=0):
instants = []
if u[0] > 0 :
signe1 = 1
else:
signe1 = -1
for i in range(1,len(t)):
if signe1>0 and u[i]<-eps:
signe1 = -1
elif signe1<0 and u[i]>eps:
signe1 = 1
instants.append(t[i])
Np = len(instants)-1
period = np.zeros(Np)
for i in range(1,len(instants)):
period[i-1] = instants[i]-instants[i-1]
return np.array(instants),np.array(period)
def decalageZeros(freq,Z1,Z2):
decal = []
dec = Z1[0]-Z2[0]
if abs(dec) > 1/(2*freq):
i0 = 1
else:
i0 = 0
N = min(len(Z1),len(Z2))
for i in range(N-i0):
decal.append(Z1[i+i0]-Z2[i])
return np.array(decal)
def dephasageCos(u1,u2):
U1_eff = np.sqrt(np.mean(u1*u1))
U2_eff = np.sqrt(np.mean(u2*u2))
cos = np.mean(u1*u2)/(U1_eff*U2_eff)
return np.arccos(cos)*RAD2DEG
def dephasageTemp(freq,t,u1,u2,eps):
Z1,T1 = passageZeros(t,u1,eps)
Z2,T2 = passageZeros(t,u2,eps)
tau = decalageZeros(freq,Z1,Z2)
return tau.mean()*freq*360 % 180
device = Device(-1)
device.open()
output = AnalogOutput(device)
analog = AnalogInput(device)
freq = 100
fe = 1000*freq
te = 1/fe
Ne = 100000
analog.channels([0,1],[10,10])
temps = analog.sampling(fe,Ne)
eps = 0.05
list_phi = np.linspace(1,90,100)
list_phi_cos = []
list_phi_temp = []
amp = 2.0
for phi in list_phi:
output.function(0,'sine',freq,amp,phase=0)
output.function(1,'sine',freq,amp,phase=phi)
output.setMaster(1,0)
output.start(0)
voltage = analog.record()
u0 = voltage[0,:]
u1 = voltage[1,:]
phi_cos = dephasageCos(u0,u1)
phi_temp = dephasageTemp(freq,temps,u0,u1,eps)
list_phi_cos.append(phi_cos)
list_phi_temp.append(phi_temp)
print(phi_cos,phi_temp)
device.close()
data = np.array([list_phi,list_phi_cos,list_phi_temp]).T
np.savetxt("dephasage-4.txt",data)
plt.figure()
plt.plot(list_phi,list_phi_cos,"ro",label="Cosinus")
plt.plot(list_phi,list_phi_temp,"bo",label="Temporel")
plt.grid()
plt.xlabel(r"$\phi (deg)$",fontsize=18)
plt.show()
[phi,phi_cos,phi_temp] = np.loadtxt("dephasage-4.txt",unpack=True)
figure(figsize=(12,6))
plot(phi,phi_cos-phi,"ro",label="Cosinus")
plot(phi,phi_temp-phi,"bo",label="Temporel")
grid()
ylim(-1,1)
legend(loc='upper right')
xlabel(r"$\phi (\rm deg)$",fontsize=18)
ylabel(r"$\Delta\phi (\rm deg)$",fontsize=18)
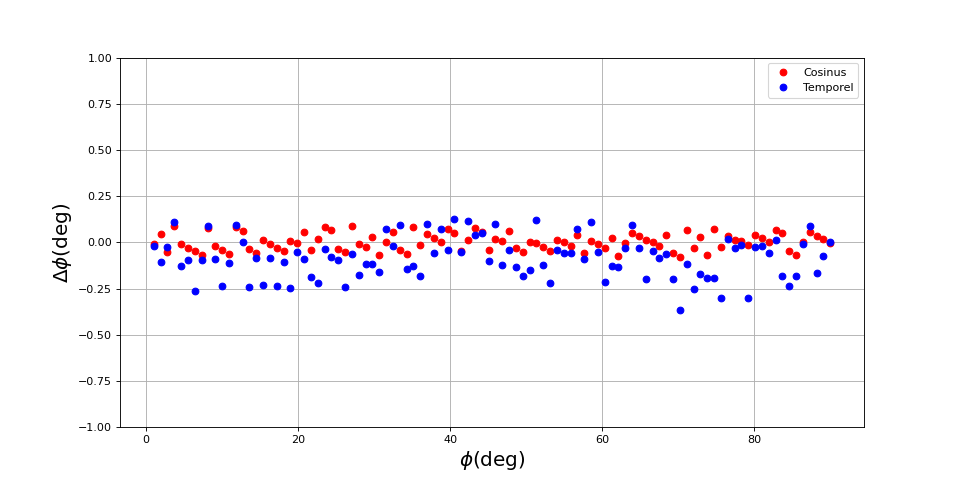 fig17.pdf
fig17.pdf
L'écart est toujours inférieur à 0,25 degrés mais n'est pas plus faible que dans le cas de la numérisation en 12 bits. Le passage de la précision de 12 à 14 bits ne semple pas apporter de gain en précision de mesure du déphasage.
Cependant, ces expériences ne font que déterminer l'écart entre le déphasage programmée et celui mesuré. Il est possible que l'écart observé avec la méthode du cosinus soit principalement dû à l'imprécision du déphasage du générateur DDS de l'Analog Discovery. Pour évaluer l'incertitude de la mesure, nous devons refaire un grand nombre de fois la mesure du déphasage pour un déphasage donné (on suppose que celui-ci reste constant, ce qui n'est pas non plus garanti). Le script suivant réalise cette opération :
from analog_0_1 import Device,AnalogOutput,AnalogInput
import matplotlib.pyplot as plt
import numpy as np
RAD2DEG = 180/np.pi
DEG2RAD = np.pi/180
def passageZeros(t,u,eps=0):
instants = []
if u[0] > 0 :
signe1 = 1
else:
signe1 = -1
for i in range(1,len(t)):
if signe1>0 and u[i]<-eps:
signe1 = -1
elif signe1<0 and u[i]>eps:
signe1 = 1
instants.append(t[i])
Np = len(instants)-1
period = np.zeros(Np)
for i in range(1,len(instants)):
period[i-1] = instants[i]-instants[i-1]
return np.array(instants),np.array(period)
def decalageZeros(freq,Z1,Z2):
decal = []
dec = Z1[0]-Z2[0]
if abs(dec) > 1/(2*freq):
i0 = 1
else:
i0 = 0
N = min(len(Z1),len(Z2))
for i in range(N-i0):
decal.append(Z1[i+i0]-Z2[i])
return np.array(decal)
def dephasageCos(u1,u2):
U1_eff = np.sqrt(np.mean(u1*u1))
U2_eff = np.sqrt(np.mean(u2*u2))
cos = np.mean(u1*u2)/(U1_eff*U2_eff)
return np.arccos(cos)*RAD2DEG
def dephasageTemp(freq,t,u1,u2,eps):
Z1,T1 = passageZeros(t,u1,eps)
Z2,T2 = passageZeros(t,u2,eps)
tau = decalageZeros(freq,Z1,Z2)
return tau.mean()*freq*360 % 180
device = Device(-1)
device.open()
output = AnalogOutput(device)
analog = AnalogInput(device)
freq = 100
fe = 1000*freq
te = 1/fe
Ne = 100000
analog.channels([0,1],[10,10])
temps = analog.sampling(fe,Ne)
eps = 0.05
list_phi_cos = []
list_phi_temp = []
amp = 2.0
phi = 20
output.function(0,'sine',freq,amp,phase=0)
output.function(1,'sine',freq,amp,phase=phi)
output.setMaster(1,0)
output.start(0)
Nt = 100
for k in range(Nt):
voltage = analog.record()
u0 = voltage[0,:]
u1 = voltage[1,:]
phi_cos = dephasageCos(u0,u1)
phi_temp = dephasageTemp(freq,temps,u0,u1,eps)
list_phi_cos.append(phi_cos)
list_phi_temp.append(phi_temp)
print(phi_cos,phi_temp)
device.close()
incert_cos = np.array(list_phi_cos).std()
incert_temp = np.array(list_phi_temp).std()
print("incert cos = %f"%incert_cos)
print("incert_temp = %f"%incert_temp)
Pour ce déphasage de 20 degrés, on obtient :
incert cos = 0.000806
incert_temp = 0.113351
Voici le résultat pour un déphasage de 60 degrés :
incert cos = 0.000747
incert_temp = 0.113259
et pour un déphasage de 1 degré :
incert cos = 0.001276
incert_temp = 0.109593
Ces valeurs sont en accord avec les résultats de la simulation : l'écart-type est beaucoup plus grand avec la méthode d'analyse temporelle. De plus, l'écart-type dans le cas de la méthode du cosinus (de l'ordre de 0,001) est nettement plus petit que les variations de Δϕ (variations de l'écart entre la mesure et le déphasage programmée) observées lorsque le déphasage varie. Celles-ci sont effet de l'ordre de grandeur de 0,1. Cela suggère que ces variations sont principalement dues à l'imprécision de la phase dans le générateur de signaux.
4. Annexe : effet du bruit
Afin de comprendre l'origine de l'erreur systématique qui apparaît sur le déphasage en présence de bruit dans les signaux, on s'intéresse au calcul du cosinus du déphasage :
Notons x(t) le bruit ajouté au signal sinusoïdal e(t) et y(t) celui ajouté à s(t). Par hypothèse, x(t) et y(t) sont des signaux stochastiques d'espérance nulle, c'est-à-dire que l'espérance d'un signal échantillonné obtenu à partir de ces signaux est nulle. Considérons tout d'abord le numérateur de l'expression du cosinus :
Cette moyenne temporelle est une variable aléatoire : pour chaque réalisation de x(t) et de y(t), la valeur est différente.
Faisons une simulation de Monte-carlo dans le cas où e(t) et s(t) ont une amplitude de 1. Dans ce cas le produit vaut 1/2 en l'absence de bruit et on évalue donc l'écart avec cette valeur. Pour chaque réalisation, on introduit une valeur aléatoire de l'origine du temps. On évalue aussi l'espérance de l'intégrale de x(t) puisque cette espérance est nulle.
fechant = 100
N = 10000 # 100 cycles
bruit = 0.1
moy = 0
moy_x = 0
list_prod = []
phi = 10
Nt = 1000 # nombre de réalisations
for i in range(Nt):
t0 = uniform(0,1,1)
t = np.arange(N)*1/fechant
e = np.sin(2*np.pi*(t+t0))
s = np.sin(2*np.pi*(t+t0)+phi*DEG2RAD)
x = normal(0,bruit,N)
y = normal(0,bruit,N)
moy_x += x.mean()
p = np.mean((e+x)*(s+y))
list_prod.append(p)
moy += p
list_prod = np.array(list_prod)
moy/= Nt
moy_x /= Nt
ecart = moy-0.5
figure(figsize=(12,6))
plot(list_prod-0.5)
grid()
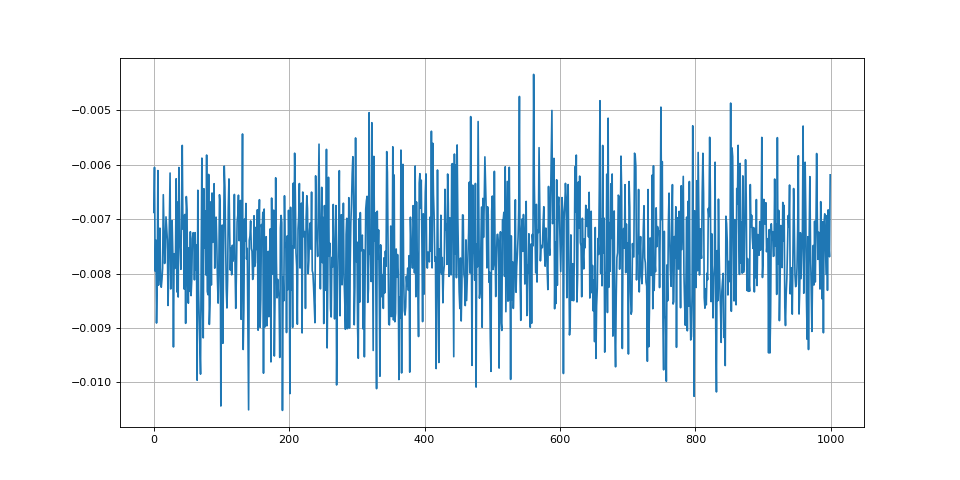 fig18.pdf
fig18.pdf
print(ecart) --> -0.007584493981533047
print(moy_x) --> -1.013117420984373e-05
fechant = 100
N = 10000 # 100 cycles
bruit = 0.1
moy = 0
moy_x = 0
list_prod = []
phi = 50
Nt = 1000 # nombre de réalisations
for i in range(Nt):
t0 = uniform(0,1,1)
t = np.arange(N)*1/fechant
e = np.sin(2*np.pi*(t+t0))
s = np.sin(2*np.pi*(t+t0)+phi*DEG2RAD)
x = normal(0,bruit,N)
y = normal(0,bruit,N)
moy_x += x.mean()
p = np.mean((e+x)*(s+y))
list_prod.append(p)
moy += p
list_prod = np.array(list_prod)
moy/= Nt
moy_x /= Nt
ecart = moy-0.5
figure(figsize=(12,6))
plot(list_prod-0.5)
grid()
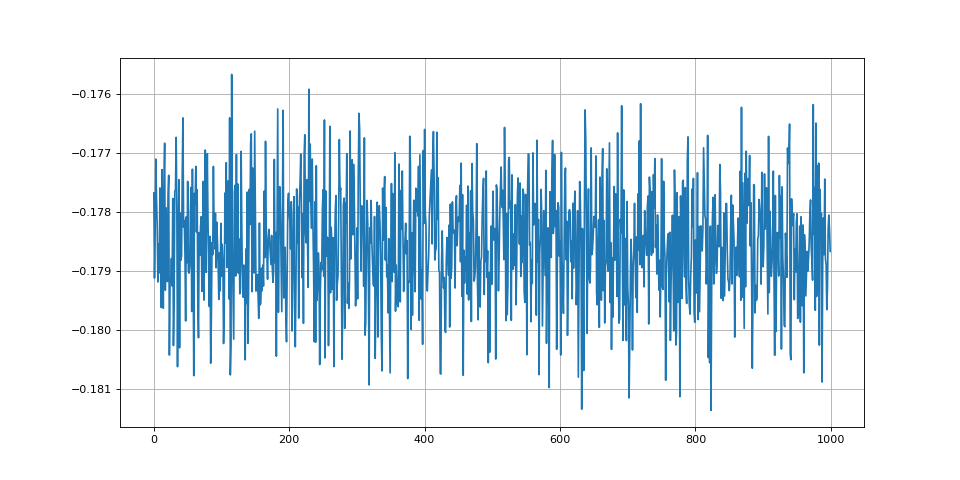 fig19.pdf
fig19.pdf
print(ecart) --> -0.1785598588930179
print(moy_x) --> -1.2056900051869646e-05
Ces deux simulations, réalisées pour deux déphasages différents, montrent que l'espérance de diffère notablement de 1/2 et que l'écart dépend du déphasage (l'écart observé est très grand devant l'évaluation de l'espérance de l'intégrale de x).
Considérons le dénominateur :
Faisons une simulation de Monte-carlo de ce terme dans le cas où les amplitudes de e et s valent 1 (la moyenne du produit vaut 1/2).
def produitEfficace(u1,u2):
U1_eff = np.sqrt(np.mean(u1*u1))
U2_eff = np.sqrt(np.mean(u2*u2))
return U1_eff*U2_eff
fechant = 100
N = 10000 # 100 cycles
bruit = 0.1
phi = 10
moy = 0
list_prod_eff = []
Nt = 1000
for i in range(Nt):
t,u1,u2 = signaux(phi,fechant,N,bruit)
p = produitEfficace(u1,u2)
list_prod_eff.append(p)
moy += p
list_prod_eff = np.array(list_prod_eff)
moy/= Nt
ecart = moy-0.5
figure(figsize=(12,6))
plot(list_prod_eff-0.5)
grid()
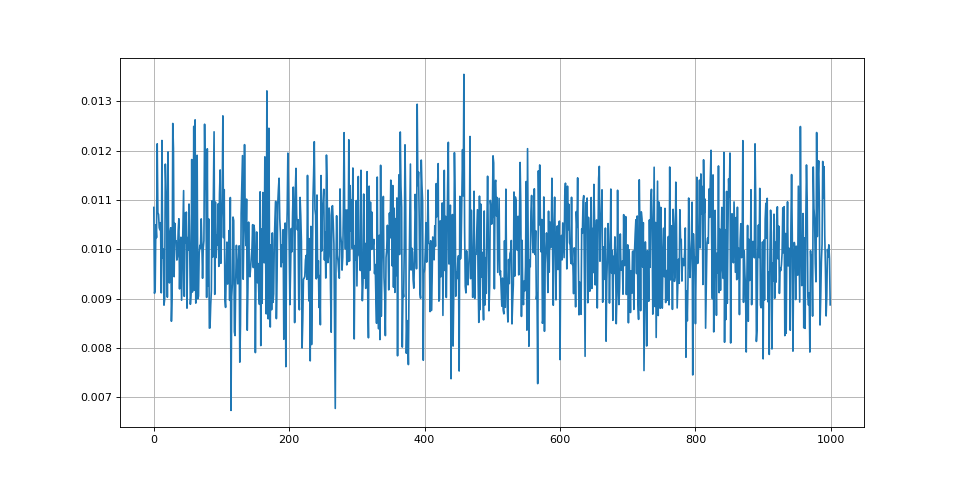 fig20.pdf
fig20.pdf
print(ecart) --> 0.01000263897846465
Cette simulation confirme que l'espérance de est légèrement différente de 1/2. D'autres calculs montrent que l'écart augmentent avec l'écart-type du bruit mais qu'il ne dépend pas du déphasage.
Faisons enfin une simulation de Monte du cosinus :
fechant = 100
N = 10000 # 100 cycles
bruit = 0.1
moy_cos = 0
list_cos = []
phi = 1
Nt = 1000 # nombre de réalisations
for i in range(Nt):
t0 = uniform(0,1,1)
t = np.arange(N)*1/fechant
e = np.sin(2*np.pi*(t+t0))
s = np.sin(2*np.pi*(t+t0)+phi*DEG2RAD)
x = normal(0,bruit,N)
y = normal(0,bruit,N)
cos = np.mean((e+x)*(s+y))/np.sqrt(np.mean((e+x)*(e+x))*np.mean((s+y)*(s+y)))
list_cos.append(cos)
moy_cos += cos
list_cos = np.array(list_cos)
moy_cos/= Nt
ecart = moy_cos-np.cos(phi*DEG2RAD)
figure(figsize=(12,6))
plot(list_cos-np.cos(phi*DEG2RAD))
grid()
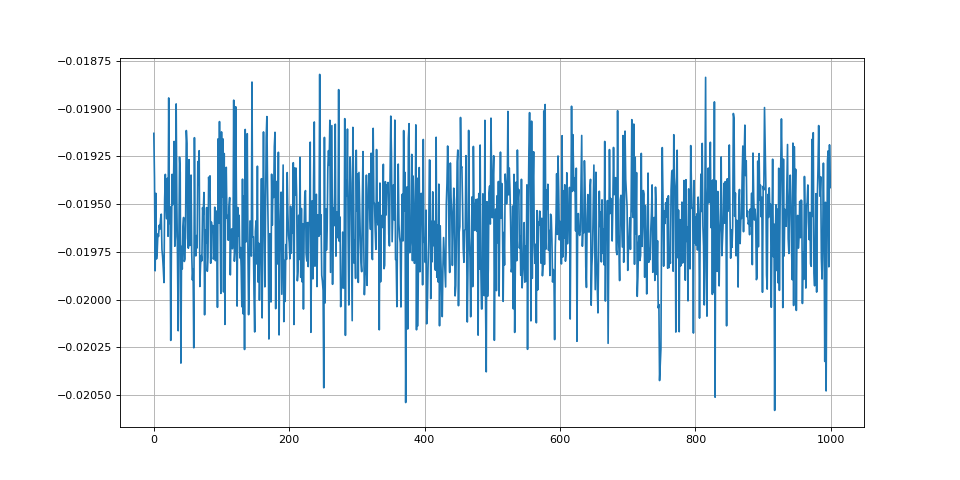 fig21.pdf
fig21.pdf
print(ecart) --> -0.019605667088419376
fechant = 100
N = 10000 # 100 cycles
bruit = 0.1
moy_cos = 0
list_cos = []
phi = 10
Nt = 1000 # nombre de réalisations
for i in range(Nt):
t0 = uniform(0,1,1)
t = np.arange(N)*1/fechant
e = np.sin(2*np.pi*(t+t0))
s = np.sin(2*np.pi*(t+t0)+phi*DEG2RAD)
x = normal(0,bruit,N)
y = normal(0,bruit,N)
cos = np.mean((e+x)*(s+y))/np.sqrt(np.mean((e+x)*(e+x))*np.mean((s+y)*(s+y)))
list_cos.append(cos)
moy_cos += cos
list_cos = np.array(list_cos)
moy_cos/= Nt
ecart = moy_cos-np.cos(phi*DEG2RAD)
figure(figsize=(12,6))
plot(list_cos-np.cos(phi*DEG2RAD))
grid()
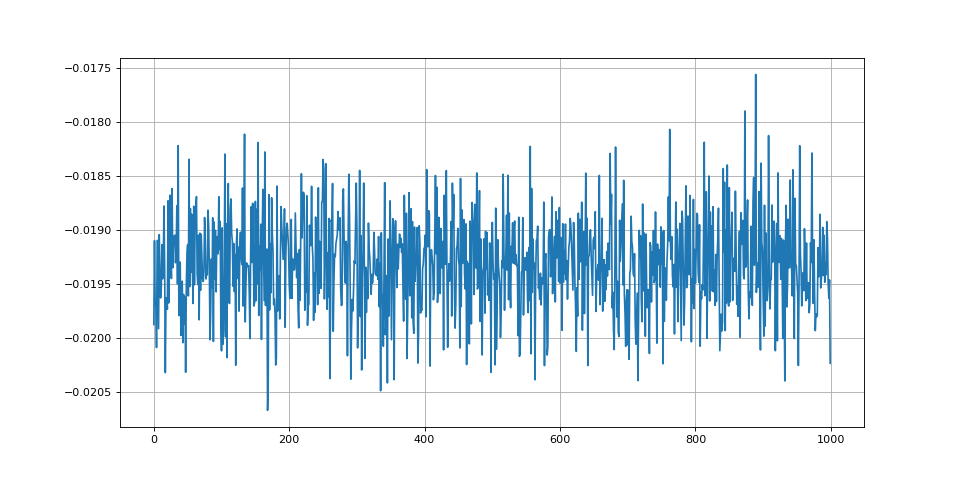 fig22.pdf
fig22.pdf
print(ecart) --> -0.019324661513326458
fechant = 100
N = 10000 # 100 cycles
bruit = 0.1
moy_cos = 0.1
list_cos = []
phi = 50
Nt = 1000 # nombre de réalisations
for i in range(Nt):
t0 = uniform(0,1,1)
t = np.arange(N)*1/fechant
e = np.sin(2*np.pi*(t+t0))
s = np.sin(2*np.pi*(t+t0)+phi*DEG2RAD)
x = normal(0,bruit,N)
y = normal(0,bruit,N)
cos = np.mean((e+x)*(s+y))/np.sqrt(np.mean((e+x)*(e+x))*np.mean((s+y)*(s+y)))
list_cos.append(cos)
moy_cos += cos
list_cos = np.array(list_cos)
moy_cos/= Nt
ecart = moy_cos-np.cos(phi*DEG2RAD)
figure(figsize=(12,6))
plot(list_cos-np.cos(phi*DEG2RAD))
grid()
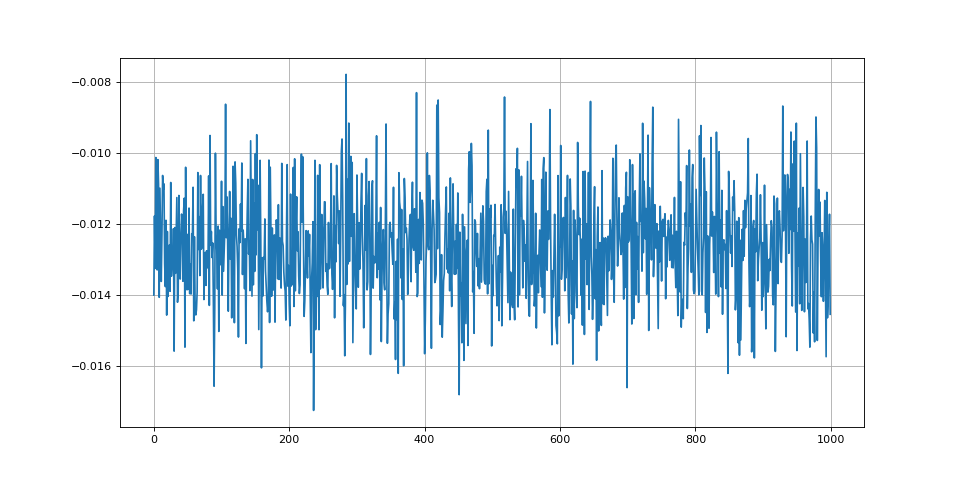 fig23.pdf
fig23.pdf
print(ecart) --> -0.012523688666517874
Ces simulations montrent un écart significatif dû à la présence du bruit. Notons qu'en absence de bruit on obtient un écart de l'ordre de 10-14 à cause des erreurs d'arrondi. L'écart dépend du déphasage : il augmente lorsque le déphasage diminue (en partant de 90 degré). Dans ces simulations, nous avons volontairement choisi un bruit très intense pour bien montrer l'effet. Lorsque le bruit est très faible, le décalage peut devenir négligeable devant l'écart-type. Remarquons aussi que lorsque le déphasage est petit, une petite variation du cosinus engendre une variation relativement grande de l'angle.