Arduino GIGA R1 : filtrage numérique
1. Introduction
Ce document montre comment réaliser un filtrage numérique avec une Arduino GIGA R1. Le processeur Arm Cortex M7 (cadencé à 480 MHz) comporte une FPU (floating point unit) double précision. Le microcontrôleur STM32H747XI comporte trois convertisseurs analogique/numérique de fréquence d'échantillonnage maximale 3,6 MHz et un convertisseur numérique/analogique de fréquence d'échantillonnage maximale 1,0 MHz. Ces caractéristiques permettent de réaliser un filtrage numérique avec calcul en virgules flottantes (beaucoup plus simple à implémenter que le calcul en virgule fixe) pour des fréquences d'échantillonnage du domaine audio (40 kHz) et au delà.
Nous réalisons un filtrage numérique avec conversion numérique/analogique du signal obtenu mais cette conversion n'est pas toujours nécessaire : dans certaines applications, le résultat du filtrage est simplement analysé pour extraire des informations utiles sur le signal.
2. Circuit d'interface
Le microcontrôleur STM32H747XI comporte deux convertisseurs analogique/numérique (ADC1 et ADC2). La tension appliquée à une entrée analogique (par exemple l'entrée A0) doit être comprise entre 0 et 3,3 V. Nous utiliserons l'ADC en mode 12 bits (car c'est la résolution du convertisseur numérique/analogique). Les nombres obtenus sont donc compris entre 0 et 4096. Si l'on souhaite filtrer un signal à valeurs positives et inférieures à 3,3 V, aucun circuit d'interface n'est nécessaire. Pour filtrer un signal alternatif, par exemple un signal audio, le circuit d'interface suivant est nécessaire :
Figure pleine pageCe circuit permet de convertir deux voies. La tension d'entrée Ve (IN0) est traitée par un circuit de type inverseur dont la tension de l'entrée non-inverseuse est ajustée par le potentiomètre. La tension de sortie (A0) s'écrit :
avec :
Les ALI sont de type rail-to-rail, c'est-à-dire que la tension en sortie doit s'étendre sur la plage définie par l'alimentation, ici la plage de 0 à 3,3 volts. L'alimentation est fournie par la carte Arduino. Si le signal est alternatif, on choisit le gain G en fonction de son amplitude maximale. Les valeurs de résistances indiquées sur le schéma correspondent à G=1. Dans ce cas, la plage de tension en entrée est [-1.65,1.65] V et le potentiomètre doit être réglé afin d'avoir (G+1)V+=1,65 V. En pratique, on utilise un voltmètre pour lire la tension de la sortie AREF (qui est une sortie par défaut), qui donne la tension de référence de l'ADC. L'entrée IN0 étant à la masse, on ajuste le potentiomètre pour que la tension en sortie soit égale à la valeur donnée par AREF divisée par deux (ce qui donnera un nombre égal à 2048).
D'autres réglages sont possibles selon la plage de tensions à traiter. Par exemple, on peut traiter un signal dont l'amplitude s'étend de -10 V à 10V avec une gain G bien choisi. Dans tous les cas, ce circuit protège parfaitement les entrées A0 et A1 de la carte Arduino car la tension en sortie d'un ALI ne peut sortir de la plage définie par l'alimentation.
Le microcontrôleur possède deux convertisseurs numérique/analogique (DAC0 et DAC1), disponibles sur les bornes A12 et A13. La tension en sortie est comprise entre 0 et 3,3 volts. Si une tension nulle en entrée donne une valeur de 2048, alors cette valeur en sortie correspond à une tension nulle.
Remarquons que l'Arduino GIGA R1 possède une prise audio jack à trois bornes (DAC0, DAC1 et A7). Cependant, cette prise a peu d'intérêt car les signaux audio doivent être alternatifs.
Le circuit précédent a l'avantage de pouvoir être alimenté directement par l'alimentation 3,3 volts de l'Arduino. Il a cependant un inconvénient : si l'on souhaite modifier le gain en changeant la résistance R2, il faut refaire le réglage du potentiomètre afin de maintenir une tension de référence de 1,65 V en sortie. Le montage suivant effectue séparément l'amplification et l'ajout du décalage de tension :
Figure pleine pageLe premier étage est un amplificateur inverseur dont le gain G est modifiable par commutation de différentes résistances. L'ALI doit être alimenté de manière symétrique car sa sortie est alternative. Le second étage est un inverseur qui ajoute un décalage. L'ALI de cet étage est alimenté par l'alimentation 3,3 V de l'Arduino, ce qui permet de garantir que la tension en sortie reste dans la plage permise par l'Arduino. La tension en sortie s'écrit :
où V+ est la tension appliquée par le potentiomètre sur l'entrée non-inverseuse.
Par exemple, la résistance R2=1,5 kΩ donne un gain G=0,15, ce qui permet de numériser un signal dont l'amplitude de crête à crête est de 22 V. Pour la résistance R5=270 kΩ, l'amplitude de crête à crête maximale est 122 mV. Remarquons que l'ALI du premier étage peut aussi être alimenté en +/- 5 V puisque l'amplitude de crête à sa sortie n'excède par 1,65 V.
3. Filtre à une voie
3.a. Conception du filtre
Dans cette partie, nous réalisons un filtre dont les coefficients sont codés en dur dans le programme arduino. Les méthodes de conception et de réalisation des filtres numériques sont exposés dans Conception et mise en œuvre des filtres numériques. On rappelle ici la formule de récurrence générale d'un filtre linéaire :
Le script Python suivant permet de calculer les coefficients d'un filtre RIF (réponse impulsionnelle infinie) par la méthode du fenêtrage et ceux d'un filtre RII (réponse impulsionnelle finie). Il trace la réponse fréquentielle de ces filtres, c'est-à-dire le gain en décibel et le déphasage en fonction du rapport de la fréquence sur la fréquence d'échantillonnage.
import numpy as np
import scipy.signal
from matplotlib.pyplot import *
def defCoeff(nom,x):
N = len(x)
s = "float %s[%d] = {"%(nom,N)
for i in range(N-1):
s += "%g,"%x[i]
s += "%g};"%x[N-1]
return s
P=40
b = scipy.signal.firwin(numtaps=2*P+1,cutoff=[0.02],window='hann',fs=1)
print(defCoeff('b',b))
w,h=scipy.signal.freqz(b)
figure()
subplot(211)
plot(w/(2*np.pi),20*np.log10(np.absolute(h)))
xlabel("f/fe")
ylabel("GdB")
grid()
subplot(212)
plot(w/(2*np.pi),np.unwrap(np.angle(h)))
xlabel("f/fe")
ylabel("phase")
grid()
b,a = scipy.signal.iirfilter(N=2,Wn=[0.1*2],btype="lowpass",ftype="butter")
print(defCoeff('b',b))
print(defCoeff('a',a))
w,h=scipy.signal.freqz(b,a)
figure()
subplot(211)
plot(w/(2*np.pi),20*np.log10(np.absolute(h)))
xlabel("f/fe")
ylabel("GdB")
grid()
subplot(212)
plot(w/(2*np.pi),np.unwrap(np.angle(h)))
xlabel("f/fe")
ylabel("phase")
grid()
show()
Voici les définitions des coefficients affichés pour le second filtre, en langage C :
float b[3] = {0.0674553,0.134911,0.0674553};
float a[3] = {1,-1.14298,0.412802};
Il suffira de copier ces deux lignes et de les coller dans le code arduino. Ce filtre comporte 3 coefficients bn et trois coefficients an. Pour le filtre RIF, on écrira float a[1] = {1};. Une valeur de a0 différente de 1 permet de modifier le gain dans la bande passante (celui-ci est égal à 1/a0).
3.b. Programme Arduino
La bibliothèque Arduino_AdvancedAnalog permet de faire fonctionner les ADC et les DAC avec une fréquence d'échantillonnage précise.
Les nombres entiers délivrés par un ADC sont disponibles dans un tampon de taille BUFSIZE. En conséquence, nous effectuerons le filtrage par bloc de BUFSIZE échantillons. Cela aura pour conséquence d'introduire un retard égal à BUFSIZE multiplié par la période d'échantillonnage, en plus du retard théorique du filtre. Pour l'implémentation du filtrage, nous utilisons la forme directe de type II (voir Conception et mise en œuvre des filtres numériques). Cette méthode consiste à faire appel à un tampon wn dont la taille est le maximum des tailles de an et ab. Les deux formules de récurrence sont :
Initialement, tous les wn sont nuls. Ce tampon sera implémenté sous la forme d'un tampon circulaire : le dernier élément, c'est-à-dire wn dans la relation ci-dessus se trouve à l'indice iw et cet indice est incrémenté d'une unité lorsque n est incrémenté de 1, avec un retour à zéro lorsqu'on atteint la taille du tampon (WSIZE).
La définition et l'initialisation d'un ADC se font par les deux lignes suivantes :
AdvancedADC adc1(A0); // entrée A0
adc1.begin(AN_RESOLUTION_12, sample_rate, BUFSIZE, NBUF) // configure et démarre l'ADC
La fréquence d'échantillonnage est définie en Hz. BUFSIZE est la taille d'un tampon et NBUF et le nombre de tampons consécutifs qui sont maintenus en mémoire. La fonction AdvancedADC.available() renvoie true lorsqu'un nouveau tampon est disponible. Le tampon est obtenu en créant un objet de la classe SampleBuffer (définie dans packages\arduino\hardware\mbed_giga\4.1.5\cores\arduino\api\DMAPool.h) :
SampleBuffer buf1 = adc1.read();
Le tampon est mémorisé sous la forme d'un tableau d'entiers 16 bits, dont on obtient le pointeur par :
uint16_t *buf1_data = buf1.data();
Lorsque le traitement des données du tampon est terminé, il faut libérer le tampon avec :
buf1.release();
Si on ne le fait pas, le tampon suivant de la liste des NBUF tampons est utilisé. Lorsque tout les tampons de cette liste sont pleins et si aucun n'est libéré, l'écriture des résultats de la conversion dans les tampons cesse. Dans le cas présent, il s'agit de faire un traitement en temps réel donc le tampon doit être libéré après usage.
Pour configurer le DAC, on procède de manière similaire :
AdvancedDAC dac0(A12); // DAC0
dac0.begin(AN_RESOLUTION_12, sample_rate, BUFSIZE, NBUF) // configure et démarre le DAC
Dans ce cas, l'instance de AdvancedDAC possède son propre jeu de tampons. La fonction AdvancedDAC.available() renvoie true lorsqu'il est possible d'écrire dans un tampon. Pour cela, on commence par récupérer un pointeur sur le tableau correspondant :
SampleBuffer buf = dac0.dequeue();
uint16_t *buf_data = buf.data();
Le tableau sera rempli avec les échantillons du signal filtré. Une fois le tampon rempli, il faut demander l'écrire de son contenu :
dac0.write(buf);
Les nombres mémorisés dans buf1_data sont en fait des entiers 12 bits (de 0 à 4096). Les valeurs que nous filtrons sont les tensions. Pour convertir les nombres en tensions, nous utilisons les deux constantes suivantes :
float offset = 2048;
float num2volt = 3.217/4096;
La tension 3.217 est mesurée sur la sortie AREF. Après filtrage, on effectue la conversion inverse de manière à obtenir des nombres entiers dans l'intervalle [0,4096]. Il faut que le filtre n'introduise pas de dépassement de l'intervalle de tensions adopté, ici -1,65 V à +1,65 V.
Voici le programme :
#include <Arduino_AdvancedAnalog.h>
#define BUFSIZE 8
#define NBUF 4
uint32_t sample_rate = 50000;
AdvancedADC adc1(A0);
AdvancedDAC dac0(A12);
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
#define FILTRE1 // choix du filtre
#ifdef FILTRE1 // filtre passe-bas RIF
#define BSIZE 81
#define ASIZE 1
#define WSIZE 81 // taille maximale de a et b
float b[81] = {-0,-1.24539e-05,-5.18658e-05,-0.000119544,-0.000214208,-0.000331776,-0.000465257,-0.000604758,-0.000737616,-0.000848639,-0.000920476,-0.000934082,-0.000869292,-0.000705464,-0.000422181,4.85048e-19,0.000578799,0.00132947,0.0022641,0.00339099,0.00471405,0.00623245,0.00794025,0.00982625,0.011874,0.0140619,0.0163636,0.0187483,0.0211816,0.023626,0.0260419,0.0283884,0.0306245,0.0327099,0.0346059,0.0362771,0.0376912,0.0388211,0.0396444,0.040145,0.040313,0.040145,0.0396444,0.0388211,0.0376912,0.0362771,0.0346059,0.0327099,0.0306245,0.0283884,0.0260419,0.023626,0.0211816,0.0187483,0.0163636,0.0140619,0.011874,0.00982625,0.00794025,0.00623245,0.00471405,0.00339099,0.0022641,0.00132947,0.000578799,4.85048e-19,-0.000422181,-0.000705464,-0.000869292,-0.000934082,-0.000920476,-0.000848639,-0.000737616,-0.000604758,-0.000465257,-0.000331776,-0.000214208,-0.000119544,-5.18658e-05,-1.24539e-05,-0};
float a[1] = {1};
#endif
#ifdef FILTRE2 // filtre passe-bas RII
#define BSIZE 3
#define ASIZE 3
#define WSIZE 3 // taille maximale de a et b
float b[3] = {0.0674553,0.134911,0.0674553};
float a[3] = {1,-1.14298,0.412802};
#endif
float w[WSIZE]; // tampon circulaire pour le filtrage
uint16_t iw; // indice de wn dans le tampon
void setup() {
pinMode(13,OUTPUT);
Serial.begin(115200);
for (int i=0; i<WSIZE; i++) w[i] = 0.0f;
iw = 0;
if (!adc1.begin(AN_RESOLUTION_12, sample_rate, BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de ADC1");
while (1);
}
if (!dac0.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC0");
while (1);
}
}
void loop() {
if (adc1.available()) {
SampleBuffer buf1 = adc1.read();
uint16_t *buf1_data = buf1.data();
int16_t jw;
float y;
if (dac0.available()) {
GPIOH->BSRR |= GPIO_BSRR_BS6; //digitalWrite(13,HIGH);
SampleBuffer buf_dac0 = dac0.dequeue();
uint16_t *buf_dac0_data = buf_dac0.data();
for (int i=0; i<buf1.size(); i++) {
w[iw] = 1.0/a[0]*(buf1_data[i]-offset)*num2volt;
jw = iw-1;
if (jw==-1) jw=WSIZE-1;
for (uint16_t k=1; k<ASIZE; k++) {
w[iw] -= a[k]*w[jw];
jw = iw-1;
if (jw==-1) jw=WSIZE-1;
}
jw = iw;
y = 0.0f;
for (uint16_t k=0; k<BSIZE; k++) {
y += b[k]*w[jw];
jw--;
if (jw==-1) jw=WSIZE-1;
}
iw++;
if (iw==WSIZE) iw=0;
buf_dac0_data[i] = y/num2volt+offset;
}
dac0.write(buf_dac0);
GPIOH->BSRR |= GPIO_BSRR_BR6; //digitalWrite(13,LOW);
}
buf1.release();
}
}
Afin de mesurer avec un oscilloscope le temps d'exécution du traitement d'un tampon, c'est-à-dire du filtrage de ses éléments, nous mettons la sortie D13 au niveau haut au début et la remettons au niveau bas à la fin.
3.c. Test du filtrage
Voici un test du filtre RIF à 81 coefficients. La fréquence d'échantillonnage est 50 kHz, donc sa fréquence de coupure est 1 kHz (rapport 0,02). Il ne faut pas oublier que si l'on veut changer la fréquence d'échantillonnage sans changer la fréquence de coupure du filtre, il faut recalculer ses coefficients. L'oscilloscope permet d'observer simultanément le signal envoyé sur IN0 (entrée du circuit de conversion) et le signal en sortie de DAC0 (sans circuit de conversion). Voici le résultat à 1000 Hz (la fréquence de coupure) :
import numpy as np
from matplotlib.pyplot import *
[t,u1,u2] = np.loadtxt("filtreRIF81-fe50kHz-1kHz.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="IN0")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
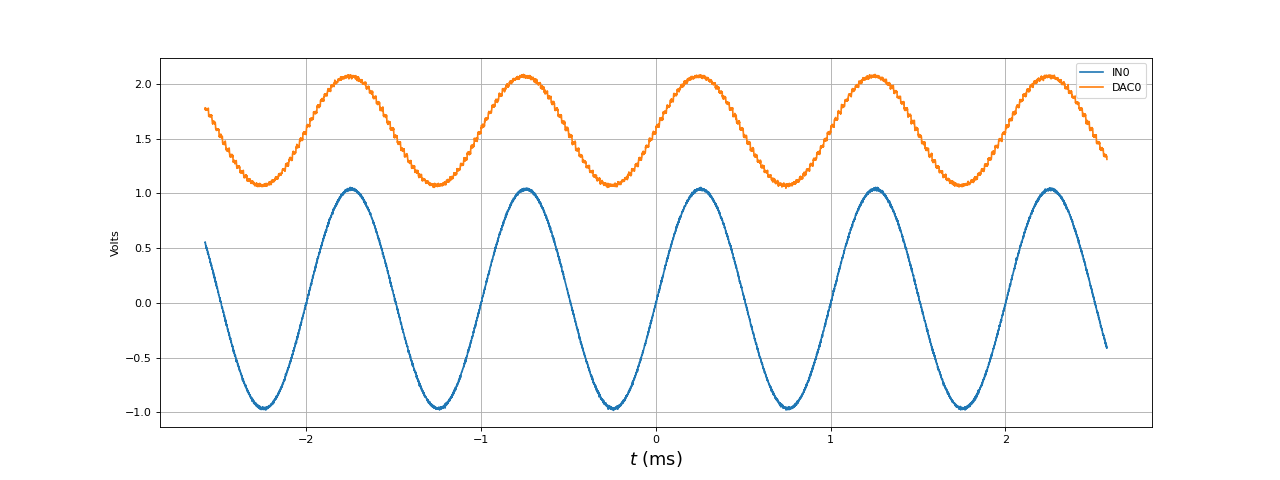 fig1.pdf
fig1.pdf
Voici le résultat à 100 Hz (dans la bande passante) :
[t,u1,u2] = np.loadtxt("filtreRIF81-fe50kHz-100Hz.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="IN0")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
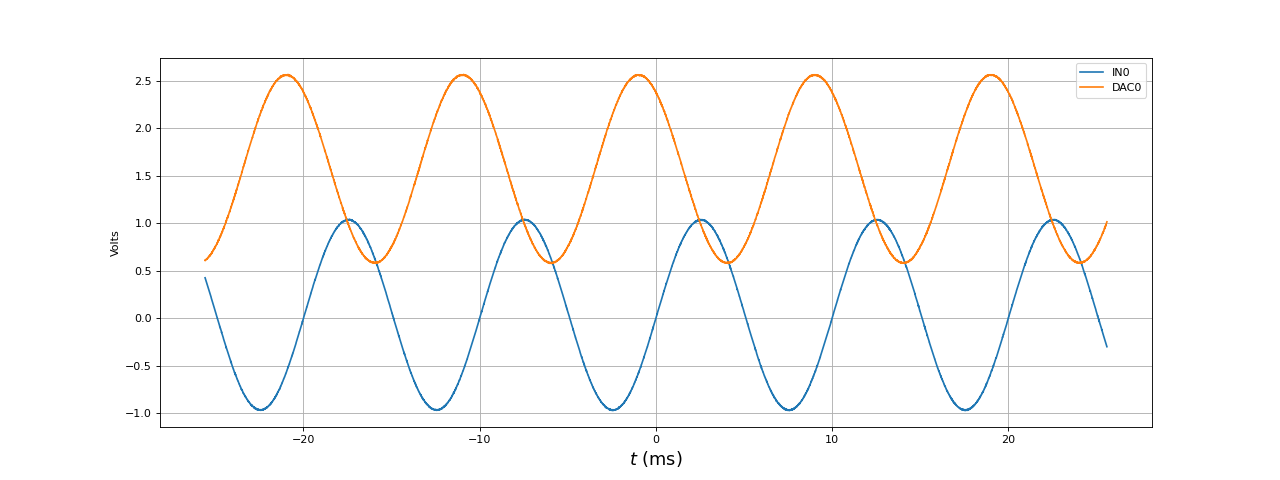 fig2.pdf
fig2.pdf
À 1000 Hz, retard entre DAC0 et IN0 semble nul mais il s'agit d'une simple coïncidence. Le retard effectif est la somme du retard intrinsèque du filtre (ici 40 fois la période d'échantillonnage), du retard dû à la taille du tampon (8 fois la période d'échantillonnage puisque le tampon comporte 8 échantillons) et du déphasage de 180 degrés dû à l'amplificateur inverseur du circuit d'interface (soit un retard égal à la moitié de la période du signal).
Voici le résultat à 2 kHz :
[t,u1,u2] = np.loadtxt("filtreRIF81-fe50kHz-2kHz.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="IN0")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
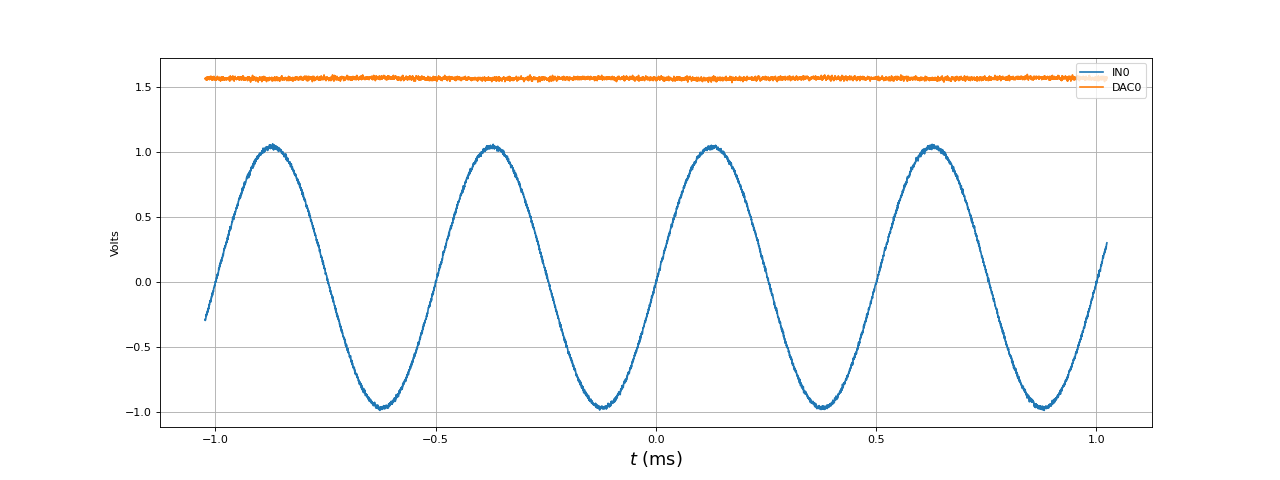 fig3.pdf
fig3.pdf
Voici le signal sur la sortie D13 (avec DAC0), à la fréquence de 1000 Hz :
[t,u1,u2] = np.loadtxt("filtreRIF81-fe50kHz-1kHz-D13.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="D13")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
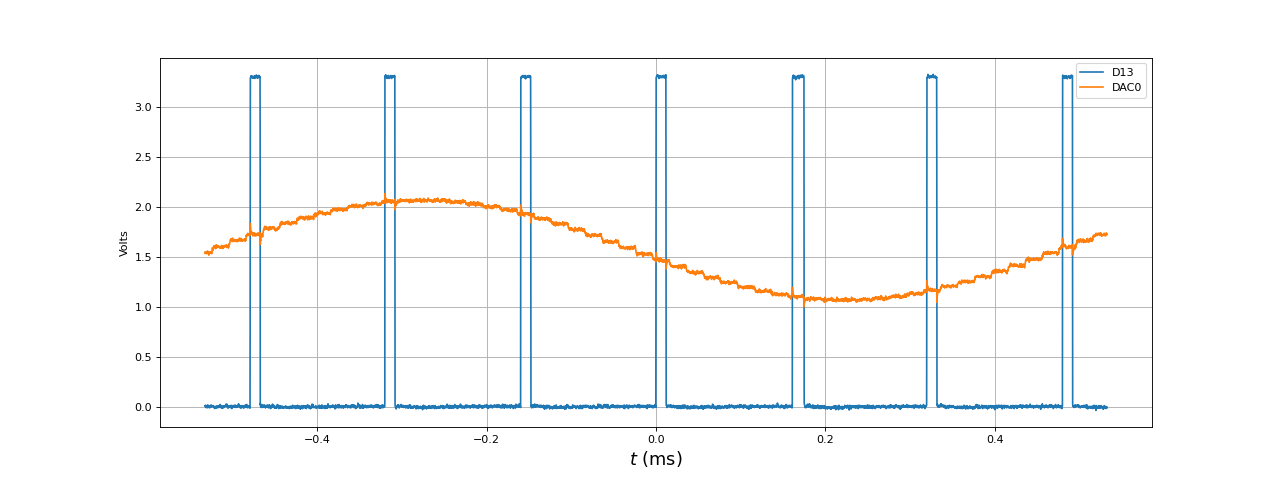 fig4.pdf
fig4.pdf
Le temps du traitement des 8 échantillons du tampon pour ce filtre RIF est de 11 microsecondes. C'est beaucoup moins que la durée de numérisation des 8 échantillons (160 microsecondes). On peut donc largement augmenter le nombre de coefficients mais il faut prévoir une marge de sécurité car la durée entre deux traitements n'est pas tout à fait constante. Un filtre RIF à 800 coefficients devrait être réalisable, car son temps d'exécution devrait logiquement être de 110 microsecondes. Si l'on augmente la fréquence d'échantillonnage d'un facteur 2, la durée entre deux traitements est divisée par deux. Voici le résultat pour une fréquence d'échantillonnage de 300 kHz (la fréquence de coupure est alors 6 kHz donc le signal à 1 kHz est dans la bande passante) :
[t,u1,u2] = np.loadtxt("filtreRIF81-fe300kHz-1kHz-D13.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="D13")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
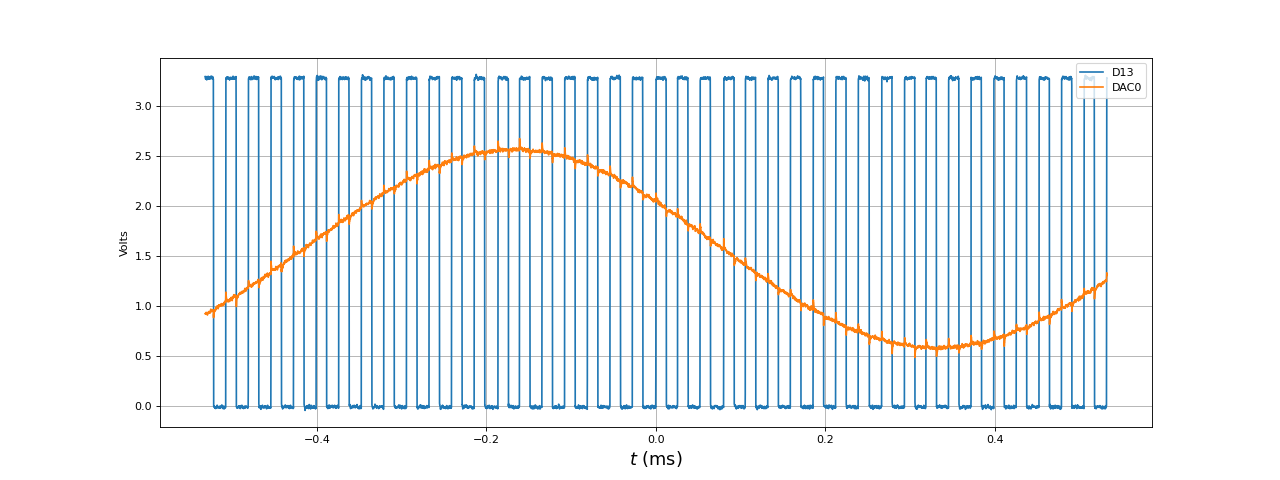 fig5.pdf
fig5.pdf
À une fréquence d'échantillonnage de 400 kHz, le filtre fonctionne encore mais le temps de latence entre deux traitements de tampon successifs peut être très faible. À 500 kHz, le filtre ne fonctionne plus.
Voici le résultat pour le filtre FIR (6 coefficients) à 500 kHz :
[t,u1,u2] = np.loadtxt("filtreFIR-fe500kHz-1kHz-D13.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="D13")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
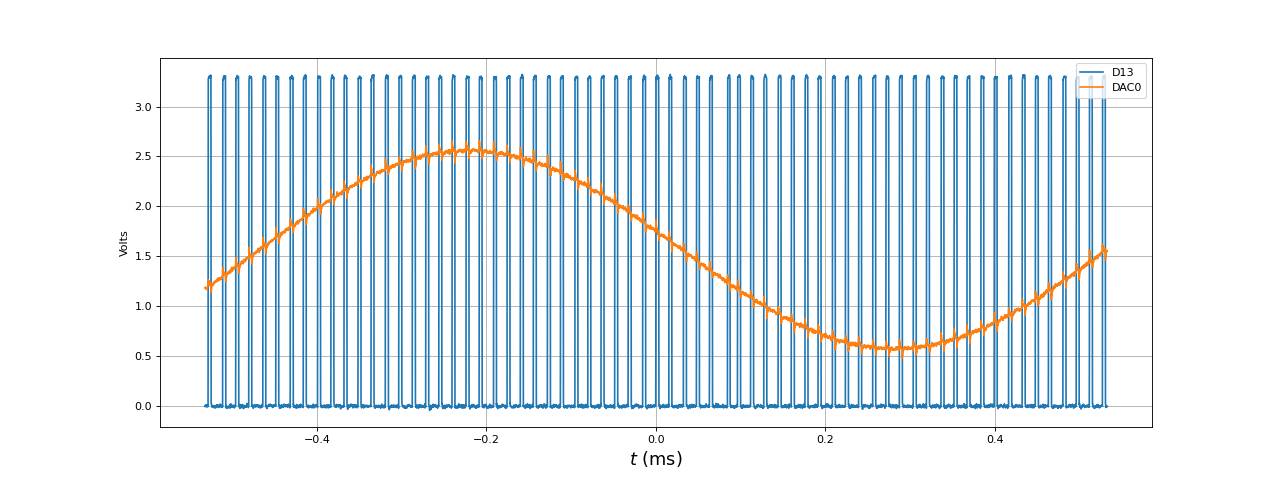 fig6.pdf
fig6.pdf
Le temps de traitement d'un tampon est évidemment beaucoup plus petit (3,5 microsecondes). Voici le résultat pour ce filtre à une fréquence d'échantillonnage de 800 kHz :
[t,u1,u2] = np.loadtxt("filtreFIR-fe800kHz-1kHz-D13.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="D13")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
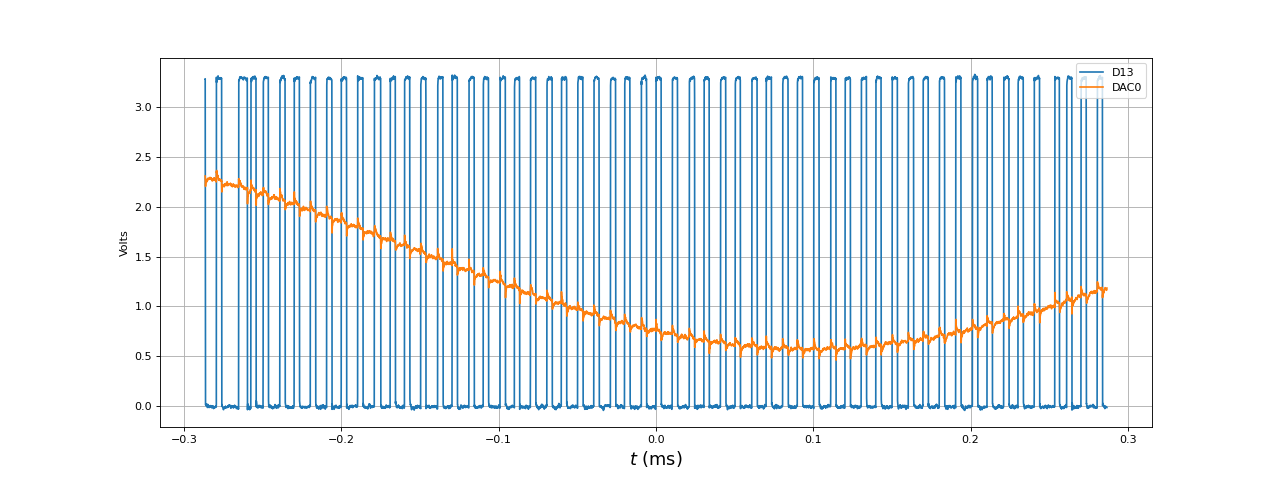 fig7.pdf
fig7.pdf
Remarque : les petits pics de tension qu'on observe sur DAC0 simultanément aux fronts sur D13 sont dûs à l'oscilloscope, pas au DAC (ils disparaissent lorsqu'on débranche D13 de l'oscilloscope).
La fréquence d'échantillonnage maximale de l'ADC est 3,6 MHz alors que celle du DAC est 1 MHz.
Conclusion : à une fréquence d'échantillonnage audio (40 kHz), un filtrage RIF comportant une centaine de coefficients fonctionne parfaitement et il reste une marge largement suffisante pour traiter une seconde voie.
Le filtre RIF ci-dessus retarde le signal (dans la bande passante) de 40 échantillons. Il faut ajouter à ce retard les 8 échantillons correspondant à la taille du tampon. L'algorithme de filtrage fonctionne quelle que soit la taille de BUFSIZE mais voici ce qu'il arrive avec BUFSIZE=4, pour le filtre RIF avec une fréquence d'échantillonnage de 50 kHz:
[t,u1,u2] = np.loadtxt("filtreRIF81-fe50kHz-1kHz-D13-BUF4.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="D13")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
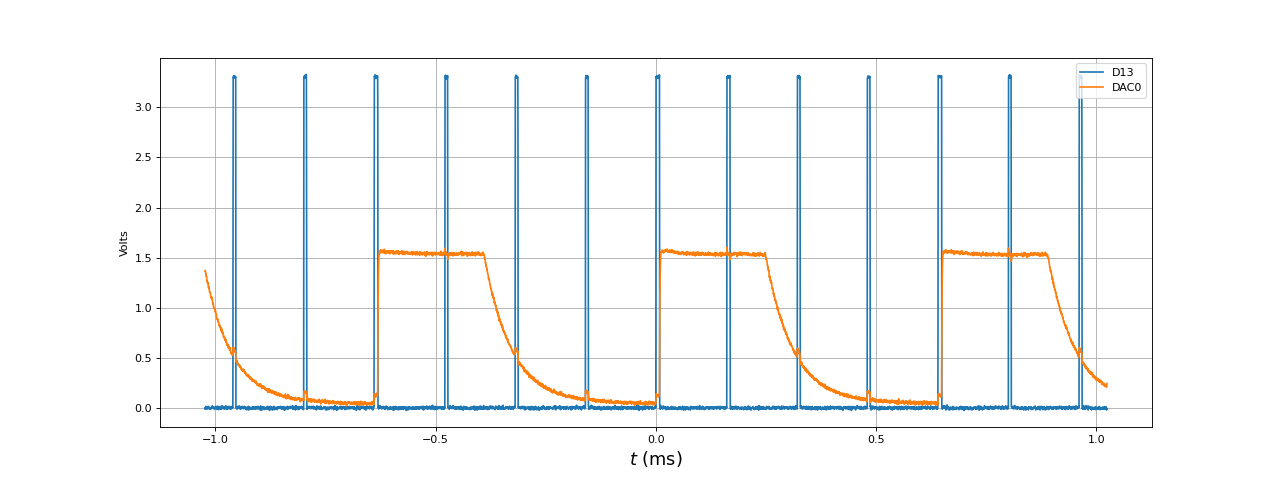 fig8.pdf
fig8.pdf
Il semble que la classe AdvancedADC ne fonctionne pas correctement lorsque le tampon a une longueur inférieure à 8 (pour une raison qui nous échappe). Cependant, le retard de 8 échantillons peut être considéré comme sans importance, surtout si on utilise un filtre RIF dont le retard intrinsèque peut être de plusieurs dizaines d'échantillons.
Afin de mesurer le retard, nous devons comparer le signal envoyé sur A0 (donc en sortie du circuit d'interface) et le signal sur DAC0. Voici les courbes à une fréquence de 100 Hz :
[t,u1,u2] = np.loadtxt("filtreRIF81-fe50kHz-100Hz-2.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="A0")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
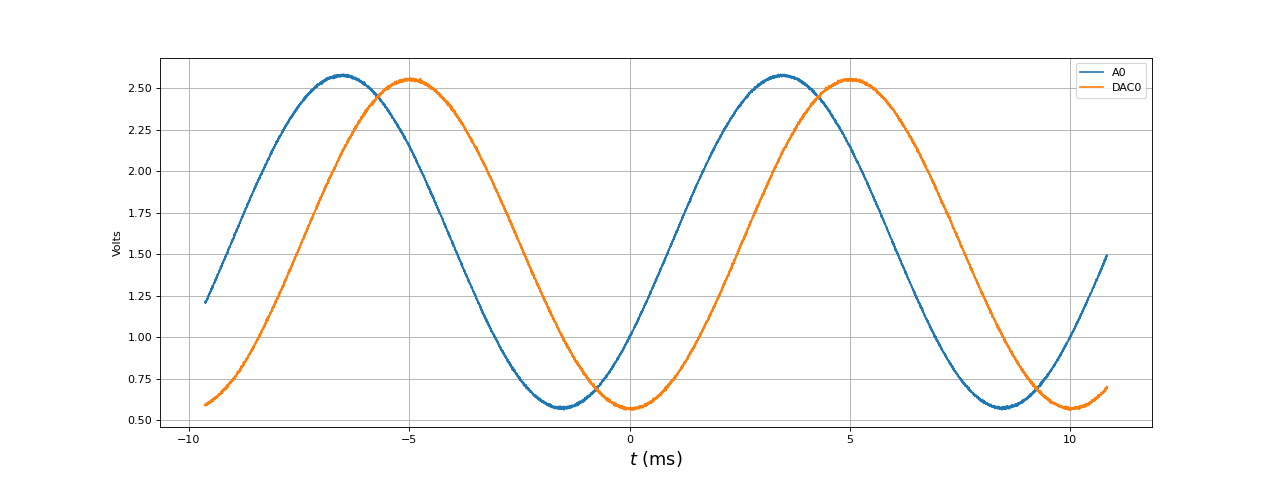 fig9.pdf
fig9.pdf
Le retard du filtre plus celui dû à la longueur du tampon (tampon de l'ADC et du DAC) est 56 fois la période d'échantillonnage, soit 1,12 ms. Or le retard observé est d'environ 1,5 ms. La différence est grande et ne peut être attribuée à la boucle de filtrage puisque son temps d'exécution est 11 microsecondes. Si nous programmons le filtre suivant :
#define BSIZE 1
#define ASIZE 1
#define WSIZE 1
float b[1] = {1.0};
float a[1] = {1.0};
Le retard mesuré est 700 microsecondes alors que le retard de 16 échantillons est de 320 microsecondes. Nous devons en conclure que les échantillons numérisés sont délivrés avec un retard d'environ 400 microsecondes (soit 20 échantillons), pour une raison qui nous échappe. Ce retard supplémentaire ne peut être dû à un temps d'exécution du code car il reste parfaitement constant (s'il ne l'était pas, on verrait des fluctuations du retard à l'oscilloscope). Si la fréquence d'échantillonnage est doublée, le retard supplémentaire est divisé par deux. Cela montre que ce retard est causé par le fonctionnement soit de l'ADC soit du DAC et cela explique qu'il est constant. Il semble que AdvancedADC et AdvancedDAC fassent appel au DMA (Direct Memory Access).
Pour finir, voici le filtrage par le filtre RIF d'un signal carré de fréquence fondamentale 100 Hz :
[t,u1,u2] = np.loadtxt("filtreRIF81-fe50kHz-1kHz-carre.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label="IN0")
plot(t*1e3,u2,label="DAC0")
legend(loc='upper right')
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts")
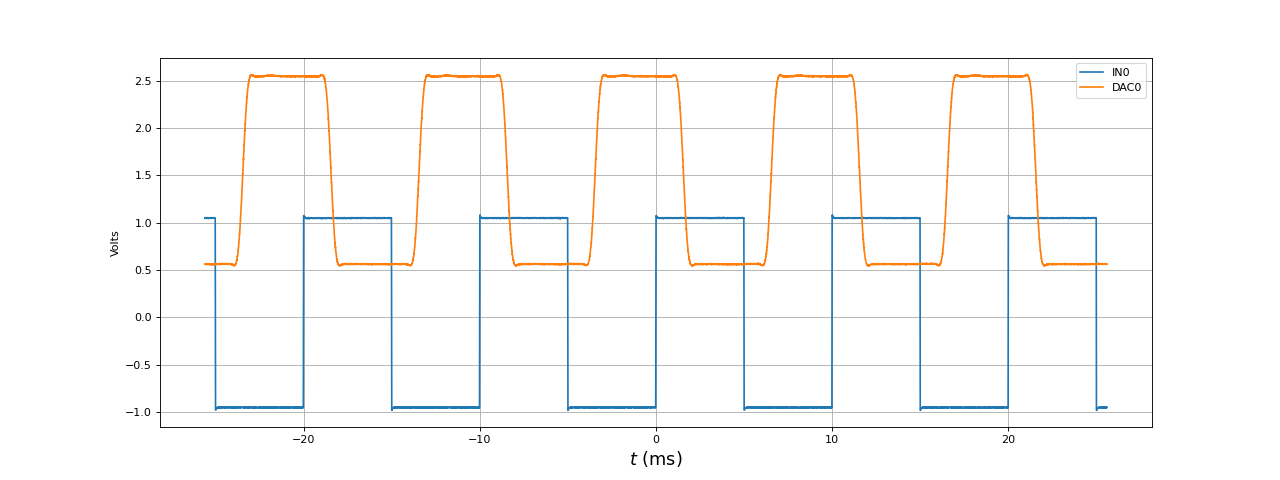 fig10.pdf
fig10.pdf