Arduino GIGA R1 : génération de signaux analogiques
1. Introduction
Ce document montre comment utiliser le convertisseur numérique/analogique (DAC) du microcontrôleur STM32H747XI pour générer des signaux. Ce DAC a une résolution de 12 bits et comporte deux sorties accessibles sur les bornes A12 et A13.
Avertissement : les sorties du DAC sont fragiles et il est donc conseillé de les utiliser avec le circuit d'interface décrit ci-dessous.
2. Circuit d'interface
Une sortie du DAC délivre une tension comprise entre 0 et 3,3 V. Si l'on souhaite obtenir une tension alternative par rapport à la masse ou si une plage de tension plus grande est nécessaire, il faut placer en sortie un circuit d'adaptation comme celui-ci :
Figure pleine pageCe circuit permet de convertir les deux voies DAC0 et DAC1. La tension d'entrée Ve (DAC0) est traitée par un circuit de type inverseur dont la tension de l'entrée non-inverseuse est ajustée par le potentiomètre. La tension de sortie (OUT0) s'écrit :
avec :
L'ALI TLV2372 est de type rail-to-rail mais cette caractéristique n'est pas indispensable pour cet usage. Les valeurs de résistances dans le circuit représenté ci-dessus donnent un gain G=1. Le potentiomètre est ajusté pour qu'une valeur convertie de 2048 conduise à 0 en sortie. La plage de tension en sortie est alors de -1,65 V à 1,65 V. Il est bien sûr possible d'obtenir une plage plus grande en augmentant le gain (il faudra alors ajuster à nouveau le potentiomètre).
Le circuit d'interface n'est pas indispensable pour une simple étude des signaux délivrés avec un oscilloscope mais sons usage est fortement conseillé pour tout application où un circuit utilise ces signaux. En effet, le circuit d'interface assure une protection du DAC, indispensable vu le prix de la carte Arduino GIGA. Notons aussi que les sorties OUT0 et OUT1 de ce circuit sont des sorties de très faible impédance mais de très faible puissance, puisque le courant délivré ne peux excéder environ 10 mA (le maximum dépendant de la charge). La conception d'un circuit de plus forte puissance dépasse le cadre de ce document. Pour envoyer le signal OUT0 sur un haut-parleur, il faudra évidemment placer un amplificateur audio. Pour les haut-parleurs de forte puissance, un ampli de classe D est conseillé.
3. Utilisation de AdvancedAnalog
3.a. Principe
La bibliothèque Arduino_AdvancedAnalog permet de faire fonctionner le DAC avec une fréquence d'échantillonnage précise. Pour utiliser les deux sorties du DAC (DAC0 et DAC1), il faut déclarer deux instances de la classe AdvancedDAC :
AdvancedDAC dac0(A12);
AdvancedDAC dac1(A13);
L'initialisation et le démarrage du DAC (pour une sortie), se fait par :
dac0.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)
La fréquence d'échantillonnage est définie en Hz. BUFSIZE est la taille d'un tampon et NBUF et le nombre de tampons qui sont maintenus en mémoire. La fonction AdvancedADC.available() renvoie true lorsque le DAC (pour la voie considérée) est disponible pour recevoir NBUF valeurs. Un tampon est un objet de la classe SampleBuffer, que l'on obtient par :
SampleBuffer buf_dac0 = dac0.dequeue();
Le pointeur sur le tableau est obtenu par :
uint16_t *buf_dac0_data = buf_dac0.data();
Une fois que ce tableau est rempli, il faut demander l'envoie de son contenu pour la conversion :
dac0.write(buf_dac0);
3.b. Signaux calculés en temps réel
La vitesse du processeur Arm Cortex M7 (cadencé à 480 MHz) et le fait qu'il possède une unité de calcul en nombres à virgule flottante double précision, permet d'envisager la génération de signaux définis par une forme mathématique, avec calcul en temps réel des valeurs des signaux. Cette méthode nécessite des temps de calcul beaucoup plus grands que l'utilisation de tables où les valeurs sont précalculées (voir plus loin) mais elle offre beaucoup plus de souplesse. Elle permet en effet de générer des signaux non périodiques, dont les propriétés peuvent être modifiées en temps réel sans interrompre le fonctionnement du DAC.
Voici un exemple de programme, qui génèrent deux signaux sinusoïdaux (dans un premier temps identiques) :
#include <Arduino_AdvancedAnalog.h>
#define BUFSIZE 8
#define NBUF 4
uint32_t sample_rate = 50000;
double sample_period;
AdvancedDAC dac0(A12);
AdvancedDAC dac1(A13);
uint32_t count;
double phi0,phi1;
double deuxpi = 2*PI;
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
float volt2num = 4096/3.217;
// définition des signaux
float f0 = 1000.0;
float f1 = 1000.0;
float signal0(float phi) {
return 0.5*sin(deuxpi*phi);
}
float signal1(float phi) {
return 0.5*sin(deuxpi*phi);
}
void setup() {
pinMode(13,OUTPUT);
count = 0;
sample_period = 1.0/sample_rate;
Serial.begin(115200);
while(!Serial);
if (!dac0.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC0");
while (1);
}
if (!dac1.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC1");
while (1);
}
}
void loop() {
if (dac0.available()&&dac1.available()) {
GPIOH->BSRR |= GPIO_BSRR_BS6; //digitalWrite(13,HIGH);
SampleBuffer buf_dac0 = dac0.dequeue();
uint16_t *buf_dac0_data = buf_dac0.data();
SampleBuffer buf_dac1 = dac1.dequeue();
uint16_t *buf_dac1_data = buf_dac1.data();
for (uint16_t i=0; i<BUFSIZE; i++) {
phi0 += f0*sample_period;
phi1 += f1*sample_period;
if (phi0 > 1) phi0 -= 1.0;
if (phi1 > 1) phi1 -= 1.0;
buf_dac0_data[i] = signal0(phi0)*volt2num + offset;
buf_dac1_data[i] = signal1(phi1)*volt2num + offset;
}
dac0.write(buf_dac0);
dac1.write(buf_dac1);
GPIOH->BSRR |= GPIO_BSRR_BR6; //digitalWrite(13,LOW);
}
}
Les deux signaux sont définis par deux fonctions qui délivrent les valeurs en volts (valeurs en sortie du circuit d'interface). Elles doivent donc être converties en nombre entier de 0 à 4096 (12 bits) lors du remplissage du tampon. La sortie D13 est placée au niveau haut au début de la boucle de remplissage des deux tampons (2 fois NBUF échantillons) puis placée au niveau bas à la fin. L'observation du signal sur D13 permettra de mesurer le temps d'exécution de cette boucle, qui doit être inférieur à NBUF fois la période d'échantillonnage.
Pour générer des signaux périodiques, on fait le calcul à partir d'une phase (phase réduite égale à la phase divisée par 2π). La phase réduite et calculée en temps réel à partir de la fréquence (qui pourra donc être modifiée). Cette phase réduite est toujours ramenée dans l'intervalle [0,1] afin d'éviter les erreurs d'arrondis qui surviendraient inévitablement pour les grandes valeurs.
Voici les signaux générés (sorties DAC0 et DAC1), numérisés avec l'Analog Discovery 2 et le logiciel Waveforms :
import numpy as np
from matplotlib.pyplot import *
[t,u1,u2] = np.loadtxt("sinus-50kHz-1000Hz.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label='DAC0')
plot(t*1e3,u2,label='DAC1')
grid()
xlabel("t (ms)",fontsize=16)
ylabel('volts')
ylim(0,3)
legend(loc='upper right')
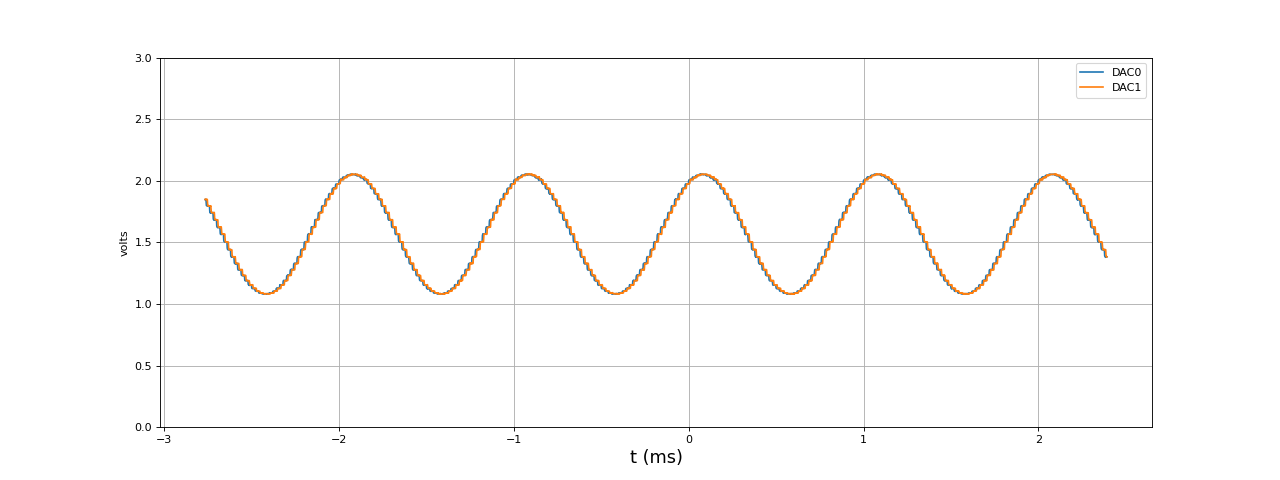 fig1.pdf
fig1.pdf
Le signal comporte 50 échantillons par cycle. Voici un détail :
figure(figsize=(16,6))
plot(t*1e3,u1,label='DAC0')
plot(t*1e3,u2,label='DAC1')
grid()
xlabel("t (ms)",fontsize=16)
ylabel('volts')
ylim(0,3)
legend(loc='upper right')
xlim(0,1)
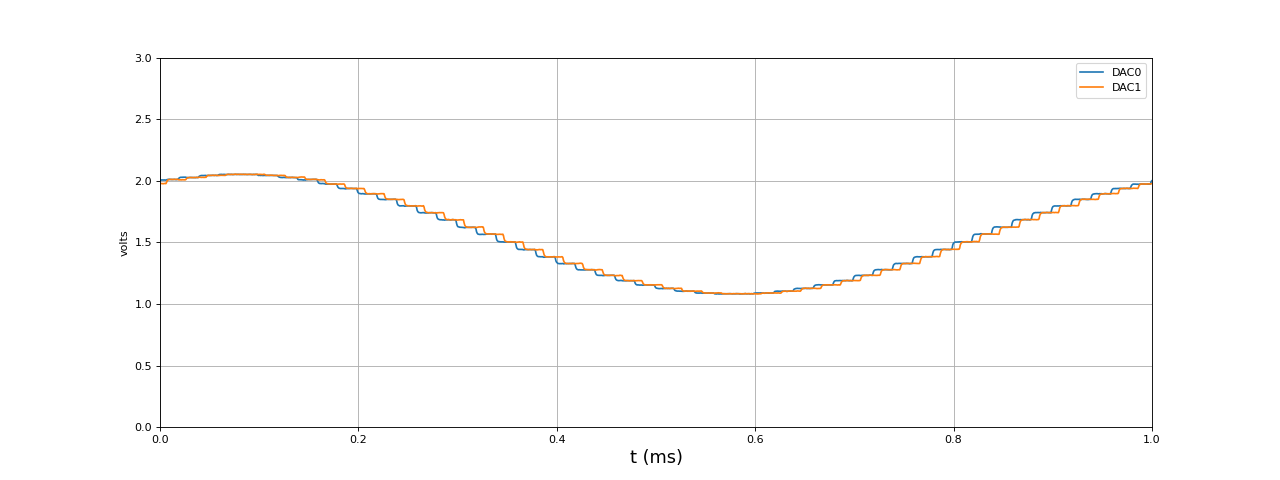 fig2.pdf
fig2.pdf
DAC1 est légèrement en retard par rapport à DAC0 : le retard est égal à 10 microsecondes, soit la moitié de la période d'échantillonnage.
Voici le signal DAC0 et le signal D13 :
import numpy as np
from matplotlib.pyplot import *
[t,u1,u2] = np.loadtxt("sinus-50kHz-1000Hz-D13.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label='DAC0')
plot(t*1e3,u2,label='D13')
grid()
xlabel("t (ms)",fontsize=16)
ylabel('volts')
ylim(0,4)
legend(loc='upper right')
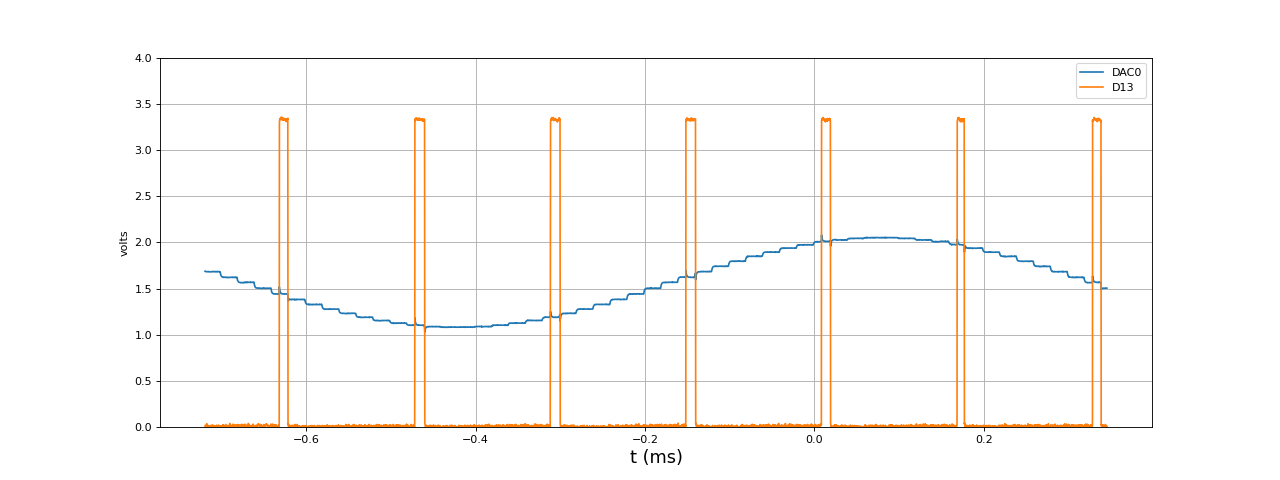 fig3.pdf
fig3.pdf
La durée d'exécution du remplissage des tampons est 11 microsecondes. Le même programme avec des calculs en double précision (type double au lieu de float pour le calcul des sinus) donne un temps de calcul de 56 microsecondes. L'utilisation des calculs en flottant 32 bits (type float) est donc justifié car il laisse une marge importante pour augmenter la complexité des calculs (mais on peut aussi réduire la fréquence d'échantillonnage si le temps de calcul est trop long).
Pour faire une analyse spectrale très précise du signal généré, les 8192 points délivrés par le logiciel Waveforms sont insuffisants. Nous utilisons l'interface Python décrite dans Interface Python pour Analog Discovery.
Voici le script d'acquisition, qui fait l'acquisition des deux voies CH1 et CH2 avec une fréquence d'échantillonnage de 50 kHz et 1 M échantillons, soit une durée de 200 s :
import numpy as np
import matplotlib.pyplot as plt
from analog_0_1 import Device,AnalogInput
from numpy.fft import fft
from scipy.signal.windows import blackman
def analyseSpectrale(t,x,nz=5):
# nz : nombre de blocs de zéros ajoutés
te = t[1]-t[0]
N=len(x)
p = int(np.log(nz*N)/np.log(2))
N1 = 2**p
x1=np.concatenate((x*blackman(N),np.zeros(N1-N)))
spectre = np.absolute(fft(x1))*2.0/N/0.42
N1 = len(x1)
T1 = N1*te
freq=np.arange(N1)*1/T1
plt.figure()
plt.plot(freq,spectre)
plt.xlabel('f (Hz)')
plt.grid()
device = Device(-1)
device.open()
analog = AnalogInput(device)
analog.channels([0,1],[5,5])
fSamp = 50000
size = 1000000
time = analog.sampling(fSamp,size)
voltage = analog.record()
u0 = voltage[0,:]
u1 = voltage[1,:]
analyseSpectrale(time,u0,nz=10)
plt.figure()
plt.plot(time,u0,label='ch 1')
plt.plot(time,u1,label='ch 2')
plt.xlabel('t (s)')
plt.ylabel('U (V)')
plt.grid()
plt.legend(loc='upper right')
plt.show()
np.save("sinus-50kHz-1000Hz-long",np.array([time,u0,u1]))
device.close()
Voici le spectre obtenu à partir de cette acquisiton (de précision 1/200 Hz) :
from numpy.fft import fft
from scipy.signal.windows import blackman
[t,u0,u1] = np.load("sinus-50kHz-1000Hz-long.npy")
def analyseSpectrale(t,x,nz=5):
# nz : nombre de blocs de zéros ajoutés
te = t[1]-t[0]
N=len(x)
p = int(np.log(nz*N)/np.log(2))
N1 = 2**p
x1=np.concatenate((x*blackman(N),np.zeros(N1-N)))
spectre = np.absolute(fft(x1))*2.0/N/0.42
N1 = len(x1)
T1 = N1*te
freq=np.arange(N1)*1/T1
return freq,spectre
freq,spectre = analyseSpectrale(t,u0-u0.mean())
figure()
plot(freq,spectre)
xlabel('f (Hz)')
grid()
xlim(999.8,1000.4)
ylim(0,1)
f0 = np.argmax(spectre)*(freq[1]-freq[0])
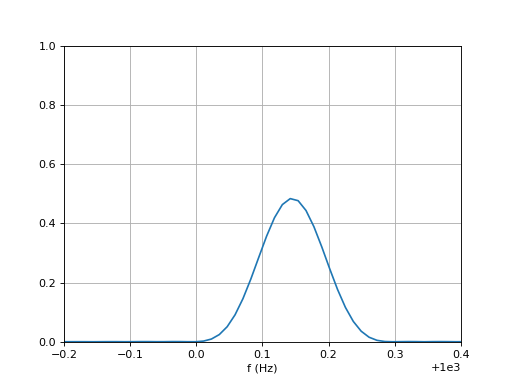 fig4.pdf
fig4.pdf
print(f0) --> np.float64(1000.1420974731444)
La fréquence donnée par ce spectre est 1000,14 Hz. L'écart avec la fréquence programmée vient très probablement de l'imprécision de l'horloge de la carte Arduino. Il est d'ailleurs confirmé par analyse spectrale sur un autre oscilloscope (PicoScope 3204B). Il est facile de corriger l'écart : la fréquence voulue doit être divisée par 1,00014 pour le calcul de la phase (cette valeur dépend évidemment de l'exemplaire de la carte Arduino).
Voici la génération d'un signal périodique comportant 3 harmoniques et d'un signal sinusoïdal, les deux de fréquence 100 Hz :
// définition des signaux
#define CORRECT 1.00014 // facteur de correction de la fréquence
float f0 = 100.0/CORRECT;
float f1 = 100.0/CORRECT;
float signal0(float phi) {
return 0.5*sin(deuxpi*phi)+0.2*sin(2*deuxpi*phi)+0.1*sin(4*deuxpi*phi+PI/3);
}
float signal1(float phi) {
return 0.5*sin(deuxpi*phi);
}
[t,u1,u2] = np.loadtxt("periodique-50kHz-100Hz.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label='DAC0')
plot(t*1e3,u2,label='DAC1')
grid()
xlabel("t (ms)",fontsize=16)
ylabel('volts')
ylim(0,3)
legend(loc='upper right')
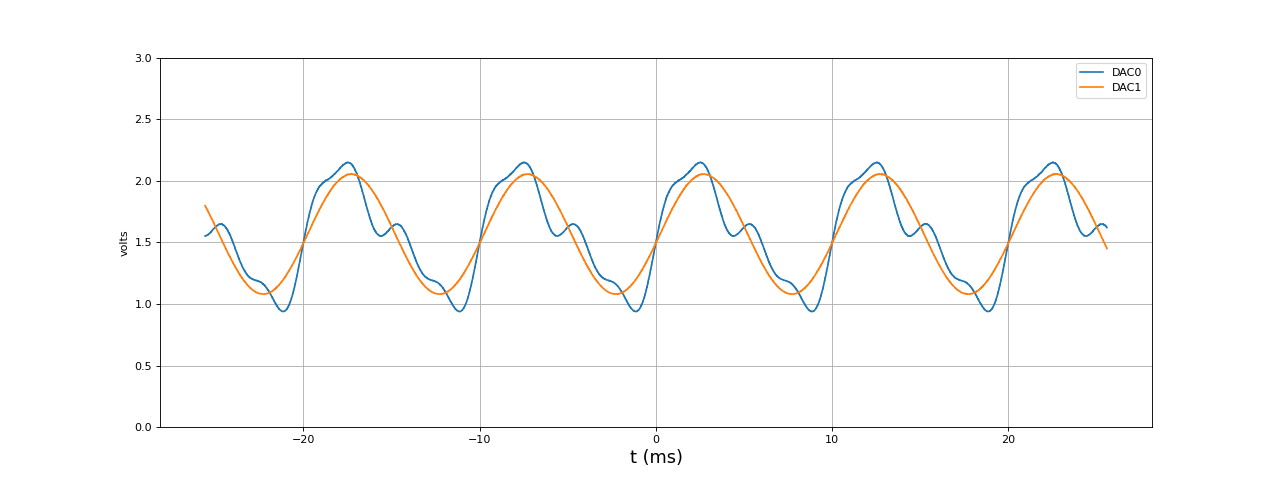 fig5.pdf
fig5.pdf
3.c. Utilisation d'une table
Pour la génération de signaux strictement périodiques et pour des grandes fréquences d'échantillonnage, la méthode précédente peut être mise en défaut. En effet, nous avons mesuré un temps de calcul pour une simple fonction sinus et pour 16 échantillons de 11 microsecondes. Si l'on adopte la fréquence d'échantillonnage maximale du DAC (1 MHz), le temps de conversion de 16 échantillons est 16 microsecondes. La génération d'un signal comportant plusieurs harmoniques risque alors d'être impossible avec la méthode précédente. Même si elle fonctionne, il peut être intéressant de libérer du temps de calcul CPU pour d'autres tâches. Nous devons dans ce cas adopter la méthode de synthèse DDS utilisant une table (voir le document Synthèse numérique d'un signal périodique, qui montre la mise en œuvre de cette méthode sur l'Arduino Due).
La méthode de synthèse d'un signal périodique par table (DDS : direct digital synthesis) consiste à placer les échantillons du signal pour une période dans une table. La table comporte des nombres entiers de 16 bits (pour un DAC 12 bits, seulement 12 bits sur les 16 sont utilisés). Le nombre d'éléments de la table doit être une puissance de deux. Nous allons utiliser une table à 256 éléments, adressée par un indice codé sur 8 bits, qui contient une période complète du signal.
Pour faire varier finement la fréquence du signal, on utilise une phase allant de 0 à 256 mais comportant aussi une partie fractionnaire, car l'incrément de phase à chaque période d'échantillonnage est en général un nombre décimal non entier. On utilise pour cela un accumulateur de phase de 32 bits à virgule fixe. Les 24 premiers bits (en partant du plus faible) codent la partie fractionnaire de la phase, les 8 derniers codent la partie entière.
Figure pleine pageL'incrément à appliquer à l'accumulateur de phase à chaque période d'échantillonnage est donné par la partie entière suivante :
où f est la fréquence du signal, c'est-à-dire la fréquence à laquelle la table complète se répète, et Te la période d'échantillonnage. L'incrément étant un entier, la résolution fréquentielle est :
Par exemple pour la fréquence d'échantillonnage maximale de 1 MHz, la résolution fréquentielle est 0,00023 Hz.
Voici le programme Arduino :
#include <Arduino_AdvancedAnalog.h>
#define BUFSIZE 8
#define NBUF 4
uint32_t sample_rate = 50000;
double sample_period;
AdvancedDAC dac0(A12);
AdvancedDAC dac1(A13);
double deuxpi = 2*PI;
#define NECHANT 256
#define SHIFT_ACCUM 24
uint16_t table0[NECHANT];
uint16_t table1[NECHANT];
uint32_t accum0,accum1;
uint32_t increm0,increm1;
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
float volt2num = 4096/3.217;
// définition des signaux
#define CORRECT 1.00014
float f0 = 100.0/CORRECT;
float f1 = 100.0/CORRECT;
float signal0(float phi) {
return 0.5*sin(deuxpi*phi)+0.2*sin(2*deuxpi*phi)+0.1*sin(4*deuxpi*phi+PI/3);
}
float signal1(float phi) {
return 0.5*sin(deuxpi*phi);
}
void setup() {
pinMode(13,OUTPUT);
sample_period = 1.0/sample_rate;
Serial.begin(115200);
while(!Serial);
for (uint16_t i=0; i<NECHANT; i++) {
table0[i] = signal0(1.0*i/NECHANT)*volt2num + offset;
table1[i] = signal1(1.0*i/NECHANT)*volt2num + offset;
}
increm0 = (uint32_t) (((float)(0xFFFFFFFF))*((float)(f0)*1.0/sample_rate)); // incrément de l'accumulateur de phase
increm1 = (uint32_t) (((float)(0xFFFFFFFF))*((float)(f1)*1.0/sample_rate));
accum0 = accum1 = 0;
if (!dac0.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC0");
while (1);
}
if (!dac1.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC1");
while (1);
}
}
void loop() {
if (dac0.available()&&dac1.available()) {
GPIOH->BSRR |= GPIO_BSRR_BS6; //digitalWrite(13,HIGH);
SampleBuffer buf_dac0 = dac0.dequeue();
uint16_t *buf_dac0_data = buf_dac0.data();
SampleBuffer buf_dac1 = dac1.dequeue();
uint16_t *buf_dac1_data = buf_dac1.data();
for (uint16_t i=0; i<BUFSIZE; i++) {
accum0 += increm0;
accum1 += increm1;
buf_dac0_data[i] = table0[accum0 >> SHIFT_ACCUM];
buf_dac1_data[i] = table1[accum1 >> SHIFT_ACCUM];
}
dac0.write(buf_dac0);
dac1.write(buf_dac1);
GPIOH->BSRR |= GPIO_BSRR_BR6; //digitalWrite(13,LOW);
}
}
Les signaux sont définis comme précédemment, avec deux fonctions d'une phase réduite (phase variant de 0 à 1) mais ces fonctions sont appelées initialement pour le remplissage des tables. Cette méthode permet de changer la fréquence en temps réel puisqu'il suffit pour cela de recalculer l'incrément de l'accumulateur de phase. En revanche, changer la forme du signal en temps réel est plus difficile puisqu'il faut changer le contenu des tables.
[t,u1,u2] = np.loadtxt("DDS-periodique-50kHz-100Hz.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label='DAC0')
plot(t*1e3,u2,label='DAC1')
grid()
xlabel("t (ms)",fontsize=16)
ylabel('volts')
ylim(0,3)
legend(loc='upper right')
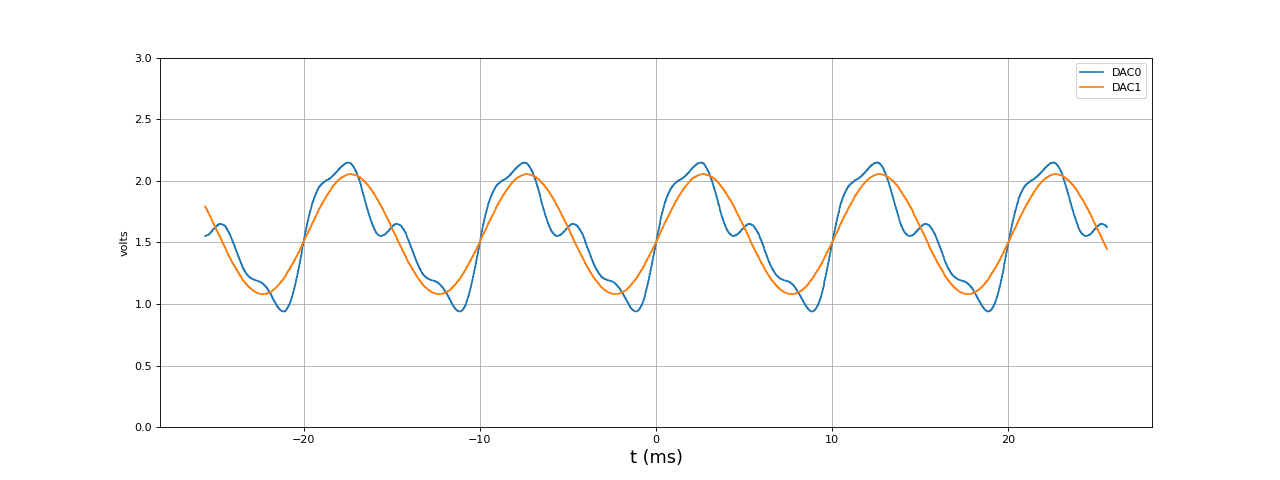 fig6.pdf
fig6.pdf
Voici DAC0 et D13 :
[t,u1,u2] = np.loadtxt("DDS-periodique-50kHz-100Hz-D13.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label='DAC0')
plot(t*1e3,u2,label='D13')
grid()
xlabel("t (ms)",fontsize=16)
ylabel('volts')
ylim(0,4)
legend(loc='upper right')
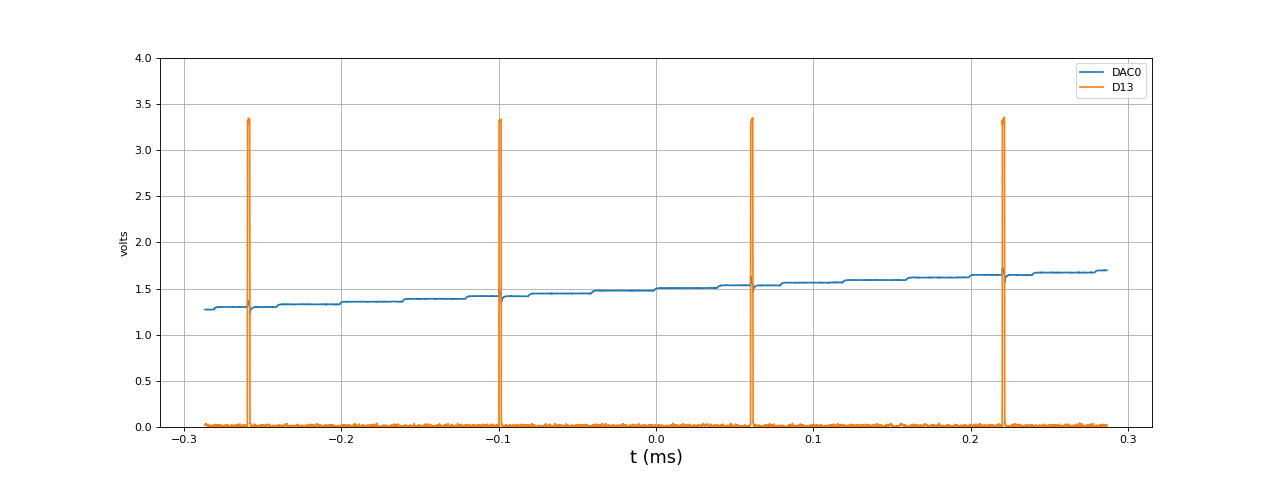 fig7.pdf
fig7.pdf
Le temps de remplissage des deux tampons de 8 échantillons est 1,4 microsecondes, ce qui est environ 8 fois plus rapide que le calcul en temps réel du signal. Avec un microcontrôleur ne possédant pas de FPU (floating point unit), comme celui de l'Arduino Due, ce rapport serait bien plus grand. Nous pouvons envisager de générer un signal de fréquence beaucoup plus élevé, avec une fréquence d'échantillonnage beaucoup plus grande :
uint32_t sample_rate = 500000;
float f0 = 10000.0/CORRECT;
float f1 = 10000.0/CORRECT;
[t,u1,u2] = np.loadtxt("DDS-periodique-500kHz-10kHz.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label='DAC0')
plot(t*1e3,u2,label='DAC1')
grid()
xlabel("t (ms)",fontsize=16)
ylabel('volts')
ylim(0,3)
legend(loc='upper right')
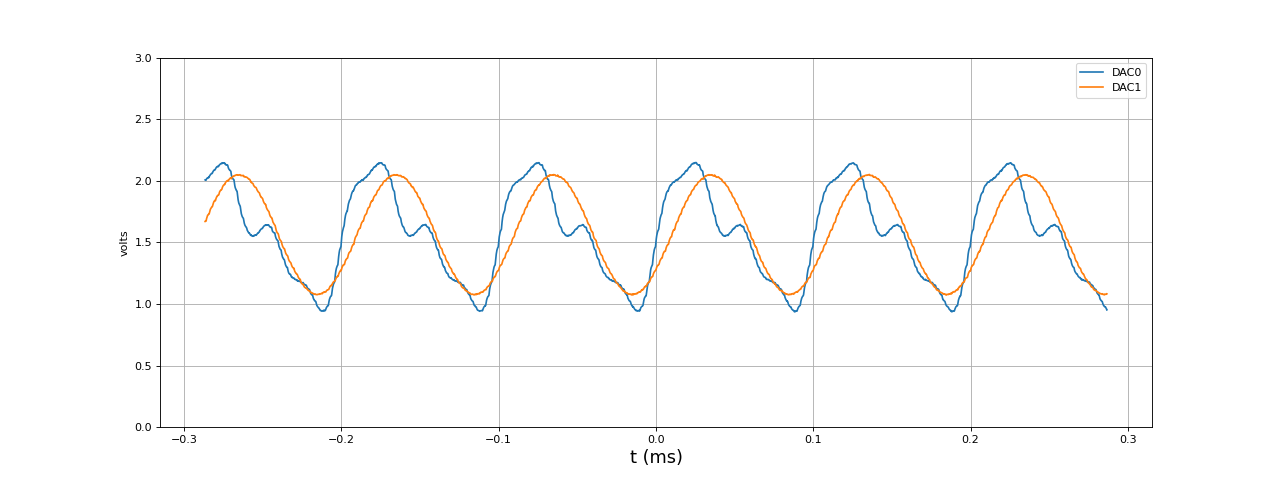 fig8.pdf
fig8.pdf
4. Applications
4.a. Génération de signaux bruités
La génération d'un signal comportant du bruit est une fonction très utile, pourtant absente sur la plupart des générateurs DDS.
La programmation du générateur de nombres aléatoires est documentée dans manuel de référence du STM32H747/757.
Il s'agit d'un générateur de nombres réellement aléatoires (True random number generator) et non simplement pseudo aléatoires comme le sont les algorithmes. Il repose sur une source de bruit analogique.
Pour configurer le générateur (RNG), on doit commencer par activer l'horloge pour RNG :
RCC->AHB2ENR |= RCC_AHB2ENR_RNGEN;
Le démarrage de RNG se fait en activant le bit RNGEN dans le registre CR :
RNG->CR |= RNG_CR_RNGEN;
Le nombre aléatoire est un nombre 32 bits accessibles dans le registre RNG->DR, de densité de probabilité uniforme. Cependant, il n'est disponible que si le bit DRDY du registre RNG->SR vaut 1, sinon le registre RNG->DR contient une valeur nulle.
Pour générer du bruit dans le cas de la synthèse par table, on doit ajouter un nombre aléatoire à la valeur récupérée dans la table. Pour cela, on définit une amplitude du bruit (en volts) par un flottant noise0. Dans la boucle de remplissage du tampon, on actualise une variable globale (uint16_t randNoise) de la manière suivante :
if (RNG->SR & RNG_SR_DRDY) randNoise = volt2num*(((double)(RNG->DR-0x7FFFFFFF))/0x7FFFFFFF)*noise0;
Si le bit DRDY vaut 0 (ce qui est très peu probable), le nombre stocké ne change pas.
Si l'on veut être certain d'obtenir un nouveau nombre aléatoire pour chaque nouvel échantillon, il suffit d'écrire :
while ((RNG->SR & RNG_SR_DRDY)==0);
randNoise = volt2num*(((double)(RNG->DR-0x7FFFFFFF))/0x7FFFFFFF)*noise0;
Après que le bit DRDY est passé à 1, le registre DR contient le nouveau nombre aléatoire tant qu'il n'est pas lu.
Voici le programme de génération par table avec génération de bruit :
#include <Arduino_AdvancedAnalog.h>
#define BUFSIZE 8
#define NBUF 4
uint32_t sample_rate = 50000;
double sample_period;
AdvancedDAC dac0(A12);
AdvancedDAC dac1(A13);
double deuxpi = 2*PI;
#define NECHANT 256
#define SHIFT_ACCUM 24
uint16_t table0[NECHANT];
uint16_t table1[NECHANT];
uint32_t accum0,accum1;
uint32_t increm0,increm1;
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
float volt2num = 4096/3.217;
// définition des signaux
#define CORRECT 1.00014
float f0 = 100.0/CORRECT;
float f1 = 100.0/CORRECT;
float noise0 = 0.05;
float noise1 = 0.05;
int16_t randNoise;
float signal0(float phi) {
return 0.5*sin(deuxpi*phi)+0.2*sin(2*deuxpi*phi)+0.1*sin(4*deuxpi*phi+PI/3);
}
float signal1(float phi) {
return 0.5*sin(deuxpi*phi);
}
void setup() {
pinMode(13,OUTPUT);
sample_period = 1.0/sample_rate;
Serial.begin(115200);
while(!Serial);
for (uint16_t i=0; i<NECHANT; i++) {
table0[i] = signal0(1.0*i/NECHANT)*volt2num + offset;
table1[i] = signal1(1.0*i/NECHANT)*volt2num + offset;
}
increm0 = (uint32_t) (((float)(0xFFFFFFFF))*((float)(f0)*1.0/sample_rate)); // incrément de l'accumulateur de phase
increm1 = (uint32_t) (((float)(0xFFFFFFFF))*((float)(f1)*1.0/sample_rate));
accum0 = accum1 = 0;
RCC->AHB2ENR |= RCC_AHB2ENR_RNGEN;
RNG->CR |= RNG_CR_RNGEN;
if (!dac0.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC0");
while (1);
}
if (!dac1.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC1");
while (1);
}
}
void loop() {
if (dac0.available()&&dac1.available()) {
GPIOH->BSRR |= GPIO_BSRR_BS6; //digitalWrite(13,HIGH);
SampleBuffer buf_dac0 = dac0.dequeue();
uint16_t *buf_dac0_data = buf_dac0.data();
SampleBuffer buf_dac1 = dac1.dequeue();
uint16_t *buf_dac1_data = buf_dac1.data();
for (uint16_t i=0; i<BUFSIZE; i++) {
accum0 += increm0;
accum1 += increm1;
if (RNG->SR & RNG_SR_DRDY) randNoise = volt2num*(((double)(RNG->DR-0x7FFFFFFF))/0x7FFFFFFF)*noise0;
buf_dac0_data[i] = table0[accum0 >> SHIFT_ACCUM]+randNoise;
if (RNG->SR & RNG_SR_DRDY) randNoise = volt2num*(((double)(RNG->DR-0x7FFFFFFF))/0x7FFFFFFF)*noise1;
buf_dac1_data[i] = table1[accum1 >> SHIFT_ACCUM]+randNoise;
}
dac0.write(buf_dac0);
dac1.write(buf_dac1);
GPIOH->BSRR |= GPIO_BSRR_BR6; //digitalWrite(13,LOW);
}
}
Voici le résultat pour une fréquence d'échantillonnage de 500 kHz (signaux de 100 Hz) :
[t,u1,u2] = np.loadtxt("DDS-periodiqueBruit-500kHz-100Hz.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label='DAC0')
plot(t*1e3,u2,label='DAC1')
grid()
xlabel("t (ms)",fontsize=16)
ylabel('volts')
ylim(0,3)
legend(loc='upper right')
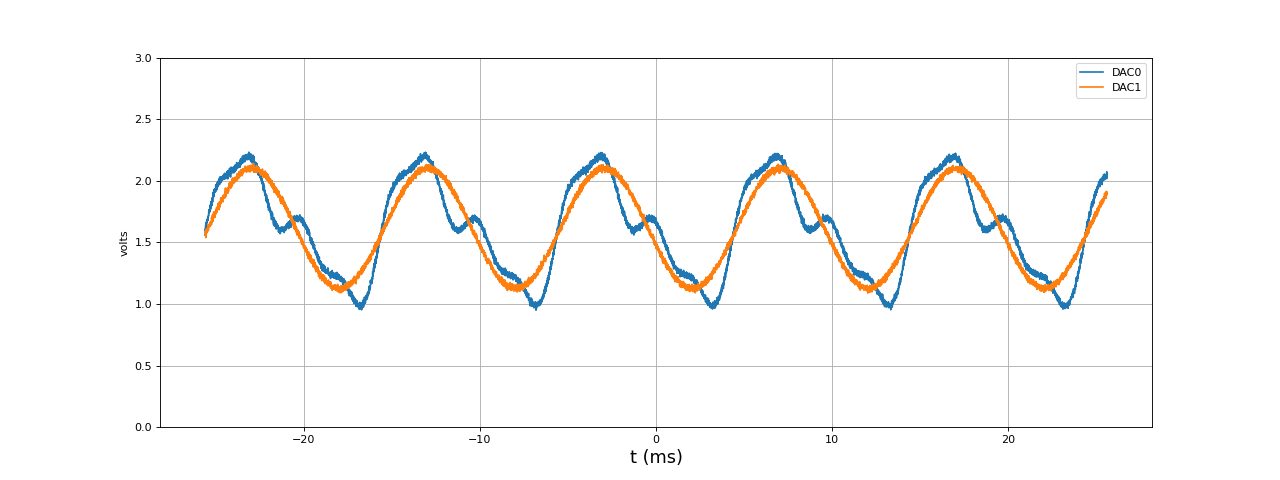 fig9.pdf
fig9.pdf
[t,u1,u2] = np.loadtxt("DDS-periodiqueBruit-500kHz-100Hz-D13.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e6,u1,label='DAC0')
plot(t*1e6,u2,label='D13')
grid()
xlabel("t (us)",fontsize=16)
ylabel('volts')
ylim(0,4)
legend(loc='upper right')
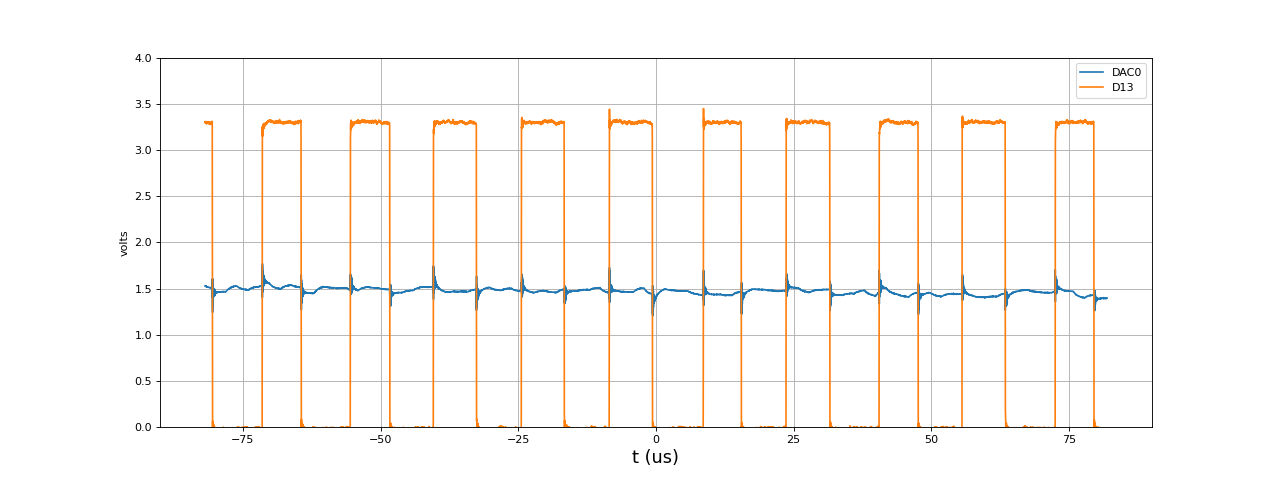 fig10.pdf
fig10.pdf
La durée de remplissage des deux tampons est de 8 microsecondes.
Il est possible de générer des nombres aléatoires à distribution gaussienne à partir de deux nombre à distribution uniforme dans l'intervalle [0,1], par la transformation suivante :
où est l'espérance et l'écart-type.
Voici la fonction faisant ce calcul :
int16_t bruitGauss(float noise, double u1, double u2) {
u1 = (u1+1)/0xFFFFFFFF;
u2 /= 0xFFFFFFFF;
return noise*sqrt(-2*log(u1))*cos(deuxpi*u2)*volt2num ;
}
L'amplitude du bruit est l'écart-type du bruit gaussien. Les deux nombres u1,u2 sont des nombres aléatoires 32 bits (convertis en double). Le temps de calcul supplémentaire oblige à diminuer la fréquence d'échantillonnage. Voici le programme complet, avec une fréquence d'échantillonnage de 200 kHz :
#include <Arduino_AdvancedAnalog.h>
#define BUFSIZE 8
#define NBUF 4
uint32_t sample_rate = 200000;
double sample_period;
AdvancedDAC dac0(A12);
AdvancedDAC dac1(A13);
double deuxpi = 2*PI;
#define NECHANT 256
#define SHIFT_ACCUM 24
uint16_t table0[NECHANT];
uint16_t table1[NECHANT];
uint32_t accum0,accum1;
uint32_t increm0,increm1;
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
float volt2num = 4096/3.217;
// définition des signaux
#define CORRECT 1.00014
float f0 = 10000.0/CORRECT;
float f1 = 10000.0/CORRECT;
float noise0 = 0.05;
float noise1 = 0.05;
int32_t rand1,rand2;
float signal0(float phi) {
return 0.5*sin(deuxpi*phi)+0.2*sin(2*deuxpi*phi)+0.1*sin(4*deuxpi*phi+PI/3);
}
float signal1(float phi) {
return 0.5*sin(deuxpi*phi);
}
int16_t bruitGauss(float noise, double u1, double u2) {
u1 = (u1+1)/0xFFFFFFFF;
u2 /= 0xFFFFFFFF;
return noise*sqrt(-2*log(u1))*cos(deuxpi*u2)*volt2num ;
}
void setup() {
pinMode(13,OUTPUT);
sample_period = 1.0/sample_rate;
Serial.begin(115200);
while(!Serial);
for (uint16_t i=0; i<NECHANT; i++) {
table0[i] = signal0(1.0*i/NECHANT)*volt2num + offset;
table1[i] = signal1(1.0*i/NECHANT)*volt2num + offset;
}
increm0 = (uint32_t) (((float)(0xFFFFFFFF))*((float)(f0)*1.0/sample_rate)); // incrément de l'accumulateur de phase
increm1 = (uint32_t) (((float)(0xFFFFFFFF))*((float)(f1)*1.0/sample_rate));
accum0 = accum1 = 0;
RCC->AHB2ENR |= RCC_AHB2ENR_RNGEN;
RNG->CR |= RNG_CR_RNGEN;
if (!dac0.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC0");
while (1);
}
if (!dac1.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC1");
while (1);
}
}
void loop() {
if (dac0.available()&&dac1.available()) {
GPIOH->BSRR |= GPIO_BSRR_BS6; //digitalWrite(13,HIGH);
SampleBuffer buf_dac0 = dac0.dequeue();
uint16_t *buf_dac0_data = buf_dac0.data();
SampleBuffer buf_dac1 = dac1.dequeue();
uint16_t *buf_dac1_data = buf_dac1.data();
double rand1,rand2;
for (uint16_t i=0; i<BUFSIZE; i++) {
accum0 += increm0;
accum1 += increm1;
while ((RNG->SR & RNG_SR_DRDY)==0);
rand1 = RNG->DR;
while ((RNG->SR & RNG_SR_DRDY)==0);
rand2 = RNG->DR;
buf_dac0_data[i] = table0[accum0 >> SHIFT_ACCUM]+bruitGauss(noise0,rand1,rand2);
while ((RNG->SR & RNG_SR_DRDY)==0);
rand1 = RNG->DR;
while ((RNG->SR & RNG_SR_DRDY)==0);
rand2 = RNG->DR;
buf_dac1_data[i] = table1[accum1 >> SHIFT_ACCUM]+bruitGauss(noise1,rand1,rand2);
}
dac0.write(buf_dac0);
dac1.write(buf_dac1);
GPIOH->BSRR |= GPIO_BSRR_BR6; //digitalWrite(13,LOW);
}
}
Avant de lire le registre RNG->DR, on attend que le bit DRDY soit à 1.
[t,u1,u2] = np.loadtxt("DDS-periodiqueBruitGauss-200kHz-100Hz.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e3,u1,label='DAC0')
plot(t*1e3,u2,label='DAC1')
grid()
xlabel("t (ms)",fontsize=16)
ylabel('volts')
ylim(0,3)
legend(loc='upper right')
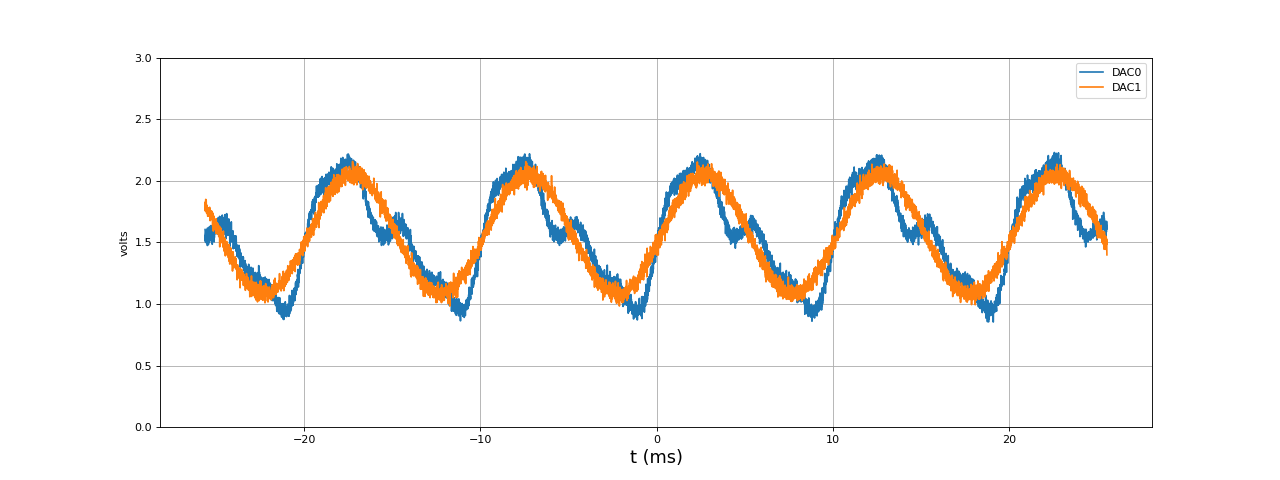 fig11.pdf
fig11.pdf
[t,u1,u2] = np.loadtxt("DDS-periodiqueBruitGauss-200kHz-100Hz-D13.txt",unpack=True,skiprows=3)
figure(figsize=(16,6))
plot(t*1e6,u1,label='DAC0')
plot(t*1e6,u2,label='D13')
grid()
xlabel("t (us)",fontsize=16)
ylabel('volts')
ylim(0,4)
legend(loc='upper right')
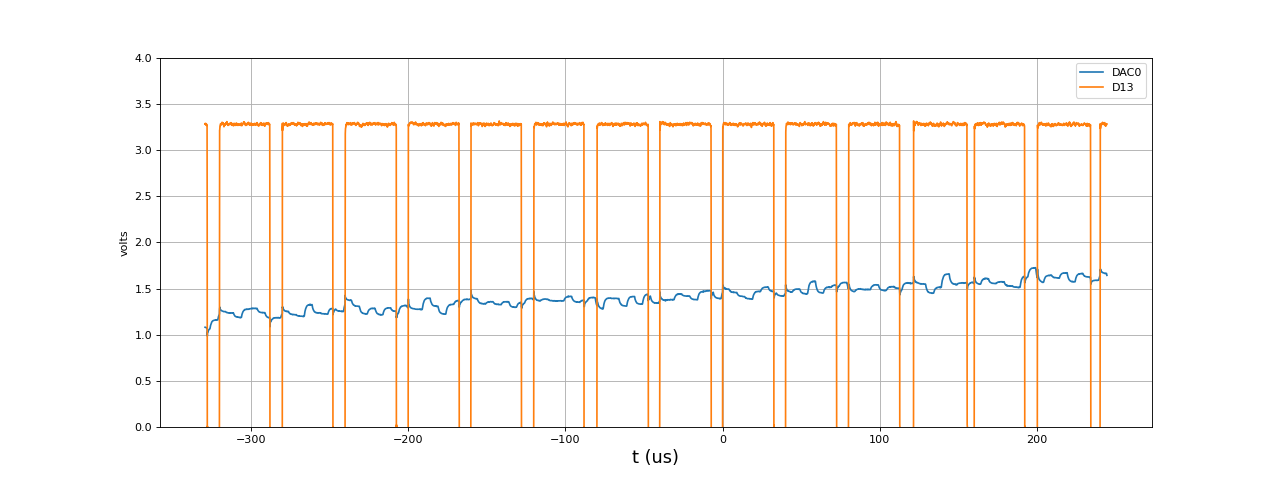 fig12.pdf
fig12.pdf
La durée de remplissage des deux tampons est 31 microsecondes, contre 8 microsecondes pour le bruit uniforme. Si l'on veut garder une marge de sécurité, la fréquence d'échantillonnage de 200 kHz ne doit pas être dépassée.
4.b. Sauts de phase aléatoire
On génère un signal stochastique défini par une forme sinusoïdale mais avec des sauts de phase aléatoires qui surviennent périodiquement. Si on définit tau0 la période des sauts de phase (appelé aussi temps de cohérence) pour DAC0, on définit le nombre d'échantillons entre deux sauts consécutifs :
uint32_t coherence0 = tau0*sample_rate;
On incrémente un compteur d'échantillons (sampleCount0). Lorsque celui-ci atteint coherence0, on le remet à zéro et on effectue le saut de phase. Celui-ci consiste simplement à ajouter le nombre aléatoire 32 bits fourni par RNG à l'accumulateur de phase.
Voici le programme :
#include <Arduino_AdvancedAnalog.h>
#define BUFSIZE 8
#define NBUF 4
uint32_t sample_rate = 200000;
double sample_period;
AdvancedDAC dac0(A12);
AdvancedDAC dac1(A13);
double deuxpi = 2*PI;
#define NECHANT 256
#define SHIFT_ACCUM 24
uint16_t table0[NECHANT];
uint16_t table1[NECHANT];
uint32_t accum0,accum1;
uint32_t increm0,increm1;
uint32_t sampleCount0,sampleCount1;
uint32_t coherence0,coherence1;
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
float volt2num = 4096/3.217;
// définition des signaux
#define CORRECT 1.00014
float f0 = 1000.0/CORRECT;
float f1 = 1000.0/CORRECT;
float tau0 = 1.0;
float tau1 = 0.1;
float signal0(float phi) {
return 0.5*sin(deuxpi*phi);
}
float signal1(float phi) {
return 0.5*sin(deuxpi*phi);
}
void setup() {
pinMode(13,OUTPUT);
sample_period = 1.0/sample_rate;
Serial.begin(115200);
while(!Serial);
for (uint16_t i=0; i<NECHANT; i++) {
table0[i] = signal0(1.0*i/NECHANT)*volt2num + offset;
table1[i] = signal1(1.0*i/NECHANT)*volt2num + offset;
}
increm0 = (uint32_t) (((float)(0xFFFFFFFF))*((float)(f0)*1.0/sample_rate)); // incrément de l'accumulateur de phase
increm1 = (uint32_t) (((float)(0xFFFFFFFF))*((float)(f1)*1.0/sample_rate));
accum0 = accum1 = 0;
sampleCount0 = sampleCount1 = 0;
coherence0 = tau0*sample_rate;
coherence1 = tau1*sample_rate;
RCC->AHB2ENR |= RCC_AHB2ENR_RNGEN;
RNG->CR |= RNG_CR_RNGEN;
if (!dac0.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC0");
while (1);
}
if (!dac1.begin(AN_RESOLUTION_12, sample_rate,BUFSIZE, NBUF)) {
Serial.println("Echec de démarrage de DAC1");
while (1);
}
}
void loop() {
if (dac0.available()&&dac1.available()) {
GPIOH->BSRR |= GPIO_BSRR_BS6; //digitalWrite(13,HIGH);
SampleBuffer buf_dac0 = dac0.dequeue();
uint16_t *buf_dac0_data = buf_dac0.data();
SampleBuffer buf_dac1 = dac1.dequeue();
uint16_t *buf_dac1_data = buf_dac1.data();
for (uint16_t i=0; i<BUFSIZE; i++) {
accum0 += increm0;
accum1 += increm1;
buf_dac0_data[i] = table0[accum0 >> SHIFT_ACCUM];
buf_dac1_data[i] = table1[accum1 >> SHIFT_ACCUM];
sampleCount0 += 1;
if (sampleCount0==coherence0) {
sampleCount0 = 0;
while ((RNG->SR & RNG_SR_DRDY)==0);
accum0 += RNG->DR;
}
if (sampleCount1==coherence1) {
sampleCount1 = 0;
while ((RNG->SR & RNG_SR_DRDY)==0);
accum1 += RNG->DR;
}
}
dac0.write(buf_dac0);
dac1.write(buf_dac1);
GPIOH->BSRR |= GPIO_BSRR_BR6; //digitalWrite(13,LOW);
}
}
Il est intéressant de faire une analyse spectrale des signaux. La fréquence étant de 1000 Hz, une fréquence d'échantillonnage de 3000 Hz est largement suffisante (elle doit être strictement supérieure à 2000 Hz). On effectue une numérisation d'un million d'échantillons (durée de 333 s) afin d'avoir un grande nombre de sauts de phases. La numérisation est faite avec l'Analog Discovery et le script donné plus haut.
[t,u0,u1] = np.load("sinus-200kHz-1000Hz-sautsPhase.npy")
freq0,spectre0 = analyseSpectrale(t,u0-u0.mean())
freq1,spectre1 = analyseSpectrale(t,u1-u1.mean())
figure(figsize=(12,8))
subplot(211)
plot(freq0,spectre0)
ylabel('DAC0')
grid()
xlim(950,1050)
ylim(0,0.1)
subplot(212)
plot(freq1,spectre1)
xlabel('f (Hz)')
ylabel('DAC1')
grid()
xlim(950,1050)
ylim(0,0.1)
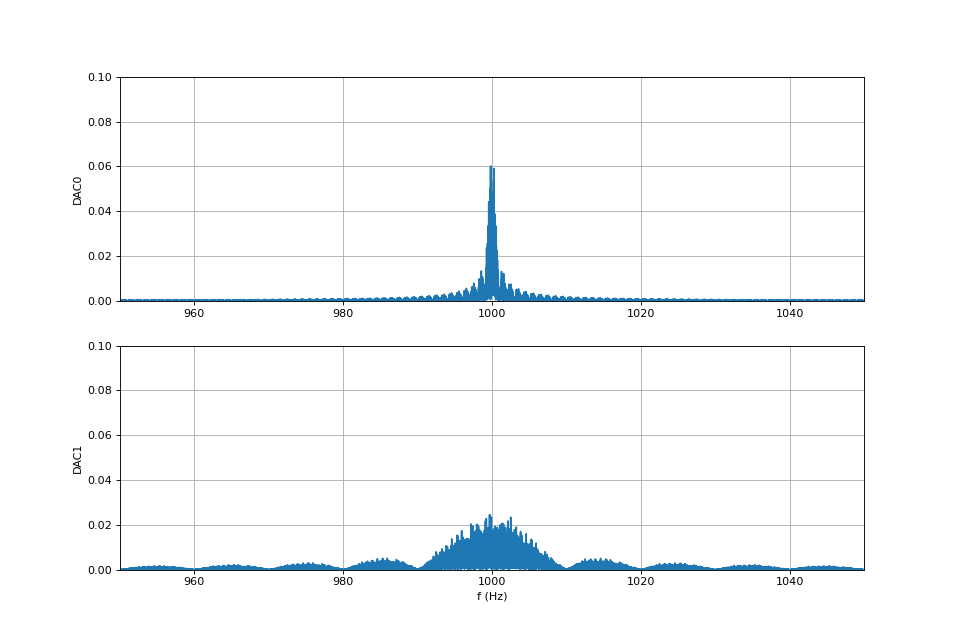 fig13.pdf
fig13.pdf
Les sauts de phases se traduisent sur le spectre par un étalement de la raie. La largeur du lobe principal est le double de l'inverse du temps de cohérence. Pour DAC1, le temps de cohérence 0,1 s et le lobe principal a une largeur de 20 Hz. Cette largeur est de 2 Hz pour DAC0. Pour comparaison, la largeur de la raie en l'absence du saut de phase est de l'ordre de 1/333 Hz.