Électrostatique

Distributions continues

1. Distributions volumiques

a. Densité volumique de charges

Échelles de longueur :

Microscopique : charges quasi ponctuelles (ions, électrons).
Mésoscopique : très grand nombre de charges ponctuelles, densité volumique de charge.
Macroscopique : la densité volumique de charge est un champ scalaire : $ρ (x, y, z)$ .

Simulation montrant le passage du microscopique au mésoscopique.

Densité volumique de charges $ρ (x, y, z)$

Quantité de charge dans le volume élémentaire $d V$ situé au point $P (x, y, z)$ :

d q = ρ (P) d V

Quantité de charge dans un volume V :

Q = ∭_{V} ρ (P) d V

Intégrale de la densité de charges sur le volume.

Distribution volumique de charges : distribution définie par une densité volumique de charges $ρ (x, y, z)$ .

Distribution dite « continue » par opposition aux distributions « discrètes » (charges ponctuelles).

La densité est continue par morceaux dans l'espace.

Théorème de Gauss pour une surface fermée $S$ dont $V$ est le volume intérieur :

\iint_{S} \vec{E} (M) \cdot \vec{n_{s}} (M) d S = \frac{1}{ε_{0}} ∭_{V} ρ (P) d V

1. Distributions volumiques

a. Densité volumique de charges

b. Sphère chargée

Sphère de centre $O$ et de rayon $R$, chargée en volume avec une densité volumique de charges uniforme $ρ_{0}$ .

Coordonnées sphériques de centre O : $r,\theta,\phi$.

Quantité de charge totale :

Q = \frac{4}{3} π R^{3} ρ_{0}

Point $M$ quelconque, tout plan contenant $M$ et $O$ est un plan de symétrie de la distribution.

Le vecteur $\vec{E} (M)$ est contenu dans ces plans de symétrie donc :

\vec{E} = E_{r} (r, θ, φ) {\vec{u}}_{r}

La distribution est invariante par rotation autour de toute droite passant par O donc :

\vec{E} = E_{r} (r) {\vec{u}}_{r}

Surface fermée pour appliquer le théorème de Gauss : sphère de centre $O$ et de rayon $r$.

\iint_{S} E_{r} (r) d S = \frac{Q_{i n t}}{ε_{0}}

E_{r} (r) 4 π r^{2} = \frac{Q_{i n t}}{ε_{0}}

Pour un point $M$ en dehors de la sphère ($r>R)$ :

Q_{i n t} = Q

E_{r} (r) = \frac{Q}{4 π ε_{0} r^{2}}

Champ identique à celui créé par une charge ponctuelle placée en $O$.

Volume de la couche comprise entre $r$ et $r+dr$ :

d V = 4 π r^{2} d r

Pour un point $M$ dans la sphère ($r\le R$) :

\begin{matrix} Q_{i n t} & = \int_{0}^{r} ρ (r) 4 π r'^{2} d r' \\ = \frac{4}{3} π r^{3} ρ_{0} \end{matrix}

Dans la sphère ($r\le R$) :

E_{r} (r) = \frac{r}{3 ε_{0}} ρ_{0}

Continuité de $\vec{E}$ en $r=R$.

Au centre de la sphère : $\vec{E} = \vec{0}$ .

Analogie avec le champ gravitationnel :

\begin{matrix} \vec{G} = - G m \frac{{\vec{u}}_{r}}{r^{2}} \\ \vec{E} = \frac{q}{4 π ε_{0}} \frac{{\vec{u}}_{r}}{r^{2}} \end{matrix}

Théorème de Gauss :

\iint_{S} \vec{G} \cdot {\vec{n}}_{s} d S = - 4 π G M_{i n t}

Théorème : le champ $\vec{E}$ créé par une distribution volumique de charges est une fonction continue des variables d'espace.

2. Distributions surfaciques

a. Densité surfacique de charges

Charges localisées au voisinage de la surface d'un conducteur

Quantité de charge portée par une surface élémentaire $dS$ :

d q = ρ_{o} e d S

Si $e$ est très petite à l'échelle macroscopique, limite $e \to 0$ et $ρ_{0} \to \infty$ :

d q = σ d S

$σ = e ρ_{o}$ densité surfacique de charges.

Distribution surfacique de charges : la charge est répartie sur une ou plusieurs surfaces et définie par une densité surfacique $σ (x, y, z)$ .

Remarque : $ρ$ est infinie sur une surface chargée et sur une charge ponctuelle (charge finie dans un volume nul).

Le champ $\vec{E}$ n'est pas continu aux points de densité infinie.

2. Distributions surfaciques

a. Densité surfacique de charges

b. Plan infini chargé

Le plan $(O x y)$ est chargé avec une densité uniforme $σ_{0}$

Point $M$ quelconque, tout plan contenant $M$ et perpendiculaire à $(O x y)$ est un plan de symétrie de la distribution. En particulier les plans :

\begin{matrix} (M, {\vec{u}}_{x}, {\vec{u}}_{z}) \\ (M, {\vec{u}}_{y}, {\vec{u}}_{z}) \end{matrix}

Le vecteur $\vec{E} (M)$ est contenu dans ces plans :

\vec{E} = E_{z} (x, y, z) {\vec{u}}_{z}

Une distribution de charges est invariante par translation dans la direction $\vec{u}$ si toute translation $ℓ \vec{u} = \vec{M M'}$ dans cette direction ne modifie pas la distribution.

Le champ électrostatique est alors invariant par translation :

$\vec{E} (M) = \vec{E} (M')$ pour toute distance $ℓ$ .

Le plan chargé est invariant par translation dans les directions ${\vec{u}}_{x}$ et ${\vec{u}}_{y}$ donc

\vec{E} = E_{z} (z) {\vec{u}}_{z}

Le plan $(O x y)$ est un plan de symétrie de la distribution donc un plan de symétrie du champ :

E_{z} (- z) = - E_{z} (z)

Surface fermée : $S = Σ_{c} \cup Σ \cup Σ'$

$Σ_{c}$ : surface cylindrique de génératrice $(O z)$

$Σ$ surface parallèle au plan à la côte $z$

$Σ'$ surface parallèle au plan à la côte $- z$

Théorème de Gauss $(z > 0)$ :

\begin{matrix} \iint_{Σ} & E_{z} (z) {\vec{u}}_{z} \cdot {\vec{u}}_{z} d S + \iint_{Σ'} E_{z} (- z) {\vec{u}}_{z} \cdot (- {\vec{u}}_{z}) d S \\ + \iint_{Σ_{c}} \vec{E} \cdot {\vec{n}}_{s} d S = \frac{A σ_{0}}{ε_{0}} \end{matrix}

2 A E_{z} (z) = \frac{A σ_{0}}{ε}

Champ électrostatique créé par le plan infini chargé :

\begin{matrix} E_{z} = \frac{σ}{2 ε_{0}} p o u r z > 0 \\ E_{z} = - \frac{σ}{2 ε_{0}} p o u r z < 0 \end{matrix}

Sur le plan chargé (plan de symétrie) : $E_{z} (0) = 0$ .

Discontinuité sur la surface chargée.

2. Distributions surfaciques

a. Densité surfacique de charges

b. Plan infini chargé

c. Condensateur plan

Condensateur : deux conducteurs métalliques auxquels une différence de potentiel est appliquée.

Q = C U

$C$ : capacité du condensateur (en Farad, ou C/V)

Modèle du condensateur plan infini, valable si $e ≪ R$ : deux conducteurs plan infinis, densités de charges $- σ_{0}$ et $σ_{0}$ sur les faces internes, pas de charges sur les faces externes.

Superposition de deux plans chargés :

\begin{matrix} z < 0, E_{z} = 0 \\ 0 < z < e, E_{z} = - \frac{σ_{0}}{ε_{0}} \\ z > e, E_{z} = 0 \end{matrix}

Circulation du champ électrostatique :

\int_{A}^{B} \vec{E} \cdot \vec{t} d l = V_{A} - V_{B} = U

E_{z} = - \frac{U}{e}

Plaques d'aire $S$, charge $Q = S σ_{0}$ .

Capacité du condensateur :

C = \frac{ε_{0} S}{e}

Potentiel ($0\le z\le e$) :

V (z) = U \frac{z}{e}

Condensateur de taille finie :

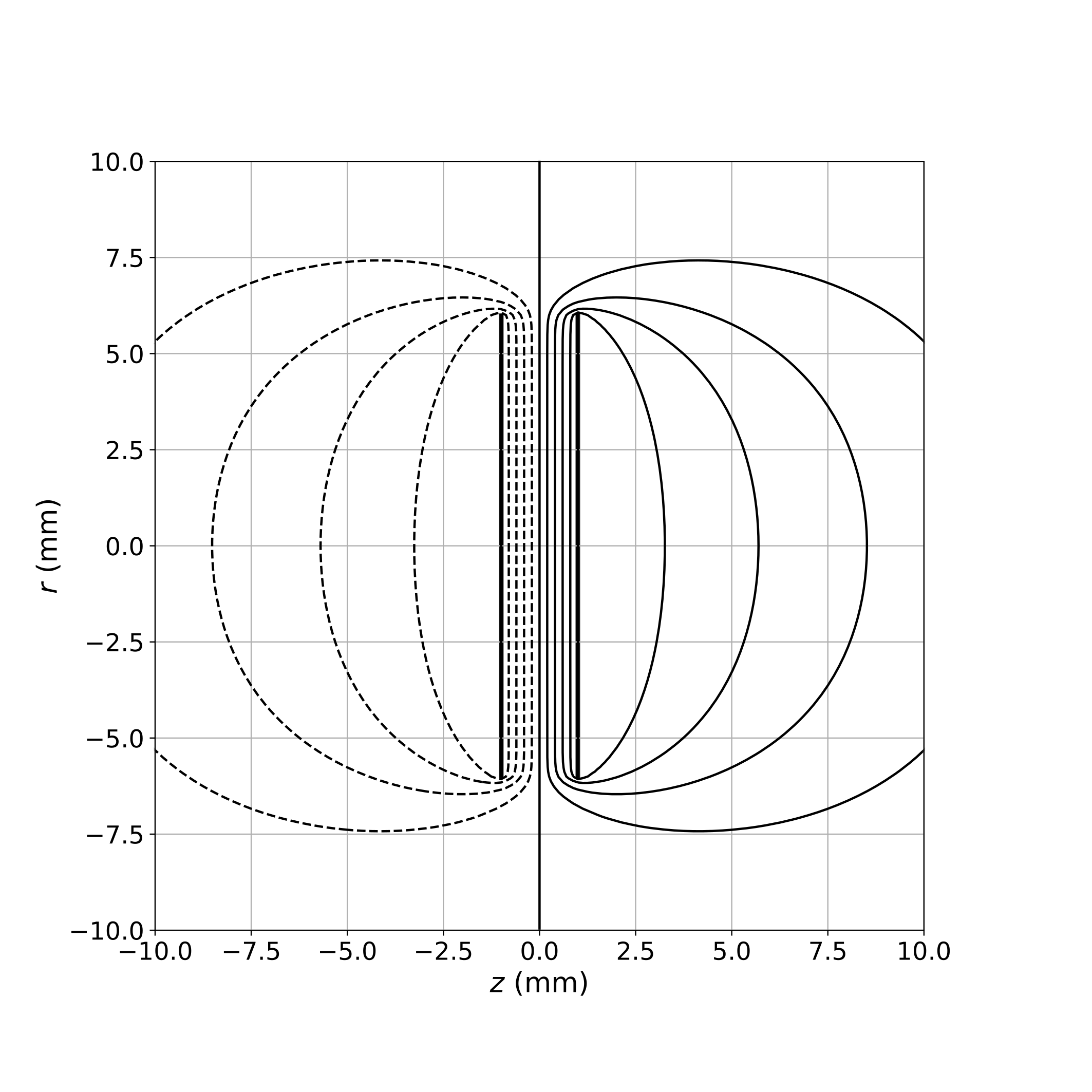
3. Distributions linéiques

a. Densité linéique de charges

Fil de rayon $r$ chargé en surface.

Courbe chargée si $r \to 0$ .

$λ$ : densité linéique de charges. Charge d'un segment élémentaire :

d q = λ d l

3. Distributions linéiques

a. Densité linéique de charges

b. Fil rectiligne infini

Coordonnées cylindriques $(r, θ, z)$

Plans de symétrie : $Π_{s} (M, {\vec{u}}_{r}, {\vec{u}}_{z})$ et $Π'_{s} (M, {\vec{u}}_{r}, {\vec{u}}_{θ})$ .

Le vecteur $\vec{E} (M)$ est contenu dans $Π_{s}$ et $Π'_{s}$ donc :

\vec{E} = E_{r} (r, θ, z) {\vec{u}}_{r}

Invariance par translation selon ${\vec{u}}_{z}$ (fil infini) :

\vec{E} = E_{r} (r, θ) {\vec{u}}_{r}

Invariance par rotation autour de (Oz):

\vec{E} = E_{r} (r) {\vec{u}}_{r}

Surface fermée S : cyclindre de révolution de rayon $r$ et de longueur $L$

S = Σ_{c} \cup Σ_{1} \cup Σ_{2}

Théorème de Gauss :

\begin{matrix} \iint_{Σ_{c}} E_{r} (r) {\vec{u}}_{r} \cdot {\vec{u}}_{r} d S = \frac{λ_{0} L}{ε_{0}} \\ E_{r} (r) 2 π r L = \frac{λ_{0} L}{ε_{0}} \\ E_{r} (r) = \frac{λ_{0}}{2 π ε_{0}} \frac{1}{r} \end{matrix}

Discontinuité de $\vec{E}$ en $r=0$.

4. Équations locales

a. Opérateur divergence

Opérateur divergence, agissant sur un champ vectoriel :

d i v \vec{E} = \frac{\partial E_{x}}{\partial x} + \frac{\partial E_{y}}{\partial y} + \frac{\partial E_{z}}{\partial z}

Autre notation (opérateur nabla) :

d i v \vec{E} = \vec{\nabla} \cdot \vec{E}

Divergence en coordonnées cylindriques :

d i v \vec{E} = \frac{1}{r} \frac{\partial (r E_{r})}{\partial r} + \frac{1}{r} \frac{\partial E_{θ}}{\partial θ} + \frac{\partial E_{z}}{\partial z}

Divergence en coordonnées sphériques :

d i v \vec{E} = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} E_{r}) + \frac{1}{r sin θ} \frac{\partial}{\partial θ} (sin θ E_{θ}) + \frac{1}{r sin θ} \frac{\partial E_{φ}}{\partial φ}

4. Équations locales

a. Opérateur divergence

b. Théorème d'Ostrogradsky

Le flux sortant d'un vecteur à travers une surface fermée est égal à l'intégrale de sa divergence dans le volume délimité par la surface :

\iint_{S} \vec{E} \cdot {\vec{n}}_{s} d S = ∭_{V} d i v \vec{E} d V

4. Équations locales

a. Opérateur divergence

b. Théorème d'Ostrogradsky

c. Théorème de Gauss

Surface fermée $S$, délimitant un volume $V$

\iint_{S} \vec{E} \cdot {\vec{n}}_{s} d S = \frac{1}{ε_{0}} ∭ ρ d V

D'après le théorème d'Ostrogradsky, pour tout volume $V$ :

\begin{matrix} ∭_{V} d i v \vec{E} d V = \frac{1}{ε_{0}} ∭ ρ d V \\ ∭_{V} (d i v \vec{E} - \frac{ρ}{ε_{0}}) d V = 0 \end{matrix}

Forme locale du théorème de Gauss :

d i v \vec{E} = \frac{ρ}{ε_{0}}

En coordonnées cartésiennes :

\frac{\partial E_{x}}{\partial x} + \frac{\partial E_{y}}{\partial y} + \frac{\partial E_{z}}{\partial z} = \frac{ρ (x, y, z)}{ε_{0}}

Si la densité $ρ$ est finie, $E_{x}, E_{y}, E_{z}$ sont des fonctions continues et dérivables.

Dans le vide $d i v \vec{E} = 0$ .

La forme locale n'est pas utilisable (discontinuité de $\vec{E}$ ) :

Sur une charge ponctuelle.
Sur une surface chargée.
Sur une charge linéique.

4. Équations locales

a. Opérateur divergence

b. Théorème d'Ostrogradsky

c. Théorème de Gauss

d. Produit vectoriel

Convention du trièdre direct.

Orientation des angles dans l'espace.

Base orthonormée directe $({\vec{u}}_{x}, {\vec{u}}_{y}, {\vec{u}}_{z})$ .

Produits vectoriels :

\begin{matrix} {\vec{u}}_{x} \land {\vec{u}}_{y} = {\vec{u}}_{z} \\ {\vec{u}}_{y} \land {\vec{u}}_{z} = {\vec{u}}_{x} \\ {\vec{u}}_{z} \land {\vec{u}}_{x} = {\vec{u}}_{y} \end{matrix}

Produit vectoriel de deux vecteurs :

C_{x} = A_{y} B_{z} - A_{z} B_{y}

4. Équations locales

a. Opérateur divergence

b. Théorème d'Ostrogradsky

c. Théorème de Gauss

d. Produit vectoriel

e. Opérateur rotationnel

Opérateur rotationnel, agissant sur un champ vectoriel :

\vec{r o t} \vec{E} = \vec{\nabla} \land \vec{E} = (\begin{matrix} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{matrix}) \land (\begin{matrix} E_{x} \\ E_{y} \\ E_{z} \end{matrix})

\begin{matrix} \vec{r o t} \vec{E} = & (\frac{\partial E_{z}}{\partial y} - \frac{\partial E_{y}}{\partial z}) {\vec{u}}_{x} \\ + (\frac{\partial E_{x}}{\partial z} - \frac{\partial E_{z}}{\partial x}) {\vec{u}}_{y} \\ + (\frac{\partial E_{y}}{\partial x} - \frac{\partial E_{x}}{\partial y}) {\vec{u}}_{z} \end{matrix}

4. Équations locales

a. Opérateur divergence

b. Théorème d'Ostrogradsky

c. Théorème de Gauss

d. Produit vectoriel

e. Opérateur rotationnel

f. Théorème de Stokes

$C$ : Courbe fermée orientée. $S$ : surface ouverte délimitée par $C$.

$C$ est le contour de la surface $S$.

Orientation de la surface par rapport au contour.

La circulation d'un vecteur sur une courbe fermée orientée est égale au flux de son rotationnel sur une surface délimitée par la courbe :

\oint_{C} \vec{E} \cdot \vec{t} d l = \iint_{S} (\vec{r o t} \vec{E}) \cdot \vec{n} d S

4. Équations locales

a. Opérateur divergence

b. Théorème d'Ostrogradsky

c. Théorème de Gauss

d. Produit vectoriel

e. Opérateur rotationnel

f. Théorème de Stokes

g. Conservation de la circulation

Propositions équivalentes pour le champ électrostatique $\vec{E}$ :

Sa circulation entre deux points ne dépend pas du chemin (circulation conservative).
Il dérive d'un potentiel.
C'est un champ conservatif.
Sa circulation sur toute courbe fermée est nulle.

Pour toute courbe fermée $C$ :

\oint_{C} \vec{E} \cdot \vec{t} d l = 0

D'après le théorème de Stokes, pour toute surface ouverte $S$ :

\iint_{S} (\vec{r o t} \vec{E}) \cdot \vec{n} d S = 0

Forme locale de la conservation de la circulation :

\vec{r o t} \vec{E} = \vec{0}

4. Équations locales

a. Opérateur divergence

b. Théorème d'Ostrogradsky

c. Théorème de Gauss

d. Produit vectoriel

e. Opérateur rotationnel

f. Théorème de Stokes

g. Conservation de la circulation

h. Équation de Poisson

Lois de l'électrostatique :

\begin{matrix} d i v \vec{E} = \frac{ρ}{ε_{0}} \\ \vec{r o t} \vec{E} = \vec{0} \Leftrightarrow i l e x i s t e V t e l q u e \vec{E} = - \vec{g r a d} V \end{matrix}

Équation aux dérivées partielles pour le potentiel :

d i v (\vec{g r a d} V) = - \frac{ρ}{ε_{0}}

Laplacien d'un champ scalaire :

Δ V = d i v (\vec{g r a d} V)

Autre notation : $\nabla^{2} V$ .

En coordonnées cartésiennes :

Δ V = \frac{\partial^{2} V}{\partial x^{2}} + \frac{\partial^{2} V}{\partial y^{2}} + \frac{\partial^{2} V}{\partial z^{2}}

Laplacien en coordonnées cylindriques :

Δ (f) = \frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial f}{\partial r}) + \frac{1}{r^{2}} \frac{\partial^{2} f}{\partial θ^{2}} + \frac{\partial^{2} f}{\partial z^{2}}

Laplacien en coordonnées sphériques :

Δ (f) = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial f}{\partial r}) + \frac{1}{r^{2} sin θ} \frac{\partial}{\partial θ} (sin θ \frac{\partial f}{\partial θ}) + \frac{1}{r^{2} {sin}^{2} θ} \frac{\partial^{2} f}{\partial φ^{2}}

Équation de Poisson de l'électrostatique :

Δ V = - \frac{ρ}{ε_{0}}

4. Équations locales

a. Opérateur divergence

b. Théorème d'Ostrogradsky

c. Théorème de Gauss

d. Produit vectoriel

e. Opérateur rotationnel

f. Théorème de Stokes

g. Conservation de la circulation

h. Équation de Poisson

i. Équation de Laplace

Problème d'électrostatique avec deux conducteurs dans le vide

Dans le vide $Δ V = 0$ (équation de Laplace).

Conditions limites :

Sur la surface d'un conducteur : $V = V_{1}$ ou $V = V_{2}$ .
À très grande distance : $V = 0$ .

Solution unique $V (x, y, z)$ .

Champ électrostatique $\vec{E} = - \vec{g r a d} V$ .