Dipôle rayonnant

1. Dipôle oscillant

a. Définition

Dipôle oscillant : dipôle électrique dont le moment dipolaire oscille à la pulsation $ω$ .

\vec{p} (t) = R e [p_{0} e^{i ω t}] {\vec{u}}_{z}

Taille du dipôle : $a$.

p (t) = a q

Oscillation de $a$ ou bien oscillation de $q$.

$(M, {\vec{u}}_{r}, {\vec{u}}_{θ})$ : plan de symétrie de $\vec{E}$ , d'antisymétrie de $\vec{B}$ .

\begin{matrix} \vec{E} = E_{r} (r, θ, t) {\vec{u}}_{r} + E_{θ} (r, θ, t) {\vec{u}}_{θ} \\ \vec{B} = B_{φ} (r, θ, t) {\vec{u}}_{φ} \end{matrix}

1. Dipôle oscillant

a. Définition

b. Rayonnement

Nombre d'onde :

k = \frac{2 π}{λ}

Rayonnement dans le vide :

k = \frac{ω}{c}

Le dipôle est très petit : $a\ll\lambda$

Approximation dipolaire :

r ≫ a

Zone de rayonnement :

r ≫ λ

\begin{matrix} \vec{\underset{̲}{E}} = - \frac{p_{0} ω^{2}}{4 π ε_{0} c^{2}} \frac{sin θ}{r} cos (ω t - k r) {\vec{u}}_{θ} \\ \vec{\underset{̲}{B}} = - \frac{p_{0} ω^{2}}{4 π ε_{0} c^{3}} \frac{sin θ}{r} cos (ω t - k r) {\vec{u}}_{φ} \end{matrix}

Localement similaire à une onde plane progressive monochromatique de vecteur d'onde :

\vec{k} = k {\vec{u}}_{r} = \frac{ω}{c} {\vec{u}}_{r}

Influence de la distance et de la colatitude :

\frac{sin (θ)}{r}

Pas de rayonnement dans l'axe du dipôle.

Vecteur de Poynting moyen :

< \vec{Π} > = \frac{p_{0}^{2} ω^{4}}{32 π^{2} ε_{0} c^{3}} \frac{{sin}^{2} θ}{r^{2}} {\vec{u}}_{r}

Puissance rayonnée à travers une sphère de rayon $r$ :

\begin{matrix} P & = \int_{0}^{π} < Π > 2 π r^{2} sin θ d θ \\ = \frac{p_{0}^{2} ω^{4}}{32 π^{2} ε_{0} c^{3}} \frac{2 π r^{2}}{r^{2}} \int_{0}^{π} {sin}^{3} θ d θ \\ = \frac{p_{0}^{2} ω^{4}}{12 π ε_{0} c^{3}} \end{matrix}

Dans la zone de rayonnement, la puissance moyenne rayonnée à travers une sphère de rayon $r$ ne dépend pas de $r$ .

Conservation de l'énergie électromagnétique : la puissance traversant une sphère de rayon $R_{1}$ est égale à la puissance traversant une sphère de rayon $R_{2} > R_{1}$ .

1. Dipôle oscillant

a. Définition

b. Rayonnement

c. Diagramme de rayonnement

Représentation de la puissance surfacique en fonction de l'angle :

ρ (θ) = \frac{< Π > (θ)}{< Π >_{m a x}} = {sin}^{2} (θ)

2. Applications

a. Antenne filaire

Émission d'une onde radio par une antenne filaire

Pour un courant sinusoïdal de pulsation $ω$ , émission d'une onde électromagnétique de longueur d'onde (dans le vide) :

λ = \frac{2 π c}{ω}

Élément de fil de longueur $d z ≪ λ$ assimilable à un dipôle oscillant.

\begin{matrix} \vec{p} = a q (t) {\vec{u}}_{z} = p (t) {\vec{u}}_{z} \\ I (t) = \frac{d q (t)}{d t} = \frac{1}{a} \frac{d p}{d t} \\ I (t) = R e [\frac{i ω p_{0}}{a} e^{i ω t}] \end{matrix}

$\underset{̲}{I} (z)$ : amplitude complexe du courant de l'élément $dz$.

Dipôle de moment :

\underset{̲}{p} (z) = \frac{\underset{̲}{I} (z)}{i ω} d z

Intégrale sur $z$ pour obtenir le champ rayonné par l'antenne.

2. Applications

a. Antenne filaire

b. Diffusion

L'onde diffusée vient de l'interaction entre l'onde incidente et la matière :

atomes et molécules,
particules solides en suspension (aérosols),
gouttelettes liquides (nuages).

Diffusion par les atomes ou les petites molécules : le champ électrique de l'onde incidente monochromatique met les électrons liés en mouvement. Chaque atome se comporte comme un dipôle oscillant qui rayonne à la fréquence de l'onde incidente.

Les différents atomes émettent de manière incohérentes (pas d'interférences).

Modèle classique (non quantique) de l'électron lié élastiquement :

Taille de l'atome ou de la molécule $\ll\lambda$.
Champ électrique de l'onde dans l'atome :

\vec{E} = E_{0} cos (ω t) {\vec{u}}_{z}

L'électron se déplace sur l'axe ($Oz$) où $O$ est le centre de l'atome.
Force de rappel élastique $- m ω_{0}^{2} z$ .
Force de frottement $- α \dot{z}$ .

Loi de Newton :

m \ddot{z} = - α \dot{z} - m ω_{0}^{2} z - e E_{0} cos (ω t)

\ddot{z} + \frac{1}{τ} \dot{z} + ω_{0}^{2} z = - \frac{e E_{0}}{m} cos (ω t)

Régime permanent :

z (t) = R e [\underset{̲}{Z} e^{i ω t}]

\underset{̲}{Z} = \frac{- e E_{0} / m}{(ω_{0}^{2} - ω^{2}) + i \frac{ω}{τ}}

Moment dipolaire dû au déplacement de l'électron :

\vec{p} = - e z {\vec{u}}_{z}

Dipôle oscillant à la pulsation $\omega$ :

\underset{̲}{p} = \frac{e^{2} E_{0} / m}{(ω_{0}^{2} - ω^{2}) + i \frac{ω}{τ}}

p_{0}^{2} = \frac{e^{4} E_{0}^{2} / m^{2}}{{(ω_{0}^{2} - ω^{2})}^{2} + \frac{ω^{2}}{τ^{2}}}

L'atome émet un rayonnement dipolaire dont l'axe $Oz$ coïncide avec la direction de $\vec{E}$ de l'onde incidente.

Puissance moyenne émise par un atome :

P = \frac{p_{0}^{2} ω^{4}}{12 π ε_{0} c^{3}}

Facteur de qualité : $Q = ω_{0} τ$ .

P = \frac{e^{4} E_{0}^{2}}{12 π ε_{0} c^{3} m^{2}} \frac{ω^{4}}{{(ω_{0}^{2} - ω^{2})}^{2} + \frac{1}{Q^{2}} ω_{0}^{2} ω^{2}}

$ω_{0}$ : fréquence d'absorption ou d'émission, liée à une transition $Δ E = ℏ ω_{0}$ .

Pour un atome $f_{0} \approx 1 0^{17} H z$ (résonance dans l'UV).

$τ \approx 1 0^{- 8} s$ .

$Q ≫ 1$ .

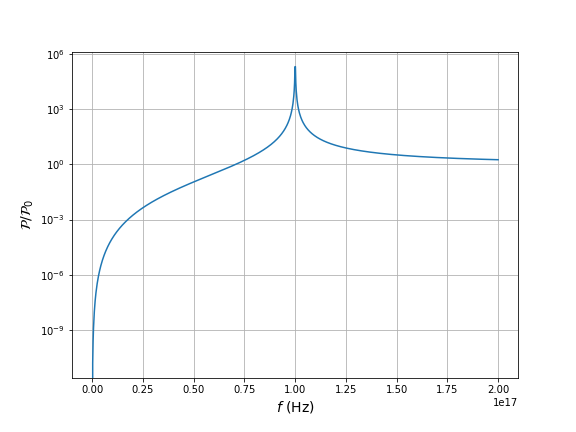
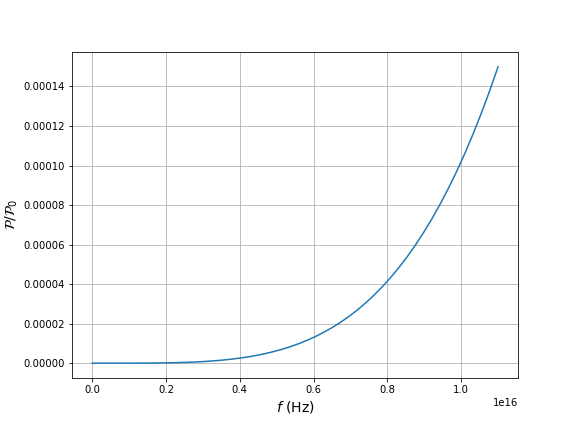
Diffusion de Rayleigh : $ω ≪ ω_{0}$ .

P \approx \frac{e^{4} E_{0}^{2}}{12 π ε_{0} c^{3} m} \frac{ω^{4}}{ω_{0}^{4}}

P \approx \frac{A}{λ^{4}}

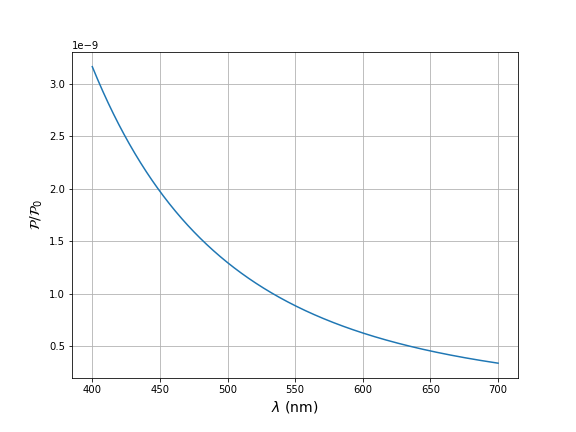
Diffusion de la lumière solaire par les molécules de l'atmosphère : couleur bleue du ciel.

Lumière solaire non polarisée : dans un plan perpendiculaire à la direction incidente, toutes les directions de $\vec{p}$ sont équiprobables.

Pour l'observateur, $\vec{E}$ est dans le plan défini par la direction du dipôle et la ligne de visée.

La diffusion à $90^{\circ}$ de la lumière incidente est minimale et de polarisation rectiligne.

L'intensité diffusée augmente avec $|\alpha|$.

La proportion de lumière polarisée rectilignement diminue avec $|\alpha|$.