Moteur synchrone à aimants permanents
1. Introduction
Ce document traite du moteur synchrone auto-piloté à commande à 6 états. Ce type de moteur est connu sous le nom de moteur à courant continu sans balais (Brushless direct current motors, BLDC).
Le bobinage du stator est triphasé. Il comporte donc au minimum trois bobines disposées à 120 degrés l'une de l'autre. L'alimentation en courant de ces trois bobines et la commutation à 6 états sont expliquées dans Commutateur triphasé à 6 états.
On s'intéresse particulièrement au cas d'un moteur à 3 bobines avec un rotor à 8 pôles (moteur 3N8P). L'alimentation du stator est pilotée par la position du rotor, laquelle est déterminée au moyen de 3 sondes à effet Hall.
La commande est effectuée par un pont de six transistors dont la commutation est pilotée par la position du rotor. Ce système permet de faire fonctionnement la machine en moteur mais aussi en générateur délivrant une tension ondulée mais de signe constant.
2. Classification des moteurs synchrones
Il est d'usage de distinguer deux types de moteurs à aimants permanents :
- BLDC : brushless direct-current motor.
- PMSM : permanent magnets synchronous motor.
Le moteur BLDC est caractérisé par une forme de force électromotrice (en fonction de l'angle du rotor) trapézoïdale. En conséquence, la commande optimale d'un moteur BLDC se fait avec des tensions de forme carrée, par une commande à 6 états. Le moteur PMSM est caractérisé par une f.é.m. de forme sinusoïdale et en conséquence, sa commande optimale est obtenue avec des tensions sinusoïdales. L'attribut direct-current pour le moteur BLDC vient du fait que ce moteur fonctionne comme un moteur à courant continu dont la commutation par balais serait remplacée par une commutation électronique.
Remarquons que la forme du couple en fonction de l'angle du rotor (pour un courant constant dans les bobines du stator) est exactement la même que celle de la f.é.m..
Cependant, les petits moteurs qualifiés de BLDC (utilisés par exemple pour le modélisme ou dans les petits drones) ont en réalité une forme de f.é.m. sinusoïdale ou quasi sinusoïdale mais pas du tout trapézoïdale (Why most hobby grade BLDC out runners are actually permanent magnet synchronous motors (PMSM)). Ces moteurs sont pourtant considérés comme de type BLDC car ils sont utilisés avec une commande à 6 états (donc une tension de forme carrée). Bien que cette commande ne soit pas optimale, principalement à cause des ondulations de couple qui en résultent, elle fonctionne très bien.
La distinction entre moteurs BLDC et PMSM n'est pas toujours faite. Par exemple, la page de présentation des circuits intégrés de pilotage de ces moteurs de Texas Instrument est intitulée Integrated control BLDC drivers alors qu'elle concerne les deux types de moteurs. Les différents types de pilotes catalogués dans cette page sont :
- Sensorless, Tapezoïdal : commande à 6 états sans capteurs.
- Sensored, Tapezoïdal : commande à 6 états avec capteurs. C'est la méthode de commande que nous utilisons dans ce document.
- Field-oriented control, Sensorless : commande sinusoïdale sans capteurs.
Finalement, la distinction entre BLDC et PMSM introduit une confusion dans la compréhension du fonctionnement de ces moteurs. Il serait selon nous plus clair d'utiliser le terme général de moteur synchrone à aimants permanents dans tous les cas. Un tel moteur, quelle que soit la forme de sa f.é.m. (trapézoïdale, sinusoïdale ou intermédiaire) peut être piloté par une commande à 6 états ou par une commande sinusoïdale, sachant que la première est optimale lorsque la f.é.m. est trapézoïdale, la seconde l'est pour une f.é.m. sinusoïdale. Dans les deux cas, l'intérêt de la commande à 6 états est sa simplicité relative. La commande sinusoïdale, plus complexe, n'est utilisée en pratique que lorsque la f.é.m. est sinusoïdale. Dans le cas d'une commande à 6 états, le synchronisme entre le champ tournant et le rotor est toujours vérifiée en moyenne bien qu'il ne le soit pas à tout instant (car le champ tourne par sauts).
Il nous semble que la confusion sur la classification de ces moteurs vient du fait que certains attribuent la distinction entre BLDC et PMSM au niveau du moteur lui-même (la forme de la f.é.m.) alors que d'autres l'attribuent à l'électronique de commande (ce qui nous semble plus pertinent).
Le moteur étudié dans ce document présente une forme de f.é.m. sinusoïdale et devrait en théorie être considéré comme PMSM. Nous allons cependant le faire fonctionner avec une commande à 6 états. La commande à 6 états est relativement aisée à réaliser car elle ne nécessite que trois capteurs à effet Hall pour déterminer la position du rotor et son algorithme de contrôle est très simple. La commande sinusoïdale est beaucoup plus difficile à réaliser : elle nécessite une détermination beaucoup plus fine de la position du rotor (avec un encodeur) et l'algorithme de calcul est beaucoup plus complexe.
Le rotor est constitué d'aimants permanents plats assemblés sur les faces d'un polygône. Ces aimants plats sont aimantés perpendiculairement à leurs faces. Les résultats que nous obtenons, en particulier la forme sinusoïdale de la f.é.m., sont liés au fait que l'aimantation est uniforme dans un aimant. Pour obtenir une forme de f.é.m. trapézoïdale, il faudrait utiliser des aimants de forme cylindrique avec une aimantation radiale. Il semble que les moteurs qualifiés BLDC bas de gamme utilisent des aimants plats (certainement moins coûteux), ce qui expliquerait la forme de f.é.m. sinusoïdale observée sur ces moteurs.
3. Modélisation du moteur
3.a. Description
La figure suivante montre une coupe transversale du moteur à 3 bobines avec un stator à 8 pôles (3N8P) :
Figure pleine pageLa longueur d'un aimant (dans la direction de l'axe de rotation) est égale à sa largeur b=30 mm (sa grande face est carrée). L'épaisseur d'un aimant est a=3 mm. Le pôle nord d'un aimant est repéré par le coloriage rouge, le pôle sud par le coloriage bleu. La distance entre le centre d'un aimant et l'axe du moteur est :
Une bobine du stator est un enroulement de spires carrées (N=250 spires). Le diamètre interne est d=50 mm et l'épaisseur e=15 mm. La longueur est c=80 mm. Ces dimensions sont celles de bobines de laboratoire d'usage général. La longueur est certainement excessive pour cette application car une grande partie de la bobine est peu sensible au champ généré par les aimants (et réciproquement). La distance entre l'axe du moteur et la face d'entrée des bobines est notée rb (elle vaut environ 55 mm). Un noyau en fer doux laminé sera ajouté à l'intérieur de chaque bobine mais nous n'en tiendrons pas compte pour la simulation.
Remarquons qu'un rotor à 8 aimants permet de s'approcher assez bien du cas idéal où les aimants forment un arc de cercle, ce qui permet de réduire la distance entre les aimants et le noyau en fer du rotor.
Dans la position du rotor représentée sur la figure précédente, l'alimentation correcte des bobine est (0,I,-I). Les deux aimants qui font face à B2 contribuent à un couple dans le même sens. Les deux aimants qui font face à B3 contribuent à un couple dans le même sens et de même sens que le précédent. Ces 4 aimants contribuent donc au couple dans le même sens. Lorsque le rotor a tourné de 15 degrés dans le sens direct, l'alimentation des bobines doit basculer à l'état (-I,I,0). le couple est alors produit par les 4 aimants qui font face à B1 d'une part, à B2. Après un cycle de 6 états de commutation, le champ statorique a tourné de 360 degrés (par saut de 60 degrés) mais le rotor a tourné de 90 degrés. La vitesse angulaire du rotor est donc le quart de la vitesse du champ statorique.
3.b. Commutation à 6 états
import numpy as np
from matplotlib.pyplot import *
DEG2RAD = np.pi/180
RAD2DEG = 180/np.pi
Dans le cas de la commutation triphasée à 6 états, les intensités des courants dans les trois bobines suivent la séquence suivante :
À chaque changement des tensions, ces courants s'établissent avec un temps supposé petit devant la durée d'un état. Par ailleurs, l'effet de la force électromotrice due au mouvement du rotor (force contre-électromotrice) est négligé. Le calcul exact du courant dans les bobines sera abordé plus loin.
L'intensité du courant I est ajustée par le rapport cyclique du découpage de la tension d'alimentation.
sequence_alim = [[1,-1,0],[1,0,-1],[0,1,-1],[-1,1,0],[-1,0,1],[0,-1,1]]
La fonction suivante donne une représentation graphique de l'état du stator :
def tracer_stator(etat):
alim = sequence_alim[etat]
styles = ["b-","k-","r-"]
for i in range(3):
a = i*120
x = np.cos(a*DEG2RAD)
y = np.sin(a*DEG2RAD)
plot([0,x],[0,y],styles[alim[i]+1])
text(x,y,"%d"%alim[i])
La fonction suivante donne une représentation graphique du rotor :
def tracer_rotor(Np,theta,R):
# Np : nombre de pôles
# theta : angle
# R : rayon
da = 360/Np
style = ["r-","b-"]
js = 0
for i in range(Np):
a = theta+i*da
x1 = np.cos((a)*DEG2RAD)
y1 = np.sin((a)*DEG2RAD)
plot([0,x1],[0,y1],"k--")
a = theta+(i-0.5)*da
x1 = R*np.cos((a)*DEG2RAD)
y1 = R*np.sin((a)*DEG2RAD)
x2 = R*np.cos((a+da)*DEG2RAD)
y2 = R*np.sin((a+da)*DEG2RAD)
plot([x1,x2],[y1,y2],style[js])
js = (js+1)%2
Voici les 6 états, sachant que le rotor tourne de 15 degrés à chaque changement d'état :
figure(figsize=(3*6,2*6))
subplot(231)
grid()
xlim(-1.1,1.1)
ylim(-1.1,1.1)
tracer_stator(0)
tracer_rotor(8,15,0.5)
subplot(232)
grid()
xlim(-1.1,1.1)
ylim(-1.1,1.1)
tracer_stator(1)
tracer_rotor(8,15*2,0.5)
subplot(233)
grid()
xlim(-1.1,1.1)
ylim(-1.1,1.1)
tracer_stator(2)
tracer_rotor(8,15*3,0.5)
subplot(234)
grid()
xlim(-1.1,1.1)
ylim(-1.1,1.1)
tracer_stator(3)
tracer_rotor(8,15*4,0.5)
subplot(235)
grid()
xlim(-1.1,1.1)
ylim(-1.1,1.1)
tracer_stator(4)
tracer_rotor(8,15*5,0.5)
subplot(236)
grid()
xlim(-1.1,1.1)
ylim(-1.1,1.1)
tracer_stator(5)
tracer_rotor(8,15*6,0.5)
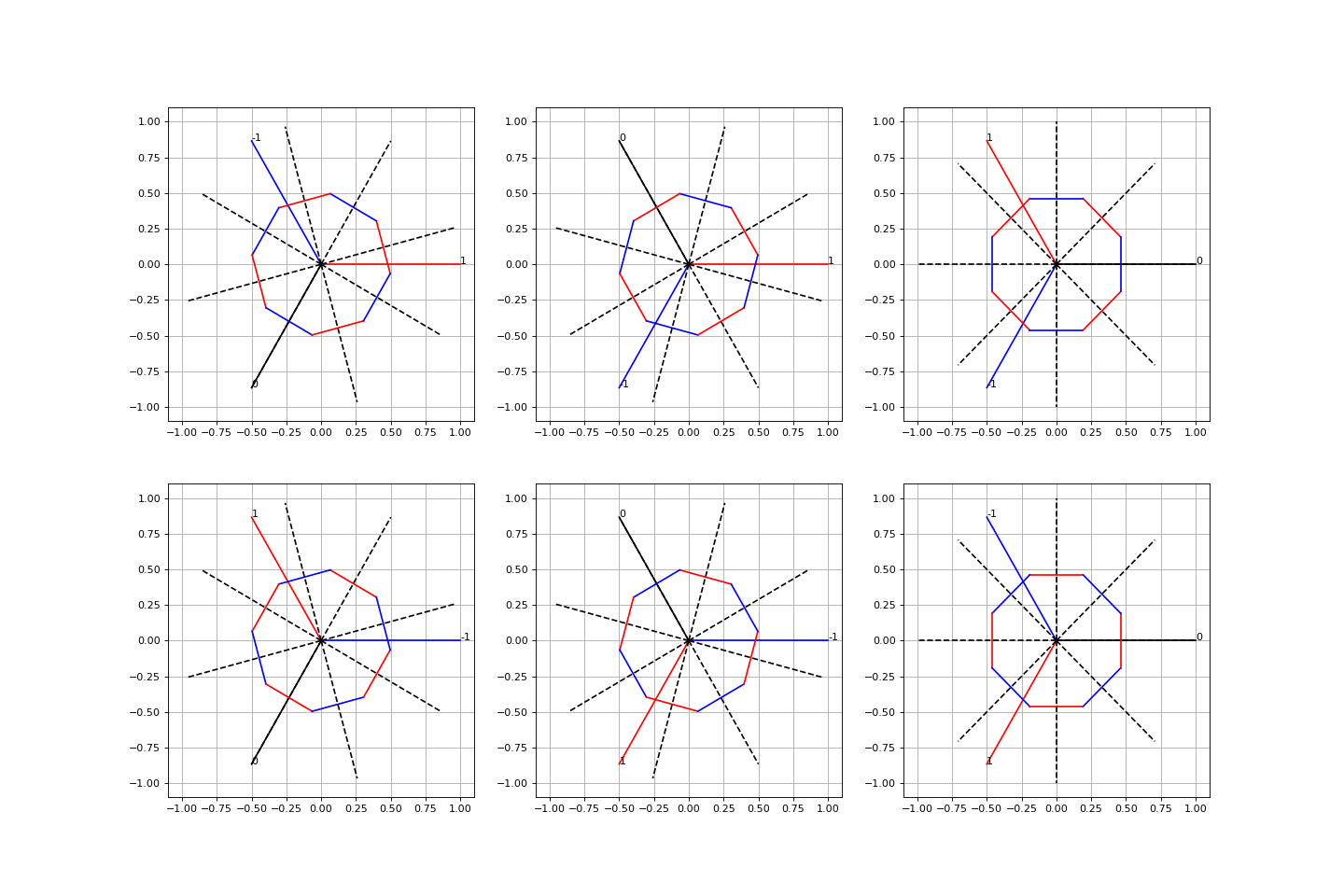 fig1.pdf
fig1.pdf
Les trois bobines du stator sont représentées par trois traits pleins partant du centre. La couleur indique le sens du champ magnétique généré. La contribution du couple d'un aimant et d'une bobine est proportionnelle au produit vectoriel du moment magnétique de l'aimant et du champ magnétique créé par la bobine. L'examen des 6 états montre que le couple est le même à chaque état (mais le rotor tourne pendant un état).
3.c. Flux magnétique et couple moteur
On adopte un modèle bidimensionnel, avec invariance par translation dans la direction Z (axe du moteur). Les aimants sont idéaux, c'est-à-dire que leur aimantation ne dépend pas du champ dans lequel il sont placés. Le champ magnétique créé par un aimant de longueur infinie et de section rectangulaire admet une expression analytique, donnée dans Flux magnétique généré par un aimant permanent. L'objectif est de calculer le flux magnétique généré par le rotor dans chaque bobine du stator. La force électromotrice développée dans chaque bobine et le moment des forces exercées par chaque bobine sur le rotor s'en déduira par dérivation (respectivement par rapport au temps et par rapport à l'angle de position du rotor).
Nous devons calculer le flux magnétique généré par un aimant quelconque du rotor dans la bobine B1 en fonction de l'angle θ définissant la position angulaire du rotor. L'angle que fait la normale de l'aimant d'indice k avec l'axe (OX) est (en degrés) :
Figure pleine pageSoit C le centre de l'aimant. Dans le repère propre à l'aimant (Cxy), le potentiel vecteur du champ créé par le courant équivalent localisé sur la face en y=b/2 s'écrit :
où est l'aimantation. Le potentiel vecteur créé par la face en y=-b/2 s'en déduit en remplaçant M par -M et b/2 par -b/2. Soient (X,Y) les coordonnées d'un point du plan dans le repère fixe (OXY). Le changement de coordonnées est une transformation affine composée d'une rotation puis d'une translation :
mu0 = 4*np.pi*1e-7
A = mu0/(2*np.pi)
Voici les fonctions permettant de calculer le potentiel vecteur en fonction de X et Y :
def f(x,y):
x += 1e-8*(x==0)
return np.float64(x)*np.log(np.float64(x)**2+np.float64(y)**2)-2*np.float64(x)+2*np.float64(y)*np.arctan(np.float64(x)/np.float64(y))
def champAz(M,a,b,alpha,ra,X,Y):
cos = np.cos(alpha)
sin = np.sin(alpha)
x = -ra+cos*X+sin*Y
y = -sin*X+cos*Y
return A*M*(f(x-a/2,y-b/2)-f(x+a/2,y-b/2)-(f(x-a/2,y+b/2)-f(x+a/2,y+b/2)))
Le flux magnétique à travers la bobine s'écrit :
où S=ce est l'aire d'une section de demi-bobine, la longueur dans la direction Z et α la compacité de l'enroulement.
La fonction suivante calcule la valeur moyenne de Az sur un rectangle constituant une demi-bobine :
def moyAz(M,a,b,alpha,ra,Xc,Yc,c,e,N):
# Xc,Yc : centre du rectangle
#c,e : dimensions du rectangle
#N : nombre de points sur chaque dimension pour le calcul de l'intégrale
X,Y = np.meshgrid(np.linspace(Xc-c/2,Xc+c/2,N),np.linspace(Yc-e/2,Yc+e/2,N))
Az = champAz(M,a,b,alpha,ra,X,Y)
return Az.mean()
La fonction suivante calcule le flux dans la bobine :
def fluxBobine(M,a,b,alpha,ra,rb,d,c,e,N):
return moyAz(M,a,b,alpha,ra,rb+c/2,d/2+e/2,c,e,N)-moyAz(M,a,b,alpha,ra,rb+c/2,-d/2-e/2,c,e,N)
Voici le flux généré par le premier aimant en fonction de l'angle θ :
a = 3e-3
b = 30e-3
d = 50e-3
e = 15e-3
c = 80e-3
ra = 38e-3
rb = 55e-3
alpha = np.arange(360)
N1 = len(alpha)
flux = np.zeros(N1)
M = 0.4/mu0
N = 100
for i in range(N1):
flux[i] = fluxBobine(M,a,b,alpha[i]*DEG2RAD,ra,rb,d,c,e,N)
figure(figsize=(16,6))
plot(alpha,flux)
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$\Phi$",fontsize=16)
grid()
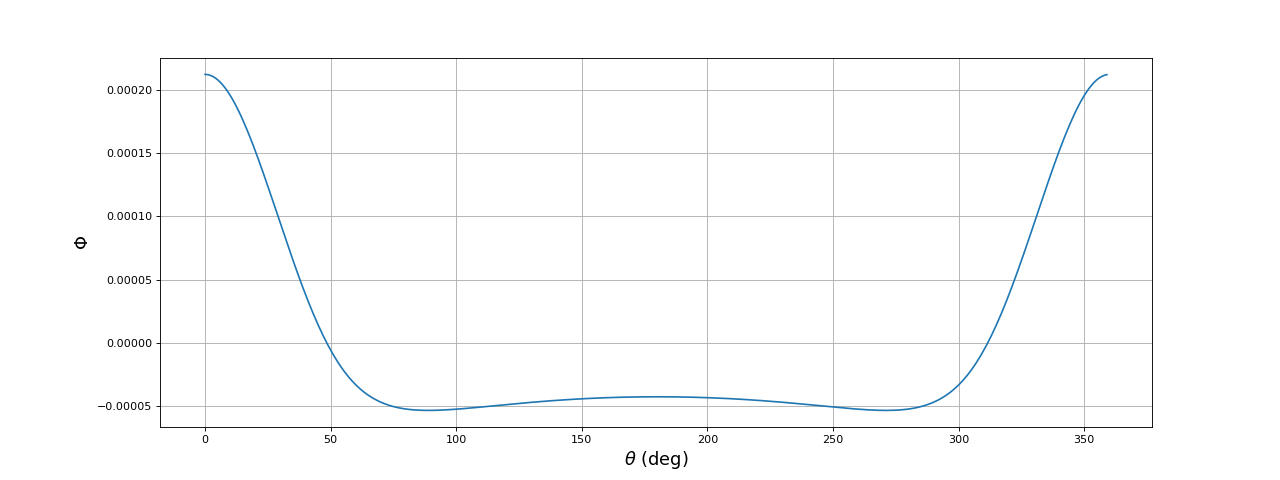 fig2.pdf
fig2.pdf
Comme attendu, le flux est maximal lorsque l'aimant est en face de la bobine. Lorsqu'il est à 180 degré, le flux est négatif mais beaucoup plus faible puisque la distance est plus grande.
La fonction suivante calcule le flux généré par les 8 aimants du rotor :
def fluxRotorBobine(M,a,b,theta,ra,rb,d,c,e,N):
flux1 = fluxBobine(M,a,b,theta,ra,rb,d,c,e,N)
flux = flux1
signe = -1
for k in range(1,8):
flux += signe*fluxBobine(M,a,b,theta+45*k*DEG2RAD,ra,rb,d,c,e,N)
signe = -signe
return flux
Voici le flux généré par le rotor en fonction de l'angle θ :
theta = np.arange(360)
N1 = len(theta)
flux = np.zeros(N1)
N = 100
for i in range(N1):
flux[i] = fluxRotorBobine(M,a,b,theta[i]*DEG2RAD,ra,rb,d,c,e,N)
figure(figsize=(16,6))
plot(theta,flux)
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$\Phi$",fontsize=16)
grid()
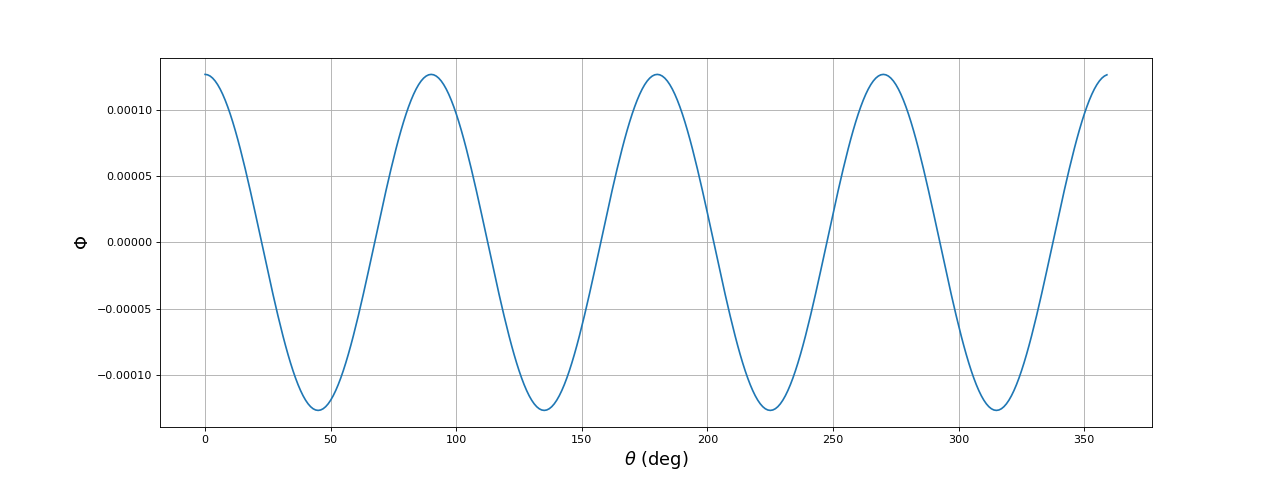 fig3.pdf
fig3.pdf
Le flux a une forme quasi sinusoïdale. Il est maximal lorsque qu'un aimant de pôle N se trouve dans l'axe de B1, ce qui se produit tous les 90 degrés, soit 4 fois par tour de rotor. Le flux s'écrit donc :
La constante dépend de l'aimantation des aimants et des caractéstiques des bobines (dimensions et bobinage).
Le flux à travers les bobines B2 et B3 se déduisent du flux à travers B1 par un déphasage de respectivement 120 et -120 degrés:
La force électromotrice dans la bobine k se déduit par dérivation :
Si le rotor tourne à une vitesse angulaire ω, la f.é.m. divisée par la vitesse angulaire du rotor s'écrit :
Voici la f.é.m. dans la bobine 1 lorsque la vitesse angulaire du rotor est constante :
from scipy.signal import convolve
fem = convolve(-flux,[1,-1],mode='same')
figure(figsize=(16,6))
fem[0] = fem[1]
plot(theta,fem)
xlabel(r"$\theta\ (\rm deg)$",fontsize=16)
ylabel(r"$\frac{e}{\omega}$",fontsize=16)
grid()
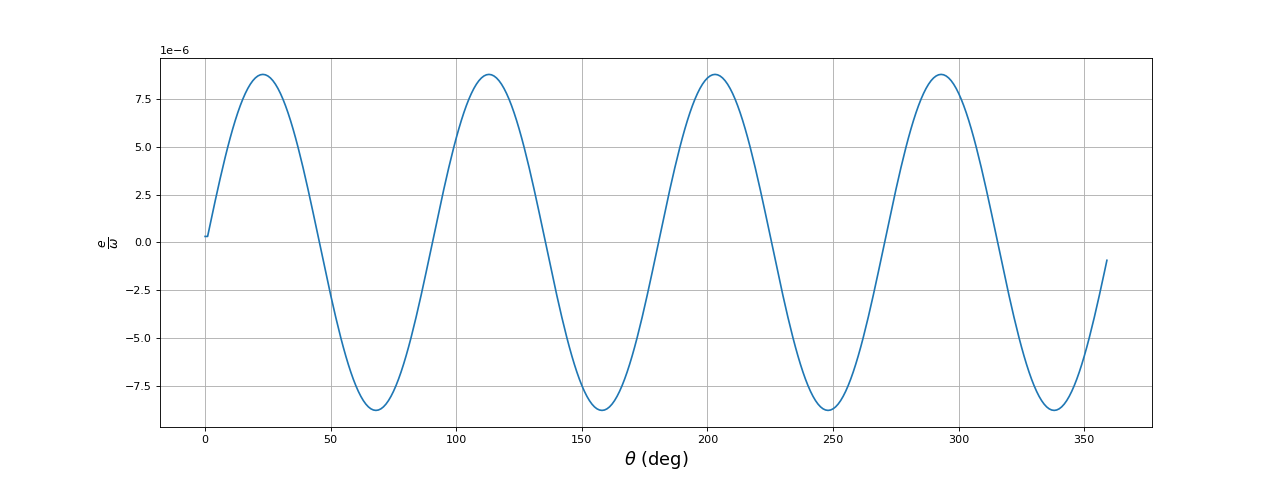 fig4.pdf
fig4.pdf
La force électromotrice en fonction de l'angle du rotor a une forme quasi sinusoïdale. Cette propriété est confirmée expérimentalement sur le moteur que nous avons réalisé (exposé plus loin). En théorie, un moteur BLDC (moteur à courant continu sans balais) a une forme d'onde trapézoïdale. Pourtant, nous avons pu aussi observer la forme sinusoïdale sur un petit moteur BLDC. En principe, si la forme de la force électromotrice est sinusoïdale, les tensions qu'il convient d'appliquer aux bobines pour obtenir un couple constant sont aussi sinusoïdales. Pour le moteur que nous étudions (et que nous avons réalisé), on applique cependant une tension de forme carrée, au moyen d'un cycle de commutation à 6 états.
Le couple moteur s'écrit :
La fonction suivante calcule le couple moteur pour un état de courant dans les bobines donné :
def coupleMoteur(fem,i1,i2,i3):
return i1*(-fem)+i2*(-np.roll(fem,120))+i3*(-np.roll(fem,240))
Voici la courbe du couple en fonction de pour six états consécutifs :
figure(figsize=(16,6))
plot(theta,coupleMoteur(fem,1,-1,0),label="I,-I,0")
plot(theta,coupleMoteur(fem,1,0,-1),label="I,0,-I")
plot(theta,coupleMoteur(fem,0,1,-1),label="0,I,-I")
plot(theta,coupleMoteur(fem,-1,1,0),label="-I,I,0")
plot(theta,coupleMoteur(fem,-1,0,1),label="-I,0,I")
plot(theta,coupleMoteur(fem,0,-1,1),label="0,-I,I")
xlabel("angle rotor (deg)",fontsize=16)
ylabel("Couple pour 1 A",fontsize=16)
legend(loc='upper right')
grid()
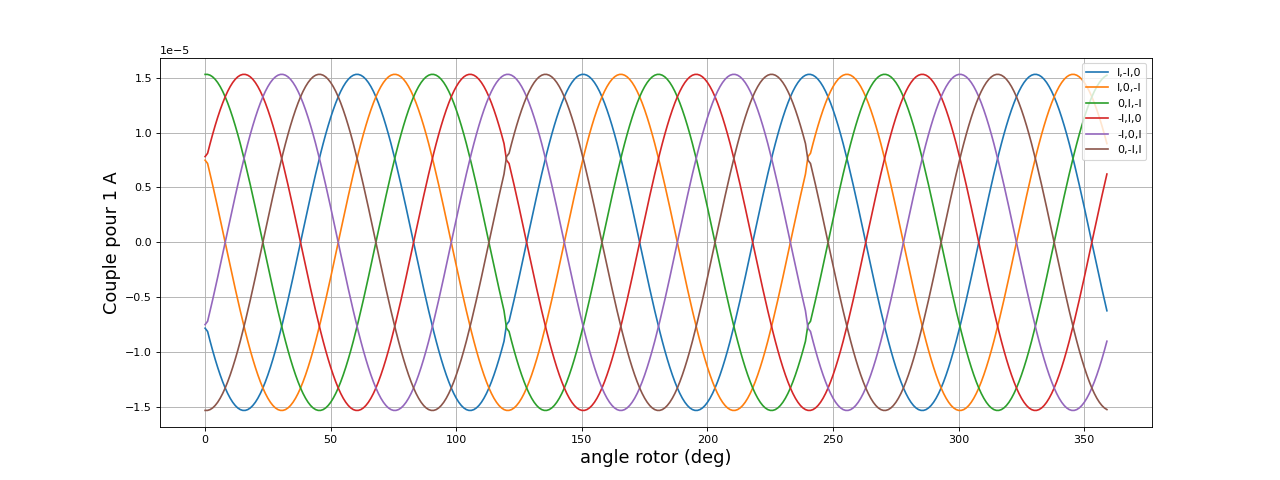 fig5.pdf
fig5.pdf
Si le rotor tourne de 15 degrés à chaque étape de la séquence de 6 états, le couple est bien constant en moyenne.
3.d. Auto-pilotage
L'auto-pilotage consiste à asservir la commutation à la position du rotor. Pendant chaque étape de la séquence de commutation des tensions appliquées aux trois bobines, le rotor doit tourner de 15 degrés. Afin de maximiser le couple, il est souhaitable que le maximum du couple se produise au milieu de chaque étape. Voyons les courbes précédentes plus en détail :
xlim(0,90)
xticks([0,15,30,45,60,75,90])
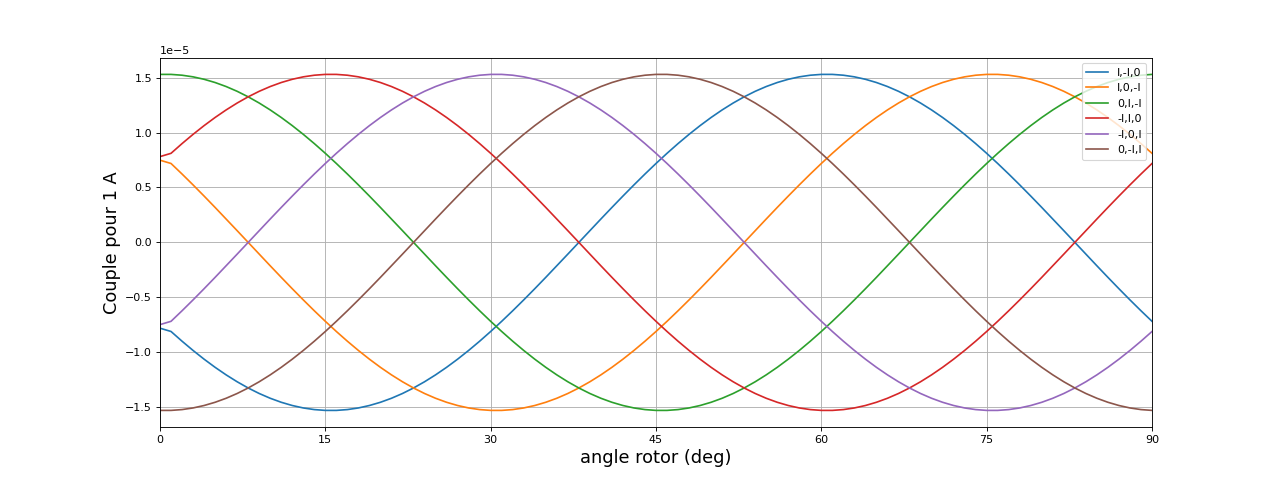 fig6.pdf
fig6.pdf
Le premier état (I,-I,0) doit être réalisé lorsque l'angle (qui définit l'angle du premier aimant) est compris entre 60-7,5 et 60+7,5. Voici les configurations pour ces deux angles limites :
figure(figsize=(2*6,6)) subplot(121) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(0) tracer_rotor(8,60-7.5,0.5) subplot(122) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(0) tracer_rotor(8,60+7.5,0.5)
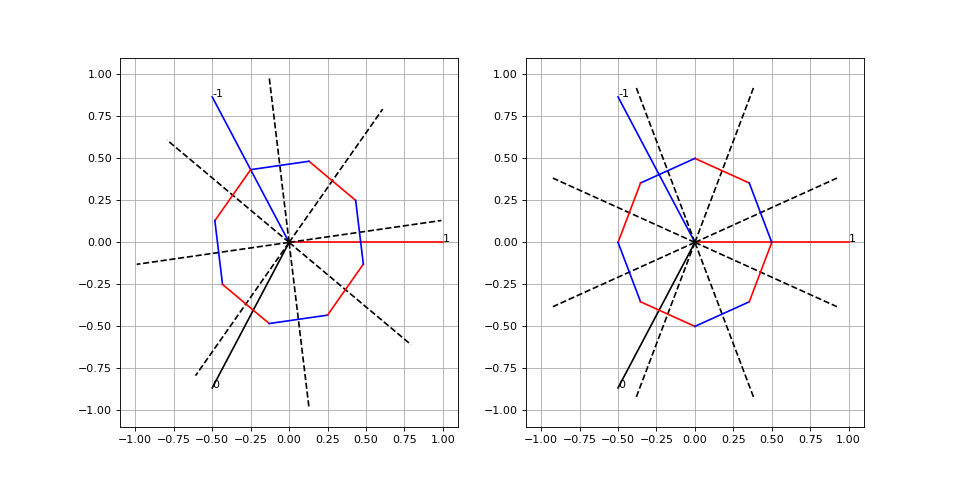 fig7.pdf
fig7.pdf
La position du rotor est déterminée par 3 capteurs à effet Hall. Chaque sonde est munie d'un comparateur et délivre donc un signal binaire : état haut si le pôle magnétique en face du capteur est un pôle nord, état bas si c'est un pôle sud. Deux capteurs doivent être dans le même état en même temps, le troisième étant dans l'autre état. Il y a donc 6 états pour les trois capteurs. Il faut choisir l'écartement angulaire des capteurs. Puisqu'un aimant occupe 45 degrés, un écartement de 30 degrés entre deux capteurs consécutifs semble un bon choix.
Voici une nouvelle version de la fonction tracer_rotor, qui représente aussi les capteurs :
def tracer_rotor(Np,theta,R,ac1,dac):
# Np : nombre de pôles
# theta : angle
# R : rayon
# ac1 : angle du premier capteur
# dac : écart angulaire entre les capteurs
da = 360/Np
style = ["r-","b-"]
js = 0
for i in range(Np):
a = theta+i*da
x1 = np.cos((a)*DEG2RAD)
y1 = np.sin((a)*DEG2RAD)
plot([0,x1],[0,y1],"k--")
a = theta+(i-0.5)*da
x1 = R*np.cos((a)*DEG2RAD)
y1 = R*np.sin((a)*DEG2RAD)
x2 = R*np.cos((a+da)*DEG2RAD)
y2 = R*np.sin((a+da)*DEG2RAD)
plot([x1,x2],[y1,y2],style[js])
js = (js+1)%2
for c in range(3):
a = (ac1+c*dac)*DEG2RAD
x = R*1.1*np.cos(a)
y = R*1.1*np.sin(a)
plot([x],[y],"ko")
text(x,y,"%d"%(c+1))
ac1 = 30 dac = 30 figure(figsize=(2*6,6)) subplot(121) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(0) tracer_rotor(8,60-7.5,0.5,ac1,dac) subplot(122) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(0) tracer_rotor(8,60+7.5,0.5,ac1,dac)
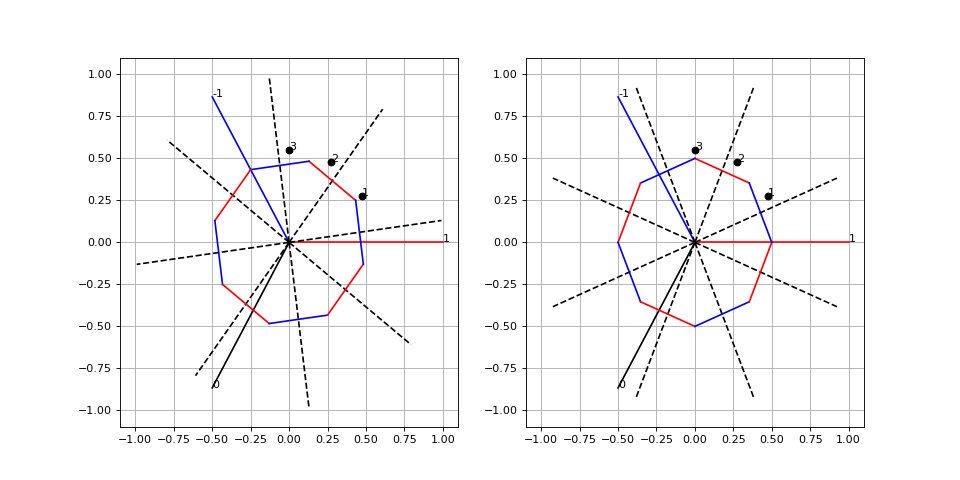 fig8.pdf
fig8.pdf
Cet état d'alimentation (I,-I,0) doit être réalisé pour l'état (0,1,0) des capteurs. Voyons l'état suivant :
figure(figsize=(2*6,6)) subplot(121) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(1) tracer_rotor(8,60-7.5+15,0.5,ac1,dac) subplot(122) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(1) tracer_rotor(8,60+7.5+15,0.5,ac1,dac)
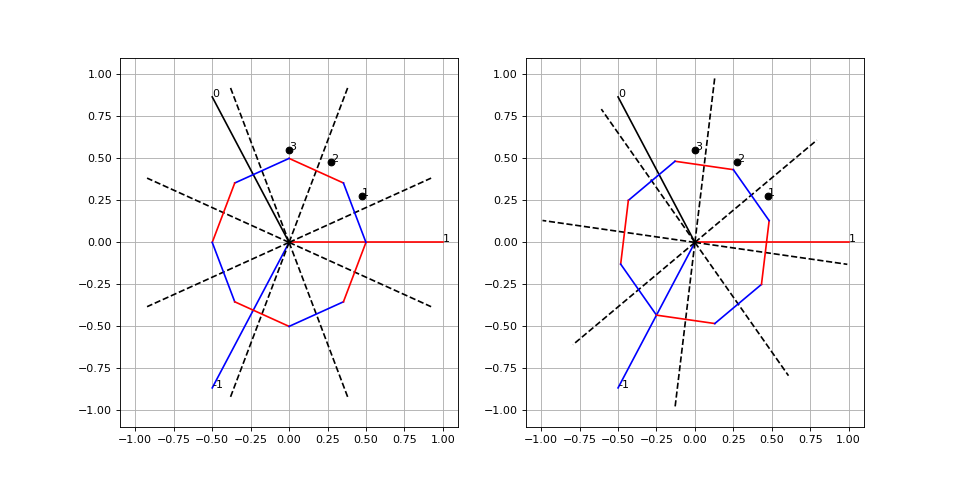 fig9.pdf
fig9.pdf
Cet état d'alimentation (I,0,-I) doit être réalisé pour l'état (0,1,1) des capteurs. Voici l'état suivant :
figure(figsize=(2*6,6)) subplot(121) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(2) tracer_rotor(8,60-7.5+15*2,0.5,ac1,dac) subplot(122) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(2) tracer_rotor(8,60+7.5+15*2,0.5,ac1,dac)
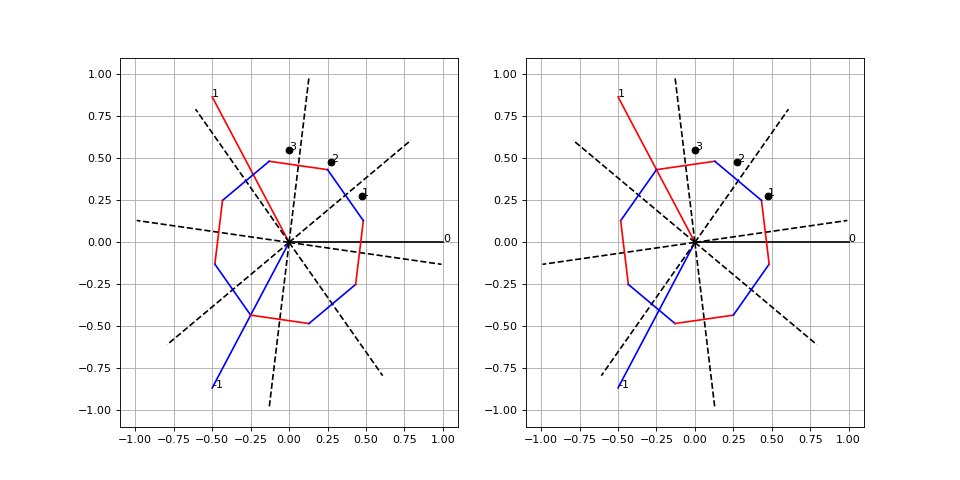 fig10.pdf
fig10.pdf
Cet état d'alimentation (0,I,-I) doit être réalisé pour l'état (0,0,1) des capteurs. Voici l'état suivant :
figure(figsize=(2*6,6)) subplot(121) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(3) tracer_rotor(8,60-7.5+15*3,0.5,ac1,dac) subplot(122) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(3) tracer_rotor(8,60+7.5+15*3,0.5,ac1,dac)
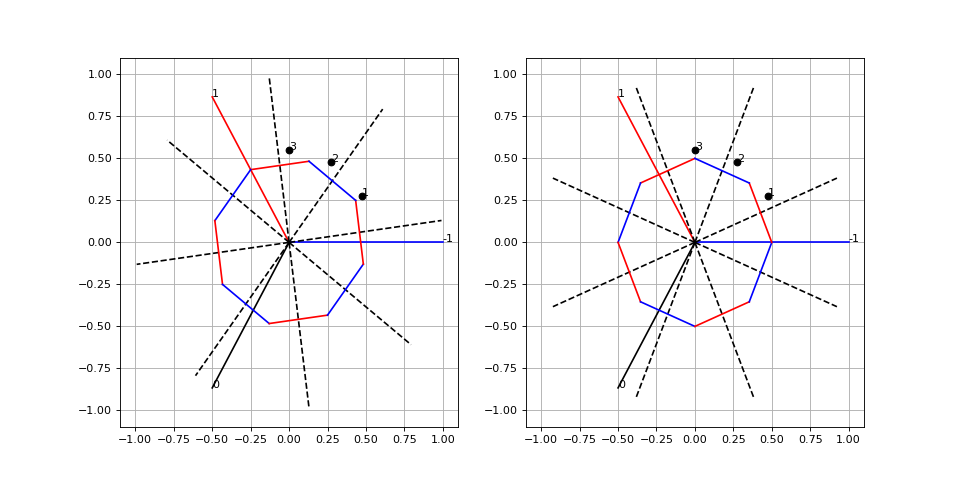 fig11.pdf
fig11.pdf
Cet état d'alimentation (-I,I,0) doit être réalisé pour l'état (1,0,1) des capteurs. Voici l'état suivant :
figure(figsize=(2*6,6)) subplot(121) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(4) tracer_rotor(8,60-7.5+15*4,0.5,ac1,dac) subplot(122) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(4) tracer_rotor(8,60+7.5+15*4,0.5,ac1,dac)
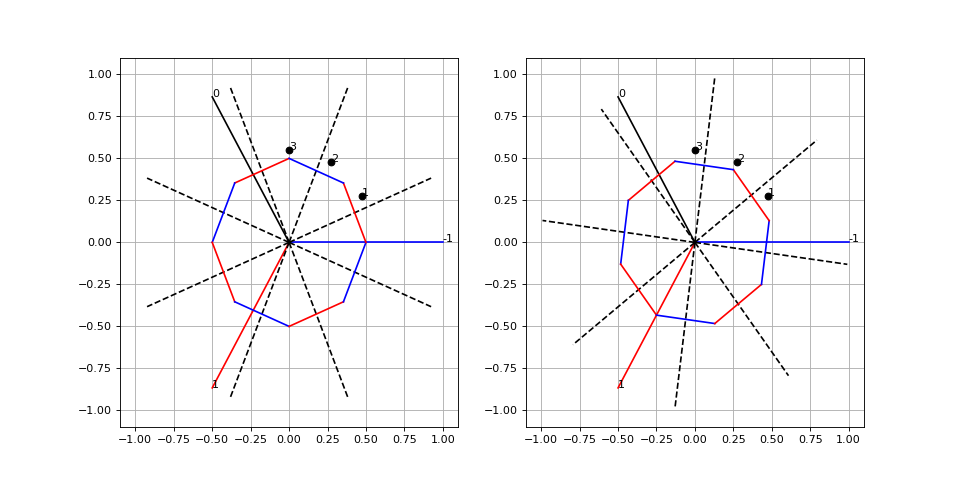 fig12.pdf
fig12.pdf
Cet état d'alimentation (-I,0,1) doit être réalisé pour l'état (1,0,0) des capteurs. Voici l'état suivant :
figure(figsize=(2*6,6)) subplot(121) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(5) tracer_rotor(8,60-7.5+15*5,0.5,ac1,dac) subplot(122) grid() xlim(-1.1,1.1) ylim(-1.1,1.1) tracer_stator(5) tracer_rotor(8,60+7.5+15*5,0.5,ac1,dac)
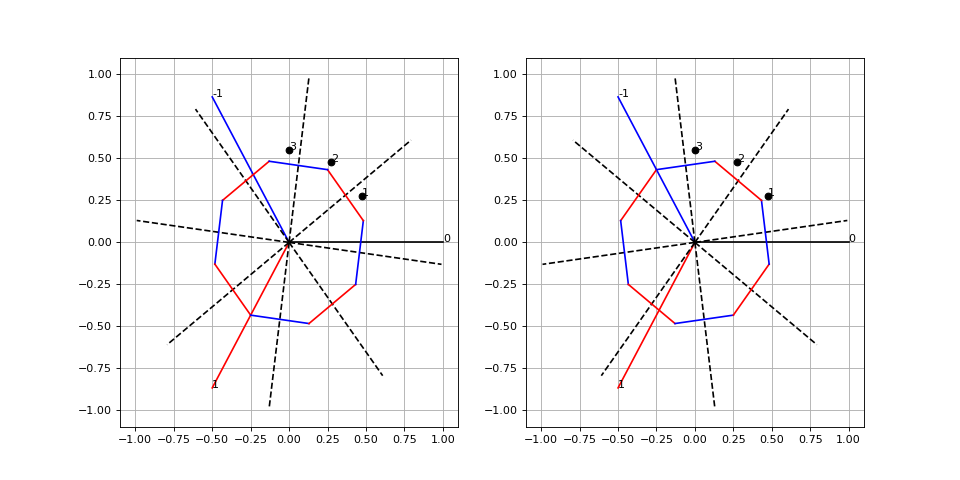 fig13.pdf
fig13.pdf
Cet état d'alimentation (0,-I,I) doit être réalisé pour l'état (1,1,0) des capteurs. Voici l'état suivant :
Voici la séquence des états des capteurs et les états correspondants des courants dans les bobines (en l'absence de force contre-électromotrice) :
En réalité, la séquence des courants dans les bobines est notablement différente de la séquence idéale donnée ci-dessus pour trois raisons :
- L'effet de la force contre-électromotrice.
- L'effet du temps de réponse de la bobine L/r.
- La source d'énergie n'applique pas une tension constante.
La source d'énergie (accumulateur ou alimentation stabilisée) alimente les bobines via un pont de 6 transistors (3 bras de 2 transistors). Un condensateur de forte capacité est généralement placé aux bornes de la source pour lisser les variations de tension mais il peut rester des variations non négligeables, dont l'amplitude dépend des caractéstiques de la source.
3.e. Simulation du moteur
Pour cette simulation, on suppose que la source délivre une tension parfaitement constante E. Chaque transistor du pont est modélisé par un interrupteur en parallèle avec une diode. Voici le schéma électrique du stator et de son circuit de commande :
Figure pleine pageLe pont de transistors comporte trois bras de deux transitors, un pour chaque bobine.
Ce modèle néglige l'inductance mutuelle entre les bobines devant leur auto-inductance mais sa prise en compte revient à diminuer l'auto-inductance de chaque bobine.
Si est la vitesse angulaire du moteur à l'instant considéré, la force électromotrice qui apparaît dans la bobine k est :
Dans le schéma électrique, cette f.é.m. est dans le même sens que l'intensité du courant. Elle est qualifiée de force contre-électromotrice car elle tend à s'opposer au passage du courant, c'est-à-dire qu'elle est de signe opposé au courant (justification donnée plus loin). On nommera force contre-électromotrice l'opposée de la f.é.m.
Les flux magnétiques sont donnés par :
La programme de commande décrit plus loin (programme Arduino) effectue une commutation dans laquelle les bornes 1,2 et 3 des trois bobines sont alternativement dans trois états différents :
- À un potentiel E par rapport à la masse (interrupteur Kk fermé et K'k ouvert).
- À un potentiel nul par rapport à la masse (interrupteur Kk ouvert et K'k fermé).
- À un potentiel libre (interrupteurs ouverts), c'est-à-dire non imposé par le pont.
Soit le temps de réponse d'une bobine. Un des 6 états d'alimentation des bobines est en fait obtenu par un découpage à une fréquence f qui doit être en principe beaucoup plus grande que . Le rapport cyclique du découpage détermine la tension effective qui est appliquée aux bobines. Dans le modèle, on fait comme si cette tension effective était directement appliquée aux bobines.
Considérons un des 6 états du cycle, où la borne m est au potentiel effectif , la borne n au potentiel nul et le bras de pont de la borne p a ses deux transistors ouverts.
On a d'une part la relation entre les tensions (loi des mailles) :
d'autre part la relation entre les courants (loi des nœuds) :
Dans le cas d'un pont de transistors à bijonction, ont ajoute des diodes de roue libre comme indiqué sur le schéma. Dans le cas d'un pont de transistors MOSFET, la diode représentée sur le schéma pour chaque transistor modélise son comportement lorsque la source a un potentiel supérieur au drain. Lorsque le transistor est bloquant (interrupteur ouvert), un courant peut donc circuler dans le sens passant de cette diode. Une des deux diodes d'un bras du pont devient passante juste après que les deux transistors deviennent bloquants (deux interrupteurs ouverts). En effet, le courant dans la bobine correspondante ne peut pas s'annuler instantanément (à cause de son auto-inductance). La figure suivante montre le chemin du courant (positif) juste après le basculement du bras à l'état libre. Le sens du courant dépend de l'état antérieur, c'est-à-dire du transistor qui était passant à l'état antérieur. La figure de gauche (respectivement de droite) montre le sens du courant positif lorsque le transistor passant à l'état antérieur est celui du haut (respectivement du bas). Dans les deux cas, la valeur absolue de l'intensité du courant est décroissante.
Figure pleine pageLe sens de la f.é.m. d'auto-induction (positive) est représenté par une flèche bleue. Dans le premier cas, le transistor du haut était passant donc le courant ip est positif. Ce courant diminue rapidement en passant par la diode du bas; en conséquence, le potentiel Vp est égal à -0,8 V (tension de seuil de la diode) tant que le courant est non nul puis la diode se bloque lorsque le courant s'annule et le potentiel Vp n'est plus imposé. Dans le second cas, le transistor du bas était passant donc le courant ip est négatif. Ce courant diminue rapidement en passant par la diode du haut; en conséquence, le potentiel Vp est égal à tant que le courant est non nul puis la diode se bloque et le potentiel devient libre (non imposé par le pont).
Les équations électriques doivent être associées à une équation mécanique, puisque les f.é.m. dépendent de la position angulaire du rotor et de sa vitesse angulaire. Cette équation est obtenue par application du théorème du moment cinétique par rapport à l'axe de rotation :
J est le moment d'inertie du rotor. est le couple moteur, donné par :
Le couple peut aussi s'exprimer en fonction des f.é.m. et des courants :
Cette relation (qui ne peut s'appliquer lorsque la vitesse angulaire est nulle) montre que le couple moyen est maximal (positif) lorsque le courant dans chaque bobine est en opposition de phase avec la f.é.m.. Cette f.é.m. est qualifiée de force contre-éloctromotrice car elle s'oppose au courant.
est le couple mécanique qu'il faut appliquer (charge mécanique). Le plus souvent, ce couple augmente avec la vitesse de manière non négligeable. Lorsque le moteur tourne à vide, le couple mécanique est dû aux frottements dans le moteur et on peut supposer qu'il s'exprime en fonction de la vitesse angulaire par :
où est le couple qu'il faut appliquer pour faire démarrer le moteur. Si le moteur est sous charge, celle-ci peut en première approche être représentée par un couple constant (c'est par exemple le cas si le moteur entraîne un monte-charge) et l'équation précédente reste pertinente. Pour que le moteur tourne à vitesse angulaire constante, il faut que . En toute rigueur, cette condition n'est pas réalisable car le couple moteur ondule nécessairement à la fréquence de commutation des 6 états (car le champ magnétique tourne par paliers). L'expérience réalisée plus loin montre cependant qu'on peut atteindre un régime où la vitesse angulaire est quasi constante (si l'inertie est assez grande). Quoi qu'il en soit, le but de la modélisation est d'obtenir le comportement du moteur lorsque sa vitesse angulaire change : au démarrage et lorsque la charge mécanique change subitement.
Les 4 équations électriques et l'équation mécanique constituent 5 équations différentielles pour les 5 inconnues . La somme des trois équations de tension et la loi des nœuds conduisent à :
On a finalement 5 équations différentielles du premier ordre pour les inconnues :
où VN est défini par et Γ par .
Les équations ci-dessus sont valables lorsque la tension Vp est fixée, c'est-à-dire lorsqu'une des diodes du bras de pont p est passante. Cette diode devient bloquante lorsque ip s'annule. En pratique, on détecte cette annulation par un changement de signe puis on annule effectivement ce courant. On a alors : et :
et la seule équation différentielle électrique est la première (celle du courant im) puisque im=-in et ip=0. On a par ailleurs :
Cette relation permet de calculer Vp lorsque les deux diodes sont bloquées.
Pour déterminer à tout instant l'état du pont de transistors, donc les valeurs de m,n,p, on fait une simulation des capteurs à effet Hall. L'angle θ indique la position d'un aimant de pôle nord (c.-à-d. dont le pôle nord est vers le stator). Cet aimant s'étend de l'angle θ-22,5 à θ+22,5. Considérons un des trois capteurs, dont la position est définie par l'angle β (30, 60 ou 90 degrés). Si β>θ-22,5, la parité de la partie entière de (β-θ+22,5)/45 indique la polarité de l'aimant qui se trouve en face du capteur : pôle nord si ce nombre est pair, pôle sud s'il est impair. Si β<θ-22,5, il faut considérer la parité de (β-θ-22,5)/45.
Il peut être intéressant de calculer l'intensité du courant i délivré par la source. Celle-ci est égale à l'intensité du courant qui traverse le transistor du haut qui est passant : . La puissance fournie par la source est donc . La puissance mécanique fournie par le moteur est .
Nous pouvons aussi simuler le fonctionnement de la machine en générateur, lorsque la source est débranchée. Dans ce cas, les courants sont nuls et on s'intéresse à la tension entre les deux bornes d'entrée du pont de transistors :
import numpy as np
class MoteurSynchrone:
def __init__(self,r,L,Phi0,J,G0,a,alphaE):
self.r = r
self.L = L
self.Phi0 = Phi0
self.J = J
self.Gamma0 = G0
self.a = a
self.Npoles = 8
self.angleAimant = 360/self.Npoles
self.DEG2RAD = np.pi/180
self.RAD2DEG = 180/np.pi
self.theta = 0 # angle rotor en degrés
self.omega = 0 # vitesse angulaire en rad/s
self.etatCapt = [0,0,0]
self.etatPont = 0 # état 0..5
self.capt2etats = [2,0,1,4,3,5] # table état des capteurs -> état du pont
self.indice_m = 0
self.indice_n = 0
self.indice_p = 0
self.tabIndice_m = [0,0,1,1,2,2]
self.tabIndice_n = [1,2,2,0,0,1]
self.tabIndice_p = [2,1,0,2,1,0]
self.alphaE = alphaE # tension effective
self.Gamma = 0 # couple moteur
self.tensions = [0,0,0]
self.courants = [0,0,0]
self.e = [0,0,0] # f.é.m.
self.VN = 0
self.potentielsBornes = [0,0,0] # 1 : potentiel haut, 0 : potentiel nul, -1 : potentiel libre
self.courantDiode = False # courant dans une diode de roue libre
self.seuilDiode = 0.8
La fonction suivante détermine l'état d'un capteur :
def etatCapteur(self,beta):
if beta >= self.theta-self.angleAimant/2:
if int((beta-self.theta+self.angleAimant/2)/self.angleAimant)%2==0:
return 1
else:
return 0
else:
if int((beta-self.theta-self.angleAimant/2)/self.angleAimant)%2==0:
return 1
else:
return 0
La fonction suivante détermine l'état du pont à partir de l'état des trois capteurs. Elle renvoie 1 si l'état a changé, 0 sinon.
def determinerEtatPont(self):
cap1 = self.etatCapteur(30)
cap2 = self.etatCapteur(60)
cap3 = self.etatCapteur(90)
bin = cap1*4+cap2*2+cap3
if (self.etatCapt[0] != cap1 or self.etatCapt[1]!=cap2 or self.etatCapt[2]!=cap3) and bin>0 and bin<=6:
self.etatCapt = [cap1,cap2,cap3]
if self.capt2etats[bin-1] != (self.etatPont+1)%6:
print("Erreur : étape sautée")
self.etatPont = self.capt2etats[bin-1]
self.indice_m = self.tabIndice_m[self.etatPont]
self.indice_n = self.tabIndice_n[self.etatPont]
self.indice_p = self.tabIndice_p[self.etatPont]
self.courantDiode = True # la diode de la borne p est passante
if self.potentielsBornes[self.indice_p] ==1 : self.potentielVp = -self.seuilDiode
else: self.potentielVp = self.alphaE + self.seuilDiode
self.potentielsBornes[self.indice_m] = 1
self.potentielsBornes[self.indice_n] = 0
self.potentielsBornes[self.indice_p] = -1
return 1 # l'état a changé
return 0 # l'état n'a pas changé
Les équations différentielles sont intégrées avec la méthode d'Euler. La fonction suivante effectue un pas de calcul de la méthode d'Euler :
def pasEuler(self):
sinphi1 = np.sin(4*self.theta*self.DEG2RAD)
sinphi2 = np.sin((4*self.theta-120)*self.DEG2RAD)
sinphi3 = np.sin((4*self.theta+120)*self.DEG2RAD)
A = self.omega*4*self.Phi0
self.e = [A*sinphi1,A*sinphi2,A*sinphi3]
em = self.e[self.indice_m]
en = self.e[self.indice_n]
ep = self.e[self.indice_p]
Im = self.courants[self.indice_m]
In = self.courants[self.indice_n]
Ip = self.courants[self.indice_p]
if self.courantDiode: # la bobine (p) se décharge dans une des deux diodes
Vp = self.potentielVp
self.VN = 1/3*(self.alphaE+Vp+em+en+ep)
deriv_Im = 1/self.L*(self.alphaE-self.VN-self.r*Im+em)
deriv_In = 1/self.L*(-self.VN-self.r*In+en)
deriv_Ip = 1/self.L*(Vp-self.VN-self.r*Ip+ep)
deriv_theta = self.omega*self.RAD2DEG
self.Gamma = -4*self.Phi0*(self.courants[0]*sinphi1+self.courants[1]*sinphi2+self.courants[2]*sinphi3)
deriv_omega = 1/self.J*(self.Gamma-self.Gamma0*(self.omega>0)-self.a*self.omega)
Im += self.h*deriv_Im
In += self.h*deriv_In
Ip += self.h*deriv_Ip
self.courantDiode = not( (Vp==-self.seuilDiode and Ip<=0) or (Vp==self.alphaE+self.seuilDiode and Ip>=0))
else: # le courant est nul dans la bobine (p)
In = -Im
Ip = 0
self.VN = 1/2*(self.alphaE+em+en)
deriv_Im = 1/self.L*(self.alphaE-self.VN-self.r*Im+em)
deriv_theta = self.omega*self.RAD2DEG
self.Gamma = -4*self.Phi0*(self.courants[0]*sinphi1+self.courants[1]*sinphi2+self.courants[2]*sinphi3)
deriv_omega = 1/self.J*(self.Gamma-self.Gamma0*(self.omega>0)-self.a*self.omega)
Im += self.h*deriv_Im
In = -Im
Vp = self.VN-ep
self.courants[self.indice_m] = Im
self.courants[self.indice_n] = In
self.courants[self.indice_p] = Ip
self.theta += self.h*deriv_theta
self.omega += self.h*deriv_omega
self.tensions[self.indice_m] = self.alphaE
self.tensions[self.indice_n] = 0
self.tensions[self.indice_p] = Vp
La fonction suivante initialise le moteur (le place au repos) :
def initialiser(self):
self.courants = [0,0,0]
self.tensions = [0,0,0]
self.theta = 0
self.omega = 0
La fonction suivante effectue la simulation jusqu'à un instant et un pas de temps donnés :
def simulation(self,tmax,h):
t = 0
i1 = []
i2 = []
i3 = []
V1 = []
V2 = []
V3 = []
e1 = []
e2 = []
e3 = []
VN = []
temps = []
theta = []
Gamma = []
omega = []
Ps = []
self.h = h
while t<tmax:
i1.append(self.courants[0])
i2.append(self.courants[1])
i3.append(self.courants[2])
V1.append(self.tensions[0])
V2.append(self.tensions[1])
V3.append(self.tensions[2])
e1.append(self.e[0])
e2.append(self.e[1])
e3.append(self.e[2])
VN.append(self.VN)
theta.append(self.theta)
omega.append(self.omega)
Gamma.append(self.Gamma)
Ps.append(self.courants[self.indice_m]*self.alphaE)
temps.append(t)
t += self.h
self.determinerEtatPont()
self.pasEuler()
return np.array(temps),np.array(i1),np.array(i2),np.array(i3),np.array(V1),np.array(V2),np.array(V3),np.array(e1),np.array(e2),np.array(e3),np.array(VN),np.array(theta),np.array(omega),np.array(Gamma),np.array(Ps)
Les tableaux sont des listes remplies avec append afin de permettre une variation du pas de temps (bien qu'il soit constant dans cette implémentation). Remarque : l'utilisation de la fonction numpy.append dans ce cas est à proscrire en raison de son inefficacité (l'espace mémoire est entièrement réaloué à chaque fois qu'un élément est ajouté).
La fonction suivante effectue une simulation sans stocker les valeurs :
def simulationVide(self,tmax,h):
t = 0
self.h = h
while t<tmax:
t += self.h
self.determinerEtatPont()
self.pasEuler()
La fonction suivante effectue le pas de calcul en l'absence de source (courants nuls) :
def pasCalculSansSource(self):
sinphi1 = np.sin(4*self.theta*self.DEG2RAD)
sinphi2 = np.sin((4*self.theta-120)*self.DEG2RAD)
sinphi3 = np.sin((4*self.theta+120)*self.DEG2RAD)
A = self.omega*4*self.Phi0
self.e = [A*sinphi1,A*sinphi2,A*sinphi3]
em = self.e[self.indice_m]
en = self.e[self.indice_n]
ep = self.e[self.indice_p]
deriv_theta = self.omega*self.RAD2DEG
self.theta += self.h*deriv_theta
self.tensions[self.indice_m] = -em
self.tensions[self.indice_n] = -en
self.tensions[self.indice_p] = -ep
Dans le cas où les courants sont nuls, il n'y a pas d'équation différentielle à intégrer, il s'agit d'un simple calcul avec augmentation itérative de l'angle du rotor.
La fonction suivante effectue la simulation en l'absence de source (courants nuls) :
def simulationSansSource(self,omega,tmax,h):
t = 0
V = []
temps = []
theta = []
self.h = h
self.omega = omega
while t < tmax:
V.append(self.tensions[self.indice_m]-self.tensions[self.indice_n])
theta.append(self.theta)
temps.append(t)
t += self.h
self.determinerEtatPont()
self.pasCalculSansSource()
return np.array(temps),np.array(V),np.array(theta)
Pour le moteur réalisé, les valeurs suivantes sont obtenues expérimentalement :
- L=10 mH.
- R=1 Ω.
- , valeur obtenue à partir de la f.é.m. (voir plus loin).
La résistance d'une bobine dépend de la fréquence. La résistance à la fréquence de découpage (environ 10 kHz) est beaucoup plus grande que la résistance DC (60 ohms). Pour le modèle, c'est la résistance à très basse fréquence qui importe et celle-ci est de l'ordre de 1 ohms.
La mesure du moment d'inertie est plus difficile à faire. Il faudrait en principe la réaliser avec un pendule de torsion préalablement étalonné. On se contente d'une évalutation de son ordre de grandeur connaissant le rayon du rotor et sa masse : J=0,001 kg⋅m2.
Pour le couple mécanique, nous commençons par un couple proportionnel à la vitesse angulaire, qui devrait représenter assez bien un moteur tournant à vide.
Voici une simulation du démarrage du moteur :
from moteurSynchrone import MoteurSynchrone
import numpy as np
r=1
L=10e-3
Phi0 = 1e-3
J=1e-3
G0 = 0
a = 1e-3
alphaE = 1 # alimentation 10 V, rapport cyclique 0.1
tmax = 5
h = 1e-5
moteur = MoteurSynchrone(r,L,Phi0,J,G0,a,alphaE)
moteur.initialiser()
temps,i1,i2,i3,V1,V2,V3,e1,e2,e3,VN,theta,omega,Gamma,Ps = moteur.simulation(tmax,h)
nom ="simulation-1.npy"
np.save(nom,np.array([temps,i1,i2,i3,V1,V2,V3,e1,e2,e3,VN,theta,omega,Gamma,Ps]))
Voici la vitesse angulaire :
temps,i1,i2,i3,V1,V2,V3,e1,e2,e3,VN,theta,omega,Gamma,Ps = np.load("simulation-1.npy")
figure(figsize=(16,6))
plot(temps,omega*RAD2DEG)
grid()
ylabel(r"$\omega \rm(deg\cdot s^{-1})$",fontsize=18)
xlabel("t (s)",fontsize=18)
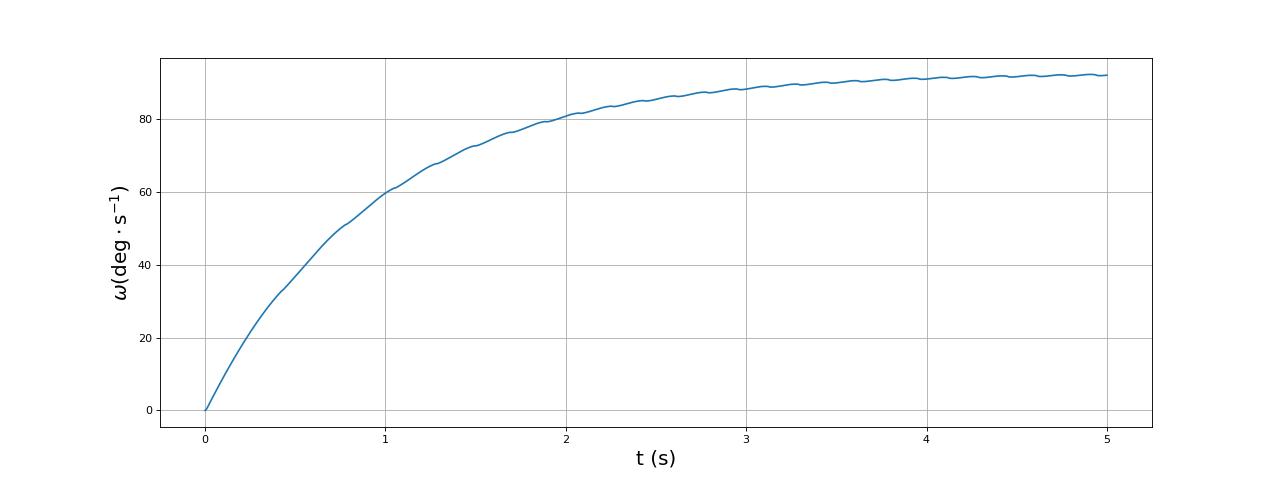 fig14.pdf
fig14.pdf
Le moteur a presque atteint le régime permanent (vitesse angulaire quasi constante).
Voici le courant dans les trois bobines :
figure(figsize=(16,6))
subplot(311)
plot(temps,i1)
grid()
ylabel(r"$i_1\ (\rm A)$",fontsize=18)
subplot(312)
plot(temps,i2)
grid()
ylabel(r"$i_2\ (\rm A)$",fontsize=18)
subplot(313)
plot(temps,i3)
grid()
ylabel(r"$i_3\ (\rm A)$",fontsize=18)
xlabel("t (s)",fontsize=18)
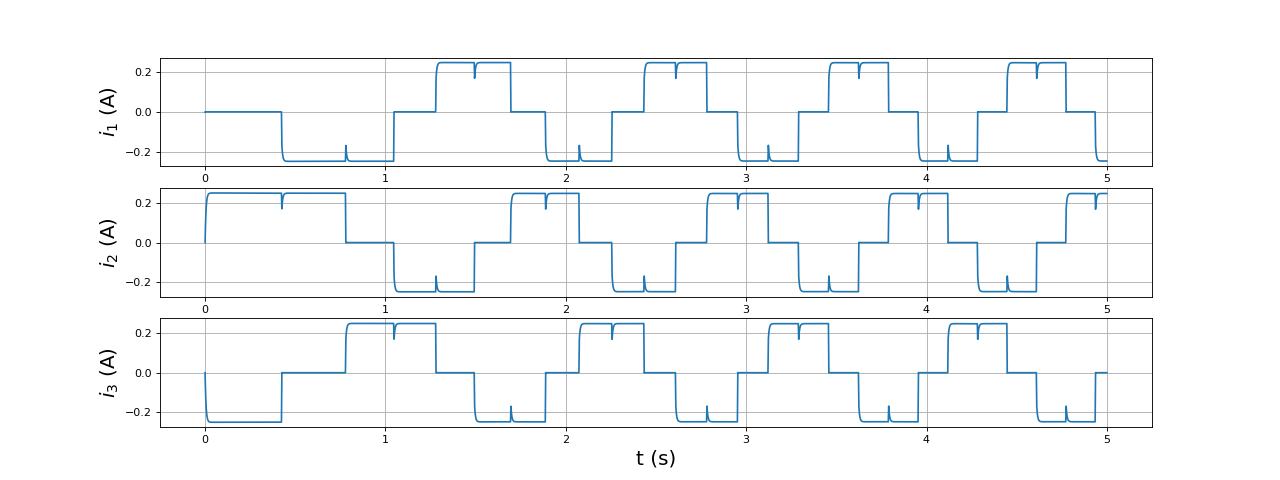 fig15.pdf
fig15.pdf
Pendant une phase du cycle à 6 états, le courant est constant (à l'exception du voisinage des commutations). Le temps de réponse d'une bobine (L/r) est en effet négligeable devant la période de commutation. Voici un détail qui montre le régime transitoire lors d'une commutation :
figure(figsize=(16,6))
subplot(311)
plot(temps,i1)
xlim(1.035,1.055)
grid()
ylabel(r"$i_1\ (\rm A)$",fontsize=18)
subplot(312)
plot(temps,i2)
xlim(1.035,1.055)
grid()
ylabel(r"$i_2\ (\rm A)$",fontsize=18)
subplot(313)
plot(temps,i3)
xlim(1.035,1.055)
grid()
ylabel(r"$i_3\ (\rm A)$",fontsize=18)
xlabel("t (s)",fontsize=18)
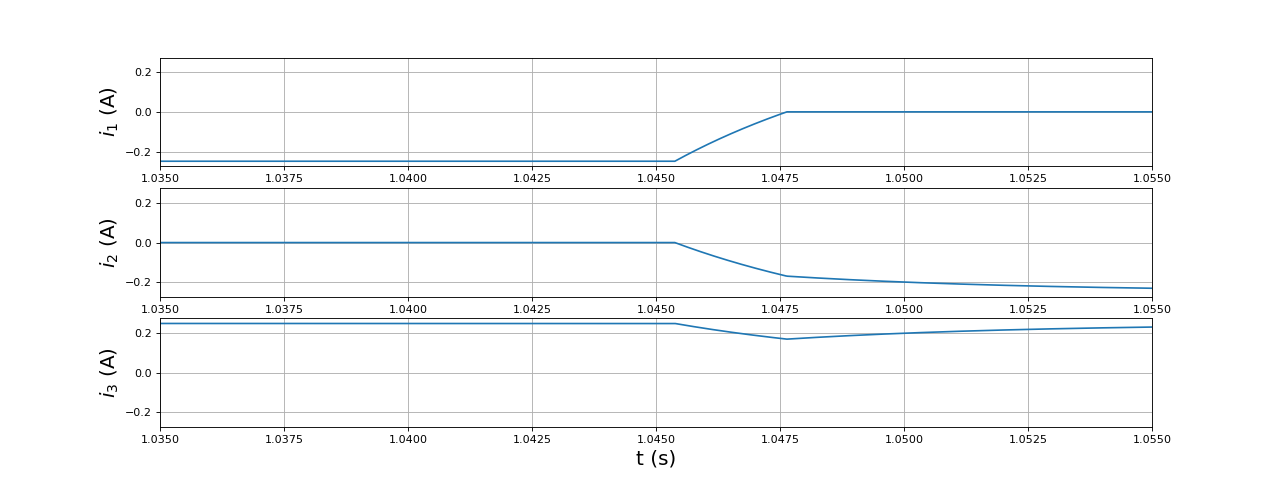 fig16.pdf
fig16.pdf
La bobine 3, dont la borne reste au potentiel haut, devrait idéalement avoir un courant constant. On observe en fait une petite diminution du courant transitoire, le temps que le courant s'établisse dans la bobine 2. En effet, la diminution du courant dans la bobine 1, qui se fait par une diode, est plus rapide que l'augmentation du courant dans la bobine 2.
Voici les tensions appliquées aux trois bobines (par rapport à la masse) :
figure(figsize=(16,6))
subplot(311)
plot(temps,V1)
grid()
ylabel(r"$V_1\ (\rm V)$",fontsize=18)
subplot(312)
plot(temps,V2)
grid()
ylabel(r"$V_2\ (\rm V)$",fontsize=18)
subplot(313)
plot(temps,V3)
grid()
ylabel(r"$V_3\ (\rm V)$",fontsize=18)
xlabel("t (s)",fontsize=18)
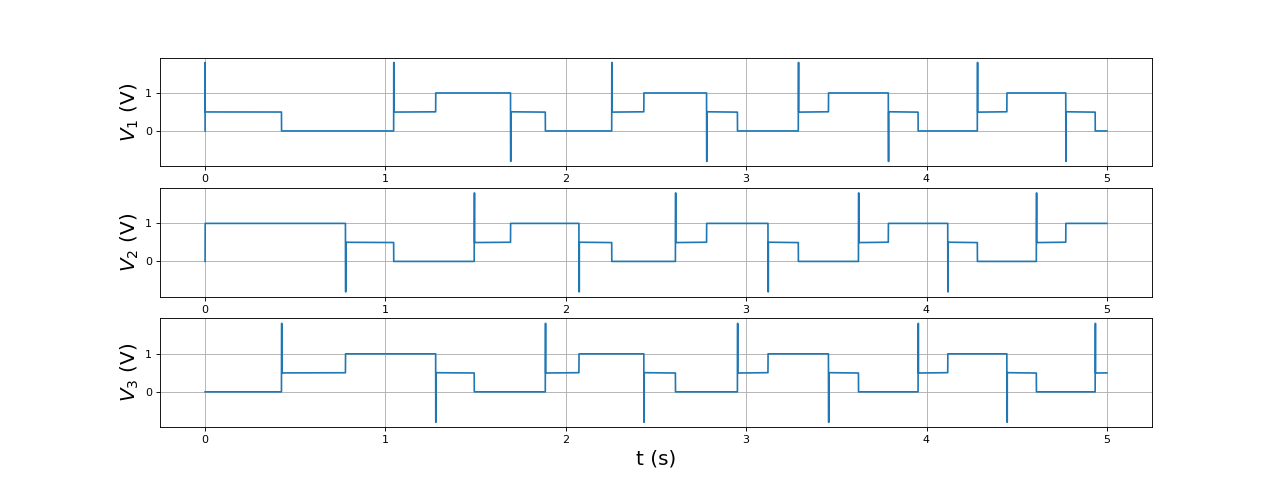 fig17.pdf
fig17.pdf
Remarquons que les f.é.m. sont très faibles devant les tensions appliquées (voir plus loin). Voici en détail le voisinage d'un changement d'état :
figure(figsize=(16,6))
subplot(311)
plot(temps,V1)
xlim(1.035,1.055)
grid()
ylabel(r"$V_1\ (\rm V)$",fontsize=18)
subplot(312)
plot(temps,V2)
xlim(1.035,1.055)
grid()
ylabel(r"$V_2\ (\rm V)$",fontsize=18)
subplot(313)
plot(temps,V3)
xlim(1.035,1.055)
grid()
ylabel(r"$V_3\ (\rm V)$",fontsize=18)
xlabel("t (s)",fontsize=18)
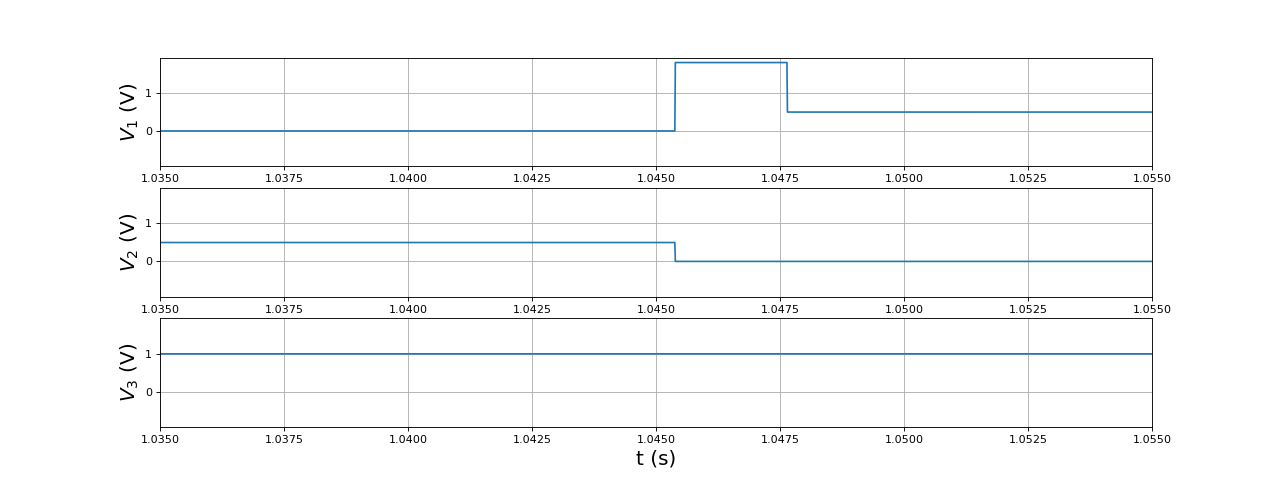 fig18.pdf
fig18.pdf
Pour ce changement, la borne 1 est celle où les deux interrupteurs basculent en position ouverte. Après la phase où la diode du haut est passante, le potentiel à cette borne prend la valeur .
Il est intéressant de tracer les tensions par rapport au point neutre (borne commune aux trois bobines montées en étoile) et les f.é.m.. Nous traçons en fait l'opposée de chaque f.é.m. (force contre électromotrice).
figure(figsize=(16,6))
subplot(311)
plot(temps,V1-VN,label=r"$V_1-V_N$")
plot(temps,-e1,label=r"$-e_1$")
legend(loc="upper right")
grid()
subplot(312)
plot(temps,V2-VN,label=r"$V_2-V_N$")
plot(temps,-e2,label=r"$-e_2$")
legend(loc="upper right")
grid()
subplot(313)
plot(temps,V3-VN,label=r"$V_3-V_N$")
plot(temps,-e3,label=r"$-e_3$")
legend(loc="upper right")
grid()
xlabel("t (s)",fontsize=18)
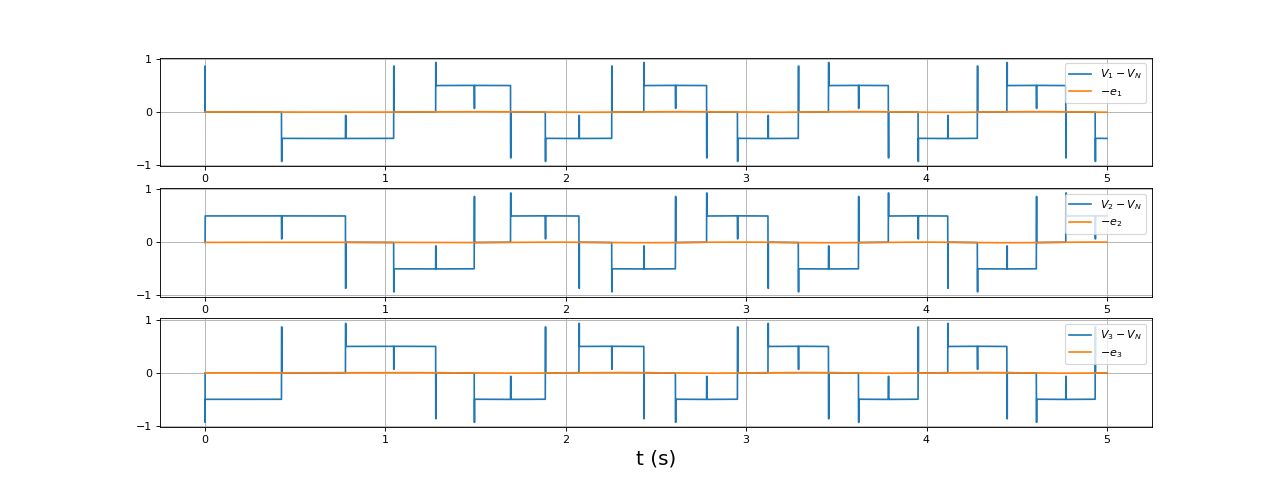 fig19.pdf
fig19.pdf
Les f.é.m. sont très faibles par rapport aux tensions appliquées aux bornes des bobines. Le courant dans les bobines est donc relativement important puisque les tensions dues à la résistance et à l'auto-inductance sont prépondérantes. C'est aussi pour cette raison que le courant est constant à chaque phase du cycle (il est peu affecté par la f.é.m.). Voici les mêmes courbes avec une échelle dilatée en ordonnée :
figure(figsize=(16,6))
subplot(311)
plot(temps,V1-VN,label=r"$V_1-V_N$",linewidth=2)
plot(temps,-e1,label=r"$-e_1$")
legend(loc="upper right")
ylim(-0.01,0.01)
grid()
subplot(312)
plot(temps,V2-VN,label=r"$V_2-V_N$",linewidth=2)
plot(temps,-e2,label=r"$-e_2$")
legend(loc="upper right")
ylim(-0.01,0.01)
grid()
subplot(313)
plot(temps,V3-VN,label=r"$V_3-V_N$",linewidth=2)
plot(temps,-e3,label=r"$-e_3$")
legend(loc="upper right")
ylim(-0.01,0.01)
grid()
xlabel("t (s)",fontsize=18)
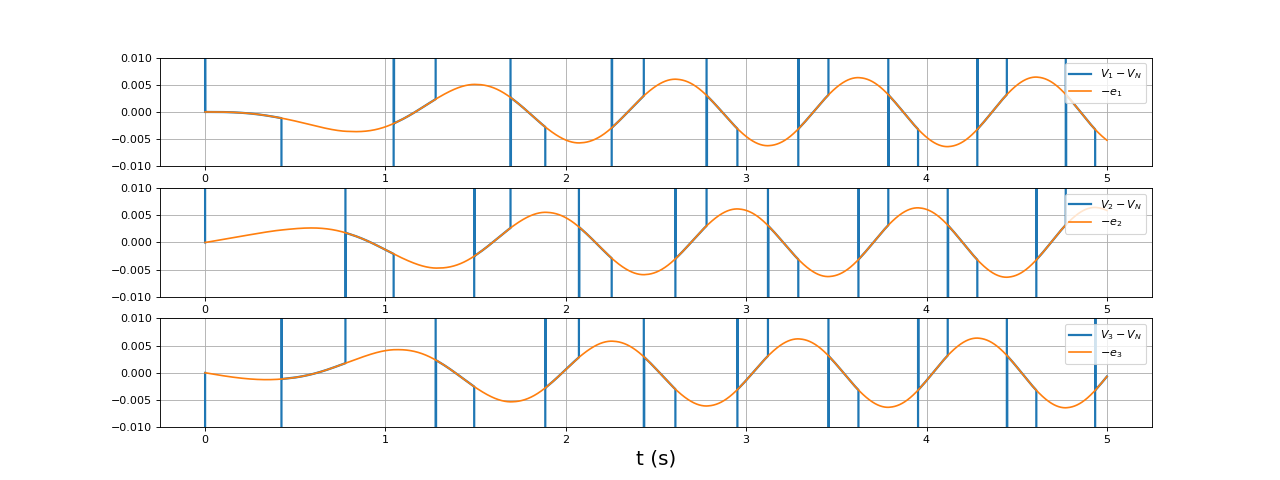 fig20.pdf
fig20.pdf
Lorsqu'une bobine est à l'état libre (après décharge dans la diode), la tension à ses bornes est égale à la f.é.m. et celle-ci passe par zéro au milieu de cette phase du cycle. La méthode de commande sans capteur repose sur la détection du passage par zéro de cette tension. Evidemment, cette méthode ne fonctionne que lorsque le moteur tourne donc elle ne permet pas à elle seule d'effectuer le démarrage du moteur.
Nous voyons par ailleurs que, dans chaque bobine, l'opposée de la f.é.m. est en phase avec le courant, ce qui est bien le comportement souhaité.
Voici le couple moteur :
figure(figsize=(16,6))
plot(temps,Gamma)
grid()
ylabel(r"$\Gamma \rm(N\cdot m)$",fontsize=18)
xlabel("t (s)",fontsize=18)
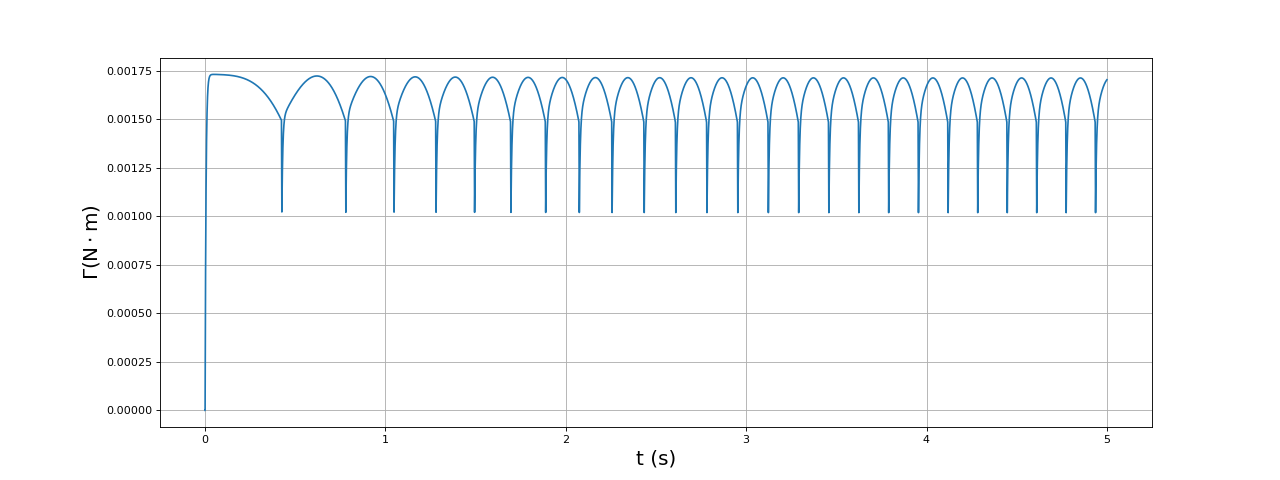 fig21.pdf
fig21.pdf
Le couple ondule avec une grande amplitude (environ , soit ) à chaque phase du cycle à 6 états. Il y a de plus une chute très brève du couple à chaque commutation, due à la chute de courant dans la bobine qui reste alimentée. Les ondulations ne sont pas dues à des variations des courants (puisque ceux-ci sont constants) mais au fait que le couple (à courant constant) dépend de l'angle du rotor de manière sinusoïdale. Rappelons que cette propriété est en fait la même que la forme sinusoïdale de la f.é.m.. Compte tenu de la forme sinusoïdale de la f.é.m. (moteur de type PMSM), la commande à 6 états conduit inévitablement à des ondulations du couple. Pour obtenir un couple constant avec ce moteur, il faudrait que le courant varie sinusoïdalement (commande sinusoïdale). Ces ondulations ont très peu d'effet sur la vitesse angulaire (en raison de l'inertie du rotor) mais elles sont généralement considérées comme indésirables en raison des vibrations qu'elles engendrent. Les chutes de courant très brèves observées juste après les commutation n'ont qu'un effet mécanique négligeable. Par ailleurs, ce phénomène est en réalité très dépendant du comportement des transitors, qui ne sont pas modélisés précisément par cette simulation.
Voici la puissance fournie par la source et la puissance mécanique fournie par le moteur :
figure(figsize=(16,6))
plot(temps,Ps,label="P source")
P = Gamma*omega
plot(temps,P,label="P mécanique")
grid()
legend(loc='upper right')
ylabel(r"$P \rm(W)$",fontsize=18)
xlabel("t (s)",fontsize=18)
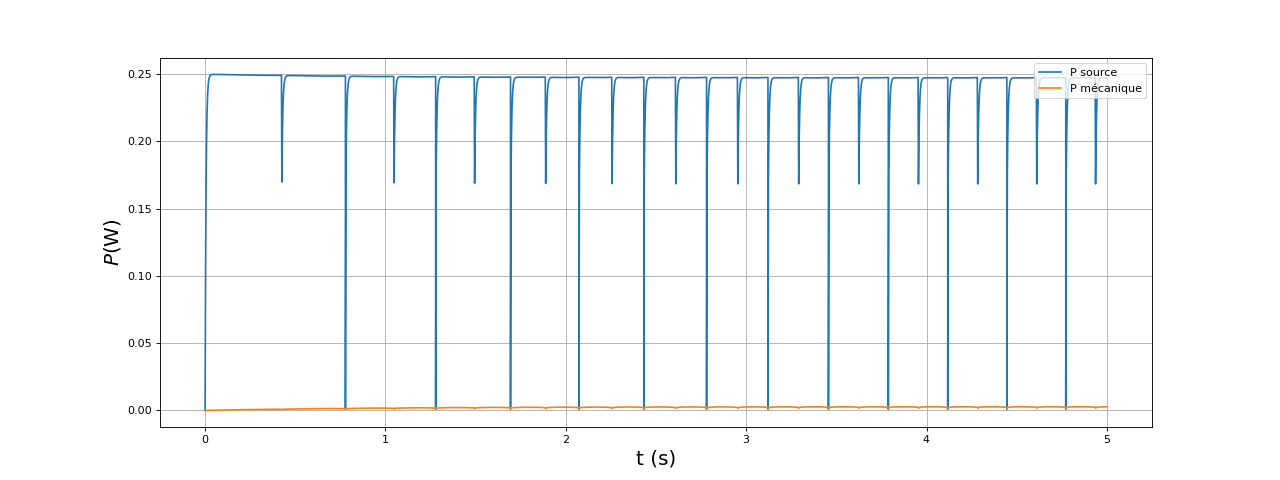 fig22.pdf
fig22.pdf
La puissance fournie par la source subit des baisses très brèves juste après les commutations. Pour calculer le rendement énergétique, il faut faire le rapport des moyennes de ces deux puissances. On voit cependant que la puissance mécanique augmente pendant le régime transitoire et que la puissance fournie par la source diminue (si l'on fait abstraction des pics). Pour calculer le rendement, nous devons moyenner sur une durée grande devant la période de commutation. Ici nous pouvons calculer les moyennes sur la deuxième partie, de 2,5 secondes à 5 secondes :
N = len(P)
rend = P[N//2:N].mean()/Ps[N//2:N].mean()
print(rend) --> 0.010443216329356705
Le rendement est très faible, ce qui n'est pas étonnant puisque les f.é.m. sont très faibles devant . L'énergie perdue est évidemment dissipée dans les résistances des bobines (le modèle n'évalue par les pertes dans les transistors).
Sans changer les caractéristiques électriques et magnétiques du moteur, le rendement devrait augmenter si le moteur tourne plus vite, car cela augmente la f.é.m.. Voici une autre simulation avec un couple mécanique nul :
r=2
L=10e-3
Phi0 = 1e-3
J=1e-3
G0 = 0
a = 0
alphaE = 1 # alimentation 10 V, rapport cyclique 0.1
tmax = 200
h = 1e-4
temps,i1,i2,i3,V1,V2,V3,e1,e2,e3,VN,theta,omega,Gamma,Ps = np.load("simulation-2.npy")
figure(figsize=(16,6))
plot(temps,omega*RAD2DEG)
grid()
ylabel(r"$\omega \rm(deg\cdot s^{-1})$",fontsize=18)
xlabel("t (s)",fontsize=18)
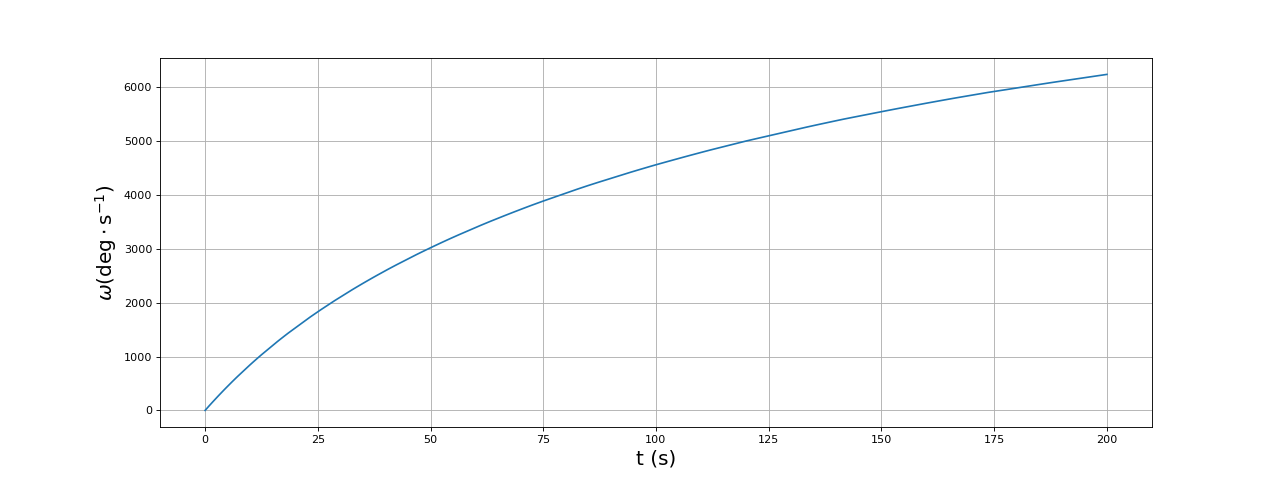 fig23.pdf
fig23.pdf
Voici le couple moteur :
figure(figsize=(16,6))
plot(temps,Gamma)
grid()
ylabel(r"$\Gamma \rm(N\cdot m)$",fontsize=18)
xlabel("t (s)",fontsize=18)
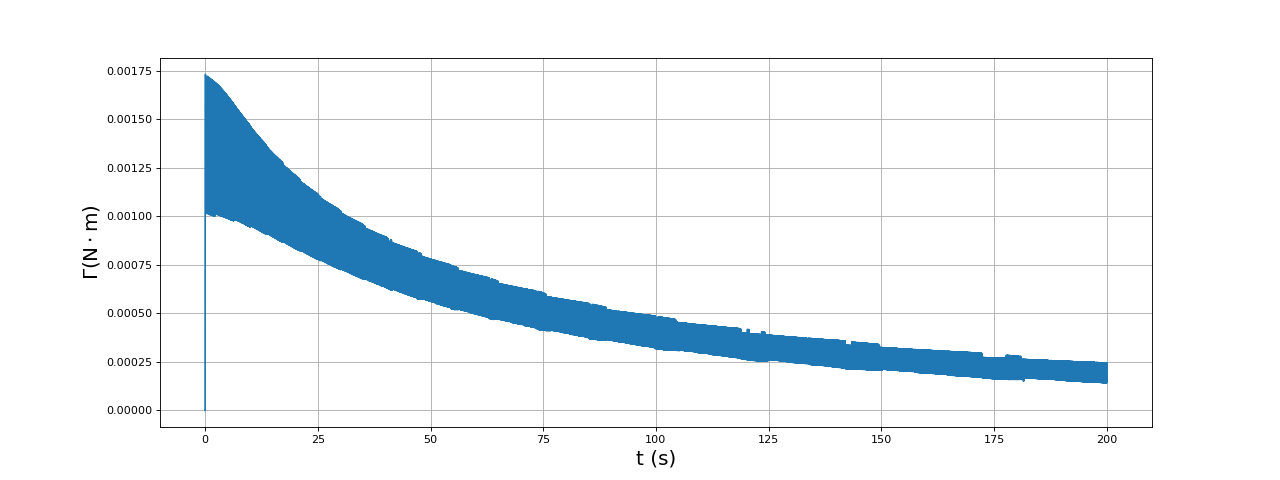 fig24.pdf
fig24.pdf
En l'absence de couple mécanique, le couple moteur diminue au fur et à mesure que la vitesse de rotation augmente. Remarquons il n'y a pas de régime stationnaire puisque la vitesse de rotation augmente indéfiniment (ce cas de figure est évidemment théorique).
Voici le courant dans les trois bobines :
figure(figsize=(16,6))
subplot(311)
plot(temps,i1)
grid()
ylabel(r"$i_1\ (\rm A)$",fontsize=18)
subplot(312)
plot(temps,i2)
grid()
ylabel(r"$i_2\ (\rm A)$",fontsize=18)
subplot(313)
plot(temps,i3)
grid()
ylabel(r"$i_3\ (\rm A)$",fontsize=18)
xlabel("t (s)",fontsize=18)
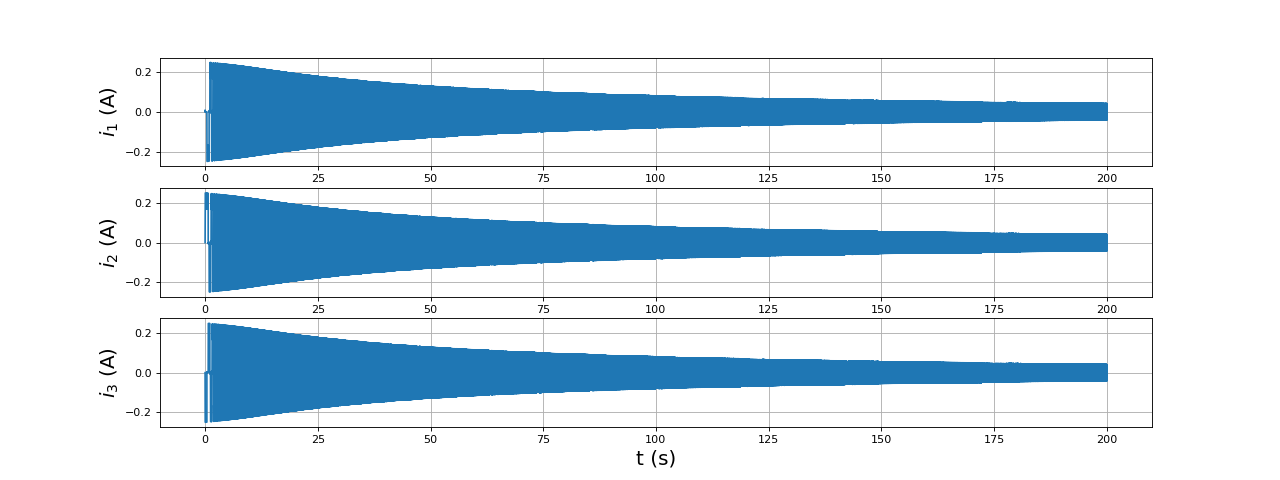 fig25.pdf
fig25.pdf
et les forces électromotrices :
figure(figsize=(16,6))
subplot(311)
plot(temps,-e1)
grid()
ylabel(r"$-e_1\ (\rm V)$",fontsize=12)
subplot(312)
plot(temps,-e2)
grid()
ylabel(r"$-e_2\ (\rm V)$",fontsize=12)
subplot(313)
plot(temps,-e3)
grid()
ylabel(r"$-e_3\ (\rm V)$",fontsize=12)
xlabel("t (s)",fontsize=18)
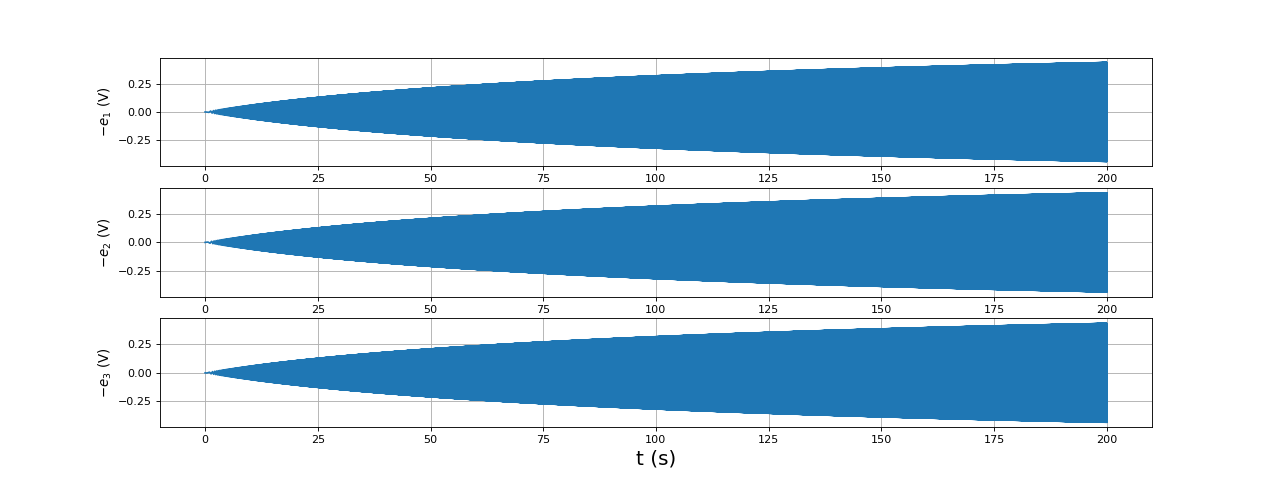 fig26.pdf
fig26.pdf
Comparé à la situation précédente (avec un couple de frottement), la vitesse du moteur atteint des valeurs beaucoup plus grandes et, en conséquence, la force électromotrice aussi. L'amplitude de crête de celle-ci atteint la moitié de l'amplitude des tensions appliquées. L'augmentation au cours du temps de l'amplitude de crête de la force électromotrice explique la diminution de celle du courant (et en conséquence la diminution du couple). Voici la forme du courant vers la fin de la simulation :
figure(figsize=(16,6))
subplot(311)
plot(temps,i1)
xlim(199.9,200)
ylim(-0.1,0.1)
grid()
ylabel(r"$i_1\ (\rm A)$",fontsize=18)
subplot(312)
plot(temps,i2)
xlim(199.9,200)
ylim(-0.1,0.1)
grid()
ylabel(r"$i_2\ (\rm A)$",fontsize=18)
subplot(313)
plot(temps,i3)
xlim(199.9,200)
ylim(-0.1,0.1)
grid()
ylabel(r"$i_3\ (\rm A)$",fontsize=18)
xlabel("t (s)",fontsize=18)
 fig27.pdf
fig27.pdf
Le courant n'est pas du tout constant pendant une phase du cycle à 6 états car la f.é.m., qui varie sinusoïdalement, est du même ordre de grandeur que la tension appliquée aux bobines.
Voici les f.é.m. :
figure(figsize=(16,6))
subplot(311)
plot(temps,-e1)
xlim(199.9,200)
grid()
ylabel(r"$-e_1\ (\rm V)$",fontsize=12)
subplot(312)
plot(temps,-e2)
xlim(199.9,200)
grid()
ylabel(r"$-e_2\ (\rm V)$",fontsize=12)
subplot(313)
plot(temps,-e3)
xlim(199.9,200)
grid()
ylabel(r"$-e_3\ (\rm V)$",fontsize=12)
xlabel("t (s)",fontsize=18)
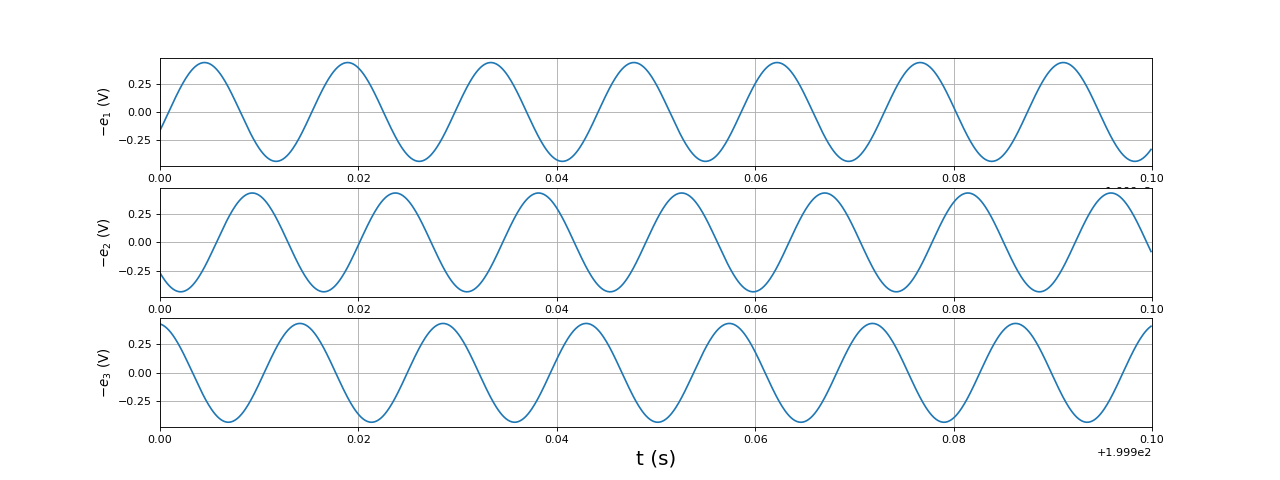 fig28.pdf
fig28.pdf
et les tensions :
figure(figsize=(16,6))
subplot(311)
plot(temps,V1)
xlim(199.9,200)
grid()
ylabel(r"$V_1\ (\rm V)$",fontsize=18)
subplot(312)
plot(temps,V2)
xlim(199.9,200)
grid()
ylabel(r"$V_2\ (\rm V)$",fontsize=18)
subplot(313)
plot(temps,V3)
xlim(199.9,200)
grid()
ylabel(r"$V_3\ (\rm V)$",fontsize=18)
xlabel("t (s)",fontsize=18)
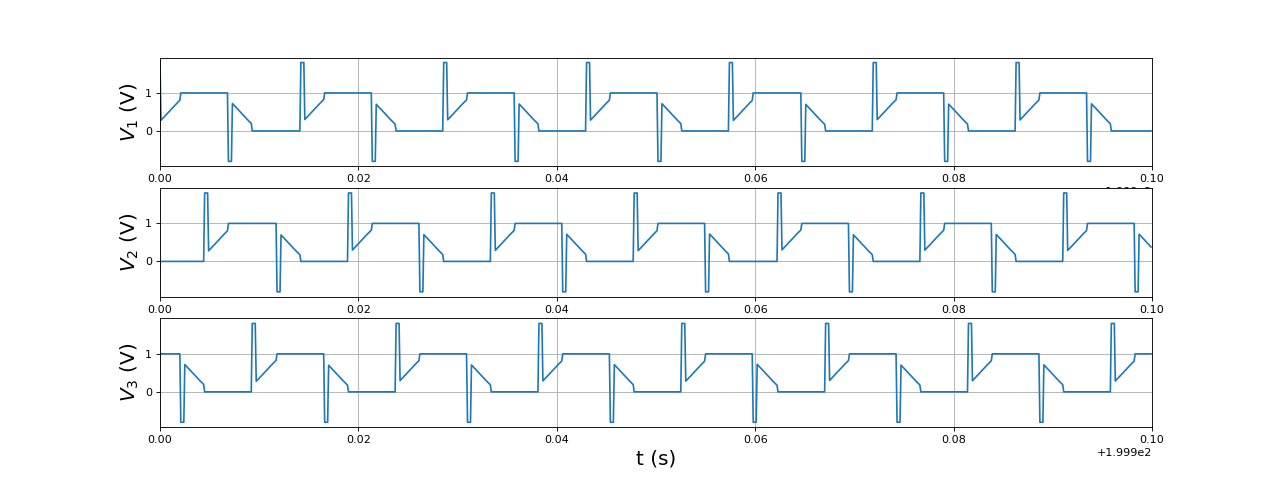 fig29.pdf
fig29.pdf
On remarque que la variation de tension lors de la phase non connectée est beaucoup plus grande que précédemment, ce qui est une conséquence de l'augmentation de la f.é.m.. De plus, le temps de conduction de la diode est plus long.
Voici les tensions par rapport au point neutre et les f.é.m. :
figure(figsize=(16,6))
subplot(311)
plot(temps,V1-VN,label=r"$V_1-V_N$")
xlim(199.9,200)
plot(temps,-e1,label=r"$-e_1$")
legend(loc="upper right")
grid()
subplot(312)
plot(temps,V2-VN,label=r"$V_2-V_N$")
xlim(199.9,200)
plot(temps,-e2,label=r"$-e_2$")
legend(loc="upper right")
grid()
subplot(313)
plot(temps,V3-VN,label=r"$V_3-V_N$")
xlim(199.9,200)
plot(temps,-e3,label=r"$-e_3$")
legend(loc="upper right")
grid()
xlabel("t (s)",fontsize=18)
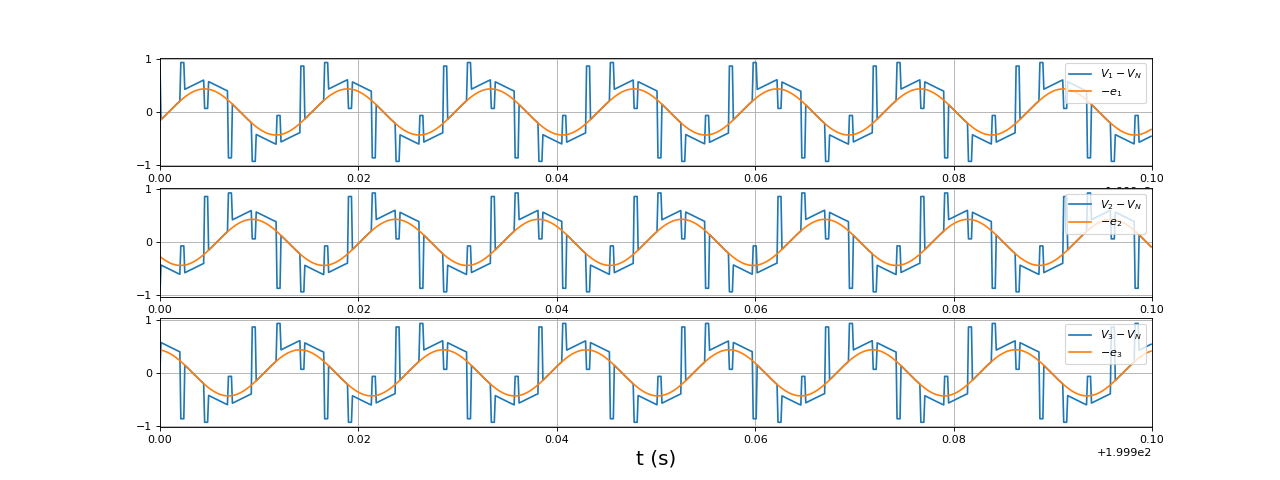 fig30.pdf
fig30.pdf
Dans ce régime de fonctionnement, où la vitesse est assez grande, les tensions par rapport au point neutre sont proches des f.é.m.., à l'exception des phases de conduction d'une diode de transistor.
Voyons le couple :
figure(figsize=(16,6))
plot(temps,Gamma)
xlim(199.9,200)
grid()
ylabel(r"$\Gamma \rm(N\cdot m)$",fontsize=18)
xlabel("t (s)",fontsize=18)
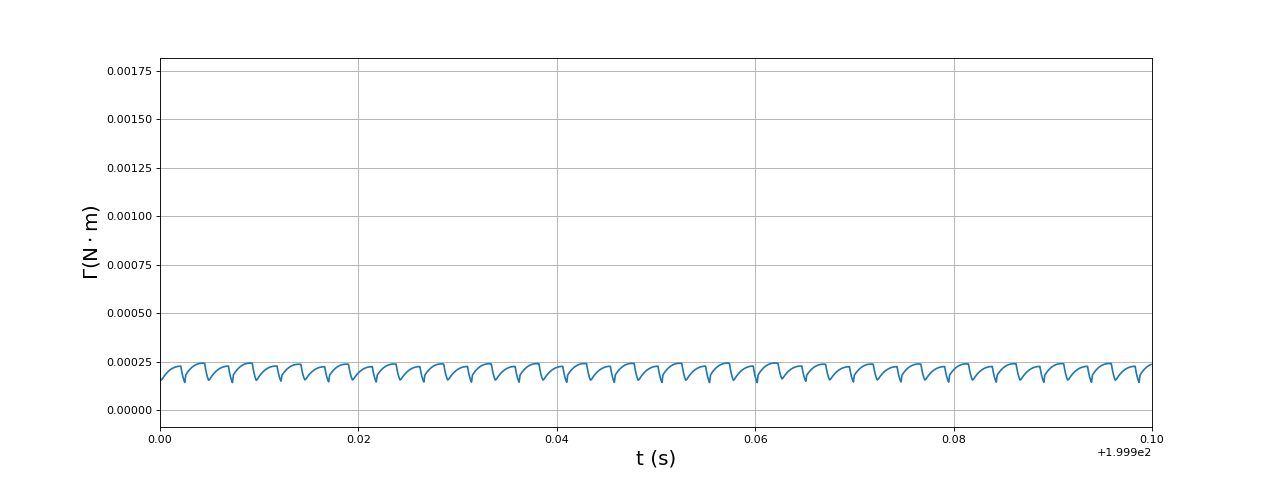 fig31.pdf
fig31.pdf
Voici la puissance fournie par la source et la puissance mécanique fournie par le moteur :
figure(figsize=(16,6))
plot(temps,Ps,label="P source")
P = Gamma*omega
plot(temps,P,label="P mécanique")
grid()
legend(loc='upper right')
ylabel(r"$P \rm(W)$",fontsize=18)
xlabel("t (s)",fontsize=18)
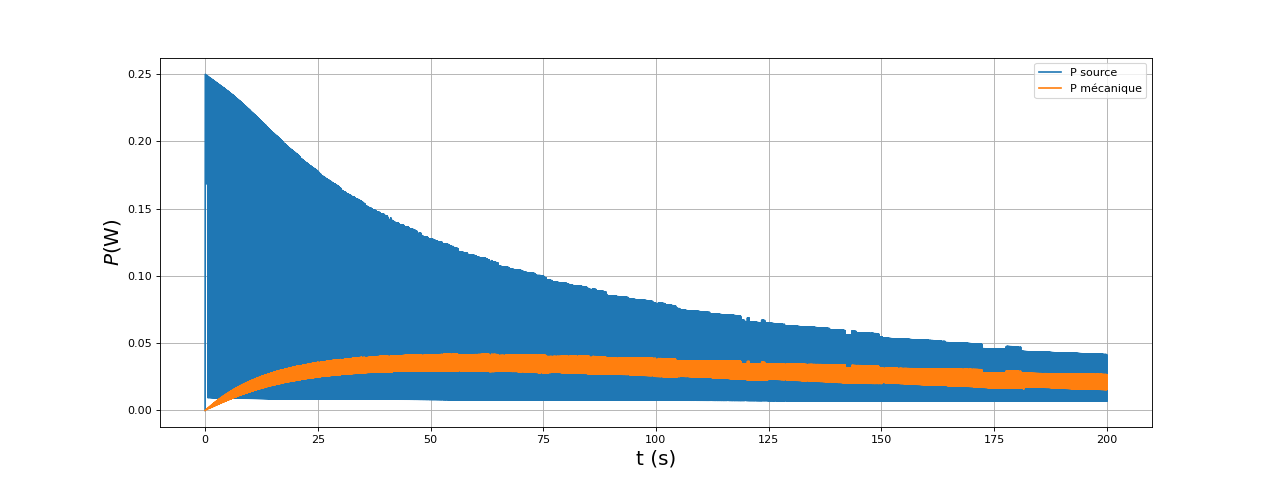 fig32.pdf
fig32.pdf
Bien qu'il n'existe pas de régime stationnaire (car le couple mécanique est nul), nous pouvons calculer un rendement en considérant les moyennes de ces puissances entre les instants 170 et 200 :
N = len(P)
k = int(175/(temps[1]-temps[0]))
rend = P[k:N].mean()/Ps[k:N].mean()
print(rend) --> 0.717692431107716
Nous obtenons bien un rendement beaucoup plus grand que précédemment mais la vitesse angulaire atteint environ 7000 deg/s, soit environ 20 tours pas secondes.
Si l'on veut augmenter le rendement à faible vitesse de rotation, il faut changer les caractéristiques du moteur, par exemple en augmentant . Voici une simulation avec dix fois plus grand et une tension effective dix fois plus petite (on revient à la valeur du coefficient de frottement de la première simulation) :
r=2
L=10e-3
Phi0 = 1e-2
J=1e-3
G0 = 0
a = 1e-3
alphaE = 1 # alimentation 10 V, rapport cyclique 0.1
tmax = 200
h = 1e-4
temps,i1,i2,i3,V1,V2,V3,e1,e2,e3,VN,theta,omega,Gamma,Ps = np.load("simulation-3.npy")
figure(figsize=(16,6))
plot(temps,omega*RAD2DEG)
grid()
ylabel(r"$\omega \rm(deg\cdot s^{-1})$",fontsize=18)
xlabel("t (s)",fontsize=18)
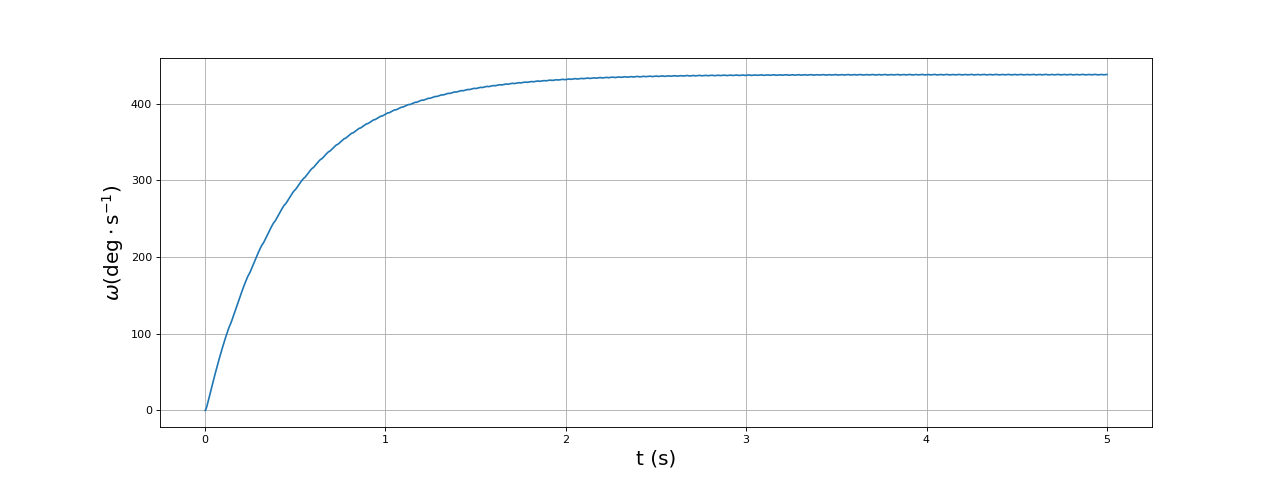 fig33.pdf
fig33.pdf
Voici les tensions aux bornes des bobines :
figure(figsize=(16,6))
subplot(311)
plot(temps,V1)
grid()
ylabel(r"$V_1\ (\rm V)$",fontsize=18)
subplot(312)
plot(temps,V2)
grid()
ylabel(r"$V_2\ (\rm V)$",fontsize=18)
subplot(313)
plot(temps,V3)
grid()
ylabel(r"$V_3\ (\rm V)$",fontsize=18)
xlabel("t (s)",fontsize=18)
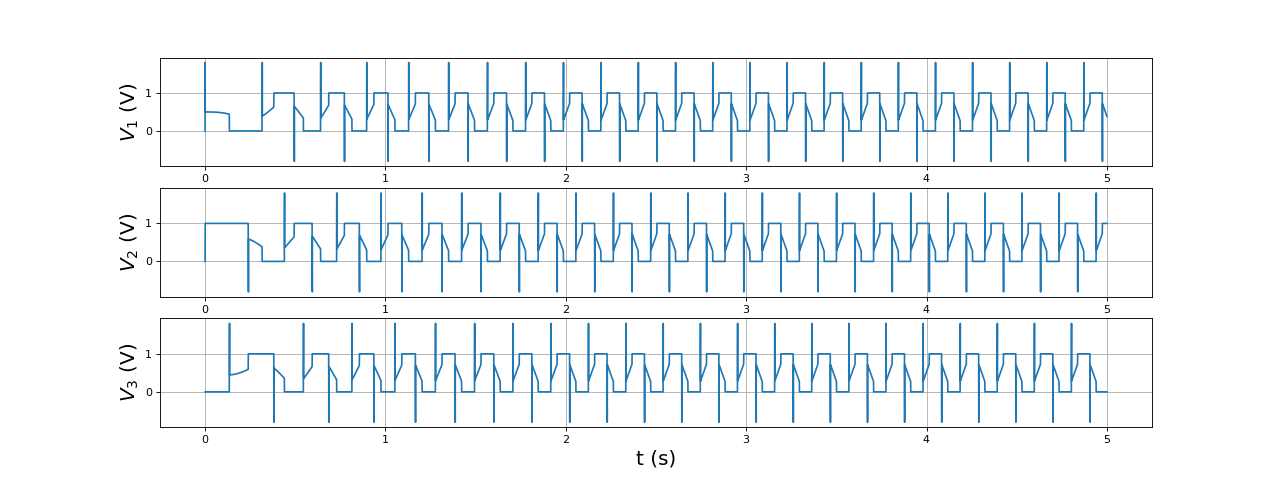 fig34.pdf
fig34.pdf
Ces courbes montrent clairement que la f.é.m. (visible sur chaque bobine pendant sont état p) est du même ordre de grandeur que la tension effective. Voici la puissance fournie par la source et la puissance mécanique fournie par le moteur :
figure(figsize=(16,6))
plot(temps,Ps,label="P source")
P = Gamma*omega
plot(temps,P,label="P mécanique")
grid()
legend(loc='upper right')
ylabel(r"$P \rm(W)$",fontsize=18)
xlabel("t (s)",fontsize=18)
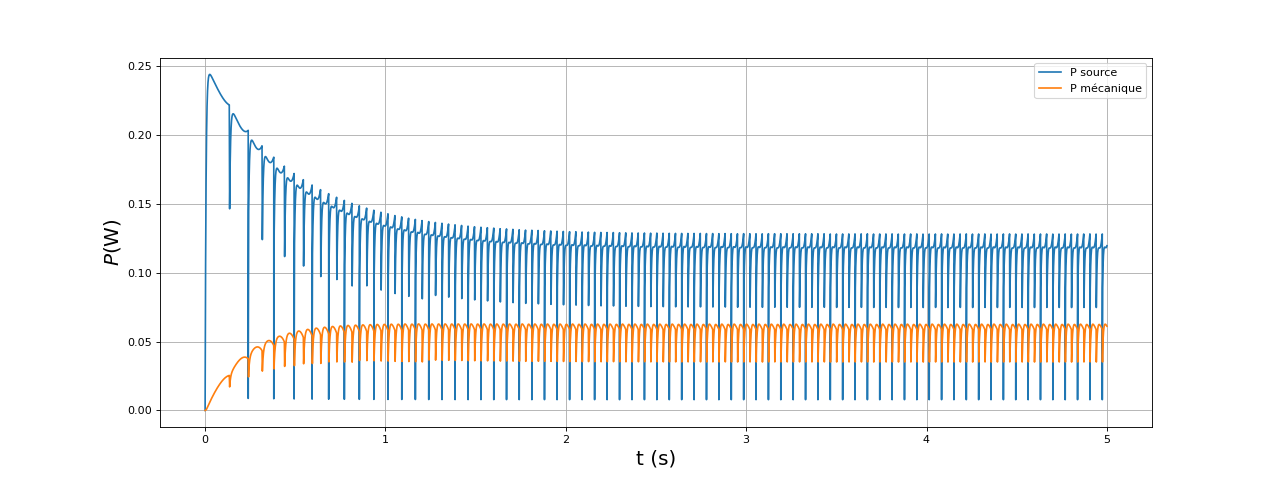 fig35.pdf
fig35.pdf
Voici le calcul du rendement :
N = len(P)
k = int(2/(temps[1]-temps[0]))
rend = P[k:N].mean()/Ps[k:N].mean()
print(rend) --> 0.508829358668254
L'augmentation de se traduit bien par une augmentation du rendement (à vitesse de rotation constante). Pour augmenter la valeur de , il faut augmenter le moment magnétique des aimants ou augmenter le captage de flux par les bobines.
La simulation Moteur synchrone permet de suivre la simulation en temps réel et de faire varier les paramètres à volonté.
3.f. Fonctionnement en générateur
Dans cette simulation, on teste le fonctionnement en générateur sans charge, c'est-à-dire sans source et sans courants dans les bobines.
r=2
L=2e-3
Phi0 = 1e-3
J=1e-3
G0 = 0.00
a = 1e-3
alphaE = 1
h = 1e-5
moteur = MoteurSynchrone(r,L,Phi0,J,G0,a,alphaE)
moteur.initialiser()
omega = 1
tmax = 10
temps,V,theta = moteur.simulationSansSource(omega,tmax,h)
nom ="simulation-4.npy"
np.save(nom,np.array([temps,V,theta]))
Voici la tension à l'entrée du pont () en fonction du temps :
[temps,V,theta] = np.load("simulation-4.npy")
figure(figsize=(16,6))
plot(temps,V)
ylabel('V')
grid()
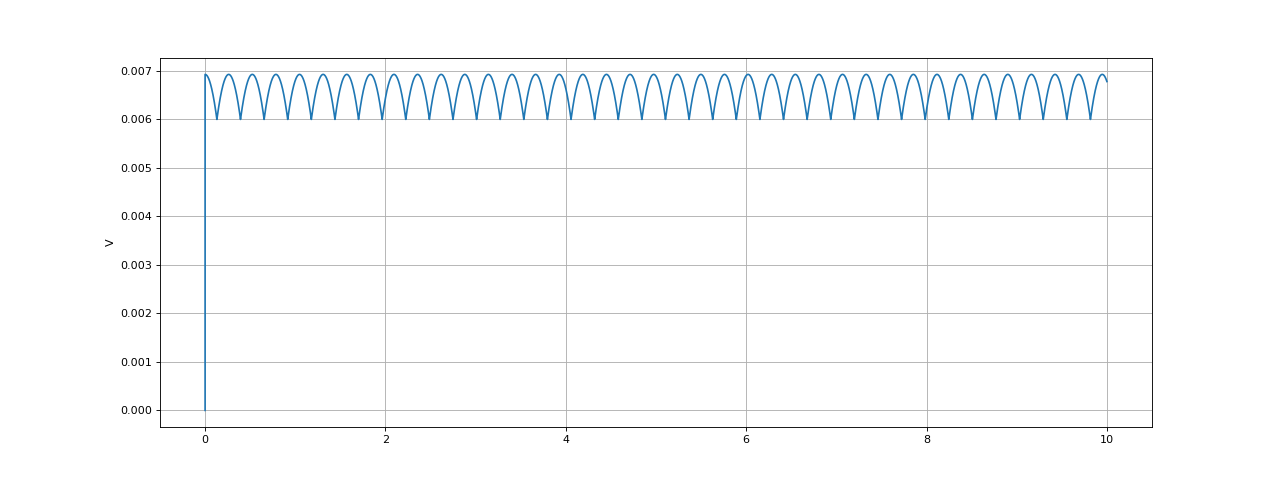 fig36.pdf
fig36.pdf
La tension a une valeur moyenne positive mais elle comporte évidemment des ondulations. Cette simulation montre que le pont de transitors auto-piloté permet de faire fonctionner la machine en générateur et de délivrer une tension redressée. Si l'on souhaite obtenir une tension constante, il faudra ajouter un filtrage passe-bas.
Une simulation plus complète doit se faire avec une charge et, en conséquence, des courants dans les bobines.
Remarquons que si le générateur était utilisé comme alternateur (sans pont de transistors), il faudrait procéder à un redressement de la tension triphasée alternative. La commande par un pont de transistors permet d'obtenir directement la tension redressée.
4. Réalisation du moteur
4.a. Description
Le moteur est réalisé par impression 3D en PLA (acide polylactique). L'image et la photo suivantes montrent le rotor et le cadre qui le tient.
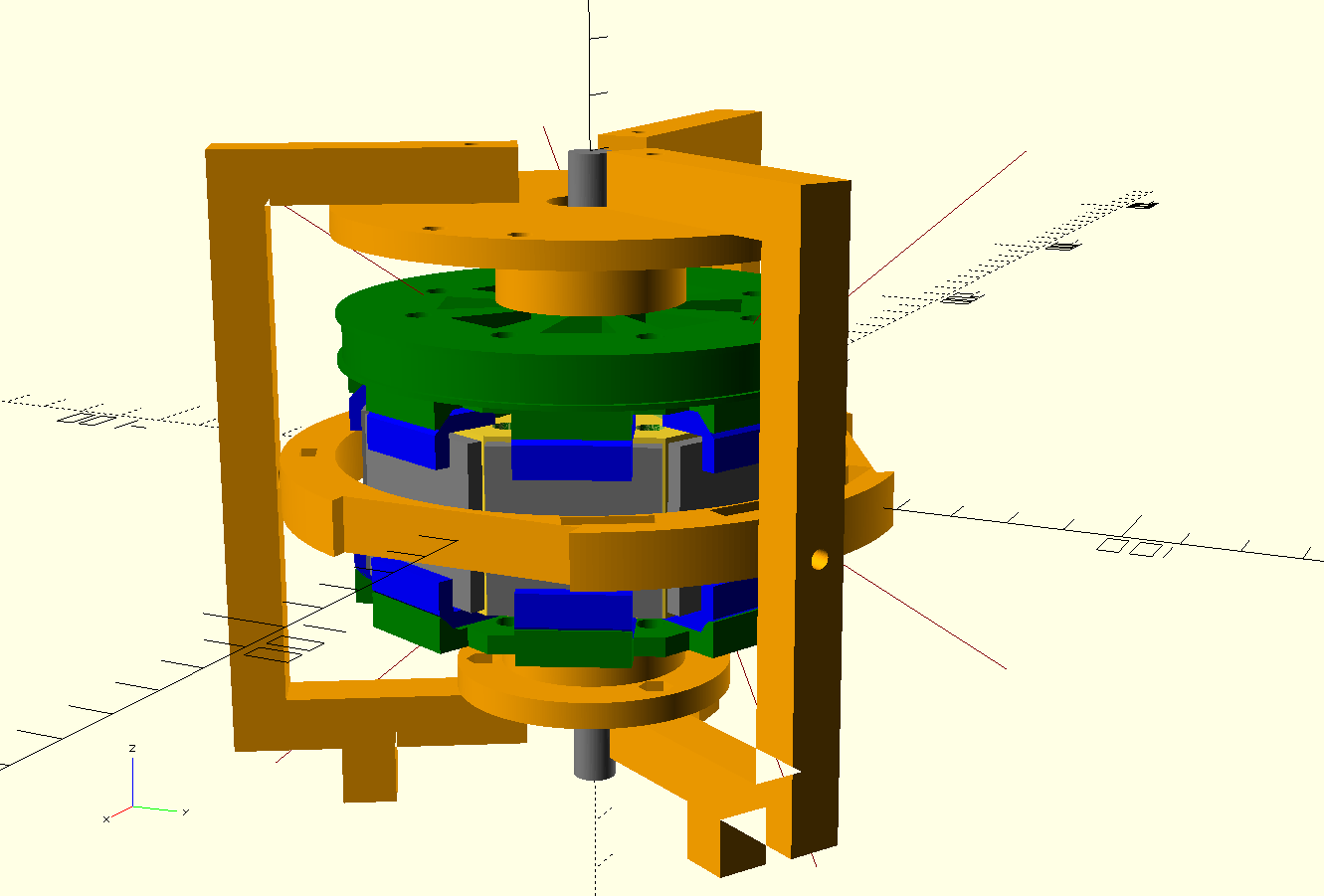

Sur la photo, l'arceau où les capteurs sont logés n'est pas encore monté.
Le rotor est muni d'un alésage de 8 mm de diamètre acceuillant un arbre en acier de même diamètre. Il est constitué de différentes parties serrées entre elles par 8 tiges filetées qui le traversent de part en part, avec un écrou de chaque côté. La partie centrale du rotor est un cyclindre octogonal (de diamètre 74 mm) sur lequel les 8 aimants sont collés (avec du ruban adhésif double face). Il s'agit d'aimants en ferrite de forme carré 30x30 mm et d'épaisseur 3 mm. Ces aimants sont maintenus en pression contre le rotor grace à des cales dont la partie supérieure comporte un biseau incliné de 45 degrés (en bleu sur l'image ci-dessus). Deux couvercles (en vert) comportent huits parties saillantes avec un biseau de 45 degrés, qui permettent d'appliquer une pression axiale dont une partie est transmise dans la direction radiale via les cales, ce qui permet de bien maintenir les aimants contre le rotor et d'avoir une transmission uniforme des efforts entre les aimants et le rotor. Le bâti est constitué de trois fourches et de deux bases dans lesquelles un roulement à bille est inséré, de diamètre interne 8 mm. La photo ci-dessous montre une vue latérale avec deux bobines :

Un arceau fixé aux fourches comporte des encoches permettant de placer précisément les noyaux des trois bobines. Nous avons en effet constaté que le placement très précis des bobines est important pour l'obtention de trois f.é.m. déphasés de 120 degrés, et en conséquence pour le bon fonctionnement du moteur. D'une manière générale, plus le nombre de pôles du rotor est grand, plus les bobines doivent être placées précisément (de même pour les capteurs). L'arceau comporte aussi trois logements permettant d'insérer les platines des trois capteurs à effet Hall à 30, 60 et 90 degrés de la première bobine.
La puissance mécanique est transmise à l'extérieur par courroie via la roue située sur la partie supérieure du rotor. Il n'est pas garanti que l'arbre soit toujours parfaitement solidaire du rotor mais cela est sans importance puisqu'il ne sert qu'à la réalisation de la liaison pivot et pas à la transmission de puissance. Par ailleurs, le poids des noyaux et des bobines est suffisant pour assurer un bon maintien du cadre par rapport au bobines. En principe, il faudrait que les bobines soient parfaitement solidaires du cadre.
La photo ci-dessous montre le côté de l'arceau où sont logés les trois capteurs :

4.b. Forces électromotrices et état des capteurs
Dans cette partie, le rotor est entraîné par un petit moteur à courant continu (le mouvement est transmis par courroie). On enregistre les tensions aux bornes des trois bobines et l'état des trois capteurs.
[t,u1,u2,u3,c1,c2,c3] = np.load("3phases3capteurs-4.npy")
c1 /= c1.max()
c2 /= c2.max()
c3 /= c3.max()
figure(figsize=(16,12))
subplot(211)
plot(t,u1,label="B1")
plot(t,u2,label="B2")
plot(t,u3,label="B3")
xlim(0,1)
grid()
legend(loc='upper right')
ylabel("U bobines (V)")
subplot(212)
plot(t,c1,label="C1")
plot(t,c2+2,label="C2")
plot(t,c3+4,label="C3")
xlabel("t (s)")
xlim(0,1)
grid()
legend(loc='upper right')
ylabel("Capteurs")
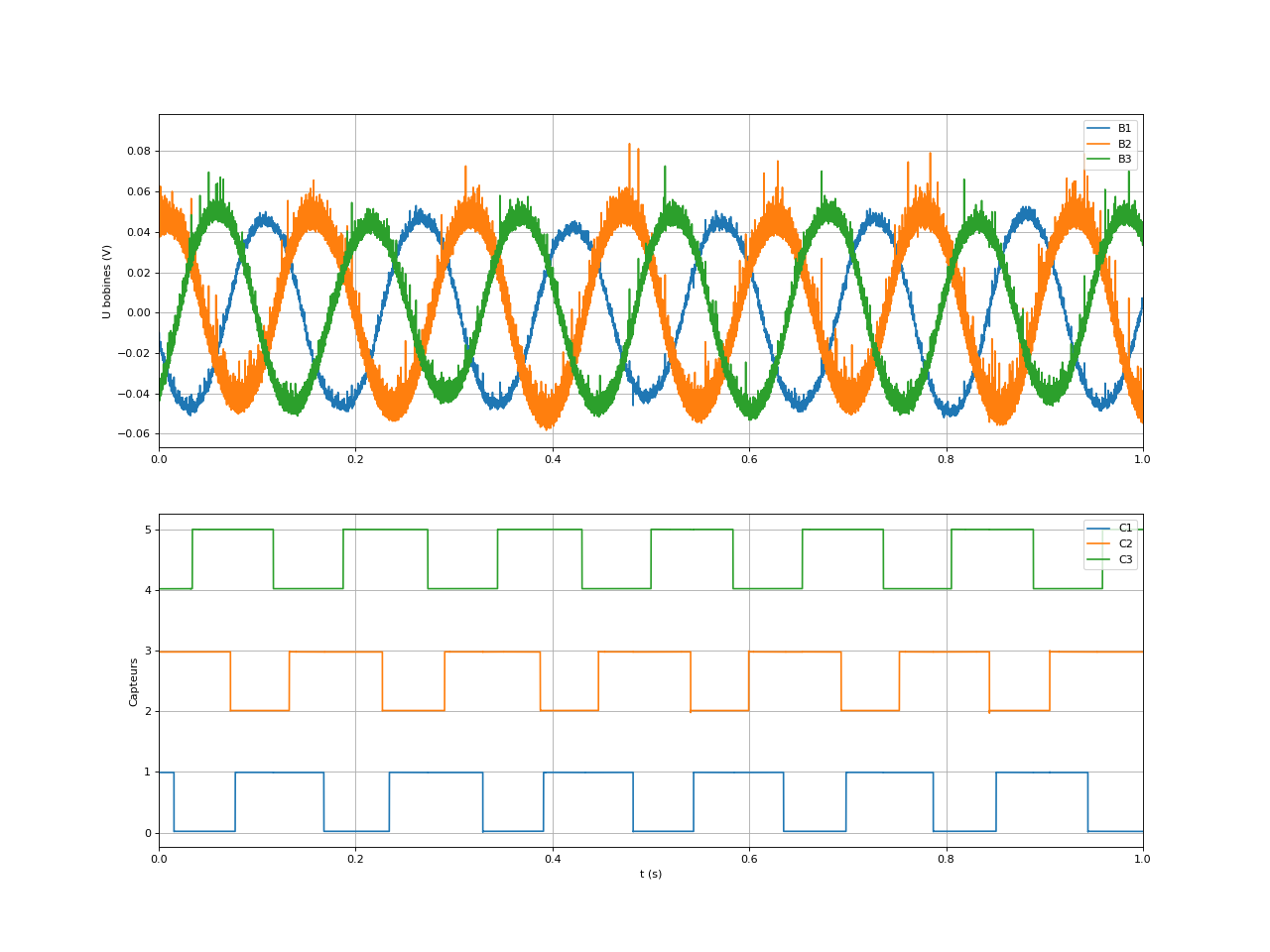 fig37.pdf
fig37.pdf
Ces résultats montrent que la force électromotrice développée dans les bobines a bien une forme sinusoïdale en fonction de l'angle du rotor, ce qui confirme les résultats obtenus pas la simulation. Le fait que la f.é.m. soit sinusoïdale et non pas trapézoïdale est dû à la forme des aimants et surtout au fait que l'aimantation d'un aimant est uniforme. Il est vraisemblable que la forme du stator soit importante aussi.
Le flux dans chaque bobine se déduit par intégration de la force électromotrice :
def integration(t,u):
te = t[1]-t[0]
v = u.copy()
for i in range(1,len(u)):
v[i] = v[i-1]+0.5*te*(u[i]+u[i-1])
return v
phi1 = -integration(t,u1)
phi2 = -integration(t,u2)
phi3 = -integration(t,u3)
phi1 -= phi1.mean()
phi2 -= phi2.mean()
phi3 -= phi3.mean()
figure(figsize=(16,6))
plot(t,phi1,label="B1")
plot(t,phi2,label="B2")
plot(t,phi3,label="B3")
xlim(0,1)
grid()
legend(loc='upper right')
ylabel(r"Flux bobines ($\rm T\cdot m^{2}$)",fontsize=18)
xlabel("t (s)",fontsize=18)
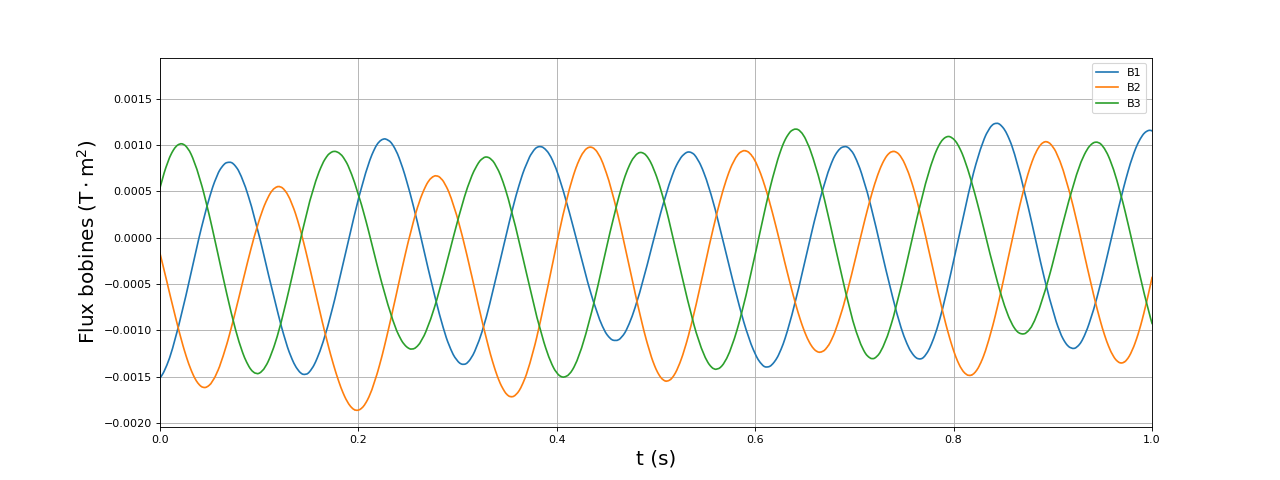 fig38.pdf
fig38.pdf
Ces courbes permettent d'évaluer la constante pour ce moteur : . Les simulations ci-dessus montrent que cette valeur est faible, ce qui implique un faible rendement énergétique. Pour augmenter cette valeur, il faudrait d'une part augmenter le moment magnétique des aimants (par exemple en utilisant des aimants au néodyme), d'autre part augmenter le flux dans les bobines en réduisant leur longueur (pour un même nombre de spires). Il faudrait aussi employer un noyau en fer faisant le tour du stator et pas simplement un noyau dans chaque bobine.
Voici la séquence des états des capteurs :
etats = [c1,c2,c3]
def sequence(etat):
N = len(etat[0])
seq = []
for i in range(1,N):
if abs(etat[0][i]-etat[0][i-1])>0.5 or abs(etat[1][i]-etat[1][i-1])>0.5 or abs(etat[2][i]-etat[2][i-1])>0.5:
e1 = (etat[0][i] > 0.5)*1
e2 = (etat[1][i] > 0.5)*1
e3 = (etat[2][i] > 0.5)*1
seq.append([e1,e2,e3])
return seq
seq = sequence(etats)
print(seq) --> [[0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0], [0, 1, 1], [0, 0, 1], [1, 0, 1], [1, 0, 0], [1, 1, 0], [0, 1, 0]]
On obtient bien la séquence de 6 états établie plus haut.
Pour chaque état des capteurs, donc pour chaque état d'alimentation des bobines, la bobine non alimentée doit avoir sa f.é.m. passant par zéro à la fin de l'état. En effet, le couple moteur développé par une bobine est proportionnel à la force électromotrice et il s'annule donc en même temps que celle-ci. Par exemple, pour le premier état des capteurs (0,1,0), l'alimentation des bobines doit être (-I,I,0) : la f.é.m. aux bornes de la bobine B3 passe par zéro à la fin de cette état. Pour l'état suivant (0,1,1) l'alimentation doit être (-I,0,I) : la f.é.m aux bornes de la bobine B2 passe par zéro à la fin de cet état.
Remarque : il est possible de réaliser l'auto-pilotage en détectant le passage par zéro de la tension aux bornes de la bobine non alimentée. Cette méthode est mise en œuvre dans les petits moteurs BLDC non munis de capteurs.
Si le sens des trois capteurs est inversé, on obtient la même séquence.
4.c. Électronique de commande et programme Arduino
La commutation à 6 états est décrite dans Commutateur triphasé à six états. Les trois bobines sont montées en étoile et on applique une séquence où deux bobines sont alimentées simultanément, la troisième restant libre (mode de conduction 120 degrés).
Si les bornes des trois bobines montées en étoile sont notées A,B,C, la séquence des états des capteurs, des courants dans les bobines et des tensions appliquées aux bornes est :
La notation AB signifie qu'on applique une tension positive entre la borne B et la borne A. La tension effective appliquée est ajustée par le rapport cyclique du découpage.
Pour un état des capteurs et son état complémentaire, il y a inversion du sens du passage du courant dans les deux bobines. Par exemple à l'état (0,1,0) correspond AB et à l'état (1,0,1) correspond BA. Or le sens du courant (qui dépend aussi du sens du bobinage) contrôle le signe du couple. En conséquence, la séquence précédente fait tourner le moteur dans un sens (à déterminer expérimentalement) et la séquence complémentaire (obtenue en inversant les 0 et les 1) le fait tourner dans l'autre sens.
Le programme Arduino reprend le programme generateurPWM-3Phases-6Etats.ino présenté dans Commutateur triphasé à six états en y ajoutant l'auto-pilotage.
Un changement d'état d'un des trois capteurs déclenche une interruption. On utilise pour cela les ports 18,19 et 20 de l'Arduino MEGA. Dans la routine de cette interruption, on détermine l'état des capteurs sous la forme d'un entier de 3 bits. La consultation d'une table indexée par cet entier permet de déterminer l'état d'alimentation des bobines qu'il faut appliquer (états numérotés de 0 à 5).
Le contrôle de la tension effective appliquée aux bobines par modulation de largeur d'impulsions est activée si la macro PWM est définie. Les timers 2,3 et 4 sont utilisés dans ce cas pour générer les signaux PWM. Dans le cas contraire, l'application des signaux de commande se fait directement avec digitalWrite. En l'absence de PWM, il est préférable de démarrer le moteur avec une tension d'alimentation faible (par exemple 1 V) et de l'augmenter progressivement pour faire augmenter la vitesse. On peut démarrer le moteur directement avec une tension de 12 V mais sa vitesse sera alors très élevée.
#include "Arduino.h"
// bras de pont phase A
#define INA_1 11 // transistor haut
#define INA_2 12 // transistor bas
// bras de pont phase B
#define INB_1 5
#define INB_2 2
// bras de pont phase C
#define INC_1 6
#define INC_2 7
// états d'un bras de pont
#define HIGH_0_LOW_1 0 // sortie à la masse (état 01)
#define HIGH_1_LOW_0 1 // sortie en PWM (état 10)
#define HIGH_0_LOW_0 2 // sortie non connectée (état 00)
uint8_t sequence_A[6] = {1,1,2,0,0,2};
uint8_t sequence_B[6] = {0,2,1,1,2,0};
uint8_t sequence_C[6] = {2,0,0,2,1,1};
uint8_t sensRot = 0;
// capteurs HALL
#define IN1 18 // PD3
#define IN2 19 // PD2
#define IN3 20 // PD1
uint8_t tableEtats[8];
uint32_t compteur;
uint32_t temps;
uint32_t period;
uint16_t icr;
uint16_t ocra,ocrb;
uint16_t diviseur[6] = {0,1,8,64,256,1024};
//#define PWM // décommenter pour activer le PWM
float periodPWM = 100;
float rapport = 0.2;
uint16_t temps_mort = 10;
La fonction suivante programme les Timers 1,3 et 4 qui servent à générer les signaux de commande du pont de transistors (voir Commutateur triphasé à six états). Elle prend en arguments la période de découpage en microsecondes et le rapport cyclique. La tension effective appliquée aux bobines est égale à la tension de l'alimentation multipliée par le rapport cyclique. Le couple moteur est proportionnel au courant dans les bobines, lui-même proportionnel en principe à la tension effective. Pour une charge mécanique donnée, la vitesse du moteur est donc proportionnelle à la tension effective (comme pour un moteur à courant continu). Le choix optimal de la fréquence de découpage dépend du rapport L/R des bobines.
void config_timers(float period, float rapport) {
// period : période du PWM en microsecondes
cli();
TCCR1A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR1B = (1 << WGM13);
TCCR3A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR3B = (1 << WGM13);
TCCR4A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR4B = (1 << WGM13);
icr = (F_CPU/1000000*period/2);
int d = 1;
while ((icr>0xFFFF)&&(d<5)) {
d++;
icr = (F_CPU/1000000*period/2/diviseur[d]);
}
TCCR1B |= d;
TCCR3B |= d;
TCCR4B |= d;
ocra = icr*rapport-temps_mort;
ocrb = icr*rapport+temps_mort;
TCNT1 = 0;
TCNT3 = 0;
TCNT4 = 0;
ICR1 = icr;
ICR3 = icr;
ICR4 = icr;
OCR1A = ocra;
OCR1B = ocrb;
OCR3A = ocra;
OCR3B = ocrb;
OCR4A = ocra;
OCR4B = ocrb;
sei();
}
Les trois fonctions suivantes permettent de placer les bras de deux transistors (respectivement les bras A, B et C) dans un état donné.
void etat_bras_A(uint8_t etat) {
#ifdef PWM
switch (etat) {
case HIGH_0_LOW_1:
OCR1A = 0;
OCR1B = 0;
break;
case HIGH_1_LOW_0:
OCR1A = ocra;
OCR1B = ocrb;
break;
case HIGH_0_LOW_0:
OCR1A = 0;
OCR1B = icr+1;
break;
}
#else
switch (etat) {
case HIGH_0_LOW_1:
digitalWrite(INA_1,LOW);
digitalWrite(INA_2,HIGH);
break;
case HIGH_1_LOW_0:
digitalWrite(INA_1,HIGH);
digitalWrite(INA_2,LOW);
break;
case HIGH_0_LOW_0:
digitalWrite(INA_1,LOW);
digitalWrite(INA_2,LOW);
break;
}
#endif
}
void etat_bras_B(uint8_t etat) {
#ifdef PWM
switch (etat) {
case HIGH_0_LOW_1:
OCR3A = 0;
OCR3B = 0;
break;
case HIGH_1_LOW_0:
OCR3A = ocra;
OCR3B = ocrb;
break;
case HIGH_0_LOW_0:
OCR3A = 0;
OCR3B = icr+1;
break;
}
#else
switch (etat) {
case HIGH_0_LOW_1:
digitalWrite(INB_1,LOW);
digitalWrite(INB_2,HIGH);
break;
case HIGH_1_LOW_0:
digitalWrite(INB_1,HIGH);
digitalWrite(INB_2,LOW);
break;
case HIGH_0_LOW_0:
digitalWrite(INB_1,LOW);
digitalWrite(INB_2,LOW);
break;
}
#endif
}
void etat_bras_C(uint8_t etat) {
#ifdef PWM
switch (etat) {
case HIGH_0_LOW_1:
OCR4A = 0;
OCR4B = 0;
break;
case HIGH_1_LOW_0:
OCR4A = ocra;
OCR4B = ocrb;
break;
case HIGH_0_LOW_0:
OCR4A = 0;
OCR4B = icr+1;
break;
}
#else
switch (etat) {
case HIGH_0_LOW_1:
digitalWrite(INC_1,LOW);
digitalWrite(INC_2,HIGH);
break;
case HIGH_1_LOW_0:
digitalWrite(INC_1,HIGH);
digitalWrite(INC_2,LOW);
break;
case HIGH_0_LOW_0:
digitalWrite(INC_1,LOW);
digitalWrite(INC_2,LOW);
break;
}
#endif
}
La fonction suivante remplit la table qui établit la correspondance entre l'état des capteurs (représenté sous la forme d'un nombre à 3 bits) et l'état du pont de transistors.
void remplir_table_etats(uint8_t sensRot) {
if (sensRot==0) {
tableEtats[B010] = 3;
tableEtats[B011] = 4;
tableEtats[B001] = 5;
tableEtats[B101] = 0;
tableEtats[B100] = 1;
tableEtats[B110] = 2;
}
else {
tableEtats[B010] = 0;
tableEtats[B011] = 1;
tableEtats[B001] = 2;
tableEtats[B101] = 3;
tableEtats[B100] = 4;
tableEtats[B110] = 5;
}
}
La fonction change_etat est appelée par interruption lorsqu'un capteur change d'état. Elle effectue la lecture de l'état des trois capteurs (sur le port D) et applique la commande du pont indiquée par la table tableEtats. De plus, elle incrémente un compteur qui atteint la valeur 24 lorsque le rotor a effectué un tour, ce qui lui permet de calculer la période de rotation en microsecondes (il faut 4 cycles de 6 états pour faire un tour de rotor).
void change_etat() {
uint32_t t;
uint8_t etat_capteurs = (PIND >> 1);
if ((etat_capteurs==0)||(etat_capteurs==0xb111)) return;
uint8_t is = tableEtats[etat_capteurs];
etat_bras_A(sequence_A[is]);
etat_bras_B(sequence_B[is]);
etat_bras_C(sequence_C[is]);
compteur += 1;
if (compteur==24) {
compteur = 0;
t = micros();
period = t-temps;
Serial.println(period/1e3);
temps = t;
}
}
Remarque : il est possible de déterminer l'état des capteurs en prenant en compte leur changement à chaque interruption. Cependant, le moteur doit continuer à fonctionner si une interruption n'est pas pris en charge : c'est pourquoi nous faisons la lecture complète des trois capteurs à chaque interruption.
Voici la fonction d'initialisation et la fonction loop (qui ne fait rien) :
void setup() {
Serial.begin(115200);
remplir_table_etats(sensRot);
pinMode(INA_1,OUTPUT);
digitalWrite(INA_1,LOW);
pinMode(INA_2,OUTPUT);
digitalWrite(INA_2,LOW);
pinMode(INB_1,OUTPUT);
digitalWrite(INB_1,LOW);
pinMode(INB_2,OUTPUT);
digitalWrite(INB_2,LOW);
pinMode(INC_1,OUTPUT);
digitalWrite(INC_1,LOW);
pinMode(INC_2,OUTPUT);
digitalWrite(INC_2,LOW);
pinMode(IN1,INPUT);
pinMode(IN2,INPUT);
pinMode(IN3,INPUT);
attachInterrupt(digitalPinToInterrupt(IN1),change_etat,CHANGE);
attachInterrupt(digitalPinToInterrupt(IN2),change_etat,CHANGE);
attachInterrupt(digitalPinToInterrupt(IN3),change_etat,CHANGE);
#ifdef PWM
config_timers(periodPWM,rapport);
#endif
compteur = 0;
temps = micros();
change_etat();
}
void loop() {
}
4.d. Étude expérimentale
Le circuit de commande est décrit dans Commutateur triphasé à six états. Il comporte 6 transistors MOSFET. Ce circuit fonctionne même si la tension d'alimentation (tension Vs) est de quelques dixièmes de volts. Le découpage des tensions appliquées aux bobines à la fréquence de 10 kHz permet de faire varier la tension effective en faisant varier le rapport cyclique. L'utilisation normale d'un moteur se fait avec une tension d'alimentation fixe et en faisant varier la vitesse au moyen du rapport cyclique du découpage. Cependant, pour une étude expérimentale, on a intérêt à ne pas utiliser de découpage et à appliquer une tension d'alimentation faible, que l'on peut augmenter pour faire monter la vitesse du moteur. En effet, les signaux électriques en présence de découpage sont souvent très confus et difficiles à analyser. Pour avoir une commande sans découpage, il suffit d'enlever la ligne #define PWM.
La vitesse de rotation du moteur est calculée à partir des signaux des capteurs et affichée sur la console.
Voici les trois tensions appliquées aux bobines par rapport à la masse, pour une tension d'alimentation Vs=1 V sans découpage :
[t,u1,u2,u3] = np.load("1V-r1-2.npy")
figure(figsize=(16,6))
plot(t,u1,label="u1")
plot(t,u2,label="u2")
plot(t,u3,label="u3")
ylabel("Volts",fontsize=16)
xlabel("t (s)",fontsize=16)
grid()
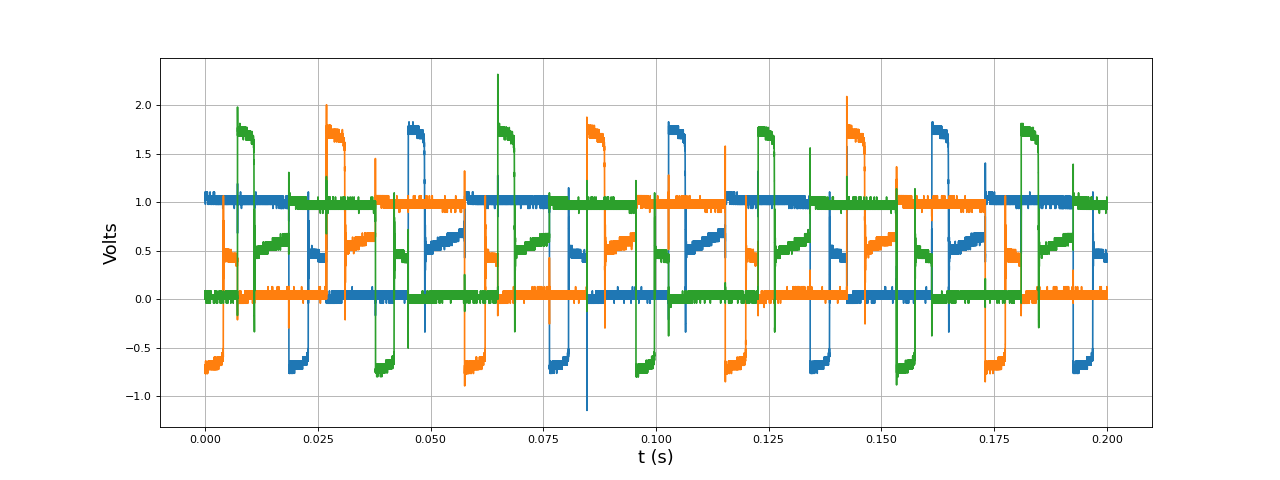 fig39.pdf
fig39.pdf
Voici les périodes de rotation affichées sur la console (en ms) :
233.07
232.80
232.57
232.07
231.68
231.28
230.94
230.61
Nous identifions sur ces signaux les 6 états du cycle. La durée d'un cycle est 58 ms, ce qui correspond à un tour en 4x63=231 ms, en accord avec la durée affichée sur la console. Au cours d'un cycle de 6 états, la tension appliquée à une bobine (par rapport à masse) est égale à 1 V pendant 2 états, elle est libre pendant 1 état, nulle pendant 2 états et libre pendant 1 état. L'état libre signifie que la tension n'est pas imposée par le pont de transistors. Lors d'un état libre, il y a une première partie où une des deux diodes du pont est passante puis une seconde partie (un peu plus longue) où cette diode est bloquante. La variation de tension pendant cette seconde partie est due aux f.é.m.. Considérons le cas d'une bobine dont la borne est au potentiel nul et qui passe à l'état libre : la diode du haut devient passante donc le potentiel de sa borne devient égal à 1,8 V puis lorsque cette diode devient bloquante, le potentiel est déterminé par les f.é.m..
La vidéo ci-dessous montre le démarrage du moteur (caméra à 120 fps donc il s'agit d'un ralenti de 4x) :
Chaque capteur comporte une LED qui s'allume lorsqu'il est à l'état haut.
Voici les tensions pour une tension d'alimentation de 2 V :
[t,u1,u2,u3] = np.load("2V-r1-2.npy")
figure(figsize=(16,6))
plot(t,u1,label="u1")
plot(t,u2,label="u2")
plot(t,u3,label="u3")
grid()
xlabel("t (s)",fontsize=16)
ylabel("Volts",fontsize=16)
xlim(0,0.2)
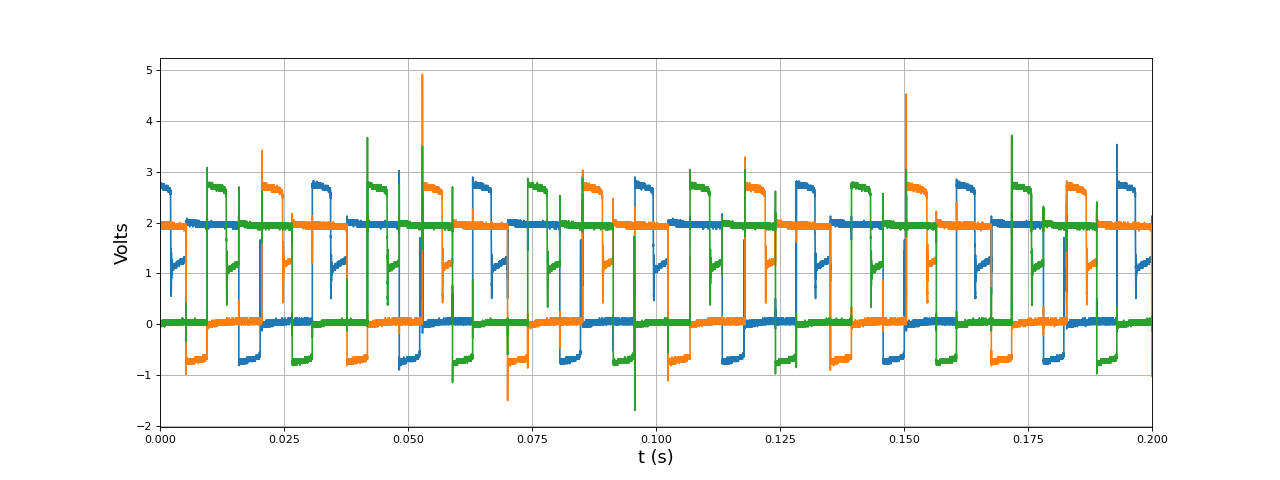 fig40.pdf
fig40.pdf
Voici les périodes de rotation affichées sur la console (en ms) :
129.67
129.76
129.84
129.89
129.91
129.91
129.8
129.87
Durée d'un cycle est 32 ms, ce qui correspond à un tour en 4*32=130 ms. Pendant la phase d'état libre d'une bobine, la conduction de la diode est plus longue.
Les trois bobines sont câblées en étoile. Afin de mesurer les tensions appliquées aux trois bobines par rapport au point neutre, nous utilisons un oscilloscope à 4 voies. Cependant, ce point neutre n'est pas à la masse. Il est donc impératif que la masse du circuit de commande, reliée à la masse de l'Arduino, elle-même reliée à la masse du PC sur lequel l'Arduino est branché par le port USB, soit indépendante de la masse de l'oscilloscope. Nous utilisons un PC portable, ce qui permet d'avoir cette indépendance (qui ne serait plus vérifiée pour un PC de bureau relié à la terre). Voici, pour une tension d'alimentation de 1 V, les trois tensions appliquées aux bobines par rapport au point neutre :
[t,u1,u2,u3] = np.load("1V-r1-N-2.npy")
figure(figsize=(16,6))
plot(t,u1,label="u1")
plot(t,u2,label="u2")
plot(t,u3,label="u3")
ylabel("Volts",fontsize=16)
xlabel("t (s)",fontsize=16)
grid()
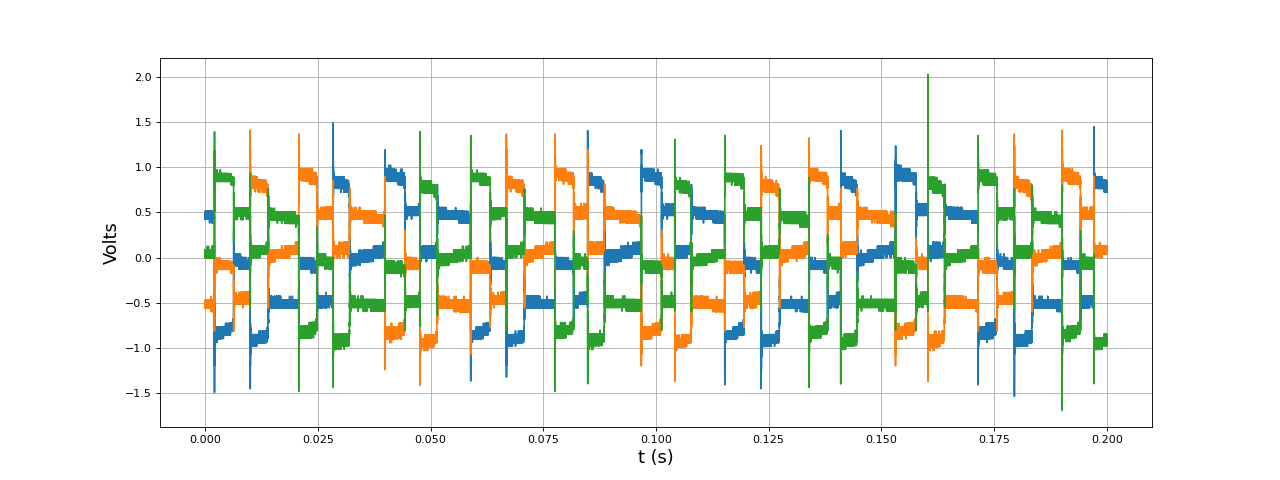 fig41.pdf
fig41.pdf
Voici les périodes de rotation affichées sur la console (en ms) :
233.02
233.08
232.91
232.87
233.18
233.32
Pour comprendre la forme de ces trois tensions, nous pouvons la rapprocher de celle obtenue plus haut pour une simulation, reproduite ci-dessous :

Pour chaque bobine, nous pouvons repérer dans la tension expérimentale la phase au cours de laquelle le potentiel sur la borne de cette bobine n'est pas imposé et une fois que la diode a cessé de conduire. Pendant cette phase, la tension par rapport au point neutre suit exactement la f.é.m. dans cette bobine (puisque le courant est nul). Le passage par zéro de cette tension peut être détecté pour piloter le moteur sans capteur mais cette méthode de pilotage ne permet pas à elle seule d'effectuer le démarrage. Le passage par zéro de la f.é.m. correspond précisément au moment où un pôle magnétique se trouve sur l'axe de la bobine.
4.e. Pilotage du moteur
La tension d'alimentation Vs est fixée. La tension effective appliquée aux bobines est ajustée au moyen du rapport cyclique de découpage. Si la fréquence de découpage est 10 kHz, nous devons estimer le temps caractéristique d'établissement du courant dans une bobine à partir de sa résistance à cette fréquence, qui est d'environ 10 ohms. La bobine ayant une auto-inductance de 10 mH, ce temps est d'environ 1 ms, soit 10 fois plus que la période de découpage. Une fréquence de 10 kHz est donc suffisante pour les bobines utilisées (qui sont relativement grosses).
Le programme Arduino ci-dessous permet de contrôler le moteur depuis un script Python. Il utilise le protocole de transmission de données décrit dans Échanges de données avec un Arduino.
Les données échangées sont :
- DATA_0 : le rapport cyclique (float).
- DATA_1 : le sens de rotation (int8, 0 ou 1).
- DATA_2 : la période en microsecondes (float), évaluée sur un tour (24 états).
- DATA_3 : mode de fonctionnement (int8, 0 ou 1).
- DATA_4 : tableau des BUFSIZE dernières périodes.
- DATA_5 : vitesse angulaire consigne (pour le mode de fonctionnement 1).
Dans le mode de fonctionnement 0, on choisit un rapport cyclique de découpage puis on récupère la période de rotation ou bien le tableau des dernières périodes (de taille BUFSIZE). Dans le mode de fonctionnement 1, on choisit vitesse de rotation et le programme effectue un ajustement du rapport cyclique (à chaque tour) de manière obtenir la vitesse demandée. Ce mode fait appel à un asservissement du rapport cyclique par la vitesse angulaire. La vitesse angulaire est évaluée à chaque tour complet. Soit la vitesse angulaire de commande (ou vitesse angulaire consigne). L'erreur est . Nous optons pour un correcteur proportionnel-intégral (PI). Le rapport cyclique du découpage est défini par la relation :
Le terme proportionnel permet d'obtenir une réponse instantanée mais conduit à une erreur non nulle en régime stationnaire. Le terme intégral permet de réduire l'erreur en régime stationnaire mais introduit un temps de retard. La mise à jour du rapport est faite après chaque tour de rotor, en fonction de la vitesse angulaire mesurée sur ce tour. Si l'on note la valeur de l'intégrale précédente, le nouveau rapport cyclique se calcule par :
Pour simuler la réponse du moteur avec le correcteur PI, on pourrait faire appel à la simulation complète introduite plus haut. En première approche, il est préférable d'introduire un modèle simplifié consistant à supposer que le couple moteur est proportionnel au rapport cyclique : . Si le couple mécanique est de la forme , l'équation mécanique s'écrit :
Cette relation et la relation conduisent à l'équation différentielle suivante :
Si le rapport cyclique est imposé (mode 0), l'équation différentielle est
L'étude du démarrage du moteur (ou de sa réponse à un changement de r) en mode 0 permet donc de déterminer le rapport et l'étude du démarrage en mode 1 permet ensuite de déterminer le rapport . Il n'est donc pas nécessaire de connaître le moment d'inertie pour obtenir les paramètres du moteur permettant de simuler la réponse du système asservi.
#include "Arduino.h"
// bras de pont phase A
#define INA_1 11 // transistor haut
#define INA_2 12 // transistor bas
// bras de pont phase B
#define INB_1 5
#define INB_2 2
// bras de pont phase C
#define INC_1 6
#define INC_2 7
#define PWM
#define TRIGGER 3 // PE5
#define CONTROL 4 // PG5
// états d'un bras de pont
#define HIGH_0_LOW_1 0 // sortie à la masse (état 01)
#define HIGH_1_LOW_0 1 // sortie en PWM (état 10)
#define HIGH_0_LOW_0 2 // sortie non connectée (état 00)
uint8_t sequence_A[6] = {1,1,2,0,0,2};
uint8_t sequence_B[6] = {0,2,1,1,2,0};
uint8_t sequence_C[6] = {2,0,0,2,1,1};
uint8_t sensRot = 0;
uint8_t etat_capteurs_anterieur;
// capteurs HALL
#define IN1 18 // PD3
#define IN2 19 // PD2
#define IN3 20 // PD1
uint8_t tableEtats[8];
uint32_t compteur;
uint32_t temps;
float period;
float omega;
float omegaDemand = 1.0;
float Kp=0.05;
float Ki=0.03;
float integOmega;
#define BUFSIZE 10
float bufPeriod[BUFSIZE];
uint8_t ibuf;
uint8_t etatControl;
uint8_t start = 0;
uint16_t icr;
uint16_t ocra,ocrb;
uint16_t temps_mort = 10;
uint16_t diviseur[6] = {0,1,8,64,256,1024};
float periodPWM = 100;
float rapport = 0.0;
uint8_t mode = 0; // mode de fonctionnement : 0 : contrôle du rapport cyclique, 1 : contrôle de la vitesse
// communication Série
#define GET_DATA 10
#define SET_DATA 11
#define DATA_0_SIZE 4 // rapport cyclique (float)
#define DATA_1_SIZE 1 // sens de rotation (int8)
#define DATA_2_SIZE 4 // période en us (float)
#define DATA_3_SIZE 1 // mode de fonctionnement (int8)
#define DATA_4_SIZE 4*BUFSIZE // tampon des périodes
#define DATA_5_SIZE 4 // vitesse en tours/s (float)
uint8_t data_0[DATA_0_SIZE];
uint8_t data_1[DATA_1_SIZE];
uint8_t data_2[DATA_2_SIZE];
uint8_t data_3[DATA_3_SIZE];
uint8_t data_5[DATA_5_SIZE];
bool data_2_ready = true;
bool data_2_request = false;
bool data_4_ready = false;
bool data_4_request = false;
void config_timers(float period, float rapport) {
// period : période du PWM en microsecondes
cli();
TCCR1A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR1B = (1 << WGM13);
TCCR3A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR3B = (1 << WGM13);
TCCR4A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR4B = (1 << WGM13);
icr = (F_CPU/1000000*period/2);
int d = 1;
while ((icr>0xFFFF)&&(d<5)) {
d++;
icr = (F_CPU/1000000*period/2/diviseur[d]);
}
TCCR1B |= d;
TCCR3B |= d;
TCCR4B |= d;
if (icr*rapport>temps_mort) {
ocra = icr*rapport-temps_mort;
ocrb = icr*rapport+temps_mort;
}
else {
ocra = icr*rapport;
ocrb = icr*rapport;
}
TCNT1 = 0;
TCNT3 = 0;
TCNT4 = 0;
ICR1 = icr;
ICR3 = icr;
ICR4 = icr;
OCR1A = ocra;
OCR1B = ocrb;
OCR3A = ocra;
OCR3B = ocrb;
OCR4A = ocra;
OCR4B = ocrb;
sei();
}
void changer_rapport_pwm(float rapport) {
if (icr*rapport>temps_mort) {
ocra = icr*rapport-temps_mort;
ocrb = icr*rapport+temps_mort;
}
else {
ocra = icr*rapport;
ocrb = icr*rapport;
}
}
void etat_bras_A(uint8_t etat) {
#ifdef PWM
switch (etat) {
case HIGH_0_LOW_1:
OCR1A = 0;
OCR1B = 0;
break;
case HIGH_1_LOW_0:
OCR1A = ocra;
OCR1B = ocrb;
break;
case HIGH_0_LOW_0:
OCR1A = 0;
OCR1B = icr+1;
break;
}
#else
switch (etat) {
case HIGH_0_LOW_1:
digitalWrite(INA_1,LOW);
digitalWrite(INA_2,HIGH);
break;
case HIGH_1_LOW_0:
digitalWrite(INA_1,HIGH);
digitalWrite(INA_2,LOW);
break;
case HIGH_0_LOW_0:
digitalWrite(INA_1,LOW);
digitalWrite(INA_2,LOW);
break;
}
#endif
}
void etat_bras_B(uint8_t etat) {
#ifdef PWM
switch (etat) {
case HIGH_0_LOW_1:
OCR3A = 0;
OCR3B = 0;
break;
case HIGH_1_LOW_0:
OCR3A = ocra;
OCR3B = ocrb;
break;
case HIGH_0_LOW_0:
OCR3A = 0;
OCR3B = icr+1;
break;
}
#else
switch (etat) {
case HIGH_0_LOW_1:
digitalWrite(INB_1,LOW);
digitalWrite(INB_2,HIGH);
break;
case HIGH_1_LOW_0:
digitalWrite(INB_1,HIGH);
digitalWrite(INB_2,LOW);
break;
case HIGH_0_LOW_0:
digitalWrite(INB_1,LOW);
digitalWrite(INB_2,LOW);
break;
}
#endif
}
void etat_bras_C(uint8_t etat) {
#ifdef PWM
switch (etat) {
case HIGH_0_LOW_1:
OCR4A = 0;
OCR4B = 0;
break;
case HIGH_1_LOW_0:
OCR4A = ocra;
OCR4B = ocrb;
break;
case HIGH_0_LOW_0:
OCR4A = 0;
OCR4B = icr+1;
break;
}
#else
switch (etat) {
case HIGH_0_LOW_1:
digitalWrite(INC_1,LOW);
digitalWrite(INC_2,HIGH);
break;
case HIGH_1_LOW_0:
digitalWrite(INC_1,HIGH);
digitalWrite(INC_2,LOW);
break;
case HIGH_0_LOW_0:
digitalWrite(INC_1,LOW);
digitalWrite(INC_2,LOW);
break;
}
#endif
}
void change_rapport() {
if (omega!=0) integOmega += (omegaDemand-omega)/omega;
rapport = Kp*(omegaDemand-omega)+Ki*integOmega;
if (rapport>1.0) rapport = 1.0;
else if (rapport<0) rapport = 0.0;
changer_rapport_pwm(rapport);
}
void change_etat() {
uint32_t t;
uint8_t etat_capteurs = (PIND >> 1)&0b111;
if (start==0) {
if (etat_capteurs==etat_capteurs_anterieur) return;
etat_capteurs_anterieur = etat_capteurs;
}
else start = 0;
if ((etat_capteurs==0)||(etat_capteurs==0xb111)) return;
uint8_t is = tableEtats[etat_capteurs];
etat_bras_A(sequence_A[is]);
etat_bras_B(sequence_B[is]);
etat_bras_C(sequence_C[is]);
compteur += 1;
if (compteur==24) { // 1 tour
if (etatControl==0) {
PORTG |= (1<<5); //digitalWrite(CONTROL,HIGH);
etatControl = 1;
}
else {
PORTG &= ~(1<<5); //digitalWrite(CONTROL,LOW);
etatControl = 0;
}
compteur = 0;
t = micros();
period = t-temps;
temps = t;
bufPeriod[ibuf] = period;
PORTE &= ~(1<<5); //digitalWrite(TRIGGER,LOW);
if (mode==1) {
omega = 1/(period*1e-6);
change_rapport();
}
ibuf++;
if (ibuf==BUFSIZE) {
ibuf = 0;
data_4_ready = true;
}
memcpy(data_2,&period,DATA_2_SIZE);
data_2_ready = true;
}
}
void remplir_table_etats(uint8_t sensRot) {
if (sensRot==0) {
tableEtats[B010] = 3;
tableEtats[B011] = 4;
tableEtats[B001] = 5;
tableEtats[B101] = 0;
tableEtats[B100] = 1;
tableEtats[B110] = 2;
}
else {
tableEtats[B010] = 0;
tableEtats[B011] = 1;
tableEtats[B001] = 2;
tableEtats[B101] = 3;
tableEtats[B100] = 4;
tableEtats[B110] = 5;
}
}
void get_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==2) data_2_request = true;
if (n==4) data_4_request = true;
}
void send_data() {
if ((data_2_ready)&&(data_2_request)) {
//data_2_ready = false;
data_2_request = false;
Serial.write(data_2,DATA_2_SIZE);
}
if ((data_4_ready)&&(data_4_request)) {
//data_4_ready = false;
data_4_request = false;
Serial.write((uint8_t *)bufPeriod,DATA_4_SIZE);
}
}
void set_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==0) {
while (Serial.available()<DATA_0_SIZE) {};
Serial.readBytes(data_0,DATA_0_SIZE);
memcpy(&rapport,data_0,DATA_0_SIZE);
digitalWrite(TRIGGER,HIGH);
changer_rapport_pwm(rapport);
period = 0.0;
change_etat();
}
else if (n==1) {
while (Serial.available()<DATA_1_SIZE) {};
Serial.readBytes(data_1,DATA_1_SIZE);
memcpy(&sensRot,data_1,DATA_1_SIZE);
remplir_table_etats(sensRot);
}
else if (n==3) {
while (Serial.available()<DATA_3_SIZE) {};
Serial.readBytes(data_3,DATA_3_SIZE);
memcpy(&mode,data_3,DATA_3_SIZE);
}
else if (n==5) {
while (Serial.available()<DATA_5_SIZE) {};
Serial.readBytes(data_5,DATA_5_SIZE);
memcpy(&omegaDemand,data_5,DATA_5_SIZE);
digitalWrite(TRIGGER,HIGH);
change_rapport();
change_etat();
}
}
void read_serial() {
char com;
if (Serial.available()>0) {
com = Serial.read();
if (com==GET_DATA) get_data();
else if (com==SET_DATA) set_data();
}
}
void setup() {
Serial.begin(115200);
while(!Serial);
remplir_table_etats(sensRot);
pinMode(INA_1,OUTPUT);
digitalWrite(INA_1,LOW);
pinMode(INA_2,OUTPUT);
digitalWrite(INA_2,LOW);
pinMode(INB_1,OUTPUT);
digitalWrite(INB_1,LOW);
pinMode(INB_2,OUTPUT);
digitalWrite(INB_2,LOW);
pinMode(INC_1,OUTPUT);
digitalWrite(INC_1,LOW);
pinMode(INC_2,OUTPUT);
digitalWrite(INC_2,LOW);
pinMode(IN1,INPUT);
pinMode(IN2,INPUT);
pinMode(IN3,INPUT);
pinMode(TRIGGER,OUTPUT);
digitalWrite(TRIGGER,LOW);
pinMode(CONTROL,OUTPUT);
digitalWrite(CONTROL,LOW);
attachInterrupt(digitalPinToInterrupt(IN1),change_etat,CHANGE);
attachInterrupt(digitalPinToInterrupt(IN2),change_etat,CHANGE);
attachInterrupt(digitalPinToInterrupt(IN3),change_etat,CHANGE);
#ifdef PWM
config_timers(periodPWM,rapport);
#endif
ibuf = 0;
compteur = 0;
temps = micros();
omega = 0;
integOmega = 0;
etatControl = 0;
etat_capteurs_anterieur = 0;
start = 1;
change_etat();
}
void loop() {
read_serial();
send_data();
}
Pour une tension d'alimentation Vs=5 V et une fréquence de découpage de 10 kHz, nous avons relevé la période de rotation pour différents rapports cycliques de découpage au moyen du script suivant :
from Arduino import Arduino
import time
import matplotlib.pyplot as plt
import numpy as np
BUFSIZE = 5
ard = Arduino('COM10',[4,1,4,1,4*BUFSIZE,4])
time.sleep(1)
RAPPORT = 0
SENS = 1
PERIOD = 2
MODE = 3
BUFPERIOD = 4
OMEGA = 5
sens = 0
list_rapport = np.linspace(0.1,0.6,10)
list_period = []
ard.write_int8(MODE,0,signed=False)
for rapport in list_rapport :
print("rapport = %f"%rapport)
ard.write_float(RAPPORT,float(rapport))
time.sleep(10)
periode = ard.read_float_array(BUFPERIOD)
periode = periode.mean()
print("periode = %f"%periode)
list_period.append(periode)
ard.write_float(RAPPORT,0)
ard.close()
list_omega = 1/(np.array(list_period)*1e-6)
np.savetxt("periodesRotation-5V-2.txt",np.array([list_rapport,list_period]).T)
plt.figure()
plt.plot(list_rapport,list_omega)
plt.ylabel("tours/s")
plt.xlabel("rapport cyclique")
plt.show()
Voici la vitesse angulaire en fonction du rapport cyclique (aucune charge externe n'est appliquée) pour deux fréquences de découpages différentes (10 et 20 kHz):
figure()
[r,P] = np.loadtxt("periodesRotation-5V-3-10kHz.txt",unpack=True)
omega = 1/(np.array(P)*1e-6)
plot(r,omega,'o')
[r,P] = np.loadtxt("periodesRotation-5V-4-20kHz.txt",unpack=True)
omega = 1/(np.array(P)*1e-6)
plot(r,omega,'+')
xlabel("rapport cyclique",fontsize=16)
ylabel(r"$\omega\ (\rm tours/s)$",fontsize=16)
grid()
xlim(0,1)
ylim(0,20)
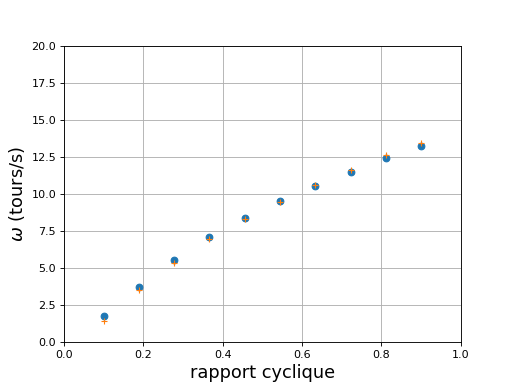 fig42.pdf
fig42.pdf
Si on se limite aux vitesses angulaires inférieures à 6 tr/s, celle-ci semble être une fonction affine du rapport cyclique. Cela est compatible avec un couple moteur de la forme et un couple mécanique de la forme . Ces deux relations impliquent en effet une vitesse angulaire en régime stationnaire :
Voici une régression linéaire faite sur les trois premiers points :
coef,cov = np.polyfit(r[0:3],omega[0:3],1,cov='unscaled')
print(coef) --> array([22.15093324, -0.76767069])
Cette expérience nous donne donc accès à et à . Dans le cas présent, le couple mécanique provient uniquement des frottements internes aux moteur. Si une charge mécanique externe est appliquée, avec un couple contrôlé, il faut évidemment refaire ces mesures de vitesse angulaire stationnaire.
La mesure du courant dans une bobine, c'est-à-dire du champ magnétique qu'elle génère, peut se faire au moyen d'une sonde à effet Hall placée à l'arrière de son noyau.
Voici la tension fournie par la sonde à effet Hall (proportionnelle au champ magnétique) et par le capteur Hall situé à côté de la bobine. pour une tension d'alimentation Vs=5 V, une fréquence de découpage de 20 kHz et un rapport cyclique de 0,1 :
figure(figsize=(16,6))
[t,ui,uc] = np.loadtxt("champB-20kHz-5V-r0,1.txt",unpack=True,skiprows=1)
ui = ui-2.46
title("Vs = 5 V, 20 kHz, rapport=0,1")
plot(t,ui,label="B")
plot(t,uc/10,label="Capteur")
xlabel("t (s)",fontsize=16)
ylabel("u (V)",fontsize=16)
grid()
legend(loc="upper right")
ylim(-0.5,0.5)
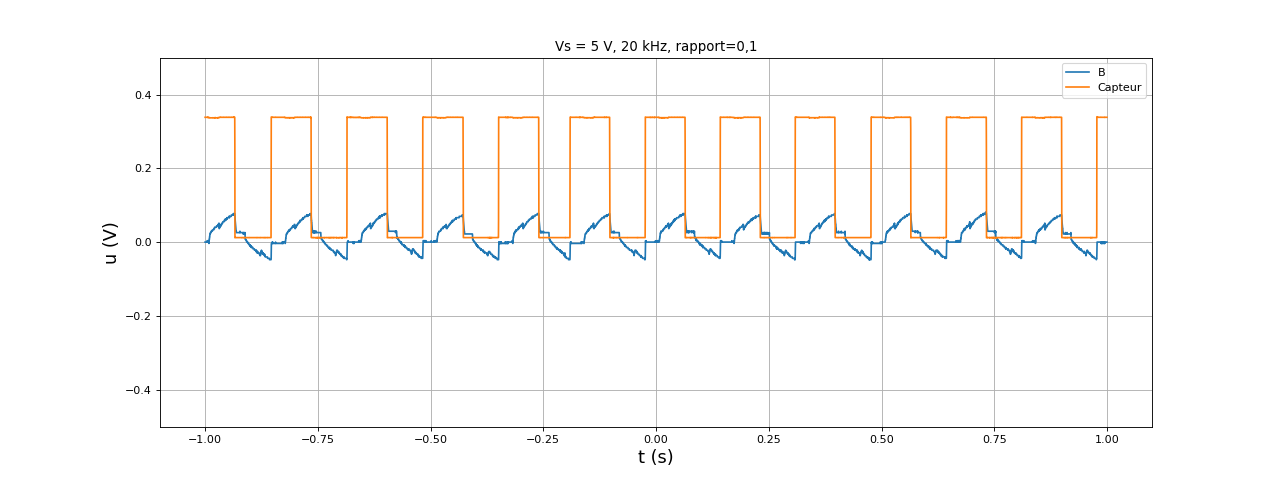 fig43.pdf
fig43.pdf
Le capteur change d'état 2 fois par cycle. À un des états (haut ou bas) correspond donc 3 états de commutation. On repère l'état où le courant dans la bobine est nul, suivi des deux états où le courant est positif. Ce courant est loin d'être constant. En effet, la bobine a une auto-inductance de 9,8 mH et une résistance à 100 Hz de 0,8 ohms, ce qui donne un temps de réponse du courant de 12 ms. Ces deux états sont en principe suivi d'un état où le courant est nul mais le capteur à effet Hall donne une tension légèrement décalée (la tension de référence en sortie du capteur est 2,46 V (la moitié de sa tension d'alimentation). Une bobine plus petite, avec un facteur de qualité plus grand, aurait un temps de réponse plus court mais nécessiterait aussi d'augmenter la fréquence de découpage (pour la même raison, bien que le découpage fasse intervenir la résistance à la fréquence de découpage). Les variations de courant pendant un état de conduction d'un bobine sont indésirables car elles impliquent une variation du couple.
Voici le signal pour un rapport cyclique de 0,5 :
figure(figsize=(16,6))
[t,ui,uc] = np.loadtxt("champB-20kHz-5V-r0,5.txt",unpack=True,skiprows=1)
ui = ui-2.46
title("Vs = 5 V, 20 kHz, rapport=0,5")
plot(t,ui,label="B")
plot(t,uc/10,label="Capteur")
xlabel("t (s)",fontsize=16)
ylabel("u (V)",fontsize=16)
grid()
legend(loc="upper right")
ylim(-0.5,0.5)
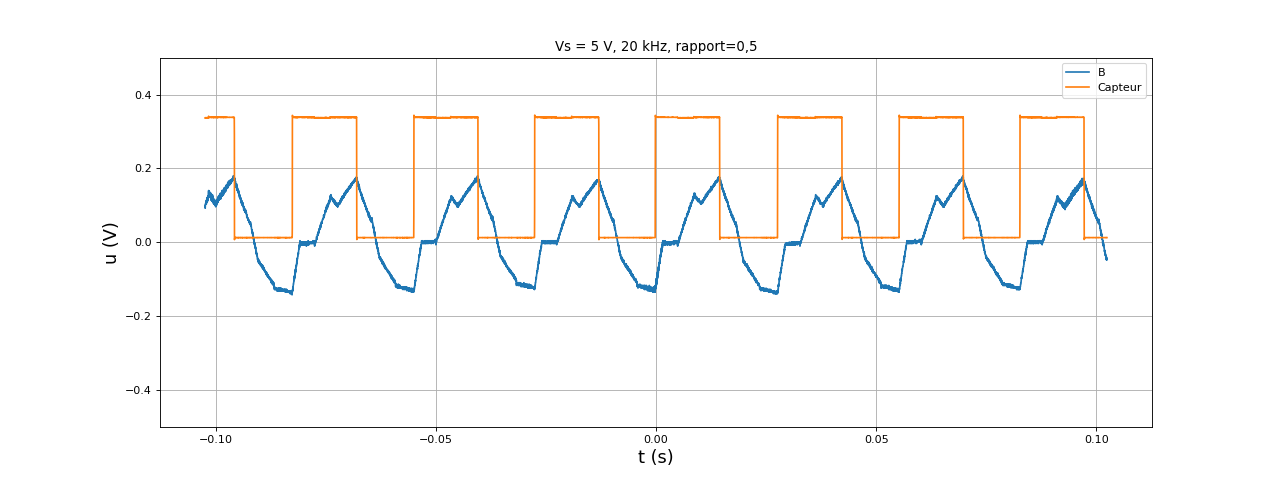 fig44.pdf
fig44.pdf
et pour un rapport cyclique de 0,9 :
figure(figsize=(16,6))
[t,ui,uc] = np.loadtxt("champB-20kHz-5V-r0,9.txt",unpack=True,skiprows=1)
ui = ui-2.46
title("Vs = 5 V, 20kHz, rapport=0,9")
plot(t,ui,label="B")
plot(t,uc/10,label="Capteur")
xlabel("t (s)",fontsize=16)
ylabel("u (V)",fontsize=16)
grid()
legend(loc="upper right")
ylim(-0.5,0.5)
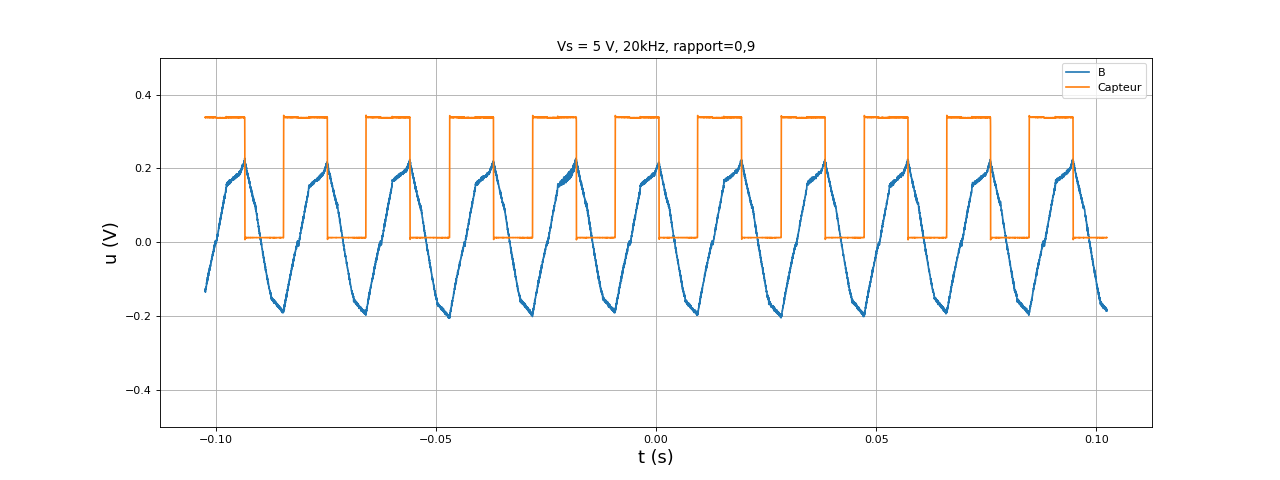 fig45.pdf
fig45.pdf
Pour tester la régulation de vitesse, on utilise le script suivant :
from Arduino import Arduino
import time
BUFSIZE = 5
ard = Arduino('COM10',[4,1,4,1,4*BUFSIZE,4])
RAPPORT = 0
SENS = 1
PERIOD = 2
MODE = 3
BUFPERIOD = 4
OMEGA = 5
sens = 0
time.sleep(1)
ard.write_int8(MODE,0,signed=False)
ard.write_float(RAPPORT,0.0)
while True:
r = input('Omega en tr/s ?')
if r=='n': break
elif r=='p':
periode = ard.read_float_array(BUFPERIOD)
periode = periode.mean()
print("periode = %f"%periode)
else:
omega = float(r)
ard.write_float(OMEGA,omega)
ard.write_int8(MODE,1,signed=False)
ard.write_int8(MODE,0,signed=False)
ard.write_float(RAPPORT,0.0)
ard.close()
Les signaux des trois capteurs sont enregistrés avec un analyseur logique (Analog Discovery 2). Le déclenchement de l'enregistrement est fait à partir du front montant émis sur D3 lorsque la commande de changement de vitesse est reçue. En réalité, le déclenchement peut être positionné comme on le souhaite sur la fenêtre d'acquisition (pas nécessairement au début). L'analyse des signaux des trois capteurs permet de déterminer la vitesse angulaire du moteur en fonction du temps. La période de changement d'état (soit 1/24 de la période de rotation) est évaluée à chaque changement d'état d'un des capteurs. L'échantillonnage du temps qui en résulte n'est évidemment pas régulier. L'enregistrement a une durée de 50 secondes et la fréquence d'échantillonnage est de 80 Hz. Cette fréquence relativement basse conduit à un bruit de quantification sur la période très fort, qui nous oblige à effectuer un filtrage passe-bas. On utilise pour cela un filtre RIF, bien que ce type de filtre soit en principe prévu pour filtre des signaux échantillonnés à période d'échantillonnage constante. Voici la fonction qui effectuer l'analyse des trois signaux. Elle renvoit le temps et la période (filtrée).
from scipy.signal import firwin,convolve
def analyseCapteurs(t,u0,u1,u2):
periode = []
temps = []
tchange = t[0]
etat0 = u0[0] > 0.5
etat1 = u1[0] > 0.5
etat2 = u2[0] > 0.5
for i in range(1,len(t)):
if (u0[i] < 0.5 and etat0) or (u0[i] > 0.5 and not(etat0)):
periode.append(t[i]-tchange)
temps.append(t[i])
tchange = t[i]
etat0 = not(etat0)
if (u1[i] < 0.5 and etat1) or (u1[i] > 0.5 and not(etat1)):
periode.append(t[i]-tchange)
temps.append(t[i])
tchange = t[i]
etat1 = not(etat1)
if (u2[i] < 0.5 and etat2) or (u2[i] > 0.5 and not(etat2)):
periode.append(t[i]-tchange)
temps.append(t[i])
tchange = t[i]
etat2 = not(etat2)
j = 0
periode = periode[j:len(periode)-j]
temps = temps[j:len(temps)-j]
P = 30
b = firwin(2*P+1,cutoff=[0.01],window='hann',fs=0.5)
periode = convolve(periode,b,mode='valid')
temps = temps[P:len(temps)-P]
return np.array(temps),np.array(periode)
Voici l'évolution de la vitesse du moteur (à vide) au démarrage lorsque le rapport cyclique est imposé (mode 0) :
def plotOmega(filename,label):
[t,u0,u1,u2] = np.loadtxt(filename,skiprows=1,unpack=True)
temps,periode = analyseCapteurs(t,u0,u1,u2)
plot(temps,1/(periode*24),label=label)
figure()
plotOmega("start-r0,1-1.txt",r"$r=0,1$")
plotOmega("start-r0,2-1.txt",r"$r=0,2$")
plotOmega("start-r0,3-1.txt",r"$r=0,3$")
plotOmega("start-r0,4-1.txt",r"$r=0,4$")
plotOmega("start-r0,5-1.txt",r"$r=0,5$")
plotOmega("start-r0,6-1.txt",r"$r=0,6$")
ylim(0,12)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
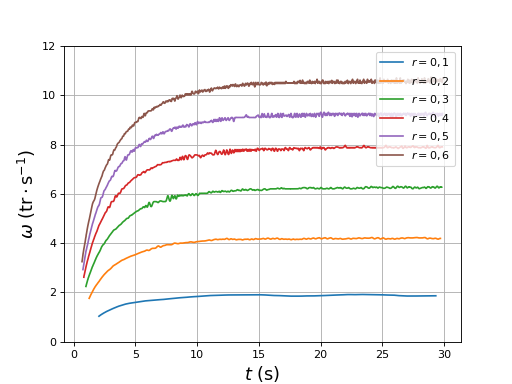 fig46.pdf
fig46.pdf
Voici le démarrage du moteur en mode 1, pour une vitesse angulaire commandée de 2 tr/s, pour différentes valeurs de Kp et Kp :
figure()
plotOmega("start-w2-Kp0,05-Ki0,01-1.txt",r"$K_p=0,05\ K_i=0,01$")
plotOmega("start-w2-Kp0,05-Ki0,005-1.txt",r"$K_p=0,05\ K_i=0,005$")
plotOmega("start-w2-Kp0,05-Ki0,02-1.txt",r"$K_p=0,05\ K_i=0,02$")
plotOmega("start-w2-Kp0,05-Ki0,03-1.txt",r"$K_p=0,05\ K_i=0,03$")
ylim(0,4)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
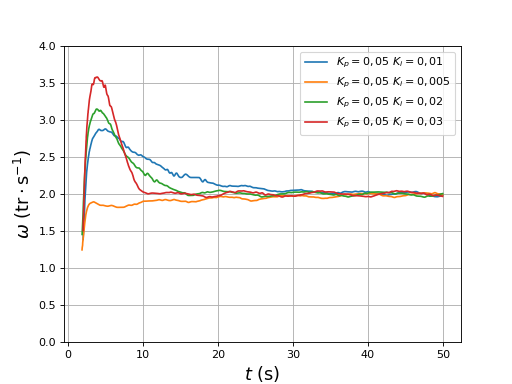 fig47.pdf
fig47.pdf
Pour la valeur Kp=0,05, la valeur Ki=0,005 donne une courbe de vitesse tendant vers la valeur commandée sans dépassement. Les autres valeurs donnent un dépassement d'autant plus grand que Ki est grand. Une valeur de Ki plus grande permet d'atteindre plus rapidement la vitesse commandée mais au prix d'un dépassement de la vitesse.
Voici la vitesse pour une vitesse angulaire commandée de 4 tr/s :
figure()
plotOmega("start-w4-Kp0,05-Ki0,01-1.txt",r"$K_p=0,05\ K_i=0,01$")
plotOmega("start-w4-Kp0,05-Ki0,005-1.txt",r"$K_p=0,05\ K_i=0,005$")
plotOmega("start-w4-Kp0,05-Ki0,02-1.txt",r"$K_p=0,05\ K_i=0,02$")
plotOmega("start-w4-Kp0,05-Ki0,03-1.txt",r"$K_p=0,05\ K_i=0,03$")
ylim(0,8)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
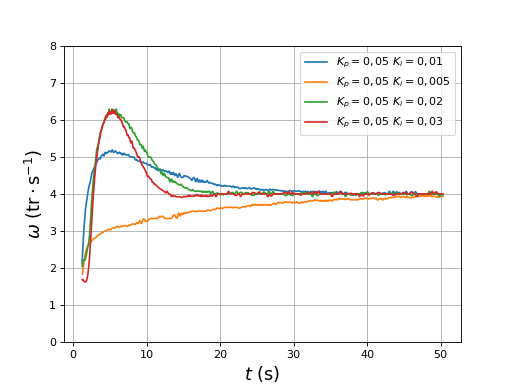 fig48.pdf
fig48.pdf
Le constat est le même que précédemment. La plus grande valeur de Ki permet d'atteindre la vitesse commandée le plus rapidement mais avec un dépassement important.
Voici la vitesse pour une vitesse angulaire commandée de 6 tr/s :
figure()
plotOmega("start-w6-Kp0,05-Ki0,01-1.txt",r"$K_p=0,05\ K_i=0,01$")
plotOmega("start-w6-Kp0,05-Ki0,005-1.txt",r"$K_p=0,05\ K_i=0,005$")
plotOmega("start-w6-Kp0,05-Ki0,02-1.txt",r"$K_p=0,05\ K_i=0,02$")
plotOmega("start-w6-Kp0,05-Ki0,03-1.txt",r"$K_p=0,05\ K_i=0,03$")
ylim(0,8)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
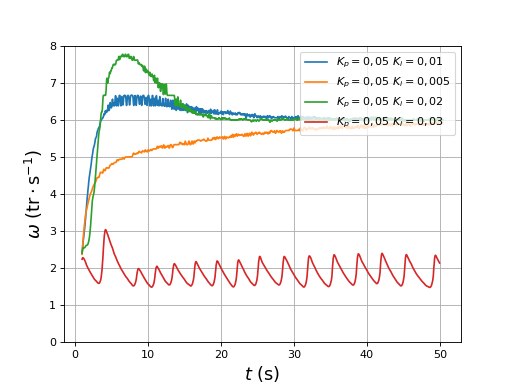 fig49.pdf
fig49.pdf
Pour cette valeur plus élevée de vitesse commandée, l'asservissement ne fonctionne pas avec Ki=0,03.
Voici les courbes de vitesse lorsqu'une consigne de 6 tr/s est appliquée alors que la vitesse est 2 tr/s :
figure()
plotOmega("change-w2-w6-Kp0,05-Ki0,01-1.txt",r"$K_p=0,05\ K_i=0,01$")
plotOmega("change-w2-w6-Kp0,05-Ki0,005-1.txt",r"$K_p=0,05\ K_i=0,005$")
plotOmega("change-w2-w6-Kp0,05-Ki0,02-1.txt",r"$K_p=0,05\ K_i=0,02$")
plotOmega("change-w2-w6-Kp0,05-Ki0,03-1.txt",r"$K_p=0,05\ K_i=0,03$")
ylim(0,8)
legend(loc="lower right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
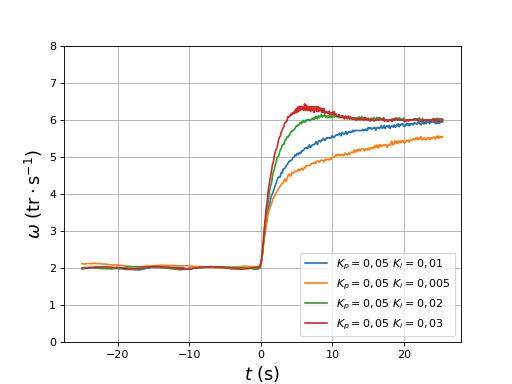 fig50.pdf
fig50.pdf
Dans le cas Ki=0,03, la vitesse 6 tr/s est atteinte sans problème et le plus rapidement. Cela montre que pour atteindre une vitesse élevée, on doit d'abord appliquer une vitesse de commande plus faible.
Voici les courbes lorsqu'une consigne de 2 tr/s est appliquée alors que la vitesse est 6 tr/s :
figure()
plotOmega("change-w6-w2-Kp0,05-Ki0,01-1.txt",r"$K_p=0,05\ K_i=0,01$")
plotOmega("change-w6-w2-Kp0,05-Ki0,005-1.txt",r"$K_p=0,05\ K_i=0,005$")
plotOmega("change-w6-w2-Kp0,05-Ki0,02-1.txt",r"$K_p=0,05\ K_i=0,02$")
plotOmega("change-w6-w2-Kp0,05-Ki0,03-1.txt",r"$K_p=0,05\ K_i=0,03$")
ylim(0,8)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
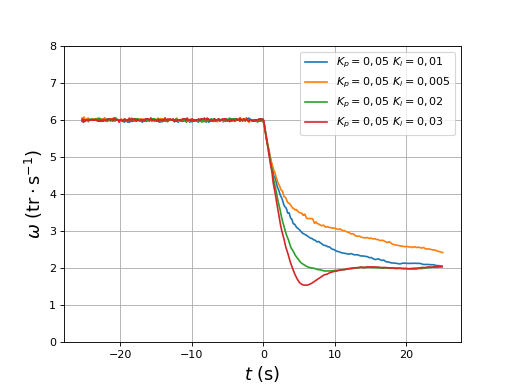 fig51.pdf
fig51.pdf