Bobine sur tore en ferrite
1. Introduction
Les noyaux toriques en ferrite permettent de réaliser des bobines d'auto-induction possédant un coefficient d'auto-inductance élevé avec peu de spires. Nous utilisons un noyau en ferrite ZnNi (alliage d'oxyde de fer avec Ni et Zn), de diamètre 25 mm, sur lequel nous enroulons un fil de cuivre de diamètre 0,5 mm. Voici par exemple d'une bobine comportant 12 spires :
Un second enroulement sur le même tore permet de réaliser un transformateur.
Ce document explore les propriétés de ce type de bobine dans le domaine des basses fréquences (dizaine de kHz) et la possibilité de s'en servir pour réaliser un onduleur à résonance destiné à exciter un transducteur piézoélectrique à 40 kHz.
Le tore utilisé possède une inductance spécifique AL=5460 nH. Un enroulement de N spires possède une auto-inductance L=N2AL. Par exemple pour N=12, l'auto-inductance est d'environ 780 μH.
2. Mesures d'impédance
On cherche à mesurer l'impédance de la bobine au voisinage de la fréquence pour laquelle on prévoit de l'utiliser, afin de savoir s'il est possible de lui attribuer une auto-inductance et une résistance interne.
Figure pleine pageLa tension sinusoïdale e(t) de pulsation ω est fournie par un générateur de fonctions. L'enregistrement de la tension u(t) aux bornes de la bobine est fait par la carte Sysam SP5 en mode différentiel (entrées EA0 et EA4). Afin d'obtenir l'intensité du courant dans la bobine i(t), on place une résistance R en série, qui doit être de l'ordre de grandeur de l'impédance de la bobine à la fréquence choisie.
Soit et , où Z est l'impédance complexe de la bobine et l'argument de Z.
L'impédance (module de l'impédance complexe) est déterminée par le rapport des grandeurs efficaces :
Considérons la moyenne du produit de u(t) et i(t) :
Le cosinus de est donc la moyenne du produit u(t)i(t) divisé par le produit des valeurs efficaces. Dans le cas d'une bobine, est petit car est proche de π/2.
Le script suivant permet d'obtenir |Z| et sur une plage de fréquence. La fréquence est déterminée par analyse spectrale, au moyen d'une transformée de Fourier discrète après avoir complété le signal échantillonné par des zéros. La fréquence est modifiée sur le générateur puis on entre 'O' pour faire une mesure, 'N' pour arrêter et enregistrer les données dans un fichier.
import numpy as np
import matplotlib.pyplot as plt
import pycanum.main as pycan
from scipy.signal import blackman
from numpy.fft import fft
def frequence(t,x):
N=len(x)
te=t[1]-t[0]
zeros=np.zeros(6*N)
X = np.concatenate((x*blackman(N),zeros))
NN=len(X)
spectre = np.absolute(fft(X))*2.0/N/0.42
freq = np.arange(NN)*1.0/(NN*te)
k=np.argmax(spectre[0:NN//2])
return freq[k]
def mesure(can,R,techant,N=50000,Np=100,plot=False):
can.config_echantillon(techant*1e6,N)
can.acquerir()
t=can.temps()[0]
signaux = can.entrees()
u=signaux[0]
ur=signaux[1]
u=u-u.mean()
ur=ur-ur.mean()
i=ur/R
N = len(t)
Z = u.std()/i.std()
cosphi = np.mean(i*u)/(u.std()*i.std())
phi = np.arccos(cosphi)
freq = frequence(t,u)
if plot:
plt.figure()
plt.plot(t,u,'b')
plt.plot(t,R*i,'r')
plt.grid()
plt.ylim(-10,10)
plt.xlim(0,20/freq)
plt.show()
return (freq,Z,cosphi,phi)
liste_f = []
liste_Z = []
liste_phi = []
R=100.7 # résistance en série
can = pycan.Sysam("SP5")
Vmax = 2
techant = 1e-6
can.config_entrees([0,1],[Vmax,Vmax],diff=[0])
r = 'O'
while r=='O':
(f,Z,cosphi,phi) = mesure(can,R,techant)
print("f = %f Hz, Z = %f, cosphi = %f, phi = %f"%(f,Z,cosphi,phi))
liste_f.append(f)
liste_Z.append(Z)
liste_phi.append(phi)
r = input("mesure (O/N) ?")
can.fermer()
liste_Z = np.array(liste_Z)
liste_phi = np.unwrap(liste_phi)
np.savetxt('impedance-E=2.txt',np.array([liste_f,liste_Z,liste_phi]).T,header='f\t Z\t phi')
plt.figure()
plt.plot(liste_f,liste_Z,'b-')
plt.grid()
plt.xlabel('f (Hz)')
plt.ylabel(r'$|Z|\ (\rm\Omega)$')
plt.figure()
plt.plot(liste_f,liste_phi/np.pi,'b-')
plt.xlabel('f (Hz)')
plt.ylabel(r'$\phi/\pi (\rm rad)$')
plt.grid()
plt.figure()
plt.plot(liste_f,liste_Z*np.cos(liste_phi),'b-')
plt.grid()
plt.xlabel('f (Hz)')
plt.ylabel(r'$Re(Z)\ (\rm\Omega)$')
plt.figure()
plt.plot(liste_f,liste_Z*np.sin(liste_phi),'b-')
plt.xlabel('f (Hz)')
plt.ylabel(r'$Im(Z)\ (\rm\Omega)$')
plt.grid()
plt.show()
Voici les résultats pour la bobine de 12 spires.
La fréquence qui nous intéresse est f=40 kHz. Compte tenu de la valeur estimée de L d'après le nombre de tours (780 μH), on devrait avoir Lω=196 Ω. On choisit donc une résistance de valeur nominale R=100 Ω, dont la valeur mesurée avec un ohmmètre est R=100,7 Ω.
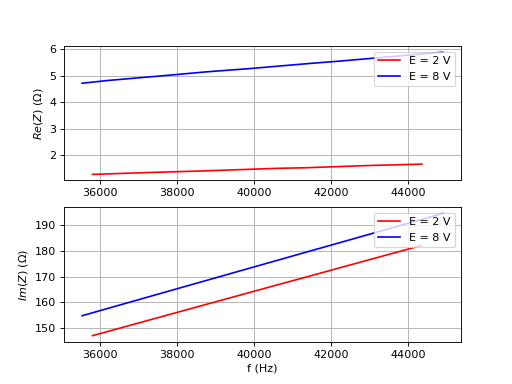
On trace les parties réelle et imaginaire de l'impédance complexe, pour une plage de fréquence de 35 kHz à 45 kHz et pour deux amplitudes de la tension d'entrée, 2 V et 8 V.
import numpy as np
from matplotlib.pyplot import *
[f1,Z1,phi1] = np.loadtxt('impedance-E=2.txt',unpack=True,skiprows=1)
[f2,Z2,phi2] = np.loadtxt('impedance-E=8.txt',unpack=True,skiprows=1)
figure()
subplot(211)
plot(f1,Z1*np.cos(phi1),"r-",label='E = 2 V')
plot(f2,Z2*np.cos(phi2),"b-",label='E = 8 V')
grid()
ylabel(r'$Re(Z)\ (\rm\Omega)$')
legend(loc='upper right')
subplot(212)
plot(f1,Z1*np.sin(phi1),"r-",label='E = 2 V')
plot(f2,Z2*np.sin(phi2),"b-",label='E = 8 V')
grid()
xlabel('f (Hz)')
ylabel(r'$Im(Z)\ (\rm\Omega)$')
legend(loc='upper right')
 impedance-bobine.pdf
impedance-bobine.pdf
Le fait que la partie imaginaire dépende linéairement de la fréquence (dans cette plage de fréquences) montre qu'il est possible de modéliser la bobine par une auto-inductance L en série avec une résistance r. Cependant, la résistance dépend à la fois de la fréquence et de l'amplitude et l'auto-inductance dépend de l'amplitude.
Si on suppose que Z=r+jLω, la valeur de L peut être obtenue à partir de la pente de la partie imaginaire de Z en fonction de la fréquence :
from scipy.stats import linregress
a1, b1, r_value, p_value, std_err = linregress(f1,Z1*np.sin(phi1))
L1 = a1/(2*np.pi)
a2, b2, r_value, p_value, std_err = linregress(f2,Z2*np.sin(phi2))
L2 = a2/(2*np.pi)
On peut aussi évaluer les valeurs de L à une fréquence donnée (40 kHz) directement à partir de la partie imaginaire de Z à cette fréquence :
print((L1,L2)) --> (0.0006531770084157831, 0.0006754092798480443)
f = 40e3
Z1_40 = a1*f+b1
Z2_40 = a2*f+b2
L1 = Z1_40/(2*np.pi*f)
L2 = Z2_40/(2*np.pi*f)
print((L1,L2)) --> (0.0006539007252220715, 0.0006916227781398327)
Les deux méthodes conduisent à une auto-inductance plus grande lorsque l'amplitude de e(t) est plus grande. Cependant, les valeurs obtenues pour E=8 V sont très différentes, ce qui montre que l'hypothèse Z=r+jLω est plutôt grossière, où en tout cas ne peut s'appliquer que sur un domaine de fréquence très étroit.
Afin d'étudier plus en détail l'influence de E, nous fixons la fréquence et utilisons la seconde méthode pour déterminer L. Le script suivant permet de déterminer L et r à une fréquence fixée, en faisant varier l'amplitude E. L'intensité efficace du courant est aussi calculée.
import numpy as np
import matplotlib.pyplot as plt
import pycanum.main as pycan
from scipy.signal import blackman
from numpy.fft import fft
def frequence(t,x):
N=len(x)
te=t[1]-t[0]
zeros=np.zeros(6*N)
X = np.concatenate((x*blackman(N),zeros))
NN=len(X)
spectre = np.absolute(fft(X))*2.0/N/0.42
freq = np.arange(NN)*1.0/(NN*te)
k=np.argmax(spectre[0:NN//2])
return freq[k]
def mesure(can,R,techant,N=50000,Np=100,plot=False):
can.config_echantillon(techant*1e6,N)
can.acquerir()
t=can.temps()[0]
signaux = can.entrees()
u=signaux[0]
ur=signaux[1]
u=u-u.mean()
ur=ur-ur.mean()
i=ur/R
N = len(t)
Z = u.std()/i.std()
cosphi = np.mean(i*u)/(u.std()*i.std())
phi = np.arccos(cosphi)
freq = frequence(t,u)
if plot:
plt.figure()
plt.plot(t,u,'b')
plt.plot(t,R*i,'r')
plt.grid()
plt.ylim(-10,10)
plt.xlim(0,20/freq)
plt.show()
u_max = u.std()*np.sqrt(2)
ur_max = ur.std()*np.sqrt(2)
return (freq,Z,cosphi,phi,i.std(),u_max,ur_max)
liste_I = []
liste_L = []
liste_r = []
R=100.7 # résistance en série
can = pycan.Sysam("SP5")
Vmax = 10
techant = 5e-7
can.config_entrees([0,1],[Vmax,Vmax],diff=[0])
r = 'O'
while r=='O':
can.config_entrees([0,1],[Vmax,Vmax],diff=[0])
(f,Z,cosphi,phi,Ieff,u_max,ur_max) = mesure(can,R,techant)
r = Z*np.cos(phi)
L = Z*np.sin(phi)/(2*np.pi*f)
print("f = %f Hz, Ieff = %f, L = %f H, r =%f Ohms "%(f,Ieff,L,r))
liste_I.append(Ieff)
liste_L.append(L)
liste_r.append(r)
r = input("mesure (O/N) ?")
can.fermer()
np.savetxt('impedance-f=40kHz.txt',np.array([liste_I,liste_L,liste_r]).T,header='I\t L\t r')
[Ieff,L,r] = np.loadtxt('impedance-f=40kHz.txt',unpack=True,skiprows=1)
figure(figsize=(10,10))
title('f = 40 kHz')
subplot(211)
plot(Ieff*1e3,L*1e6,"ro")
grid()
ylabel(r'$L\ (\rm\mu H)$')
ylim(0,1000)
subplot(212)
plot(Ieff*1e3,r,'ro')
grid()
ylabel(r"$r\ (\rm\Omega)$")
xlabel(r"$I_{eff}\ (\rm mA)$")
ylim(0,8)
 Lr-bobine-40kHz.pdf
Lr-bobine-40kHz.pdf
L'auto-inductance augmente de manière non négligeable avec l'intensité du courant efficace et la résistance augmente beaucoup.
Voici les mesures effectuées à une fréquence de 5 kHz et une résistance R=10,6 Ω.
[Ieff,L,r] = np.loadtxt('impedance-f=5kHz.txt',unpack=True,skiprows=1)
figure(figsize=(10,10))
title('f = 5 kHz')
subplot(211)
plot(Ieff*1e3,L*1e6,"ro")
grid()
ylabel(r'$L\ (\rm\mu H)$')
ylim(0,1000)
subplot(212)
plot(Ieff*1e3,r,'ro')
grid()
ylabel(r"$r\ (\rm\Omega)$")
xlabel(r"$I_{eff}\ (\rm mA)$")
ylim(0,8)
 Lr-bobine-5kHz.pdf
Lr-bobine-5kHz.pdf
À cette fréquence plus basse, l'auto-inductance est plus grande et la résistance est plus petite. On retrouve l'augmentation de ces deux grandeurs avec l'intensité du courant efficace.
Ces résultats montrent que la représentation de la bobine par L et r en série est une approximation assez grossière car ces deux grandeurs augmentent avec l'intensité du courant. Il est probable que la perméabilité magnétique du tore augmente avec l'intensité du courant (dans la gamme de courants considéré ici). Indépendamment des pertes, la bobine a donc un comportement non linéaire. La résistance interne r provient essentiellement des pertes dans la ferrite. Elles augmentent avec la fréquence et avec l'intensité du courant.
L'augmentation de la perméabilité de la ferrite avec l'excitation magnétique (H) montre qu'on est très loin de la saturation magnétique et qu'on est dans un domaine de H où la pente de la courbe B(H) augmente légèrement avec H.
3. Circuit résonant
3.a. Schéma et étude théorique
Un circuit résonant peut être obtenu en plaçant un condensateur de capacité C en parallèle avec la bobine. Une résistance R est interposée entre le générateur de signaux et le bloc LC.
Figure pleine pageL'ensemble réalise un filtre passe-bande, e(t) étant la tension d'entrée et s(t) la tension de sortie. Si la bobine est assimilée à une auto-inductance L, la fonction de transfert de ce filtre s'écrit :
fr est la fréquence de résonance et Q est le facteur de qualité. Un facteur de qualité élevé (quelques dizaines) est obtenu avec une valeur de R grande et une valeur de L petite. Ce filtre est intéressant pour le traitement des signaux car son impédance d'entrée est grande (de l'ordre de grandeur de R). En revanche, sa grande impédance de sortie le rend inapte aux applications de puissance. Notre objectif est d'utiliser ce filtre pour étudier la bobine (sans charge en sortie).
Pour le filtre idéal (sans pertes dans la bobine), le gain à la résonance est Gmax=1. En réalité, il est notablement inférieur à 1 à cause de ces pertes. La bobine est modélisée par L et une résistance r en série. Le condensateur est modélisé par une capacité en série avec une résistance. Voici les courbes de gain en fonction de la fréquence :
def modele(R,C,L,r,rc,f):
w=2*np.pi*f
Y = 1/(1/(1j*C*w)+rc)+1/(1j*L*w+r)
H = 1/(R*Y+1)
G = np.absolute(H)
return G
f = np.linspace(35e3,45e3,1000)
C=22e-9
rc=1
R=10e3
L=650e-6
fr = 1/(2*np.pi*np.sqrt(L*C))/1e3
figure()
r=0
G = modele(R,C,L,r,rc,f)
fr_0 = f[np.argmax(G)]/1e3
plot(f/1e3,G,label=r'$r = 0,\ fr=%0.2f\,\rm kHz$'%fr_0)
r=1
G = modele(R,C,L,r,rc,f)
fr_1 = f[np.argmax(G)]/1e3
plot(f/1e3,G,label=r'$r = 1\,{\rm\Omega},\ fr=%0.2f\,\rm kHz$'%fr_1)
r=5
G = modele(R,C,L,r,rc,f)
fr_5 = f[np.argmax(G)]/1e3
plot(f/1e3,G,label=r'$r = 5\,{\rm\Omega},\ fr=%0.2f\,\rm kHz$'%fr_5)
xlabel('f (kHz)')
ylabel('G')
grid()
ylim(0,1)
legend(loc='upper left')
 gainFiltreLC-1.pdf
gainFiltreLC-1.pdf
print(fr) --> 42.08740149232945
L'augmentation de la résistance de la bobine fait diminuer le gain à la résonance mais a un effet négligeable sur la fréquence de résonance. Celle-ci est donc donnée par la formule :
Voici les courbes pour une résistance R 10 fois plus grande :
R = 100e3
figure()
r=0
G = modele(R,C,L,r,rc,f)
plot(f/1e3,G,label=r'$r = 0$')
r=1
G = modele(R,C,L,r,rc,f)
plot(f/1e3,G,label=r'$r = 1\,\rm\Omega$')
r=5
G = modele(R,C,L,r,rc,f)
plot(f/1e3,G,label=r'$r = 5\,\rm\Omega$')
xlabel('f (kHz)')
ylabel('G')
grid()
ylim(0,1)
legend(loc='upper right')
 gainFiltreLC-2.pdf
gainFiltreLC-2.pdf
Ces courbes montrent que le choix de R est un compromis : une valeur grande de R permet d'augmenter le facteur de qualité du filtre idéal mais une valeur trop grande réduit le facteur de qualité du filtre à cause des pertes dans la bobine.
3.b. Courbes de gain expérimentales
La courbe de gain en fonction de la fréquence est obtenue grace à un script qui permet à la carte Sysam de délivrer une tension sinusoïdale sur sa sortie SA1 et de faire un balayage automatique de la fréquence. Le traitement des signaux et le script sont présentés dans Diagramme de Bode.
Notre objectif étant d'utiliser la bobine à 40 kHz, nous réalisons le circuit avec C=22 nF et R=10 kΩ, ce qui donne un facteur de qualité pour le filtre idéal .
On commence par obtenir la réponse à un échelon. La tension e(t) en créneau est appliquée par un générateur de fonctions. Les signaux e(t) et s(t) sont obtenus avec un oscilloscope :
 filtreLC-reponseEchelon.pdf
filtreLC-reponseEchelon.pdf
La réponse à un échelon permet de déterminer le temps de réponse du filtre : il est d'environ 0,8 ms.
Pour l'obtention de la réponse fréquentielle, l'amplitude de la tension sinusoïdale e(t) est fixée. On la note E. La grande impédance d'entrée du filtre permet en effet de maintenir cette amplitude constante quelle que soit la fréquence. Le script suivant effectue un balayage pour une valeur de E donnée :
import numpy as np
import matplotlib.pyplot as plt
import pycanum.main as pycan
import numpy.fft
def interpol(x,ninter):
N = len(x)
tfd = numpy.fft.fft(x)
N1 = N//2
tfd2 = np.concatenate((tfd[0:N1],np.zeros(N*ninter),tfd[N1:N]))
y = np.real(numpy.fft.ifft(tfd2))*(ninter+1)
return y
def mesure(can,freq,amp,delai,N=50000,Np=100,ninter=4,plot=False):
teMin = 1e-6
Np = min(Np,1/(teMin*freq))
techant = int(1/(Np*freq*teMin))*teMin
if techant==0:
techant = teMin
P = int(freq*N*techant)
freq = P/(N*techant)
Np = N/P
e1 = amp*np.cos(2*np.pi*P/N*np.arange(N))
can.config_echantillon(techant*1e6,N)
can.acquerir_avec_sorties(e1,0)
t=can.temps()[0]
signaux = can.entrees()
u=signaux[0]
s=signaux[1]
print("Seff = %f"%s.std())
N = len(t)
n1 = int(delai/techant)
t=t[n1:N]
t=t-t[0]
e=u[n1:N]
s=s[n1:N]
N=len(e)
r = ninter+1
if ninter>0:
e = interpol(e,ninter)
s = interpol(s,ninter)
t = np.arange(len(e))*t[len(t)-1]/len(e)
d = int(Np*r/4)
E=e.std()
S=s.std()
G=S/E
z=s[d:N]*(e[d:N]-1j*e[0:N-d])
Z = z.mean()
phi = np.angle(Z)
H = Z/E**2
if plot:
plt.figure()
plt.plot(t,e,'b')
plt.plot(t,s,'r')
plt.grid()
plt.ylim(-10,10)
plt.xlim(0,10/freq)
plt.show()
return(freq,G,phi,H,techant,Np)
can = pycan.Sysam("SP5")
liste_f = []
liste_G = []
liste_phi = []
frequences = np.linspace(35e3,45e3,200)
E = 1 # amplitude de la tension d'entrée
delai = 1e-3 # délai pour le régime transisoire
ninter=0
for f in frequences:
can.config_entrees([0,1],[E*1.1,E*1.1])
(f,G,phi,H,te,Np) = mesure(can,f,E,delai,ninter=ninter)
print("f = %f Hz, G = %f, phi = %f, te = %f, Np = %f"%(f,G,phi,te,Np))
liste_f.append(f)
liste_G.append(G)
liste_phi.append(phi)
can.fermer()
np.savetxt('filtreLC-1-E=1V.txt',np.array([liste_f,liste_G,liste_phi]).T,header='f\t G\t phi')
GdB = 20*np.log10(liste_G)
liste_phi = np.unwrap(liste_phi)
plt.figure()
plt.plot(liste_f,GdB,'b-')
plt.xscale('log')
plt.grid()
plt.xlabel('f (Hz)')
plt.ylabel('G (dB)')
plt.figure()
plt.plot(liste_f,liste_phi,'b-')
plt.xscale('log')
plt.xlabel('f (Hz)')
plt.ylabel('phi (rad)')
plt.grid()
plt.show()
La courbe de réponse fréquentielle est obtenue pour les amplitudes E de 1,2,5 et 9 volts. Pour chacune de ces courbes de gain, on détermine la fréquence de résonance (maximum du gain) et on en déduit la valeur correspondante de L, grace à la relation :
Les courbes de gain du modèle tracées ci-dessus montrent en effet que la valeur de r a un effet négligeable sur la fréquence de résonance.
On recherche la résistance r du modèle qui permet de minimiser l'écart entre le gain maximal expérimental et le gain maximal du modèle. Dans la partie précédente, nous avons montré que l'auto-inductance de la bobine en régime sinusoïdal dépend du courant efficace. Dans ce filtre, le courant efficace dans la bobine n'est évidemment pas constant et il n'est pas accessible directement. Nous estimons le courant efficace à la résonance à partir de la fréquence de résonance et de la valeur de L obtenue à partir de cette fréquence.
Pour chaque valeur de E, la courbe de gain du modèle pour la valeur optimale de r est tracée en trait pointillé.
R=10000
C=22e-9
styles = ['r','b','k','g']
styles_mod = ['r--','b--','k--','g--']
E = [1,2,5,9]
def traceGain(n):
[f,G,phi] = np.loadtxt('filtreLC-1-E=%dV.txt'%E[n],skiprows=1,unpack=True)
fr = f[np.argmax(G)]
L = 1/(4*np.pi**2*fr**2*C)
Gmax = G.max()
ecart = 10
kopt = 0
r = np.linspace(1,8,1000)
for k in range(len(r)):
Gmodele = modele(R,C,L,r[k],rc,f)
Gmodele_max = Gmodele.max()
if abs(Gmodele_max-Gmax) < ecart:
kopt = k
ecart = abs(Gmodele_max-Gmax)
ropt = r[kopt]
Gmodele = modele(R,C,L,ropt,rc,f)
Ieff = E[n]*Gmax/(L*2*np.pi*fr)/np.sqrt(2)
plot(f,G,styles[n],label='E = %d V'%E[n]+', Ieff = %0.1f mA, L = %0.0f uH'%(Ieff*1e3,L*1e6))
plot(f,Gmodele,styles_mod[n],label=r"$r=%0.1f\,\rm\Omega$"%ropt)
figure(figsize=(16,6))
grid()
xlabel('f (Hz)')
ylabel('G')
ylim(0,0.5)
for n in range(4):
traceGain(n)
legend(loc='upper right')
 filtreLC-courbesGain.pdf
filtreLC-courbesGain.pdf
Ces courbes confirment que l'auto-inductance L est d'autant plus grande que l'intensité du courant dans la bobine est grande, ce qui a pour effet de réduire la fréquence de résonance lorsque l'amplitude de la tension d'entrée est plus grande. Ces variations de fréquence de résonance sont loin d'être négligeables et il est quasi impossible de les prévoir par le calcul. Il faut remarquer que l'intensité efficace du courant dans la bobine varie avec la fréquence donc que l'auto-inductance L n'est pas une constante.
La comparaison avec le modèle (maximum du gain) permet d'estimer la résistance r. Cette résistance augmente avec l'intensité du courant efficace, conformément aux résultats obtenus plus haut. On constate cependant que la correpondance entre le modèle et la courbe expérimentale est assez mauvaise, ce qui n'est pas étonnant car ni L ni r ne sont constantes lorsque la fréquence varie : elles dépendent intrinsèquement de la fréquence et l'intensité du courant varie avec la fréquence. Les valeurs de L et r obtenues doivent être interprétées comme les valeurs à la résonance. Par ailleurs, il faut remarquer que la valeur de r est beaucoup plus grande que la résistance du fil en courant continu (130 mΩ). Bien que la résistance du fil augmente avec la fréquence à cause de l'effet de peau, cette augmentation ne peut expliquer les valeurs de plusieurs ohms que nous obtenons. La résistance r est en effet principalement due aux pertes dans le noyau en ferrite, qui dépendent à la fois de la fréquence et du flux magnétique.
Les valeurs de L obtenues d'après la fréquence de résonance et l'estimation du courant efficace à la résonance sont-elles en accord avec les courbes L(Ieff) obtenue précédemment pour une fréquence de 40 kHz ? La réponse est clairement négative. Si on prend l'exemple de la courbe pour E=9 V, l'estimation de L d'après la fréquence de résonance est de 755 uH, ce qui est nettement plus grand que la valeur de L mesurée pour un courant efficace de 12 mA, qui était d'environ 660 uH.
3.c. Application
Ce filtre passe-bande est assez sélectif pour extraire le fondamental d'un signal en créneaux.
Voici la réponse du filtre pour un signal e(t) en créneaux, avec une fréquence accordée sur la fréquence de résonance du filtre :
 filtreLC-filtrageCreneau-1.pdf
filtreLC-filtrageCreneau-1.pdf
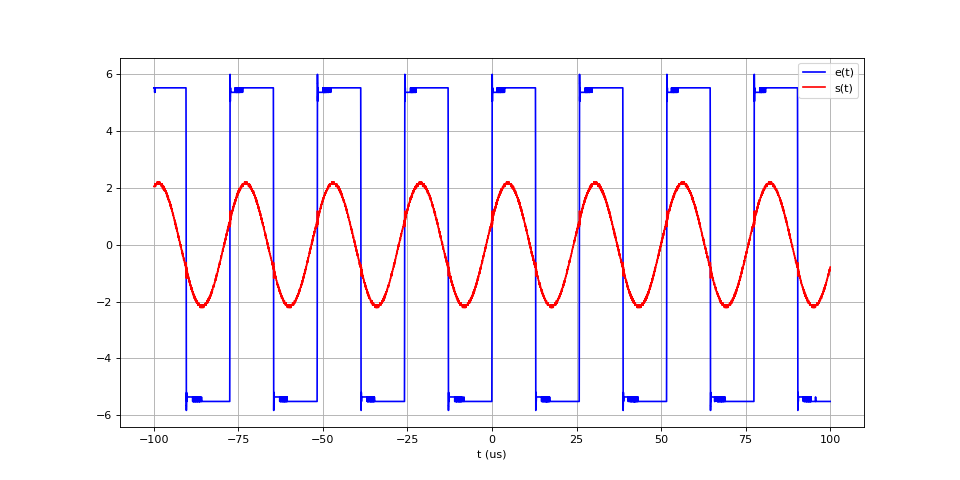
Pour la même fréquence, abaissons l'amplitude de e(t) :
 filtreLC-filtrageCreneau-2.pdf
filtreLC-filtrageCreneau-2.pdf
Comme prévu d'après la partie précédente, l'abaissement de l'amplitude a pour effet d'augmenter la fréquence de résonance, ce qui se traduit par une sortie s(t) de moins grande amplitude et déphasée par rapport à l'entrée.
Ce filtre pourrait servir à obtenir un signal quasi sinusoïdal à partir de la tension en créneau délivrée par un oscillateur à relaxation. Dans ce cas, l'amplitude du signal e(t) est fixée et il est donc possible d'ajuster la fréquence de l'oscillateur pour qu'elle corresponde à celle du filtre. Ajuster la fréquence de résonance du filtre pour qu'elle soit égale à une valeur prédéterminée, par exemple 40 kHz, est beaucoup plus difficile. En effet, l'ajout ou le retrait d'une spire de la bobine aurait un effet beaucoup trop grand sur L. Cependant, en jouant à la fois sur le nombre de spires et sur l'ajustement de C (avec plusieurs condensateurs), il est possible d'obtenir une fréquence assez proche d'une fréquence choisie. De ce point de vue, une bobine sans noyau offrirait beaucoup plus de souplesse car, le nombre de spires étant beaucoup plus grand, il est possible d'ajuster finement L (qui de plus ne dépend pas du courant ni de la fréquence). La bobine à noyau en ferrite est cependant beaucoup moins encombrante et plus facile à réaliser.
4. Application : onduleur à résonance
4.a. Circuit résonant
L'objectif est d'obtenir un courant dans la bobine de fréquence 40 kHz avec une tension assez grande (plusieurs dizaines de volts). On considère tout d'abord le circuit suivant :
Figure pleine pageCe filtre, dont la tension d'entrée est e(t) et la tension de sortie s(t) a une impédance d'entrée très faible au voisinage de la résonance. En conséquence, il est impossible de maintenir une amplitude constante en entrée sur toute la plage de fréquences. Cela n'empêche pas d'obtenir la réponse fréquentielle. Voici la courbe de gain en fonction de la fréquence pour la bobine à N=12 spires et deux valeurs de C : C=18,8 nF (4 condensateurs de 4,7 nF en parallèle) et C=21 nF (4 condensateurs de 4,7 nF et un de 2,2 nF en parallèle). L'amplitude programmée sur la carte est 2 V. L'amplitude de e(t) diminue fortement à la résonance et l'amplitude de s(t) atteint environ 9 V.
figure()
[f,G,phi] = np.loadtxt('filtreLC-2-E=2V.txt',unpack=True,skiprows=1)
plot(f/1e3,G,label='C=18,8 nF')
[f,G,phi] = np.loadtxt('filtreLC-3-E=2V.txt',unpack=True,skiprows=1)
plot(f/1e3,G,label='C=21 nF')
grid()
xlabel('f (kHz)')
ylabel('G')
ylim(0,25)
legend(loc='upper right')
 filtreLC-2-Gain.pdf
filtreLC-2-Gain.pdf
Afin d'effectuer une isolation galvanique entre l'entrée et la sortie, et d'offrir une amplification supplémentaire de la tension, on réalise un transformateur en enroulant sur le tore un bobinage secondaire, comportant aussi 12 spires :
Figure pleine pagePour l'étude de ce filtre, la masse est reliée à une borne de l'enroulement primaire et à une borne de l'enroulement secondaire. L'intérêt de l'isolation galvanique apparaîtra plus loin.
figure()
[f,G,phi] = np.loadtxt('filtreLC-transfo-2-E=2V.txt',unpack=True,skiprows=1)
plot(f/1e3,G,label='C=18,8 nF')
[f,G,phi] = np.loadtxt('filtreLC-transfo-3-E=2V.txt',unpack=True,skiprows=1)
plot(f/1e3,G,label='C=21 nF')
grid()
xlabel('f (kHz)')
ylabel('G')
ylim(0,25)
legend(loc='upper right')
 filtreLC-transfo-Gain.pdf
filtreLC-transfo-Gain.pdf
4.b. Onduleur
Le générateur de signaux est remplacé par un pont de transistors en H.
Figure pleine pageNous utilisons le pont de transistors à jonctions L298, dont le fonctionnement et le pilotage est décrit dans Pilotage d'un pont L298.
L'alimentation délivre une tension Vs pouvant aller de 7,5 V à 50 V.
Pour un pont idéal, la tension e(t), qui est la tension entre les sorties OUT1 et OUT2 du pont, devrait alterner entre -Vs et +Vs. En réalite, la forme exacte de e(t) dépend évidemment de la charge du pont (ici le condensateur et la bobine en série). On remarque qu'aucune des deux bornes du bobinage primaire ne peut être reliée à la masse. L'isolation galvanique permet de relier à la masse une des bornes du bobinage secondaire. La tension s(t) peut atteindre plusieurs dizaines de volts. On place donc en sortie un potentiomètre avec un rapport de division 1/10 afin de visualiser la tension u(t), 10 fois plus petite que s(t).
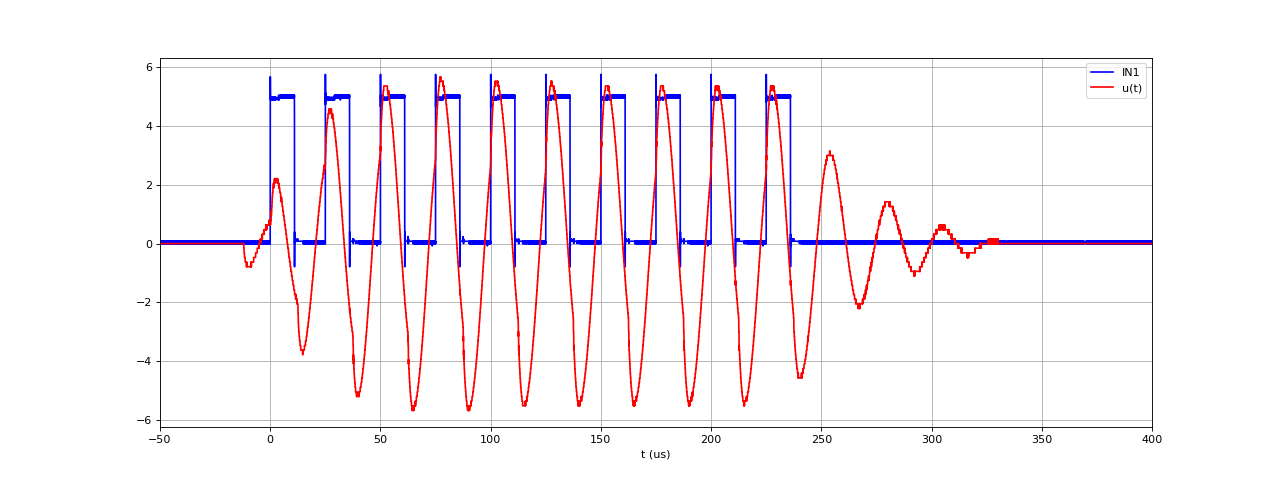
Voici la tension u(t) et la tension de commande IN1 du pont (plus précisément de la moité du pont), pour une tension d'alimentation Vs=10 V. Le programme Arduino qui pilote le pont envoie un signal comportant 10 cycles de période 25 microsecondes (fréquence 40 kHz). La capacité est C=18,8 nF.
 onduleur40kHz-Vs10.pdf
onduleur40kHz-Vs10.pdf
Après un régime transitoire d'environ 3 cycles, la tension s(t) atteint une amplitude de 55 V et sa forme est quasi sinusoïdale. Il est difficile de savoir si la tension e(t) est en phase avec s(t) (ce qui doit être vrai à la résonance), car il y a un léger décalage entre la tension de commande et la tension en sortie du pont (le rapport cyclique de la tension de commande est inférieur à 1/2, comme expliqué dans Pilotage d'un pont L298). Il semble cependant qu'on soit proche de la résonance. En tout cas, la tension atteinte en sortie répond bien à notre objectif. Si on la trouve trop grande, il suffit de réduire le nombre de spires du bobinage secondaire. On pourra aussi l'augmenter en augmentant ce nombre de spires ou en augmentant la tension Vs.
Voici le résultat pour un tension Vs=15 V :
 onduleur40kHz-Vs15.pdf
onduleur40kHz-Vs15.pdf
La tension s(t) atteint 80 volts, mais il semble que la fréquence de résonance se soit légèrement décalée, ce qui n'est pas étonnant compte tenu des observations faites précédemment (influence du courant sur la valeur de L).
Voici le résultat pour Vs=20 V :
 onduleur40kHz-Vs20.pdf
onduleur40kHz-Vs20.pdf
Cette augmentation de la tension d'alimentation n'apporte pas de gain de l'amplitude en sortie, bien au contraire, et il y a de plus une distorsion importante. On constate que l'onduleur est utilisable jusqu'à Vs=16 volts.
Voici le résultat pour Vs=10 V mais avec 6 spires dans le bobinage secondaire :
 onduleur40kHz-Vs10-6sp.pdf
onduleur40kHz-Vs10-6sp.pdf
L'amplitude est bien deux fois plus petite qu'avec 12 spires et atteint 25 V.
Cet onduleur est destiné à alimenter un transducteur piézoélectrique pour émettre des ultrasons à 40 kHz. Nous branchons donc le transducteur en sortie :
Figure pleine pageVoici le résultat pour Vs=10 V mais avec 6 spires dans le bobinage secondaire :
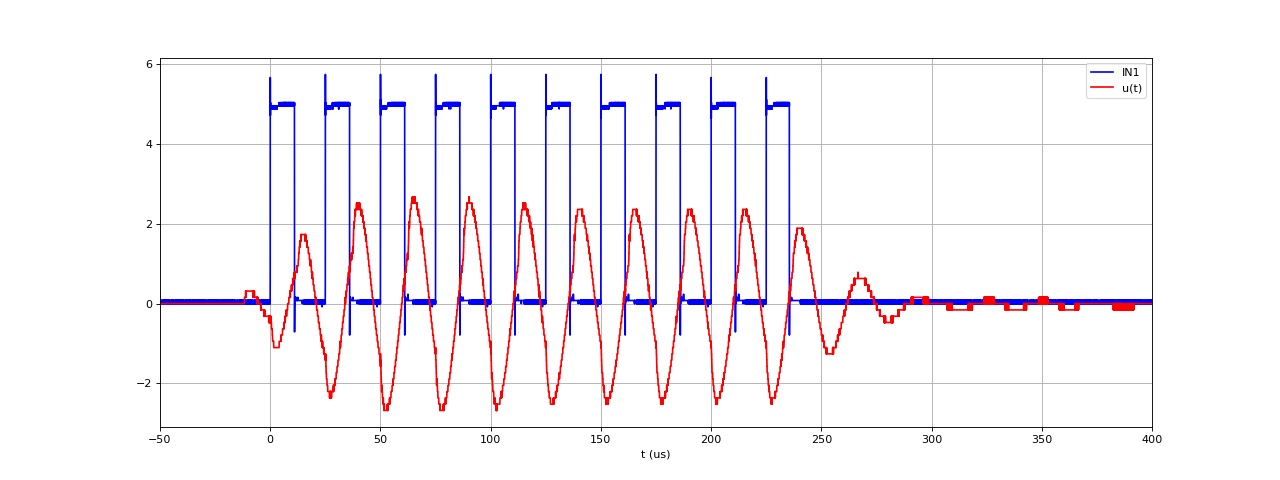 onduleur40kHz-Vs10-6sp-piezo.pdf
onduleur40kHz-Vs10-6sp-piezo.pdf
La présence du transducteur n'affecte pas la tension s(t).
4.c. Augmentation de l'inductance
Dans le cadre de l'excitation d'un transducteur pour l'émission d'ultrasons à 40 kHz, le circuit précédent comporte un inconvénient : l'impédance de la bobine secondaire à 40 kHz est très faible (5 Ω pour 6 spires). Cette faible impédance rend impossible l'utilisation du même transducteur en réception. Il faut donc augmenter le nombre de spires du primaire et du secondaire, de manière à atteindre une impédance assez grande. Une auto-inductance de 10 mH (primaire et secondaire) est facile à atteindre : pour le tore que nous avons utilisé, il faut enrouler 43 spires, ce qui est faisable avec un fil émaillé. Un moyen plus simple est d'utiliser une bobine d'arrêt double (Power Line Choke Coil) :

Il s'agit d'un transformateur avec des enroulements primaire et secondaire identiques. Ce type de transformateur est habituellement utilisé pour filtrer des perturbations de haute fréquence, par exemple celles provenant des alimentations à découpage. Nous utilisons une bobine EPCOS dont les enroulements primaire et secondaire ont une auto-inductance de L=10 mH, et pouvant supporter 1 A.
Nous étudions tout d'abord le circuit résonant avec un condensateur en série, de capacité C=1,31 nF (3 fois 4,7 nF et 10 nF en série). Pour l'obtention de la courbe de gain avec la carte SysamSP5, nous devons réduire la tension d'entrée car le gain du filtre à la résonance est très grand. Un diviseur de tension suivi d'un suiveur de tension permet d'abaisser la tension délivrée sur la sortie SA1 d'un facteur 10 (environ).
Figure pleine page
figure()
[f,G,phi] = np.loadtxt('filtreLC-epcos10mH-E=2V.txt',unpack=True,skiprows=1)
plot(f/1e3,G)
grid()
xlabel('f (kHz)')
ylabel('G')
ylim(0,40)
 filtreLC-10mH-Gain.pdf
filtreLC-10mH-Gain.pdf
La résonance n'est pas à 40 kHz mais le gain à cette fréquence est tout de même très élevé. La valeur de L étant fixée, on peut modifier C pour que le gain à la fréquence de 40 kHz soit plus ou moins grand, en fonction de l'amplitude de tension souhaitée en sortie de l'onduleur. Pour le bon fonctionnement de l'onduleur, il est préférable que la fréquence de découpage soit légèrement supérieure à la fréquence de résonance et non pas inférieure. Par ailleurs, cette courbe de gain est établie avec une amplitude de la tension d'entrée très faible (environ 0,2 V), donc avec un courant très faible dans l'enroulement primaire. Or on a vu que l'augmentation du courant réduit la fréquence de résonance. On doit donc s'attendre à une fréquence de résonance plus basse lorsque le transformateur est incorporé dans l'onduleur. Voici le schéma de l'onduleur :
Figure pleine pageVoici les tensions IN1 (commande d'un demi-pont) et u(t) (égal à s(t) divisée par 10) pour une période de 25 microsecondes et une tension d'alimentation Vs=10 V.
 onduleur40kHz-10mH-Vs10-T25.pdf
onduleur40kHz-10mH-Vs10-T25.pdf
La présence de distorsion indique que la fréquence (40 kHz) est en dessous de la fréquence de résonance. Voici le résultat pour une période de 24 microsecondes (41,6 kHz) :
 onduleur40kHz-10mH-Vs10-T24.pdf
onduleur40kHz-10mH-Vs10-T24.pdf
La tension s(t) atteint 100 V. On remarque par ailleurs que le temps de réponse du circuit résonant est un peu plus grand que celui étudié précemment (L plus petite).
Cet onduleur devrait convenir pour exciter un transducteur piézoélectrique qui nécessite ce niveau de tension. Comment abaisser la tension maximale en sortie ? La première solution est de réduire le nombre de spires du bobinage secondaire. On peut aussi abaisser la fréquence de résonance en augmentant la capacité C. Voici le résultat avec C=3,3 nF, pour une fréquence de 40 kHz et Vs=10 V :
 onduleur40kHz-10mH-Vs10-T25-2.pdf
onduleur40kHz-10mH-Vs10-T25-2.pdf
et pour C=2,2 nF :
 onduleur40kHz-10mH-Vs10-T25-3.pdf
onduleur40kHz-10mH-Vs10-T25-3.pdf
Dans ce cas, la valeur atteinte par s(t) est d'environ 22 V. On est assez loin de la résonance mais cela représente tout de même un gain d'un facteur 2 par rapport à la tension d'alimentation.
Si l'objectif est de piloter un transducteur piézoélectrique pour émettre des ultrasons (à 40 kHz), la forme d'onde n'a pas d'importance, seule la fréquence d'excitation importe. On peut d'ailleurs se passer de la résonance et utiliser le circuit suivant :
Figure pleine pageVoici les signaux pour une fréquence de 40 kHz et une tension d'alimentation Vs=10 V :
 pont40kHz-10mH-Vs10-T25.pdf
pont40kHz-10mH-Vs10-T25.pdf
Comme prévu, la tension de crête de s(t) est beaucoup moins grande. Elle atteint ici 10 V, qui est la tension d'alimentation. On voit aussi un avantage de ce circuit par rapport au circuit avec résonance : la durée des oscillations de s(t) est limitée par la durée de l'excitation. Pour augmenter la tension de crête, il faut augmenter Vs. Voici le résultat pour Vs=20 V :
 pont40kHz-10mH-Vs20-T25.pdf
pont40kHz-10mH-Vs20-T25.pdf
Si le transducteur est branché en sortie, voici la forme de u(t) :
 pont40kHz-10mH-Vs20-T25-piezo.pdf
pont40kHz-10mH-Vs20-T25-piezo.pdf
La tension s(t) présente des oscillations d'environ 300 kHz. Il semble y avoir un phénomène de résonance entre la bobine secondaire de 10 mH et le transducteur. Cependant, nous avons constaté que ces oscillations indésirables sont absentes dans le signal électrique fourni par le transducteur de réception, et sont donc probablement absentes de l'onde acoustique émise.
Avec ce montage à excitation directe (sans résonance), il existe un moyen d'augmenter l'amplitude de la tension s(t) sans changer celle de l'alimentation : augmenter le nombre de spires du bobinage secondaire.