Redressement

2.a. Redressement avec filtrage inductif

Dans le circuit suivant, le redressement est effectué par une seule diode. R peut être la résistance de charge et l'ajout de L permet d'effectuer un filtrage RL. Dans certains cas, la charge elle-même est inductive.

Figure pleine page

La tension d'entrée est $V_e\left(t\right)=Esin\left(\omega t\right)$. À l'instant initial (t=0), cette tension est nulle et toutes les autres grandeurs sont supposées nulles. Au début, on a V=0 et V_e>0 donc la diode est passante (état 1). L'équation différentielle vérifiée par le courant dans la charge (qui est aussi le courant débité par la source) est :

$$L\frac{di}{dt}+Ri=V_e\left(t\right)\text{(1)}$$

La diode passe à l'état bloquant (état 2) lorsque i s'annule pour devenir négatif. Lorsque cela se produit, la tension V_e est nécessairement négative. Dans l'état 2, on a simplement i=0 et V=0. La diode passe à l'état passant lorsque V_e devient nulle ou positive.

La fonction suivante effectue la simulation en intégrant l'équation différentielle par la méthode d'Euler. Pour ce circuit simple, une résolution entièrement analytique est possible mais dans d'autres circuits la détermination de l'état du circuit (tensions et courants) au moment d'un changement d'état peut nécessiter une résolution numérique d'équations algébriques. La méthode de simulation pas à pas par la méthode d'Euler dispense de ce type de résolution et permet donc, de manière simple et universelle, d'effectuer la simulation de ce type de circuits.

import numpy as np
from matplotlib.pyplot import *
                    
def simulation1(E,f,L,R,tmax,dt):
    w = 2*np.pi*f
    etat = 1
    t = 0
    i = 0
    data = [[0,0,0,0]] #t,i,Ve,V
    while t<tmax:
        t += dt
        Ve = E*np.sin(w*t)
        if etat==1:
            i += (Ve/L-R/L*i)*dt
            data.append([t,i,Ve,Ve])
            if i<=0: etat+=1
        elif etat==2:
            i = 0
            data.append([t,i,Ve,0])
            if Ve>=0: etat=1
    data = np.array(data)
    return data[:,0],data[:,1],data[:,2],data[:,3]
                    

Le facteur de puissance est défini comme le rapport de la puissance moyenne délivrée par la source par le produit de la tension efficace et du courant efficace. Pour un circuit linéaire, le facteur de puissance est égale à $cos\left(\phi \right)$, où $\phi$ est le déphasage entre la tension et le courant de la source. Pour un circuit non linéaire, il s'agit du déphasage entre la tension (qui est sinusoïdale) et du fondamental du courant. La fonction suivante calcule le facteur de puissance en utilisant la dernière période des signaux :

def facteurP(t,Us,Is,f):
    dt = t[1]-t[0]
    N = int(1/(f*dt))
    i = len(Us)-N
    j = len(Us)
    Ueff = np.std(Us[i:j])
    Ieff = np.std(Is[i:j])
    return np.mean(Us[i:j]*Is[i:j])/(Ueff*Ieff)
                      

Le facteur de puissance est compris entre 0 et 1. Plus il est proche de 1, moins la source devra fournir un courant important pour fournir une puissance donnée, ce qui est souhaitable. Certaines sources ont une limite du courant et si le facteur de qualité est bas il s'en suit une limite de la puissance délivrable relativement basse.

L'efficacité du filtrage est évaluée en comparant la période avec le rapport L/R. Voici une simulation avec une valeur de L relativement faible :

f=100
E=10
L=10e-3
R = 5
t,i,Ve,V = simulation1(E,f,L,R,0.05,1e-5)
figure(figsize=(16,6)) 
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,i,f)
title("Kp = %0.2f"%Kp)
                    

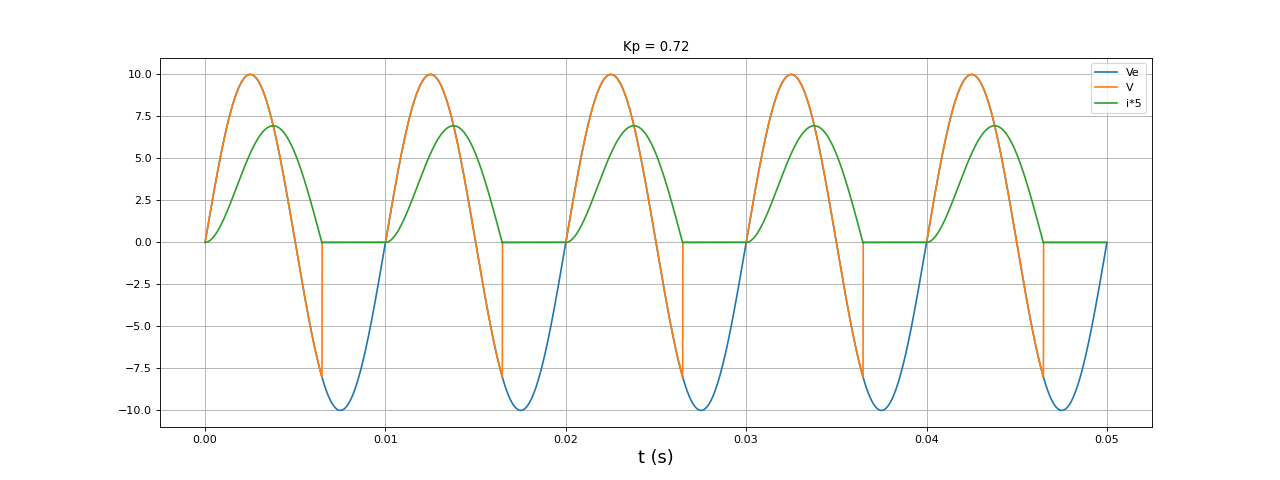fig1.pdf

Voici la simulation avec une valeur de L dix fois plus grande :

f=100
E=10
L=100e-3
R = 5
t,i,Ve,V = simulation1(E,f,L,R,0.05,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,i,f)
title("Kp = %0.2f"%Kp)
                    

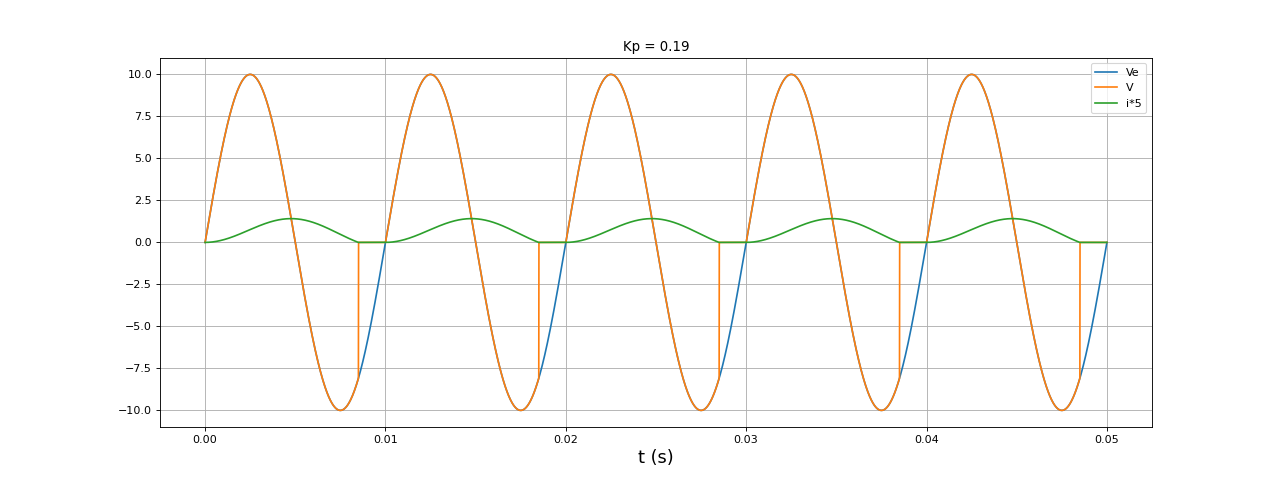fig2.pdf

L'intervalle de temps où le courant est nul est moins grand mais sa valeur moyenne est plus basse. Le déphasage entre le fondamental du courant et la tension est à l'évidence proche de 90 degrés, ce qui explique la faiblesse du facteur de puissance. Par ailleurs, la valeur moyenne de la tension V dépend de la résistance de charge R. Voici la simulation précédente avec une résistance 10 fois plus grande :

R = 50
t,i,Ve,V = simulation1(E,f,L,R,0.05,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,i,f)
title("Kp = %0.2f"%Kp)
                    

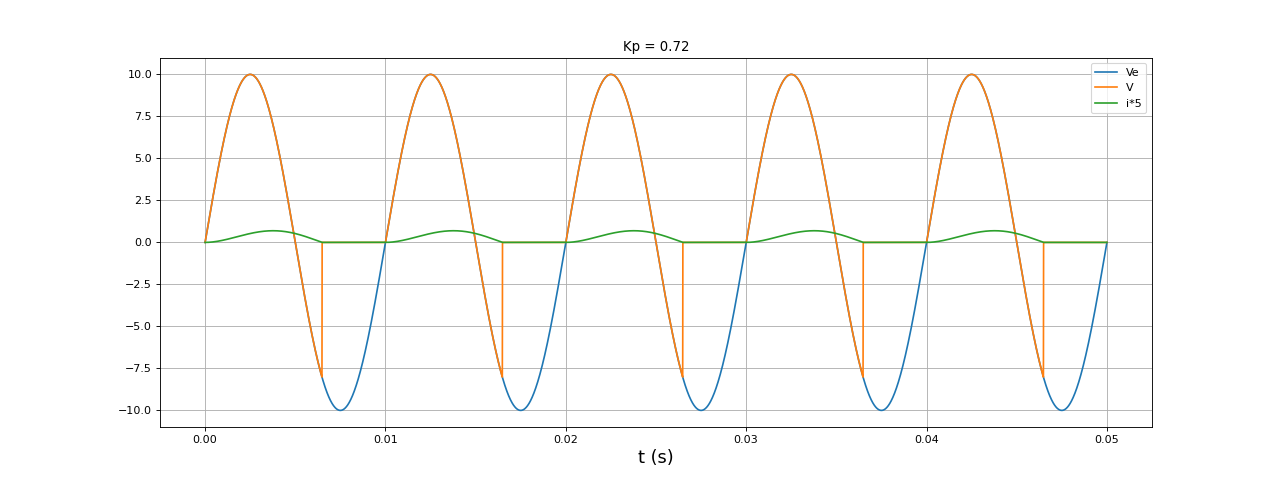fig3.pdf

La valeur moyenne de V (qui est positive) est d'autant plus grande que la résistance de charge est grande. Autrement dit, la moyenne de V est d'autant plus basse que le courant est grand. La simulation suivante permet de calculer les valeurs moyennes pour différentes valeurs de la résistance de charge :

Vmoy = []
Imoy = []
for R in [1,5,10,20,40,80]:
    t,i,Ve,V = simulation1(E,f,L,R,0.05,1e-5)
    Vmoy.append(V.mean())
    Imoy.append(i.mean())
figure()
plot(Imoy,Vmoy,"o")
grid()
xlim(0,0.2)
ylim(0,3)
xlabel("I moy (A)",fontsize=16)
ylabel("V moy (V)",fontsize=16)
                     

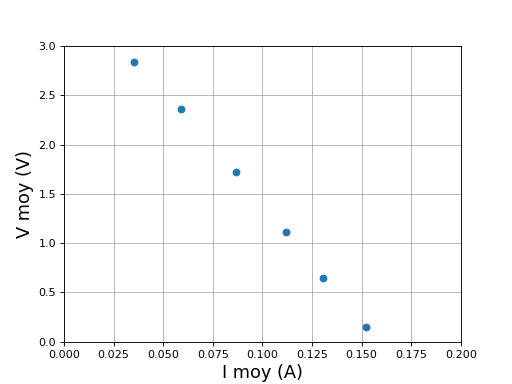fig4.pdf

Une première amélioration de ce circuit consiste à ajouter une diode de roue libre :

Figure pleine page

Dans ce circuit qui comporte deux diodes, il y a a priori quatre états de commutation mais seulement deux sont possibles.

Au début, la diode D₁ est passante donc V=V_e (état 1). En conséquence, la diode D₂ devient passante lorsque V_e devient négatif. Mais si D₂ est passante alors V=0, ce qui est incompatible avec D₁ passante. En conséquence, la fermeture de D₂ s'accompagne de l'ouverture de D₁ (état 2). Lorsque V_e redevient positif, la diode D₁ devient à nouveau passante et, pour la même raison que précédemment, D₂ est nécessairement bloquante. On a donc deux états possibles. Les deux diodes commutent en opposition et la commutation est commandée par le signe de V_e.

Dans l'état 1, l'équation différentielle pour i(t) est la même que précédemment. Dans l'état 2, elle est :

$$L\frac{di}{dt}+Ri=0\text{(2)}$$

Contrairement au circuit précédent, il faut distinguer le courant i dans la charge et le courant i_e qui sort de la source (courant d'entrée).

def simulation2(E,f,L,R,tmax,dt):
    w = 2*np.pi*f
    etat = 1
    t = 0
    i = 0
    data = [[0,0,0,0,0]] #t,i,ie,Ve,V
    while t<tmax:
        t += dt
        Ve = E*np.sin(w*t)
        if etat==1:
            i += (Ve/L-R/L*i)*dt
            data.append([t,i,i,Ve,Ve])
            if Ve <=0: etat+=1
        elif etat==2:
            i += -R/L*i*dt
            data.append([t,i,0,Ve,0])
            if Ve>=0: etat=1
    data = np.array(data)
    return data[:,0],data[:,1],data[:,2],data[:,3],data[:,4]
                    

Voici une simulation avec L faible :

f=100
E=10
L=10e-3
R = 5
t,i,ie,Ve,Vd = simulation2(E,f,L,R,0.05,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,Vd,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

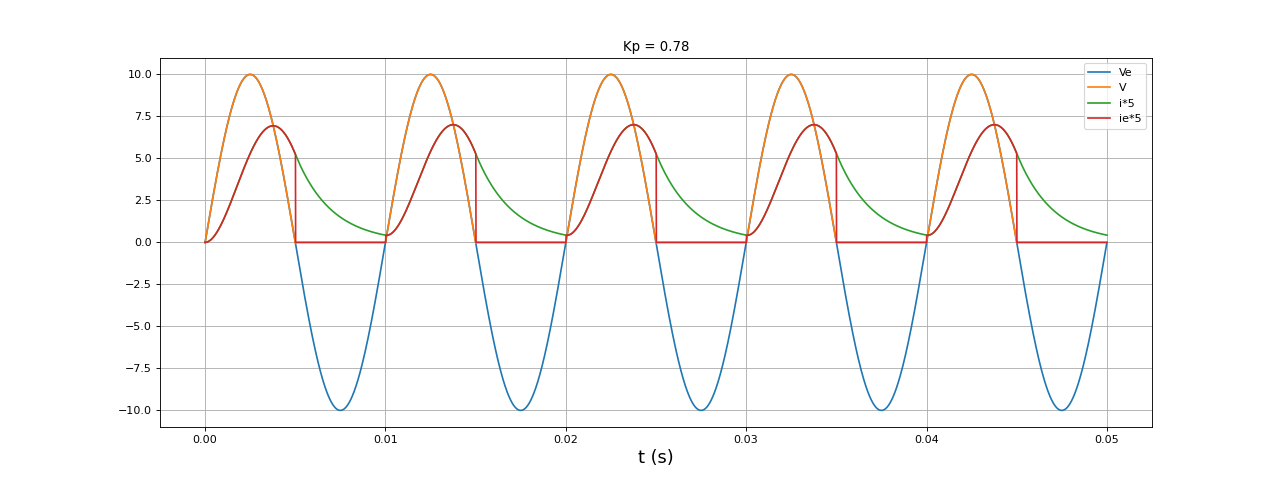fig5.pdf

L'effet le plus important de l'ajout d'une diode de roue libre est le fait que la tension V s'annule pour les valeurs négatives de la tension d'entrée. En conséquence, la valeur moyenne de V ne dépend que de l'amplitude de la tension d'entrée et pas de la résistance de charge (elle en dépend dans le circuit sans diode de roue libre).

Voici une simulation avec L 10 fois plus grand (on doit augmenter la durée de la simulation) :

f=100
E=10
L=100e-3
R = 5
t,i,ie,Ve,V = simulation2(E,f,L,R,0.1,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

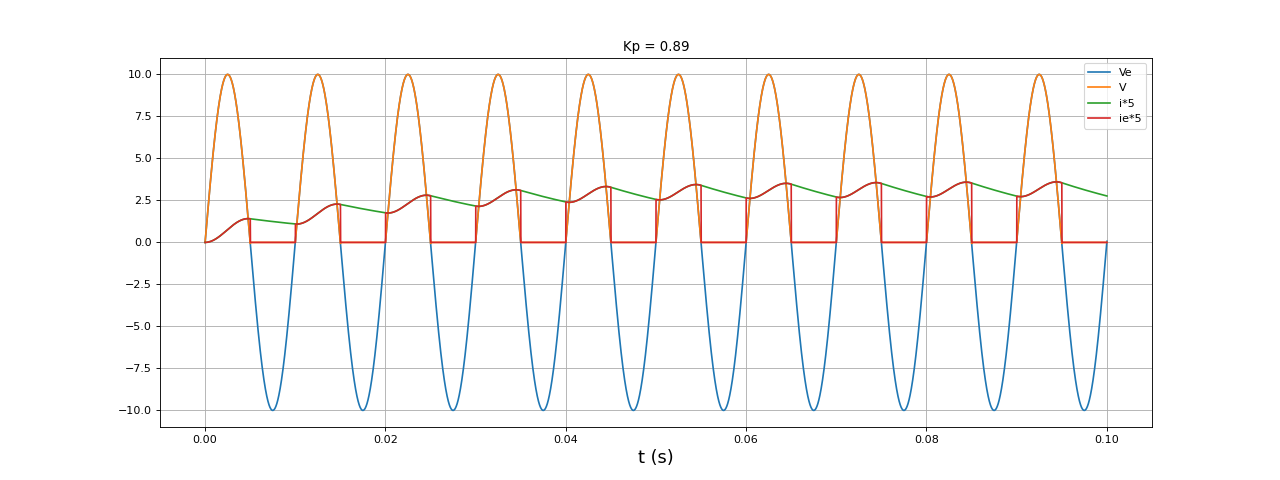fig6.pdf

À même fréquence, le facteur de puissance de ce circuit (avec la diode de roue libre) est beaucoup plus grand que celui du circuit sans la diode de roue libre. Cela signifie que, pour une puissance moyenne reçue par la charge donnée, la source aura moins de courant à fournir.

Avec la diode de roue libre ajoutée, on obtient un courant dont le taux d'ondulation est nettement plus bas et dont la valeur moyenne est plus élevée. En augmentant, la fréquence, on devrait réduire encore le taux d'ondulation du courant :

f=500
E=10
L=100e-3
R = 5
t,i,ie,Ve,V = simulation2(E,f,L,R,0.1,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

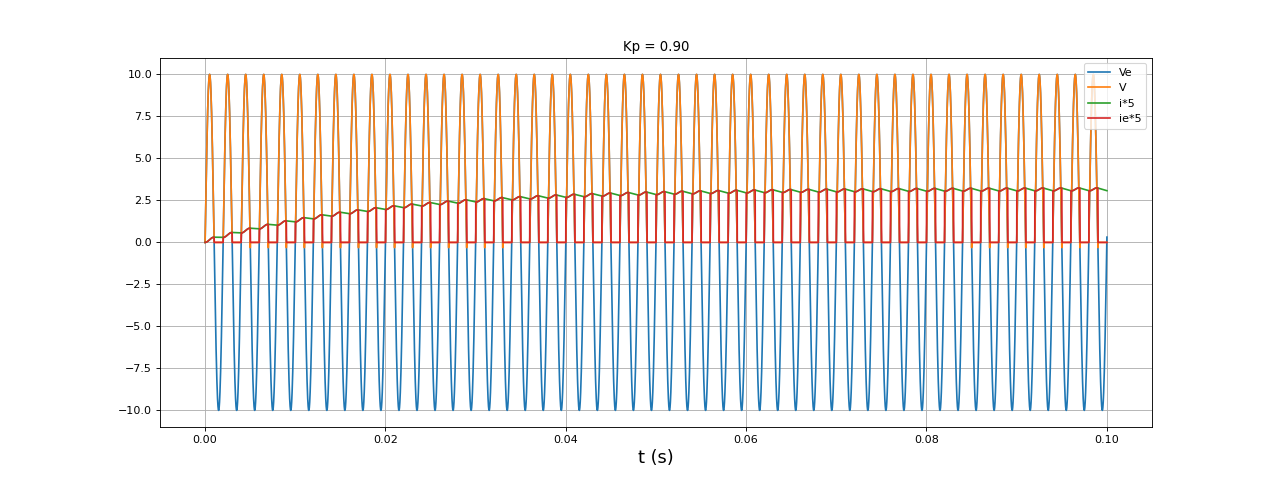fig7.pdf

Le circuit précédent peut être modifié en ajoutant une inductance de commutation [1] :

Figure pleine page

Dans l'état 1 (D1 passante et D2 bloquante) on a i₁=i et :

$$\begin{array}{ccc}\hfill & V_e=(L_e+L)\frac{di}{dt}+Ri\hfill & \hfill \text{(3)}\\ \hfill & V=L\frac{di}{dt}+Ri\hfill & \hfill \text{(4)}\end{array}$$

donc :

$$V=\frac{L}{L_e+L}{V}_e+\frac{R{L}_e}{L_e+L}i\text{(5)}$$

i est toujours positif car un courant négatif serait incompatible avec les diodes. Lorsque V s'annule la diode D₂ devient passante. La diode D₁ reste passante car son ouverture violerait la continuité du courant dans L_e. À l'état 2, les deux diodes sont donc passantes. On a dans cet état :

$$\begin{array}{ccc}\hfill & 0=L\frac{di}{dt}+Ri\hfill & \hfill \text{(6)}\\ \hfill & V_e=L_e\frac{d{i}_e}{dt}\hfill & \hfill \text{(7)}\end{array}$$

L'état 2 cesse lorsque i_e s'annule pour devenir négatif car la diode D₁ devient alors bloquante alors que la diode D₂ reste passante (état 3). Dans l'état 3 on a :

$$0=L\frac{di}{dt}+Ri\text{(8)}$$

L'état 3 cesse lorsque V_e s'annule pour devenir positif. On passe alors à l'état 4, où les deux diodes sont passantes. Les équations différentielles dans l'état 4 sont les mêmes que dans l'état 2. L'état 4 cesse lorsque le courant dans D₂ s'annule pour devenir négatif, c'est-à-dire lorsque $i_e-i\ge 0$.

def simulation3(E,f,Le,L,R,tmax,dt):
    w = 2*np.pi*f
    etat = 1
    t = 0
    i = 0
    ie = 0
    data = [[0,0,0,0,0]] #t,i,ie,Ve,V
    while t<tmax:
        t += dt
        Ve = E*np.sin(w*t)
        if etat==1:
            i += (Ve/(L+Le)-R/(L+Le)*i)*dt
            ie = i
            V = L/(L+Le)*Ve+R*Le/(L+Le)*i
            data.append([t,i,ie,Ve,V])
            if V <=0: etat+=1
                
        elif etat==2:
            i += -R/L*i*dt
            ie += Ve/Le*dt
            V = 0
            data.append([t,i,ie,Ve,V])
            if ie<=0: etat+=1
        elif etat==3:
            i += -R/L*i*dt
            ie = 0
            data.append([t,i,ie,Ve,0])
            if Ve>=0: etat+=1
        elif etat==4:
            i += -R/L*i*dt
            ie += Ve/Le*dt
            V = 0
            data.append([t,i,ie,Ve,V])
            if ie>=i: etat=1
                
    data = np.array(data)
    return data[:,0],data[:,1],data[:,2],data[:,3],data[:,4]
                    

Voici une simulation avec L faible :

f=100
E=10
Le = 10e-3
L=10e-3
R = 5
t,i,ie,Ve,V = simulation3(E,f,Le,L,R,0.05,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

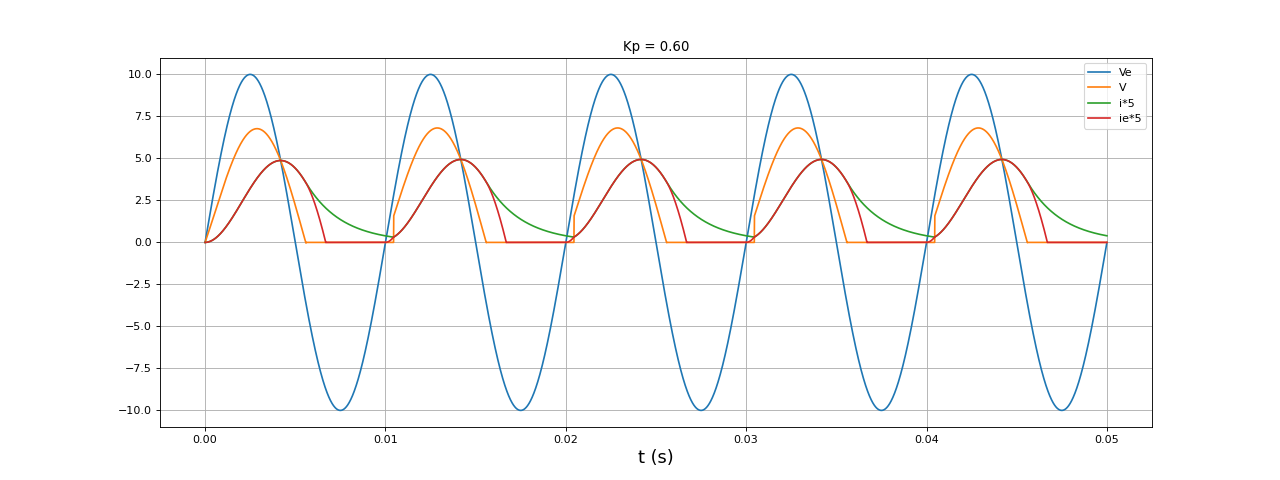fig8.pdf

et une autre avec L 10 fois plus grand :

f=100
E=10
Le = 10e-3
L=100e-3
R = 5
t,i,ie,Ve,V = simulation3(E,f,Le,L,R,0.1,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

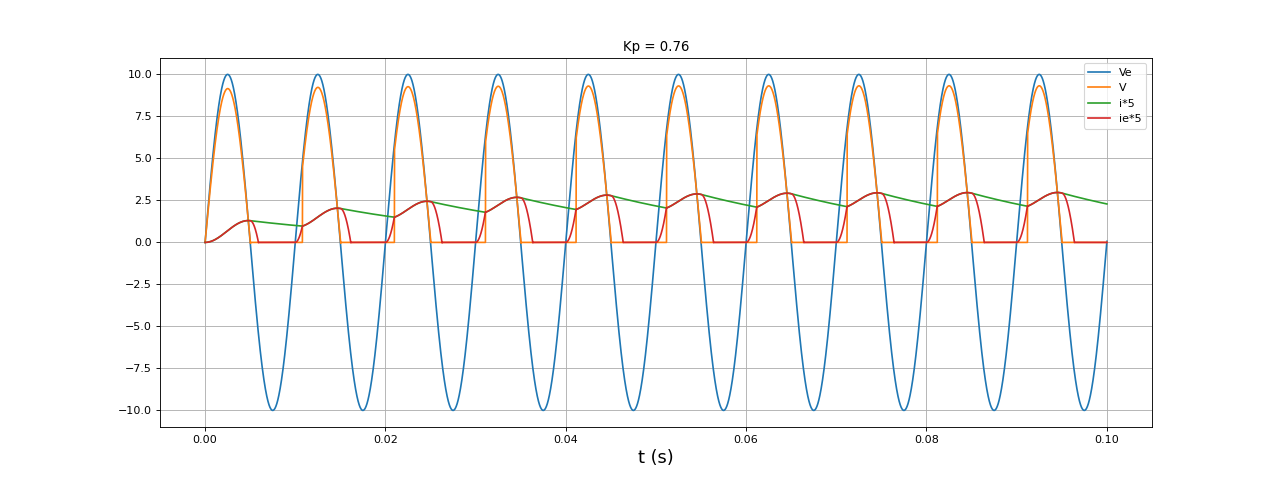fig9.pdf

Voici la tension V moyenne en fonction du courant i moyen :

Vmoy = []
Imoy = []
for R in [1,2,5,10,20,40,80]:
    t,i,ie,Ve,V = simulation3(E,f,Le,L,R,0.1,1e-5)
    N = len(V)
    Vmoy.append(V[N//2:N].mean())
    Imoy.append(i[N//2:N].mean())
figure()
plot(Imoy,Vmoy,"o")
grid()
xlim(0,3)
ylim(0,7)
xlabel("I moy (A)",fontsize=16)
ylabel("V moy (V)",fontsize=16)
                     

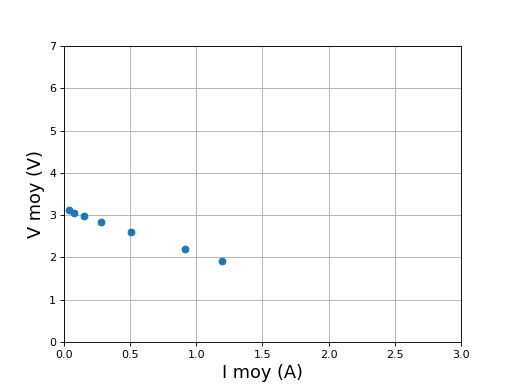fig10.pdf

2.b. Redressement avec filtrage capacitif

Dans le circuit suivant, R est la résistance de charge. Le filtrage est réalisé par la capacité C.

Figure pleine page

La tension d'entrée est $V_e\left(t\right)=Esin\left(\omega t\right)$. À l'instant initial (t=0), cette tension est nulle et toutes les autres grandeurs sont supposées nulles. Au début, on a V=0 et V_e>0 donc la diode est passante (état 1) et V=V_e. Dans cet état, on a :

$$\begin{array}{ccc}\hfill & i_e=\frac{V_e}{R}+C\frac{d{V}_e}{dt}\hfill & \hfill \text{(9)}\\ \hfill & i=\frac{V_e}{R}\hfill & \hfill \text{(10)}\end{array}$$

La diode devient bloquante lorsque V_e commence à décroître, c'est-à-dire lorsque sa dérivée s'annule. On passe alors à l'état 2, pour lequel i_e=0 et :

$$RC\frac{di}{dt}+i=0\text{(11)}$$

On revient à l'état 1 lorsque V devient inférieur ou égal à V_e.

Juste après le passage à l'état 1, la tension V décroît car la capacité se décharge dans la résistance. Si cette décroissance est plus rapide que la décroissance de V_e (si C ou R ne sont pas assez grandes), la diode revient immédiatement l'état passant (état 1) puis à l'état bloquant puisque la dérivée de V_e est toujours négative. Il se produit donc, pendant un court intervalle de temps, une alternance des deux états, mais il s'agit d'un artefact dû au modèle de diode idéale.

def simulation4(E,f,C,R,tmax,dt):
    w = 2*np.pi*f
    etat=1
    t = 0
    i = 0
    data = [[0,0,0,0,0]] #t,i,ie,Ve,V
    while t<tmax:
        t += dt
        Ve = E*np.sin(w*t)
        dVe = E*w*np.cos(w*t)
        if etat==1:
            ie = Ve/R+C*dVe
            i = Ve/R
            V = Ve
            data.append([t,i,ie,Ve,V])
            if dVe<=0: etat+=1
        elif etat==2:
            ie = 0
            i += -i/(R*C)*dt
            V = R*i
            data.append([t,i,ie,Ve,V])
            if Ve>V: etat=1
    data = np.array(data)
    return data[:,0],data[:,1],data[:,2],data[:,3],data[:,4]
                    

f=100
E=10
C=2e-3
R = 5
t,i,ie,Ve,V = simulation4(E,f,C,R,0.1,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i,label="i")
plot(t,ie,label="ie")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

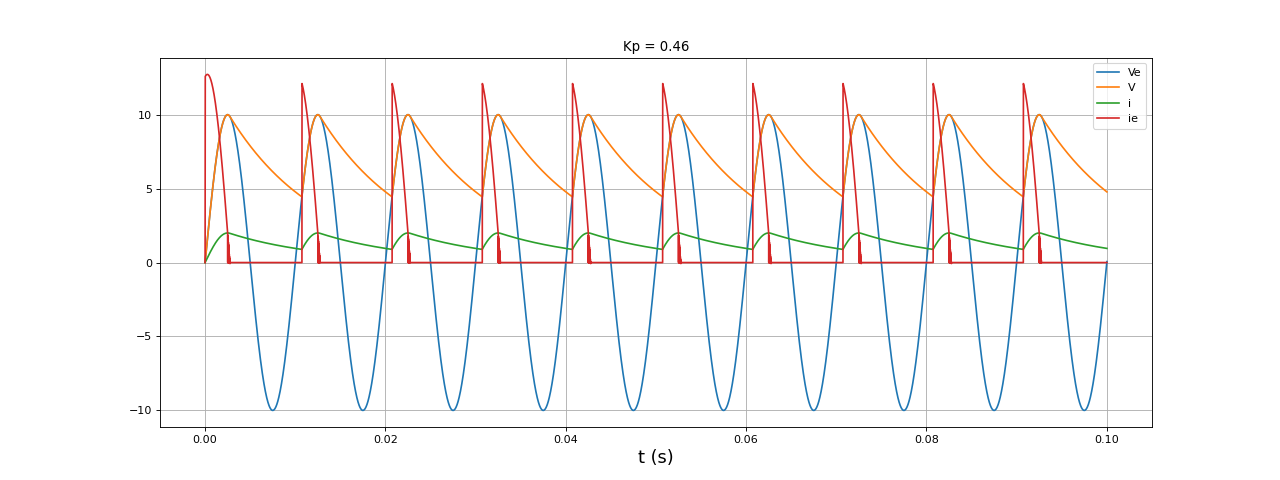fig11.pdf

On observe bien sur le courant i₁, comme prévu, une alternance des deux états juste après le maximum de V_e :

figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i,label="i")
plot(t,ie,label="ie")
xlabel("t (s)",fontsize=16)
grid()
xlim(0.09,0.1)
legend(loc="upper right")
title("Kp = %0.2f"%Kp)
                    

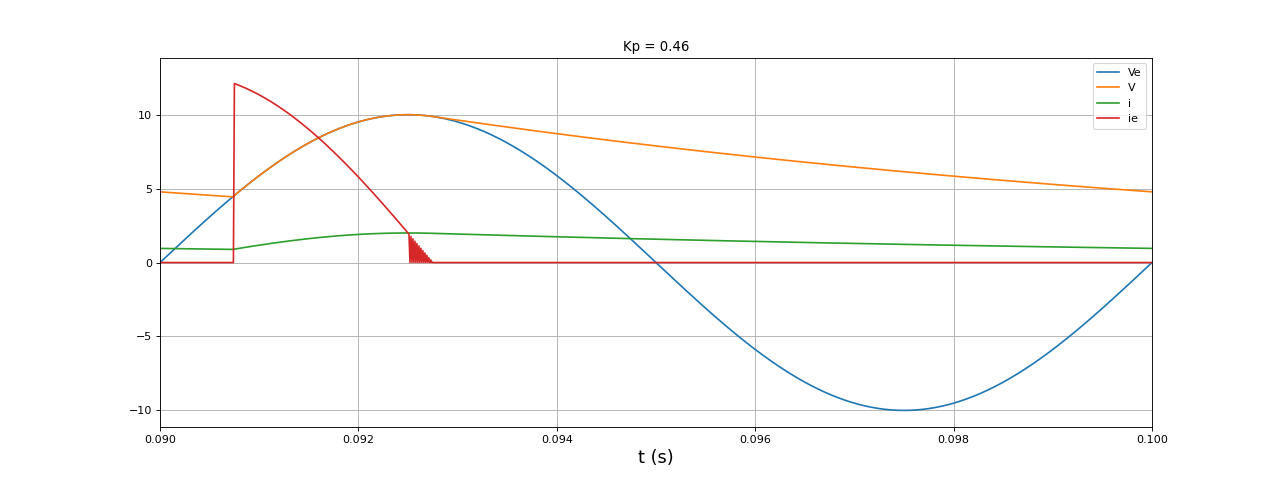fig12.pdf

Voici une simulation avec une valeur de capacité plus grande :

f=100
E=10
C=10e-3
R = 5
t,i,ie,Ve,V = simulation4(E,f,C,R,0.1,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i,label="i")
plot(t,ie,label="ie")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

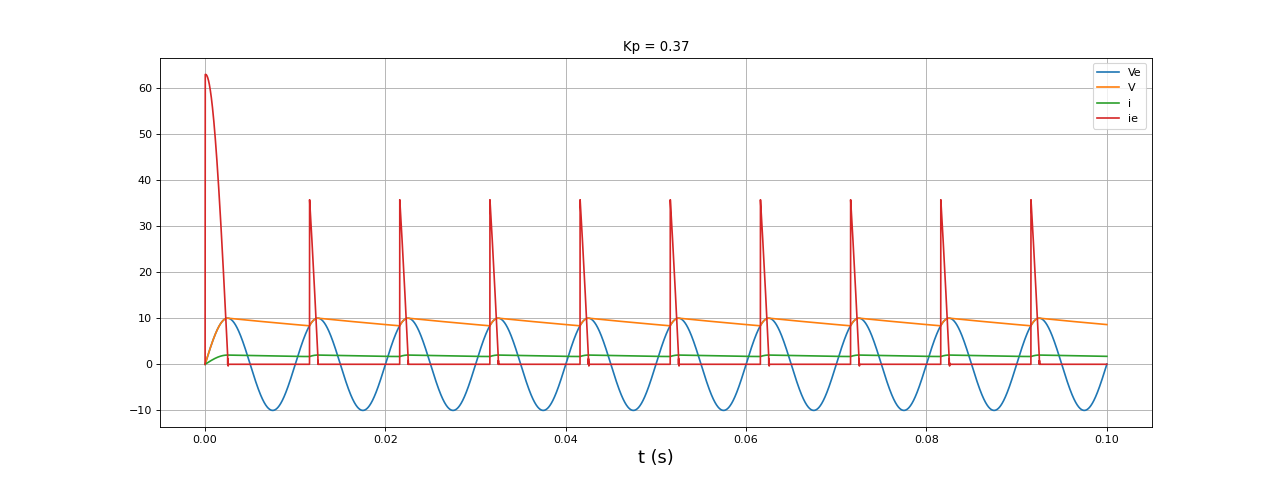fig13.pdf

Le principal inconvénient de ce circuit apparaît sur ces courbes : la source doit fournir un courant très fort lorsque la diode est passante.

Voici une simulation de ce circuit avec LTspice :

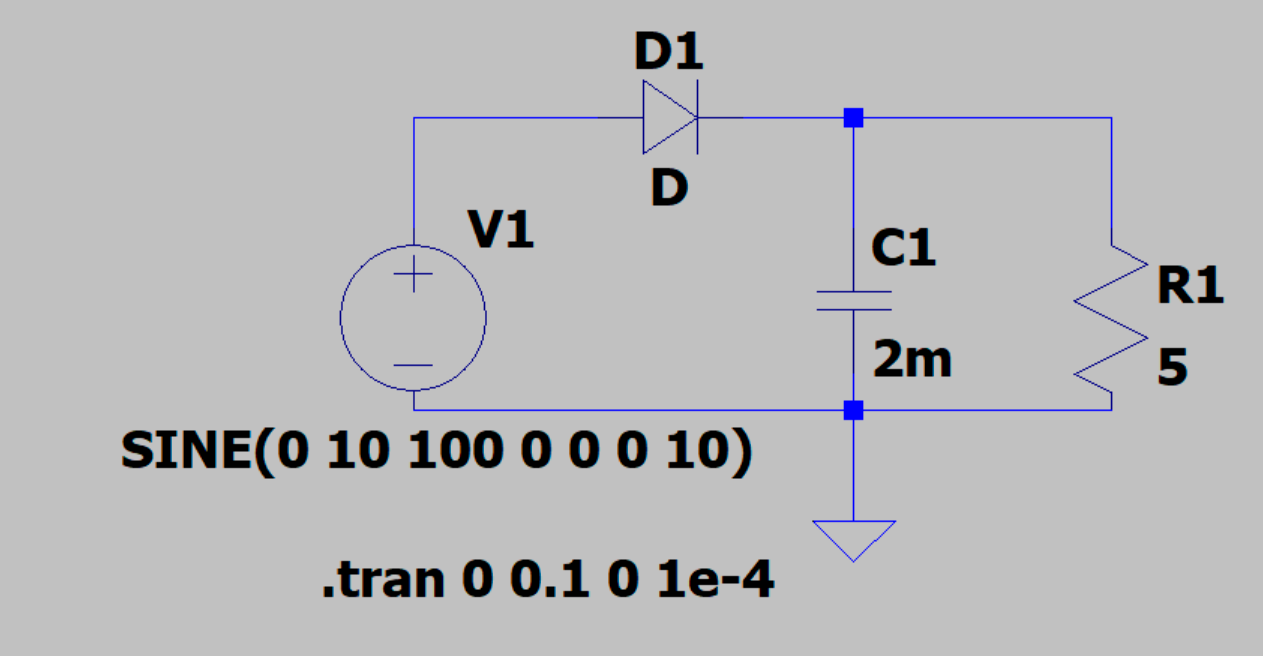
[t,Ve,V,i,ie] = np.loadtxt("demiOnde-RC-1.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i,label="i")
plot(t,-ie,label="ie")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
                    

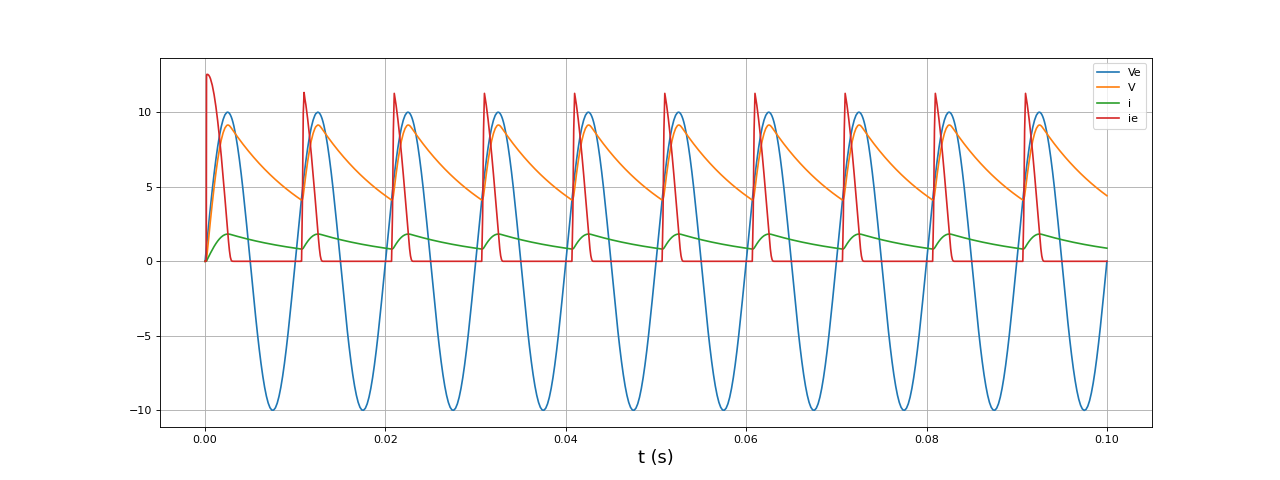fig14.pdf

Cette simulation montre l'effet du seuil de tension de la diode. On voit aussi que les bascules de la diode après le passage de V_e par son maximum ne se produisent pas et qu'ils sont bien dûs au modèle de la diode idéale.

3.a. Filtrage inductif

Le circuit 2 présenté plus haut (avec deux diodes) peut être complété afin de faire passer le courant aussi pour les alternances négatives de la tension d'entrée. Le circuit obtenu comporte quatre diodes formant un pont de diodes :

Figure pleine page

Le prix à payer pour obtenir le redressement double alternance et l'impossibilité d'avoir une masse commune entre la source et la charge.

Comme précédemment, on pose $V_e\left(t\right)=Esin\left(\omega t\right)$ et on suppose qu'à l'instant initial toutes les grandeurs sont nulles. Au début (état 1), seules les diodes D₁ et D₄ sont passantes. On a donc V=V_e et l'équation différentielle suivante :

$$L\frac{di}{dt}+Ri=V_e\left(t\right)\text{(12)}$$

La diode D₂ devient passante lorsque V_e s'annule pour devenir négative, ce qui a pour effet d'annuler la tension sur la cathode de D₁ donc de rendre celle-ci bloquante (puisque la tension sur son anode est négative). Simultanément, D₃ devient passante puisque la tension à son anode est nulle et la tension à sa cathode devient négative. La tension à l'anode de D₄ devient donc négative alors que sa cathode est à la masse (de la source) donc D₄ devient bloquante. On a donc un état 2 où seules les diodes D₂ et D₃ sont passante. Dans l'état 2, on a V=-V_e, i_e=-i et :

$$L\frac{di}{dt}+Ri=-V_e\left(t\right)\text{(13)}$$

Le retour à l'état 1 se fait lorsque la tension V_e s'annule pour devenir positive.

La simulation est similaire à celle donnée plus haut pour le redressement mono-alternance avec la diode de roue libre : l'état est simplement déterminé par le signe de V_e.

def simulation5(E,f,L,R,tmax,dt):
    w = 2*np.pi*f
    etat=1
    t = 0
    i = 0
    data = [[0,0,0,0,0]] #t,i,ie,Ve,V
    while t<tmax:
        t += dt
        Ve = E*np.sin(w*t)
        if etat==1:
            i += (Ve/L-R/L*i)*dt
            data.append([t,i,i,Ve,Ve])
            if Ve <=0: etat+=1
        elif etat==2:
            i += (-Ve/L-R/L*i)*dt
            data.append([t,i,-i,Ve,-Ve])
            if Ve>=0: etat=1
    data = np.array(data)
    return data[:,0],data[:,1],data[:,2],data[:,3],data[:,4]
                    

Voici une simulation avec L faible :

f=100
E=10
L=10e-3
R = 5
t,i,ie,Ve,V = simulation5(E,f,L,R,0.1,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

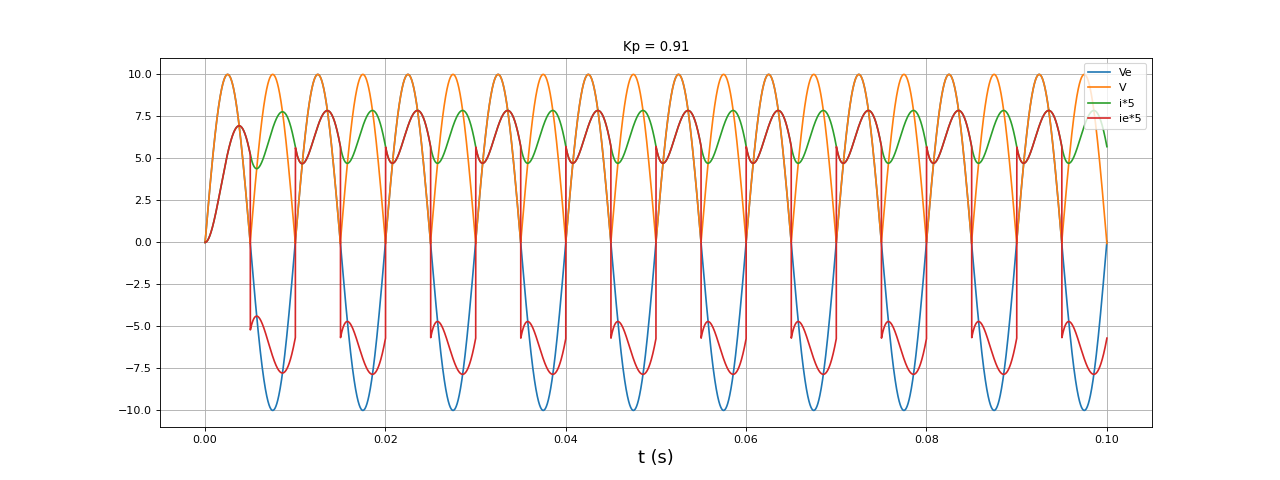fig15.pdf

puis avec une valeur de L dix fois plus grande :

f=100 
E=10
L=100e-3
R = 5
t,i,ie,Ve,V = simulation5(E,f,L,R,0.1,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

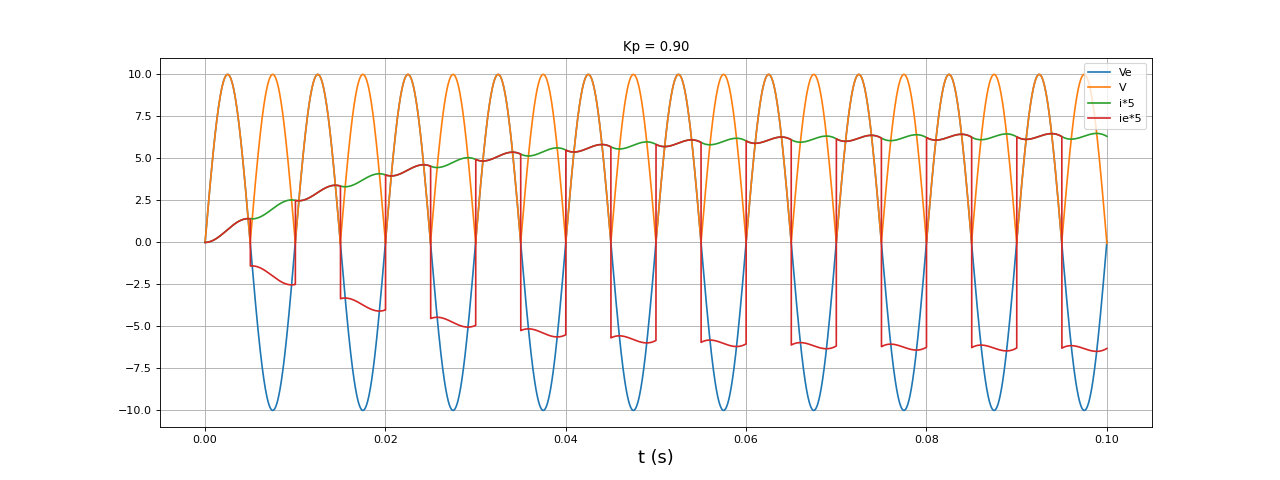fig16.pdf

Lorsque $\frac{Lf}{R}\gg 1$, le courant i dans la charge est quasi constant. Ce courant dépend de l'amplitude de la tension d'entrée et de R.

Voici la tension V moyenne en fonction du courant i moyen (on fait varier la résistance de charge):

Vmoy = []
Imoy = []
for R in [1,2,5,10,20,40,80]:
    t,i,ie,Ve,V = simulation5(E,f,L,R,0.1,1e-5)
    N = len(V)
    Vmoy.append(V[N//2:N].mean())
    Imoy.append(i[N//2:N].mean())
figure()
plot(Imoy,Vmoy,"o")
grid()
xlim(0,3)
ylim(0,7)
xlabel("I moy (A)",fontsize=16)
ylabel("V moy (V)",fontsize=16)
                     

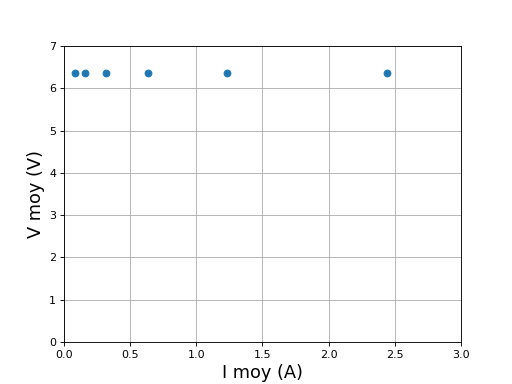fig17.pdf

La valeur moyenne de la tension V ne dépend pas du courant moyen dans la charge, ce qui est logique puisque V est simplement a valeur absolue de V_e.

Voici une simulation du même circuit avec LTspice :

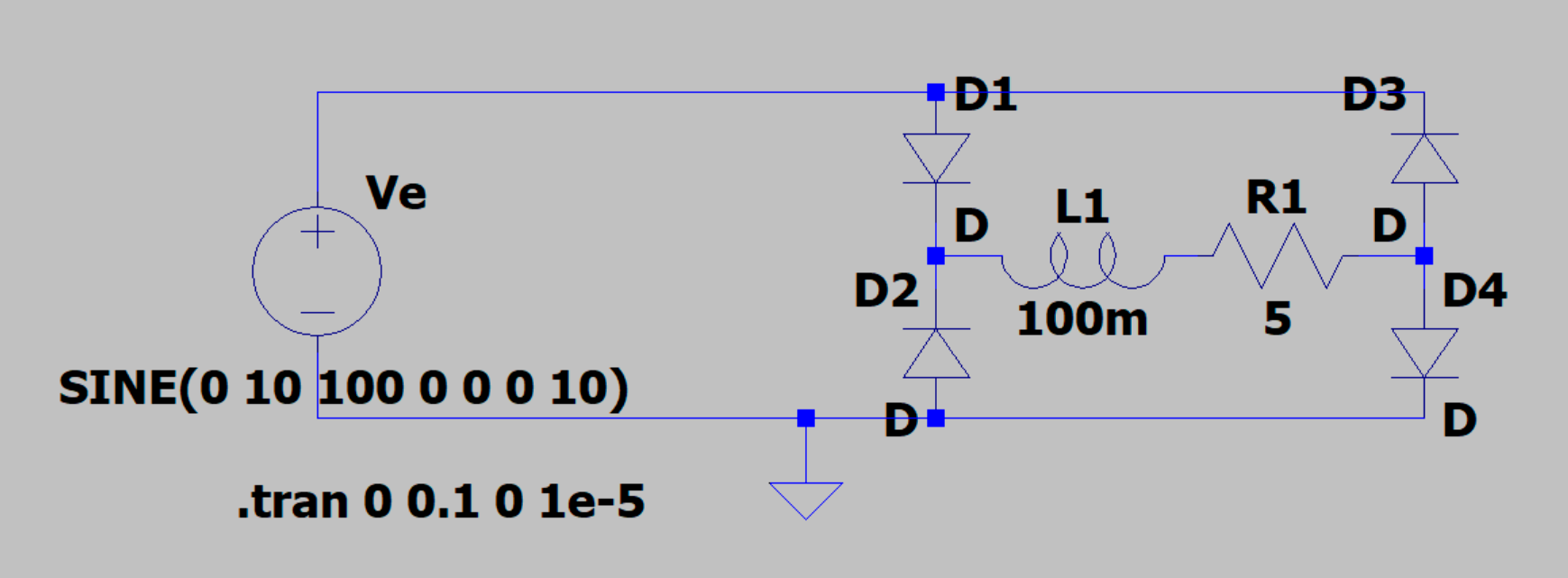
[t,Ve,Vp,Vm,i,ie] = np.loadtxt("pleineOnde-LR-1.txt",unpack=True,skiprows=1)
V = Vp-Vm
figure(figsize=(16,6))
plot(t,Ve,label="Ve") 
plot(t,V,label="V")
plot(t,-i*5,label="i*5")
plot(t,-ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
                    

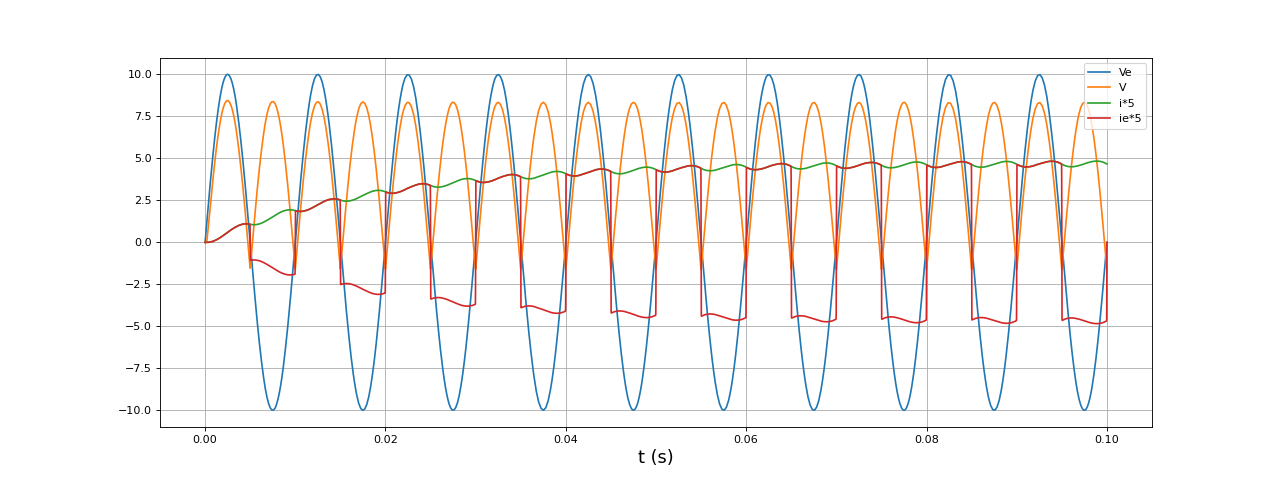fig18.pdf

Cette simulation montre l'effet du seuil de tension des diodes : la tension V passe (très brièvement) par des valeurs négatives et le courant dans la charge est moins grand.

Dans le circuit suivant, une inductance de commutation est ajoutée :

Figure pleine page

Dans l'état 1, seules les diodes D₁ et D₄ sont passantes. On a donc i_e=i et

$$\begin{array}{ccc}\hfill & V_e=(L_e+L)\frac{di}{dt}+Ri\hfill & \hfill \text{(14)}\\ \hfill & V=L\frac{di}{dt}+Ri\hfill & \hfill \text{(15)}\end{array}$$

donc :

$$V=\frac{L}{L_e+L}{V}_e+\frac{R{L}_e}{L_e+L}i\text{(16)}$$

Lorsque V s'annule pour devenir négative, D₂ devient passante mais D₁ reste passante car le courant dans L_e est continu (l'intensité est positive). La cathode de D₃ est à une différence de potentiel V par rapport à son anode donc cette diode devient passante et, comme i est positif et continu, la diode D₄ reste passante. On a donc un état 2 où toutes les diodes sont passantes. Dans l'état 2, on a V=0 et

$$\begin{array}{ccc}\hfill & \frac{d{i}_e}{dt}=\frac{V_e\left(t\right)}{L_e}\hfill & \hfill \text{(17)}\\ \hfill & \frac{di}{dt}=-\frac{R}{L}i\hfill & \hfill \text{(18)}\end{array}$$

Notons i₁,i₂,i₃,i₄ les courants dans les diodes, dans le sens positif indiqué par les flèches rouges sur le schéma. La loi des nœuds conduit aux équations suivantes :

$$\begin{array}{cc}\hfill & i_1+i_2=i\hfill \\ \hfill & i_3+i_4=i\hfill \\ \hfill & i_1-i_3=i_e\hfill \\ \hfill & -i_2+i_4=i_e\hfill \end{array}$$

mais ce système n'admet pas de solution unique (son déterminant est nul). Il faut donc une condition supplémentaire pour déterminer les courants dans les diodes. En réalité, la tension aux bornes d'une diode n'est pas nulle et le courant est déterminée par la valeur de cette tension. Comme le montre la simulation Spice présentée plus loin, on a en fait i₁=i₄ et i₂=i₃. Dans l'état 2, on a donc :

$$\begin{array}{cc}\hfill & i_1=i_4=\frac{i+i_e}{2}\hfill \\ \hfill & i_2=i_3=\frac{i-i_e}{2}\hfill \end{array}$$

L'état 2 cesse lorsque i₁ s'annule pour devenir négative, ce qui provoque le bloquage de la diode D₁ et celui de D₄. La diode D₃ reste passante pour maintenir la continuité de i. On a donc un état 3 où seules les diodes D₂ et D₃ sont passantes. Dans l'état 3, on a i_e=-i et :

$$\begin{array}{ccc}\hfill & -V_e=(L_e+L)\frac{di}{dt}+Ri\hfill & \hfill \text{(19)}\\ \hfill & V=L\frac{di}{dt}+Ri\hfill & \hfill \text{(20)}\end{array}$$

donc :

$$V=-\frac{L}{L_e+L}{V}_e+\frac{R{L}_e}{L_e+L}i\text{(21)}$$

L'état 3 cesse lorsque V s'annule pour devenir négatif et on passe alors à l'état 4 où toutes les diodes sont passantes. Les équations pour l'état 4 sont données plus ci-dessus. On passe de l'état 4 à l'état 1 lorsque i₂ s'annule pour devenir négatif.

def simulation6(E,f,Le,L,R,tmax,dt): 
    w = 2*np.pi*f
    etat=1
    t = 0
    i = 0
    ie = 0
    data = [[0,0,0,0,0]] #t,i,ie,Ve,V
    while t<tmax:
        t += dt
        Ve = E*np.sin(w*t)
        if etat==1:
            i += (Ve/(L+Le)-R/(L+Le)*i)*dt
            ie = i
            V = L/(L+Le)*Ve+R*(1-L/(L+Le))*i
            data.append([t,i,ie,Ve,V])
            if V <=0: etat+=1
        elif etat==2:
            i += -R/L*i*dt
            ie += Ve/Le*dt
            V = 0
            data.append([t,i,ie,Ve,V])
            if i+ie<=0: etat+=1
        elif etat==3:
            i += (-Ve/(L+Le)-R/(L+Le)*i)*dt
            ie = -i
            V = -L/(L+Le)*Ve+R*(1-L/(L+Le))*i
            data.append([t,i,ie,Ve,V])
            if V<=0: etat+=1
        elif etat==4:
            i += -R/L*i*dt
            ie += Ve/Le*dt
            V = 0
            data.append([t,i,ie,Ve,V])
            if i-ie<=0: etat=1
            
    data = np.array(data)
    return data[:,0],data[:,1],data[:,2],data[:,3],data[:,4]
                    

Voici une simulation avec L faible :

f=100
E=10
Le = 10e-3
L=10e-3
R = 5
t,i,ie,Ve,V = simulation6(E,f,Le,L,R,0.05,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

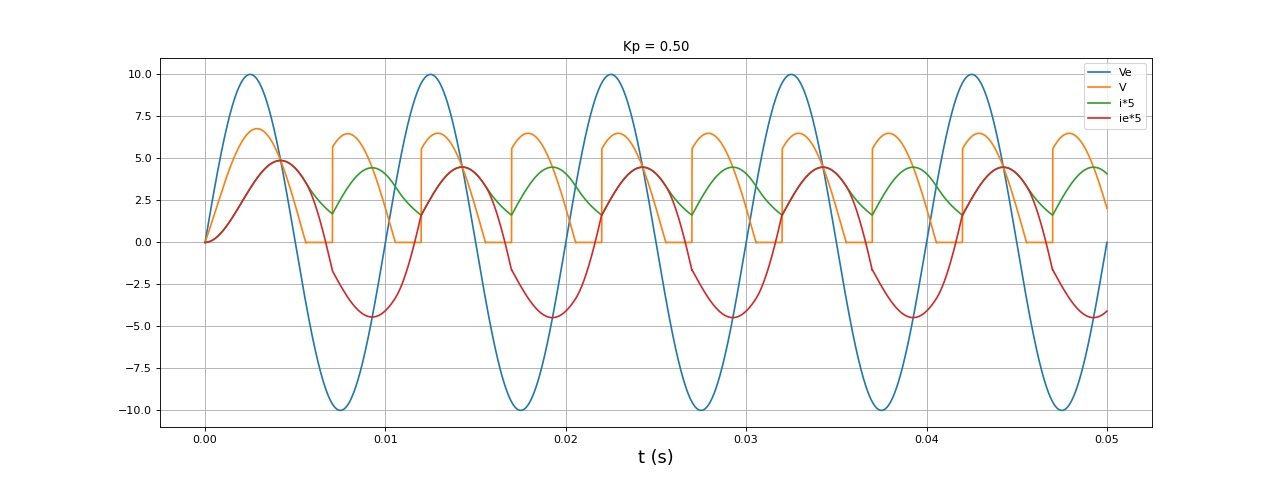fig19.pdf

puis L dix fois plus grand :

f=100
E=10
Le = 10e-3
L=100e-3
R = 5
t,i,ie,Ve,V = simulation6(E,f,Le,L,R,0.1,1e-5)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

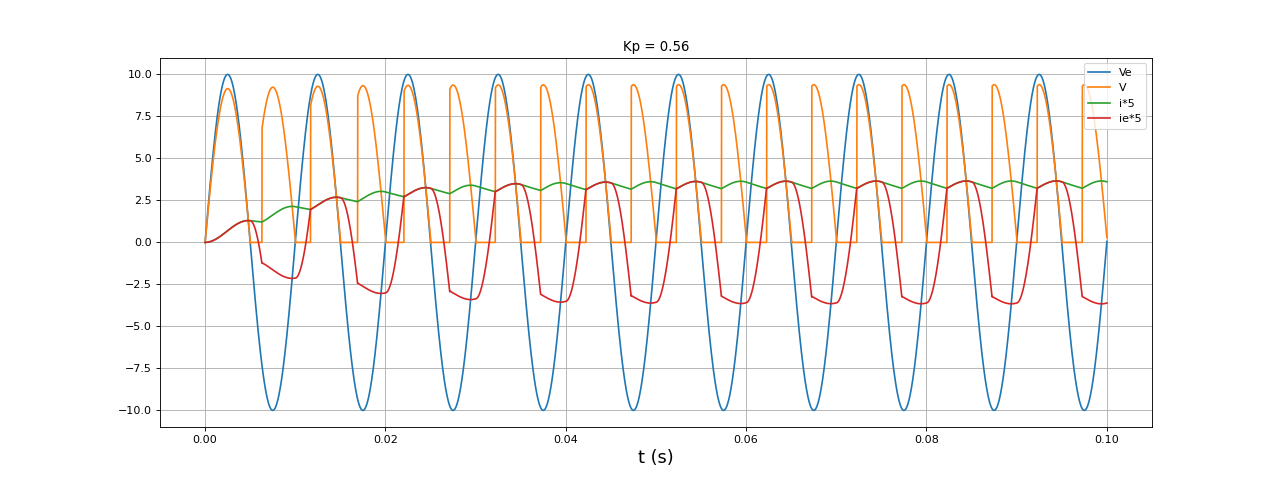fig20.pdf

Voici la tension V moyenne en fonction du courant i moyen :

Vmoy = []
Imoy = []
for R in [1,2,5,10,20,40,80]:
    t,i,ie,Ve,V = simulation6(E,f,Le,L,R,0.1,1e-5)
    N = len(V)
    Vmoy.append(V[N//2:N].mean())
    Imoy.append(i[N//2:N].mean())
figure()
plot(Imoy,Vmoy,"o")
grid()
xlim(0,3)
ylim(0,7)
xlabel("I moy (A)",fontsize=16)
ylabel("V moy (V)",fontsize=16)
                     

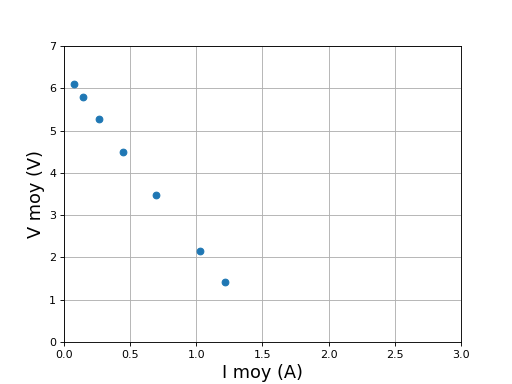fig21.pdf

Contrairement au circuit sans l'inductance de commutation L_e, la moyenne de V dépend de la moyenne de i (elle décroît linéairement avec le courant).

Voici une simulation du même circuit avec LTspice :

[t,Ve,Vp,Vm,i,ie] = np.loadtxt("pleineOnde-LLR-1.txt",unpack=True,skiprows=1)
V = Vp-Vm
figure(figsize=(16,6))
plot(t,Ve,label="Ve") 
plot(t,V,label="V")
plot(t,-i*5,label="i*5")
plot(t,-ie*5,label="ie*5")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
                    

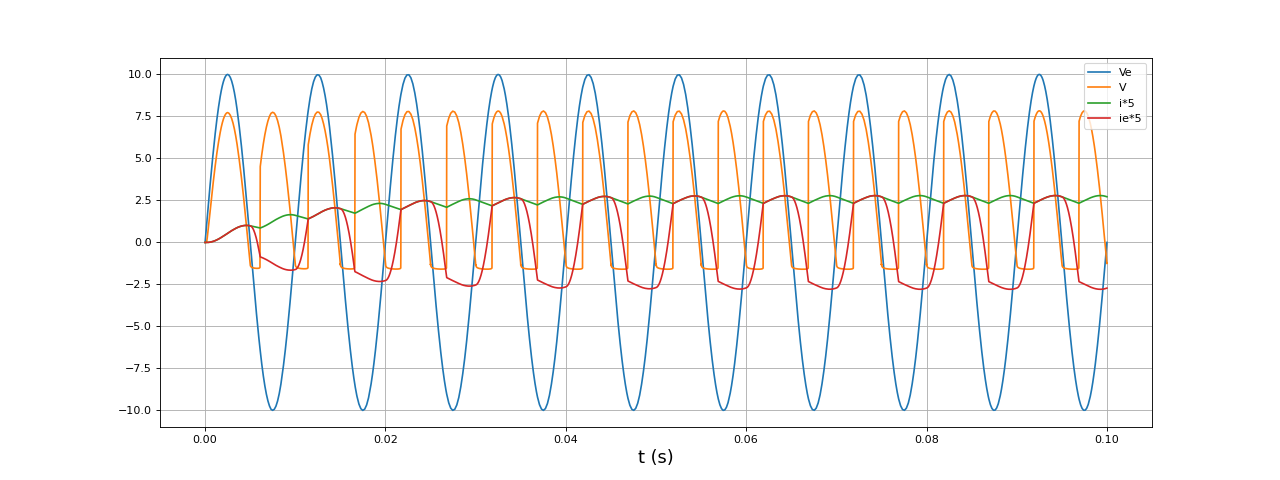fig22.pdf

Cette simulation montre l'effet des seuils de tension des diodes : la tension V est négative dans les états 2 et 4 et le courant dans la charge est plus bas.

Voici les courants dans les diodes :

[t,i1,i2,i3,i4] = np.loadtxt("pleineOnde-LLR-diodes.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(t,i1,label="i1")
plot(t,i2,label="i2")
plot(t,i3,label="i3")
plot(t,i4,label="i4")
ylabel("i (A)",fontsize=16)
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
                    

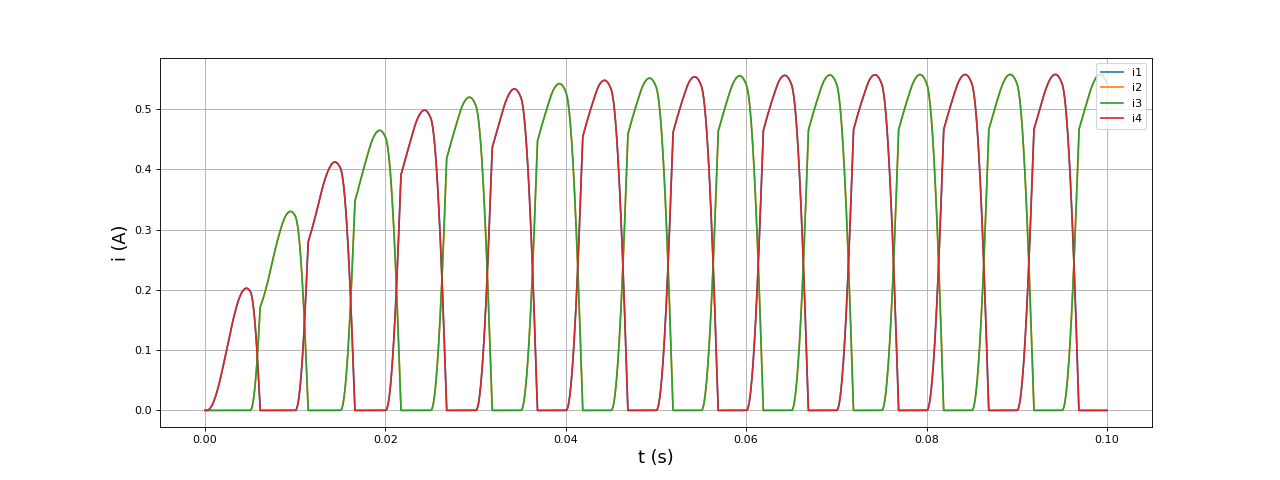fig23.pdf

On a bien i₁=i₄ et i₂=i₃, ce qui est évident dans les états 1 et 3 mais ne l'est pas dans les états 2 et 4.

4.a. Algorithme

Dans les simulations précédentes, reposant sur le modèle de diode idéale, les états des diodes sont déterminés au préalable ainsi que les conditions qui déclenchent le passage d'un état au suivant. Le dernier exemple montre que cette tâche n'est pas toujours aisée.

Les simulations effectuées par Spice reposent sur la mise en équation complète du système. Il faut pour cela disposer d'une caractéristique de la diode permettant d'obtenir le courant sans ambiguité à partir de la tension (ou l'inverse). Autrement dit, la fonction I=f(U) doit être bijective. Voici une version simplifiée du modèle de diode utilisé par Spice [2] :

$$\begin{array}{ccc}\hfill & f\left(U\right)=I_s(e^{\frac{U}{U_0}}-1)+U{G}_{min}siU>-5U_0\hfill & \hfill \text{(22)}\\ \hfill & f\left(U\right)=-I_s+U{G}_{min}siU\le -5U_0\hfill & \hfill \text{(23)}\end{array}$$

avec les valeurs suivantes : $I_s=10^{-14}A$, $U_0=2,6\cdot 10^{-2}V$ et $G_{min}=10^{-4}{\Omega }^{-1}$. Cette fonction admet une fonction inverse f^-1 mais il semble qu'il n'existe pas de forme analytique de cette fonction. Déterminer U si I est donné nécessite donc la résolution d'une équation algébrique non linéaire.

def Idiode(U,Is=1e-14,U0=2.6e-2,Gmin=1e-3):
    if U > -5*U0:
        return Is*(np.exp(U/U0)-1)+U*Gmin 
    else:
        return -Is+U*Gmin
        
U = np.linspace(-1,1,1000)
I = np.zeros(len(U))
for k in range(len(U)):
    I[k] = Idiode(U[k])
figure()
plot(U,I)
grid()
ylabel("I (A)",fontsize=16)
xlabel("U (V)",fontsize=16)
                    

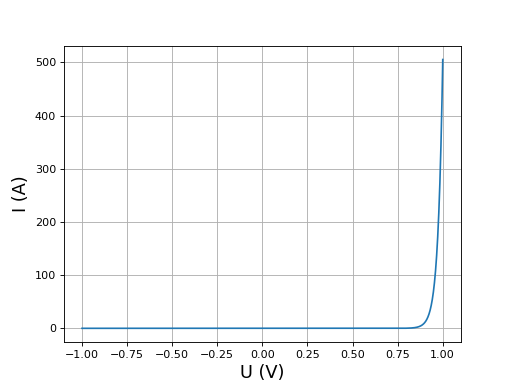fig24.pdf

La conductance G_min a un effet très faible sur la caractéristique mais permet d'assurer la bijectivité. Remarquons que la fonction présente une petite discontinuité en U=-U₀.

Considérons comme premier exemple le circuit de redressement suivant :

Figure pleine page

Les trois inconnues étant V,i,i_e, les trois équations sont :

$$\begin{array}{ccc}\hfill & V=L\frac{di}{dt}+Ri\hfill & \hfill \text{(24)}\\ \hfill & i_e=f(V_e-V)\hfill & \hfill \text{(25)}\\ \hfill & i-i_e=f(-V)\hfill & \hfill \text{(26)}\end{array}$$

Ces équations sont bien évidemment non linéaires en raison de la non linéarité de la fonction f.

L'équation différentielle peut être intégrée par la méthode d'Euler. La valeur de i étant connue, les valeurs de V et i_e sont obtenues par résolution du système d'équations suivant :

$$\begin{array}{ccc}\hfill & i_e-f(V_e-V)=0\hfill & \hfill \text{(27)}\\ \hfill & f(-V)+i_e-i=0\hfill & \hfill \text{(28)}\end{array}$$

Les trois inconnues varient continûment (contrairement au cas du modèle à diode idéale) donc, à chaque itération et si le pas de temps est assez petit, on connaît une valeur de (V,i_e) très proche de la solution du système ci-dessus. La méthode de Newton-Raphson [3] permet d'obtenir rapidement cette solution.

Notons x_i les inconnues (ici x₀=V et x₁=i_e). Le système s'écrit :

$$\begin{array}{cc}\hfill & F_0(x_0,x_1)=0\hfill \\ \hfill & F_1(x_0,x_1)=0\hfill \end{array}$$

Le développement de Taylor à l'ordre 1 s'écrit :

$$F_i(x_0+\delta x_0,x_1+\delta x_1)=F_i(x_0,x_1)+\sum _{j=0}^1\frac{\partial F_i}{\partial x_j}\delta x_i\text{(29)}$$

La matrice jacobienne est définie par :

$$J_{ij}=\frac{\partial F_i}{\partial x_j}\text{(30)}$$

On doit avoir :

$$0=F_i(x_0,x_1)+\sum _{j=0}^1\frac{\partial F_i}{\partial x_j}\delta x_i\text{(31)}$$

donc $\delta X={(\delta x_0,\delta x_1)}^T$ est obtenu par résolution du système linéaire suivant :

$$J\delta X=-F\text{(32)}$$

où $F={(F_0(x_0,x_1),F_1(x_0,x_1))}^T$.

Afin de contrôler la convergence vers la solution, on calcule le nombre suivant [3] :

$$res=\sum _{i=0}^1{F}_i^2(x_0,x_1)\text{(33)}$$

Si res est supérieur à une tolérance $\epsilon$, on refait une itération avec un nouveau déplacement $\delta X$.

Pour l'exemple traité, on a :

$$\begin{array}{cc}\hfill & F_0(x_0,x_1)=x_1-f(V_e-x_0)\hfill \\ \hfill & F_1(x_0,x_1)=f(-x_0)+x_1-i=0\hfill \end{array}$$

La fonction f est définie par :

$$\begin{array}{ccc}\hfill & f\left(U\right)=I_s(e^{\frac{U}{U_0}}-1)+U{G}_{min}siU>-5U_0\hfill & \hfill \text{(34)}\\ \hfill & f\left(U\right)=-I_s+U{G}_{min}siU\le -5U_0\hfill & \hfill \text{(35)}\end{array}$$

et sa dérivée :

$$\begin{array}{ccc}\hfill & f\text{'}\left(U\right)=\frac{I_s}{U_0}{e}^{\frac{U}{U_0}}+G_{min}siU>-5U_0\hfill & \hfill \text{(36)}\\ \hfill & f\text{'}\left(U\right)=G_{min}siU\le -5U_0\hfill & \hfill \text{(37)}\end{array}$$

La matrice jacobienne est :

$$\begin{array}{cc}\hfill & \frac{\partial F_0}{\partial x_0}=f\text{'}(V_e-x_0)\hfill \\ \hfill & \frac{\partial F_0}{\partial x_1}=1\hfill \\ \hfill & \frac{\partial F_1}{\partial x_0}=-f\text{'}(-x_0)\hfill \\ \hfill & \frac{\partial F_1}{\partial x_1}=1\hfill \end{array}$$

Voici la fonction qui calcule la dérivée de f :

def deriv_Idiode(U,Is=1e-14,U0=2.6e-2,Gmin=1e-3):
    if U > -5*U0:
        return Is/U0*np.exp(U/U0)+Gmin
    else:
        return Gmin
        
        

La valeur de G_min doit être assez petite pour ne pas modifier notablement la caractéristique de la diode mais elle doit être assez grande pour permettre la convergence de la méthode de Newton-Raphson.

Voici la fonction qui effectue une itération de Newton-Raphson :

from numpy.linalg import solve

def iteration_newton(V,ie,i,Ve,Gmin):
    J = np.array([[deriv_Idiode(Ve-V,Gmin=Gmin),1],[-deriv_Idiode(-V,Gmin=Gmin),1]])
    B = -np.array([ie-Idiode(Ve-V,Gmin=Gmin),Idiode(-V,Gmin=Gmin)+ie-i])
    deltaX = solve(J,B)
    V += deltaX[0]
    ie += deltaX[1]
    F = np.array([ie-Idiode(Ve-V,Gmin=Gmin),Idiode(-V,Gmin=Gmin)+ie-i])
    res = F[0]*F[0]+F[1]*F[1]
    return [V,ie],res
            

Voici la fonction qui donne la solution approchée par la méthode de Newton-Raphson. Un nombre d'itérations maximal est imposé, ce qui est utile en cas de non convergence de la méthode de Newton-Raphson. La fonction renvoie les valeurs de V,i_e, le nombre d'itérations effectuées et la dernière valeur de res.

def newton(V,ie,i,Ve,eps=1e-4,maxiter=30,Gmin=1e-3):
    next,res = iteration_newton(V,ie,i,Ve,Gmin)
    niter = 1
    while res > eps and niter<maxiter:
        next,res = iteration_newton(next[0],next[1],i,Ve,Gmin)
        niter+=1
    return next[0],next[1],niter,res
             

Voici la fonction qui effectue la simulation du circuit :

def simulation2complete(E,f,L,R,tmax,dt,Gmin=1e-3):
    w = 2*np.pi*f
    t = 0
    i = 0
    ie = 0
    V = 0
    Ve = 0
    data = [[t,i,ie,Ve,V,0,0]]
    while t<tmax:
        Ve = E*np.sin(w*t)
        V,ie,niter,res = newton(V,ie,i,Ve,Gmin=Gmin)
        i= i+(V-R*i)/L*dt
        t +=dt
        data.append([t,i,ie,Ve,V,niter,res])
    data = np.array(data)
    return data[:,0],data[:,1],data[:,2],data[:,3],data[:,4],data[:,5],data[:,6]
             

Voici une simulation, pour les mêmes paramètres qu'une simulation présentées plus haut avec les diodes idéales.

f=100
E=10
L=100e-3
R = 5
t,i,ie,Ve,V,niter,res = simulation2complete(E,f,L,R,0.1,1e-5,Gmin=1e-4)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
plot(t,niter,label="niter")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

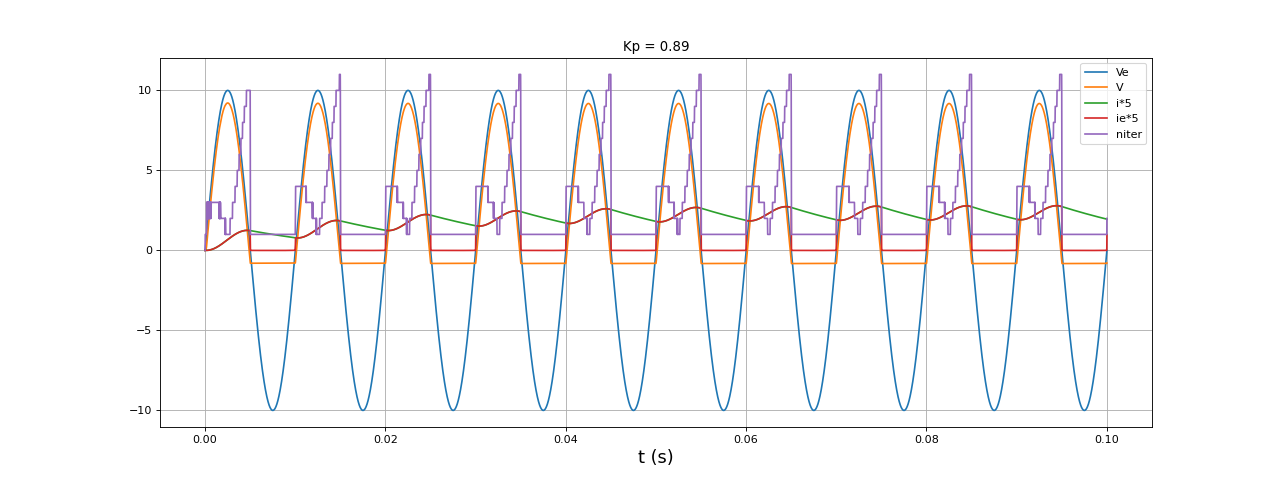fig25.pdf

Le tracé du nombre d'itération dans la recherche de racines permet de contrôler le bon déroulement de l'algorithme de Newton-Raphson. Le nombre d'itérations augmente à certains moments du cycle mais sans jamais atteindre la limite (30), ce qui montre que tout fonctionne correctement. Voici le tracé de res en fonction du temps :

figure(figsize=(16,6))
plot(t,res)
grid()
xlabel("t (s)",fontsize=16)
ylabel("res",fontsize=16)
                    

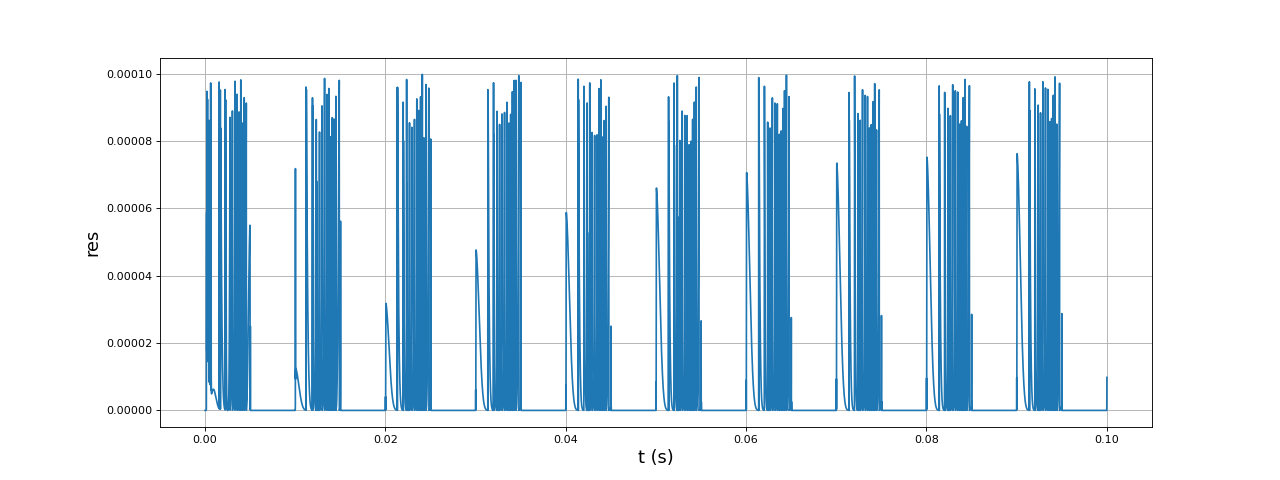fig26.pdf

Les valeurs les plus grandes de res (toujours inférieures à la tolérance $\epsilon$) surviennent pendant la phase de conduction de la diode D₁ et c'est aussi pendant cette phase que le nombre d'itération augmente (surtout au début et à la fin de cette phase).

Si on abaisse la valeur de G_min jusqu'à 10^-6, la simulation fonctionne et donne les mêmes courbes. En dessous de cette valeur, la convergence de la méthode de Newton-Raphson ne se fait plus. Inversement, une valeur trop grande modidie le résultat car la caractéristique de la diode est trop modifiée :

f=100
E=10
L=100e-3
R = 5
t,i,ie,Ve,V,niter,res = simulation2complete(E,f,L,R,0.1,1e-5,Gmin=1e-2)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
plot(t,niter,label="niter")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

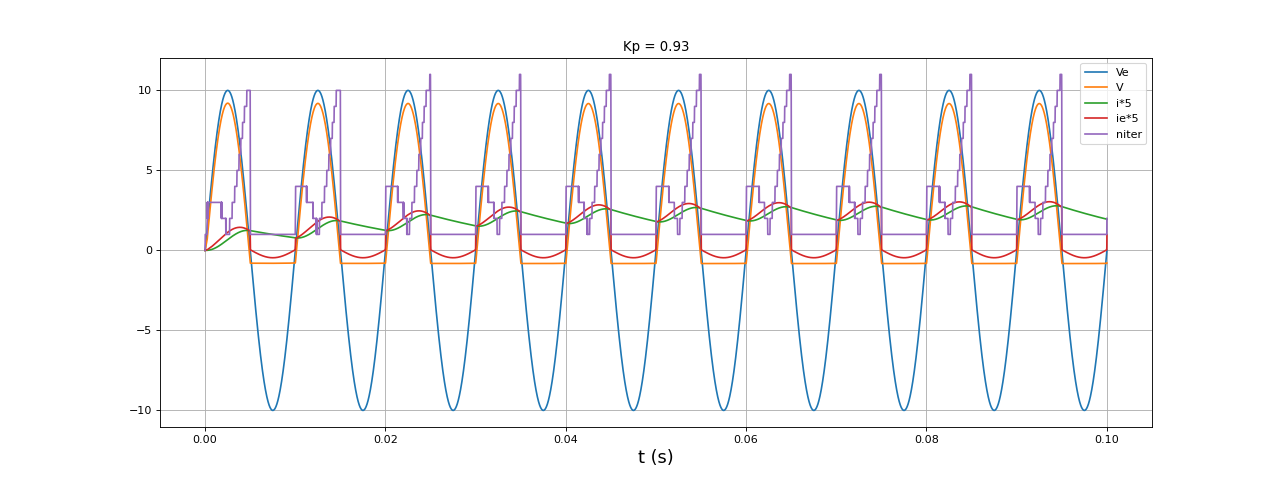fig27.pdf

4.b. Exemple : redressement mono-alternance avec inductance de commutation

On reprend le circuit précédent en lui ajoutant une inductance de commutation :

Figure pleine page

Les inconnues sont V,i,i_e,U₁, soit une de plus que dans l'exemple précédent. Les équations sont :

$$\begin{array}{ccc}\hfill & V_e=L_e\frac{d{i}_e}{dt}+U_1+V\hfill & \hfill \text{(38)}\\ \hfill & V=L\frac{di}{dt}+Ri\hfill & \hfill \text{(39)}\\ \hfill & f\left(U_1\right)-i_e=0\hfill & \hfill \text{(40)}\\ \hfill & f(-V)+i_e-i=0\hfill & \hfill \text{(41)}\end{array}$$

Si i et i_e sont connus, les deux dernières équations permettent de déterminer U₁ et V. Contrairement à l'exemple précédent, ces deux équations sont indépendantes (non couplées). Cela vient de l'introduction de la tension U₁ comme nouvelle variable, qui évite d'avoir une dérivée dans l'équation algébrique de la relation courant-tension de la diode D₁. On utilisera cependant l'algorithme général de Newton-Raphson pour un système d'équations. Si l'on pose x₀=U₁ et x₁=V on a :

$$\begin{array}{ccc}\hfill & F_0(x_0,x_1)=f\left(x_0\right)-i_e\hfill & \hfill \text{(42)}\\ \hfill & F_1(x_0,x_1)=f(-x_1)+i_e-i\hfill & \hfill \text{(43)}\end{array}$$

La matrice jacobienne est :

$$\begin{array}{cc}\hfill & \frac{\partial F_0}{\partial x_0}=f\text{'}\left(x_0\right)\hfill \\ \hfill & \frac{\partial F_0}{\partial x_1}=0\hfill \\ \hfill & \frac{\partial F_1}{\partial x_0}=0\hfill \\ \hfill & \frac{\partial F_1}{\partial x_1}=-f\text{'}(-x_1)\hfill \end{array}$$

C'est bien sûr une matrice diagonale puisque les deux équations sont indépendantes.

Le calcul de i et i_e par la méthode d'Euler se fait par les deux équations :

$$\begin{array}{ccc}\hfill & \frac{d{i}_e}{dt}=\frac{1}{L_e}(V_e-U_1-V)\hfill & \hfill \text{(44)}\\ \hfill & \frac{di}{dt}=\frac{1}{L}(V-Ri)\hfill & \hfill \text{(45)}\\ \hfill & \hfill \text{(46)}\end{array}$$

Ces deux équations sont non couplées mais la méthode d'Euler s'appliquerait sans difficultés à des équations couplées. Il faut remarquer que ces équations sont très différentes de celles du même circuit sans L_e (on ne pourra pas passer de celui-ci au précédent simplement en posant L_e=0).

Cet exemple nous permet d'introduire des fonctions permettant de résoudre un système de N équations algébriques pour N variables.

def iteration_newton_N(X,F,J,N,param):
    # X : liste de N nombres
    # F : liste de N fonction de la forme F(X,param)
    # J : liste de N listes de N fonctions de la forme F(X,param)
    # param : liste de paramètres (variables intervenant comme paramètres constants dans la résolution)
    matJ = np.zeros((N,N))
    matF = np.zeros(N)
    for i in range(N): # équation i
        for j in range(N): # variable j
            matJ[i,j] = J[i][j](X,param)
    B = np.zeros(N)
    for i in range(N):
        B[i] = -F[i](X,param)
    deltaX = solve(matJ,B)
    nextX = X+deltaX
    for i in range(N):
        matF[i] = F[i](nextX,param)
    res = np.sum(matF**2)
    return nextX,res
    
def newton_N(X,F,J,N,param,eps=1e-4,maxiter=30):
    niter = 0
    start = True
    while start or (res > eps and niter < maxiter):
        start = False
        nextX,res = iteration_newton_N(X,F,J,N,param)
        X = nextX
        niter += 1
    return nextX,niter,res
    
    

Voici la fonction qui effectue la simulation du circuit :

def simulation3complete(E,f,Le,L,R,tmax,dt,Gmin=1e-3):
    # param[0] : ie
    # param[1] : i
    # parama[2] : Gmin
    def F0(X,param): return Idiode(X[0],Gmin=param[2])-param[0]
    def F1(X,param): return Idiode(-X[1],Gmin=param[2])+param[0]-param[1]
    F = [F0,F1]
    def J00(X,param): return deriv_Idiode(X[0],Gmin=param[2])
    def J01(X,param): return 0
    def J10(X,param): return 0
    def J11(X,param): return -deriv_Idiode(-X[1],Gmin=param[2])
    J = [[J00,J01],[J10,J11]]
    N = 2
    w = 2*np.pi*f
    t = 0
    i = 0
    ie = 0
    V = 0
    U1 = 0
    Ve = 0
    data = [[t,i,ie,Ve,V,U1,0,0]]
    while t<tmax:
        Ve = E*np.sin(w*t)
        
        param = [ie,i,Gmin]
        X = [U1,V]
        nextX,niter,res = newton_N(X,F,J,N,param)
        U1,V = nextX[0],nextX[1]
        i= i+(V-R*i)/L*dt
        ie = ie+(Ve-U1-V)/Le*dt
        t +=dt
        data.append([t,i,ie,Ve,V,U1,niter,res])
    
    data = np.array(data)
    return data[:,0],data[:,1],data[:,2],data[:,3],data[:,4],data[:,5],data[:,6],data[:,7]

f=100
E=10
Le = 10e-3
L=100e-3
R = 5
t,i,ie,Ve,V,U1,niter,res = simulation3complete(E,f,Le,L,R,0.1,1e-5,Gmin=1e-3)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
plot(t,niter,label="niter")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

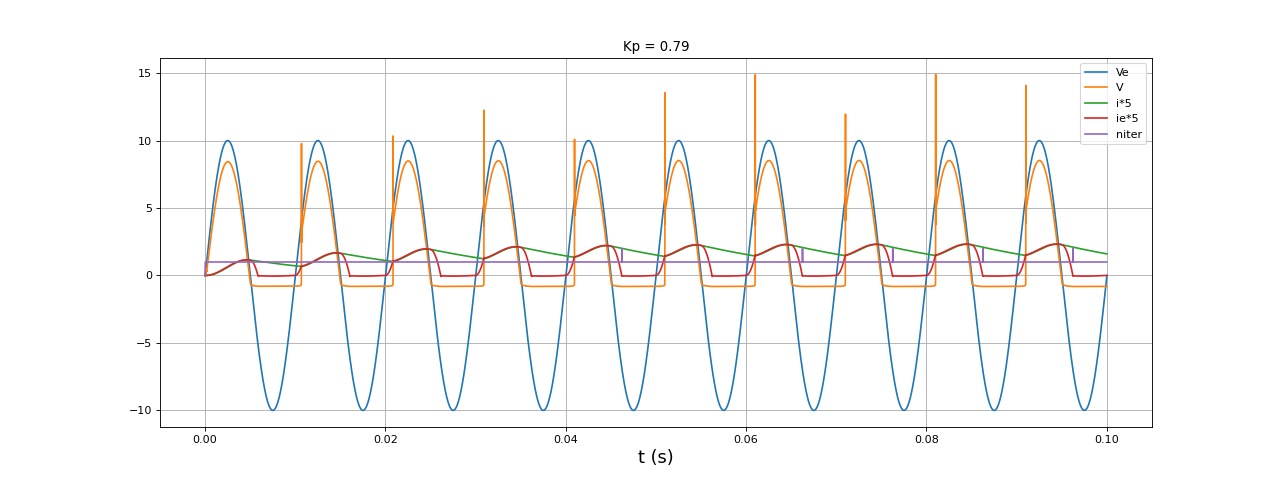fig28.pdf

Pour ce circuit, une valeur G_min de 10^-4 ne fonctionne pas. Le résultat n'est pas satisfaisant : on observe un pic de la tension V à la fin de l'état 2. Réduisons le pas de temps :

f=100
E=10
Le = 10e-3
L=100e-3
R = 5
t,i,ie,Ve,V,U1,niter,res = simulation3complete(E,f,Le,L,R,0.1,1e-6,Gmin=1e-3)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
plot(t,niter,label="niter")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

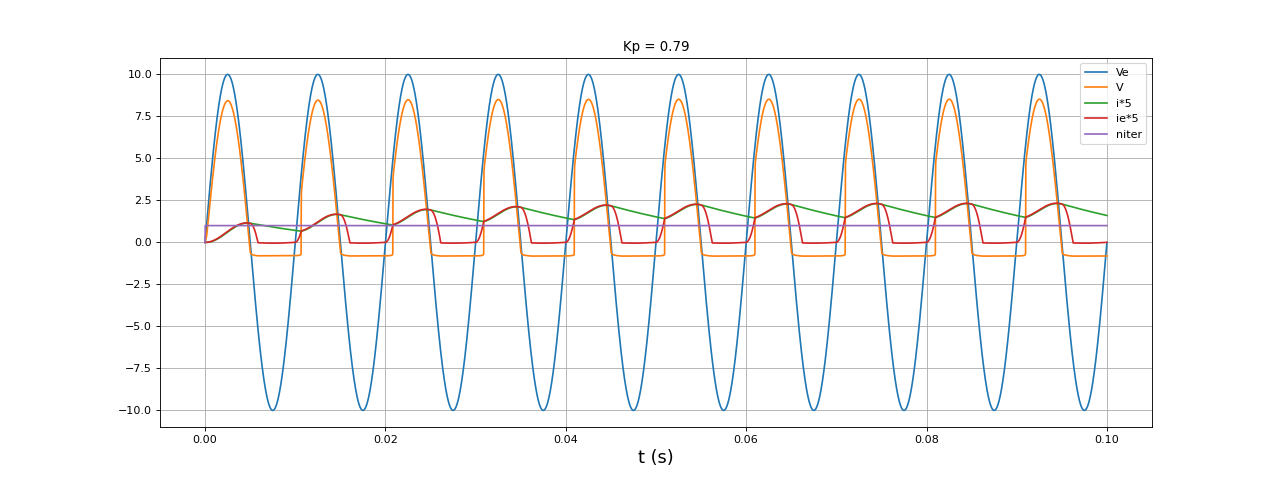fig29.pdf

Le problème est bien résolu par abaissement du pas de temps mais le calcul est beaucoup plus long. Une méthode de Runge-Kutta avec adaptation du pas est donc indispensable.

4.c. Exemple : redressement double-alternance avec inductance de commutation

Figure pleine page

Les 11 variables sont :

$$i_e,i,i_1,i_2,i_3,i_4,V,V_1,V_2,V_3,V_4\text{(47)}$$

Voici les 11 équations :

$$\begin{array}{cc}\hfill & V_e=L_e\frac{d{i}_e}{dt}+V_1-V_2\hfill \\ \hfill & V=L\frac{di}{dt}+Ri\hfill \\ \hfill & V+V_1+V_3=0\hfill \\ \hfill & V+V_2+V_4=0\hfill \\ \hfill & i_e+i_3-i_1=0\hfill \\ \hfill & i-i_1-i_2=0\hfill \\ \hfill & i-i_3-i_4=0\hfill \\ \hfill & i_1=f\left(V_1\right)\hfill \\ \hfill & i_2=f\left(V_2\right)\hfill \\ \hfill & i_3=f\left(V_3\right)\hfill \\ \hfill & i_4=f\left(V_4\right)\hfill \end{array}$$

Nous pouvons immédiatement éliminer les variables i₃,i₄,V₃,V₄ :

$$\begin{array}{cc}\hfill & V_e=L_e\frac{d{i}_e}{dt}+V_1-V_2\hfill \\ \hfill & V=L\frac{di}{dt}+Ri\hfill \\ \hfill & i-i_1-i_2=0\hfill \\ \hfill & i_1=f\left(V_1\right)\hfill \\ \hfill & i_2=f\left(V_2\right)\hfill \\ \hfill & i-i_e=f(-V-V_1)\hfill \\ \hfill & i-i_1+i_e=f(-V-V_2)\hfill \end{array}$$

Il reste 7 variables, c'est-à-dire le nombre de mailles (3) et de nœuds (4) du circuit.

À chaque itération, les valeurs de i et i_e sont obtenues par la méthode d'Euler avec les deux premières équations. Les 5 autres équations sont résolues par la méthode de Newton-Raphson. Voici les variables et leur correspondance avec les variables notées x_i :

$\begin{array}{ccccc}\hfill x_0\hfill & \hfill x_1\hfill & \hfill x_2\hfill & \hfill x_3\hfill & \hfill x_4\hfill \\ \hfill i_1\hfill & \hfill i_2\hfill & \hfill V\hfill & \hfill V_1\hfill & \hfill V_2\hfill \end{array}$

Voici les fonctions F :

$$\begin{array}{cc}\hfill & F_0\left(X\right)=i-x_0-x_1\hfill \\ \hfill & F_1\left(X\right)=f\left(x_3\right)-x_0\hfill \\ \hfill & F_2\left(X\right)=f\left(x_4\right)-x_1\hfill \\ \hfill & F_3\left(X\right)=f(-x_2-x_3)-x_0+i_e\hfill \\ \hfill & F_4\left(X\right)=f(-x_2-x_4)+x_0-i-i_e\hfill \\ \hfill \end{array}$$

Voici le programme de simulation.

def simulation6complete(E,f,Le,L,R,tmax,dt,Gmin=1e-3):
    # param[0] : ie
    # param[1] : i
    # parama[2] : Gmin
    def F0(X,param): return param[1]-X[0]-X[1]
    def F1(X,param): return Idiode(X[3])-X[0]
    def F2(X,param): return Idiode(X[4])-X[1]
    def F3(X,param): return Idiode(-X[2]-X[3])-X[0]+param[0]
    def F4(X,param): return Idiode(-X[2]-X[4])+X[0]-param[0]-param[1]
    
    F = [F0,F1,F2,F3,F4]
    def J00(X,param): return -1
    def J01(X,param): return -1
    def J02(X,param): return 0
    def J03(X,param): return 0
    def J04(X,param): return 0
    
    def J10(X,param): return -1
    def J11(X,param): return 0
    def J12(X,param): return 0
    def J13(X,param): return deriv_Idiode(X[3])
    def J14(X,param): return 0
    
    
    def J20(X,param): return 0
    def J21(X,param): return -1
    def J22(X,param): return 0
    def J23(X,param): return 0
    def J24(X,param): return deriv_Idiode(X[4])
    
    def J30(X,param): return -1
    def J31(X,param): return 0
    def J32(X,param): return -deriv_Idiode(-X[2]-X[3])
    def J33(X,param): return -deriv_Idiode(-X[2]-X[3])
    def J34(X,param): return 0
    
    def J40(X,param): return 1
    def J41(X,param): return 0
    def J42(X,param): return -deriv_Idiode(-X[2]-X[4])
    def J43(X,param): return 0
    def J44(X,param): return -deriv_Idiode(-X[2]-X[4])
    
    
    J=[[J00,J01,J02,J03,J04],[J10,J11,J12,J13,J14],[J20,J21,J22,J23,J24],[J30,J31,J32,J33,J34],[J40,J41,J42,J43,J44]]
    N = 5
    w = 2*np.pi*f
    t = 0
    i = 0
    ie = 0
    V = 0
    V1,V2 = 0,0
    i1,i2 = 0,0
    Ve = 0
    data = [[t,i,ie,Ve,V,0,0]]
    
    while t<tmax:
        Ve = E*np.sin(w*t)
        param = [ie,i,Gmin]
        X = [i1,i2,V,V1,V2]
        nextX,niter,res = newton_N(X,F,J,N,param)
        i1,i2,V,V1,V2 = nextX[0],nextX[1],nextX[2],nextX[3],nextX[4]
        i= i+(V-R*i)/L*dt
        ie = ie+(Ve-V1+V2)/Le*dt
        t +=dt
        data.append([t,i,ie,Ve,V,niter,res])
    
    data = np.array(data)
    return data[:,0],data[:,1],data[:,2],data[:,3],data[:,4],data[:,5],data[:,6]

f=100
E=10
Le = 10e-3
L=100e-3
R = 5
t,i,ie,Ve,V,niter,res = simulation6complete(E,f,Le,L,R,0.1,1e-6,Gmin=1e-3)
figure(figsize=(16,6))
plot(t,Ve,label="Ve")
plot(t,V,label="V")
plot(t,i*5,label="i*5")
plot(t,ie*5,label="ie*5")
plot(t,niter,label="niter")
xlabel("t (s)",fontsize=16)
grid()
legend(loc="upper right")
Kp = facteurP(t,Ve,ie,f)
title("Kp = %0.2f"%Kp)
                    

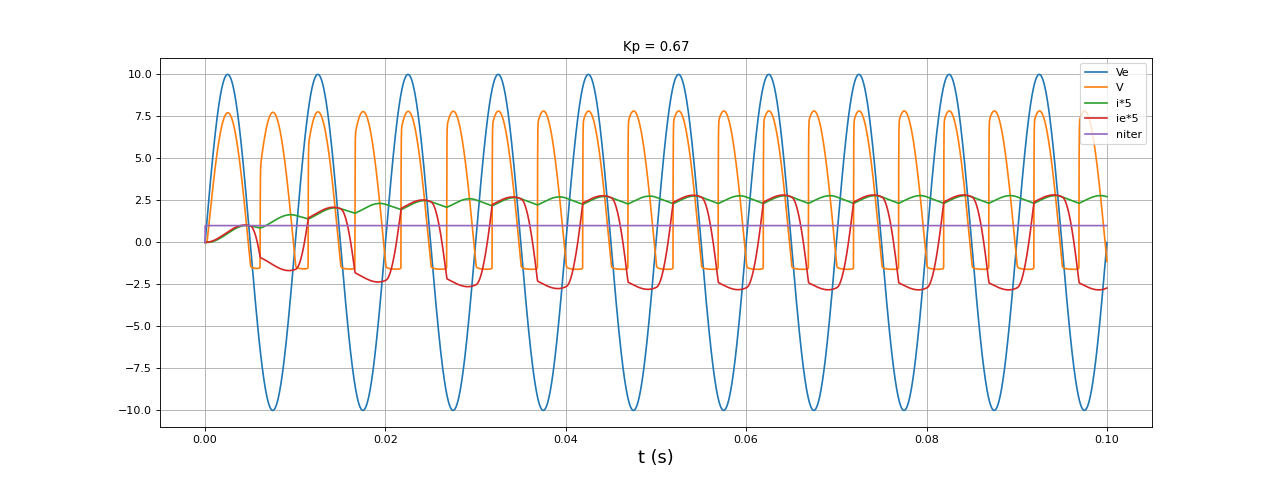fig30.pdf