Pendule double

1. Introduction

Ce document est une introduction à la simulation des systèmes de solides indéformables en liaison. L'exemple traité est un pendule double.

La première méthode de mise en équation consiste à utiliser pour chaque solide tous ses degrés de liberté (3 pour un mouvement plan) et à introduire les forces de liaison. Cette méthode conduit à un nombre d'inconnues beaucoup plus grand que le nombre de degrés de liberté du système. Elle a cependant l'avantage de se prêter à un traitement automatique pour N solides. L'intégration numérique nécessite la résolution d'un système linéaire à chaque pas de temps, qui permet de calculer les accélérations et les forces.

La deuxième méthode consiste à utiliser les équations de Lagrange. Les inconnues sont les degrés de liberté du système (2 pour le pendule double). Les équations obtenues sont plus faciles à intégrer, mais la méthode nécessite beaucoup de calculs manuels, et ne se prête pas à un traitement automatique pour N solides.

En troisième partie, nous aborderons une méthode adapté au traitement général des systèmes de solides en liaison. Elle consiste à calculer directement les forces de liaison au moyen d'équations traduisant les liaisons en terme d'accélération.

2. Équations de Newton et d'Euler

2.a. Équations du mouvement

On considère un système en mouvement plan constitué de deux barres. La première barre (notée 2) est en liaison pivot avec le support (noté 1). La seconde barre (notée 3) est en liaison pivot avec la première. Pour simplifier, on assimile les liaisons pivot à des liaisons ponctuelles, ce qui revient à supposer qu'elles sont parfaites. Le support est fixe dans le référentiel galiléen. On note C₂ et C₃ les centres de masse des deux barres. Les longueurs des barres sont notées l₁ et l₂ et on suppose que les centres de masse sont au milieu. On introduit les composantes des forces agissant sur les points de liaison. Par exemple F_x¹² est la composante sur x de la force exercée par le support 1 sur la barre 2.

Figure pleine page

Le système a deux degrés de liberté, représentés par les angles θ₂ et θ₃. On commence par exprimer l'accélération des centres de masse en fonction des angles et de leurs dérivées :

\begin{matrix} a_{2 x} = \frac{l_{2}}{2} (- {\ddot{θ}}_{2} sin θ_{2} - {\dot{θ}}_{2}^{2} cos θ_{2}) & (1) \\ a_{2 y} = \frac{l_{2}}{2} ({\ddot{θ}}_{2} cos θ_{2} - {\dot{θ}}_{2}^{2} sin θ_{2}) & (2) \\ a_{3 x} = l_{2} (- {\ddot{θ}}_{2} sin θ_{2} - {\dot{θ}}_{2}^{2} cos θ_{2}) + \frac{l_{3}}{2} (- {\ddot{θ}}_{3} sin θ_{3} - {\dot{θ}}_{3}^{2} cos θ_{3}) & (3) \\ a_{3 y} = l_{2} ({\ddot{θ}}_{2} cos θ_{2} - {\dot{θ}}_{2}^{2} sin θ_{2}) + \frac{l_{3}}{2} ({\ddot{θ}}_{3} cos θ_{3} - {\dot{θ}}_{3}^{2} sin θ_{3}) & (4) \end{matrix}

Pour la barre 2, on écrit le théorème de la résultante cinétique et le théorème du moment cinétique au centre de masse (appelés aussi équation de Newton et d'Euler) :

\begin{matrix} m_{2} a_{2 x} = F_{x}^{12} - F_{x}^{23} + m_{2} g & (5) \\ m_{2} a_{2 y} = F_{y}^{12} - F_{y}^{23} & (6) \\ J_{2} {\ddot{θ}}_{2} = \frac{l_{2}}{2} (F_{x}^{12} sin θ_{2} - F_{y}^{12} cos θ_{2} + F_{x}^{23} sin θ_{2} - F_{y}^{23} cos θ_{2}) & (7) \end{matrix}

On procède de même pour la barre 3 :

\begin{matrix} m_{3} a_{3 x} = F_{x}^{23} + m_{3} g & (8) \\ m_{3} a_{3 y} = F_{y}^{23} & (9) \\ J_{3} {\ddot{θ}}_{3} = \frac{l_{3}}{2} (F_{x}^{23} sin θ_{3} - F_{y}^{23} cos θ_{3}) & (10) \end{matrix}

On obtient ainsi 10 équations pour les 10 inconnues suivantes :

X = {(a_{2 x}, a_{2 y}, {\ddot{θ}}_{2}, a_{3 x}, a_{3 y}, {\ddot{θ}}_{3}, F_{x}^{12}, F_{y}^{12}, F_{x}^{23}, F_{y}^{23})}^{T} (11)

Le système d'équations est linéaire. On peut donc le mettre sous la forme matricielle AX=B avec :

A = (\begin{matrix} 1 & 0 & \frac{l_{2}}{2} sin θ_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & - \frac{l_{2}}{2} cos θ_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & l_{2} sin θ_{2} & 1 & 0 & \frac{l_{3}}{2} sin θ_{3} & 0 & 0 & 0 & 0 \\ 0 & 0 & - l_{2} cos θ_{2} & 0 & 1 & - \frac{l_{3}}{2} cos θ_{3} & 0 & 0 & 0 & 0 \\ m_{2} & 0 & 0 & 0 & 0 & 0 & - 1 & 0 & 1 & 0 \\ 0 & m_{2} & 0 & 0 & 0 & 0 & 0 & - 1 & 0 & 1 \\ 0 & 0 & J_{2} & 0 & 0 & 0 & - \frac{l_{2}}{2} sin θ_{2} & \frac{l_{2}}{2} cos θ_{2} & - \frac{l_{2}}{2} sin θ_{2} & \frac{l_{2}}{2} cos θ_{2} \\ 0 & 0 & 0 & m_{3} & 0 & 0 & 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 0 & m_{3} & 0 & 0 & 0 & 0 & - 1 \\ 0 & 0 & 0 & 0 & 0 & J_{3} & 0 & 0 & - \frac{l_{3}}{2} sin θ_{3} & \frac{l_{3}}{2} cos θ_{3} \end{matrix}) (12)

B = (\begin{matrix} - \frac{l_{2}}{2} {\dot{θ}}_{2}^{2} cos θ_{2} \\ - \frac{l_{2}}{2} {\dot{θ}}_{2}^{2} sin θ_{2} \\ - l_{2} {\dot{θ}}_{2}^{2} cos θ_{2} - \frac{l_{3}}{2} {\dot{θ}}_{3}^{2} cos θ_{3} \\ - l_{2} {\dot{θ}}_{2}^{2} sin θ_{2} - \frac{l_{3}}{2} {\dot{θ}}_{3}^{2} sin θ_{3} \\ m_{2} g \\ 0 \\ 0 \\ m_{3} g \\ 0 \\ 0 \end{matrix}) (13)

Il est en principe possible de résoudre ce système formellement pour exprimer les accélérations angulaires en fonction des angles. Une approche plus simple et plus générale pour les problèmes de systèmes de solides ([1]) consiste à laisser le système d'équations sous cette forme. Il comporte 8 inconnues de plus que les deux degrés de liberté du système : les accélérations des centres de masse et les forces de liaison. Les équations sont intégrées par une méthode numérique à un pas (méthode d'Euler ou Runge-Kutta). À chaque pas de temps, le système AX=B est résolu numériquement pour obtenir les accélérations angulaires.

2.b. Intégration numérique

L'évaluation des accélérations angulaires est très coûteuse puisqu'elle nécessite la résolution d'un système linéaire à 10 inconnues. Une methode à un pas et à une seule évaluation de la dérivée par pas, comme la méthode d'Euler, est donc recommandée. Le système étant conservatif, on a intérêt à utiliser une méthode d'Euler symplectique. À chaque pas de temps, on calcule les nouveaux angles avant de calculer les accélérations angulaires par résolution du système linéaire, puis on calcule les nouvelles vitesses angulaires.

from scipy.linalg import solve
import math
import numpy
from matplotlib.pyplot import *

class PenduleDouble:
    def __init__(self,l2,l3,m2,m3,J2,J3):
        self.A = numpy.zeros((10,10))
        self.B = numpy.zeros((10,1))
        self.A[0,0] = 1.0
        self.A[1,1] = 1.0
        self.A[2,3] = 1.0
        self.A[3,4]= 1.0
        self.A[4,0] = m2
        self.A[4,6] = -1.0
        self.A[4,8] = 1.0
        self.A[5,1] = m2
        self.A[5,7] = -1.0
        self.A[5,9] = 1.0
        self.A[6,2] = J2
        self.A[7,3] = m3
        self.A[7,8] = -1.0
        self.A[8,4] = m3
        self.A[8,9] = -1.0
        self.A[9,5] = J3
        self.B[4] = m2
        self.B[7] = m3
        self.l2 = l2
        self.l3 = l3
        self.theta2 = 0.0
        self.theta3 = 0.0
        self.dtheta2 = 0.0
        self.dtheta3 = 0.0
        
    def pas_euler(self,h):
        self.theta2 += self.dtheta2*h
        self.theta3 += self.dtheta3*h
        sin2 = math.sin(self.theta2)
        cos2 = math.cos(self.theta2)
        sin3 = math.sin(self.theta3)
        cos3 = math.cos(self.theta3)
        l2 = self.l2*0.5
        l3 = self.l3*0.5
        self.A[0,2] = l2*sin2
        self.A[1,2] = -l2*cos2
        self.A[2,2] = self.l2*sin2
        self.A[2,5] = l3*sin3
        self.A[3,2] = -self.l2*cos2
        self.A[3,5] = -l3*cos3
        self.A[6,6] = -l2*sin2
        self.A[6,7] = l2*cos2
        self.A[6,8] = -l2*sin2
        self.A[6,9] = l2*cos2
        self.A[9,8] = -l3*sin3
        self.A[9,9] = l3*cos3
        dtheta2_2 = self.dtheta2**2
        dtheta3_2 = self.dtheta3**2
        self.B[0] = -l2*dtheta2_2*cos2
        self.B[1] = -l2*dtheta2_2*sin2
        self.B[2] = self.B[0]*2-l3*dtheta3_2*cos3
        self.B[3] = self.B[1]*2-l3*dtheta3_2*sin3
        x = solve(self.A,self.B)
        self.dtheta2 += x[2][0]*h
        self.dtheta3 += x[5][0]*h
        
        
    def euler(self,T,Yi,h):
        Y = Yi
        t = 0.0
        liste_y = [[Yi[0],Yi[1],Yi[2],Yi[3]]]
        liste_t = [t]
        self.theta2 = Yi[0]
        self.dtheta2 = Yi[1]
        self.theta3 = Yi[2]
        self.dtheta3 = Yi[3]
        while t < T:
            self.pas_euler(h)
            t += h
            liste_y.append([self.theta2,self.dtheta2,self.theta3,self.dtheta3])
            liste_t.append(t)
        return (numpy.array(liste_t),numpy.array(liste_y))

pendule = PenduleDouble(1.0,1.0,1.0,1.0,1.0,1.0)
Yi = [1.0,0.0,0.0,0.0]
(t,y) = pendule.euler(50,Yi,1e-3)

figure()
plot(t,y[:,0],label="theta2")
plot(t,y[:,2],label="theta3")
legend(loc="upper right")
xlabel("t")
grid()

figA.pdf

Yi = [3.0,0.0,2.0,0.0]
(t,y) = pendule.euler(100,Yi,1e-3)
figure()
plot(t,y[:,0],label="theta2")
plot(t,y[:,2],label="theta3")
legend(loc="upper right")
xlabel("t")
grid()

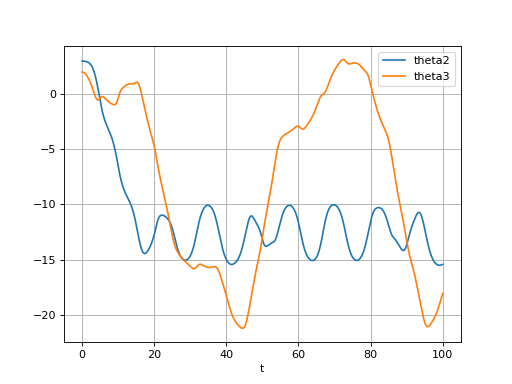figB.pdf

3. Équations de Lagrange

3.a. Équations du mouvement

Les équations de Lagrange permettent d'obtenir directement des équations du mouvement ne faisant intervenir que les degrés de liberté, ici les angles θ₂,θ₃. Elle s'applique pour des liaisons dont la puissance totale des forces est nulle, c'est-à-dire pour des liaisons parfaites.

Le lagrangien est la différence entre l'énergie cinétique et l'énergie potentielle :

L (θ_{2}, θ_{3}, {\dot{θ}}_{2}, {\dot{θ}}_{3}) = E_{c} (θ_{2}, θ_{3}, {\dot{θ}}_{2}, {\dot{θ}}_{3}) - E_{p} (θ_{2}, θ_{3}) (14)

Pour ce système à deux degrés de liberté, les deux équations de Lagrange ([2]) sont :

\begin{matrix} \frac{d}{d t} \frac{\partial L}{\partial {\dot{θ}}_{2}} - \frac{\partial L}{\partial θ_{2}} = 0 & (15) \\ \frac{d}{d t} \frac{\partial L}{\partial {\dot{θ}}_{3}} - \frac{\partial L}{\partial θ_{3}} = 0 & (16) \end{matrix}

Pour exprimer l'énergie cinétique, il faut tout d'abord écrire les vitesses des centres de masse :

\begin{matrix} v_{2 x} = - \frac{l_{2}}{2} {\dot{θ}}_{2} sin θ_{2} & (17) \\ v_{2 y} = \frac{l_{2}}{2} {\dot{θ}}_{2} cos θ_{2} & (18) \\ v_{3 x} = - l_{2} {\dot{θ}}_{2} sin θ_{2} - \frac{l_{3}}{2} {\dot{θ}}_{3} sin θ_{3} & (19) \\ v_{3 y} = l_{2} {\dot{θ}}_{2} cos θ_{2} + \frac{l_{3}}{2} {\dot{θ}}_{3} cos θ_{3} & (20) \end{matrix}

Pour chaque solide, l'énergie cinétique est la somme de l'énergie cinétique du centre de masse affecté de la masse du solide et de l'énergie cinétique de rotation autour du centre de masse :

\begin{matrix} E_{c} = & \frac{1}{2} m_{2} v_{2}^{2} + \frac{1}{2} m_{3} v_{3}^{2} + \frac{1}{2} J_{2} {\dot{θ}}_{2}^{2} + \frac{1}{2} J_{3} {\dot{θ}}_{3}^{2} & (21) \\ = & \frac{1}{2} m_{2} (\frac{l_{2}}{2})^{2} {\dot{θ}}_{2}^{2} + \frac{1}{2} m_{3} l_{3}^{2} {\dot{θ}}_{2}^{2} + \frac{1}{2} m_{3} (\frac{l_{2}}{2})^{2} {\dot{θ}}_{3}^{2} + \frac{1}{2} m_{3} l_{2} l_{3} {\dot{θ}}_{2} {\dot{θ}}_{3} (sin θ_{2} sin θ_{3} + cos θ_{2} cos θ_{3}) + \frac{1}{2} J_{2} {\dot{θ}}_{2}^{2} + \frac{1}{2} J_{3} {\dot{θ}}_{3}^{2} & (22) \end{matrix}

L'énergie potentielle, due à la pesanteur, est :

E_{p} = - m_{2} g \frac{l_{2}}{2} cos θ_{2} - m_{3} g (l_{2} cos θ_{2} + \frac{l_{3}}{2} cos θ_{3}) (23)

Les deux équations de Lagrange conduisent à :

\begin{matrix} a_{11} {\ddot{θ}}_{2} + a_{12} {\ddot{θ}}_{3} = b_{1} & (24) \\ a_{21} {\ddot{θ}}_{2} + a_{22} {\ddot{θ}}_{3} = b_{2} & (25) \end{matrix}

avec :

\begin{matrix} a_{11} = m_{2} \frac{l_{2}^{2}}{4} + m_{3} l_{2}^{2} + J_{2} & (26) \\ a_{22} = m_{3} \frac{l_{3}^{2}}{4} + J_{3} & (27) \\ a_{21} = a_{12} = \frac{1}{2} m_{3} l_{2} l_{3} (sin θ_{2} sin θ_{3} + cos θ_{2} cos θ_{3}) & (28) \\ b_{1} = \frac{1}{2} m_{3} l_{2} l_{3} (cos θ_{2} sin θ_{3} - sin θ_{2} cos θ_{3}) {\dot{θ}}_{3}^{2} - m_{2} g \frac{l_{2}}{2} sin θ_{2} - m_{3} g l_{2} sin θ_{2} & (29) \\ b_{2} = \frac{1}{2} m_{3} l_{2} l_{3} (sin θ_{2} cos θ_{3} - cos θ_{2} sin θ_{3}) {\dot{θ}}_{2}^{2} - m_{3} g \frac{l_{3}}{2} sin θ_{3} & (30) \end{matrix}

On obtient finalement les accélérations angulaires :

\begin{matrix} {\ddot{θ}}_{2} = \frac{a_{22} b_{1} - a_{12} b_{2}}{a_{11} a_{22} - a_{12}^{2}} & (31) \\ {\ddot{θ}}_{3} = \frac{a_{11} b_{2} - a_{21} b_{1}}{a_{11} a_{22} - a_{12}^{2}} & (32) \end{matrix}

3.b. Intégration numérique

class PenduleDouble2:
    def __init__(self,l2,l3,m2,m3,J2,J3):
        self.a11 = m2*l2**2/4+m3*l2**2+J2
        self.a22 = m2*l2**2/4+J3
        self.d = self.a11*self.a22
        self.u = 0.5*m3*l2*l3
        self.v = m2*l2*0.5+m3*l2
        self.w = m3*l3*0.5
        self.theta2 = 0.0
        self.theta3 = 0.0
        self.dtheta2 = 0.0
        self.dtheta3 = 0.0
        
    def pas_euler(self,h):
        self.theta2 += self.dtheta2*h
        self.theta3 += self.dtheta3*h
        sin2 = math.sin(self.theta2)
        cos2 = math.cos(self.theta2)
        sin3 = math.sin(self.theta3)
        cos3 = math.cos(self.theta3)
        a12 = self.u*(sin2*sin3+cos2*cos3)
        det = self.d-a12**2
        b1 = self.u*(cos2*sin3-sin2*cos3)*self.dtheta3**2-self.v*sin2
        b2 = self.u*(sin2*cos3-cos2*sin3)*self.dtheta2**2-self.w*sin3
        self.dtheta2 += (self.a22*b1-a12*b2)/det*h
        self.dtheta3 += (self.a11*b2-a12*b1)/det*h
        
    def euler(self,T,Yi,h):
        Y = Yi
        t = 0.0
        liste_y = [Yi]
        liste_t = [t]
        self.theta2 = Yi[0]
        self.dtheta2 = Yi[1]
        self.theta3 = Yi[2]
        self.dtheta3 = Yi[3]
        while t < T:
            self.pas_euler(h)
            t += h
            liste_y.append([self.theta2,self.dtheta2,self.theta3,self.dtheta3])
            liste_t.append(t)
        return (numpy.array(liste_t),numpy.array(liste_y))

pendule = PenduleDouble2(1.0,1.0,1.0,1.0,1.0,1.0)
Yi = [1.0,0.0,0.0,0.0]
(t,y) = pendule.euler(50,Yi,1e-3)

figure()
plot(t,y[:,0],label="theta2")
plot(t,y[:,2],label="theta3")
legend(loc="upper right")
xlabel("t")
grid()

figC.pdf

Yi = [3.0,0.0,2.0,0.0]
(t,y) = pendule.euler(100,Yi,1e-3)
figure()
plot(t,y[:,0],label="theta2")
plot(t,y[:,2],label="theta3")
legend(loc="upper right")
xlabel("t")
grid()

figD.pdf

4. Méthode générale

4.a. Principe

On recherche une méthode générale permettant de traiter par un algorithme un nombre quelconque de solides en liaisons, par différents types de liaison. La méthode exposée ci-dessus (partie 2) se prête bien au cas de N solides en liaison pivot. L'obtention des équations (1) à (4), qui expriment les accélérations des centres de masse en fonction des angles, des vitesses et des accélérations angulaires, est cependant laborieuse pour N solides. Par ailleurs, d'autres types de liaisons (comme la liaison glissière), ne permettraient pas d'obtenir des relations de cette forme.

Une autre méthode consiste à calculer directement les forces de liaison en fonction de la configuration des solides et de leur vitesse angulaire ([3]). Dans la méthode précédente (partie 2), les liaisons apparaissent implicitement dans les équations (1) à (4). Il nous faut une équation traduisant explicitement une liaison pivot. Considérons la liaison entre les solides i et j. Soit P_ij le point du pivot lié au solide i, et P_ji le point du pivot lié au solide j. Ces deux points doivent être condondus à tout instant mais il ne le seront que si une force de liaison convenable est appliquée. Introduisons les vecteurs ${\vec{R}}_{P_{i j}} = \vec{O P_{i j}}$ et ${\vec{R}}_{P_{j i}} = \vec{O P_{j i}}$ . Les dérivées premières par rapport aux temps sont les vitesses ${\vec{V}}_{P_{i j}}$ et ${\vec{V}}_{P_{j i}}$ . Les dérivées secondes sont les accélérations ${\vec{A}}_{P_{i j}}$ et ${\vec{A}}_{P_{j i}}$ . Le maintient de la liaison implique que les trois équations suivantes soient vérifiées à tout instant :

\begin{matrix} {\vec{R}}_{P_{i j}} = {\vec{R}}_{P_{j i}} & (33) \\ {\vec{V}}_{P_{i j}} = {\vec{V}}_{P_{j i}} & (34) \\ {\vec{A}}_{P_{i j}} = {\vec{A}}_{P_{j i}} & (35) \end{matrix}

La première de ces équations implique la deuxième et la troisième. Elle est donc suffisante pour exprimer la liaison. L'objectif étant de calculer les forces de liaison, il nous faut une équation faisant intervenir les forces. Seule la troisième (égalité des accélérations) convient pour cela. Supposons qu'à l'instant t=0, les deux premières équations soient vérifiées (cette condition est facile à obtenir si toutes les vitesses initiales sont nulles). Si la troisième équation est vérifiée à tout instant, la deuxième le sera automatiquement et la première aussi, ce qui assure la maintient de la liaison. Nous allons donc expliciter la troisième équation, qui exprime l'égalité des accélérations.

4.b. Force de liaison

Considérons l'égalité des accélérations pour deux solides i et j :

{\vec{A}}_{P_{i j}} = {\vec{A}}_{P_{j i}} (36)

où P_ij est un point lié au solide i et P_ji un point lié au solide j. Cette égalité permet d'assurer la liaison pivot entre les deux solides. Ces deux points sont alors confondus à tout instant.

Afin d'utiliser les équations de Newton et d'Euler (théorèmes de la résultante et du moment cinétique), il faut faire intervenir le centre de masse. Partons de la relation suivante (relation classique de la cinématique du solide, que nous admettrons) :

{\vec{V}}_{P_{i j}} = {\vec{V}}_{C_{i}} + {\vec{ω}}_{i} \land \vec{C_{i} P_{i j}} = {\vec{V}}_{C_{i}} + {\vec{ω}}_{i} \land ({\vec{R}}_{P_{i j}} - {\vec{R}}_{C_{i}}) (37)

Dérivons par rapport au temps pour obtenir l'accélération :

{\vec{A}}_{P_{i}} = {\vec{A}}_{C_{i}} + \frac{d {\vec{ω}}_{i}}{d t} \land ({\vec{R}}_{P_{i j}} - {\vec{R}}_{C_{i}}) + {\vec{ω}}_{i} \land ({\vec{V}}_{P_{i j}} - {\vec{V}}_{C_{i}}) = {\vec{A}}_{C_{i}} + \frac{d {\vec{ω}}_{i}}{d t} \land ({\vec{R}}_{P_{i j}} - {\vec{R}}_{C_{i}}) + {\vec{ω}}_{i} \land ({\vec{ω}}_{i} \land ({\vec{R}}_{P_{i j}} - {\vec{R}}_{C_{i}})) (38)

En première approche, nous supposons que chaque solide est en liaison avec au plus deux solides. Le solide i est en liaison pivot avec le solide j et le solide k. Écrivons les lois de Newton et d'Euler pour le solide i :

\begin{matrix} m_{i} {\vec{A}}_{C_{i}} = {\vec{F}}^{e i} + {\vec{F}}^{j i} + {\vec{F}}^{k i} & (39) \\ J_{i} \frac{d {\vec{ω}}_{i}}{d t} = {\vec{M}}^{e i} + \vec{C_{i} P_{i j}} \land {\vec{F}}^{j i} + \vec{C_{i} P_{i k}} \land {\vec{F}}^{k i} & (40) \end{matrix}

La seconde équation n'est valable que pour un problème bidimensionnel (problème plan). Le vecteur ${\vec{F}}^{e i} = F_{x}^{e i} {\vec{u}}_{x} + F_{y}^{e i} {\vec{u}}_{y}$ est la résultante des forces extérieures agissant sur le solide i et le vecteur ${\vec{M}}^{e i} = M^{e i} {\vec{u}}_{z}$ est le moment résultant des forces extérieures par rapport au centre de masse. Dans le cas du pendule double, la seule force extérieure est le poids.

Nous obtenons finalement l'expression suivante de l'accélération du point P_ij :

{\vec{A}}_{P_{i j}} = \frac{1}{m_{i}} ({\vec{F}}^{e i} + {\vec{F}}^{j i} + {\vec{F}}^{k i}) + \frac{1}{J_{i}} ({\vec{M}}^{e i} + \vec{C_{i} P_{i j}} \land {\vec{F}}^{j i} + \vec{C_{i} P_{i k}} \land {\vec{F}}^{k i}) \land \vec{C_{i} P_{i j}} + {\vec{ω}}_{i} \land ({\vec{ω}}_{i} \land \vec{C_{i} P_{i j}}) (41)

Considérons à présent le solide j, qui est en liaison avec le solide i et avec le solide l. Compte tenu de la relation ${\vec{F}}^{j i} = - {\vec{F}}^{i j}$ (principe des actions réciproques), l'accélération de son point de liaison avec le solide i s'écrit :

{\vec{A}}_{P_{j i}} = \frac{1}{m_{j}} ({\vec{F}}^{e j} - {\vec{F}}^{j i} + {\vec{F}}^{l j}) + \frac{1}{J_{j}} ({\vec{M}}^{e j} - \vec{C_{j} P_{j i}} \land {\vec{F}}^{j i} + \vec{C_{j} P_{j l}} \land {\vec{F}}^{l j}) \land \vec{C_{j} P_{j i}} + {\vec{ω}}_{j} \land ({\vec{ω}}_{j} \land \vec{C_{i} P_{j i}}) (42)

L'égalité des accélérations $(36)$ s'écrit donc :

\begin{matrix} \frac{1}{m_{i}} ({\vec{F}}^{e i} + {\vec{F}}^{j i} + {\vec{F}}^{k i}) + \frac{1}{J_{i}} ({\vec{M}}^{e i} + \vec{C_{i} P_{i j}} \land {\vec{F}}^{j i} + \vec{C_{i} P_{i k}} \land {\vec{F}}^{k i}) \land \vec{C_{i} P_{i j}} + {\vec{ω}}_{i} \land ({\vec{ω}}_{i} \land \vec{C_{i} P_{i j}}) & (43) \\ = & \frac{1}{m_{j}} ({\vec{F}}^{e j} - {\vec{F}}^{j i} + {\vec{F}}^{l j}) + \frac{1}{J_{j}} ({\vec{M}}^{e j} - \vec{C_{j} P_{j i}} \land {\vec{F}}^{j i} + \vec{C_{j} P_{j l}} \land {\vec{F}}^{l j}) \land \vec{C_{j} P_{j i}} + {\vec{ω}}_{j} \land ({\vec{ω}}_{j} \land \vec{C_{j} P_{j i}}) & (44) \end{matrix}

Posons $\vec{C_{i} P_{i j}} = K_{i j} {\vec{u}}_{x} + L_{i j} {\vec{u}}_{y}$ . La projection sur les deux axes conduit aux deux équations suivantes :

\begin{matrix} \frac{1}{m_{i}} (F_{x}^{e i} + F_{x}^{j i} + F_{x}^{k i}) - \frac{1}{J_{i}} M^{e i} L_{i j} - \frac{1}{J_{i}} (L_{i j} (K_{i j} F_{y}^{j i} - L_{i j} F_{x}^{j i})) - \frac{1}{J_{i}} (L_{i j} (K_{i k} F_{y}^{k i} - L_{i k} F_{x}^{k i})) - ω_{i}^{2} K_{i j} = \frac{1}{m_{j}} (F_{x}^{e j} - F_{x}^{j i} + F_{x}^{l j}) - \frac{1}{J_{j}} M^{e j} L_{j i} + \frac{1}{J_{j}} (L_{j i} (K_{j i} F_{y}^{j i} - L_{j i} F_{x}^{j i})) - \frac{1}{J_{j}} (L_{j i} (K_{j l} F_{y}^{l j} - L_{j l} F_{x}^{l j})) - ω_{j}^{2} K_{j i} & (45) \\ \frac{1}{m_{i}} (F_{y}^{e i} + F_{y}^{j i} + F_{y}^{k i}) + \frac{1}{J_{i}} M^{e i} K_{i j} + \frac{1}{J_{i}} (K_{i j} (K_{i j} F_{y}^{j i} - L_{i j} F_{x}^{j i})) + \frac{1}{J_{i}} (K_{i j} (K_{i k} F_{y}^{k i} - L_{i k} F_{x}^{k i})) - ω_{i}^{2} L_{i j} = \frac{1}{m_{j}} (F_{y}^{e j} - F_{y}^{j i} + F_{y}^{l j}) + \frac{1}{J_{j}} M^{e j} K_{j i} - \frac{1}{J_{j}} (K_{j i} (K_{j i} F_{y}^{j i} - L_{j i} F_{x}^{j i})) + \frac{1}{J_{j}} (K_{j i} (K_{j l} F_{y}^{l j} - L_{j l} F_{x}^{l j})) - ω_{j}^{2} L_{j i} & (46) \end{matrix}

Les deux équations sont finalement :

(\frac{1}{m_{i}} + \frac{1}{m_{j}} + \frac{L_{i j}^{2}}{J_{i}} + \frac{L_{j i}^{2}}{J_{j}}) F_{x}^{j i} + (- \frac{L_{i j} K_{i j}}{J_{i}} - \frac{L_{j i} K_{j i}}{J_{j}}) F_{y}^{j i} + (\frac{1}{m_{i}} + \frac{L_{i j} L_{i k}}{J_{i}}) F_{x}^{k i} + (- \frac{L_{i j} K_{i k}}{J_{i}}) F_{y}^{k i} + (- \frac{1}{m_{j}} - \frac{L_{j i} L_{j l}}{J_{j}}) F_{x}^{l j} + (\frac{L_{j i} K_{j l}}{J_{j}}) F_{y}^{l j} = - \frac{F_{x}^{e i}}{m_{i}} + \frac{F_{x}^{e j}}{m_{j}} + \frac{M^{e i} L_{i j}}{J_{i}} - \frac{M^{e j} L_{j i}}{J_{j}} + ω_{i}^{2} K_{i j} - ω_{j}^{2} K_{j i} (47)

(- \frac{K_{i j} L_{i j}}{J_{i}} - \frac{K_{j i} L_{j i}}{J_{j}}) F_{x}^{j i} + (\frac{1}{m_{i}} + \frac{1}{m_{j}} + \frac{K_{i j}^{2}}{J_{i}} + \frac{K_{j i}^{2}}{J_{j}}) F_{y}^{j i} + (- \frac{K_{i j} L_{i k}}{J_{i}}) F_{x}^{k i} + (\frac{1}{m_{i}} + \frac{K_{i j} K_{i k}}{J_{i}}) F_{y}^{k i} + (\frac{K_{j i} L_{j l}}{J_{j}}) F_{x}^{l j} + (- \frac{1}{m_{j}} - \frac{K_{j i} K_{j l}}{J_{j}}) F_{y}^{l j} = - \frac{F_{y}^{e i}}{m_{i}} + \frac{F_{y}^{e j}}{m_{j}} - \frac{M^{e i} K_{i j}}{J_{i}} + \frac{M^{e j} K_{j i}}{J_{j}} + ω_{i}^{2} L_{i j} - ω_{j}^{2} L_{j i} (48)

Pour résumer, une liaison pivot dans un problème bidimensionnel se traduit par deux équations pour les composantes des forces de liaison. Il faut remarquer que la condition $(36)$ appliquée à un problème tridimensionnel traduit une liaison rotule et non pas une liaison pivot.

Si l'un des solides (disons le solide j) est fixe, la condition de la liaison pivot s'écrit :

{\vec{A}}_{P_{i} j} = \vec{0} (49)

Pour obtenir ce cas, il faut poser dans les équations précédentes : $\frac{1}{m_{j}} = 0$ , $\frac{1}{J_{j}} = 0$ , $ω_{j} = 0$ .

Ces deux équations font intervenir six inconnues (les composantes de trois forces de liaison). Si l'un des solides n'a qu'une seule liaison, il y a une force en moins. On remarque par ailleurs, en vertu du principe des actions réciproques, que l'inversion des indices dans une composante d'une force revient à changer le signe du terme correspondant.

4.c. Algorithme

Pour chaque solide du système, les variables sont : la position du centre de masse, l'orientation et les dérivées premières correspondantes :

(X_{i}, Y_{i}, θ_{i}, V X_{i}, V Y_{i}, ω_{i}) = (X_{C_{i}}, Y_{C_{i}}, θ_{i}, {\dot{X}}_{C_{i}}, {\dot{Y}}_{C_{i}}, ω_{i}) (50)

À l'instant t où la configuration du système est connue, ces variables sont déterminées pour chaque solide. Pour chaque liaison ij du système, il est alors possible de calculer $F_{x}^{j i}$ et $F_{y}^{j i}$ à l'aide du système linéaire constitué des équations $(47)$ et $(48)$ . Il s'agit d'un système linéaire pour les composantes de toutes les forces de liaison du système.

Les équations différentielles du premier ordre à intégrer sont :

\begin{matrix} \frac{d X_{i}}{d t} = V X_{i} & (51) \\ \frac{d Y_{i}}{d t} = V Y_{i} & (52) \\ \frac{d θ_{i}}{d t} = ω_{i} & (53) \\ \frac{d V X_{i}}{d t} = \frac{1}{m_{i}} (F_{x}^{e i} + \sum_{j} F_{x}^{j i}) & (54) \\ \frac{d V Y_{i}}{d t} = \frac{1}{m_{i}} (F_{y}^{e i} + \sum_{j} F_{y}^{j i}) & (55) \\ \frac{d ω_{i}}{d t} = \frac{1}{J_{i}} (M^{e i} + \sum_{j} K_{i j} F_{y}^{j i} - L_{i j} F_{x}^{j i}) & (56) \end{matrix}

Pour chaque solide, on doit sommer sur les points de liaison avec les autres solides (somme sur j).

On remarque que cette méthode comporte des variables de configuration redondantes : les coordonnées des centres de masses apparaissent explicitement dans le système alors qu'elles pourraient en principe s'exprimer en fonction des angles. Le calcul de ces coordonnées à partir des angles n'est donc pas nécessaire pour l'intégration numérique mais il faudra tout de même l'effectuer pour le calcul de la condition initiale.

Une méthode d'Euler ou de Runge-Kutta est utilisable pour l'intégration numérique. Le calcul des forces de liaison doit se faire à chaque changement de configuration du système.

4.d. Pendule double

Reprenons l'exemple du pendule double. Voici les expressions des coefficients K_ij et L_ij pour ce système :

\begin{matrix} K_{21} = - \frac{l_{2}}{2} cos (θ_{2}) & (57) \\ L_{21} = - \frac{l_{2}}{2} sin (θ_{2}) & (58) \\ K_{23} = - K_{21} & (59) \\ L_{23} = - L_{21} & (60) \\ K_{32} = - \frac{l_{3}}{2} cos (θ_{3}) & (61) \\ L_{32} = - \frac{l_{3}}{2} sin (θ_{3}) & (62) \end{matrix}

Les forces extérieures et les moments associés s'écrivent :

\begin{matrix} F_{x}^{e 2} = m_{2} g & (63) \\ F_{y}^{e 2} = 0 & (64) \\ M^{e 2} = 0 & (65) \\ F_{x}^{e 3} = m_{3} g & (66) \\ F_{y}^{e 3} = 0 & (67) \\ M^{e 3} = 0 & (68) \end{matrix}

Écrivons le système linéaire à résoudre pour déterminer les 4 composantes de forces de liaison :

(\begin{matrix} \frac{1}{m_{2}} + \frac{L_{21}^{2}}{J_{2}} & - \frac{L_{21} K_{21}}{J_{2}} & \frac{1}{m_{2}} + \frac{L_{21} L_{23}}{J_{2}} & - \frac{L_{21} K_{23}}{J_{2}} \\ - \frac{K_{21} L_{21}}{J_{2}} & \frac{1}{m_{2}} + \frac{K_{21}^{2}}{J_{2}} & - \frac{K_{21} L_{23}}{J_{2}} & \frac{1}{m_{2}} + \frac{K_{21} K_{23}}{J_{2}} \\ \frac{1}{m_{2}} + \frac{L_{23} L_{21}}{J_{2}} & - \frac{L_{23} K_{21}}{J_{2}} & \frac{1}{m_{2}} + \frac{1}{m_{3}} + \frac{L_{23}^{2}}{J_{2}} + \frac{L_{32}^{2}}{J_{3}} & - \frac{L_{23} K_{23}}{J_{2}} - \frac{L_{32} K_{32}}{J_{3}} \\ - \frac{K_{23} L_{21}}{J_{2}} & \frac{1}{m_{2}} + \frac{K_{23} K_{21}}{J_{2}} & - \frac{K_{23} L_{23}}{J_{2}} - \frac{K_{32} L_{32}}{J_{3}} & \frac{1}{m_{2}} + \frac{1}{m_{3}} + \frac{K_{23}^{2}}{J_{2}} + \frac{K_{32}^{2}}{J_{3}} \end{matrix}) (\begin{matrix} F_{x}^{12} \\ F_{y}^{12} \\ F_{x}^{32} \\ F_{y}^{32} \end{matrix}) = (\begin{matrix} - \frac{F_{x}^{e 2}}{m_{2}} + \frac{M^{e 2} L_{21}}{J_{2}} + ω_{2}^{2} K_{21} \\ - \frac{F_{y}^{e 2}}{m_{2}} - \frac{M^{e 2} K_{21}}{J_{2}} + ω_{2}^{2} L_{21} \\ - \frac{F_{x}^{e 2}}{m_{2}} + \frac{F_{x}^{e 3}}{m_{3}} + \frac{M^{e 2} L_{23}}{J_{2}} - \frac{M^{e 3} L_{32}}{J_{3}} + ω_{2}^{2} K_{23} - ω_{3}^{2} K_{32} \\ - \frac{F_{y}^{e 2}}{m_{2}} + \frac{F_{y}^{e 3}}{m_{3}} - \frac{M^{e 2} K_{23}}{J_{2}} + \frac{M^{e 3} K_{32}}{J_{3}} + ω_{2}^{2} L_{23} - ω_{3}^{2} L_{32} \end{matrix}) (69)

class PenduleDouble3:
    def __init__(self,l2,l3,m2,m3,J2,J3):
        self.m2 = m2
        self.m3 = m3
        self.l2 = l2
        self.l3 = l3
        self.J2 = J2
        self.J3 = J3
        self.X2 = 0
        self.Y2 = 0
        self.theta2 = 0
        self.VX2 = 0
        self.VY2 = 0
        self.omega2 = 0
        self.X3 = 0
        self.Y3 = 0
        self.theta3 = 0
        self.VX3 = 0
        self.VY3 = 0
        self.omega3 = 0
        self.g = 1
        self.A = numpy.zeros((4,4))
        self.B = numpy.zeros((4,1))
        
    def pas_euler(self,h):
        self.X2 += h*self.VX2
        self.Y2 += h*self.VY2
        self.theta2 += h*self.omega2
        self.X3 += h*self.VX3
        self.Y3 += h*self.VY3
        self.theta3 += h*self.omega3
        
        K21 = -self.l2*0.5*numpy.cos(self.theta2)
        L21 = -self.l2*0.5*numpy.sin(self.theta2)
        K23 = -K21
        L23 = -L21
        K32 = -self.l3*0.5*numpy.cos(self.theta3)
        L32 = -self.l3*0.5*numpy.sin(self.theta3)
        Fxe2 = self.g*self.m2
        Fye2 = 0
        Me2 = 0
        Fxe3 = self.g*self.m3
        Fye3 = 0
        Me3 = 0
        
        self.A[0,0] = 1/self.m2+L21*L21/self.J2
        self.A[0,1] = -L21*K21/self.J2
        self.A[0,2] = 1/self.m2+L21*L23/self.J2
        self.A[0,3] = -L21*K23/self.J2
        self.A[1,0] = self.A[0,1]                   
        self.A[1,1] = 1/self.m2+K21*K21/self.J2
        self.A[1,2] = -K21*L23/self.J2
        self.A[1,3] = 1/self.m2+K21*K23/self.J2
        self.A[2,0] = 1/self.m2+L23*L21/self.J2
        self.A[2,1] = -L23*K21/self.J2
        self.A[2,2] = 1/self.m2+1/self.m3+L23*L23/self.J2+L32*L32/self.J3
        self.A[2,3] = -L23*K23/self.J2-L32*K32/self.J3
        self.A[3,0] = -K23*L21/self.J2
        self.A[3,1] = 1/self.m2+K23*K21/self.J2
        self.A[3,2] = self.A[2,3]
        self.A[3,3] = 1/self.m2+1/self.m3+K23*K23/self.J2+K32*K32/self.J3
        self.B[0] = -Fxe2/self.m2+Me2*L21/self.J2+self.omega2**2*K21
        self.B[1] = -Fye2/self.m2-Me2*K21/self.J2+self.omega2**2*L21
        self.B[2] = -Fxe2/self.m2+Fxe3/self.m3+Me2*L23/self.J2-Me3*L32/self.J3+self.omega2**2*K23-self.omega3**2*K32
        self.B[3] = -Fye2/self.m2+Fye3/self.m3-Me2*K23/self.J2+Me3*K32/self.J3+self.omega2**2*L23-self.omega3**2*L32
        F = solve(self.A,self.B)
        Fx12 = F[0][0]
        Fy12 = F[1][0]
        Fx32 = F[2][0]
        Fy32 = F[3][0]
        
        self.VX2 += h/self.m2*(Fxe2+Fx12+Fx32)
        self.VY2 += h/self.m2*(Fye2+Fy12+Fy32)
        self.omega2 += h/self.J2*(Me2+K21*Fy12-L21*Fx12+K23*Fy32-L23*Fx32)
        self.VX3 += h/self.m3*(Fxe3-Fx32)
        self.VY3 += h/self.m3*(Fye3-Fy32)
        self.omega3 += h/self.J3*(Me3-K32*Fy32+L32*Fx32)   
        
    def euler(self,T,theta2,theta3,h):
        self.theta2 = theta2
        self.theta3 = theta3
        self.omega2 = 0
        self.omega3 = 0
        self.X2 = self.l2*0.5*numpy.cos(self.theta2)
        self.Y2 = self.l2*0.5*numpy.sin(self.theta2)
        self.X3 = self.l2*numpy.cos(self.theta2)+self.l3*0.5*numpy.cos(self.theta3)
        self.Y3 = self.l2*numpy.sin(self.theta2)+self.l3*0.5*numpy.sin(self.theta3)
        self.VX2 = 0
        self.VY2 = 0
        self.VX3 = 0
        self.VY3 = 0
        t = 0.0
        liste_y = [[self.X2,self.Y2,self.theta2,self.X3,self.Y3,self.theta3]]
        liste_t = [t]
        while t < T:
            self.pas_euler(h)
            t += h
            liste_y.append([self.X2,self.Y2,self.theta2,self.X3,self.Y3,self.theta3])
            liste_t.append(t)
        return (numpy.array(liste_t),numpy.array(liste_y))
        
pendule = PenduleDouble3(1.0,1.0,1.0,1,1.0,1)
(t,y) = pendule.euler(50,1,0,1e-3)

figure()
plot(t,y[:,2],label="theta2")
plot(t,y[:,5],label="theta3")
legend(loc="upper right")
xlabel("t")
grid()

figE.pdf

figure()
plot(y[:,1],-y[:,0])
plot(y[:,4],-y[:,3])
axes().set_aspect('equal')
xlabel('y')
ylabel('x')
grid()

figF.pdf

Il est intéressant de comparer cette méthode à celle utilisée en partie 2. Le système linéaire à résoudre comporte 4 équations (autant que de composantes de forces inconnues), alors qu'il en comportait 10 dans la première méthode. Par ailleurs, le remplissage de la matrice est beaucoup plus simple car il ne nécessite pas d'analyse cinématique du système. Il sera aisé de construire un algorithme permettant de remplir cette matrice dans le cas général, par exemple pour traiter le cas du pendule à N bras.

Références

[1] A.A. Shabana, Computational dynamics, (John Wiley and Sons, 2001)

[2] H. Goldstein, Classical mechanics, (Addison-Wesley, 1980)

[3] M. G. Coutinho, Guide to dynamic simulations of rigids bodies and particle systems, (Springer, 2013)