Gaz parfait

1. Définition du modèle

On considère un modèle de gaz parfait classique, constitué de N particules ponctuelles se déplaçant sur un domaine bidimensionnel. Les coordonnées (x,y) des particules sont dans l'intervalle [0,1]. Les particules ont la même probabilité de se trouver en tout point de ce domaine (la densité de probabilité est uniforme).

Soit ${\vec{v}}_{i}$ la vitesse de la particule i. Pour un gaz parfait, il n'y a pas d'énergie d'interaction entre les particules, donc l'énergie totale du système est la somme des énergies cinétiques des particules :

E = \frac{1}{2} \sum_{i = 1}^{N} {\vec{v}}_{i}^{2} (1)

L'énergie totale est supposée constante. Toutes les configurations de vitesse qui vérifient cette équation sont équiprobables.

On se propose de faire une simulation de Monte-Carlo, consistant à échantillonner les positions et les vitesses aléatoirement afin de faire des calculs statistiques. Il faudra pour cela respecter les deux hypothèses d'équiprobabilité énoncées précédemment.

La distribution des positions est indépendante de la distribution des vitesses. On peut donc traiter séparément l'échantillonnage des positions et celui des vitesses.

2. Distribution des positions

2.a. Objectif

On doit générer P configurations de position de N particules, sachant que toutes les positions dans le domaine [0,1]x[0,1] ont la même probabilité.

On s'intéresse à la fraction n de particules qui sont dans la première moitié du domaine, c'est-à-dire dont l'abscisse vérifie :

x \in [0, \frac{1}{2}] (2)

Pour les P configurations, on calcule la valeur moyenne $\bar{n}$ et l'écart-type Δn.

L'échantillonnage doit être fait pour un nombre P de configurations assez grand, et répété pour plusieurs valeurs de N. L'objectif est de tracer la moyenne et l'écart-type en fonction de N, pour un nombre P fixé.

2.b. Échantillonnage direct

Dans cette méthode, on génère aléatoirement les positions de toutes les particules pour chaque nouvelle configuration.

import numpy
import numpy.random
import random
import math
from matplotlib.pyplot import *

La fonction suivante effectue l'échantillonnage direct. Elle renvoit la moyenne de n et son écart-type :

def position_direct(N,P):

def position_direct(N,P):
    somme_n = 0
    somme_n2 = 0
    for k in range(P):
        x = numpy.random.random_sample(N)
        n = 0
        for i in range(N):
            if x[i]<0.5:
                n += 1
        somme_n += n*1.0/N
        somme_n2 += n*n*1.0/(N*N)
    moy_n = somme_n/P
    var_n = somme_n2/P-moy_n**2
    dn = math.sqrt(var_n)
    print(moy_n,dn)
    return (moy_n,dn)

Voici un exemple. On calcule la moyenne et l'écart-type pour trois valeurs différentes de N :

liste_N = [10,100,1000,10000]
liste_n = []
liste_dn = []
P = 1000
for N in liste_N:
    (n,dn) = position_direct(N,P)
    liste_n.append(n)
    liste_dn.append(dn)
         
figure()
errorbar(liste_N,liste_n,yerr=liste_dn,fmt=None)
xlabel("N")
ylabel("n")
xscale('log')
grid()
axis([1,1e4,0,1])

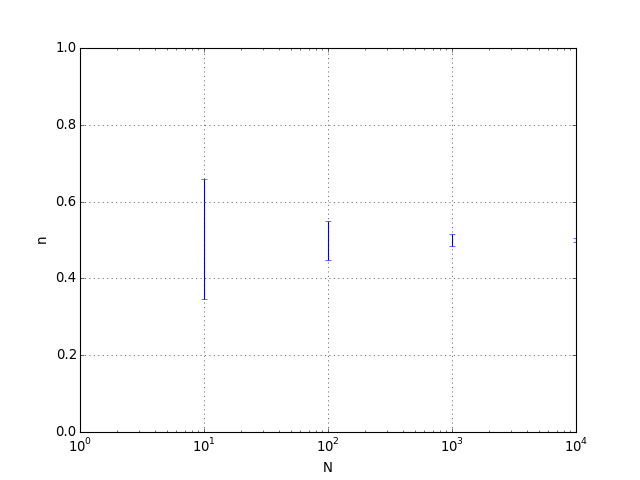fig1.pdf

On voit la décroissance de l'écart-type lorsque N augmente. Il décroît comme l'inverse de la racine carré de N. Physiquement, cet écart représente l'amplitude des fluctuations de densité dans le gaz. Lorsque le nombre de particule est de l'ordre du nombre d'Avogadro, ces fluctuations sont extrêmement faibles.

2.c. Échantillonnage de Metropolis

Dans cette méthode, la position des particules est mémorisée. Au départ, on les répartit aléatoirement. Pour obtenir une nouvelle configuration, on ne déplace qu'une seule particule. Pour cela, on tire aléatoirement une particule parmi les N particules, puis on choisi aléatoirement un déplacement $\vec{d}$ limité à l'intérieur d'un carré, c'est-à-dire dont les composantes vérifient :

\begin{matrix} | d_{x} | < d_{m} & (3) \\ | d_{y} | < d_{m} & (4) \end{matrix}

La distance maximale d_m pourra être modifiée. Tous les déplacements vérifiant cette condition sont équiprobables.

Lorsque le déplacement conduit à placer la particule en dehors du domaine, ce déplacement n'est pas effectué et la nouvelle configuration est identique à la précédente.

La fonction suivante effectue l'échantillonnage de Metropolis :

def position_metropolis(N,P,dm):

def position_metropolis(N,P,dm):
    somme_n = 0
    somme_n2 = 0
    x = numpy.random.random_sample(N)
    y = numpy.random.random_sample(N)
    for k in range(P):
        i = random.randint(0,N-1)
        dx = (random.random()*2-1)*dm
        dy = (random.random()*2-1)*dm
        x1 = x[i]+dx
        y1 = y[i]+dy
        if ((x1<1)and(x1>0)and(y1<1)and(y1>0)):
            x[i] = x1
            y[i] = y1
        n = 0
        for i in range(N):
            if x[i]<0.5:
                n += 1
        somme_n += n*1.0/N
        somme_n2 += n*n*1.0/(N*N)
    moy_n = somme_n/P
    var_n = somme_n2/P-moy_n**2
    dn = math.sqrt(var_n)
    print(moy_n,dn)
    return (moy_n,dn)

Par rapport à l'échantillonnage direct, il faut un nombre de tirages plus grand :

liste_N = [10,100,1000,10000]
liste_n = []
liste_dn = []
P = 10000
for N in liste_N:
    (n,dn) = position_metropolis(N,P,0.2)
    liste_n.append(n)
    liste_dn.append(dn)
         
figure()
errorbar(liste_N,liste_n,yerr=liste_dn,fmt=None)
xlabel("N")
ylabel("n")
xscale('log')
grid()
axis([1,1e4,0,1])

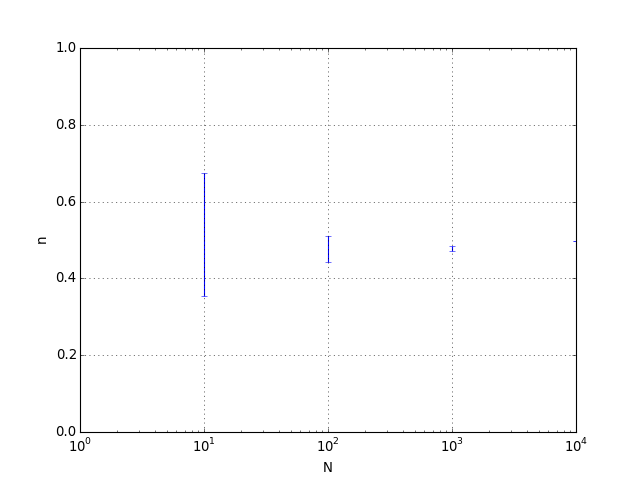fig2.pdf

3. Distribution des vitesses

3.a. Distribution des énergies cinétiques

On s'intéresse à présent à la distribution des vitesses des N particules, sans se préoccuper de leurs positions. L'énergie totale E est constante. On note e_i l'énergie cinétique de la particule i. Il faut répartir l'énergie E en N énergies cinétiques de particules, sachant que toutes les configurations de vitesse sont équiprobables. Pour cela, on doit choisir aléatoirement N-1 frontières sur l'intervalle [0,E], comme le montre la figure suivante :

Figure pleine page

Les intervalles obtenus définissent les énergies cinétiques des particules. Les N-1 frontières sont tirées aléatoirement avec une densité de probabilité uniforme sur l'intervalle [0,E]. Il faut trier les valeurs puis calculer les énergies cinétiques des N particules en parcourant la liste des frontières par valeurs croissantes.

L'objectif est de calculer un histogramme représentant la distribution des énergies cinétiques. Notons H cet histogramme, e_m l'énergie cinétique maximale et nh le nombre d'intervalles qu'il contient. L'histogramme est un tableau à nh cases. Chaque case correspond à un intervalle d'énergie de largeur h=e_m/nh. La case H[i] correspond à l'intervalle d'énergie cinétique [hi,h(i+1)].

On fait P tirages de N énergies cinétiques. Pour chacune des énergies cinétiques obtenues, on complète l'histogramme en incrémentant d'une unité la case correspondant à cette énergie.

Lorsque les P tirages sont effectués, on divise les valeurs de l'histogramme par la somme de toutes ses valeurs, de manière à obtenir des probabilités pour chaque intervalle d'énergie cinétique. Enfin on trace l'histogramme en fonction de l'énergie cinétique.

import numpy
import numpy.random
import math
from matplotlib.pyplot import *

La fonction suivante effectue les P tirages. Elle renvoit l'histogramme et les énergies cinétiques correspondantes.

def distribution_energies(N,E,ecm,nh,P):

def distribution_energies(N,E,em,nh,P):
    histogramme = numpy.zeros(nh)
    h = em*1.0/nh
    energies = numpy.arange(nh)*h    
    for k in range(P):
        partition = numpy.random.random_sample(N-1)*E
        partition = numpy.sort(partition)
        partition = numpy.append(partition,E)
        p = 0
        for i in range(N):
            e = partition[i]-p
            p = partition[i]
            m = math.floor(e/h)
            if m<nh:
                histogramme[m] += 1
    return (energies,histogramme/(P*N))

Voici un exemple :

E=1.0
N=1000
ecm=0.01
nh=100
P=1000
(e,h)= distribution_energies(N,E,ecm,nh,P)
figure()
plot(e,h,'o')
xlabel('ec')
ylabel('proba')
grid()

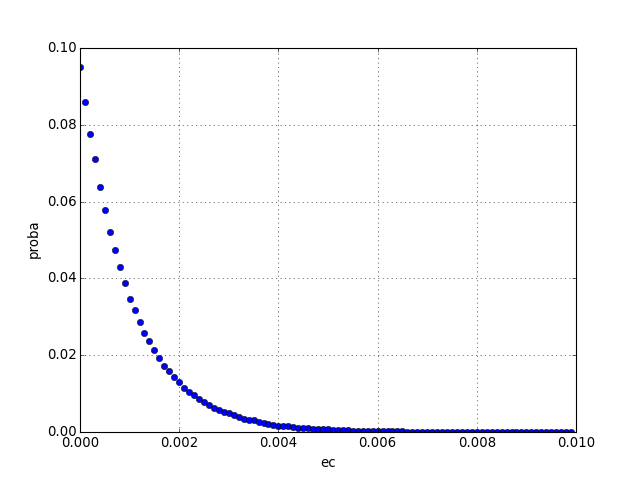figA.pdf

Les énergies cinétiques obéissent à la distribution de Boltzmann (distribution exponentielle). La température est T=E/N, l'énergie cinétique moyenne des particules. Pour le vérifier, on divise l'histogramme par sa première valeur, on le multiplie par E/N, puis on trace le logarithme népérien :

figure()
plot(e,numpy.log(h/h[0])*E/N,'o')
xlabel('ec')
ylabel('ln(p/p0)')
grid()

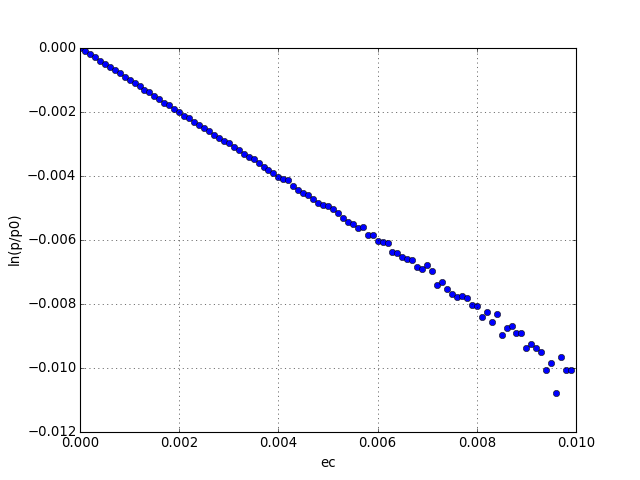figB.pdf

La probabilité pour une particule d'avoir l'énergie cinétique e est bien :

p (e) = p (0) e^{- \frac{e}{T}} (5)

3.b. Distribution des vitesses

On cherche la distribution de la norme du vecteur vitesse. La fonction suivante calcule l'histogramme. vm est la vitesse maximale.

def distribution_vitesses(N,E,vm,nh,P)

def distribution_vitesses(N,E,vm,nh,P):
    histogramme = numpy.zeros(nh)
    h = vm*1.0/nh
    energies = numpy.arange(nh)*h    
    for k in range(P):
        partition = numpy.random.random_sample(N-1)*E
        partition = numpy.sort(partition)
        partition = numpy.append(partition,E)
        p = 0
        for i in range(N):
            e = partition[i]-p
            p = partition[i]
            m = math.floor(math.sqrt(2*e)/h)
            if m<nh:
                histogramme[m] += 1
    return (energies,histogramme/(P*N))

Voici un exemple

vm = math.sqrt(2*ecm)
(v,h) = distribution_vitesses(N,E,vm,nh,P)
figure()
plot(v,h,'o')
xlabel('v')
ylabel('proba')
grid()

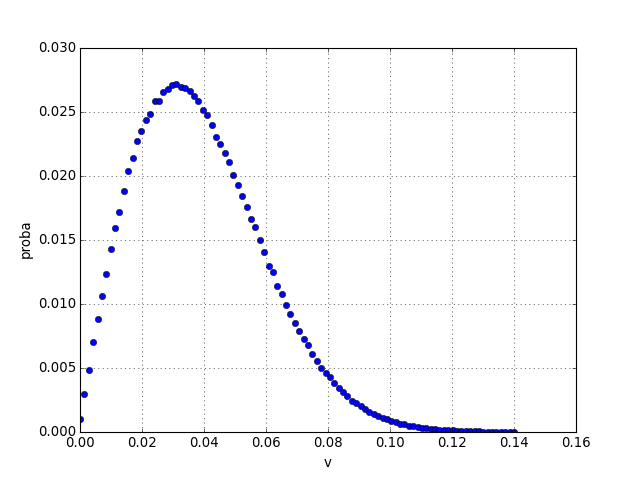figC.pdf

C'est la distribution des vitesses de Maxwell.

Simulation de Monte-Carlo d'un gaz parfait