Schrödinger

Équation de Schrödinger

1. Rayonnement électromagnétique

a. Quantum de rayonnement

Plus petite énergie dans un rayonnement électromagnétique de fréquence $ν$ :

E = h ν = ℏ ω

Constante de Planck :

h = 6, 626 \cdot 1 0^{- 34} J \cdot s, ℏ = \frac{h}{2 π}

L'échange d'énergie matière-rayonnement est quantifié. Photon : quantum d'énergie $E$ .

Quantité de mouvement d'un photon :

\vec{p} = ℏ \vec{k} = \frac{h}{λ} \vec{u}

Le photon est une particule de rayonnement, de masse nulle, dont la vitesse est $c$ dans tout référentiel.

1. Rayonnement électromagnétique

a. Quantum de rayonnement

b. Amplitude complexe de l'onde électromagnétique

Onde électromagnétique polarisée rectilignement.

Amplitude complexe du champ électrique :

\underset{̲}{E_{x}} (x, y, z, t)

Équation des ondes dans le vide :

\nabla^{2} \underset{̲}{E_{x}} = \frac{1}{c^{2}} \frac{\partial^{2} \underset{̲}{E_{x}}}{\partial t^{2}}

Interprétation probabiliste : la probabilité de détecter un photon sur un capteur plan en $z=0$, en un point $M (x, y)$ , à l'instant $t$ , est :

d P = | \underset{̲}{E_{x}} (x, y, 0, t) |^{2} d x d y

$| \underset{̲}{E_{x}} |^{2}$ est une densité de probabilité, proportionnelle à l'intensité lumineuse.

Simulation : Diffraction de photons.

2. Comportement ondulatoire des particules

a. Relation de de Broglie

Particule matérielle : électron, neutron, proton, atome, ion, etc.

Quantité de mouvement (ou impulsion) d'une particule matérielle (de masse $m$ ) non relativiste :

\vec{p} = m \vec{v}

Relation de de Broglie (1923) : une particule matérielle possède des propriétés ondulatoires.

\begin{matrix} λ = \frac{h}{p} \\ \vec{p} = ℏ \vec{k} \end{matrix}

2. Comportement ondulatoire des particules

a. Relation de de Broglie

b. Fonction d'onde

Il est impossible de prévoir la position d'une particule même si son état initial est connu.

La physique quantique donne des lois de probabilité pour les résultats des mesures physiques.

Fonction d'onde associée à une particule matérielle :

\underset{̲}{ψ} (x, y, z, t)

La probabilité de détecter la particule dans le volume élémentaire $d V$ situé en $(x, y, z)$ , à l'instant $t$ , est :

d P = | \underset{̲}{ψ} (x, y, z, t) |^{2} d V

Densité de probabilité associée à la mesure de position de la particule à l'instant t :

ρ (x, y, z, t) = | \underset{̲}{ψ} (x, y, z, t) |^{2} = \underset{̲}{ψ} {\underset{̲}{ψ}}^{*}

La fonction d'onde est une amplitude complexe de probabilité et rien d'autre (pas de champ physique associé).

2. Comportement ondulatoire des particules

a. Relation de de Broglie

b. Fonction d'onde

c. Onde de de Broglie

Onde de de Broglie : onde associée à une particule matérielle libre dont l'impulsion est $\vec{p}$ .

Énergie de la particule libre (non relativiste) :

E = E_{c} = \frac{p^{2}}{2 m}

Pulsation de l'onde : $ω = \frac{E}{ℏ}$

Vecteur d'onde : $\vec{k} = \frac{\vec{p}}{ℏ}$

Fonction d'onde pour une particule libre d'impulsion $\vec{p} = p \vec{u_{x}}$ :

\underset{̲}{ψ} (x, t) = \underset{̲}{ψ_{0}} e^{i (k x - ω t)} = \underset{̲}{ψ_{0}} e^{i (\frac{p}{ℏ} x - \frac{E}{ℏ} t)}

Densité de probabilité uniforme dans tout l'espace :

| \underset{̲}{ψ} |^{2} = | \underset{̲}{ψ_{0}} |^{2}

Physiquement impossible.

Une fonction d'onde physiquement possible doit être normalisée

\int_{- \infty}^{\infty} | \underset{̲}{ψ} (x) |^{2} d x = 1

L'onde de de Broglie n'est pas normalisable.

2. Comportement ondulatoire des particules

a. Relation de de Broglie

b. Fonction d'onde

c. Onde de de Broglie

d. Preuves expérimentales

Exemple : électron accéléré par une d.d.p. de 10 V :

\begin{matrix} m = 9, 31 \cdot 1 0^{- 31} k g \\ E = 10 e V \\ v = \sqrt{\frac{2 E}{m}} = 1, 8 \cdot 1 0^{6} m \cdot s^{- 1} \\ λ = \frac{h}{m v} = 0, 38 n m \\ ν = 2, 4 \cdot 1 0^{15} H z \end{matrix}

Diffraction d'électrons par un cristal : expérience de Davisson et Germer (1927).

L'onde associée aux électrons est diffractée par le réseau cristallin de la cible.

Maximum d'électrons reçus dans des directions correspondant aux interférences constructives.

Expérience de Young avec des électrons de longueur d'onde $λ = 50 p m$ et deux fentes d'espacement $a = 272 n m$

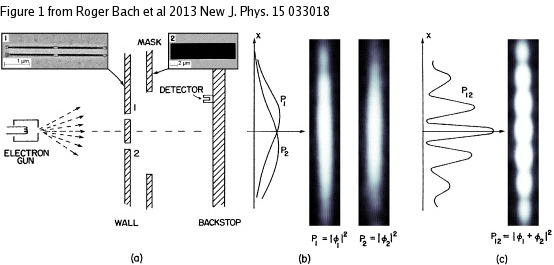
Probabilité d'impact sur le détecteur : $| \underset{̲}{ψ} (x) |^{2}$ .

Franges d'interférence.

Pas de franges avec une seule fente.

3. Équation de Schrödinger

a. Particule libre

Équation différentielle pour la fonction d'onde d'une particule ?

Particule libre d'impulsion $\vec{p} = p {\vec{u}}_{x}$ :

\underset{̲}{ψ} (x, t) = \underset{̲}{ψ_{0}} e^{i (\frac{p}{ℏ} x - \frac{E}{ℏ} t)}

\begin{matrix} i ℏ \frac{\partial \underset{̲}{ψ}}{\partial t} = E \underset{̲}{ψ} \\ - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} \underset{̲}{ψ}}{\partial x^{2}} = \frac{p^{2}}{2 m} \underset{̲}{ψ} \end{matrix}

Pour une particule libre non relativiste :

E = \frac{p^{2}}{2 m}

Équation aux dérivées partielles pour la fonction d'onde d'une particule (matérielle) libre non relativiste :

i ℏ \frac{\partial \underset{̲}{ψ} (x, t)}{\partial t} = - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} \underset{̲}{ψ} (x, t)}{\partial x^{2}}

3. Équation de Schrödinger

a. Particule libre

b. Particule dans un potentiel

Particule non relativiste se déplaçant sur un axe $(O x)$ .

Fonction d'onde $\underset{̲}{ψ} (x, t)$ .

Probabilité de détecter la particule entre $x$ et $x+dx$ à l'instant $t$ :

d P = | \underset{̲}{ψ} (x, t) |^{2} d x

Hypothèse : l'interaction de la particule avec son environnement peut être modélisée par une énergie potentielle $V (x)$ .

Équation de Schrödinger (1925) pour une particule de masse $m$ non relativiste se déplaçant sur un axe $(O x)$ dans une énergie potentielle $V (x)$ :

i ℏ \frac{\partial \underset{̲}{ψ} (x, t)}{\partial t} = - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} \underset{̲}{ψ} (x, t)}{\partial x^{2}} + V (x) \underset{̲}{ψ} (x, t)

3. Équation de Schrödinger

a. Particule libre

b. Particule dans un potentiel

c. État stationnaire

L'état stationnaire d'une particule est un état d'énergie déterminée :

\underset{̲}{ψ} (x, t) = e^{- i \frac{E}{ℏ} t} \underset{̲}{φ} (x)

La fonction d'onde est sinusoïdale par rapport au temps.

Équation de Schrödinger indépendante du temps :

\frac{d^{2} \underset{̲}{φ} (x)}{d x^{2}} + \frac{2 m (E - V (x))}{ℏ^{2}} \underset{̲}{φ} (x) = 0

La densité de probabilité est stationnaire :

ρ = \underset{̲}{ψ} {\underset{̲}{ψ}}^{*} = \underset{̲}{φ} {\underset{̲}{φ}}^{*}

Exemple : particule dans un potentiel uniforme $V = V_{o}$ (particule libre), d'énergie $E > V_{0}$ :

\begin{matrix} k = \frac{\sqrt{2 m (E - V_{o})}}{ℏ} \\ \underset{̲}{φ} (x) = A e^{i k x} + B e^{- i k x} \end{matrix}

État quantique de superposition de deux impulsions :

\begin{matrix} \vec{p} = ℏ k {\vec{u}}_{x} e t \vec{p}' = - ℏ k {\vec{u}}_{x} \end{matrix}

Si $B = 0$ , le sens de l'impulsion est déterminé.

E = \frac{p^{2}}{2 m} + V_{o}

3. Équation de Schrödinger

a. Particule libre

b. Particule dans un potentiel

c. État stationnaire

d. Principe de superposition

Soient ${\underset{̲}{ψ}}_{1} (x, t)$ et ${\underset{̲}{ψ}}_{2} (x, t)$ deux solutions de l'équation de Schrödinger pour un potentiel $V (x)$

\underset{̲}{ψ} (x, t) = {\underset{̲}{ψ}}_{1} (x, t) + {\underset{̲}{ψ}}_{2} (x, t)

est solution de l'équation de Schrödinger pour le même potentiel.

Densité de probabilité de la position :

ρ = | {\underset{̲}{ψ}}_{1} |^{2} + | \underset{̲}{ψ_{2}} |^{2} + ({\underset{̲}{ψ}}_{1} {\underset{̲}{ψ}}_{2}^{*} + {\underset{̲}{ψ}}_{1}^{*} {\underset{̲}{ψ}}_{2})

Existence d'un terme d'interférence.

Les probabilités ne s'ajoutent pas.

Exemple : expérience de Young avec des électrons.

Une seule fente ouverte :

Fente 1 seule : densité de probabilité $ρ_{1} (x)$ .

Fente 2 seule : densité de probabilité $ρ_{2} (x)$ .

Avec les deux fentes :

ρ \neq ρ_{1} + ρ_{2}

L'affirmation «la particule passe par une des deux fentes» est fausse.

Notion de trajectoire d'une particule invalide lorsque la longueur d'onde n'est pas négligeable devant la taille des objets.

La particule est détectée en un point du capteur (résolution plus ou moins grande) mais le mouvement de la particule entre la source et le détecteur ne peut être représenté par une courbe dans l'espace.

Le phénomène d'interférence devient négligeable si les fentes sont très espacées (par rapport à la longueur d'onde).

La diffraction est négligeable si la largeur des fentes est grande devant la longueur d'onde.

Approximation de la trajectoire de la mécanique classique.

4. Paquet d'ondes

a. Normalisation de la fonction d'onde

La densité de probabilité associée aux mesures de position doit être normalisée :

\int_{- \infty}^{+ \infty} | \underset{̲}{ψ} (x, t) |^{2} d x = 1

La fonction d'onde doit être normalisable :

| | \underset{̲}{ψ} | | = \sqrt{\int_{- \infty}^{+ \infty} | \underset{̲}{ψ} (x, t) |^{2} d x}

doit être définie.

Fonction d'onde normalisée :

{\underset{̲}{ψ}}_{n} (x, t) = \frac{\underset{̲}{ψ} (x, t)}{| | \underset{̲}{ψ} | |}

L'onde de de Broglie :

\underset{̲}{ψ} (x, t) = \underset{̲}{ψ_{0}} e^{i (\frac{p}{ℏ} x - \frac{E}{ℏ} t)}

n'est pas normalisable.

Comment définir une fonction d'onde normalisable pour une particule libre ?

4. Paquet d'ondes

a. Normalisation de la fonction d'onde

b. Paquet d'ondes

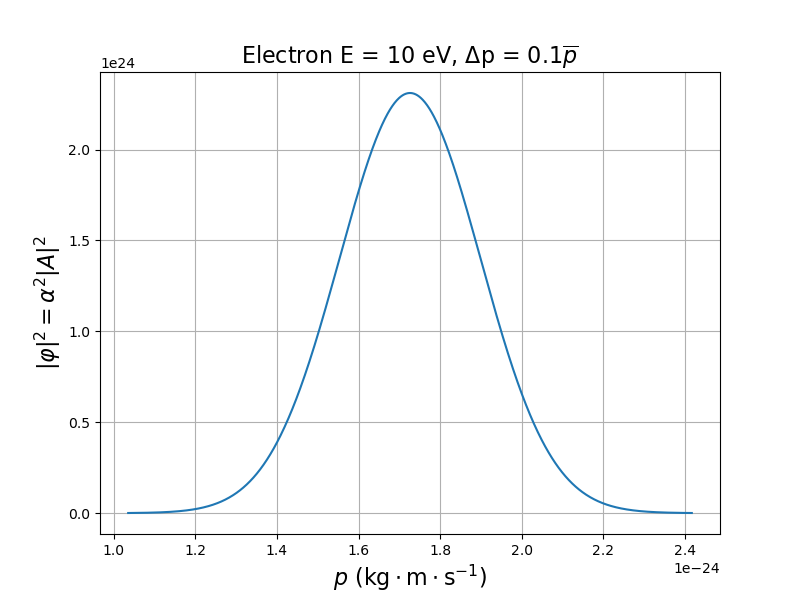
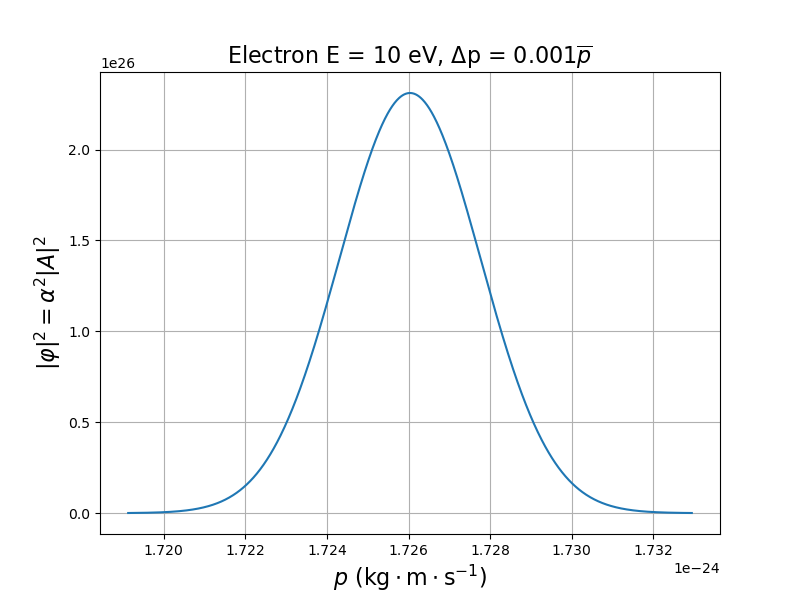
Somme continue d'ondes de de Broglie de différentes impulsions :

\underset{̲}{ψ} (x, t) = \int_{- \infty}^{+ \infty} \underset{̲}{A} (p) e^{i (\frac{p}{ℏ} x - \frac{E (p)}{ℏ} t)} d p

Spectre en impulsion : $\underset{̲}{A} (p)$ .

Relation de dispersion :

E (p) = \frac{p^{2}}{2 m}

$\underset{̲}{φ} (p) = α \underset{̲}{A} (p)$ est une amplitude de probabilité relative aux mesures d'impulsions.

$α$ : facteur de normalisation.

Probabilité qu'une mesure de l'impulsion donne une valeur comprise entre $p$ et $p + d p$ :

α^{2} | \underset{̲}{A} (p) |^{2} d p

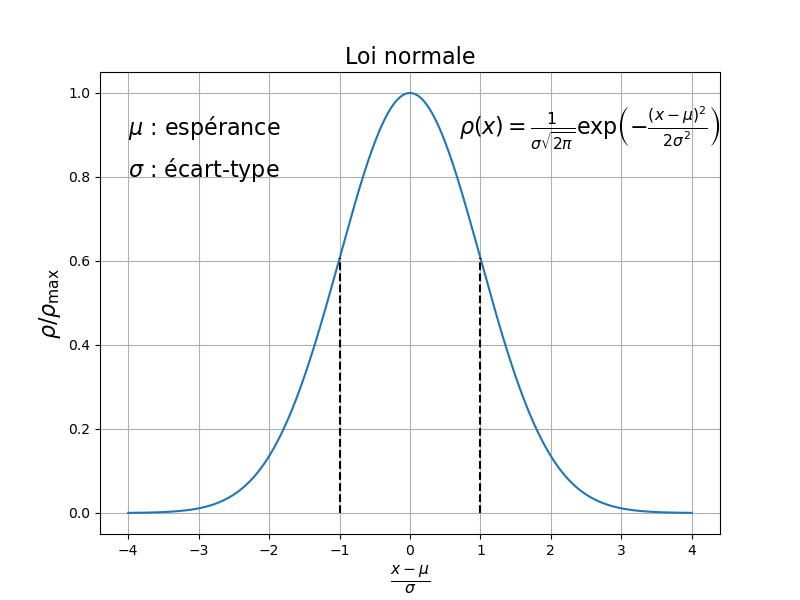
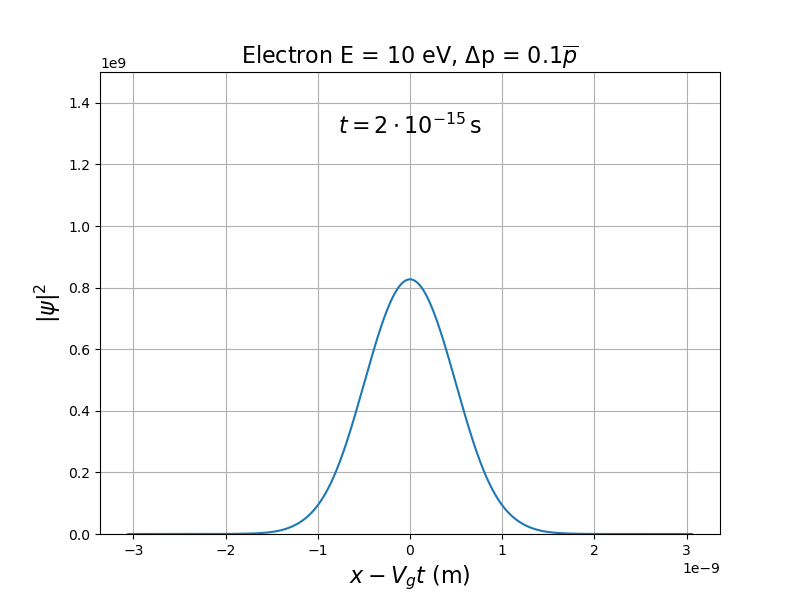
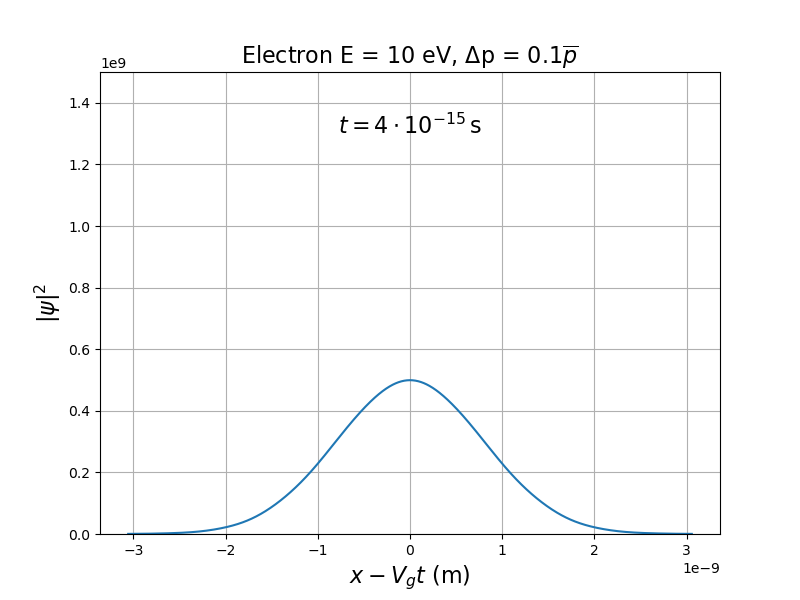
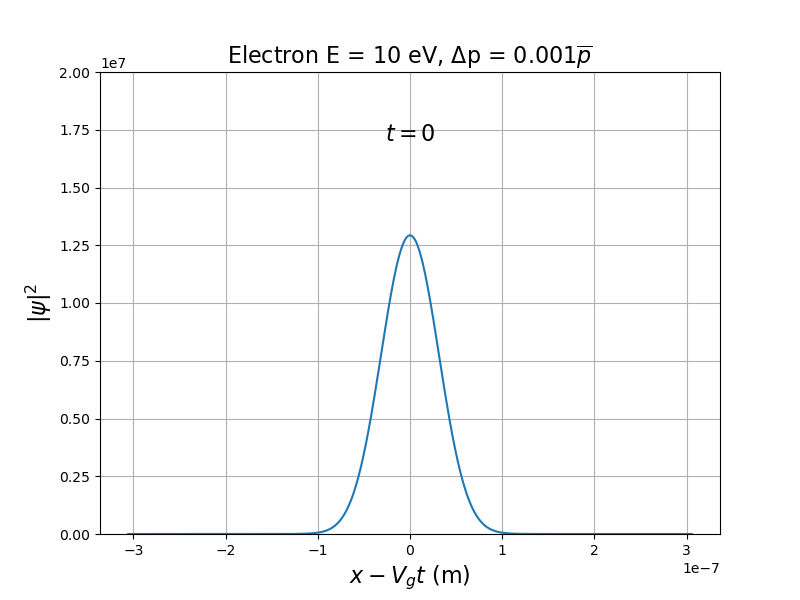
Paquet d'ondes gaussien : $| \underset{̲}{φ} (p) |^{2}$ est définie par la loi normale.

$| \underset{̲}{ψ} (x, t) |^{2}$ (à t fixé) suit aussi la loi normale.

Les ondes de de Broglie sont dispersives.

Vitesse de groupe :

v_{g} = \frac{d ω}{d k} = \frac{d E}{d p} = \frac{\bar{p}}{m}

$v_{g}$ est la vitesse moyenne de la particule.

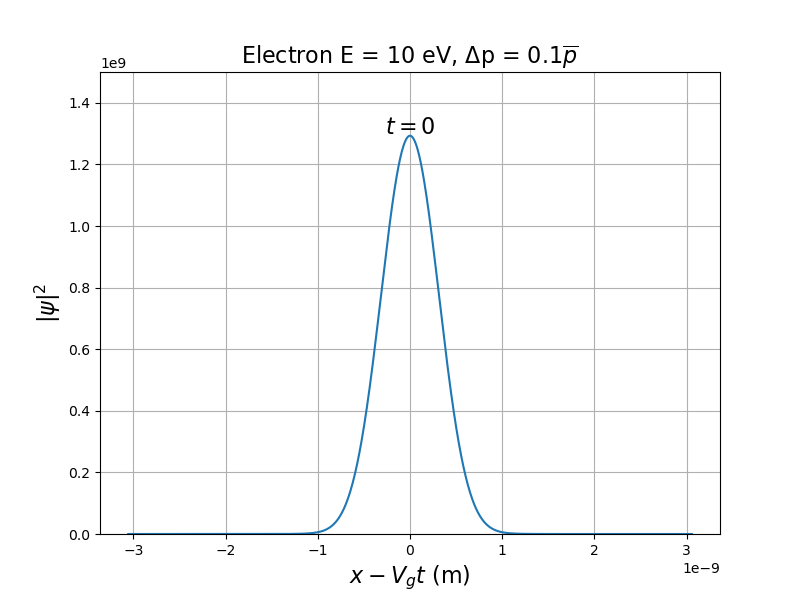
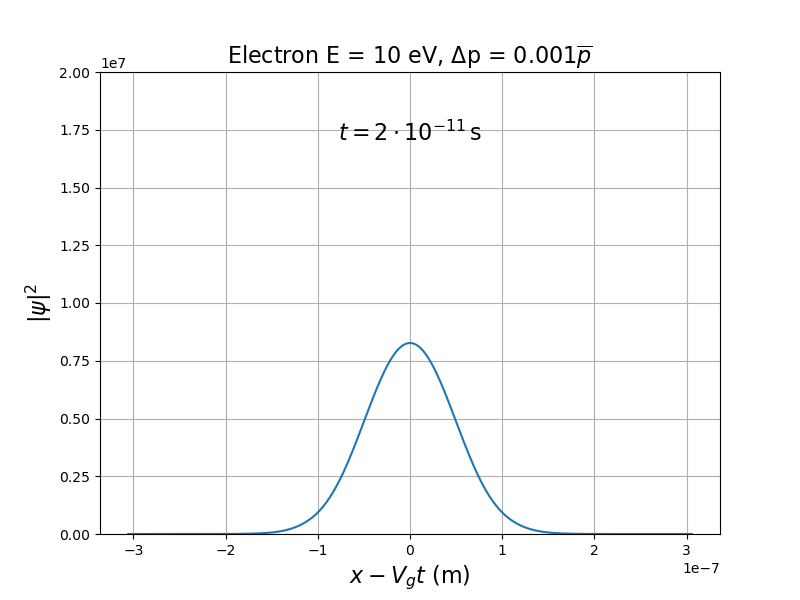
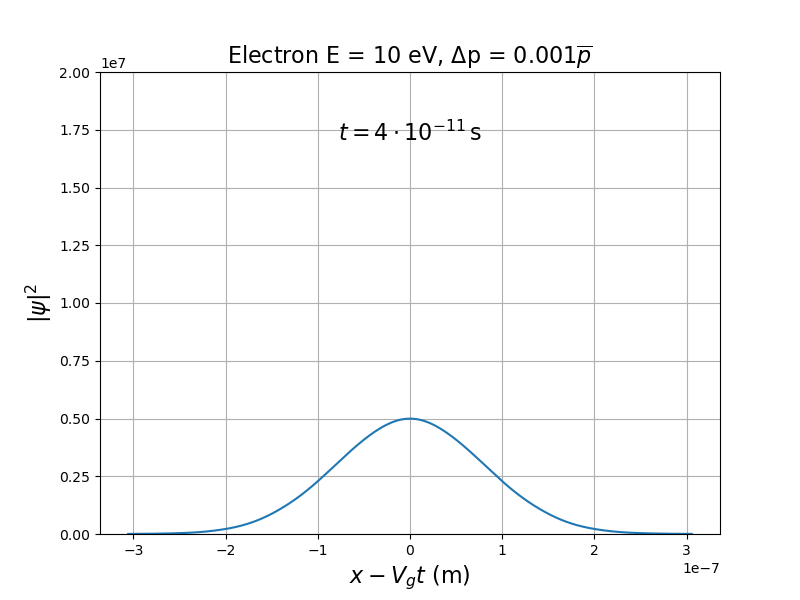
Étalement du paquet d'ondes.

Simulation : Paquet d'ondes de matière

4. Paquet d'ondes

a. Normalisation de la fonction d'onde

b. Paquet d'ondes

c. Ecart-types des résultats de mesures

Pour une particule dans un état donné (fonction d'onde donnée), le résultat d'une mesure de position est aléatoire (imprévisible).

Position moyenne (espérance) : $\bar{x}$ .

Écart-type des mesures de position :

Δ x = \sqrt{\bar{x^{2}} - {\bar{x}}^{2}}

Pour un paquet d'ondes gaussien : probabilité de 0,68 que le résultat de la mesure soit dans l'intervalle $[\bar{x} - Δ x, \bar{x} + Δ x]$ .

$2 Δ x$ est l'ordre de grandeur de la largeur du paquet d'ondes.

Pour une particule dans un état donné, le résultat d'une mesure d'impulsion est aléatoire.

Écart-type des mesures d'impulsion :

Δ p = \sqrt{\bar{p^{2}} - {\bar{p}}^{2}}

$Δ x$ et $Δ p$ quantifient les indéterminations quantiques de $x$ et $p$ , dues à leur caractère fondamentalement aléatoire.

Ne pas confondre avec l'incertitude des instruments de mesure (supposée négligeable).

4. Paquet d'ondes

a. Normalisation de la fonction d'onde

b. Paquet d'ondes

c. Ecart-types des résultats de mesures

d. Inégalité d'Heisenberg

Inégalité d'Heisenberg (1927), ou relation d'indétermination d'Heisenberg :

Δ x Δ p \geq \frac{ℏ}{2}

Plus l'indétermination sur l'impulsion est faible, plus celle sur la position est grande, et inversement.

En mécanique newtonienne, la position et l'impulsion sont parfaitement déterminées.

Pour un paquet d'ondes gaussien avant l'étalement :

Δ x Δ p = \frac{ℏ}{2}

Si le spectre $\underset{̲}{A} (p)$ est fixé, $Δ p$ est constant mais $Δ x$ augmente au cours du temps (étalement du paquet).

Simulation : Paquet d'ondes de matière

Exemple : électron d'énergie moyenne 10 eV :

\begin{matrix} \bar{E} = 10 e V \\ \bar{p} = \sqrt{2 m \bar{E}} = 1, 7 \cdot 1 0^{- 24} k g \cdot m \cdot s^{- 1} \\ \bar{λ} = \frac{h}{\bar{p}} = 0, 38 n m \\ Δ p = 0, 1 \bar{p} = 1, 7 \cdot 1 0^{- 25} k g \cdot m \cdot s^{- 1} (h y p o t h è s e) \\ Δ x \approx \frac{ℏ}{2 Δ p} = 0, 31 n m \end{matrix}

Nanoparticule sphérique :

\begin{matrix} r = 100 n m \\ m = 4, 2 \cdot 1 0^{- 18} k g \\ \frac{{\bar{p}}^{2}}{2 m} = \frac{3}{2} k_{B} T \\ \bar{p} = 2, 3 \cdot 1 0^{- 19} k g \cdot m \cdot s^{- 1} \\ Δ p = 1 0^{- 4} \bar{p} = 2, 3 \cdot 1 0^{- 23} k g \cdot m \cdot s^{- 1} \\ Δ x = \frac{ℏ}{2 Δ p} = 2, 3 \cdot 1 0^{- 12} m = 2, 3 \cdot 1 0^{- 3} n m \end{matrix}

Particule non quantique : $Δ x$ et $Δ p$ négligeables devant la précision des instruments de mesure.

Les lois de Newton s'appliquent.

4. Paquet d'ondes

a. Normalisation de la fonction d'onde

b. Paquet d'ondes

c. Ecart-types des résultats de mesures

d. Inégalité d'Heisenberg

e. Particule délocalisée

Particule dont l'impulsion est peu indéterminée :

\begin{matrix} Δ p ≪ p \\ \frac{ℏ}{2 Δ x} ≪ ℏ k \\ Δ x ≫ λ \end{matrix}

Fonction d'onde approximative :

\underset{̲}{ψ} (x, t) \approx \underset{̲}{ψ_{0}} e^{i (\frac{p}{ℏ} x - \frac{E}{ℏ} t)}

limitée sur une longueur de l'ordre de $4 Δ x$ .

4. Paquet d'ondes

a. Normalisation de la fonction d'onde

b. Paquet d'ondes

c. Ecart-types des résultats de mesures

d. Inégalité d'Heisenberg

e. Particule délocalisée

f. Réduction et étalement du paquet d'ondes

Inégalités d'Heisenberg pour un mouvement dans l'espace :

\begin{matrix} Δ x Δ p_{x} \geq \frac{ℏ}{2} \\ Δ y Δ p_{y} \geq \frac{ℏ}{2} \\ Δ z Δ p_{z} \geq \frac{ℏ}{2} \end{matrix}

Aucune relation entre $Δ x$ et $Δ p_{y}$ .

Diffraction de particules par une ouverture de diamètre $b$ .

Largeur du paquet d'ondes incident grande devant $b$ .

L'ouverture permet de déterminer (mesurer) la position transversale avec une précision $b$ .

Juste après l'ouverture, la largeur du paquet d'onde est réduite à $b$ .

L'indétermination $Δ p_{y}$ est augmentée.

L'étalement du paquet dans la direction $y$ devient plus rapide : phénomène de diffraction.

4. Paquet d'ondes

a. Normalisation de la fonction d'onde

b. Paquet d'ondes

c. Ecart-types des résultats de mesures

d. Inégalité d'Heisenberg

e. Particule délocalisée

f. Réduction et étalement du paquet d'ondes

g. Densité de courant de probabilité

Densité de probabilité pour la position : $ρ (x, t) = | \underset{̲}{ψ} (x, t) |^{2}$

\int_{- \infty}^{+ \infty} ρ (x, t) d x = 1

Si la densité diminue dans une région, elle doit augmenter dans une autre.

Équation locale de conservation de la probabilité :

\frac{\partial ρ}{\partial t} + \frac{\partial j_{x}}{\partial x} = 0

$\vec{j}$ : vecteur densité de courant de probabilité.

Pour une particule libre d'impulsion parfaitement déterminée, la densité de courant de probabilité est :

\vec{j} = ρ \vec{v} = | \underset{̲}{ψ} |^{2} \frac{\vec{p}}{m}

5. Annexe

a. Séparation des variables

i ℏ \frac{\partial \underset{̲}{ψ} (x, t)}{\partial t} = - \frac{ℏ^{2}}{2 m} \frac{\partial^{2} \underset{̲}{ψ} (x, t)}{\partial x^{2}} + V (x) \underset{̲}{ψ} (x, t)

Recherche d'une solution de la forme :

\underset{̲}{ψ} (x, t) = \underset{̲}{φ} (x) \underset{̲}{χ} (t)

N'est pas nécessairement une onde stationnaire.

i ℏ \frac{1}{\underset{̲}{χ}} \frac{d \underset{̲}{χ}}{d t} = - \frac{ℏ^{2}}{2 m} \frac{1}{\underset{̲}{φ}} \frac{d^{2} \underset{̲}{φ}}{d x^{2}} + V (x)

Fonction de $x$ égale à une fonction de $t$.

i ℏ \frac{1}{\underset{̲}{χ}} \frac{d \underset{̲}{χ}}{d t} = E

$E$ est une constante homogène à une énergie.

\frac{d \underset{̲}{χ}}{d t} + i \frac{E}{ℏ} \underset{̲}{χ} = 0

\underset{̲}{χ} (t) = exp (- i \frac{E}{ℏ} t)

D'après la relation de Planck-Einstein $E=\hbar\omega$ est l'énergie de la particule.

- \frac{ℏ^{2}}{2 m} \frac{1}{\underset{̲}{φ}} \frac{d^{2} \underset{̲}{φ}}{d x^{2}} + V (x) = E

\frac{d^{2} \underset{̲}{φ} (x)}{d x^{2}} + \frac{2 m (E - V (x))}{ℏ^{2}} \underset{̲}{φ} (x) = 0