Équation de Schrödinger

1.a. Quantum de rayonnement

L'hypothèse de quantification du rayonnement électromagnétique a été introduite en 1905 par Einstein, pour interpréter les résultats obtenus par Planck sur le rayonnement thermique du corps noir.

Dans une onde électromagnétique monochromatique de pulsation ω, l'énergie est quantifiée, c'est-à-dire qu'elle ne peut prendre que des valeurs multiples du quantum d'énergie :

$h=6,626\cdot 10^{-34}J\cdot s$ est la constante de Planck et $\hslash =h/2\pi$.

Cette relation entre l'énergie et la pulsation est la relation de Planck-Einstein. Elle précise la plus petite énergie qui peut être échangée entre une onde électromagnétique de pulsation ω et la matière (par ex. l'absorption ou l'émission de lumière par un atome). On dit que l'énergie d'une onde électromagnétique est quantifiée. Le quantum d'énergie de valeur E est appelé photon.

Dans certaines expériences, les photons se comportent comme des particules qui ont l'énergie E ci-dessus et la quantité de mouvement (ou impulsion) :

$$\overrightarrow{p}=\hslash \overrightarrow{k}\text{(2)}$$

où $\overrightarrow{k}$ est le vecteur d'onde.

Par exemple, une expérience de diffraction par une ouverture sur un écran, réalisée avec une source de très faible intensité, permet d'observer les impacts des photons sur un capteur, comme le montre la simulation Diffraction par une ou plusieurs ouvertures (sélectionner une ouverture à deux cercles et cocher particules pour simuler les impacts des photons dans une expérience de trous d'Young). Les impacts obtenus sur le capteur sont une manifestation corpusculaire de la lumière. En revanche, la répartition des impacts ne peut s'expliquer que par le caractère ondulatoire de la lumière. Les impacts des photons se répartissent sur le capteur en suivant une loi de probabilité qui correspond à l'intensité lumineuse.

Considérons par exemple l'expérience des fentes d'Young réalisée avec une source de lumière dont la puissance est si faible que les photons parviennent sur le capteur un par un. L'impact d'un photon sur le capteur est clairement discernable. Le point d'impact d'un photon est aléatoire, c'est-à-dire qu'il est imprévisible, mais la probabilité d'impact est plus forte là où l'intensité lumineuse (calculée avec la formule de Fresnel) est plus forte. Plus précisément, la densité de probabilité de répartition des impacts est proportionnelle à l'intensité lumineuse (ce point sera précisé plus loin).

Ainsi la lumière possède un double aspect, ondulatoire (phénomène d'interférence) et corpusculaire (impacts des photons).

On remarque que le photon possède une impulsion alors que sa masse est nulle. Il s'agit en effet d'une particule relativiste, puisqu'elle se déplace à la vitesse de la lumière dans le vide. Pour une particule relativiste sans masse, la relation entre l'énergie et l'impulsion est E=pc. Cette impulsion se manifeste par une force ressentie par une cible sur laquelle des photons sont envoyés.

Avec les sources de lumière usuelles (comme les lampes et les lasers), la quantification de l'énergie est imperceptible. Considérons par exemple une onde de lumière de puissance P=1 μW et de longueur d'onde λ=500 nm. L'énergie d'un photon est :

$$E=h\frac{c}{\lambda }=4\cdot 10^{-19}J\text{(3)}$$

Le flux de photons est donc P/E=2 10¹² photons par seconde. Sur un capteur, le taux d'arrivé des photons est beaucoup trop rapide pour qu'on puisse les détecter individuellement. Le capteur est sensible au flux d'énergie moyen, c'est-à-dire à l'intensité lumineuse (multipliée par la surface du capteur).

La quantification de l'énergie du rayonnement apparaît dans l'effet photoélectrique : lorsque la surface d'un métal est éclairée par un rayonnement ultraviolet, des électrons du métal sont extraits et éjectés dans le vide avec une énergie cinétique non nulle. Le dispositif suivant permet d'étudier le phénomène :

Figure pleine page

Les électrons éjectés sont collectés par l'anode et détectés par l'ampèremètre. Lorsqu'elle est positive, la différence de potentiel U permet de déccélerer les électrons éjectés. S'ils sont assez déccélérés, il ne parviennent pas à l'anode et l'intensité du courant dans l'ampèremètre est nulle. L'expérience montre que des électrons parviennent à l'anode seulement si U est en dessous d'une valeur bien précise et si la longueur d'onde est inférieure à une valeur bien précise. Si la longueur d'onde est supérieure à cette valeur, aucun effet photoélectrique n'est observé, même si l'intensité du rayonnement est augmentée. Ces résultats s'expliquent si l'on admet que l'éjection d'un électron du métal ne peut être provoquée que par un seul photon. Pour cela, le photon du rayonnement doit posséder une énergie qui excède une valeur W_s, appelée énergie d'extraction. L'excédent d'énergie apportée par le photon est converti en énergie cinétique de l'électron :

$$h\nu =W_s+E_c\text{(4)}$$

Par exemple, pour le zinc W_s=4,33 eV et la fréquence du rayonnement doit vérifier :

$$\nu >1,05\cdot 10^{15}Hz\text{(5)}$$

soit pour la longueur d'onde :

$$\lambda <287nm\text{(6)}$$

L'énergie cinétique E_c (exprimée en eV) est égale à la tension seuil en dessous de laquelle les électrons parviennent à l'anode. On constate en effet que la tension seuil augmente avec la fréquence de la lumière.

1.b. Ondes de de Broglie

En 1923, de Broglie (physicien français 1892-1987) a émis l'hypothèse que les particules matérielles, de masse non nulle, comme les électrons, les protons ou les neutrons, ont aussi des propriétés ondulatoires, qui se manifestent par une longueur d'onde donnée par la relation :

$$\lambda =\frac{h}{p}\text{(7)}$$

ou plus précisément par un vecteur d'onde relié à l'impulsion par la relation :

Pour définir une onde plane progressive monochromatique à partir de la relation de de Broglie, on doit aussi utiliser la relation de Planck-Einstein. Pour une particule se déplaçant dans une seule direction, la fonction d'onde s'écrit :

En mécanique quantique, la fonction d'onde associée à une particule est nécessairement à valeurs complexes. Pour un photon (et seulement dans ce cas), il s'agit de la représentation complexe du champ électrique de l'onde électromagnétique (approximation scalaire) mais pour une particule matérielle il ne s'agit pas d'une onde électromagnétique. Nous verrons plus loin la signification exacte de cette fonction d'onde.

Pour une particule libre non relativiste de masse m, l'énergie est égale à l'énergie cinétique :

$$E=\frac{p^2}{2m}\text{(10)}$$

En introduisant la pulsation et le nombre d'onde, on en déduit la relation suivante :

$$k^2=\frac{2m}{\hslash }\omega \text{(11)}$$

Cette équation est la relation de dispersion d'une onde de de Broglie associée à une particule libre (non relativiste). On voit ainsi que la propagation de cette onde dans le vide se fait de manière dispersive, puisque la vitesse de phase dépend de la pulsation.

Le comportement ondulatoire de la matière se manifeste avec des objets microscopiques (électrons, atomes, etc.). Considérons par exemple l'hélium gazeux à température ambiante. La masse d'un atome d'hélium est $m=6,6\cdot 10^{-27}kg$. L'impulsion quadratique moyenne est :

$$p=\sqrt{2mE}=\sqrt{3mkT}\text{(12)}$$

où $k=1,38\cdot 10^{-23}J\cdot K^{-1}$ est la constante de Boltzmann. On en déduit la longueur d'onde de de Broglie :

$$\lambda =\frac{h}{\sqrt{3mkT}}=7,3\cdot 10^{-2}nm\text{(13)}$$

Cette longueur d'onde est très petite, bien plus petite que la distance moyenne entre les atomes du gaz, mais pas assez pour que l'on puisse négliger le comportement ondulatoire à l'échelle atomique. Il est possible d'obtenir une longueur d'onde beaucoup plus grande en refroidissant le gaz à une température proche de zéro kelvin.

Avec des électrons, dont la masse est $m=9,1\cdot 10^{-31}kg$, les longueurs d'onde sont beaucoup plus grandes. Les électrons sont généralement accélérés par des systèmes électrostatiques, et leur énergie est donc donnée en électron-volts. La longueur d'onde se calcule avec :

$$\lambda =\frac{h}{\sqrt{2mE}}\text{(14)}$$

Par exemple, avec E=100 eV, on obtient λ=0,12 nm, une longueur d'onde de l'ordre de la distance interatomique dans un cristal. Le comportement des électrons de conduction dans un métal est donc très fortement ondulatoire. Un modèle corpusculaire n'est pas du tout adapté à ce cas.

Pour un objet de taille mésoscopique, et à plus forte raison de taille macroscopique, la longueur de de Broglie est complètement négligeable, même devant l'échelle atomique. Pour ce type d'objet, le caractère ondulatoire est complètement négligeable.

1.c. Diffraction d'électrons par un cristal

La première preuve expérimentale du comportement ondulatoire des électrons a été donnée en 1927, par Davisson et Germer, qui ont effectué la diffraction d'électrons par un cristal de nickel. La longueur d'onde de de Broglie des électrons étaient de l'ordre de la distance interatomique. Dans ces conditions, on observe des phénomènes de diffraction analogues à ceux de la lumière sur un réseau de fentes.

Dans cette expérience, les électrons sont émis par un filament métallique chauffé, puis accélérés par une différence de potentiel de l'ordre de 100 V. Les électrons réfléchis par la cible sont reçus sur un détecteur dont la position angulaire peut être variée.

Figure pleine page

Les électrons sont détectés seulement dans des directions bien précises, de manière analogue à la diffraction d'une onde électromagnétique par un réseau de fentes. Les directions de détection correspondent aux conditions d'interférence constructive des ondes diffractées par les atomes du cristal. L'analyse de la figure de diffraction permet de déterminer la structure du réseau cristallin et les distances entre les atomes. L'expérience est analogue à celle de la diffraction de la lumière par un réseau de fentes, mais la figure de diffraction est plus complexe en raison de la répartition tri-dimensionnelle des atomes dans le cristal.

Aujourd'hui, la diffraction de particules matérielles est courramment utilisée pour explorer la structure de la matière aux échelles microscopiques et mésoscopiques. En particulier, la diffraction de neutrons (Institut Laue-Langevin) est utilisée en raison de leur neutralité électrique, qui leur permet de pénétrer dans la matière beaucoup plus profondément que les électrons.

La diffraction de rayons X est aussi utilisée pour explorer la matière, mais la diffraction d'électrons permet d'atteindre des longueurs d'onde beaucoup plus petites (en augmentant la différence de potentiel), ce qui permet d'accéder à des détails plus fins.

1.d. Diffraction de particules par une fente double

Il est possible de faire des expériences de type fentes d'Young avec des particules, mais leur réalisation est relativement récente en raison des difficultés technologiques. Les longueurs d'onde étant au plus de l'ordre du nanomètre, il faut deux fentes dont la distance est de l'ordre du micromètre (environ mille fois plus petit que l'expérience de Young avec la lumière).

F. Shimizu et al. ont effectué en 1992 ([1]) une expérience de double fente avec des atomes de néon ultrafroids (dont la vitesse est inférieure à 1 m/s). Les deux fentes avaient une largeur de 2 μm et étaient espacées de 6 μm.

Plus récemment, une expérience de double fente a été faite avec des électrons d'énergie 600 eV, de longueur d'onde 50 pm, avec deux fentes espacées de 272 nm ([2]). L'expérience montre clairement une figure d'interférence similaire à celle des fentes d'Young en optique.

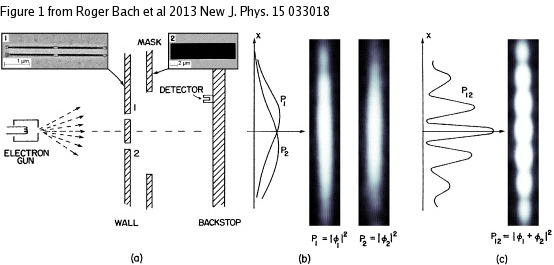
Un masque mobile permet de sélectionner une ou deux fentes. L'image suivante montre les figures d'interférence obtenue :

Lorsque l'écran ne comporte qu'une seule fente, aucune frange d'interférence n'est visible.

2.a. Particule libre

Schrödinger (physicien autrichien 1887-1961) a établi en 1927 une équation différentielle linéaire permettant de déterminer de manière générale la fonction d'onde associée à une particule.

Considérons tout d'abord le cas d'une particule libre en mouvement unidirectionnel ayant une impulsion p bien définie, dont la fonction d'onde est celle de de Broglie :

$$\psi (x,t)={\psi }_0{e}^{i(\frac{p}{\hslash }x-\frac{E}{\hslash }t)}\text{(15)}$$

Considérons alors les dérivées suivantes :

$$\begin{array}{ccc}\hfill & i\hslash \frac{\partial \psi }{\partial t}=E\psi \hfill & \hfill \text{(16)}\\ \hfill & -\frac{{\hslash }^2}{2m}\frac{{\partial }^2\psi }{\partial x^2}=\frac{p^2}{2m}\psi \hfill & \hfill \text{(17)}\end{array}$$

Compte tenu de la relation entre l'énergie et l'impulsion pour une particule libre non relativiste, on en déduit que la fonction d'onde vérifie l'équation différentielle suivante :

$$i\hslash \frac{\partial \psi }{\partial t}=-\frac{{\hslash }^2}{2m}\frac{{\partial }^2\psi }{\partial x^2}\text{(18)}$$

Par généralisation, cette équation permet de déterminer la fonction d'onde d'une particule matérielle non relativiste en mouvement libre (non soumis à une action extérieure).

Cette équation ressemble à l'équation des ondes (équation de d'Alembert) mais la dérivée temporelle est du premier ordre. Elle ressemble aussi à l'équation de diffusion mais la dérivée temporelle est multipliée par i, ce qui permet d'obtenir des solutions ondulatoires. L'équation obtenue est l'équation linéaire la plus simple qui conduit aux ondes de de Broglie pour une particule libre. En dérivant deux fois par rapport au temps, on obtient :

$$\frac{{\partial }^2\psi }{\partial t^2}=-\frac{E^2}{{\hslash }^2}\psi \text{(19)}$$

On voit qu'il n'est pas possible de construire une équation linéaire avec une dérivée seconde. La nécessité d'une équation linéaire est liée au principe de superposition, qui sera expliqué plus loin.

2.b. Particule dans un potentiel

L'équation de Schrödinger généralise l'équation précédente à une particule soumise à un potentiel V(x). Le potentiel correspond à l'énergie potentielle en mécanique classique, reliée à la force par :

$$F_x=-\frac{dV}{dx}\text{(20)}$$

La théorie de Schrödinger conserve la notion d'énergie potentielle utilisée en mécanique classique (mais pas celle de force). En mécanique quantique, il est d'usage de noter V le potentiel, mais il faut ne pas le confondre avec le potentiel électrique, qui est une énergie potentielle par unité de charge.

Voici l'équation de Schrödinger à une dimension, qui s'applique à une particule non relativiste :

Le terme ajouté est l'énergie potentielle multipliée par la fonction d'onde. On vérifie facilement l'homogénéité de ce terme avec les deux autres.

L'équation de Schrödinger se résout sur un intervalle $x\in (a,b)$, dont les bornes sont éventuellement à l'infini. Il faut disposer de conditions limites sur ces bords et d'une condition initiale.

2.c. États stationnaires

Comme l'équation des ondes, l'équation de Schrödinger est souvent résolue par une méthode spectrale, qui consiste à rechercher des solutions de la forme suivante :

$$\psi (x,t)=e^{-i\omega t}\phi \left(x\right)\text{(22)}$$

L'état de la particule représenté par cette solution, dont les variables temps et espace sont séparées, est appelée en mécanique quantique état stationnaire (pour une raison qu'on verra plus loin). Il faut remarquer qu'il y a une discordance avec le vocabulaire utilisé en physique ondulatoire, où une onde stationnaire est un type plus particulier d'onde. La solution stationnaire de la mécanique quantique ondulatoire est en fait l'équivalent de l'onde sinusoïdale de la physique ondulatoire classique.

En reportant l'expression $\mathrm{(22)}$ dans l'équation de Schrödinger, on obtient :

$$\hslash \omega \phi =-\frac{{\hslash }^2}{2m}\frac{d^2\phi }{d{x}^2}+V\left(x\right)\phi \text{(23)}$$

La relation de Planck-Einstein permet de définir l'énergie de la particule par

$$E=\hslash \omega \text{(24)}$$

On obtient alors l'équation suivante, appelée équation de Schrödinger indépendante du temps :

$$E\phi =-\frac{{\hslash }^2}{2m}\frac{d^2\phi }{d{x}^2}+V\left(x\right)\phi \text{(25)}$$

qu'on écrira sous la forme :

$$\frac{d^2\phi }{d{x}^2}+\frac{2m(E-V\left(x\right))}{{\hslash }^2}\phi =0\text{(26)}$$

L'équation de Schrödinger indépendante du temps est très importante en mécanique quantique, car l'énergie E est souvent la seule grandeur observable. Par exemple, la spectroscopie de la lumière (visible et UV) permet d'accéder aux niveaux d'énergie des électrons dans les atomes. Cette équation a permis a Schrödinger d'expliquer ces niveaux d'énergie, ce qui a constitué un des premiers succès de la mécanique quantique.

3.a. Amplitude et densité de probabilité

L'équation de Schrödinger a permis à ce dernier d'expliquer les niveaux d'énergie des électrons dans les atomes. Il restait cependant à donner une interprétation physique à la fonction d'onde dans le cas d'une particule libre, par exemple dans une expérience de diffraction par un cristal. La question se pose aussi pour l'expérience plus récente de diffraction par une bi-fente. Cette interprétation a été donnée par Born (physicien allemand 1882-1970).

On se place dans le cas tridimensionnel où la fonction d'onde dépend des trois coordonnées dans l'espace et du temps :

$$\psi (x,y,z,t)\text{(27)}$$

Supposons que l'on dispose d'un capteur permettant de détecter la particule au voisinage d'un point de l'espace, par exemple le capteur dans l'expérience de Davisson et Germer. Suivant la position du détecteur, on détecte en général un nombre variable d'impacts pour une durée donnée. Pour certaines positions (correspondant aux interférences constructives), le nombre d'impacts est très élevé alors qu'il est très faible pour d'autres positions.

La détection d'une particule par le capteur à un instant t est un phénomène aléatoire : il n'est pas possible de prévoir si une particule parvient ou pas sur le capteur, même si sa condition initiale de la particule est connue. Il est en revanche possible de définir une loi de probabilité pour la détection des particules. Ce caractère aléatoire des résultats de mesure est fondamental en mécanique quantique. En mécanique classique (mécanique de Newton), la connaissance de la condition initiale d'une particule suffit pour savoir si elle parvient ou pas dans la fenêtre d'un capteur. Ce n'est pas le cas en physique quantique, et il faut bien comprendre que ce caractère aléatoire ne vient pas d'une variation aléatoire de la condition initiale, mais d'une propriété fondamentale du mouvement des particules : deux particules qui sont exactement dans la même condition initiale conduiront en général à deux résultats différents, c'est-à-dire qu'une particule peut être détecté par le capteur alors que l'autre ne l'est pas.

La probabilité de détecter la particule en (x,y,z) à (dx,dy,dz) près s'écrit :

$$\rho (x,y,z,t)dxdydz\text{(28)}$$

où ρ(x,y,z,t) est la densité de probabilité de détection de la particule. Elle est aussi appelée densité de probabilité de présence, bien que la notion de présence de la particule en un point n'ait pas de sens en dehors de sa détection par un capteur.

La densité de probabilité de détection de la particule est égale au module au carré de la fonction d'onde :

Pour cette raison, la fonction d'onde constitue une amplitude de probabilité. Cette relation entre la fonction d'onde et la densité de probabilité est similaire à la relation entre la fonction d'onde et l'intensité en optique. Cependant, la fonction d'onde de la physique quantique est par nature une fonction à valeurs complexes, dont la partie réelle n'a aucune signification particulière.

Expérimentalement, cette densité de probabilité est obtenue avec un grand nombre de particules préparées dans les mêmes conditions. Par exemple, dans l'expérience de diffraction des électrons, il faut détecter un grand nombre d'électrons, pour différentes positions du capteur, afin obtenir la distribution des impacts.

Comme nous allons le voir, le fait d'identifier la densité de probabilité au module au carré de la fonction d'onde est une propriété physique fondamentale, qui vient de la manière particulière dont les probabilités se composent dans les expériences de physique quantique (c'est-à-dire les expérience dont l'explication relève de la physique quantique).

Considérons le cas particulier d'une fonction d'onde d'un état stationnaire d'énergie E, pour une particule se déplaçant sur un axe, qui s'écrit :

$$\psi (x,t)=e^{-i\frac{E}{\hslash }t}\phi \left(x\right)\text{(30)}$$

La densité de probabilité est :

$$\rho \left(x\right)=|\phi \left(x\right){|}^2\text{(31)}$$

Elle est indépendante du temps, c'est pourquoi on parle d'état stationnaire. Cela signifie que la probabilité de détecter la particule entre x et x+dx ne dépend pas du temps.

3.b. Superposition des fonctions d'onde

Pour comprendre comment les probabilités quantiques se composent, considérons l'expérience de diffraction d'électrons par un écran percé de deux fentes F₁ et F₂ (expérience de Young avec des particules). Les électrons sont émis par un filament chauffé puis accélérés par un champ électrostatique. Le plan de détection est situé en arrrière des fentes. Soit un repère (Oxyz) où l'axe Oz est perpendiculaire au plan de détection. Par convention, on place l'origine z=0 sur ce plan (donc z<0 pour les électrons).

Figure pleine page

Lorsque seule la fente F₁ est présente, on observe sur l'écran une tache de diffraction sans franges, c'est-à-dire un étalement des impacts qui suit une loi de probabilité ρ₁(x,y,0,t) présentant un maximum dans la direction du faisceau incident, mais pas de variations périodiques. De même, lorsque seule la fente F₂ est présente, on observe une densité ρ₂(x,y,0,t) similaire. À supposer que l'électron soit émis à l'instant 0, cette densité est non nulle seulement au voisinage d'un instant t correspondant au temps de trajet de l'électron entre la source et le plan de détection (ce temps est aussi une variable aléatoire). Pour obtenir expérimentalement ces densités, il faut enregistrer les points d'impact (et le temps d'arrivé) pour un très grand nombre d'électrons.

Figure pleine page

En présence des deux fentes, une particule décrite par la cinématique classique franchit soit la première fente, soit la seconde. Avec une composition classique des probabilités, on devrait observer une densité de probabilité de détection somme de ρ₁(x,y,0,t) et ρ₂(x,y,0,t). Or ce n'est pas du tout ce qu'on observe puisque la densité avec deux fentes présente des variations périodiques (des franges d'interférence) :

$$\rho (x,y,0,t)\ne {\rho }_1(x,y,0,t)+{\rho }_2(x,y,0,t)\text{(32)}$$

Les résultats expérimentaux s'expliquent en appliquant le principe de superposition non pas aux densités de probabilité mais aux fonctions d'onde :

C'est pour cela que la densité de probabilité est définie comme le module au carré de la fonction d'onde. La fonction d'onde obéit à une équation différentielle linéaire, l'équation de Schrödinger, et vérifie donc le principe de superposition.

La densité de probabilité de détection en présence des deux fentes s'écrit donc :

$$\rho (x,y,0,t)=|{\psi }_1(x,y,0,t)+{\psi }_2(x,y,0,t){|}^2={\rho }_1(x,y,0,t)+{\rho }_2(x,y,0,t)+2Re\left({\psi }_1(x,y,0,t){\psi }_2^{*}(x,y,0,t)\right)\text{(34)}$$

Le dernier terme comporte les modulations sous forme de franges d'interférence.

La composition des probabilités montre qu'il n'est pas possible d'affirmer que les électrons passent soit par un trou soit par un autre. Autrement dit, la notion de trajectoire d'un électron n'a plus de sens. De manière générale, la trajectoire d'une particule telle qu'elle est définie en cinématique classique n'est plus valable en mécanique quantique. Il n'est pas possible d'attribuer à l'électron le parcours d'une courbe bien définie avec une vitesse définie en tout point. Bien que cela heurte nos habitudes de pensée, il a été démontré expérimentalement que les particules comme les électrons ou les atomes n'ont pas de trajectoire (au sens de la cinématique classique).

L'expérience de la fente double a été considérée bien avant sa réalisation expérimentale, comme une expérience de pensée pour expliquer les fondements de la mécanique quantique ([3]). Il a été objecté qu'il serait possible de déterminer par quelle fente chaque électron passe, en éclairant les fentes à l'arrière par de la lumière et en détectant la lumière diffusée par les électrons.

Figure pleine page

La diffusion de la lumière est une collision élastique entre un photon et un électron. Si un photon diffusé est détecté au niveau de la fente F₁, on peut en déduire que l'électron est passé par cette fente. Cette expérience de pensée met en évidence un paradoxe : si la fente de passage peut être déterminée, comment les probabilités peuvent-elles se composer par addition des amplitudes de probabilité (et non pas addition des probabilités) ? La solution de ce paradoxe est la suivante : lorsqu'on détermine par quelle fente chaque électron passe, les interférences observées sur le plan de détection disparaissent, et les probabilités s'ajoutent ρ=ρ₁+ρ₂. Physiquement, cela vient du fait que la diffusion des électrons par les photons de la lumière modifie le comportement des électrons de manière à faire disparaître les interférences. Pour employer le langage de l'optique, on peut dire que le dispositif d'observation détruit la cohérence des deux ondes issues des deux fentes.

Le comportement ondulatoire ne se manifeste que si la distance entre les fentes n'est pas trop grande par rapport à la longueur d'onde des particules. Dans l'expérience mentionnée plus haut, le rapport entre la distance des fentes et la longueur d'onde est d'environ 5000, ce qui fait un interfrange d'environ 0,2 mrad. C'est aussi l'ordre de grandeur pour l'expérience de Young effectuée avec de la lumière. Lorsque ce rapport est beaucoup plus grand, la notion de trajectoire classique s'applique à nouveau. Pour reprendre le dispositif précédent, où les électrons ont une longueur d'onde de 50 pm, une distance entre les fentes de l'ordre du millimètre ne donne pas d'interférences.

Figure pleine page

La distribution des impacts sur le plan de détection vérifie alors l'addition $\rho (x,y)={\rho }_1(x,y)+{\rho }_2(x,y)$. Autrement-dit, il n'y a plus de terme d'interférence dans la densité de probabilité.

Pour les objets mésoscopiques ou macroscopiques, la longueur d'onde est tellement petite que les phénomènes ondulatoires sont inexistants. Pour ces objets, la notion de trajectoire s'applique parfaitement. À l'échelle moléculaire, les phénomènes ondulatoires ne sont plus négligeables mais l'approche classique est encore valable, du moins en première approximation. Par exemple, la simulation de la dynamique des molécules par la mécanique classique donne (pour un gaz ou un liquide) des résultats conformes aux observations. Pour les solides, en particulier les métaux, la mécanique quantique est en revanche prépondérante. À l'intérieur de l'atome, les phénomènes ondulatoires sont prépondérants et la mécanique classique ne s'applique pas du tout. C'est d'ailleurs l'étude des spectres énergétiques des atomes qui a conduit à la naissance de la mécanique quantique.

3.c. Normalisation de la fonction d'onde

La fonction d'onde est une amplitude de probabilité, dont le module au carré constitue une densité de probabilité de détection des particules (ou densité de probabilité de présence). La fonction d'onde n'est pas directement accessible expérimentalement. C'est son module au carré qui est accessible, par une répétition d'émission de particules et une étude statistique des points d'impact sur un détecteur.

On reprend le cas d'une particule ayant un mouvement unidirectionnel. Dans ce cas, la fonction d'onde dépend de x et de t. On suppose de plus que l'état est stationnaire : la densité de probabilité ne dépend pas du temps. La probabilité de détecter la particule entre x et x+dx est :

$$\rho \left(x\right)dx=\psi (x,t){\psi }^{*}(x,t)dx=|\psi {|}^{2}dx\text{(35)}$$

Si la particule est confinée dans l'intervalle (a,b), la somme des probabilités sur cet intervalle doit être égale à 1 :

$${\int }_a^b|\psi {|}^{2}dx=1\text{(36)}$$

Cette équation est la condition de normalisation de la fonction d'onde.

Si la particule n'est pas confinée, les bornes de l'intervalle sont infinie et :

$${\int }_{-\infty }^{+\infty }|\psi {|}^{2}dx=1\text{(37)}$$

La fonction d'onde doit être de carré sommable, une condition mathématique qu'il est parfois impossible à réaliser. Considérons par exemple l'état stationnaire pour une particule libre ayant une impulsion p parfaitement déterminée, et une énergie $E=\frac{p^2}{2m}$ (fonction d'onde de de Broglie) :

$$\psi (x,t)={\psi }_0{e}^{i(\frac{p}{\hslash }x-\frac{E}{\hslash }t)}\text{(38)}$$

La densité de probabilité associée est :

$$\rho \left(x\right)=|{\psi }_0{|}^2\text{(39)}$$

La probabilité de détecter la particule est uniforme : la probabilité de détecter la particule sur un intervalle de largeur Δx centré à l'absisse x est indépendante de x. Cela correspond à une particule complètement délocalisée, ce qui est physiquement impossible. Pour cette fonction d'onde, le carré n'est pas sommable. Cette fonction d'onde ne peut donc représenter un état physique réel, mais elle a tout de même un intérêt mathématique puisqu'il s'agit d'une solution de l'équation de Schrödinger (pour une particule libre). De manière similaire aux ondes planes progressives monochromatiques en optique, les ondes de de Broglie sont utilisées comme fonctions de base pour écrire des solutions physiquement acceptables, dont le carré est sommable.

3.d. Paquet d'onde

Pour une onde électromagnétique, on obtient une fonction d'onde physiquement acceptable en sommant des ondes planes progressives monochromatiques de différentes fréquences. La somme est soit discrète (série de Fourier), soit continue (intégrale de Fourier). La même démarche est utilisée en mécanique quantique : on somme des ondes planes progressives sinusoïdales pour obtenir une solution de carré sommable ayant une signification physique. Une somme discrète s'écrit de la manière suivante :

$$\psi (x,t)=\sum _{j}A\left(p_j\right)e^{i(\frac{p_j}{\hslash }x-\frac{E_j}{\hslash }t)}\text{(40)}$$

où p_j est l'impulsion de la composante d'indice j. Pour obtenir une fonction d'onde de carré sommable, on est amené à écrire des intégrales de la forme :

$$\psi (x,t)=\int A\left(p\right)e^{i(\frac{p}{\hslash }x-\frac{E\left(p\right)}{\hslash }t)}dp\text{(41)}$$

La fonction $A\left(p\right)$ constitue le spectre en impulsion de l'onde. Pour une particule libre, l'énergie et l'impulsion sont reliées par la relation de dispersion :

$$E\left(p\right)=\frac{p^2}{2m}\text{(42)}$$

Les différentes composantes de ces sommes ont des vitesses de propagation différentes (les ondes de de Broglie sont dispersives).

Un exemple important est une superposition de solutions stationnaires constituant un paquet d'ondes. La simulation Paquet d'onde de matière montre un paquet gaussien obtenu par une somme discrète (dans ce cas les paquets s'enchaînent périodiquement).

Le paquet d'ondes est d'autant plus étroit que son spectre en impulsion est large.

En première approximation, un paquet d'ondes se déplace à la vitesse de groupe, définie par :

$$v_g=\frac{d\omega }{dk}=\frac{dE}{dp}\text{(43)}$$

En dérivant la relation $\mathrm{(42)}$ on obtient :

$$v_g=\frac{p}{m}\text{(44)}$$

La vitesse de groupe correspond à la vitesse de la cinématique classique.

Un paquet d'ondes se déforme au cours du temps : il se produit un phénomène d'étalement progressif du paquet, qui vient de la relation de dispersion non linéaire. Plus le paquet d'ondes est étroit (plus son spectre en impulsion est large), plus le phénomène d'étalement est rapide.

Pour le calcul d'un paquet d'ondes gaussien, voir Paquet d'onde d'une particule matérielle.

3.e. Inégalités d'Heisenberg

Considérons un paquet d'ondes à une dimension (une seule variable d'espace x) et l'interprétation probabiliste de la fonction d'onde. Pour cela, on représente, à un instant donné, le module au carré de la fonction d'onde en fonction de x. Pour un paquet d'ondes gaussien, cette courbe a une forme gaussienne (à l'instant t=0). On représente parallèlement le module au carré du spectre en impulsion, qui est une fonction d'onde associée à la variable impulsion, mais qui ne dépend pas du temps.

Figure pleine page

La probabilité de détecter la particule dans l'intervalle (x,x+dx) est représentée par l'aire hachurée. On définit de manière analogue une probabilité de mesurer l'impulsion dans l'intervalle (p,p+dp). Pour une distribution gaussienne, la valeur la plus probable coïncide avec la valeur moyenne. Si l'on mesure la position de la particule (au même instant) pour un grand nombre d'expériences réalisées dans les mêmes conditions, la moyenne des valeurs obtenues est $\overline{x}$.

Supposons que l'on dispose d'un capteur permettant de mesurer la position x (à l'instant t) et d'un capteur permettant de mesurer l'impulsion p. L'expérience est répétée N fois (N très grand), avec à chaque fois une particule préparée dans les mêmes conditions, pour obtenir N mesures de x puis elle répétée à nouveau N fois pour obtenir N valeurs de p. La mesure de la position et de l'impulsion doivent être faites dans des expériences distinctes (mais avec la même condition initiale de préparation de la particule) car la mesure de l'une place la particule dans un état très particulier, qui n'est plus celui que l'on veut étudier. Le résultat de la mesure de position est imprévisible : il s'agit d'une variable aléatoire dont la densité de probabilité est donnée par $|\psi (x,t){|}^2$. Il est important de bien comprendre que la dispersion des valeurs de x obtenues pour ces N mesures est due au caractère fondamentalement imprévisible de l'évolution de la particule et pas à une incertitude expérimentale du capteur ou du processus de préparation de la particule. Dans toute la discussion qui suit, les incertitudes expérimentales (au sens classique) sont supposées négligeables. Les valeurs de l'impulsion, qui sont également imprévisibles, sont réparties selon la densité de probabilité définie par |A|². Chaque mesure (soit de la position, soit de l'impulsion) donne une valeur bien précise puisqu'on néglige l'incertitude expérimentale.

L'impulsion moyenne obtenue est $\overline{p}$. Les densités de probabilité en position et en impulsion du paquet d'ondes permettent de définir des écarts-types (racine carré de la variance) :

$$\begin{array}{ccc}\hfill & \Delta x=\sqrt{\overline{x^2}-{\overline{x}}^2}\hfill & \hfill \text{(45)}\\ \hfill & \Delta p=\sqrt{\overline{p^2}-{\overline{p}}^2}\hfill & \hfill \text{(46)}\end{array}$$

Pour une densité de probabilité gaussienne, le double de l'écart-type correspond à un probabilité de 68 pour cent. La largeur spatiale du paquet est donc 2Δx et la largeur du spectre en impulsion est 2Δp, si l'on définit la largeur comme l'intervalle donnant 68 pour cent des résultats.

L'écart-type représente la dispersion des valeurs mesurées autour de la valeur moyenne. En mécanique quantique, cette dispersion vient du caractère probabiliste des prévisions qui peuvent être faites à partir de la fonction d'onde, et pas de l'imprécision des appareils de mesure. On suppose ici que l'incertitude des appareils de mesure est négligeable par rapport à l'écart-type. L'écart-type Δx est aussi appelé indétermination de la position et Δp est l'indétermination de l'impulsion.

Le paquet d'ondes a une largeur spatiale d'autant plus grande que son spectre en impulsion est étroit. Plus précisément, les deux écarts-types vérifient l'inégalité suivante, établie par Heisenberg (physicien allemand 1901-1976) :

Le produit des deux écarts-types ne peut être inférieur à la moitié de la constante de Planck réduite. L'égalité est vérifiée dans un cas particulier : le paquet d'ondes gaussien à l'instant initial, avant qu'il ne commence à s'étaler. Si le spectre en impulsion est indépendant du temps, l'écart-type Δp est constant. L'étalement du paquet d'ondes au cours du temps fait que l'écart-type Δx augmente au cours du temps. La valeur minimale est donnée par l'inégalité d'Heisenberg mais elle peut atteindre des valeurs beaucoup plus grande lorsque le paquet devient très étalé. On pourra sans conséquence retenir l'inégalité avec $\hslash$ à la place de $\hslash /2$ car on s'intéresse en général à un ordre de grandeur de la plus petite valeur du produit des écart-types.

Cette relation est appelée inégalité spatiale d'Heisenberg, ou encore relation d'indétermination d'Heisenberg. On rencontre ausi l'appellation relation d'incertitude, qu'il faudrait éviter car les indéterminations ne sont pas des incertitudes au sens classique du terme d'incertitudes expérimentales liées à la précision de la mesure. Elle montre que la dispersion des valeurs de position mesurées est d'autant plus grande que celle des valeurs d'impulsion mesurées est faible. Autrement dit, si une expérience conduit à une position très bien déterminée (à un instant t), alors il y a une forte indétermination sur l'impulsion. Inversement, si l'expérience conduit à une faible dispersion des valeurs de l'impulsion, alors la position et fortement indéterminée.

Autrement dit, il n'est pas possible d'obtenir des mesures de la position et de l'impulsion avec une indétermination aussi faible qu'on le souhaite sur ces deux grandeurs. Bien entendu, une seule mesure conduit bien à une valeur précise de x et une valeur précise de p. L'inégalité d'Heisenberg concerne les écart-types obtenus par analyse d'un grand nombre de mesures.

En raison de l'inégalité d'Heisenberg, il n'est pas possible d'attribuer à une particule une position parfaitement déterminée (à l'instant t) avant d'avoir effectivement mesuré cette position. En effet, cela impliquerait Δx=0 et par conséquence $\Delta p\to \infty$. De même, il est impossible de lui attribuer une impulsion déterminée. Cela est clairement en contradiction avec les principes de la cinématique classique, où la position et la vitesse d'un point matériel sont par principe parfaitement déterminées à tout instant.

Plus généralement, pour une particule se déplaçant dans un espace à 3 dimensions, les inégalités d'Heisenberg sont :

$$\begin{array}{ccc}\hfill & \Delta x\Delta p_x\ge \frac{\hslash }{2}\hfill & \hfill \text{(48)}\\ \hfill & \Delta y\Delta p_y\ge \frac{\hslash }{2}\hfill & \hfill \text{(49)}\\ \hfill & \Delta z\Delta p_z\ge \frac{\hslash }{2}\hfill & \hfill \text{(50)}\end{array}$$

Chaque inégalité concerne l'abscisse sur un axe et l'impulsion correspondante. En revanche, aucune relation ne lie la position sur un axe à l'impulsion sur un autre axe.

Les inégalités d'Heisenberg sont fondamentales en mécanique quantique car elles montrent les limites de l'approche cinématique classique. En mécanique classique, la position et la vitesse d'une particule peuvent être en principe définies toutes les deux simultanément avec une précision arbitraire. En pratique, on est bien sûr limité par la précision des appareils de mesure, mais aucune limitation de principe n'existe. En mécanique quantique, il n'est pas possible, même en principe, de définir simultanément la position et l'impulsion (sur le même axe).

Pour une fonction d'onde plane de la forme :

$$\psi (x,t)={\psi }_0{e}^{i(kx-\omega t)}={\psi }_0{e}^{i(\frac{p}{\hslash }x-\frac{E}{\hslash }t)}\text{(51)}$$

l'écart-type sur l'impulsion est nul car celle-ci est parfaitement définie. On a donc un écart-type sur la position infini : $\Delta x\to \infty$, ce qui correspond au fait que la particule est complètement délocalisée (la densité de probabilité est indépendante de x et de t). En tout point de l'axe x, on a la même probabilité de détecter la particule, ce qui est physiquement absurde. En réalité, une particule ne peut être représentée par une onde de ce type. Il faut construire un paquet d'ondes pour obtenir une fonction d'onde physiquement acceptable. Comme nous l'avons vu, un paquet d'ondes a bien une indétermination Δx finie.

Pour voir les ordres de grandeur, considérons un atome d'hélium à température ambiante. Sa quantité de mouvement moyenne est

$$p=\sqrt{3mkT}=10^{-23}J\cdot s^{-2}\cdot m^{-1}\text{(52)}$$

Considérons une expérience dans laquelle on détermine la position de l'atome avec une indétermination de l'ordre de 10 nm. Par exemple, on peut laisser le gaz s'échapper d'un récipient par un orifice de cette taille. L'indétermination sur l'impulsion est (au mieux) de l'ordre de :

$$\Delta p\simeq \frac{\hslash }{2\Delta x}=5\cdot 10^{-27}J\cdot s^{-2}\cdot m^{-1}\text{(53)}$$

L'indétermination sur l'impulsion est petite par rapport à l'impulsion. Il n'en est plus de même pour un atome ultrafroid. Par exemple pour T=0,01 K, l'impulsion est :

$$5\cdot 10^{-26}J\cdot s^{-2}\cdot m^{-1}\text{(54)}$$

Dans ce cas, l'indétermination sur l'impulsion est environ un dixième de la valeur de l'impulsion, ce qui n'est pas négligeable.

Comme deuxième exemple, considérons un faisceau d'électrons d'énergie E (acquise par une différence de potentiel), envoyé sur un écran percé d'une ouverture de diamètre b. L'indétermination relative sur l'impulsion est :

$$\frac{\Delta p}{p}=\frac{\hslash }{2b\sqrt{2mE}}\text{(55)}$$

Par exemple pour un électron d'énergie 100 eV on obtient :

$$\frac{\Delta p}{p}=\frac{6\cdot 10^{-11}}{b}\text{(56)}$$

Pour une ouverture de diamètre b=60 nm, l'indétermination relative est de 0,001. Il faut donc descendre à l'échelle de l'atome (quelques picomètres) pour que l'indétermination sur l'impulsion soit très importante.

L'expérience suivante montre le lien entre l'inégalité d'Heisenberg et les propriétés ondulatoires des particules. Il s'agit d'une expérience de diffraction d'électrons par une petite ouverture de largeur b. On raisonne à deux dimensions (x,y). L'expérience consiste à envoyer des électrons sur l'écran percé et à les détecter sur un capteur plan situé plus loin.

Figure pleine page

Les électrons incidents ont une impulsion moyenne $\overrightarrow{p}$ perpendiculaire à l'écran (incidence normale). Si le faisceau est bien collimaté, la dispersion Δp_y est très faible et Δy (la largeur transversale du paquet d'ondes) est plus grande que le diamètre de l'ouverture. Il y a donc une grande indétermination de la coordonnée y des électrons. Juste à la sortie de l'ouverture (en x=0⁺), l'indétermination sur y se réduit et devient Δy'=b (à peu près). En effet, on est certain que l'électron passe par l'ouverture car il ne peut traverser la partie pleine de l'écran. Nous insistons sur le fait qu'il s'agit de l'indétermination de y juste derrière l'ouverture. L'inégalité d'Heisenberg donne l'indétermination sur l'impulsion transversale (on suppose que le paquet d'ondes est gaussien) :

$$\Delta p_y\text{'}=\frac{\hslash }{2b}\text{(57)}$$

Il s'agit bien sûr d'un ordre de grandeur donc on aurait put omettre le facteur 1/2. Lors du passage par l'ouverture, il y a donc une forte réduction de l'indétermination sur y, associée à une forte augmentation de l'indétermination sur l'impulsion correspondante. Ce phénomène est appelé réduction du paquet d'ondes. Au cours de la propagation dans la direction x il se produit un étalement du paquet d'ondes dans la direction y, analogue au phénomène de diffraction observé en optique. Cet étalement est une conséquence de la dispersion Δp_y' de l'impulsion transversale. Lorsqu'on relève les impacts des électrons sur l'écran, il y a une dispersion Δy'' supérieure à la largeur de l'ouverture.

Plus l'ouverture est petite, moins la valeur y (en sortie de l'ouverture) est indéterminée et plus la valeur de p_y est indéterminée, ce qui se traduit par un plus grand étalement des impacts sur l'écran. Rappelons que la position du point d'impact d'un électron sur l'écran est une variable aléatoire, et que ce caractère aléatoire est une propriété quantique fondamentale, qui n'a rien à voir avec une incertitude expérimentale classique.

La vidéo suivante montre l'évolution de la densité de probabilité au cours du temps pour un paquet d'ondes gaussien, obtenue par une simulation numérique :

Si un écran avec deux ouvertures proches est utilisé, on observe des impacts répartis statistiquement en franges d'interférence, à condition que la largeur transversale du paquet d'ondes initial couvre bien les deux ouvertures. Lorsqu'une particule est détectée sur l'écran, elle apparaît sous forme d'un point avec une position bien déterminée (le point d'impact). En revanche, le modèle de la particule ponctuelle ne permet pas d'expliquer la formation de franges d'interférences pour la densité de probabilité des impacts. Les phénomènes d'interférence ne peuvent s'expliquer que par les propriétés ondulatoires de la particule. Comme nous l'avons vu plus haut, le concept de particule ponctuelle et de trajectoire associée n'est plus valable. On ne peut affirmer que la particule passe par l'une ou l'autre ouverture. Pour décrire cette situation paradoxale, on parle de dualité onde-corpuscule. L'aspect corpusculaire intervient au moment de l'impact, c'est-à-dire au moment où l'on mesure la position de la particule sur un écran. Le mouvement de la particule entre la source et l'écran ne peut s'expliquer que par l'aspect ondulatoire.

Pour d'autres exemples de diffraction, voir Diffraction d'un paquet d'ondes de matière.

Pour un objet mésoscopique ou macroscopique, les indéterminations imposées par les inégalités d'Heisenberg sont tellement petites qu'on peut tout à fait les négliger. Pour un tel objet, la notion classique de trajectoire s'applique parfaitement. Dans ce cas, on peut d'ailleurs montrer (théorème d'Ehrenfest [4]) que l'équation de Schrödinger conduit à la loi de Newton du mouvement. La mécanique classique est donc un cas limite de la mécanique quantique, valable lorsque les écarts-types sur les positions et les impulsions sont négligeables.

3.f. Densité de courant de probabilité

Dérivons par rapport au temps la densité de probabilité :

$$\frac{\partial \rho }{\partial t}=\frac{\partial \psi }{\partial t}{\psi }^{*}+\frac{\partial {\psi }^{*}}{\partial t}\psi \text{(58)}$$

Considérons l'équation de Schrödinger et son complexe conjugué :

$$\begin{array}{ccc}\hfill & i\hslash \frac{\partial \psi }{\partial t}=-\frac{{\hslash }^2}{2m}\frac{{\partial }^2\psi }{\partial x^2}+V\psi \hfill & \hfill \text{(59)}\\ \hfill & -i\hslash \frac{\partial {\psi }^{*}}{\partial t}=-\frac{{\hslash }^2}{2m}\frac{{\partial }^2{\psi }^{*}}{\partial x^2}+V{\psi }^{*}\hfill & \hfill \text{(60)}\end{array}$$

On en déduit les expressions de $\frac{\partial \psi }{\partial t}$ et $\frac{\partial {\psi }^{*}}{\partial t}$ que l'on reporte dans $\mathrm{(58)}$ :

$$\frac{\partial \rho }{\partial t}=\frac{i\hslash }{2m}{\psi }^{*}\frac{{\partial }^2\psi }{\partial x^2}-\frac{i\hslash }{2m}\psi \frac{{\partial }^2{\psi }^{*}}{\partial x^2}\text{(61)}$$

On définit un vecteur densité de courant de probabilité. Pour un problème unidirectionnel, sa composante sur l'axe est :

$$j_x=\frac{\hslash }{2im}{\psi }^{*}\frac{\partial \psi }{\partial x}-\frac{\hslash }{2im}\psi \frac{\partial {\psi }^{*}}{\partial x}\text{(62)}$$

Ce vecteur permet d'écrire la forme locale de la conservation de la densité :

$$\frac{\partial \rho }{\partial t}+\frac{\partial j_x}{\partial x}=0\text{(63)}$$

Cette équation est similaire à la forme locale de la conservation de la charge électrique.

Lorsque la fonction d'onde est normalisée, il faut que l'intégrale de la densité sur l'intervalle accessible à la particule soit constante au cours du temps, car cette intégrale doit rester égale à 1 :

$$\frac{d}{dt}{\int }_a^b\rho dx=0\text{(64)}$$

En utilisant la densité de courant de probabilité, on obtient :

$$\frac{d}{dt}{\int }_a^b\rho dx={\int }_a^b\frac{\partial \rho }{\partial t}dx=-{\int }_a^b\frac{\partial j_x}{\partial x}dx=j_x\left(a\right)-j_x\left(b\right)\text{(65)}$$

Pour que la condition de normalisation soit maintenue au cours du temps, il faut que la densité de courant de probabilité soit nulle sur les bords du domaine (qui peuvent être à l'infini).

Pour une solution stationnaire, la densité de probabilité est constante donc la densité de courant de probabilité est uniforme.

Voyons le cas de l'onde de de Broglie, qui est associée à une particule libre d'impulsion parfaitement déterminée :

$$\psi (x,t)={\psi }_0{e}^{i(kx-\omega t)}\text{(66)}$$

On obtient la densité de courant de probabilité suivante :

$$j_x=\frac{\hslash k}{m}{\psi }_0{\psi }_0^{*}=\frac{p}{m}|{\psi }_0{|}^2=\rho \frac{p}{m}\text{(67)}$$

Il faut remarquer que cette relation n'est valable que si l'impulsion est parfaitement déterminée. Elle n'est donc pas applicable à un paquet d'ondes, qui comporte une indétermination de l'impulsion. On a vu que la valeur de $\left|{\psi }_0\right|$ ne peut être déterminée par la condition de normalisation. En conséquence, la norme de la densité de probabilité, pour une particule d'impulsion déterminée, est définie à une constante multiplicative près indéterminée. Cependant, nous serons toujours amené à calculer des rapports de densité de probabilité, ce qui fait que cette indétermination n'a pas d'importance.

Pour finir, on constate que la densité de courant de probabilité est égale à la densité de probabilité multipliée par l'équivalent de la vitesse de la particule. Dans ce cas, la densité de probabilité et la densité de courant associée sont les mêmes en tout point de l'espace car la particule est complètement délocalisée. L'impulsion de cette onde plane est en effet parfaitement définie. D'après l'inégalité d'Heisenberg, on a donc un écart-type sur la position infini. Physiquement, une telle onde ne peut représenter une particule. Comme nous l'avons vu plus haut, les ondes planes sont utilisées comme solutions de base pour obtenir, par superposition, des solutions sous forme de paquet d'ondes.