Second principe

Transformation chimique -- second principe

1. Enthalpie libre d'un système chimique

a. Potentiel thermodynamique

Transformation chimique monobare et monotherme : l'enthalpie libre du mélange en fonction de l'avancement est un potentiel thermodynamique.

1. Enthalpie libre d'un système chimique

a. Potentiel thermodynamique

b. Potentiel chimique

Constituant d'un mélange : espèce chimique dans un état physique donné.

$n_{i}$ : nombre de moles du constituant $i$.

$μ_{i}$ : potentiel chimique du constituant $i$.

Différentielle de l'énergie interne :

d U = T d S - P d V + \sum_{i = 1}^{N} μ_{i} d n_{i}

Dérivées partielles :

\begin{matrix} T = (\frac{\partial U}{\partial S})_{V, n_{i}} \\ P = - (\frac{\partial U}{\partial V})_{S, n_{i}} \\ μ_{i} = (\frac{\partial U}{\partial n_{i}})_{S, V, n_{j \neq i}} \end{matrix}

Enthalpie libre du mélange : $G = U + P V - T S$

G = \sum_{i = 1}^{N} n_{i} μ_{i}

$μ_{i}$ est l'enthalpie libre molaire partielle du constituant $i$ dans le mélange.

Variables de l'enthalpie libre :

G (T, P, n_{1}, n_{2}, \dots n_{N})

Différentielle de l'enthalpie libre :

d G = - S d T + V d P + \sum_{i = 1}^{N} μ_{i} d n_{i}

Dérivées partielles :

\begin{matrix} S = - (\frac{\partial G}{\partial T})_{P, n_{i}} \\ V = (\frac{\partial G}{\partial P})_{T, n_{i}} \\ μ_{i} = (\frac{\partial G}{\partial n_{i}})_{T, P, n_{j \neq i}} \end{matrix}

Potentiel chimique d'un constituant (résultat admis) :

μ_{i} = μ_{i}^{\circ} (T) + R T ln (a_{i})

$μ_{i}^{\circ}$ : potentiel chimique standard.

$a_{i}$ : activité du constituant $i$ dans le mélange, en général fonction de la composition et de la pression.

1. Enthalpie libre d'un système chimique

a. Potentiel thermodynamique

b. Potentiel chimique

c. Mélanges idéaux

Mélange idéal de gaz parfaits

\begin{matrix} P V = n R T = \sum_{i} n_{i} R T \\ P_{i} V = n_{i} R T \end{matrix}

Pression partielle du gaz $i$

P_{i} = \frac{n_{i}}{n} P = x_{i} P

a_{i} = \frac{P_{i}}{P_{0}} = x_{i} \frac{P}{P_{0}}

Solution diluée idéale

$c_{i}$ concentration (mol/L) du soluté $i$

a_{i} = \frac{c_{i}}{c_{0}}

a_{s o l v a n t} = 1

a_{s o l i d e} = 1

2. Enthalpie libre de réaction

a. Définition

Enthalpie libre de réaction d'un système chimique où une réaction d'avancement $ξ$ se déroule :

Δ_{r} G = (\frac{\partial G}{\partial ξ})_{T, P}

Grandeur intensive (molaire).

À T et P constantes :

d G = \sum_{i = 1}^{N} μ_{i} d n_{i} = \sum_{i = 1}^{N} μ_{i} ν_{i} d ξ

Δ_{r} G = \sum_{i = 1}^{N} ν_{i} μ_{i}

2. Enthalpie libre de réaction

a. Définition

b. Évolution d'un système chimique

Pour une transformation monobare et monotherme, l'enthalpie libre $G (ξ)$ est minimale à l'équilibre et la fonction est dérivable pour tout $ξ$ donc :

(\frac{\partial G}{\partial ξ})_{T, P} = 0

Premier et second principes appliqués au système chimique :

d G < 0

Équilibre chimique :

Δ_{r} G = 0

Sens d'évolution d'un système hors d'équilibre :

Si $Δ_{r} G < 0$ alors $d ξ > 0$ .
Si $Δ_{r} G > 0$ alors $d ξ < 0$ .

2. Enthalpie libre de réaction

a. Définition

b. Évolution d'un système chimique

c. Loi de l'équilibre chimique

Enthalpie libre standard de réaction

Δ_{r} G^{\circ} (T) = \sum_{i = 1}^{N} ν_{i} μ_{i}^{\circ} (T)

Enthalpie libre de réaction :

Δ_{r} G = Δ_{r} G^{\circ} (T) + R T ln (Q_{r})

Quotient de réaction :

Q_{r} = Π_{i = 1}^{N} a_{i}^{ν_{i}}

Exemple : synthèse de l'ammoniac

N_{2} (g) + 3 H_{2} (g) = 2 N H_{3} (g)

Pour un mélange idéal de gaz parfaits :

Q_{r} = \frac{(\frac{P (N H_{3})}{P_{0}})^{2}}{(\frac{P (N_{2})}{P_{0}}) (\frac{P (H_{2})}{P_{0}})^{3}}

Mélange initial : $n$ mole de $N_{2}$ et $3n$ moles de $H_{2}$ .

\begin{matrix} N_{2} (g) & 3 H_{2} (g) & 2 N H_{3} (g) & n_{g} \\ n & 3 n & 0 & 4 n \\ n - ξ & 3 n - 3 ξ & 2 ξ & 4 n - 2 ξ \end{matrix}

Quotient de réaction en fonction de l'avancement :

Q_{r} (ξ, P) = \frac{{(2 ξ)}^{2} {(4 n - 2 ξ)}^{2} P_{0}^{2}}{{(3 n - 3 ξ)}^{3} (n - ξ) P^{2}}

Constante d'équilibre : $K^{\circ} (T)$ .

Δ_{r} G^{\circ} (T) + R T ln (K^{\circ} (T)) = 0

K^{\circ} (T) = exp (- \frac{Δ_{r} G^{\circ} (T)}{R T})

Enthalpie libre de réaction :

Δ_{r} G (T, P, ξ) = R T ln (\frac{Q_{r} (ξ, P)}{K^{\circ} (T)})

Condition d'équilibre :

Q_{r} (ξ_{e}, P) = K^{\circ} (T)

Sens d'évolution d'un système hors d'équilibre :

Si $Q_{r} < K^{\circ}$ alors $d ξ > 0$ .
Si $Q_{r} > K^{\circ}$ alors $d ξ < 0$ .

Taux de conversion de $H_{2}$ :

α = \frac{3 ξ}{3 n}

Q_{r} = \frac{{(2 α)}^{2} {(4 - 2 α)}^{2} P_{0}^{2}}{{(2 - 2 α)}^{3} (1 - α) P^{2}}

Le taux de conversion ne dépend que des proportions initiales (variables intensives).

2. Enthalpie libre de réaction

a. Définition

b. Évolution d'un système chimique

c. Loi de l'équilibre chimique

d. Enthalpie libre standard de réaction

Enthalpie libre standard de réaction :

Δ_{r} G^{\circ} = \sum_{i = 1}^{N} ν_{i} μ_{i}^{\circ}

$μ_{i}^{\circ}$ : enthalpie libre molaire de l'espèce dans l'état standard (gaz pur parfait ou soluté infiniment dilué).

μ_{i}^{\circ} = G_{i, m}^{\circ} = H_{i, m}^{\circ} - T S_{i, m}^{\circ}

Entropie standard de réaction

Δ_{r} S^{\circ} (T) = \sum_{i = 1}^{N} ν_{i} S_{i, m}^{\circ}

Les entropies molaires standards sont obtenues expérimentalement : table thermodynamique à 298 K.

Signe de $Δ_{r} S^{\circ}$ pour une réaction en phase gazeuse :

Positif si $\sum ν_{g a z} > 0$ .
Négatif si $\sum ν_{g a z} < 0$ .
Indéterminé si $\sum ν_{g a z} = 0$ .

Exemple : $N_{2} (g) + 3 H_{2} (g) = 2 N H_{3} (g)$ à 298 K

\begin{matrix} Δ_{r} H^{\circ} = \\ Δ_{r} S^{\circ} = \\ Δ_{r} G^{\circ} = \\ K^{\circ} = \end{matrix}

Enthalpie libre standard de réaction :

Δ_{r} G^{\circ} (T) = Δ_{r} H^{\circ} - T Δ_{r} S^{\circ}

L'enthalpie et l'entropie standard de réaction dépendent de $T$ mais cette dépendance est souvent négligée. L'enthalpie libre standard de réaction dépend fortement de $T$.

Réaction thermodynamiquement favorable :

K^{\circ} > 1

Δ_{r} G^{\circ} < 0

Facteur énergétique : le caractère exothermique tend à rendre la réaction favorable.

Facteur entropique : une variation d'entropie positive tend à rendre la réaction favorable, d'autant plus que la température est élevée.

Une réaction endothermique peut être favorable grace au facteur entropique.

Attention : ne pas confondre réaction rapide (cinétique) et réaction thermodynamiquement favorable, très souvent lente à température ambiante.

3. Équilibre chimique

a. Influence de la température

Influence de la température sur l'enthalpie libre standard de réaction :

Δ_{r} G^{\circ} (T) = Δ_{r} H^{\circ} - T Δ_{r} S^{\circ}

Signe de l'entropie standard de réaction :

$Δ_{r} S^{\circ} > 0$ : augmentation de $T$ favorable
$Δ_{r} S^{\circ} < 0$ : augmentation de $T$ défavorable

Exemple : $N_{2} (g) + 3 H_{2} (g) = 2 N H_{3} (g)$

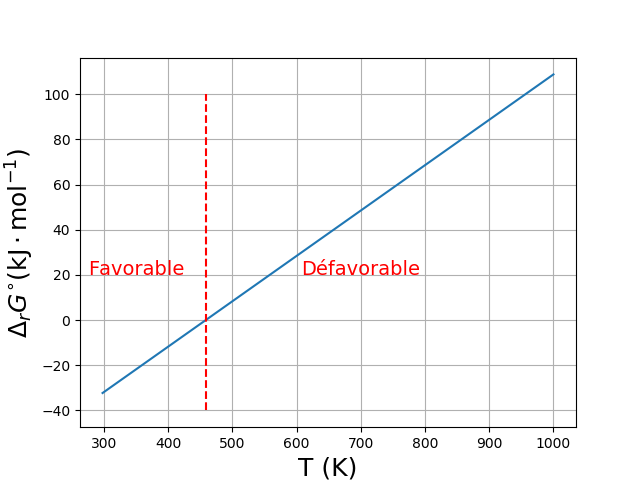
Influence de la température sur la constante d'équilibre

ln K^{\circ} (T) = - \frac{Δ_{r} G^{\circ} (T)}{R T} = - \frac{Δ_{r} H^{\circ}}{R T} + \frac{Δ_{r} S^{\circ}}{R}

Loi de van't Hoff :

\frac{d ln K^{\circ} (T)}{d T} = \frac{Δ_{r} H^{\circ}}{R T^{2}}

Pour une réaction exothermique, $K^{\circ} (T)$ est une fonction décroissante de la température.

Dans un réacteur adiabatique, $K^{\circ} (T)$ diminue au cours de la transformation.

Exemple : $N_{2} (g) + 3 H_{2} (g) = 2 N H_{3} (g)$

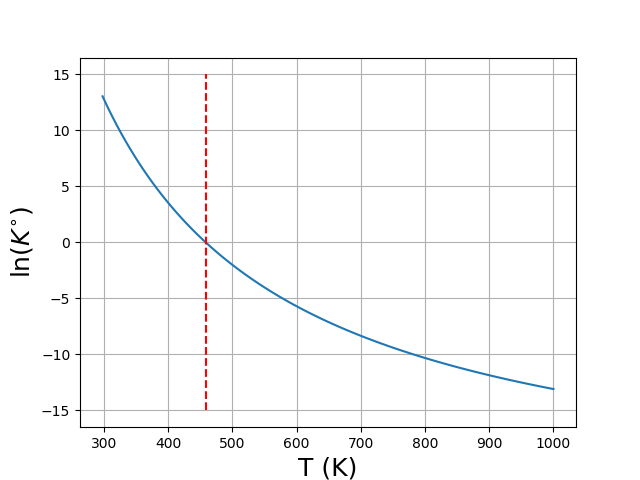
Influence de la température sur l'avancement à l'équilibre :

Δ_{r} G = Δ_{r} G^{\circ} (T) + R T ln (Q_{r} (ξ, P)) = R T ln (\frac{Q_{r} (ξ, P)}{K^{\circ} (T)})

À l'équilibre : $Δ_{r} G = 0$ .

Augmentation de $T$ : le système n'est plus à l'équilibre. Le signe de $Δ_{r} G$ permet de déterminer le sens d'évolution :

Si $K^{\circ}$ augmente alors $Δ_{r} G < 0$ et $d ξ > 0$ .
Si $K^{\circ}$ diminue alors $Δ_{r} G > 0$ et $d ξ < 0$ .

3. Équilibre chimique

a. Influence de la température

b. Influence de la pression

La constante d'équilibre $K^{\circ} (T)$ ne dépend pas de $P$. Le quotient de réaction dépend de $P$ si au moins un constituant du mélange est gazeux.

Δ_{r} G = R T ln (\frac{Q_{r} (ξ, P)}{K^{\circ} (T)})

Augmentation de $P$ : le système n'est plus à l'équilibre. Le signe de $Δ_{r} G$ permet de déterminer le sens d'évolution :

Si $Q_{r}$ augmente alors $Δ_{r} G > 0$ et $d ξ < 0$ .
Si $Q_{r}$ diminue alors $Δ_{r} G < 0$ et $d ξ > 0$ .

Exemple : $N_{2} (g) + 3 H_{2} (g) = 2 N H_{3} (g)$

Mélange initial : $n$ mole de $N_{2}$ et $3n$ moles de $H_{2}$ .

Q_{r} (ξ, P) = \frac{{(2 ξ)}^{2} {(4 n - 2 ξ)}^{2} P_{0}^{2}}{{(3 n - 3 ξ)}^{3} (n - ξ) P^{2}}

Si $P$ augmente $Q_{r}$ diminue donc $Δ_{r} G < 0$ et $d ξ > 0$ .

L'avancement augmente avec la pression.

3. Équilibre chimique

a. Influence de la température

b. Influence de la pression

c. Influence des proportions initiales

Exemple : $N_{2} (g) + 3 H_{2} (g) = 2 N H_{3} (g)$

Mélange initial : $n_1$ moles de $N_{2}$ et $n_2$ moles de $H_{2}$ .

\begin{matrix} N_{2} (g) & 3 H_{2} (g) & 2 N H_{3} (g) & n_{g} \\ n_{1} & n_{2} & 0 & n_{1} + n_{2} \\ n_{1} - ξ & n_{2} - 3 ξ & 2 ξ & n_{1} + n_{2} - 2 ξ \end{matrix}

Q_{r} (ξ, P) = \frac{{(2 ξ)}^{2} {(n_{1} + n_{2} - 2 ξ)}^{2} P_{0}^{2}}{{(n_{2} - 3 ξ)}^{3} (n_{1} - ξ) P^{2}}

Influence de $n_{1}$ ?

\frac{\partial ln (Q_{r})}{\partial n_{1}} = \frac{n_{1} - n_{2}}{(n_{1} + n_{2} - 2 ξ) (n_{1} - ξ)}

Si $n_{1} < n_{2}$ , une augmentation de $n_{1}$ fait diminuer $Q_{r}$ donc $d ξ > 0$ .

Si $n_{1} > n_{2}$ , une augmentation de $n_{1}$ fait augmenter $Q_{r}$ donc $d ξ < 0$ .

Si $N_{2}$ est en excès ( $n_{1} > n_{2} / 3$ ), l'avancement est maximal pour $n_1=n_2$.