TP 3 - Analyse spectrale des signaux périodiques - Partie II
1. Introduction
Dans cette seconde partie, on verra comment utiliser la transformée de Fourier discrète pour faire l'analyse spectrale d'un signal expérimental périodique ou quasi périodique, dont la période n'est pas connue. La méthode permettra plus généralement de faire l'analyse spectrale d'un signal non périodique.
Matériel :
- Générateur de signaux.
- Oscilloscope.
- Carte SysamSP5.
2. Principe
Lorsqu'on analyse un signal réel, on ne connaît pas en général sa période exacte et la périodicité peut d'ailleurs être imparfaite. Il est donc impossible de réaliser un échantillonnage de N points sur exactement une période. On réalise alors l'échantillonnage sur une durée T grande devant la période du signal. La durée T=NTe définit la largeur de la fenêtre d'analyse. La résolution fréquentielle du spectre obtenu est 1/T, donc plus T est grand plus l'analyse fréquentielle est fine. Par exemple, avec T=1 s, on obtient un spectre de résolution 1 Hz. Remarquons que la durée du signal analysée est volontairement notée T, comme la période du signal périodique étudié précédemment. En effet, l'analyse de ce signal par tranformée de Fourier discrète donne les coefficients de Fourier d'une fonction de période T dont le signal analysé définit la forme (signal analysé prolongé par périodicité).
Figure pleine pageLa limite correspond au passage à un spectre continu (par opposition au spectre de raies). En réalité, la durée T est nécessairement finie mais, si elle est assez grande par rapport à la période du signal, le spectre discret obtenu peut être considéré comme une approximation du spectre continu qui serait obtenu avec une durée infinie. On trace donc le spectre en reliant les points par des segments, ce qui correspond à une interpolation linéaire. On verra cependant qu'une interpolation linéaire n'est pas toujours satisfaisante.
La fréquence d'échantillonnage doit respecter la condition de Nyquist-Shannon pour les signaux à bande de fréquences limitée. Elle doit donc être d'autant plus grande que le signal comporte des hautes fréquences dans son spectre. Obtenir un spectre de bonne résolution exige une durée T grande. Obtenir un spectre de bonne résolution d'un signal dont la fréquence fmax est grande nécessite donc un nombre d'échantillons N très grand. En conséquence, la capacité de stockage en mémoire est un paramètre important, avec la fréquence d'échantillonnage, pour la performance d'un système numérique d'analyse spectrale. Les meilleurs systèmes sont capables de mémoriser plusieurs millions d'échantillons et de calculer la TFD de ces échantillons.
3. Spectre d'un signal sinusoïdal
Nous allons voir comment cela fonctionne avec un signal réel, dont on fait la numérisation avec la carte Sysam-SP5.
La fréquence d'échantillonnage est fixée à fe=10 kHz. La durée T de la numérisation est variable. Voici le script (à télécharger) qui fait la numérisation, trace le signal échantillonné et l'enregistre dans un fichier. Ce script doit être exécuté en local avec IDLE. Pour chaque expérience, le signal échantillonné est enregistré dans un fichier NPY. Il faudra donc faire attention à modifier le nom du fichier avant chaque expérience, pour ne pas écraser le fichier de l'expérience précédente.
L'enregistrement du signal numérique dans un fichier permettra son traitement dans un notebook du Jupyter Hub. Ce notebook constitue un compte rendu du TP. Il devra contenir les analyses de tous les signaux étudiés dans ce TP, les uns à la suite des autres. En ouvrant le notebook, on devra donc voir les analyses de tous les signaux et les commentaires associés.
import numpy as np
import matplotlib.pyplot as plt
import pycanum.main as pycan
can = pycan.Sysam("SP5")
Vmax = 10.0
can.config_entrees([0],[Vmax])
fe = 10e3
te = 1/fe
T=0.1
N = int(T/te)
can.config_echantillon(te*1e6,N)
can.acquerir()
t=can.temps()[0]
u0=can.entrees()[0]
can.fermer()
# modifier le nom du fichier fichier pour chaque expérience
np.save('sinus-875Hz-T=0,1.npy',np.array([t,u0]))
plt.figure()
plt.plot(t,u0)
plt.grid()
plt.xlabel('t (s)')
plt.ylabel('u (V)')
plt.xlim(0,1e-2) # échelle à choisir en fonction de la période du signal
plt.show()
[1] Utiliser le générateur de signaux pour générer un signal sinusoïdal de fréquence f1=875 Hz et d'amplitude 4,0 V (8 Vpp). Le visualiser avec l'oscilloscope.
[2] Effectuer la numérisation de ce signal pour fe=10 kHz et T=0,1 s.
[3] Exporter le fichier NPY contenant le signal vers le Jupyter Hub, dans le dossier partage/TP/TP3 et dans le sous-dossier NOM1-NOM2. Créer dans ce dossier un notebook intitulé AnalyseSignaux, dans lequel on écrira le code d'analyse spectrale de ce signal et des suivants.
[4] Après avoir importé les modules nécessaires, récupérer le signal de la manière suivante : [t,x]=np.load('nom_fichier.npy'). Faire le tracé de sa représentation temporelle (ne pas oublier les légendes et le bon choix des échelles).
[5] Calculer la TFD puis le spectre de la manière suivante :
tfd = fft(x)
N = len(x)
te = t[1]-t[0]
T = N*te
spectre = np.absolute(tfd)*2/N
freq = np.arange(N)*1.0/T
[6] Tracer le spectre avec la fonction plot, qui relie les points par des segments rectilignes. Reconnaître dans la courbe tracée le spectre d'une sinusoïde mais dont la raie a une largeur non nulle.
L'analyse spectrale permet d'obtenir la fréquence du signal. Il s'agit de la fréquence qui correspond au maximum du spectre :
i = np.argmax(spectre[0:N//2])
f = freq[i]
print(f)
La précision de cette valeur est .
Si la durée T est assez grande, la hauteur de la raie est en principe égale à l'amplitude de la sinusoïde. On l'obtient par :
A = np.max(spectre[0:N//2])
print(A)
[7]
Obtenir la fréquence et la hauteur de la raie et comparer aux valeurs programmées sur le générateur.
[8]
Augmenter la durée T d'analyse afin d'obtenir une résolution fréquentielle de 1 Hz.
Obtenir la fréquence et la hauteur de la raie et comparer aux valeurs programmées sur le générateur. Y-a-t-il une amélioration par rapport à la durée précédente ?
[9]
Refaire la numérisation avec une fréquence f1 plus grande, telle que la condition de Nyquist-Shannon soit satisfaite
mais avec une marge d'une centaine de Hertz. Relever la fréquence du maximum et comparer à la fréquence programmée sur le générateur.
[10]
Refaire la numérisation avec une fréquence f1 plus grande, telle que la condition de Nyquist-Shannon ne soit pas satisfaite.
On pourra par exemple choisir f1 telle que f1-fe/2 soit de l'ordre de quelques centaines d'Hertz. Quelle est la fréquence
relevée sur le spectre ? Vérifier que cette fréquence est égale à fe-f1.
Lorsque la condition de Nyquist-Shannon n'est pas vérifiée, on observe un repliement de spectre : la raie de fréquence f1 se trouve dans la bande [fe/2,fe], alors que la raie de fréquence fe-f1 se retrouve dans la bande [0,fe/2], là où on s'attend à voir le spectre du signal analogique.
[11]
Observer la représentation temporelle du signal échantillonné sur une dizaine de cycles. Peut-on déduire une fréquence de cette observation ? Comparer à la fréquence obtenue sur le spectre.
Le spectre du signal échantillonné a une période égale à fe. Il comporte donc les raies identiques aux fréquences suivantes (où p est un nombre entier) :
Dans l'exemple précédent, le repliement de la raie de fréquence fe-f1 est observé. Si l'on augmente encore la fréquence f1, on peut observer le repliement de la raie de fréquence 2fe-f1. Cela se produit lorsque : , soit .
[12] Choisir une fréquence f1 permettant d'observer ce repliement.
4. Amélioration de l'analyse spectrale
Le calcul du spectre fournit bien la fréquence de la raie avec une précision de 1/(2T) mais la hauteur de la raie est plus ou moins sous-estimée.
L'estimation de la hauteur de la raie est améliorée en augmentant la durée T. Cependant, si la fréquence d'échantillonnage est très grande (si le signal comporte des très hautes fréquences), la durée T est limitée par la taille de la mémoire associée au convertisseur analogique-numérique.
Il est possible d'améliorer la précision de la hauteur de raie, et même de sa fréquence, sans augmenter la durée de la numérisation. La méthode consiste à faire une interpolation du spectre discret, comme le montre la figure ci-dessous.
Figure pleine pageLe spectre interpolé correspond au spectre du signal de durée T mais qui serait prolongé par des zéros afin que sa durée soit infinie. Pour l'obtenir, il faut donc ajouter des zéros au signal échantillonné (après le dernier échantillon) avant de calculer sa transformée de Fourier discrète. Pour obtenir un bon résultat, il est préférable d'appliquer une fonction de fenêtrage au signal. Le fenêtrage consiste à multiplier le signal par une fonction de pondération qui réduit sa valeur aux bords de la fenêtre d'analyse. Voici par exemple la fonction de fenêtrage de Blackman, pour N=1000 échantillons :
from scipy.signal.windows import get_window
from matplotlib.pyplot import *
figure()
N = 1000
w = get_window('blackman',N)
plot(w)
grid()
xlabel('n')
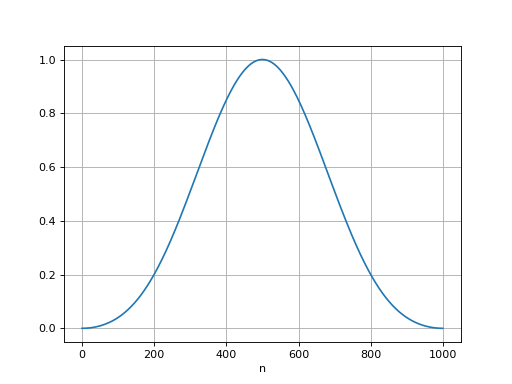 blackman.pdf
blackman.pdf
La figure suivante illustre les deux étapes de l'interpolation :
Figure pleine pageSi x désigne le tableau contenant les échantillons, le fenêtrage et l'ajout de zéros est réalisé par :
N=len(x)
w = get_window('blackman',N))
x1=np.concatenate(x*w,np.zeros(6*N)))
On a choisit d'ajouter un nombre de zéros égal à 6 fois la taille du signal.
Le spectre se calcule avec la TFD, mais il faut appliquer un facteur correctif (qui dépend du type de fenêtrage utilisé) :
spectre = np.absolute(fft(x1))*2.0/N/0.42
La nouvelle durée T1 du signal échantillonné est la taille du nouveau signal (tableau x) multipliée par la période d'échantillonnage. Les valeurs de fréquences sont donc obtenues par :
N1 = len(x1) T1 = N1*te freq=np.arange(N1)*1/T1
[13]
Appliquer cette méthode de calcul du spectre et comparer la hauteur de la raie à l'amplitude de la sinusoïde.
[14]
Ajouter un décalage au signal (offset) et obtenir son spectre. Ajuster l'échelle de fréquence du tracé de manière à bien faire apparaître les deux raies du spectre. Comparer l'amplitude de la raie de fréquence nulle à la valeur
du décalage.
Dans la suite du TP et dans les TP suivants, on utilisera cette méthode de calcul du spectre car elle permet d'optimiser la précision pour une durée T donnée.
Remarque : l'ajout de zéros permet d'améliorer la précision de la mesure de la hauteur de la raie et de celle de la fréquence. Cependant, la durée du signal analysée reste T et la résolution fréquentielle reste 1/T. Il sera donc impossible de discerner deux raies dont les fréquences sont plus proches que 1/T. Autrement dit, il ne faut pas confondre résolution en fréquence et précision en fréquence. La seule manière d'augmenter la résolution fréquentielle est d'augmenter la durée T de l'enregistrement du signal.
5. Spectre d'un signal périodique
Pour faire l'analyse spectrale d'un signal périodique, la fréquence d'échantillonnage doit en principe être supérieure au double de la plus grande fréquence présente dans le signal. Théoriquement, des fonctions périodiques comme le créneau ou le triangle n'ont pas de fréquence maximale (ne sont pas à bande de fréquences limitée). Cependant, un signal réel possède toujours une fréquence maximale mais celle-ci peut être plus grande que la fréquence d'échantillonnage maximale (10 MHz pour la carte SysamSP5, 2 GHz pour l'oscilloscope).
S'il est impossible d'échantillonner correctement les harmoniques de rang élevé du signal, un compromis doit être trouvé. Le repliement de ces harmoniques sera inévitable mais il faut que les raies repliées soient assez faibles ou bien clairement identifiables.
L'amplitude des harmoniques de rang élevé est généralement très faible par rapport à celle du fondamental. On est alors amené à représenter l'amplitude en échelle logarithmique :
spectre_db = 20*np.log10(spectre)
[15] Faire la numérisation d'un signal triangulaire d'une fréquence d'environ 90 Hz et d'amplitude 4,0 V, à la fréquence d'échantillonnage fe=10 kHz et pour une durée T=1 s.
[16] Obtenir le spectre du signal échantillonné en échelle décibel.
[17]
Quelle est en théorie la différence en décibel entre la raie du fondamental et la raie de l'harmonique de rang 3 ? Retrouve-t-on cette différence
sur le spectre ?
[18]
Repérer sur le spectre les raies qui viennent du repliement. Jusqu'à quelle fréquence peut-on considérer que ces raies sont négligeables (c.a.d. au moins
-20 dB en dessous des raies du signal analogique voisines) ?
Remarque : si la fréquence d'échantillonnage est multiple de la fréquence du signal, les raies repliées ne sont pas discernables.
[19]
Refaire la numérisation du même signal mais avec une fréquence d'échantillonnage fe=100 kHz. Le nombre d'échantillons est alors N=100000.
Tracer le spectre en décibel pour des fréquences de 0 à 5000 Hz. Comparer au spectre obtenu avec fe=10 kHz.
Faire l'analyse spectrale du même signal avec l'oscilloscope (voir Annexe). Mesurer le rapport d'amplitude entre l'harmonique de rang $n$ et le fondamental, jusqu'à $n=9$ (utiliser les outils de mesure). Entrer ces valeurs dans un tableau numpy et vérifier la loi en pour l'amplitude des harmoniques.
6. Annexe : fonction FFT de l'oscilloscope
La fonction FFT (Fast Fourier Transform) permet d'obtenir le spectre d'un signal. L'oscilloscope trace le spectre pour des fréquences dans l'intervalle , qui est le domaine de fréquence correspondant au spectre du signal analogique qu'on étudie.
- Appuyer sur FFT pour activer le calcul du spectre.
- Si le signal à analyser est sur la voie 1, sélectionner la voie 1 comme source.
- Il est conseillé de garder la trace du signal mais de la décaler vers le haut.
- L'échelle verticale du spectre (l'amplitude) est en décibel ou bien en Volts (RMS). Pour changer le type d'échelle, aller dans Param. Le bouton Echelle permet de modifier cette échelle.
- La durée T du signal échantillonné (signal dont la TFD est calculée) correspond à la totalité du signal visible sur l'écran. Si on augmente cette durée en tournant le bouton de réglage de l'échelle de temps, la résolution fréquentielle du spectre augmente (celle-ci est affichée sur l'écran).
- L'intervalle de fréquences du spectre tracé à l'écran se règle avec les boutons Plage et Centre.
- Le bouton Décal permet de décaler le spectre verticalement.