TP 20 : Spectroscope à réseau

1. Introduction

L'objectif de ce TP est d'apprendre à utiliser un spectroscope-goniomètre à réseau, pour observer un spectre de raies, puis pour faire des mesures de longueur d'onde.

Les simulations et le traitement des résultats expérimentaux seront faits dans un notebook intitulé spectroscope à placer dans un dossier à votre nom, qu'il faudra créer dans partage/TP/TP20 Spectroscope.

2. Principe

Le spectroscope est constitué d'un collimateur et d'une lunette montés sur un goniomètre. Le collimateur est fixe alors que la lunette tourne autour de l'axe du goniomètre. L'angle de rotation de l'axe de la lunette peut être mesuré au soixantième de degré près.

Figure pleine page

Le collimateur est constitué d'une fente, dont la largeur est ajustable, et d'une lentille convergente. Une molette permet d'ajuster la distance entre la fente et la lentille. La source de lumière à étudier est placée juste derrière la fente. Lorsque le collimateur est réglé, il forme l'image de la fente à l'infini. Observés dans un plan perpendiculaire à la fente, les rayons sont collimatés, c'est-à-dire parallèles entre eux.

La lunette sert à faire une observation visuelle à l'infini. Elle est constituée d'un objectif (une lentille convergente), d'un plan image contenant un réticule, et d'un oculaire. Le réticule est formé de deux fils montés en croix. Il sert à régler la lunette et à viser précisément les raies du spectre. La lunette comporte aussi un rétroéclairage du réticule (non représenté sur la figure) : une lame semi-réfléchissante est interposée entre le réticule et l'oculaire pour éclairer le réticule par l'arrière. Le bloc oculaire, comportant l'oculaire, le réticule et son rétroéclairage, peut être déplacé par rapport à l'objectif afin de faire la mise au point.

3. Réglages

L'observateur doit tout d'abord régler le tirage de l'oculaire (par rapport au réticule) pour voir une image nette du réticule, puis régler la lunette à l'infini par autocollimation. Cette méthode consiste à placer un miroir plan contre la lentille de l'objectif, et à déplacer le bloc oculaire (par rapport à l'objectif) afin que l'image du réticule par réflexion soit nette.

[1] Régler le tirage de l'oculaire en le tournant.

[2] Faire la mise au point de la lunette à l'infini par autocollimation.

Le collimateur doit former l'image de la fente à l'infini. On se sert donc de la lunette déjà réglée pour faire son réglage.

[3] Observer l'image de la fente par la lunette et régler le collimateur. Affiner la fente.

Le goniomètre est un instrument permettant de mesurer des angles de déviation de la lumière. Il est constitué d'un axe de rotation vertical, autour duquel le plateau central et la lunette tournent. La mesure d'angle se fait au moyen de deux cercles. Le premier cercle, gradué en degrés, est fixe. Le second cercle entraîne en rotation la lunette et comporte un vernier qui permet de lire l'angle au soixantième de degré près. La référence de l'angle étant une direction arbitraire, on doit toujours mesurer une différence d'angles de deux directions visées.

[4] Se familiariser avec les vis de réglage du plateau. Un niveau à bulle permet de faire un premier réglage (approximatif) du plateau, qui doit être horizontal puisque l'axe de rotation est vertical.

[5] Le support de la lunette possède une vis de réglage. Comprendre son utilité en observant l'image de la fente.

[6] Apprendre à lire un angle au moyen du cercle gradué et du vernier.

4. Réseau de diffraction

Un réseau de diffraction est un écran opaque sur lequel un très grand nombre de fentes (appelées aussi traits) sont tracées. On note n le nombre de traits par millimètre et a=1/n l'espacement des fentes (en millimètres). Par exemple, pour un réseau comportant 100 traits par millimètre a=10 μm.

Le réseau est posé verticalement sur le plateau central. La fente du collimateur doit être parallèle aux traits du réseau. La lumière issue du collimateur arrive sur le réseau avec un angle d'incidence (par rapport à la normale) noté i. Une raie de longueur d'onde λ est observée dans une direction α_p vérifiant la condition d'interférence constructive :

$$sin{\alpha }_p-sini=p\frac{\lambda }{a}\text{(1)}$$

où p est un nombre entier (l'ordre d'interférence).

Figure pleine page

Pour p=0 (ordre 0), on observe l'image de la fente, là où elle serait en l'absence du réseau, et sans aucune dispersion de la lumière. Le spectre de raies d'ordre 1 comporte les raies observées aux angles α₁. Le spectre d'ordre -1 comporte les raies d'angles α_-1.

Les angles α₁ et α_-1 ne sont pas directement mesurables. On mesure les angles par rapport à l'ordre 0, notés β₁ et β_-1, et définis par :

$$\begin{array}{cc}\hfill & {\beta }_1={\alpha }_1-i\hfill \\ \hfill & {\beta }_{-1}={\alpha }_{-1}-i\hfill \end{array}$$

Idéalement, le réseau doit être éclairé en incidence normale (i=0). Dans ce cas, α₁=β₁ et α_-1=β_-1. Étant donné que l'angle d'incidence n'est pas mesurable, il faut disposer d'une procédure permettant de l'annuler, ou au moins de le rendre assez faible.

[7] Pour un réseau de 300 traits par millimètre et un angle d'incidence i=10 degrés, calculer les angles β₁ et β_-1 pour la longueur d'onde λ=500 nm.

[8] De quel côté l'angle le plus grand en valeur absolue (|β₁| ou |β_-1|) se trouve-t-il ?

[9] Après avoir mesuré β_-1 et β₁, dans quel sens faut-il tourner le réseau pour réduire l'angle i afin de se rapprocher de l'incidence normale ?

5. Mesure des longueurs d'onde

On dispose d'une lampe spectrale à vapeur de mercure (Hg) ou d'une lampe à vapeur de mercure-cadmium (Hg-Cd).

[10] Placer le réseau à peu près perpendiculairement au faisceau incident. Observer l'ordre 0, image de la fente du collimateur. Affiner la fente si nécessaire. Constater que la rotation du réseau n'affecte pas la direction de l'ordre 0.

[11] Observer le spectre à l'ordre 1 puis son symétrique à l'ordre -1.

[12] Observer le spectre à l'ordre 1 à l'œil nu (sans la lunette) et comparer à celui vu avec la lunette. Pourquoi le spectre est-il inversé ?

[13] Observer les spectres à l'ordre 2 et 3 et constater qu'ils se chevauchent. Expliquer à l'aide de la formule du réseau.

[14] Choisir une raie et la pointer à l'ordre 1 puis à l'ordre -1. Relever ainsi les angles β₁ et β_-1. Augmenter l'angle d'indidence i et vérifier le résultat obtenu à la question 8.

[15] Replacer le réseau en incidence normale puis mesurer précisément β₁ et β_-1. Corriger l'orientation du réseau en tournant la vis de rotation du plateau dans le sens qui convient. Refaire la mesure et corriger l'orientation. En répétant plusieurs fois cette opération, il est possible en principe d'annuler l'angle d'incidence, à la précision du goniomètre près.

Pour mesurer une longueur d'onde, on fait l'hypothèse que i=0, ce qui conduit à :

$$\begin{array}{ccc}\hfill & sin\left({\alpha }_1\right)=sin\left({\beta }_1\right)=\frac{\lambda }{a}\hfill & \hfill \text{(2)}\\ \hfill & sin\left({\alpha }_{-1}\right)=sin\left({\beta }_{-1}\right)=-\frac{\lambda }{a}\hfill & \hfill \text{(3)}\end{array}$$

On a donc dans ce cas :

$${\beta }_1=-{\beta }_{-1}et{\alpha }_1={\beta }_1=\frac{{\beta }_1-{\beta }_{-1}}{2}$$

Afin de minimiser l'erreur causée par l'angle i pas tout à fait nul, on relève directement la différence β₁-β_-1 en pointant la raie à l'ordre 1 puis à l'ordre -1, et on calcule la longueur d'onde avec la relation :

$$\lambda =asin\left(\frac{{\beta }_1-{\beta }_{-1}}{2}\right)\text{(4)}$$

[16] Repérer les raies les plus intenses du spectre et leur attribuer un nom de couleur.

[17] Choisir une raie et mesurer pour cette raie β₁ et β_-1. La différence $\left|{\beta }_1\right|-\left|{\beta }_{-1}\right|$ permet d'estimer l'angle d'incidence i. Pour cela, utiliser le script Python donné en annexe A.

[18] D'après la précision du goniomètre et la précision du pointage de la raie, donner l'incertitude $u\left(\beta \right)$ sur les valeurs de ${\beta }_1$ et ${\beta }_{-1}$. On admet que le nombre de traits du réseau par millimètre est connu avec une incertitude $u\left(n\right)=0,5m{m}^{-1}$. D'après l'estimation de l'angle d'incidence, quelle incertitude $u\left({\lambda }_i\right)$ sur la longueur d'onde peut-on attribuer au fait que l'angle d'incidence n'est pas parfaitement nul ?

[19] Calculer l'incertitude de la longueur d'onde par une simulation de Monte-Carlo.

[20] Mesurer les longueurs d'onde des raies identifiées et présenter les résultats dans le notebook.

6. Annexe : simulation d'une mesure

import numpy as np
from matplotlib.pyplot import *

L = 500 # longueur d'onde (nm)
n = 100 # nombre de traits par mm
a = 1/n
i = np.linspace(-2,2,1000) # angle d'incidence en degrés
alpha_1 = np.arcsin(L*1e-6/a+np.sin(i*np.pi/180))*180/np.pi
alpha_m1 = np.arcsin(-L*1e-6/a+np.sin(i*np.pi/180))*180/np.pi
figure()
plot(i,np.absolute(alpha_1)-np.abs(alpha_m1),'k-')
xlabel(r"$i\ (\rm deg)$",fontsize=16)
ylabel(r"$|\beta_1|-|\beta_{-1}|\ (\rm deg)$",fontsize=16)
grid()
            

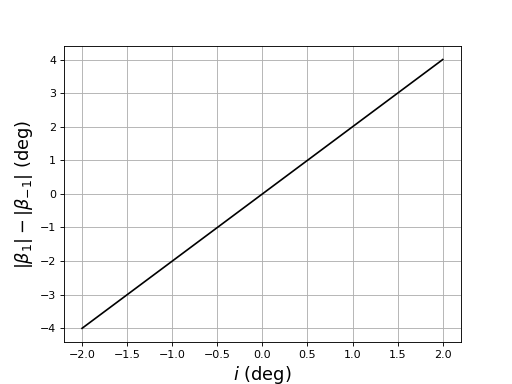differenceBeta.pdf

Mesure d'une longueur d'onde avec la relation $\mathrm{(4)}$ :

Lmesuree = a*1e6*np.sin((alpha_1-alpha_m1)/2*np.pi/180)
figure()
plot(i,Lmesuree-L,'k-')
xlabel(r"$i\ (\rm deg)$",fontsize=16)
ylabel(r"$\lambda_{\rm mes}-\lambda\ (\rm nm)$",fontsize=16)
grid()
              

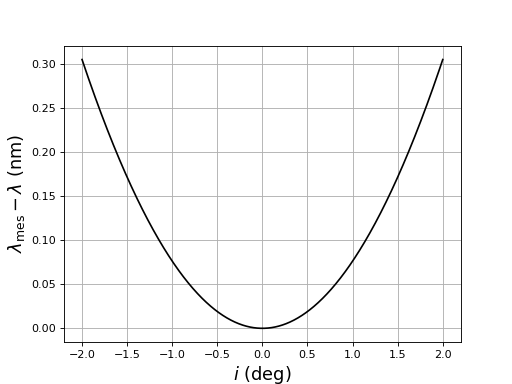ecartLongueurOnde.pdf

Cette courbe donne l'écart entre la longueur d'onde et la longueur d'onde mesurée en supposant que l'angle d'incidence est nul et en utilisant la relation $\mathrm{(4)}$.

Pour comparaison, voici l'écart si on utilise seulement l'angle β₁, que l'on assimile à α₁, pour déterminer la longueur d'onde :

Lmesuree = a*1e6*np.sin(alpha_1*np.pi/180)
figure()
plot(i,Lmesuree-L,'k-')
xlabel(r"$i\ (\rm deg)$",fontsize=16)
ylabel(r"$\lambda_{\rm mes}-\lambda\ (\rm nm)$",fontsize=16)
grid()
              

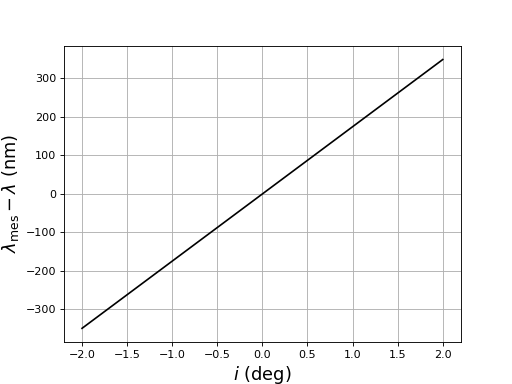ecartLongueurOnde-bis.pdf

Dans ce cas, l'erreur est beaucoup plus grande, ce qui confirme l'intérêt de mesurer β₁-β_-1 et d'appliquer la relation $\mathrm{(4)}$. La différence β₁-β_-1 est très peu sensible à l'angle d'incidence, contrairement à β₁.