Triangulation de Delaunay
1. Introduction
Ce document montre comment générer un maillage triangulaire (pour la méthode des éléments finis) au moyen de la triangulation de Delaunay.
L'objectif est de réaliser une implémentation en Python. Les théorèmes utilisés sont simplement énoncés.
2. Définition
Soit S un ensemble de points du plan. Une triangulation de S est un ensemble de triangles dont les sommets sont les points de S et dont la réunion est l'intérieur de l'enveloppe convexe de S.
On appelle cercle circonscrit d'un triangle l'unique cercle qui contient ses trois sommets.
Par définition, une triangulation de Delaunay possède la propriété suivant : pour tous ses triangles, l'intérieur du cercle circonscrit, c'est-à-dire le disque ouvert circonscrit, ne contient aucun point de S.
Pour un ensemble de points donné, il existe une seule triangulation de Delaunay si et seulement si sur aucun cercle circonscit il n'y a plus de 3 points (les trois sommets du triangle).
Dans ce document, nous appelerons nœuds les sommets des triangles car il s'agit des nœuds du maillage que l'on veut générer.
Un triangle d'une triangulation quelconque est dit Delaunay si son disque ouvert circonscrit ne contient aucun nœud.
Soit un triangle constitué des trois nœuds N1,N2,N3, rangés dans le sens direct, c'est-à-dire que . Le centre du cercle circonscrit est l'intersection des médiatrices des segments N1N2 et N1N3. Si C12 désigne le centre du segment N1N2 et C le centre du cercle circonscrit, on a . Il en est de même pour le segment N1N3, ce qui conduit aux deux équations linéaires suivantes pour les coordonnées (xc,yc) du point C :
Le déterminant de ce système est :
Il est nul si et seulement si les trois points sont alignés, une situation qui ne doit pas survenir. Le système se résout sans difficultés au moyen des règles de Cramer.
Le rayon du cercle est bien évidemment la distance entre le centre et un des nœuds.
Pour savoir si un nœud N(x,y) est à dans le disque ouvert circonscrit d'un triangle, il suffit de comparer sa distance au centre du cercle avec le rayon. En pratique, on compare la distance au carré avec le rayon au carré. Cette condition peut s'exprimer au moyen du déterminant suivant :
Le nœud N(x,y) est à l'intérieur du disque ouvert circonscrit si ce déterminant est strictement positif. Il n'est pas rare que le point testé se trouve théoriquement sur le cercle circonscrit. Considérons par exemple 4 nœuds formant un carré :
Figure pleine pageOn voit facilement sur cet exemple qu'il y a deux triangulations de Delaunay pour ces quatre points car ils sont sur un même cercle. Le point N n'est pas à l'intérieur du cercle circonscrit du triangle N1,N2,N3 mais le test ci-dessus peut renvoyer un résultat positif à cause des erreurs d'arrondi. Pour éviter ce problème, on utilise le test suivant pour savoir si le nœud est dans le disque circonscrit :
avec par exemple . De cette manère, on évite qu'un nœud situé sur le disque circonscrit soir déclaré interne au cercle à cause d'une erreur d'arrondi.
La fonction scipy.spatial.Delaunay permet d'obtenir une triangulation de Delaunay d'un ensemble de points.
import numpy as np from matplotlib.pyplot import * from scipy.spatial import Delaunay from scipy.linalg import det from numpy.random import uniform import random import time
Nous définissons une classe Noeud. Chaque nœud est une instance de cette classe. Chaque instance est transmise dans les fonctions et stockée dans les listes sous la forme d'une référence. Par exemple, si l'on écrit L=[n1,n2,n3] où n1,n2,n3 sont trois instances de la classe Noeud, ce sont en fait les références de ces instances qui sont stockées dans la liste. Ainsi n1 désigne un objet similaire au pointeur du langage C/C++. Le test n1==n2 permet de savoir si deux références pointent le même nœud, sans réaliser aucun test sur les coordonnées. Deux nœuds différents qui ont exactement les mêmes coordonnées seront bien traités comme distincts. La classe contient les coordonnées du nœud et la liste des triangles auxquels il appartient.
class Noeud:
def __init__(self,x,y):
self.x = x
self.y = y
self.triangles = []
def draw(self,style):
plot([self.x],[self.y],style)
La classe Triangle représente un triangle. Les nœuds du triangle sont stockés dans une liste et sont rangés dans le sens direct. Chaque triangle comporte une liste de ses triangles voisins, c'est-à-dire des triangles avec lesquels il a au moins un sommet commun. Voici la première version de cette classe, qui comporte une fonction permettant de tester si un nœud se trouve dans le disque ouvert circonscrit et une fonction qui calcule le centre et le rayon de ce cercle (utilisée pour tracer le cercle) :
class Triangle:
def __init__(self,n1,n2,n3):
self.noeuds = [n1,n2,n3]
self.detT = n2.x*n3.y-n2.x*n1.y-n1.x*n3.y-n2.y*n3.x+n2.y*n1.x+n1.y*n3.x
self.ST = 0.5*abs(self.detT) # aire du triangle
if self.detT<0:
(n2,n3) = (n3,n2)
self.noeuds = [n1,n2,n3]
self.detT = n2.x*n3.y-n2.x*n1.y-n1.x*n3.y-n2.y*n3.x+n2.y*n1.x+n1.y*n3.x
self.voisins = []
self.virtuel = False # voir plus loin
for i in range(3):
self.noeuds[i].triangles.append(self)
if self.detT==0:
print("triangle avec 3 points alignés")
def triangleVoisin(self,tr):
# test si un triangle est voisin
return (self.noeuds[0] in tr.noeuds) or (self.noeuds[1] in tr.noeuds) or (self.noeuds[2] in tr.noeuds)
def ajouterVoisin(self,triangle):
self.voisins.append(triangle)
def enleverVoisin(self,triangle):
self.voisins.remove(triangle)
def dansCercle(self,n):
n1 = self.noeuds[0]
n2 = self.noeuds[1]
n3 = self.noeuds[2]
M = np.array([[n1.x,n1.y,n1.x**2+n1.y**2,1],[n2.x,n2.y,n2.x**2+n2.y**2,1],[n3.x,n3.y,n3.x**2+n3.y**2,1],[n.x,n.y,n.x**2+n.y**2,1]])
m = max(n1.x,n1.y,n2.x,n2.y,n3.x,n3.y,n.x,n.y)
return det(M) > 1e-11*m*m
def cercle(self):
x1 = self.noeuds[0].x
y1 = self.noeuds[0].y
x2 = self.noeuds[1].x
y2 = self.noeuds[1].y
x3 = self.noeuds[2].x
y3 = self.noeuds[2].y
det = (x2-x1)*(y3-y1)-(y2-y1)*(x3-x1)
xc = ((x2*x2-x1*x1+y2*y2-y1*y1)/2*(y3-y1)-(x3*x3-x1*x1+y3*y3-y1*y1)/2*(y2-y1))/det
yc = ((x3*x3-x1*x1+y3*y3-y1*y1)/2*(x2-x1)-(x2*x2-x1*x1+y2*y2-y1*y1)/2*(x3-x1))/det
R = np.sqrt((x1-xc)**2+(y1-yc)**2)
return xc,yc,R
def contientCote(self,na,nb):
return (na in self.noeuds) and (nb in self.noeuds)
def coteCommun(self,tr):
# test si un autre triangle comporte un côté commun avec le triangle
return self.contientCote(tr.noeuds[0],tr.noeuds[1]) or self.contientCote(tr.noeuds[0],tr.noeuds[2]) or self.contientCote(tr.noeuds[1],tr.noeuds[2])
def draw(self,style=None,linewidth=1):
if style==None:
plot([self.noeuds[0].x,self.noeuds[1].x,self.noeuds[2].x,self.noeuds[0].x],[self.noeuds[0].y,self.noeuds[1].y,self.noeuds[2].y,self.noeuds[0].y],linewidth=linewidth)
else:
plot([self.noeuds[0].x,self.noeuds[1].x,self.noeuds[2].x,self.noeuds[0].x],[self.noeuds[0].y,self.noeuds[1].y,self.noeuds[2].y,self.noeuds[0].y],style,linewidth=linewidth)
def drawCercle(self,style):
xc,yc,R = self.cercle()
theta = np.linspace(0,2*np.pi,360)
x = xc+R*np.cos(theta)
y = yc+R*np.sin(theta)
if style!=None:
plot(x,y,style)
else:
plot(x,y)
def print(self):
print("Triangle : ",self)
for n in self.noeuds:
print(n.x,n.y)
La classe Maillage représente le maillage, c'est-à-dire la triangulation. Voici la première version de cette classe :
class Maillage:
def __init__(self):
self.triangles = []
self.retire = []
def fromList(self,noeuds,simplices):
triangles = []
for t in simplices:
n1 = noeuds[t[0]]
n2 = noeuds[t[1]]
n3 = noeuds[t[2]]
tr = Triangle(n1,n2,n3)
triangles.append(tr)
for i in range(len(triangles)): #recherche des voisins
for j in range(len(triangles)):
if i!=j and triangles[i].triangleVoisin(triangles[j]):
triangles[i].ajouterVoisin(triangles[j])
self.triangles = triangles
def draw(self,style,linewidth=1):
for tr in self.triangles:
tr.draw(style,linewidth)
def drawCercles(self,style):
for tr in self.triangles:
tr.drawCercle(style)
def verifierDelaunay(self):
i = 0
test = True
for tr in self.triangles:
for n in tr.noeuds:
for t in self.triangles:
if t!=tr:
if not(n in t.noeuds) and (n!=None) and t.dansCercle(n) :
test=False
i += 1
if t.virtuel:
t.noeuds[0].draw("ro")
t.noeuds[1].draw("ro")
else:
t.drawCercle("r-")
return i
Le maillage est une liste de triangles, c'est-à-dire une liste d'objets de la classe Triangle. La fonction fromList permet de générer le maillage à partir d'une liste de nœuds et d'une liste de triangles, chacun ayant la forme d'une liste de trois indices. Cette liste sera fournie par la fonction scipy.spatial.Delaunay. On pourra ainsi disposer d'une triangulation de Delaunay déjà faite pour tester les algorithmes. La génération du maillage consiste à placer les triangles dans la liste et à remplir la liste voisins de chaque triangle. D'une manière générale, toute modification du maillage devra s'accompagner d'une mise à jour de cette liste, une opération relativement délicate car chaque voisin doit apparaître une seule fois dans la liste. Par ailleurs, retirer un voisin de la liste de voisins se fait sans difficultés avec la fonction de liste remove, qui prend en argument le nom du voisin, c'est-à-dire en fait une référence de l'objet représentant le triangle voisin. La fonction verifierDelaunay renvoie le nombre de triangles qui ne sont pas Delaunay, qui doit être nul pour une triangulation de Delaunay. Cette fonction permettra de vérifier le bon fonctionnement d'algorithmes qui transforment la triangulation tout en maintenant une triangulation de Delaunay.
Voici un exemple :
points = []
noeuds = []
N = 10
x = uniform(-10,10,N)
y = uniform(-10,10,N)
for i in range(N):
points.append([x[i],y[i]])
noeuds.append(Noeud(x[i],y[i]))
points = np.array(points)
tri = Delaunay(points)
figure(figsize=(8,8))
maillage = Maillage()
maillage.fromList(noeuds,tri.simplices)
maillage.draw("k-")
xlim(-10,10)
ylim(-10,10)
invalid = maillage.verifierDelaunay()
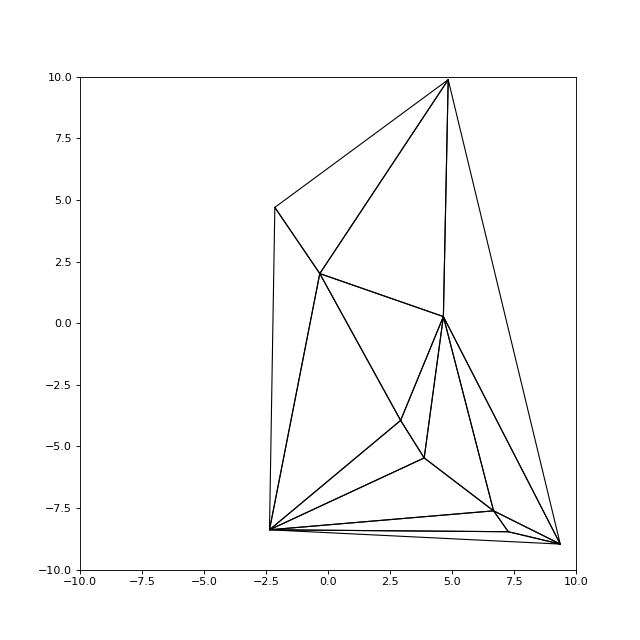 fig1.pdf
fig1.pdf
print(invalid) --> 0
Voici le tracé des cercles circonscrits :
figure(figsize=(8,8))
maillage.draw("k-")
maillage.drawCercles(None)
xlim(-10,10)
ylim(-10,10)
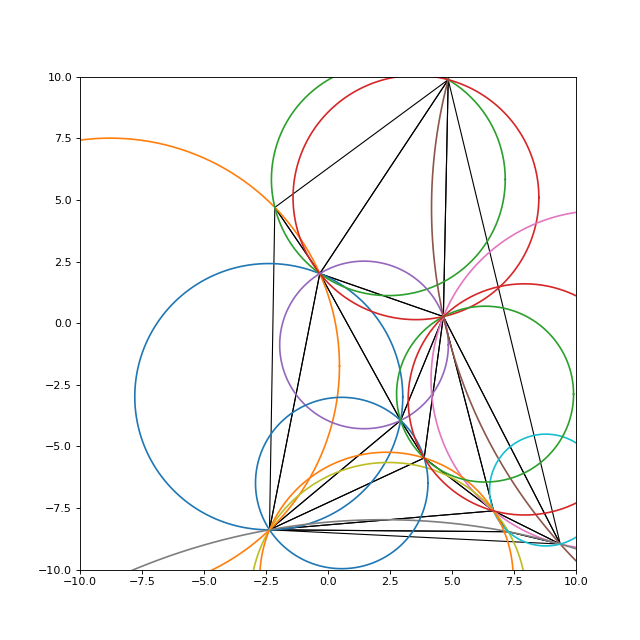 fig2.pdf
fig2.pdf
3. Algorithme de Bowyer-Watson
3.a. Insertion d'un nœud interne
L'algorithme de Bowyer-Watson permet d'ajouter à une triangulation un nouveau nœud et de mettre à jour la triangulation de Delaunay de manière efficace. Dans un premier temps, on traite le cas où le nœud ajouté se trouve dans la triangulation, c'est-à-dire dans l'enveloppe convexe de l'ensemble des nœuds.
Soit N le nouveau nœud. La première étape consiste à repérer un triangle dont le disque ouvert circonscrit contient N. Un tel triangle existe évidemment puisque N se trouve dans l'enveloppe convexe des nœuds.
La deuxième étape consiste à trouver tous les triangles dont le disque ouvert circonscrit contient N. Pour obtenir ces triangles on les recherche tout d'abord parmi les voisins du premier triangle, puis parmi les voisins des voisins et ainsi de suite. La recherche se fait donc de manière récursive.
Les triangles dont le disque ouvert circonscrit contient N forment une cavité polyhédrique, comme illusté sur la figure suivante. Plus précisément, enlever ces triangles donne une cavité polyhédrique.
La troisième étape consiste à générer des nouveaux triangles. Il s'agit des triangles formés du nœud N et des nœuds de la cavité polyhédrique. Ces triangles sont Delaunay. La nouvelle triangulation est donc Delaunay. Pour générer ces triangles, il suffit de repérer le côté des triangles enlevés (les triangles de la cavité) qui ne sont partagés par aucun autre côté des autres triangles enlevés. Ces côtés sont en effet ceux du polyhèdre.
La figure suivante montre une triangulation de Delaunay avec un nœud ajouté N. Les triangles dont le disque ouvert circonscrit contient N sont grisés et leur cercle tracé. Les bords de la partie grisée forment la cavité.
Figure pleine pageLa figure suivante montre les nouveaux triangles (grisés) et leur cercle circonscrit, qui effectivement ne contiennent aucuns nœuds.
Figure pleine pagePour résumer, voici les quatre parties de l'algorithme :
- (1) Recherche d'un triangle dont le disque ouvert circonscrit contient N.
- (2) Recherche récursive de tous les triangles dont le disque ouvert circonscrit contient N. Ces triangles forment une cavité polyhédrique.
- (3) Retrait des triangles de la cavité.
- (4) Génération des triangles constitués de N et des côtés non partagés des triangles de la cavité.
La partie la moins efficace de l'algorithme est (1) car elle se fait a priori en itérant sur tous les nœuds de la triangulation. Il sera donc souhaitable d'accélérer cette étape en recherchant les triangles dans une zone particulière (mais cette optimisation dépendera de la méthode de maillage). Si le nouveau nœud est inséré dans un triangle particulier connu, cette recherche n'est évidemment plus nécessaire. On verra plus loin une méthode d'accélération de cette recherche dans le cas où les nœuds ajoutés sont connus à l'avance.
Nous ajoutons à la classe Maillage la fonction enleverTriangle, qui permet d'enlever un triangle de la liste des triangles, de la listes de voisins des triangles voisins et de la liste des triangles des nœuds sommets de ce triangle. La fonction ajouterNoeud permet d'ajouter un nœud et de mettre à jour la triangulation au moyen de l'algorithme de Bowyer-Watson.
class Maillage2(Maillage):
def __init__(self):
Maillage.__init__(self)
def enleverTriangle(self,tr):
self.retire.append(tr)
self.triangles.remove(tr)
for trv in tr.voisins:
trv.enleverVoisin(tr)
for i in range(3):
if tr.noeuds[i]!=None:
tr.noeuds[i].triangles.remove(tr)
def ajouterNoeud(self,n):
def rechercheCavite(n,tr,trCavite):
for t in tr.voisins:
if not(t in trCavite) and t.dansCercle(n):
trCavite.append(t)
rechercheCavite(n,t,trCavite)
trCavite = []
for tr in self.triangles: # recherche d'un triangle dont le cercle circonscrit contient le nouveau noeud
if tr.dansCercle(n):
trCavite.append(tr)
rechercheCavite(n,tr,trCavite) # recherche récursive des autres triangles
break
nouveaux = []
for i in range(len(trCavite)):
tr = trCavite[i]
self.enleverTriangle(tr)
for c in [[0,1],[0,2],[1,2]]: # recherche du côté non partagé
na = tr.noeuds[c[0]]
nb = tr.noeuds[c[1]]
ajout = True
for j in range(len(trCavite)):
if i!=j:
if trCavite[j].contientCote(na,nb):
ajout = False
break
if ajout:
nouvTr = Triangle(n,na,nb)
nouveaux.append(nouvTr)
self.triangles.append(nouvTr)
# recherche des voisins du nouveau triangle parmi les voisins des triangles enlevés
voisins = []
for t in trCavite:
for trv in t.voisins:
if not(trv in trCavite) and not(trv in voisins) and trv.triangleVoisin(nouvTr):
nouvTr.ajouterVoisin(trv)
trv.ajouterVoisin(nouvTr)
voisins.append(trv)
# les nouveaux triangles sont voisins
for i in range(len(nouveaux)):
for j in range(len(nouveaux)):
if i!=j:
nouveaux[i].ajouterVoisin(nouveaux[j])
La recherche des voisins des nouveaux triangles se fait en deux étapes : on recherche tout d'abord les voisins parmi les voisins des triangles enlevés puis parmi les nouveaux triangles. Il est important qu'aucun voisin n'apparaisse plusieurs fois dans une liste de voisins.
Voici un exemple : on génére tout d'abord une triangulation de Delaunay aléatoire avec une enveloppe convexe carrée puis on ajute quelques nœuds de positions aléatoires :
points = []
noeuds = []
N = 10
x = uniform(-10,10,N)
y = uniform(-10,10,N)
for i in range(N):
points.append([x[i],y[i]])
noeuds.append(Noeud(x[i],y[i]))
for x,y in [(-10,-10),(-10,10),(10,10),(10,-10)]:
points.append([x,y])
noeuds.append(Noeud(x,y))
points = np.array(points)
tri = Delaunay(points)
figure(figsize=(8,8))
maillage = Maillage2()
maillage.fromList(noeuds,tri.simplices)
maillage.draw("k-")
 fig3.pdf
fig3.pdf
N = 5
x = uniform(-10,10,N)
y = uniform(-10,10,N)
noeuds = []
for i in range(N):
n = Noeud(x[i],y[i])
maillage.ajouterNoeud(n)
noeuds.append(n)
figure(figsize=(8,8))
maillage.draw("k-")
for n in noeuds:
n.draw("ro")
invalid = maillage.verifierDelaunay()
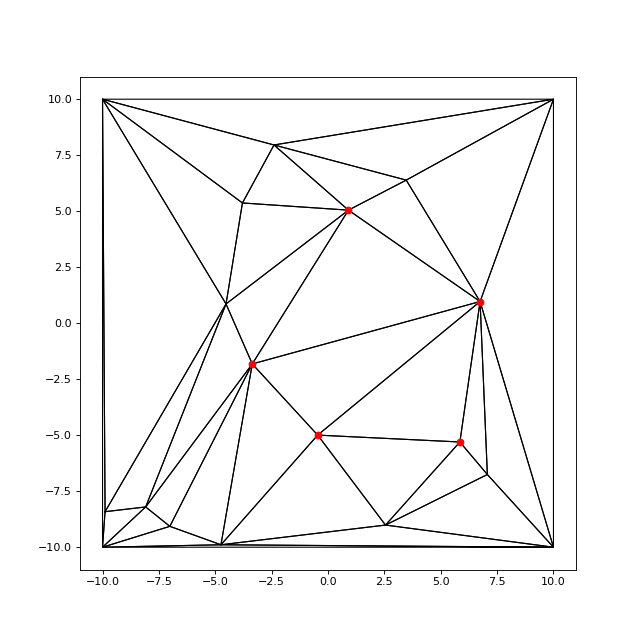 fig4.pdf
fig4.pdf
print(invalid) --> 0
3.b. Insertion d'un nœud externe
Un nœud externe n'est pas dans l'enveloppe convexe de l'ensemble initial. Dans ce cas, il s'agit d'ajouter des triangles qui comportent le nœud N ajouté et un segment de la frontière de la triangulation initiale (si le disque ouvert circonscrit du triangle associé à ce segment ne contient pas N). De plus, il faut supprimer les triangles dont le disque ouvert circonscrit contient N.
La figure suivante représente la situation dans le cas où aucun disque ouvert circonscrit ne contient N :
Figure pleine pageLes triangles à ajouter sont tracés en trait pointillé. Pour savoir avec quels segments de la frontière les nouveaux triangles doivent être créés, il suffit de déterminer de quel côté de la droite formé par le segment le nœud N se situe. Par exemple pour le segment N1N2, cette droite est tracée en trait pointillé rouge sur la figure. La droite en trait pointillé bleu est celle d'un segment avec lequel le nœud N ne formera pas un nouveau triangle.
Un nouveau triangle doit être créé si N se trouve à droite de la droite orientée (N1N2). La condition s'écrit :
Si N se trouve sur le segment N1N2 alors il se trouve aussi dans disque ouvert circonscrit du triangle auquel le segment appartient et ce triangle doit être enlevé (c'est ausi le cas si N est très proche du segment).
Le cas du nœud ajouté externe peut être intégré à l'algoritme de Bowyer-Watson en introduisant des triangles virtuels. À chaque segment de la frontière on associe un triangle virtuel dont le troisième sommet est un nœud virtuel. Ce nœud n'a pas de position particulière, son rôle est de permettre d'intégrer le segment dans un triangle qui sera traité comme tous les triangles par l'algorithme. La condition d'appartenance au disque ouvert circonscrit, qui permet de savoir si un triangle doit être enlevé, est remplacée par la condition . Si cette condition est vérifiée, le triangle virtuel est retiré. Les deux côtés virtuels de ce triangles deviennent des segments de bord s'il ne sont communs avec aucun autre côté de triangles enlevés. Si le nœud N se trouve sur le segment N1N2, il faut enlever le triangle réel auquel ce segment appartient mais aussi le triangle virtuel (car il aura deux segments à la place d'un seul). La condition pour que N appartienne au segment est :
C'est cependant une condition théorique qui a peu de change de se produire à cause des erreurs d'arrondis. Il est bien plus probable que N se trouve à proximité du segment. La figure suivante montre cette situation après retrait des triangles de la cavité :
Figure pleine pageDans ce cas, deux triangles sont enlevés, un triangle virtuel et un triangle réel, et quatre sont créés : deux triangles virtuels (associés au deux nouveaux segments de la frontière) et deux triangles réels (qui remplissent l'espace laissé par le triangle réel enlevé).
Nous devons implémenter une classe pour les triangles virtuels, qui comporte les mêmes fonctions que celle du triangle réel, en particulier la fonction dansCercle mais celle-ci fera le test décrit ci-dessus. On définit donc une nouvelle classe avec la même interface (en C++, il faudrait faire une classe virtuelle de base et deux classes dérivées) :
class TriangleVirtuel(Triangle):
def __init__(self,n1,n2):
self.noeuds = [n1,n2,None] # noeud virtuel = None
self.voisins = []
self.virtuel = True
n1.triangles.append(self)
n2.triangles.append(self)
def triangleVoisin(self,tr):
# test si un triangle est voisin
return (self.noeuds[0] in tr.noeuds) or (self.noeuds[1] in tr.noeuds)
def ajouterVoisin(self,triangle):
self.voisins.append(triangle)
def enleverVoisin(self,triangle):
self.voisins.remove(triangle)
def dansCercle(self,n):
x1 = self.noeuds[0].x
y1 = self.noeuds[0].y
x2 = self.noeuds[1].x
y2 = self.noeuds[1].y
test = (n.x-x1)*(y2-y1)-(n.y-y1)*(x2-x1)
m = max(x1,x2,y1,y2)
eps = 1e-11*m*m
if test > eps :
return True
surSeg = -eps < test < eps and (x2-x1)*(n.x-x1)+(y2-y1)*(n.y-y1) > 0 and (x1-x2)*(n.x-x2)+(y1-y2)*(n.y-y2) > 0
#print(surSeg,x1,y1,x2,y2,n.x,n.y)
return surSeg
def cercle(self):
return None
def contientCote(self,na,nb):
return (na in self.noeuds) and (nb in self.noeuds)
def coteCommun(self,tr):
# test si un autre triangle comporte un côté commun avec le triangle
return self.contientCote(tr.noeuds[0],tr.noeuds[1]) or self.contientCote(tr.noeuds[0],tr.noeuds[2]) or self.contientCote(tr.noeuds[1],tr.noeuds[2])
def draw(self,style=None,linewidth=1):
if style:
plot([self.noeuds[0].x,self.noeuds[1].x],[self.noeuds[0].y,self.noeuds[1].y],style,linewidth=linewidth)
else:
plot([self.noeuds[0].x,self.noeuds[1].x],[self.noeuds[0].y,self.noeuds[1].y],linewidth=linewidth)
def drawCercle(self,style):
pass
def print(self):
print("Triangle : ",self)
for n in self.noeuds[0:2]:
print(n.x,n.y)
Pour mettre au point la nouvelle version de la classe Maillage, nous lui ajoutons une fonction triangleInitial, qui permet de créer un maillage comportant seulement un triangle réel et trois triangles virtuels, un pour chaque côté. Bien évidemment, on pourra plus tard définir une forme initiale quelconque.
Bien que l'algorithme soit le même, la fonction ajouterNoeud doit être légèrement modifiée car certains nouveaux triangles sont virtuels. L'algorithme permet de générer automatiquement les triangles virtuels associés aux nouveaux segments de la frontière. La figure suivante représente la situation où 3 segments de la frontière, et seulement 3, ne sont plus sur la frontière après la transformation. Le triangle virtuel associé à un segment de la frontière est représenté sous la forme d'une flèche, le sens de celle-ci indiquant l'ordre des nœuds dans le triangle virtuel (le nœud virtuel est toujours le troisième).
Figure pleine pagePar exemple, le triangle virtuel A est constitué des nœuds N1,N2,V où V désigne le nœud virtuel (représenté par l'objet None). Les triangles virtuels A,B et C sont dans la cavité et sont donc enlevés, indépendamment du fait que le segment correspondant reste ou pas dans la triangulation (il est retiré si le triangle réel auquel il appartient est dans la cavité). Un nouveau triangle est obtenu à partir d'un segment non partagé par d'autres triangles de la cavité auquel on ajoute le nœud N. Dans le cas du triangle virtuel A, les côtés N1V et N1N2 ne sont pas partagés. Il y a donc un nouveau triangle réel N1,N,N2 et un nouveau triangle virtuel N1,N,V (triangle D). Dans le cas du triangle B, les deux côtés N2V et N3V sont partagés respectivement avec les triangles A et C; seul son côté N2N2 n'est pas partagé donc il y a un nouveau triangle réel N2,N,N3 mais aucun triangle virtuel. Dans le cas du triangle C, les côtés non partagés sont N3N4 et N3V donc il y a un nouveau triangle réel N,N4,N3 et un nouveau triangle virtuel N,N4,V. Nous voyons donc que l'algorithme génère bien un triangle virtuel pour chaque nouveau segment de la frontière. Il faut remarquer que le nœud virtuel doit être considéré comm un seul et même nœud pour tous les triangles virtuels, ce qui est facile à obtenir si le nœud virtuel est toujours représenté par l'objet None. Lors de la création d'un triangle virtuel, il faut faire en sorte que ses deux premiers nœuds définissent un segment de la frontière parcouru dans le sens direct. Pour cela, il faut que le nœud du triangle enlevé (autre que V) qui appartient au nouveau triangle garde sa position dans le nouveau triangle, la troisième position étant toujours occupée par V et la position restante par N. Par exemple pour le nouveau triangle D, le premier nœud est N1 puisque ce nœud avait la première position dans le triangle A. Pour le nouveau triangle E, le nœud N4 est en deuxième position puisque c'était sa position dans le triangle C.
class Maillage3(Maillage):
def __init__(self):
Maillage.__init__(self)
def enleverTriangle(self,tr):
self.retire.append(tr)
self.triangles.remove(tr)
for trv in tr.voisins:
trv.enleverVoisin(tr)
for i in range(3):
if tr.noeuds[i]!=None:
tr.noeuds[i].triangles.remove(tr)
def triangleInitial(self,n1,n2,n3):
tr = Triangle(n1,n2,n3)
self.triangles.append(tr)
bord1 = TriangleVirtuel(tr.noeuds[0],tr.noeuds[1])
bord2 = TriangleVirtuel(tr.noeuds[1],tr.noeuds[2])
bord3 = TriangleVirtuel(tr.noeuds[2],tr.noeuds[0])
bords = [bord1,bord2,bord3]
for b in bords:
self.triangles.append(b)
b.ajouterVoisin(tr)
tr.ajouterVoisin(b)
bord1.ajouterVoisin(bord2)
bord2.ajouterVoisin(bord1)
bord1.ajouterVoisin(bord3)
bord3.ajouterVoisin(bord1)
bord2.ajouterVoisin(bord3)
bord3.ajouterVoisin(bord2)
def ajouterNoeud(self,n):
def rechercheCavite(n,tr,trCavite):
for t in tr.voisins:
if not(t in trCavite) and t.dansCercle(n):
trCavite.append(t)
rechercheCavite(n,t,trCavite)
trCavite = []
for tr in self.triangles: # recherche d'un triangle dont le cercle circonscrit contient le nouveau noeud
if tr.dansCercle(n):
trCavite.append(tr)
rechercheCavite(n,tr,trCavite) # recherche récursive des autres triangles
break
nouveaux = []
for i in range(len(trCavite)):
tr = trCavite[i]
self.enleverTriangle(tr)
for c in [[0,1],[0,2],[1,2]]: # recherche du côté non partagé
na = tr.noeuds[c[0]]
nb = tr.noeuds[c[1]]
ajout = True
for j in range(len(trCavite)):
if i!=j:
if trCavite[j].contientCote(na,nb):
ajout = False
break
if ajout:
if nb!=None:
nouvTr = Triangle(n,na,nb)
else :
if tr.noeuds[0]==na:
nouvTr = TriangleVirtuel(na,n)
else:
nouvTr = TriangleVirtuel(n,na)
nouveaux.append(nouvTr)
self.triangles.append(nouvTr)
# recherche des voisins du nouveau triangle parmi les voisins des triangles enlevés
voisins = []
for t in trCavite:
for trv in t.voisins:
if not(trv in trCavite) and not(trv in voisins) and trv.triangleVoisin(nouvTr):
nouvTr.ajouterVoisin(trv)
trv.ajouterVoisin(nouvTr)
voisins.append(trv)
# les nouveaux triangles sont voisins
for i in range(len(nouveaux)):
for j in range(len(nouveaux)):
if i!=j:
nouveaux[i].ajouterVoisin(nouveaux[j])
return len(nouveaux)
maillage = Maillage3()
n1 = Noeud(-10,-10)
n2 = Noeud(10,-10)
n3 = Noeud(0,10)
maillage.triangleInitial(n1,n2,n3)
maillage.draw("k-")
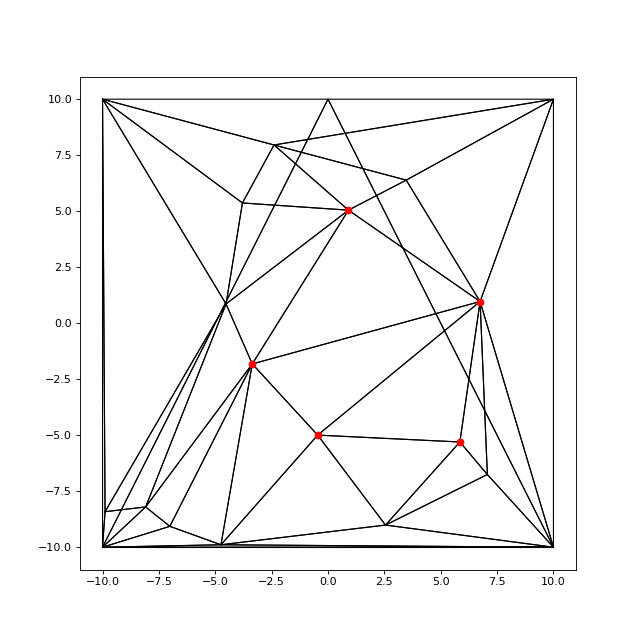 fig5.pdf
fig5.pdf
On commence par ajouter des nœuds à l'intérieur :
figure(figsize=(8,8))
maillage.ajouterNoeud(Noeud(0,0))
maillage.ajouterNoeud(Noeud(1,-5))
maillage.draw("k-")
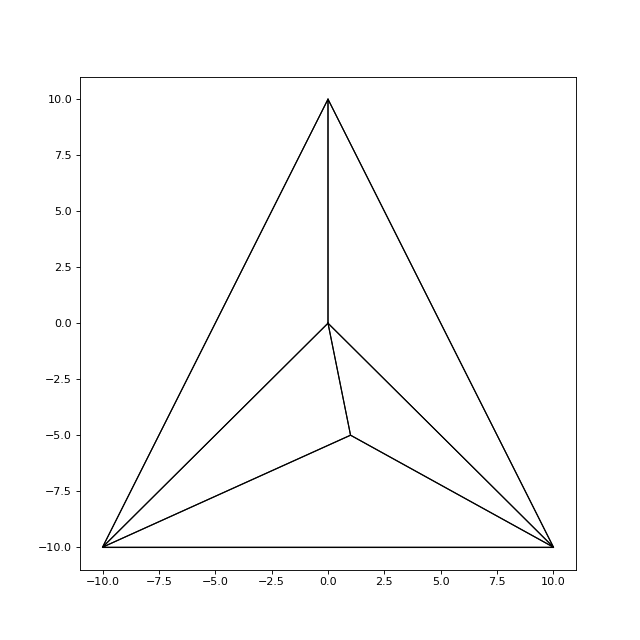 fig6.pdf
fig6.pdf
puis un nœud à l'extérieur :
figure(figsize=(8,8))
maillage.ajouterNoeud(Noeud(5,5))
maillage.draw("k-")
xlim(-10,10)
ylim(-10,10)
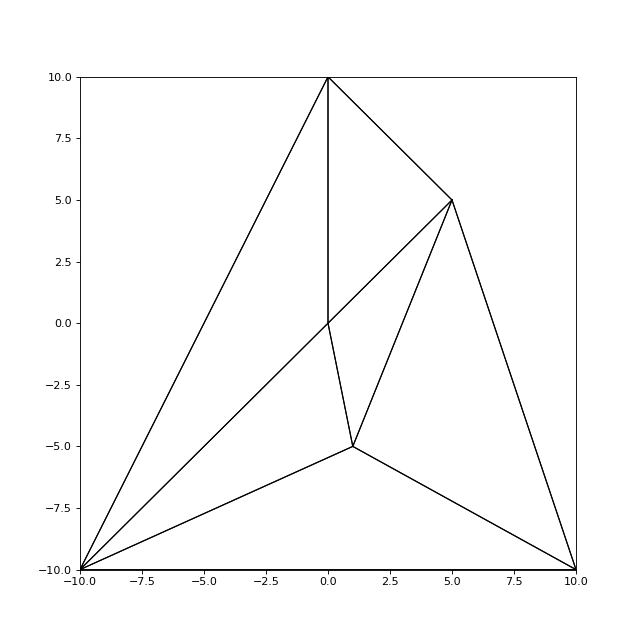 fig7.pdf
fig7.pdf
figure(figsize=(8,8))
maillage.ajouterNoeud(Noeud(9,6))
maillage.draw("k-")
xlim(-10,10)
ylim(-10,10)
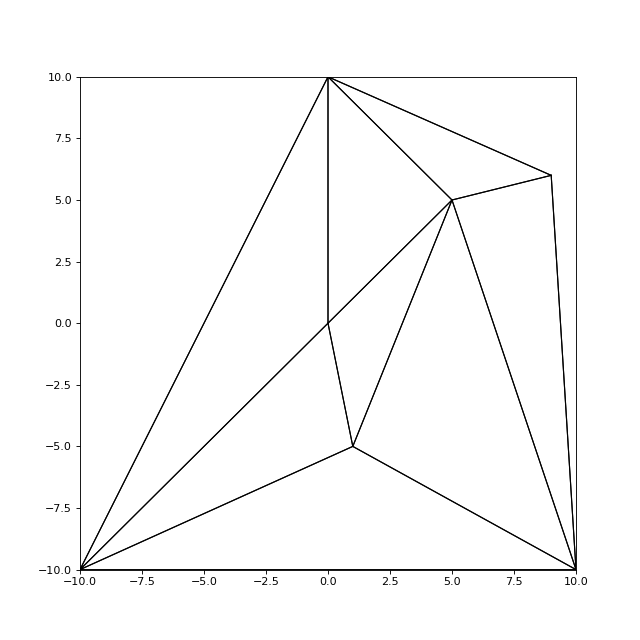 fig8.pdf
fig8.pdf
Pour vérifier que tout fonctionne bien, on ajoute un nœd à l'intérieur d'un des nouveaux triangles :
figure(figsize=(8,8))
maillage.ajouterNoeud(Noeud(5,6))
maillage.draw("k-")
xlim(-10,10)
ylim(-10,10)
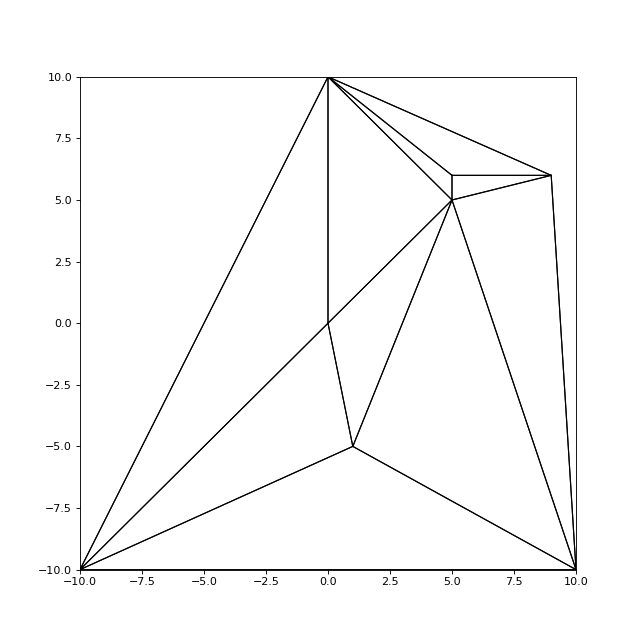 fig9.pdf
fig9.pdf
Un cas particulier à vérifier est celui d'un nouveau nœud situé exactement sur un segment de la frontière. Ajoutons un nœud sur la frontière horizontale (sans erreur d'arrondi possible dans ce cas) :
figure(figsize=(8,8))
maillage.ajouterNoeud(Noeud(-1,-10))
maillage.draw("k-")
xlim(-10,10)
ylim(-10,10)
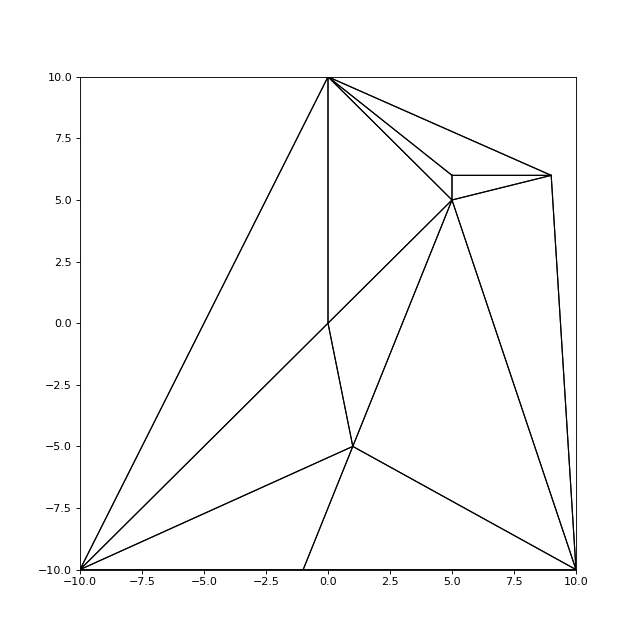 fig10.pdf
fig10.pdf
Finalement, l'algorithme permet de générer une triangulation de Delaunay d'un ensemble de points aléatoires quelconque, à condition de partir d'un triangle initial, qui sont évidemment les trois premiers nœuds :
maillage = Maillage3()
n1 = Noeud(-10,-10)
n2 = Noeud(10,-10)
n3 = Noeud(0,10)
maillage.triangleInitial(n1,n2,n3)
N = 10
x = uniform(-10,10,N)
y = uniform(-10,10,N)
noeuds = [n1,n2,n3]
for i in range(N):
n = Noeud(x[i],y[i])
maillage.ajouterNoeud(n)
noeuds.append(n)
figure(figsize=(8,8))
maillage.draw("k-")
for n in noeuds:
n.draw("ro")
invalid = maillage.verifierDelaunay()
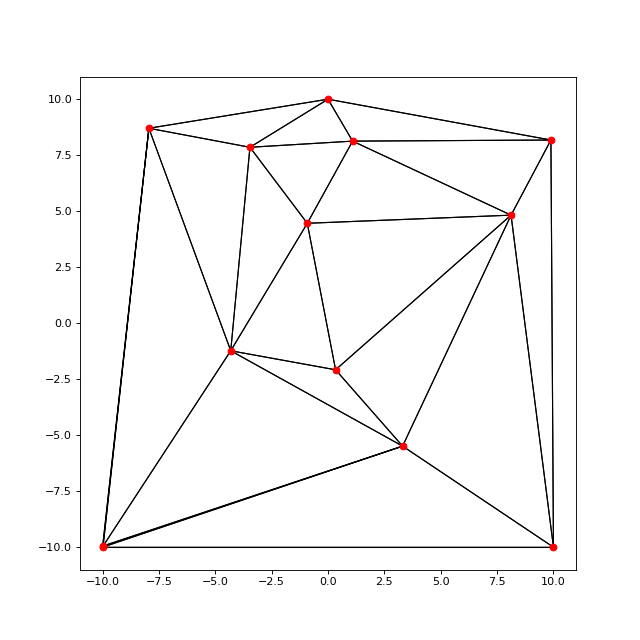 fig11.pdf
fig11.pdf
print(invalid) --> 0
C'est vraisemblablement l'algorithme implémenté par la fonction scipy.spatial.Delaunay mais nous disposons ici d'un algorithme qui permet de construire un maillage de Delaunay nœud par nœud.
3.c. Insertion aléatoire
L'efficacité de la génération des maillages est une question importante car les maillages pour la méthode des éléments finis peuvent comporter plusieurs centaines de milliers de nœuds.
Outre l'étape de localisation du premier triangle dont le disque ouvert circonscrit contient le nouveau nœud, la destruction et l'ajout de triangles peut être très inefficace lorsque leur nombre est trop grand. Cela se produit pour l'ajout de nœuds externes lorsqu'il sont répartis sur une grille (ou à peu près). Voici un exemple :
N = 20
x = np.linspace(-10,10,N)
y = np.linspace(-10,10,N)
maillage = Maillage3()
noeuds = []
n1 = Noeud(x[0],y[0])
n2 = Noeud(x[1],y[0])
n3 = Noeud(x[0],y[1])
maillage.triangleInitial(n1,n2,n3)
for j in range(N):
for i in range(N):
if not((i,j) in [(0,0),(1,0),(0,1)]):
n = Noeud(x[i],y[j])
noeuds.append(n)
Voici un état intermédiaire du maillage :
P = 4*N+3
nNouv = 0
for k in range(P):
nNouv += maillage.ajouterNoeud(noeuds[k])
figure(figsize=(8,8))
maillage.draw("k-")
xlim(-10,10)
ylim(-10,10)
nNouv /= P
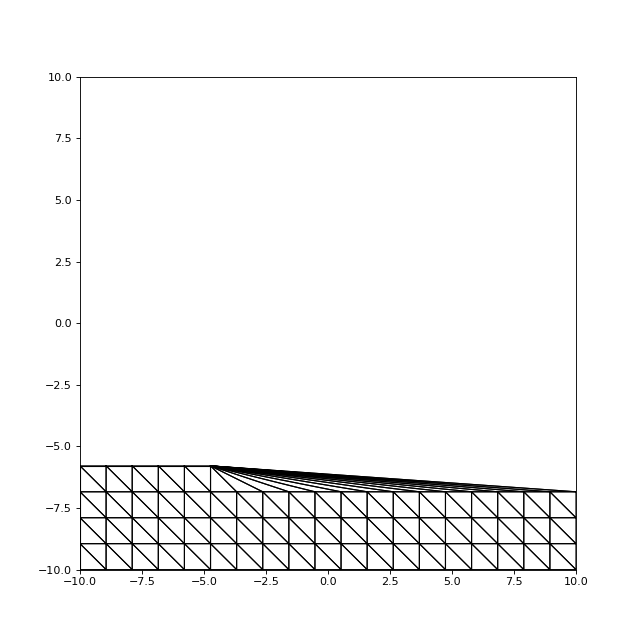 fig12.pdf
fig12.pdf
print(nNouv) --> 10.795180722891565
Le nombre de nouveaux triangles créés à chaque insertion est très grand (le nombre de triangles enlevés est quasiment le même). Dans le cas présent, il est en moyenne égale au nombre de nœuds par rangée divisé par 2.
Une solution simple pour augmenter l'efficacité est d'ajouter les nœuds dans un ordre aléatoire. Bien évidemment, cela n'est possible que pour les nœuds dont les positions sont connues dès le début. Nous ajoutons à la classe Maillage une fonction prenant en argument une liste de nœuds à ajouter et qui les ajoute après avoir effectué des permuations aléatoires (autant que le nombre de nœuds de la liste).
class Maillage4(Maillage3):
def __init__(self):
Maillage3.__init__(self)
def ajouterListeNoeuds(self,noeuds,P):
# P : nombre de noeuds ajoutés
N = len(noeuds)
for p in range(N):
i = random.randint(0,N-1)
j = random.randint(0,N-1)
noeuds[i],noeuds[j] = noeuds[j],noeuds[i]
nNouv = 0
for k in range(P):
nNouv += self.ajouterNoeud(noeuds[k])
return nNouv/P
Voici un état intermédiaire du maillage :
N = 20
x = np.linspace(-10,10,N)
y = np.linspace(-10,10,N)
maillage = Maillage4()
noeuds = []
n1 = Noeud(x[0],y[0])
n2 = Noeud(x[1],y[0])
n3 = Noeud(x[0],y[1])
maillage.triangleInitial(n1,n2,n3)
for j in range(N):
for i in range(N):
if not((i,j) in [(0,0),(1,0),(0,1)]):
n = Noeud(x[i],y[j])
noeuds.append(n)
P = 4*N+3
nNouv = maillage.ajouterListeNoeuds(noeuds,P)
figure(figsize=(8,8))
maillage.draw("k-")
xlim(-10,10)
ylim(-10,10)
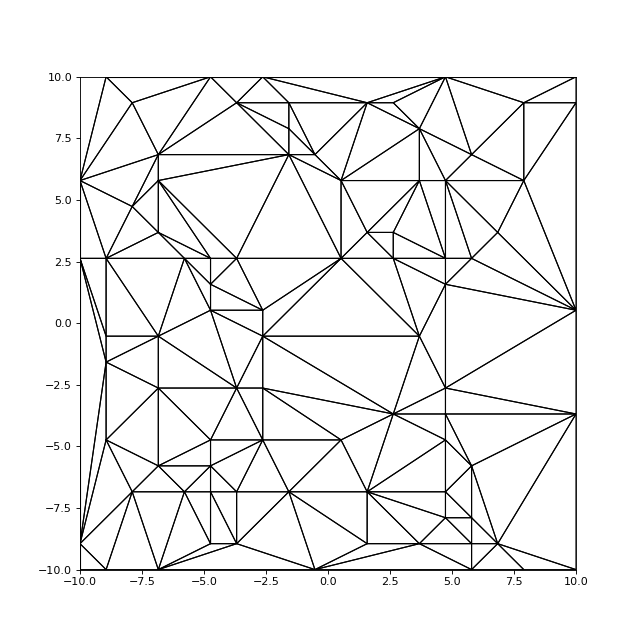 fig13.pdf
fig13.pdf
print(nNouv) --> 5.397590361445783
On comprend aisément l'intérêt de l'ajout aléatoire : la plupart des nœuds ajoutés sont internes.
Voici le maillage complet :
N = 20
x = np.linspace(-10,10,N)
y = np.linspace(-10,10,N)
maillage = Maillage4()
noeuds = []
n1 = Noeud(x[0],y[0])
n2 = Noeud(x[1],y[0])
n3 = Noeud(x[0],y[1])
maillage.triangleInitial(n1,n2,n3)
for j in range(N):
for i in range(N):
if not((i,j) in [(0,0),(1,0),(0,1)]):
n = Noeud(x[i],y[j])
noeuds.append(n)
P = N*N-3
nNouv = maillage.ajouterListeNoeuds(noeuds,P)
figure(figsize=(8,8))
maillage.draw("k-")
xlim(-10,10)
ylim(-10,10)
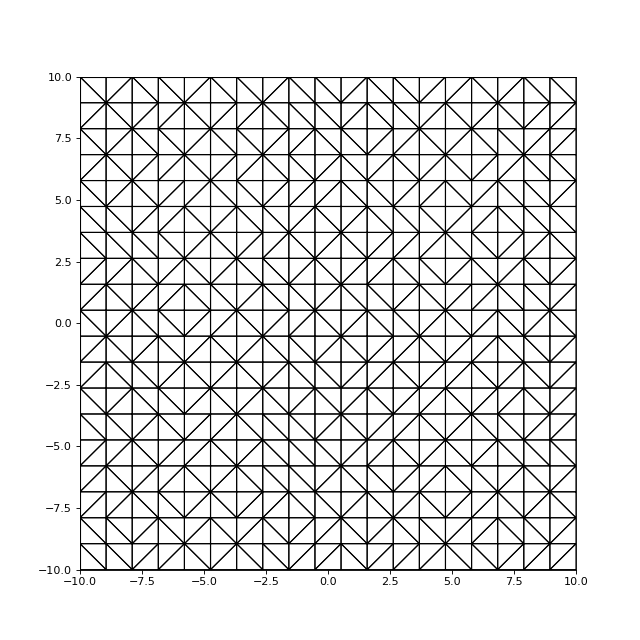 fig14.pdf
fig14.pdf
print(nNouv) --> 4.944584382871536
Le nombre moyen de triangles créés à chaque insertion est réduit. On est ici dans un cas où il existe plusieurs triangulations de Delaunay : les cercles circonscrits des triangles non situés près des bords contiennent en effet 4 nœuds (sur le cercle).
Il peut être montré que si les nœuds sont insérés dans un ordre aléatoire, le nombre moyen de triangles créés à chaque insertion est inférieur à 6. Ainsi, si le nombre de nœuds par rangée est beaucoup plus grand que 12, le gain en efficacité est très important. Voici un exemple avec 40 nœuds par rangée :
N = 20#N = 40
x = np.linspace(-10,10,N)
y = np.linspace(-10,10,N)
maillage = Maillage4()
noeuds = []
n1 = Noeud(x[0],y[0])
n2 = Noeud(x[1],y[0])
n3 = Noeud(x[0],y[1])
maillage.triangleInitial(n1,n2,n3)
for j in range(N):
for i in range(N):
if not((i,j) in [(0,0),(1,0),(0,1)]):
n = Noeud(x[i],y[j])
noeuds.append(n)
P = N*N-3
t1 = time.time()
nNouv = maillage.ajouterListeNoeuds(noeuds,P)
t1 = time.time()-t1
figure(figsize=(8,8))
maillage.draw("k-")
xlim(-10,10)
ylim(-10,10)
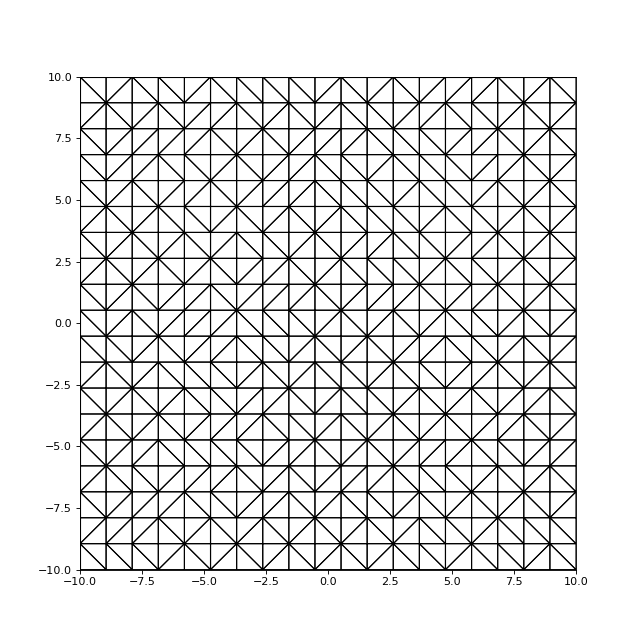 fig15.pdf
fig15.pdf
print(nNouv) --> 4.9773299748110835
Cette méthode a cependant un inconvénient : il est plus difficile d'accélérer l'étape de recherche du premier triangle car la position de chaque nœud ajouté est aléatoire. Pour accélérer la première étape, il faut localiser le nœud inséré dans la triangulation, c'est-à-dire déterminer efficacement un triangle dont le cercle circonscrit contient ce nœud. Si on exclut cette étape de localisation (si on la suppose O(1)), la complexité temporelle de l'insertion aléatoire est O(N) où N est le nombres de nœuds insérés. Si l'insertion n'est pas aléatoire, la complexité peut être O(N2) dans le pire des cas (nœuds sur une grille).
3.d. Accélération de la recherche du premier triangle
Lorsqu'un nouveau nœud N est ajouté, il faut tout d'abord trouver un triangle dont le disque ouvert circonscrit contienne N. La recherche par parcours systématique de tous les triangles est très inefficace. L'utilisation d'un graphe de conflits permet d'accélérer cette recherche. Il s'agit d'un graphe biparti qui relie les nœuds non encore ajoutés aux triangles de la triangulation (réels ou virtuels). Chaque nœud non encore ajouté (mais connu à l'avance) est relié à un et un seul triangle, avec lequel il est en conflit, c'est-à-dire que son disque ouvert circonscrit contient le nœud.
Figure pleine pageUn nœud est connecté à un seul triangle mais un triangle peut avoir plusieurs nœuds avec lequel il est en conflit. Par exemple le triangle T2 est en conflit avec les nœuds N1 et N3. Lorsqu'un nœud est ajouté à la triangulation, le graphe des conflits donne immédiatement un triangle dont le disque circonscrit contient ce nœud. Par exemple si le nœud N7 est ajouté, ce triangle est T6.
Le graphe doit être mis à jour après chaque insertion d'un nouveau nœud Ni. La première mise à jour évidente consiste à enlever ce nœud du graphe. Il faut aussi enlever les triangles qui sont supprimés, ceux dont le disque circonscrit contient Ni et qui sont déterminé à partir du premier par recherche récursive par voisinage, comme expliqué plus haut. Enfin il faut ajouter les nouveaux triangles. Enlever un nœud est une opération très simple, consistant à enlever une seule liaison. Enlever un triangle consiste à enlever les liaisons de tous les nœuds avec lesquels ce triangle est en conflit mais cette opération laisse des nœuds sans conflit. Il faut donc attribuer un nouveau triangle à ces nœuds orphelins. Par ailleurs, de nouveaux triangles sont ajoutés au graphe et ces triangles sont des canditats pour les conflits attribués aux nœuds orphelins.
Pour reprendre la figure ci-dessus, supposons qu'on enlève le nœud du graphe N6 (c'est-à-dire que ce nœud est ajouté à la triangulation) et que les triangles enlevés soient T3 (déterminé d'après le graphe), T4 et T6. On suppose par ailleurs que 3 triangles sont ajoutés, les triangles T10,T11,T12. L'état du graphe devient :
Figure pleine pageIl faut ensuite attribuer un triangle à chacun des nœuds N4,N5,N7,N8. Soit Nk l'un de ces nœud. Il était en conflit avec un des triangles de la cavité (qui a été enlevé), de sommets A,B,C. Les points Ni et Nk appartiennent au disque ouvert circonscrit de ce triangle. Considérons la droite NiNk: elle coupe un côté de la cavité polyhédrique, qui est un côté d'un nouveau triangle et aussi un côté non partagé des triangles enlevés. Notons T le nouveau triangle construit à partir de ce côté, colorié en gris sur la figure suivante :
Figure pleine pageSi Nk est à l'intérieur de la cavité, alors il est dans le triangle T, donc dans son disque circonscrit. C'est le cas du point Nk sur la figure ci-dessus (à gauche). Le nœud Nk est donc en conflit avec le triangle T. Si le nœud Nk n'est pas à l'intérieur de la cavité (point Nk' sur la figure à droite), alors ce nœuds est aussi en conflit à avec le triangle T (démonstration ?). Nous voyons donc que, pour chaque nœud qui n'a plus de conflit, il est possible d'en trouver un parmi les triangles ajoutés dans la cavité, ce qui permet de mettre à jours de graphe des conflits.
Un nœud peut avoir un triangle virtuel enregistré comme conflit s'il se trouve à droite du segment de frontière associé à ce triangle (le demi-plan est l'équivalent du cercle circonscrit). Lorsqu'une cavité contient des triangles virtuels (c.-à-d. des bords de la triangulation), il peut arriver qu'un nouveau triangle virtuel soit attribué à un nœud orphelin (qui étaient en conflit avec un triangle de la cavité, réel ou virtuel). La figure suivante montre un exemple où la cavité comporte trois triangles virtuels et un triangle réel :
Figure pleine pageLe cercle circonscrit du triangle réel est tracé en pointillé. Les trois triangles virtuels sont représentés par une flèche bleue. Les nouveaux triangles sont représentés à droite, avec en vert les côtés qui partagent le nœud ajouté Ni. Comme précédemment, Nk est un nœud qui était en conflit avec un triangle (figure de gauche) et, puisque ce triangle est supprimé, il faut lui attribuer un nouveau triangle avec lequel il est en conflit. Prenons l'exemple du nœud Nk représenté sur la figure. Avant suppression des triangles, ce nœud avait peut-être comme triangle associé dans le graphe des conflits le triangle virtuel situé en haut (mais cela peut être un autre triangle). Considérons, pour chaque nœud réel du triangle virtuel, la droite passant par un nœud du segment et par un point quelconque P situé dans la triangulation (le même point pour tous les triangles). Ces droites sont représentées en trait pointillé sur la figure ci-dessus. Elles permettent de partager l'extérieur de la triangulation en domaines, chacun étant associé à un trianle virtuel. Le côté virtuel du triangle est ainsi une demi-droite. Si le nœud Nk est dans le domaine d'un triangle virtuel, celui-ci est en conflit avec lui. Conclusion : si aucun triangle réel créé n'est en conflit avec le nœud Nk alors il existe un nouveau nœud virtuel qui l'est. L'attribution dans le graphe des conflits d'un triangle au nœud Nk consiste donc à en chercher un parmi les nouveaux nœuds. Bien qu'il soit possible d'accélérer cette recherche, nous la ferons par un parcours linéaire des nouveaux triangles car le nombre de ceux-ci est en moyenne inférieur à 6.
Pour implémenter l'algorithme, il n'est pas nécessaire de disposer explicitement d'un graphe biparti. Il suffit que chaque nœud dispose d'une référence d'un triangle avec lequel il est en conflit et que chaque triangle dispose d'une liste de références de nœuds qui sont en conflit avec lui. Voici la nouvelle classe Noeud :
class Noeud:
def __init__(self,x,y):
self.x = x
self.y = y
self.triangleConflit = None
self.triangles = []
def definirConflit(self,tr):
self.triangleConflit = tr
def enleverConflit(self):
self.triangleConflit = None
def draw(self,style):
plot([self.x],[self.y],style)
Voici la nouvelle classe Triangle, dérivée de la première :
class Triangle2(Triangle):
def __init__(self,n1,n2,n3):
Triangle.__init__(self,n1,n2,n3)
self.noeudsConflit = []
def ajouterConflit(self,n):
self.noeudsConflit.append(n)
def enleverConflit(self,n):
self.noeudsConflit.remove(n)
et la nouvelle classe pour les triangles virtuels :
class TriangleVirtuel2(TriangleVirtuel):
def __init__(self,n1,n2):
TriangleVirtuel.__init__(self,n1,n2)
self.noeudsConflit = []
def ajouterConflit(self,n):
self.noeudsConflit.append(n)
def enleverConflit(self,n):
self.noeudsConflit.remove(n)
La classe Maillage3 doit être revue entièrement. Dans la fonction ajouterListNoeuds, il faut initialiser le graphe des conflits (cette fonction est appelée après que le premier triangle réel soit créé, avec trois triangles virtuels). Dans la fonction ajouterNoeud, la recherche des triangles en conflit avec le nœud ajouté est beaucoup plus rapide que précédemment puisque le premier triangle en conflit est mémorisé dans le graphe des conflits, c'est-à-dire dans l'object Noeud. les autres triangles sont trouvés par recherche récursive comme précédemment. Une liste de nœuds en conflit avec les triangles de la cavité, qui sont enlevé, est établie (noeudsSansConflit). La création des nouveaux triangles se fait comme précédemment mais, dès qu'un triangle est créé, on parcours la liste noeudsSansConflit pour attribuer éventuellement ce triangle à un des nœuds de cette liste, à condition que l'attribution n'ait pas déjà été faite. Le nombre de triangles créés est en moyenne inférieur à 6 donc cette mise à jour du graphe des conflits se fait en temps constant.
class Maillage5(Maillage):
def __init__(self):
Maillage.__init__(self)
def enleverTriangle(self,tr):
self.retire.append(tr)
self.triangles.remove(tr)
for trv in tr.voisins:
trv.enleverVoisin(tr)
for i in range(3):
if tr.noeuds[i]!=None:
tr.noeuds[i].triangles.remove(tr)
def triangleInitial(self,n1,n2,n3):
tr = Triangle2(n1,n2,n3)
self.triangles.append(tr)
bord1 = TriangleVirtuel2(tr.noeuds[0],tr.noeuds[1])
bord2 = TriangleVirtuel2(tr.noeuds[1],tr.noeuds[2])
bord3 = TriangleVirtuel2(tr.noeuds[2],tr.noeuds[0])
bords = [bord1,bord2,bord3]
for b in bords:
self.triangles.append(b)
b.ajouterVoisin(tr)
tr.ajouterVoisin(b)
bord1.ajouterVoisin(bord2)
bord2.ajouterVoisin(bord1)
bord1.ajouterVoisin(bord3)
bord3.ajouterVoisin(bord1)
bord2.ajouterVoisin(bord3)
bord3.ajouterVoisin(bord2)
self.P = Noeud((n1.x+n2.x+n3.x)/3,(n1.y+n2.y+n3.y)/3)
def ajouterListeNoeuds(self,noeuds,P):
# P : nombre de noeuds ajoutés
self.noeuds = noeuds
for n in noeuds: #initialisation du graphe des conflits avec les 4 premiers triangles
for i in range(4):
if self.triangles[i].dansCercle(n):
n.definirConflit(self.triangles[i])
self.triangles[i].ajouterConflit(n)
break
N = len(noeuds)
for p in range(N):
i = random.randint(0,N-1)
j = random.randint(0,N-1)
noeuds[i],noeuds[j] = noeuds[j],noeuds[i]
nNouv = 0
for k in range(P):
nNouv += self.ajouterNoeud(noeuds[k])
return nNouv/P
def printConflits(self):
for i in range(len(self.noeuds)):
print("noeud ",i," conflit :")
self.noeuds[i].triangleConflit.print()
for i in range(len(self.triangles)):
print("triangle ",i)
for n in self.triangles[i].noeudsConflit:
print("noeud : ",n.x,n.y)
def ajouterNoeud(self,n):
def rechercheCavite(n,tr,trCavite):
for t in tr.voisins:
if not(t in trCavite) and t.dansCercle(n):
trCavite.append(t)
rechercheCavite(n,t,trCavite)
trCavite = []
tr = n.triangleConflit
# bug : noeud sans conflit ?
trCavite.append(tr)
rechercheCavite(n,tr,trCavite) # recherche récursive des autres triangles
nouveaux = []
# mise à jour du graphe des conflits
noeudsSansConflit = [] # noeuds n'ayant plus de triangle associé dans le graphe des conflits
for tr in trCavite:
for no in tr.noeudsConflit:
if no!=n:
noeudsSansConflit.append(no)
no.enleverConflit()
for i in range(len(trCavite)):
tr = trCavite[i]
self.enleverTriangle(tr)
for c in [[0,1],[0,2],[1,2]]: # recherche du côté non partagé
na = tr.noeuds[c[0]]
nb = tr.noeuds[c[1]]
ajout = True
for j in range(len(trCavite)):
if i!=j:
if trCavite[j].contientCote(na,nb):
ajout = False
break
if ajout:
if nb!=None:
nouvTr = Triangle2(n,na,nb)
else :
if tr.noeuds[0]==na:
nouvTr = TriangleVirtuel2(na,n)
else:
nouvTr = TriangleVirtuel2(n,na)
nouveaux.append(nouvTr)
self.triangles.append(nouvTr)
# recherche d'un triangle en conflit pour chaque noeud qui n'en a plus
# nouvTr est-il en conflit avec l'un de ces noeuds ?
for nsc in noeudsSansConflit:
if nouvTr.virtuel==False:
if nsc.triangleConflit==None and nouvTr.dansCercle(nsc):
nsc.definirConflit(nouvTr)
nouvTr.ajouterConflit(nsc)
else:
if nsc.triangleConflit==None and nouvTr.dansCercle(nsc) :
nsc.definirConflit(nouvTr)
nouvTr.ajouterConflit(nsc)
# recherche des voisins du nouveau triangle parmi les voisins des triangles enlevés
voisins = []
for t in trCavite:
for trv in t.voisins:
if not(trv in trCavite) and not(trv in voisins) and trv.triangleVoisin(nouvTr):
nouvTr.ajouterVoisin(trv)
trv.ajouterVoisin(nouvTr)
voisins.append(trv)
# les nouveaux triangles sont voisins
for i in range(len(nouveaux)):
for j in range(len(nouveaux)):
if i!=j:
nouveaux[i].ajouterVoisin(nouveaux[j])
return len(nouveaux)
N = 40
x = np.linspace(0,10,N)
y = np.linspace(0,10,N)
maillage = Maillage5()
noeuds = []
n1 = Noeud(x[0],y[0])
n2 = Noeud(x[1],y[0])
n3 = Noeud(x[0],y[1])
maillage.triangleInitial(n1,n2,n3)
for j in range(N):
for i in range(N):
if not((i,j) in [(0,0),(1,0),(0,1)]):
n = Noeud(x[i],y[j])
noeuds.append(n)
P = N*N-3
figure(figsize=(8,8))
t2 = time.time()
nNouv = maillage.ajouterListeNoeuds(noeuds,P)
t2 = time.time()-t2
maillage.draw("k-")
xlim(-1,11)
ylim(-1,11)
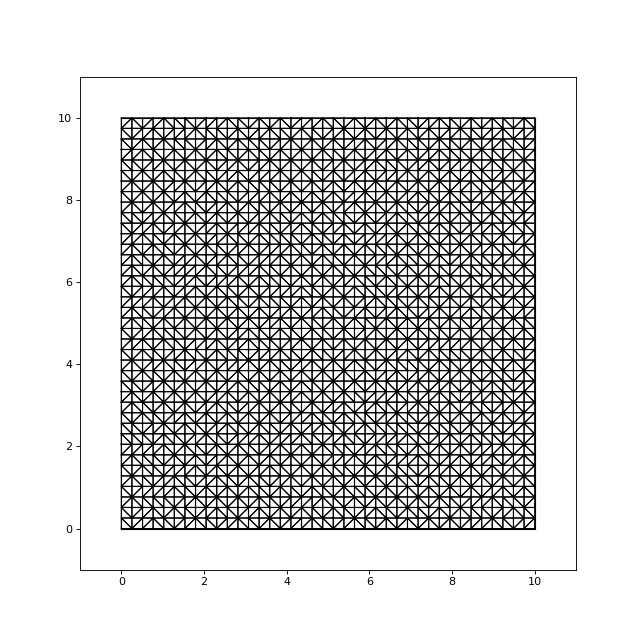 fig16.pdf
fig16.pdf
print(nNouv) --> 5.028804007514089
Voici les temps de calcul sans l'accélération de la recherche du premier triangle et avec :
print(t1) --> 0.4074852466583252
print(t2) --> 0.807161808013916
Voici la génération d'une triangulation avec deux fois plus de nœuds que ci-dessus :
N = int(N*np.sqrt(2))
x = np.linspace(0,10,N)
y = np.linspace(0,10,N)
maillage = Maillage5()
noeuds = []
n1 = Noeud(x[0],y[0])
n2 = Noeud(x[1],y[0])
n3 = Noeud(x[0],y[1])
maillage.triangleInitial(n1,n2,n3)
for j in range(N):
for i in range(N):
if not((i,j) in [(0,0),(1,0),(0,1)]):
n = Noeud(x[i],y[j])
noeuds.append(n)
P = N*N-3
figure(figsize=(8,8))
t3 = time.time()
nNouv = maillage.ajouterListeNoeuds(noeuds,P)
t3 = time.time()-t3
maillage.draw("k-")
xlim(-1,11)
ylim(-1,11)
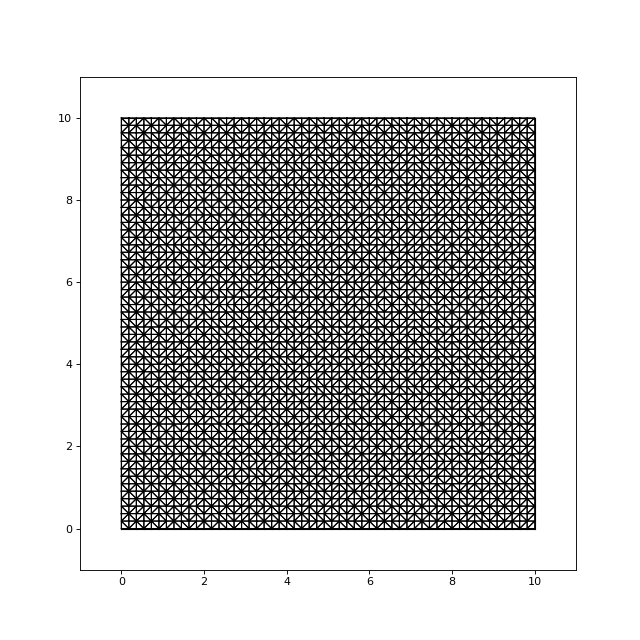 fig17.pdf
fig17.pdf
print(t3) --> 1.6960170269012451
3.e. Retrait d'un nœud
Lorsque le maillage n'est pas satisfaisant, on peut être amené à supprimer un nœud. Cette suppression a pour conséquence immédiate la suppression de tous les triangles qui ont ce nœud comme sommet. Ceux-ci sont immédiatement disponibles car il sont stockés dans une liste associée à chaque nœud. La suppression de ces triangles conduit à une cavité polyhédrique (pas nécessairement convexe) définie par les nœuds des triangles enlevés autres que le nœud enlevé. Ces nœuds sont rangés afin que le polyhèdre soit parcouru dans le sens direct. La figure suivante représente le nœud N à enlever et les triangles auxquels il appartient, qu'il faut aussi enlever.
Figure pleine pageOn part du premier triangle rencontré dans la liste des triangles du nœud N, le triangle T1 sur la figure. Dans ce triangle, on considère le nœud N1 qui suit N et le nœud suivant N2. Les nœuds N1 et N2 constituent les deux premiers nœuds du polyèdre. Parmis les triangles auxquels N appartient, on recherche celui qui contient N2, le triangle T2, dans lequel on trouve le nœud N3. La recherche est ainsi répété itérativement jusqu'à obtenir à nouveau le nœud N1. On obtient ainsi la liste des nœuds du polyèdre rangés dans le sens direct. Si le nœud N se trouve sur la frontière de la triangulation, il y a exactement deux triangles virtuels auxquels ce nœud appartient (figure ci-dessus à droite). Lorsqu'on parvient à un triangle virtuel (T4), qui correspond à un segment de bord, on identifie l'indice dans le triangle virtuel du nœuds de ce segment autre que N (nœud N3). Si cet indice vaut 0, comme c'est le cas pour T4 alors le triangle suivant est l'autre triangle virtuel (triangle T5) de la liste des triangles auxquels N appartient. Pour le triangle T5, cet indice vaut 1 donc le triangle suivant est un triangle réel contenant le nœud N4.
Il faut ensuite triangulariser la cavité avec l'algorithme de Bowyer-Watson en traitant les nœuds du polyhèdre comme des nouveaux nœuds, bien qu'ils ne soient pas globalement nouveaux puisqu'ils appartiennent à d'autres triangles (éventuellement à des triangles virtuels). Les trois premiers nœuds du polyèdre définissent le premier triangle (à condition qu'ils ne soient pas alignés).
La triangulation par l'algorithme de Bowyer-Watson, à partir de ce premier triangle et par ajout des nœuds restant du polyèdre, permet d'obtenir une triangulation de Delaunay de la cavité. Cependant, la triangulation obtenue est convexe alors que la cavité ne l'est pas toujours. Cette situation est illustée sur la figure suivante, dans le cas où aucun nœud de la cavité n'est sur un bord de la triangulation :
Figure pleine pageLes deux nouveaux triangles coloriés en rouge doivent être éliminés. Il s'agit de triangles qui ont une intersection avec au moins un des triangles de la triangulation après retrait de ceux de la cavité, ou bien de triangles identiques à un de ces triangles. Il faut détecter efficacement ces triangles. Deux triangles ont une intersection si et seulement si un côté de l'un coupe un côté de l'autre (voir annexe). Pour chaque nouveau triangle, il faut faire ce test avec les triangles auxquels les nœud du triangle appartiennent (qui sont mémorisés dans les nœuds). Par ailleurs, les triangles virtuels générés lors de la triangulation de la cavité, représentés par une flèche rouge dur la figure, doivent aussi être élminés (on verra plus loin qu'on les élimine même s'ils sont au bord).
Il faut aussi considérer le cas où le nœud enlevé se trouve sur la frontière :
Figure pleine pageL'intérieur de la triangulation se trouve à droite. Les triangles enlevés sont représentés en trait pointillé. Les triangles virtuels qui définissaient les bords sont aussi enlevé puisque le nœud enlevé en fait partie. Le polyèdre définissant la cavité contient donc les nœuds 1,2,3 et 4. Les nouveaux triangles apparaissant lors de la triangulation de la cavité sont, par exemple, les triangles 1,2,3 et 2,4,3. Le premier, tracé en bleu, doit être conservé. Le second, tracé en rouge, doit être éliminé. On a aussi représenté les nouveaux triangles virtuels qui doivent être éliminés en rouge et ceux qui doivent être conservés en bleu.
Nous ne voyons pas de méthode simple pour décider si un triangle virtuel doit être gardé ou pas. De plus, ces triangles virtuels ne sont pas toujours orientés convenablement. La stratégie la plus simple est donc de supprimer tous les triangles virtuels générés par la triangulation de la cavité puis de générer des triangles virtuels pour les bords.
Le premier triangle est similaire au premier triangle introduit précédemment pour l'algorithme de Bowyer-Watson, avec un triangle virtuel associé à chacun de ses trois côtés. Il reste à introduire les autres nœuds (nombre de nœuds du polyèdre moins 3) en suivant l'algorithme exposé ci-dessus et implémenté dans la classe Maillage5. La cavité est donc triangularisé indépendamment du reste de la triangulation. Lorsqu'un nœud du polyèdre est ajouté, il n'appartient évidemment à aucun disque circonscrit des triangles situés hors de la cavité. Grace à l'algorithme de Bowyer-Watson, il n'appartient à aucun disque circonscrit des nouveaux triangles. De plus, aucun nœud à l'extérieur de la cavité n'est dans le disque ouvert circonscrit d'un des nouveaux triangles (démonstration ?). En conséquence, la triangulation de la cavité conduit bien à une triangulation globalement Delaunay.
L'implémentation de la triangulation de la cavité est immédiate : il suffit de créer une instance de la classe Maillage5 et de l'utiliser pour générer les triangles, à la suite de quoi ceux-ci sont récupérés et insérés dans la triangulation globale s'ils sont valides. Il faut faire attention au fait que les nœuds du polyèdre sont modifiés par la triangulation de la cavité : il faut donc enlever les triangles invalides de la triangulation de la cavité. Les potentiels voisins des nouveaux triangles sont parmi ces nouveaux triangles et parmi ceux qui étaient voisins des triangles enlevés.
Les triangles virtuels générés par la triangulation de la cavité permettent d'obtenir les nœuds des bords de cette cavité. Lorsqu'un segment de bord appartient à un et un seul triangle, un nouveau triangle virtuel doit être généré pour ce bord, car il s'agit d'un nouveau bord de la triangulation.
Lorsque le nœud est enlevé, les triangles contenant ce nœud sont enlevés et une liste de leurs voisins est générée. Après création des nouveaux triangles, les voisins de ceux-ci sont recherchés dans cette liste.
La classe Maillage6, dérivée de la classe Maillage5, comporte en plus la fonction pour enlever un nœud. Elle comporte aussi une fonction pour détecter l'intersection de deux triangles, bien que celle-ci devrait plutôt être placée dans la classe Triangle.
class Maillage6(Maillage5):
def __init__(self):
Maillage5.__init__(self)
def intersectionSegments(self,A,B,C,D):
det = (B.y-A.y)*(C.x-D.x)-(D.y-C.y)*(A.x-B.x)
if det==0: return False
x = (((B.y-A.y)*A.x+(A.x-B.x)*A.y)*(C.x-D.x)-((D.y-C.y)*C.x+(C.x-D.x)*C.y)*(A.x-B.x))/det
y = (((D.y-C.y)*C.x+(C.x-D.x)*C.y)*(B.y-A.y)-((B.y-A.y)*A.x+(A.x-B.x)*A.y)*(D.y-C.y))/det
test1 = (x-A.x)*(B.x-A.x)+(y-A.y)*(B.y-A.y) > 0
test2 = (x-B.x)*(A.x-B.x)+(y-B.y)*(A.y-B.y) > 0
test3 = (x-C.x)*(D.x-C.x)+(y-C.y)*(D.y-C.y) > 0
test4 = (x-D.x)*(C.x-D.x)+(y-D.y)*(C.y-D.y) > 0
test = test1 and test2 and test3 and test4
return test
def intersectionTriangles(self,tr1,tr2):
if tr1.virtuel or tr2.virtuel:
return False
if tr1==tr2: return False
paires = [(0,1),(0,2),(1,2)]
if (tr1.noeuds[0] in tr2.noeuds) and (tr1.noeuds[1] in tr2.noeuds) and (tr1.noeuds[2] in tr2.noeuds): # triangles identiques
return True
for p in paires:
for q in paires:
A = tr1.noeuds[p[0]]
B = tr1.noeuds[p[1]]
C = tr2.noeuds[q[0]]
D = tr2.noeuds[q[1]]
if A!=C and A!=D and B!=C and B!=D and self.intersectionSegments(A,B,C,D): return True
return False
def enleverNoeud(self,n):
voisins = [] # voisins des triangles enlevés
retrait = [] # triangles à enlever
for tr in n.triangles:
for trv in tr.voisins:
if not(n in trv.noeuds) and not(trv in voisins):
voisins.append(trv)
retrait.append(tr)
# recherche des noeuds du polyèdre dans le sens direct
polyedre = []
recherche = True
premier = None
k = 0
while recherche:
i = 0
while tr.noeuds[i]!=n: i = (i+1)%3
# i : indice du noeud dans le triangle
k += 1
if not(tr.virtuel):
i1 = (i+1)%3
i2 = (i1+1)%3
n1 = tr.noeuds[i1]
if n1==premier:
recherche = False
break
if premier==None : premier = n1
n2 = tr.noeuds[i2]
polyedre.append(n1)
suivant = False
for t in n.triangles: # recherche du triangle suivant
if t!=tr and n2 in t.noeuds:
tr = t
suivant = True
break
else:
i1 = abs(i-1)
n1 = tr.noeuds[i1] # l'autre noeud réel
if i1==1:
for t in n.triangles:
if t!=tr and not(t.virtuel) and n1 in t.noeuds:
tr = t
break
else:
polyedre.append(n1)
for t in n.triangles:
if t!=tr and t.virtuel:
tr = t
break
N = len(polyedre)
for tr in retrait:
self.enleverTriangle(tr)
cavite = Maillage6()
cavite.triangleInitial(polyedre[0],polyedre[1],polyedre[2])
try:
if len(polyedre) > 3:
cavite.ajouterListeNoeuds(polyedre[3::],len(polyedre)-3)
except:
print("échec de triangulation de la cavité")
return
#cavite.draw("g-",linewidth=3)
# recherche des triangles générés à conserver
insert = []
retraitCavite = []
bordsCavite = []
for tr in cavite.triangles:
insertion = True
if tr.virtuel:
insertion=False
bordsCavite.append([tr.noeuds[0],tr.noeuds[1]])
else:
for tv in voisins:
if self.intersectionTriangles(tv,tr):
insertion = False
break
if insertion:
insert.append(tr)
else:
retraitCavite.append(tr)
# on enlève les triangles inutiles de la cavité (pour la mise à jour des noeuds)
for tr in retraitCavite:
cavite.enleverTriangle(tr)
#recherche des bords pour créer les nouveaux triangles virtuels.
trianglesVirtuels = []
for seg in bordsCavite:
n1 = seg[0]
n2 = seg[1]
num = 0
for tr in n1.triangles:
if n2 in tr.noeuds:
num += 1
if num==1: # segment appartenant à un seul triangle
tv = TriangleVirtuel2(n1,n2)
#if not(tv.dansCercle(n)):
# tv.noeuds[0],tv.noeuds[1] = tv.noeuds[1],tv.noeuds[0]
trianglesVirtuels.append(tv)
for tr in trianglesVirtuels:
insert.append(tr)
self.nouvTriangles = insert
self.voisins = voisins
self.polyedre = polyedre
self.trianglesVirtuels = trianglesVirtuels
# insertion des nouveaux triangles dans la triangulation
for tr in insert:
self.triangles.append(tr)
for tv in voisins:
if tv.triangleVoisin(tr):
tr.ajouterVoisin(tv)
tv.ajouterVoisin(tr)
Voici un exemple, comportant deux nœuds qui vont être enlevés :
maillage = Maillage6()
n1 = Noeud(-10,-10)
n2 = Noeud(10,-10)
n3 = Noeud(0,10)
maillage.triangleInitial(n1,n2,n3)
N = 30
x = uniform(-10,10,N)
y = uniform(-10,10,N)
noeuds = []
for i in range(N):
n = Noeud(x[i],y[i])
noeuds.append(n)
n1 = Noeud(0,0) # noeud central à enlever
noeuds.append(n1)
n2 = Noeud(-11,11) # noeud de bord à enlever
noeuds.append(n2)
maillage.ajouterListeNoeuds(noeuds,len(noeuds))
figure(figsize=(8,8))
maillage.draw("k-")
n1.draw("ro")
n2.draw("ro")
xlim(-12,12)
ylim(-12,12)
 fig18.pdf
fig18.pdf
Les nœuds à enlever sont marqués en rouge. On enlève le nœud situé au centre :
figure(figsize=(8,8))
noeuds.remove(n1)
n1.draw("ro")
maillage.enleverNoeud(n1)
maillage.draw("k-")
for tr in maillage.nouvTriangles:
tr.draw("r-")
xlim(-12,12)
ylim(-12,12)
invalid = maillage.verifierDelaunay()
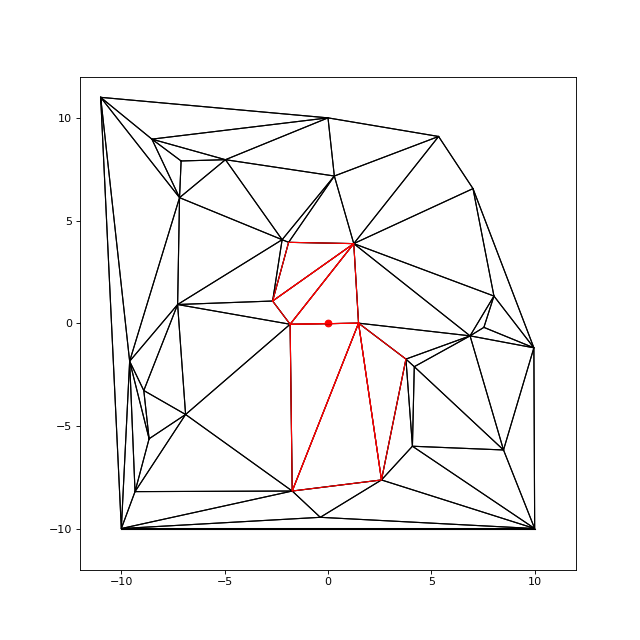 fig19.pdf
fig19.pdf
print(invalid) --> 0
Les nouveaux triangles sont tracés en rouge. On retire le nœud du bord :
figure(figsize=(8,8))
noeuds.remove(n2)
n2.draw("ro")
maillage.enleverNoeud(n2)
maillage.draw("k-")
for tr in maillage.nouvTriangles:
tr.draw("r-")
xlim(-12,12)
ylim(-12,12)
invalid = maillage.verifierDelaunay()
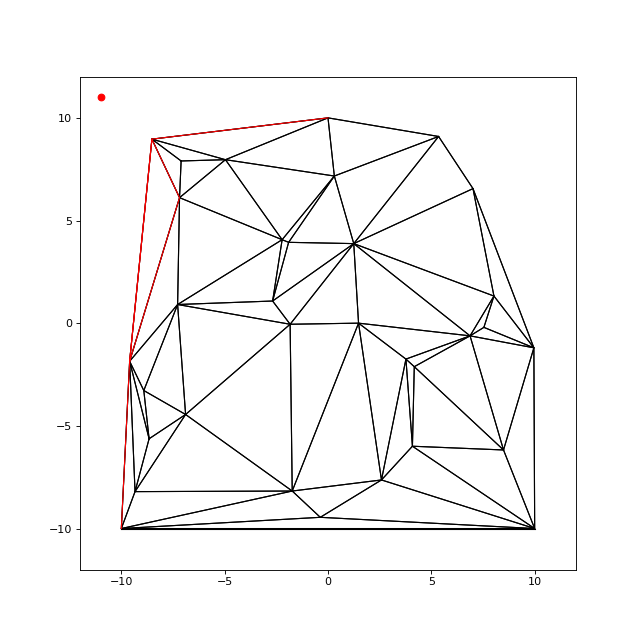 fig20.pdf
fig20.pdf
print(invalid) --> 0
Parmi les nouveaux triangles, il y a les nouveaux triangles virtuels, correspondant aux nouveaux bords. On enlève quelques nœuds sélectionnés au hasard
for k in range(10):
i = random.randint(0,len(noeuds)-1)
n = noeuds[i]
noeuds.remove(n)
maillage.enleverNoeud(n)
figure(figsize=(8,8))
maillage.draw("k-")
xlim(-12,12)
ylim(-12,12)
invalid = maillage.verifierDelaunay()
 fig21.pdf
fig21.pdf
print(invalid) --> 0
4. Annexes
4.a. Test d'intersection de deux triangles
Deux triangles ont une intersection si et seulement si un côté de l'un coupe un côté de l'autre. Il faut donc détecter l'intersection entre un segment AB et un segment CD. On commence par rechercher le point d'intersection des droites (AB) et (BC), dont les coordonnées sont solutions du système suivant :
Le déterminant de ce système est :
S'il est nul, les deux droites sont parallèles. C'est en particulier le cas lorsqu'on teste deux côtés communs de deux triangles. En conséquence, si le déterminant est nul les deux côtés ne se coupent pas. S'il est non nul, on obtient les coordonnées du point d'intersection avec la règle de Cramer :
Les deux segments se coupent si et seulement si le point d'intersection M appartient aux deux segments (ouverts) :
c'est-à-dire :
Si un des nœuds du segment AB est aussi un nœud du segment DC, par exemple si A=C, le test risque de conclure à une intersection à cause des erreurs d'arrondi, alors qu'il n'y a pas d'intersection dans ce cas (puisqu'on considère les segments ouverts). Il faut donc exclure du test ce cas.