Arduino GIGA R1 : mesure de la période d'un signal analogique
1. Introduction
Ce document montre comment mesurer la période d'un signal analogique périodique (ou quasi périodique) dont la numérisation est faite sur le convertisseur analogique/numérique (ADC) du microcontrôleur STM32H747XI. Les deux méthodes développées sont :
- Méthode d'analyse temporelle, consistant à détecter les passages par zéro du signal ou bien les extrémas.
- Méthode d'analyse fréquentielle, consistant à analyser le spectre obtenu par une acquisition sur un grand nombre de cycles.
La méthode temporelle se limite aux signaux sinusoïdaux et aux signaux qui présentent deux passages par zéro par cycle et deux extréma par cycle. Lorsque la durée entre deux passages par zéro (ou deux maxima) varie d'un cycle à l'autre, le signal est dit quasi périodique. Cette méthode permet de suivre précisément ces variations de période (au sens de durée d'un cycle). Elle nécessite une période d'échantillonnage très petite devant la période (au moins 100 fois plus petite). Cette méthode demande peu de mémoire.
La méthode fréquentielle est plus générale puisqu'elle permet de déterminer la fréquence fondamentale d'un signal périodique quelle que soit sa forme. En revanche, elle ne permet évidemment pas de suivre les fluctuations de la durée des cycles, ce qu'on peut appeler la période locale. La période d'échantillonnage doit être strictement inférieure à la moitié de la période fondamentale du signal. Une détermination précise de la fréquence exige de calculer la transformée de Fourier discrète du signal numérisé sur une grande durée (par rapport à la période). Pour cette raison, cette méthode demande une grande capacité de mémoire.
2. Méthode d'analyse temporelle
2.a. Algorithme
Le signal est supposé quasi sinusoïdal et de valeur moyenne nulle. On cherche les passages par zéro. Un passage par zéro par valeurs croissantes est suivi d'un passage par valeur décroissante. En principe, la détection d'un passage par zéro se fait en détectant un changement de signe d'un échantillon par rapport à celui qui le précède. En pratique, cette approche est mise en défaut lorsque le signal comporte du bruit. Une solution à cette difficulté est d'introduire une marge (positive). Notons xn la valeur du signal numérique à l'instant n. Si le signal est négatif alors il faut que xn>ε pour qu'un changement de signe soit détecté. Si le signal est positif alors il faut que xn<ε pour qu'un changement de signe soit détecté. Cette méthode est illustrée sur la figure suivante. La variable s contient le signe.
Figure pleine pageLe succès de cette algorithme repose sur une hypothèse : une fois que x a dépassé ε (le signe devient s = 1), il doit descendre en dessous de -ε à la fin du cycle et non pas à cause du bruit. Plus le bruit a une grande amplitude plus ε doit être grand mais il ne doit pas être trop grand non plus. Il n'est pas toujours aisé de connaître a priori la bonne valeur de ε donc des essais sont nécessaires. Remarquons que les comparateurs à hystéris, utilisés en électronique analogique, fonctionnent de cette manière.
La seconde méthode pour traiter les signaux bruités est d'effectuer un filtrage numérique passe-bas avant de faire l'analyse. On peut alors abaisser la valeur de ε où même la prendre nulle :
Figure pleine pagePour détecter les maxima et les minima, on peut dériver le signal avant d'appliquer l'algorithme précédent. Cependant, la dérivation augmente considérablement le bruit dans un signal donc le filtrage passe-bas sera probablement indispensable. L'avantage de la mesure de période à partir des extréma est qu'elle fonctionne aussi si la valeur moyenne du signal n'est pas nulle, voire si elle fluctue au cours du temps. Considérer la dérivée du signal plutôt que le signal lui-même revient simplement à considérer xn+1-xn à la place de xn.
2.b. Programme Arduino
Le filtrage numérique est exposé dans Arduino GIGA R1 : filtrage numérique. Dans le cas présent, le signal obtenu par filtrage, constitué de valeurs représentant les tensions en volts, est analysé pour la détection des changements de signes.
Si nous optons pour une fréquence d'échantillonnage de 100 kHz, la méthode fonctionnera avec une bonne précision pour des signaux de fréquences inférieures à 1 kHz (au moins 100 échantillons par cycle). Un filtre RIF avec une fréquence de coupure de 1 kHz semple a priori un bon choix. Voici le calcul d'un tel filtre avec 41 coefficients :
import numpy as np
from matplotlib.pyplot import *
import scipy.signal
def defCoeff(nom,x): # pour définir un tableau en langage C
N = len(x)
s = "float %s[%d] = {"%(nom,N)
for i in range(N-1):
s += "%g,"%x[i]
s += "%g};"%x[N-1]
return s
P=20
b = scipy.signal.firwin(numtaps=2*P+1,cutoff=[0.1],window='hann',fs=1)
print(defCoeff('b',b))
fe = 100e3
w,h=scipy.signal.freqz(b)
figure(figsize=(12,8))
subplot(211)
plot(w/(2*np.pi)*fe,20*np.log10(np.absolute(h)))
ylabel("GdB")
grid()
subplot(212)
plot(w/(2*np.pi)*fe,np.unwrap(np.angle(h)))
xlabel("f (Hz)")
ylabel("phase")
grid()
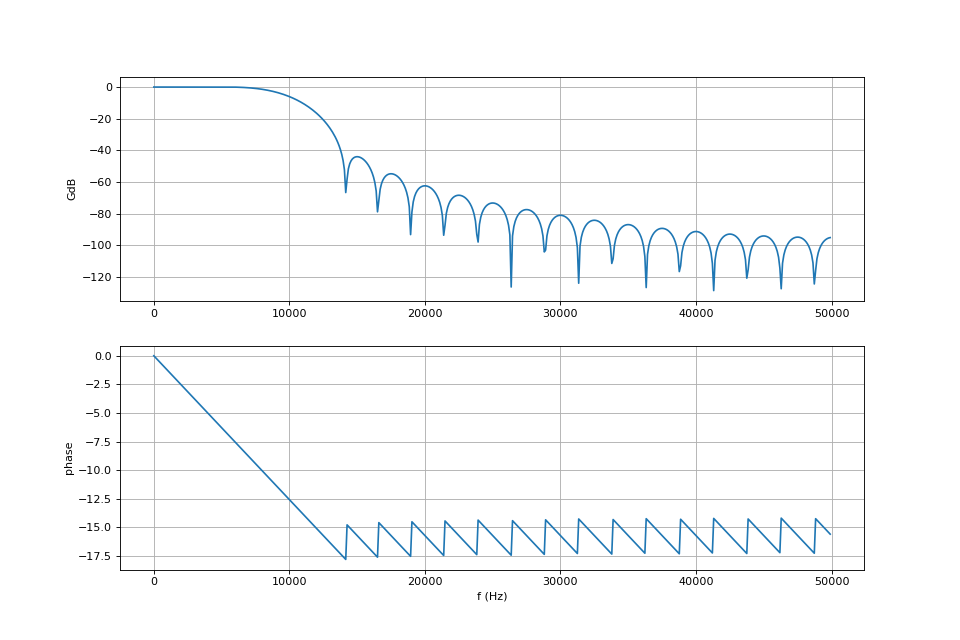fig1.pdf
L'utilisation de l'ADC et le filtrage numérique sont expliqués dans Arduino GIGA R1 : filtrage numérique. La détection des passages par zéro se fait sur les valeurs converties en volts (la valeur zéro correspond à 2048). La détermination des périodes se fait en comptant le nombre d'échantillons entre un passage par zéro par valeur croissante et le suivant. Les valeurs (entiers 32 bits) sont stockées dans un tampon et affichées dès que le tampon est plein.
#include <Arduino_AdvancedAnalog.h>
#define BUFSIZE 8 // tampon pour l'ADC
#define NBUF 4
uint32_t sample_rate = 100000;
AdvancedADC adc1(A0);
#define PERIODBUFSIZE 100 // tampon pour les périodes
uint32_t period[2][PERIODBUFSIZE];
uint32_t period_index;
uint8_t period_nbuf;
bool period_buffer_ready = false;
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
int8_t signe;
bool derive = false;
float epsilon = 1e-3;
uint32_t sample_count;
float last_sample;
#define BSIZE 41
#define ASIZE 1
#define WSIZE 41 // taille maximale de a et b
float b[41] = {-0,-6.05231e-05,-0.00041093,-0.000968941,-0.00111489,1.13996e-18,0.00275013,0.0063475,0.00870225,0.00716282,-3.89207e-18,-0.0120015,-0.0247287,-0.0313913,-0.0247172,6.64417e-18,0.0422416,0.0952615,0.14743,0.185655,0.199687,0.185655,0.14743,0.0952615,0.0422416,6.64417e-18,-0.0247172,-0.0313913,-0.0247287,-0.0120015,-3.89207e-18,0.00716282,0.00870225,0.0063475,0.00275013,1.13996e-18,-0.00111489,-0.000968941,-0.00041093,-6.05231e-05,-0};
float a[1] = {1.0};
float w[WSIZE];
uint16_t iw; // indice de wn
void setup() {
pinMode(13,OUTPUT);
Serial.begin(115200);
while(!Serial);
for (int i=0; i<WSIZE; i++) w[i] = 0.0f;
iw = 0;
last_sample = 0;
signe = 2;
sample_count = 0;
period_index = 0;
period_nbuf = 0;
if (!adc1.begin(AN_RESOLUTION_12, sample_rate, BUFSIZE, NBUF)) {
Serial.println("Impossible d'ouvrir ADC");
while (1);
}
}
void analyse() {
GPIOH->BSRR |= GPIO_BSRR_BS6; //digitalWrite(13,HIGH);
SampleBuffer buf1 = adc1.read();
uint16_t *buf1_data = buf1.data();
int16_t jw;
float y;
float ytemp;
for (int i=0; i<buf1.size(); i++) {
w[iw] = 1.0/a[0]*(buf1_data[i]-offset)*num2volt;
jw = iw-1;
if (jw==-1) jw=WSIZE-1;
for (uint16_t k=1; k<ASIZE; k++) {
w[iw] -= a[k]*w[jw];
jw = iw-1;
if (jw==-1) jw=WSIZE-1;
}
jw = iw;
y = 0.0f;
for (uint16_t k=0; k<BSIZE; k++) {
y += b[k]*w[jw];
jw--;
if (jw==-1) jw=WSIZE-1;
}
iw++;
if (iw==WSIZE) iw=0;
if (derive) {
ytemp = y;
y = (y-last_sample)*sample_rate; // dérivée
last_sample = ytemp;
}
sample_count++;
if (signe==2) { // initialisation
if (y>epsilon) signe=1;
else if (y<-epsilon) signe=-1;
}
else {
if ((signe>0)&&(y<-epsilon)) signe=-1;
else if ((signe<0)&&(y>epsilon)) { // passage par zéro par valeur croissante
signe=1;
period[period_nbuf][period_index] = sample_count; // sauvegarde dans le tampon
sample_count = 0;
period_index++;
if (period_index==PERIODBUFSIZE) {
period_index = 0;
if (period_nbuf==0) period_nbuf=1; else period_nbuf = 0;
period_buffer_ready = true;
}
}
}
}
buf1.release();
GPIOH->BSRR |= GPIO_BSRR_BR6; //digitalWrite(13,LOW);
}
void loop() {
if (adc1.available()) analyse();
if (period_buffer_ready) {
period_buffer_ready = false;
uint8_t nbuf;
if (period_nbuf==0) nbuf=1; else nbuf=0;
for (int i=0; i<PERIODBUFSIZE; i++) {
Serial.print(period[nbuf][i]);
Serial.print(", ");
}
}
}
Pour tester ce programme, nous utilisons l'Analog Discovery comme générateur de signal et le circuit d'interface (voir Arduino GIGA R1 : filtrage numérique) qui permet de décaler les tensions de manière à ramener la tension nulle à la valeur médiane (donnant le nombre 2048). Voici le résultat de la sortie console pour une sinusoïde de fréquence 1000 Hz et d'amplitude de crête 1 V :
1000, 1000, 1000, 1001, 1000, 1000, 999, 1002, 1000, 1000, 999, 1001, 1000, 1001, 999, 1000, 1001, 999, 1001, 1000, 999, 1001, 1000, 1000, 1001, 1000, 999
Il s'agit des nombres d'échantillons par cycle (la fréquence d'échantillonnage est 1000 kHz). Pour cette sinusoïde de 1000 Hz, il y a 100 échantillons par cycle. La précision relative de la mesure de période est bien meilleur que le centième : elle est de l'ordre de 2/1000 (sous réserve que la précision du générateur soit bien meilleure).
Voici le résultat pour une sinusoïde de 10 Hz :
10005, 9997, 10005, 10000, 10001, 10010, 9995, 10001, 10005, 9999, 10000, 10002, 10007, 10000, 10001, 9998, 10004, 10000, 10003, 10001, 9998, 10004, 10007, 9992
2.c. Transfert des données
Le programme suivant ajoute au précédent le transfert de données avec le PC par le protocole décrit dans Échanges de données avec un Arduino.
#include <Arduino_AdvancedAnalog.h>
#define BUFSIZE 8 // tampon pour l'ADC
#define NBUF 4
uint32_t sample_rate = 10000;
AdvancedADC adc1(A0);
#define PERIODBUFSIZE 100 // tampon pour les périodes
uint32_t period[2][PERIODBUFSIZE];
uint32_t period_index;
uint8_t period_nbuf;
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
int8_t signe;
uint8_t derive = 0;
float epsilon = 1e-3;
uint32_t sample_count;
float last_sample;
#define BSIZE 41
#define ASIZE 1
#define WSIZE 41 // taille maximale de a et b
float b[41] = {-0,-6.05231e-05,-0.00041093,-0.000968941,-0.00111489,1.13996e-18,0.00275013,0.0063475,0.00870225,0.00716282,-3.89207e-18,-0.0120015,-0.0247287,-0.0313913,-0.0247172,6.64417e-18,0.0422416,0.0952615,0.14743,0.185655,0.199687,0.185655,0.14743,0.0952615,0.0422416,6.64417e-18,-0.0247172,-0.0313913,-0.0247287,-0.0120015,-3.89207e-18,0.00716282,0.00870225,0.0063475,0.00275013,1.13996e-18,-0.00111489,-0.000968941,-0.00041093,-6.05231e-05,-0};
float a[1] = {1.0};
float w[WSIZE];
uint16_t iw; // indice de wn
// transferts des données
#define GET_DATA 10
#define SET_DATA 11
#define DATA_0_SIZE PERIODBUFSIZE*4 // périodes
#define DATA_1_SIZE 4 // uint32_t, sample_rate
#define DATA_2_SIZE 1 // uint8_t, derive
#define DATA_3_SIZE 4 // float, epsilon
uint8_t data_1[DATA_1_SIZE];
uint8_t data_2[DATA_2_SIZE];
uint8_t data_3[DATA_3_SIZE];
bool data_0_ready = false;
bool data_0_request = false;
void get_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==0) data_0_request = true;
}
void send_data() {
if ((data_0_ready)&&(data_0_request)) {
data_0_ready = false;
data_0_request = false;
uint8_t nbuf;
if (period_nbuf==0) nbuf=1; else nbuf=0;
Serial.write((uint8_t*)(period[nbuf]),DATA_0_SIZE);
}
}
void set_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==1) {
while (Serial.available()<DATA_1_SIZE) {};
Serial.readBytes(data_1,DATA_1_SIZE);
memcpy(&sample_rate,data_1,DATA_1_SIZE);
adc1.stop();
adc1.begin(AN_RESOLUTION_12, sample_rate, BUFSIZE, NBUF);
}
else if (n==2) {
while (Serial.available()<DATA_2_SIZE) {};
Serial.readBytes(data_2,DATA_2_SIZE);
memcpy(&derive,data_2,DATA_2_SIZE);
}
else if (n==3) {
while (Serial.available()<DATA_3_SIZE) {};
Serial.readBytes(data_3,DATA_3_SIZE);
memcpy(&epsilon,data_3,DATA_3_SIZE);
}
}
void read_serial() {
char com;
if (Serial.available()>0) {
com = Serial.read();
if (com==GET_DATA) get_data();
else if (com==SET_DATA) set_data();
}
}
void setup() {
pinMode(13,OUTPUT);
Serial.begin(500000);
while(!Serial);
for (int i=0; i<WSIZE; i++) w[i] = 0.0f;
iw = 0;
last_sample = 0;
signe = 2;
sample_count = 0;
period_index = 0;
period_nbuf = 0;
if (!adc1.begin(AN_RESOLUTION_12, sample_rate, BUFSIZE, NBUF)) {
Serial.println("Impossible d'ouvrir ADC");
while (1);
}
}
void analyse() {
GPIOH->BSRR |= GPIO_BSRR_BS6; //digitalWrite(13,HIGH);
SampleBuffer buf1 = adc1.read();
uint16_t *buf1_data = buf1.data();
int16_t jw;
float y;
float ytemp;
for (int i=0; i<buf1.size(); i++) {
w[iw] = 1.0/a[0]*(buf1_data[i]-offset)*num2volt;
jw = iw-1;
if (jw==-1) jw=WSIZE-1;
for (uint16_t k=1; k<ASIZE; k++) {
w[iw] -= a[k]*w[jw];
jw = iw-1;
if (jw==-1) jw=WSIZE-1;
}
jw = iw;
y = 0.0f;
for (uint16_t k=0; k<BSIZE; k++) {
y += b[k]*w[jw];
jw--;
if (jw==-1) jw=WSIZE-1;
}
iw++;
if (iw==WSIZE) iw=0;
if (derive) {
ytemp = y;
y = (y-last_sample)*sample_rate; // dérivée
last_sample = ytemp;
}
sample_count++;
if (signe==2) { // initialisation
if (y>epsilon) signe=1;
else if (y<-epsilon) signe=-1;
}
else {
if ((signe>0)&&(y<-epsilon)) signe=-1;
else if ((signe<0)&&(y>epsilon)) { // passage par zéro par valeur croissante
signe=1;
period[period_nbuf][period_index] = sample_count; // sauvegarde dans le tampon
sample_count = 0;
period_index++;
if (period_index==PERIODBUFSIZE) {
period_index = 0;
if (period_nbuf==0) period_nbuf=1; else period_nbuf = 0;
data_0_ready = true;
}
}
}
}
buf1.release();
GPIOH->BSRR |= GPIO_BSRR_BR6; //digitalWrite(13,LOW);
}
void loop() {
if (adc1.available()) analyse();
read_serial();
send_data();
}
Les données sont échangées avec un script Python au moyen de la classe Python accessible dans le fichier Arduino.py. Les données échangées sont :
- Data 0 : le tampon de PERIODBUFSIZE périodes (tableau de uint32).
- Data 1 : la période d'échantillonnage (uint32).
- Data 1 : derive (0 ou 1, uint8).
- Data 2 : epsilon (float).
Il faut remarquer que le changement de la fréquence d'échantillonnage modifie la fréquence de coupure du filtre. Celui-ci a en effet une fréquence de coupure égale à un dixième de la fréquence d'échantillonnage.
Voici le script qui configure l'analyseur et fait l'acquisition d'un nombre nb de tampons consécutifs.
from Arduino import Arduino
import matplotlib.pyplot as plt
import numpy as np
from numpy.fft import fft
PERIODBUFSIZE = 100
ard = Arduino('COM5',[PERIODBUFSIZE*4,4,1,4],baudrate=500000)
ard.write_int32(1,10000,signed=False) # sample_rate
ard.write_int8(2,0,signed=False) # signe
ard.write_float(3,1e-3) # epsilon
ard.read_int32_array(0,signed=False)
ard.read_int32_array(0,signed=False)
nb = 5
N = nb*PERIODBUFSIZE
period = np.zeros(N)
i = 0
for k in range(nb):
data = ard.read_int32_array(0,signed=False)
period[i:i+PERIODBUFSIZE] = data
i += PERIODBUFSIZE
ard.close()
plt.figure()
plt.plot(period,"r.")
plt.grid()
plt.ylim(0,200)
np.savetxt("periodes-fe10kHz-100Hz.txt",period)
plt.show()
Voici les périodes pour une sinusoïde de fréquence 100 Hz et d'amplitude de crête 1 V. La fréquence d'échantillonnage est 10 kHz.
period = np.loadtxt("periodes-fe10kHz-100Hz.txt")
figure(figsize=(16,6))
plot(period,"b.")
grid()
ylim(90,110)
xlabel("cycle")
ylabel("Période")
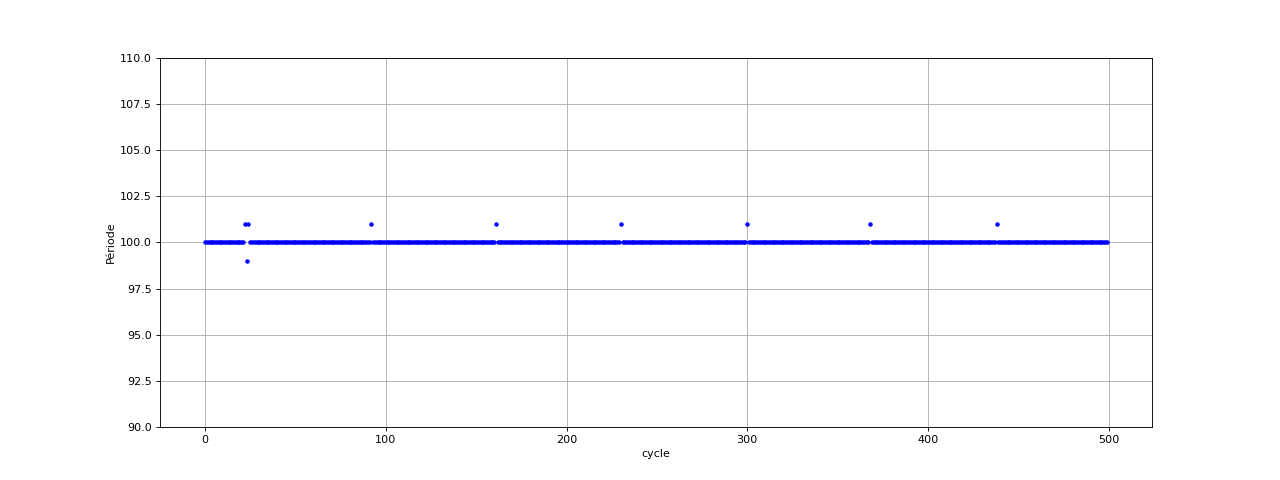fig2.pdf
Voici les périodes déterminées à partir des maxima (derive = 1) :
period = np.loadtxt("periodes-fe10kHz-100Hz-derive.txt")
figure(figsize=(16,6))
plot(period,"b.")
grid()
ylim(90,110)
xlabel("cycle")
ylabel("Période")
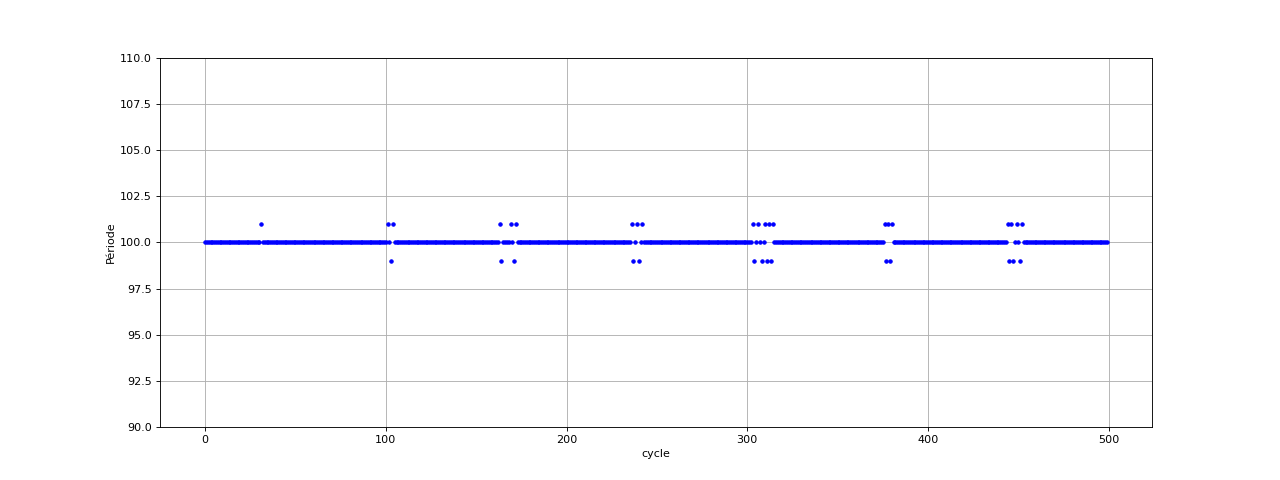fig3.pdf
La détection des maxima a l'avantage de fonctionner sur un signal comportant un décalage. Voici le résultat pour une sinusoïde d'amplitude de crête 500 mV avec un offset de 1 V (la valeur maximale, ici 1,5 V, ne doit pas dépasser la moitié de la plage de tensions du convertisseur avec son circuit d'interface).
period = np.loadtxt("periodes-fe10kHz-100Hz-offset-derive.txt")
figure(figsize=(16,6))
plot(period,"b.")
grid()
ylim(90,110)
xlabel("cycle")
ylabel("Période")
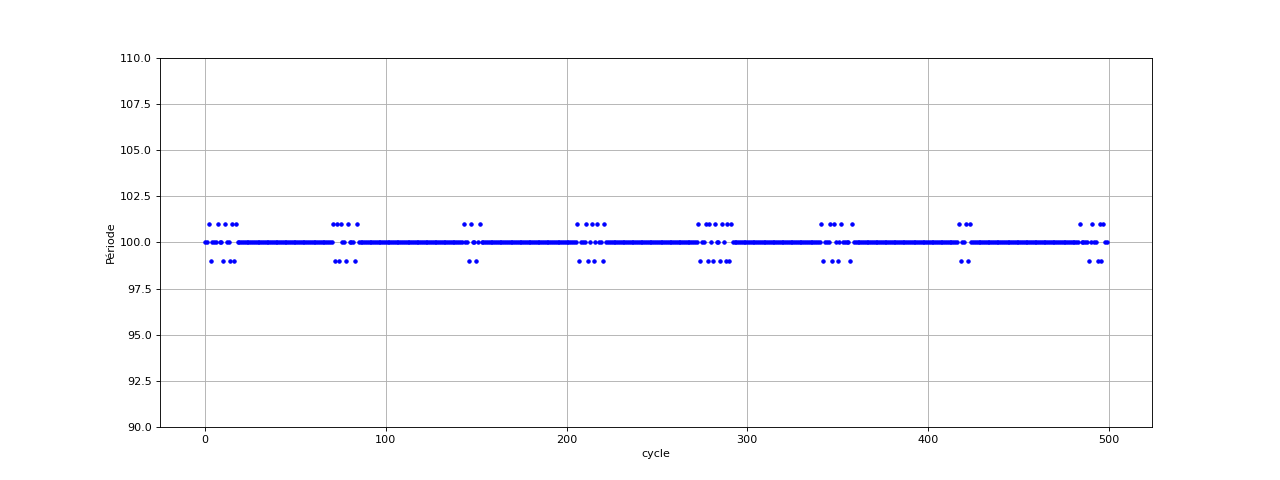fig4.pdf
Voici les périodes avec une fréquence d'échantillonnage de 20 kHz :
period = np.loadtxt("periodes-fe20kHz-100Hz-offset-derive.txt")
figure(figsize=(16,6))
plot(period,"b.")
grid()
ylim(180,220)
xlabel("cycle")
ylabel("Période")
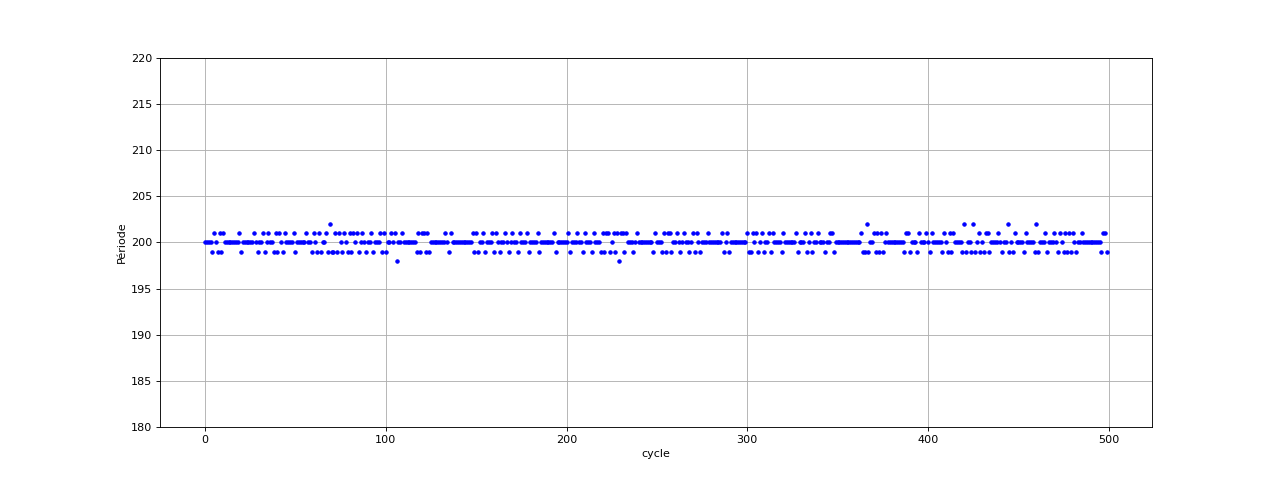fig5.pdf
Les écarts par rapport à la valeur attendue (200) sont plus nombreux mais leur amplitude relative est plus faible.
Voici les périodes avec une fréquence d'échantillonnage de 40 kHz (ε est toujours égal à 1e-3) :
period = np.loadtxt("periodes-fe40kHz-100Hz-offset-derive.txt")
figure(figsize=(16,6))
plot(period,"b.")
grid()
ylim(0,500)
xlabel("cycle")
ylabel("Période")
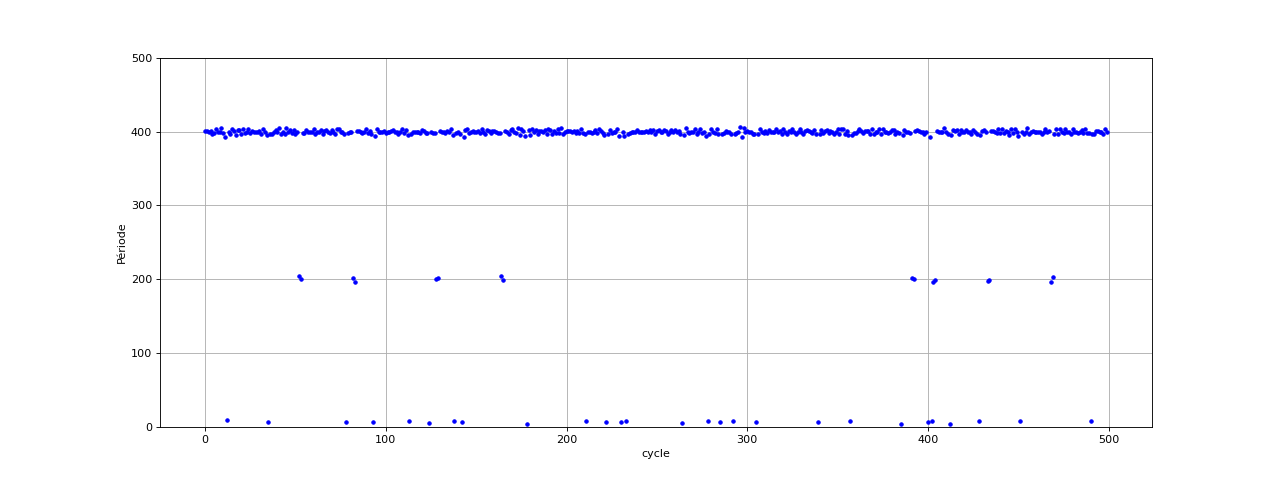fig6.pdf
Il y a des erreurs dues à une valeur de ε trop faible. En effet, la valeur de crête de la dérivée est 314 donc il faut augmenter ε. Voici le résultat pour ε=10 :
period = np.loadtxt("periodes-fe40kHz-100Hz-offset-derive-2.txt")
figure(figsize=(16,6))
plot(period,"b.")
grid()
ylim(0,500)
xlabel("cycle")
ylabel("Période")
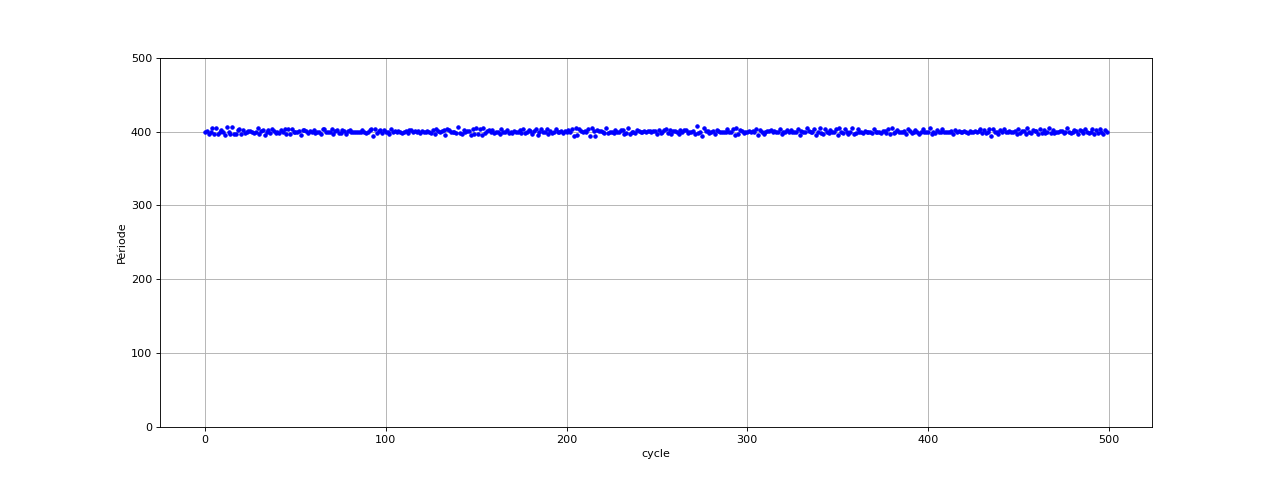fig7.pdf
period = np.loadtxt("periodes-fe40kHz-100Hz-offset-derive-2.txt")
figure(figsize=(16,6))
plot(period,"b.")
grid()
ylim(360,440)
xlabel("cycle")
ylabel("Période")
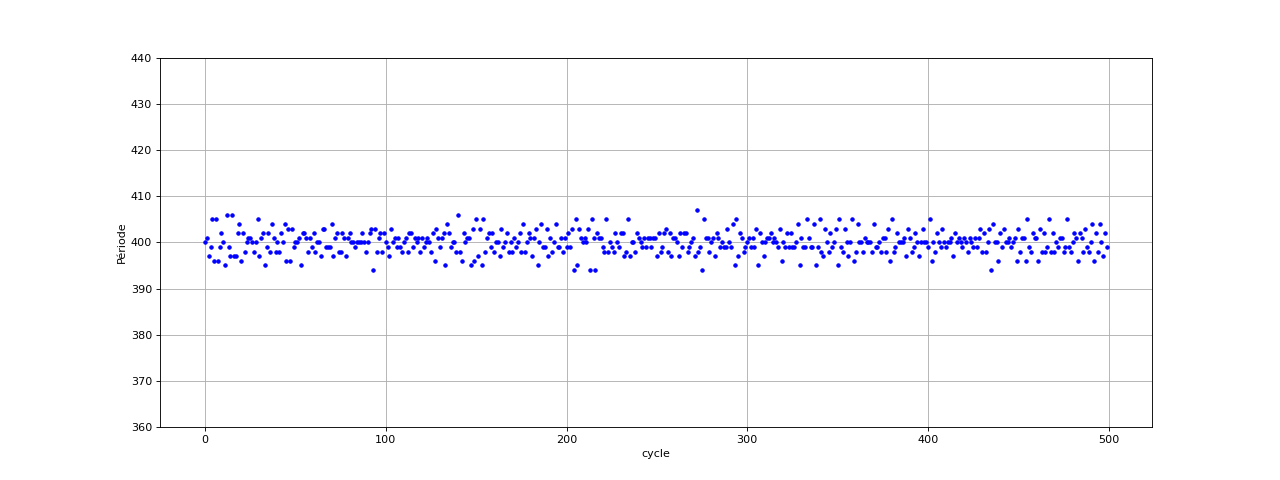fig8.pdf
Cette valeur de ε donne de bons résutats puisque les fluctuations relatives sont du même ordre de grandeur que précédemment. Cependant, cette fréquence d'échantillonnage plus élevée devrait conduire à une meilleure précision. Nous pouvons essayer d'améliorer la précision en accentuant le filtrage. Voici le résultat avec une filtre RIF de 161 coefficients, dont la fréquence de coupure est 1 kHz, et avec ε=1 :
period = np.loadtxt("periodes-fe40kHz-100Hz-offset-derive-3.txt")
figure(figsize=(16,6))
plot(period,"b.")
grid()
ylim(360,440)
xlabel("cycle")
ylabel("Période")
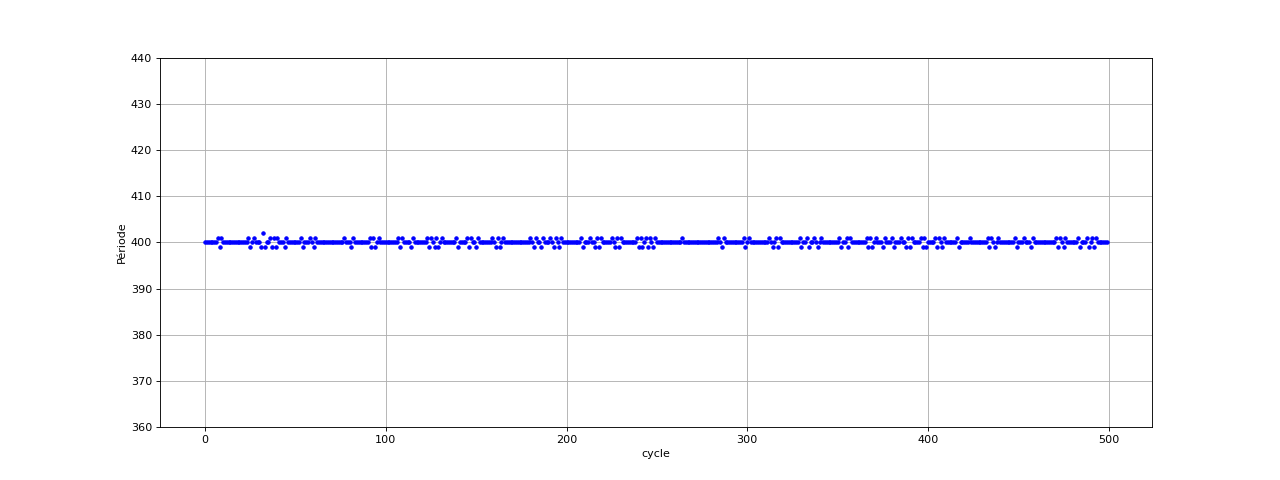fig9.pdf
Nous pouvons conclure de ces résultats que la précision est augmentée si on augmente la fréquence d'échantillonnage mais qu'il faut en même temps augmenter la sélectivité du filtre (en augmentant le nombre de coefficients) de manière à maintenir une valeur de ε faible devant l'amplitude de crête de la dérivée.
3. Méthode d'analyse fréquentielle
3.a. Principe
Cette méthode consiste à faire l'analyse fréquentielle au moyen de la transformée de Fourier discrète (voir Analyse spectrale d'un signal numérique).
Si le signal est périodique, la détermination de sa fréquence consiste à repérer la raie fondamentale dans le spectre puis à déterminer la fréquence correspondant à son maximum le plus précisément possible. Il y deux conditions à respecter :
- La fréquence d'échantillonnage doit être strictement supérieure au double de la fréquence du signal étudié. Comme celle-ci est inconnue, il faut évidemment prévoir une marge de sécurité.
- La durée du signal échantillonnée doit être la plus grande possible puisque la précision en fréquence est égale à l'inverse de cette durée.
La seconde condition est difficile à réaliser car la mémoire disponible sur un microcontrôleur est relativement faible. La méthode classique permettant d'augmenter la précision du spectre (sans pour autant augmenter la résolution) sans augmenter la durée analysée consiste à ajouter des zéros au signal avant de calculer sa TFD mais cela ne résout évidemment pas le problème de la mémoire disponible.
Considérons l'échantillonnage d'un signal périodique comportant 3 harmoniques :
from numpy.random import normal
f = 105.3
def signal(t):
return 0.5+np.sin(2*np.pi*f*t)+0.3*np.sin(3*2*np.pi*f*t)+0.1*np.sin(5*2*np.pi*f*t+np.pi/3)
te = 1e-3 #période d'échantillonnage
N = 4096 # nombre d'échantillons (puissance de 2)
t = np.arange(N)*te
u = signal(t)+normal(0,1e-2,N)
On calcule sa transformée de Fourier discrète et on trace le spectre (module de la TFD en fonction de la fréquence) :
from numpy.fft import fft
tfd = fft(u)*2/N
spectre = np.absolute(tfd)
freq = np.arange(N)*1/(N*te)
figure(figsize=(16,6))
plot(freq,spectre)
grid()
xlabel("f (Hz)")
ylabel("A (V)")
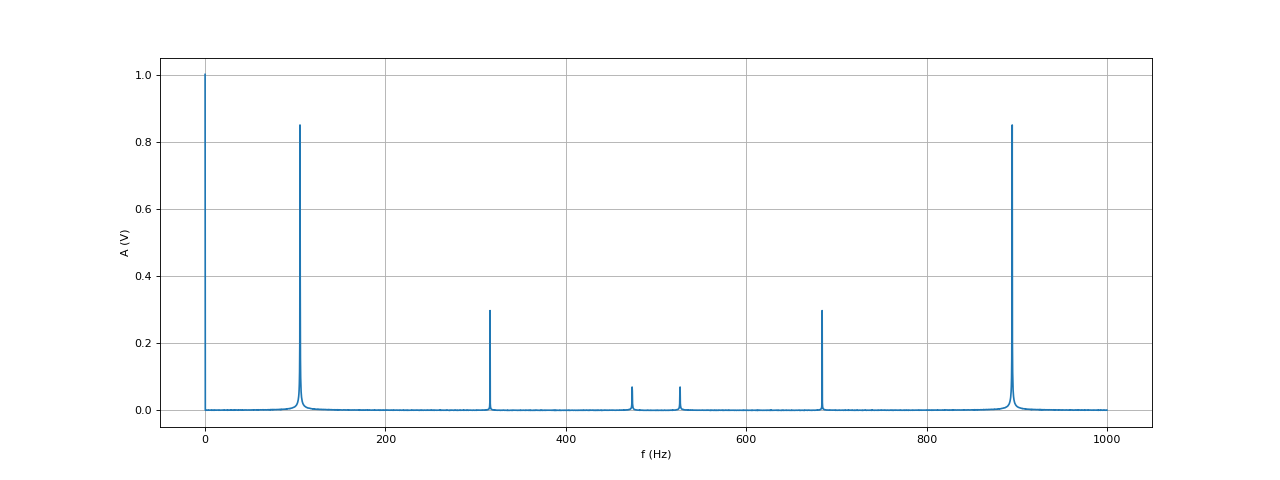fig10.pdf
La valeur à l'indice 0 correspond à la fréquence nulle (c'est le double de la composante continue). Pour extraire les harmoniques, on commence par calculer l'amplitude en décibel, en prenant comme référence la plus grande valeur du spectre :
Amax = np.max(spectre)
spectre_db = 20*np.log10(spectre/Amax)
figure(figsize=(16,6))
plot(freq,spectre_db)
grid()
xlabel("f (Hz)")
ylabel("dB")
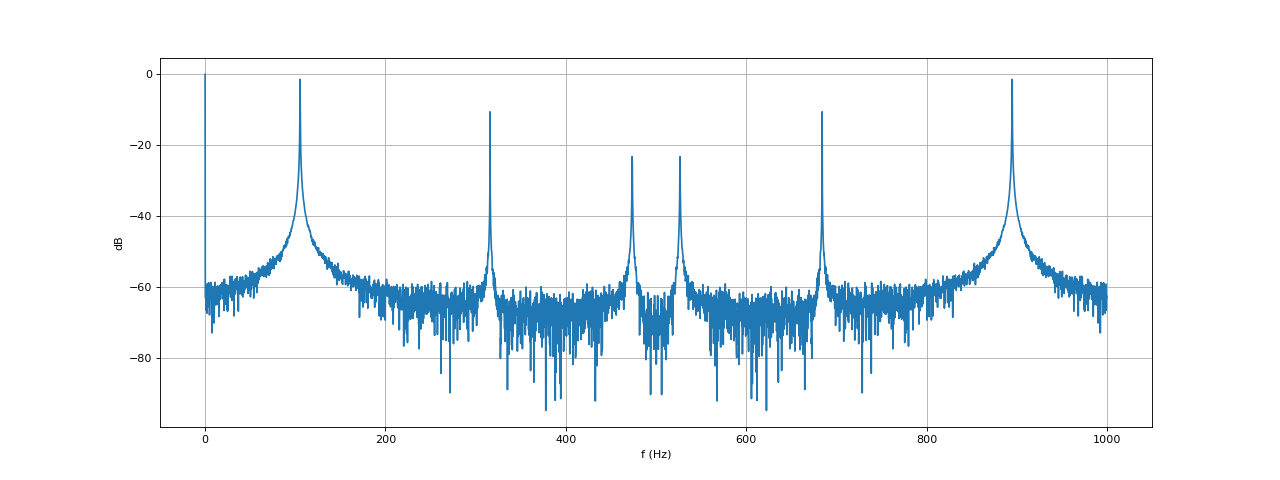fig11.pdf
Remarque : on pourrait penser qu'il est aisé de ne pas tenir compte de la raie d'ordre 0. C'est en effet possible si celle-ci occupe seulement le premier terme de la TFD comme c'est le cas ici mais il en va autrement si le spectre est calculé après ajout de zéro : dans ce cas, la composante de fréquence nulle doit être traitée comme les harmoniques. Pour extraire les raies, on doit décider d'une valeur maximale en décibel par rapport au maximum. Dans cet exemple, si l'on choisi un maximum de 40 dB, les trois harmoniques du signal seront extraite. Il faut ensuite déterminer les maxima en parcourant le spectre depuis l'indice 1 jusqu'à l'indice N/2. L'algorithme de recherche des maxima est similaire à celui exposé plus haut pour la recherche d'extréma d'un signal :
def rechercheRaies(spectre_db,freq,maxdb,epsilon):
raies = []
i = 1
N = len(spectre_db)//2
while i<N-1:
if spectre_db[i] > -maxdb:
deriv = spectre_db[i]-spectre_db[i-1]
if deriv > 0 : signe = 1
else : signe = -1
deriv = spectre_db[i+1]-spectre_db[i]
if signe>0 and deriv < -epsilon:
signe = -1
raies.append(freq[i])
i += 1
while i < N-1 and spectre_db[i] > -maxdb :
deriv = spectre_db[i]-spectre_db[i-1]
if signe>0 and deriv<-epsilon:
signe = -1
raies.append(freq[i])
elif signe<0 and deriv>epsilon:
signe = 1
i += 1
else:
i += 1
return raies
raies = rechercheRaies(spectre_db,freq,40,1e-2)
print(raies) --> [105.46875, 316.162109375, 473.6328125]
La résolution fréquentielle est :
print(freq[1]-freq[0]) --> 0.244140625
Le bon fonctionnement de l'extraction des raies repose sur le bon choix de ε. Il est en effet possible de détecter des maxima de petite amplitude en dehors des raies, d'autant plus que maxdb est grand.
Il n'est pas nécessaire de calculer le spectre en décibel pour implémenter cet algorithme. Si spectre est le tableau contenant le module de la TFD, l'évaluation de la dérivée s'écrit aussi :
deriv = 20*np.log10(spectre[i]/spectre[i-1])
La valeur minimale de l'amplitude étant connue, le test de validité s'écrit :
if spectre[i] > Amin:
Il est aussi possible de faire la détection des maxima en évaluant la dérivée du module et non pas du module en décibel :
def rechercheRaies2(spectre,freq,Amin,epsilon):
raies = []
i = 1
N = len(spectre)//2
while i<N-1:
if spectre[i] > Amin:
deriv = spectre[i]-spectre[i-1]
if deriv > 0 : signe = 1
else : signe = -1
deriv = spectre[i+1]-spectre[i]
if signe>0 and deriv < -epsilon:
signe = -1
raies.append(freq[i])
i += 1
while i < N-1 and spectre[i] > Amin :
deriv = spectre[i]-spectre[i-1]
if signe>0 and deriv<-epsilon:
signe = -1
raies.append(freq[i])
elif signe<0 and deriv>epsilon:
signe = 1
i += 1
else:
i += 1
return raies
raies = rechercheRaies2(spectre,freq,1e-2,1e-2)
print(raies) --> [105.46875, 316.162109375, 473.6328125]
Cette méthode est préférable à la première car elle est moins sensible aux maxima locaux accidentels.
L'estimation de la fréquence d'une raie peut être améliorée par interpolation quadratique. Soit b le module de l'élement de la TFD d'indice imax. Le module de l'élément précédent, d'indice imax-1, est noté a, celui de l'élément suivant, d'indice imax+1, est noté c. L'interpolation quadratique consiste à chercher la parabole qui passe par ces trois points. Le maximum de cette parabole donne une estimation du maximum de la raie. On obtient la position du maximum sous la forme d'un décalage compris entre -1/2 et 1/2 :
qui permet de calculer l'indice interpolé (nombre réel) du maximum i=imax+p puis la fréquence associée. Une estimation de la hauteur de la raie est donnée par :
3.b. Programme Arduino avec CMSIS DSP
Le calcul de la TFD par transformée de Fourier rapide (FFT) peut être effectué avec des fonctions de la bibliothèque CMSIS DSP Software Library (CMSIS : Cortex Microcontroller Software Interface Standard, DSP : Digital Signal Processing).
Le programme suivant montre comment se programme le calcul de la FFT pour un signal à valeurs réelles. Le nombre d'échantillons doit être une puisssance de 2 et sa valeur maximale est 4096 (nous ne connaissons pas la raison de cette limitation).
#include <arm_math.h>
#define NSAMPLES 4096
arm_rfft_fast_instance_f32 rfft_instance;
float fft[NSAMPLES*2];
float fft_amp[NSAMPLES];
float sig[NSAMPLES];
void setup() {
Serial.begin(115200);
while(!Serial);
for (int i=0; i<NSAMPLES; i++) sig[i] = sin(2*PI*i/NSAMPLES);
arm_rfft_fast_init_f32(&rfft_instance,NSAMPLES);
arm_rfft_fast_f32(&rfft_instance,sig,fft,0);
arm_cmplx_mag_f32(fft,fft_amp,NSAMPLES/2);
for (int i=0; i<NSAMPLES/2; i++) {
Serial.println(fft_amp[i]*2.0/NSAMPLES);
}
}
void loop() {
}
Le signal échantillonné est une sinusoïde d'amplitude de crête 1, échantillonnée précisément sur une période. La TFD (après normalisation) est donc constitué de zéros et de la valeur 1 à l'indice 1.
Le programe suivant effect la numérisation d'un signal (voie A0) et la détection des raies.
#include <Arduino_AdvancedAnalog.h>
#include <arm_math.h> // CMSIS DSP
#define BUFSIZE 32
#define NBUF 10
#define NSAMPLES 4096
AdvancedADC adc1(A0);
float sig[NSAMPLES];
uint32_t sample_rate = 40000;
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
// paramètres de détection des raies
float Amin = 0.01;
float epsilon = 1e-2;
uint16_t indice;
arm_rfft_fast_instance_f32 rfft_instance;
float fft[NSAMPLES*2];
float fft_amp[NSAMPLES];
float deltaf;
float Veff = 0;
void setup() {
Serial.begin(115200);
while(!Serial);
indice = 0;
deltaf = sample_rate*1.0/NSAMPLES;
if (!adc1.begin(AN_RESOLUTION_12, sample_rate, BUFSIZE, NBUF)) {
while (1);
}
}
void printRaie(float f,float amp) {
Serial.print(f,6);
Serial.print(" +/- ");
Serial.print(deltaf,4);
Serial.print(" Hz, ");
Serial.println(amp,8);
}
void interpolRaie(int i) {
#define a fft_amp[i-1]
#define b fft_amp[i]
#define c fft_amp[i+1]
float p = 0.5*(a-c)/(1-2*b+c);
float f = (i+p)*deltaf;
float A = b-0.25*(a-c)*p;
printRaie(f,A);
}
void loop() {
if (adc1.available()) {
SampleBuffer buf1 = adc1.read();
uint16_t *buf1_data = buf1.data();
for (uint16_t i=0; i<BUFSIZE; i++) {
sig[indice] = (buf1_data[i]-offset)*num2volt;
Veff += sig[indice]*sig[indice];
indice++;
}
buf1.release();
if (indice==NSAMPLES) {
indice = 0;
arm_rfft_fast_init_f32(&rfft_instance,NSAMPLES);
arm_rfft_fast_f32(&rfft_instance,sig,fft,0);
arm_cmplx_mag_f32(fft,fft_amp,NSAMPLES/2);
float f;
uint16_t N = NSAMPLES/2;
uint16_t i;
for (i=0; i<N; i++) {
fft_amp[i] *= 2.0/NSAMPLES;
}
Serial.println("---------------");
Veff = sqrt(Veff/NSAMPLES);
Serial.print("Veff = "); Serial.println(Veff,5);
float deriv;
int8_t signe;
i = 1;
while (i<N-1) {
if (fft_amp[i]>Amin) {
deriv = fft_amp[i]-fft_amp[i-1];
if (deriv > 0) signe=1; else signe = -1;
deriv = fft_amp[i+1]-fft_amp[i];
if ((signe>0)&&(deriv<-epsilon)) {
signe = -1;
interpolRaie(i);
i++;
}
while ((i<N-1)&&(fft_amp[i]>Amin)) {
deriv = fft_amp[i]-fft_amp[i-1];
if ((signe>0)&&(deriv<-epsilon)) {
signe = -1;
interpolRaie(i-1);
}
else if ((signe<0)&&(deriv>epsilon)) signe = 1;
i++;
}
}
else i++;
}
delay(1000);
}
}
}
La fréquence d'échantillonnage est 40 kHz et le nombre d'échantillons 4096 (le maximum permis par la fonction fft de CMSIS DSP). On peut donc faire l'analyse d'un signal audio, dont les harmoniques ne dépassent pas 20 kHz. Voici par exemple le résultat pour un signal sinusoïdal de fréquence 945 Hz (le seuil de détection Amin vaut 0,01) :
Veff = 0.70583
925.157104 +/- 12.2070 Hz, 0.57885599
---------------
Veff = 0.70622
951.427307 +/- 12.2070 Hz, 0.83815831
---------------
Veff = 0.70578
926.095703 +/- 12.2070 Hz, 0.57822084
---------------
Veff = 0.70525
926.009766 +/- 12.2070 Hz, 0.57816601
---------------
Veff = 0.70532
925.793030 +/- 12.2070 Hz, 0.57828152
Voici le résultat pour une sinusoïde de 125 Hz :
124.948982 +/- 12.2070 Hz, 0.87352687
---------------
Veff = 0.70944
128.857880 +/- 12.2070 Hz, 0.85340077
---------------
Veff = 0.70774
124.801125 +/- 12.2070 Hz, 0.87536836
---------------
Veff = 0.70897
124.941628 +/- 12.2070 Hz, 0.87360168
---------------
Veff = 0.70452
124.225739 +/- 12.2070 Hz, 0.88600892
---------------
Veff = 0.70441
125.999146 +/- 12.2070 Hz, 0.86315364
---------------
Veff = 0.70146
124.936867 +/- 12.2070 Hz, 0.87353915
---------------
Veff = 0.70636
123.551414 +/- 12.2070 Hz, 0.90065420
---------------
Veff = 0.70424
125.221596 +/- 12.2070 Hz, 0.87035614
et pour une sinusoïde de 10539 Hz :
Veff = 0.70740
10536.966797 +/- 12.2070 Hz, 0.88593704
---------------
Veff = 0.70722
10535.416992 +/- 12.2070 Hz, 0.92799354
---------------
Veff = 0.70746
10537.369141 +/- 12.2070 Hz, 0.87906498
---------------
Veff = 0.70731
10535.414063 +/- 12.2070 Hz, 0.92809892
---------------
Veff = 0.70735
10537.368164 +/- 12.2070 Hz, 0.87901253
La précision de détermination de la hauteur de la raie (en théorie égale à 1) est assez médiocre, ce qui est attendu pour une analyse spectrale avec aussi peu d'échantillons.
La précision en fréquence est limitée par le nombre d'échantillons (4096). On voit bien sur cet exemple que la méthode d'analyse spectrale est beaucoup moins précise que la méthode d'analyse temporelle pour un signal sinusoïdal. Elle a en revanche l'avantage de s'appliquer à un signal périodique quelconque.
Voici le résultat pour un signal triangulaire de 548 Hz et d'amplitude de crête 1 V, avec un seuil de détection toujours égal à 0,01 :
Veff = 0.57784
547.311523 +/- 12.2070 Hz, 0.72562325
1647.967285 +/- 12.2070 Hz, 0.08207195
3833.024658 +/- 12.2070 Hz, 0.01764415
---------------
Veff = 0.57612
546.719727 +/- 12.2070 Hz, 0.71083432
1648.155029 +/- 12.2070 Hz, 0.06805015
---------------
Veff = 0.57808
547.176758 +/- 12.2070 Hz, 0.72135019
1648.027222 +/- 12.2070 Hz, 0.07765958
3832.998779 +/- 12.2070 Hz, 0.01522910
Les raies de rang 1,3 et 7 sont détectées. Étrangement, l'harmonique de rang 5 n'est pas détectée mais cela peut provenir de la sous-estimation de la hauteur des raies, qui est sans doute plus marquée pour la raie de rang 5 (pour cette fréquence). Divisons par deux le seuil de détection (0,001) :
2746.696289 +/- 12.2070 Hz, 0.01691139
3832.992920 +/- 12.2070 Hz, 0.01490011
---------------
Veff = 0.57600
546.453796 +/- 12.2070 Hz, 0.70721757
1648.095825 +/- 12.2070 Hz, 0.07272713
2746.689941 +/- 12.2070 Hz, 0.01738855
---------------
Veff = 0.57596
547.858948 +/- 12.2070 Hz, 0.74331230
1648.171753 +/- 12.2070 Hz, 0.06668762
2746.680664 +/- 12.2070 Hz, 0.01808655
---------------
Veff = 0.57638
548.937317 +/- 12.2070 Hz, 0.78415877
1648.119873 +/- 12.2070 Hz, 0.07075486
3833.005615 +/- 12.2070 Hz, 0.01605066
---------------
Veff = 0.57768
546.863647 +/- 12.2070 Hz, 0.71360606
1648.015015 +/- 12.2070 Hz, 0.07879218
2746.640137 +/- 12.2070 Hz, 0.02145945
---------------
Veff = 0.57599
546.811951 +/- 12.2070 Hz, 0.71347934
1648.132080 +/- 12.2070 Hz, 0.06989212
2746.678223 +/- 12.2070 Hz, 0.01829096
3833.007813 +/- 12.2070 Hz, 0.01603375
On voit sur cet exemple que la détection des raies de rangs 5 et 7 est plutôt aléatoire. Seules les raies de rang 1 et 3 sont systématiquement détectées. Il serait intéressant de mettre en place un algorithme qui rassemble les raies détectées sur plusieurs acquisitions successives.
3.c. Amélioration de l'analyse spectrale
L'exemple précédent montre que la limitation à 4096 du nombre d'échantillons du signal analysé a, en plus de l'effet évident sur la précision de fréquence, un effet considérable sur la hauteur des raies et donc au final sur la reproductibilité de la détection des raies. Afin d'augmenter le nombre d'échantillons, nous reprenons notre propre implémentation de la FFT, déjà utilisée dans Analyse spectrale sur Arduino.
La fonction fft effectue le calcul de la TFD. L'algorithme FFT nécessite deux tableaux (notés A et B). À chaque niveau de TFD, l'un des deux tableaux contient les TFD de niveau inférieur (TFD à N termes) et l'autre tableau reçoit les nouvelles TFD (TFD à 2N termes). Il faut donc alterner le rôle de A et B (source ou destination) à chaque niveau de TFD. En principe, cela se fait en langage C par un échange des pointeurs sur A et B. Cependant, le compilateur de l'IDE Arduino considère comme incompatibles les types float * (pointeur sur un flottant) et float[256] (pointeur sur un tableau de flottants), ce qui empêche de procéder à un échange de pointeurs sur deux tableaux, à moins de créer un troisième tableau de taille égale aux deux premier, ce qui est ici exclu pour des raisons d'économie de la mémoire. La fonction suivante attribue le rôle de source ou de destination aux tableaux A ou B en fonction de la valeur de parite (0 ou 1). Il est convenu que les échantillons du signal sont au départ dans le tableau A (variables globales A_re et A_im) et que la TFD finale se trouve dans le tableau B (variables globales B_re et B_im). Les valeurs initiales du tableau A sont bien sûr perdues.
#include <Arduino_AdvancedAnalog.h>
#define BUFSIZE 32
#define NBUF 10
#define NSAMPLES 16384
#define P 14 // NSAMPLE = 2**P
AdvancedADC adc1(A0);
float A_re[NSAMPLES];
float A_im[NSAMPLES];
float B_re[NSAMPLES];
float B_im[NSAMPLES];
uint32_t sample_rate = 50000;
// transformation nombre -> tension
float offset = 2048;
float num2volt = 3.217/4096;
uint16_t indice;
float fft_amp[NSAMPLES/2];
float deltaf;
float Amin = 0.001;
float epsilon = 1e-2;
float Veff = 0;
int inversion(uint16_t i) {
uint8_t bi;
int8_t b;
uint8_t bits[P];
for (b=0; b<P; b++) {
bi = i & 0b1;
i = i >> 1;
bits[b] = bi;
}
uint16_t facteur = 1;
uint16_t j = 0;
for (b=P-1; b>=0; b--) {
j += bits[b]*facteur;
facteur *= 2;
}
return j;
}
void fft() {
uint16_t j;
for (int k=0; k<NSAMPLES; k++) {
j = inversion(k);
B_re[j] = A_re[k];
B_im[k] = A_im[k];
}
uint16_t taille = 1;
uint16_t taille_precedente;
uint16_t nombre_tfd = NSAMPLES;
uint16_t position;
float phi, W_re, W_im;;
float x,y;
uint8_t parite = 0;
for (uint16_t q=0; q<P; q++) {
taille_precedente = taille;
taille *= 2;
nombre_tfd /= 2;
for (uint16_t m=0; m<nombre_tfd; m++) {
phi = -2*PI/taille;
position = m*taille;
uint16_t i,j,k;
for (i=0; i<taille_precedente; i++) {
W_re = cos(phi*i);
W_im = sin(phi*i);
j = position+taille_precedente+i;
k = position +i;
if (parite==0) {
x = B_re[j];
y = B_im[j];
A_re[k] = B_re[k] + x*W_re-y*W_im;
A_im[k] = B_im[k] + x*W_im+y*W_re;
}
else {
x = A_re[j];
y = A_im[j];
B_re[k] = A_re[k] + x*W_re-y*W_im;
B_im[k] = A_im[k] + x*W_im+y*W_re;
}
}
for (i=taille_precedente; i<taille; i++) {
W_re = cos(phi*i);
W_im = sin(phi*i);
j = position+i;
k = position+i-taille_precedente;
if (parite==0) {
x = B_re[j];
y = B_im[j];
A_re[j] = B_re[k] + x*W_re-y*W_im;
A_im[j] = B_im[k] + x*W_im+y*W_re;
}
else {
x = A_re[j];
y = A_im[j];
B_re[j] = A_re[k] + x*W_re-y*W_im;
B_im[j] = A_im[k] + x*W_im+y*W_re;
}
}
}
parite = ~parite;
}
if (parite) {
for (int k=0; k<NSAMPLES; k++) {B_re[k] = A_re[k]; B_im[k] = A_im[k];}
}
}
void setup() {
Serial.begin(115200);
while(!Serial);
indice = 0;
deltaf = sample_rate*1.0/NSAMPLES;
for (int i=0; i<NSAMPLES; i++) A_im[i] = 0.0;
if (!adc1.begin(AN_RESOLUTION_12, sample_rate, BUFSIZE, NBUF)) {
while (1);
}
}
void printRaie(float f,float amp) {
Serial.print(f,6);
Serial.print(" +/- ");
Serial.print(deltaf,4);
Serial.print(" Hz, ");
Serial.println(amp,8);
}
void interpolRaie(int i) {
#define a fft_amp[i-1]
#define b fft_amp[i]
#define c fft_amp[i+1]
float p = 0.5*(a-c)/(1-2*b+c);
float f = (i+p)*deltaf;
float A = b-0.25*(a-c)*p;
printRaie(f,A);
}
void loop() {
if (adc1.available()) {
SampleBuffer buf1 = adc1.read();
uint16_t *buf1_data = buf1.data();
for (uint16_t i=0; i<BUFSIZE; i++) {
A_re[indice] = (buf1_data[i]-offset)*num2volt;
A_im[indice] = 0.0;
Veff += A_re[indice]*A_re[indice];
indice++;
}
buf1.release();
if (indice==NSAMPLES) {
indice = 0;
Veff = sqrt(Veff/NSAMPLES);
Serial.println("---------------");
Serial.print("Veff = "); Serial.println(Veff,5);
Veff = 0;
fft();
float f;
uint16_t N = NSAMPLES/2;
uint16_t i;
for (i=0; i<N; i++) {
fft_amp[i] = sqrt(B_re[i]*B_re[i]+B_im[i]*B_im[i])*2.0/NSAMPLES;
}
float deriv;
int8_t signe;
i = 1;
while (i<N-1) {
if (fft_amp[i]>Amin) {
deriv = fft_amp[i]-fft_amp[i-1];
if (deriv > 0) signe=1; else signe = -1;
deriv = fft_amp[i+1]-fft_amp[i];
if ((signe>0)&&(deriv<-epsilon)) {
signe = -1;
interpolRaie(i);
i++;
}
while ((i<N-1)&&(fft_amp[i]>Amin)) {
deriv = fft_amp[i]-fft_amp[i-1];
if ((signe>0)&&(deriv<-epsilon)) {
signe = -1;
interpolRaie(i-1);
}
else if ((signe<0)&&(deriv>epsilon)) signe = 1;
i++;
}
}
else i++;
}
delay(1000);
}
}
}
L'arduino GIGA possède une mémoire RAM de 1 MB. Le programme nécessite 4 tableaux de NSAMPLES flottants 32 bits et un tableau de NSAMPLES/2 flottants 32 bits (fft_amp, dont on pourrait se passer en réutilisant un des autres tableaux). NSAMPLES = 16384 demande donc 295 kOctets, ce qui est très en dessous de 1 Moctets.
Voici le résultat pour le signal triangulaire de fréquence 548 Hz, d'amplitude de crête 1 V, avec un seuil de détection de 0,001 :
Veff = 0.57686
556.400208 +/- 3.0518 Hz, 0.38135472
1644.937378 +/- 3.0518 Hz, 0.07052437
2740.488037 +/- 3.0518 Hz, 0.02763718
3836.063232 +/- 3.0518 Hz, 0.01483563
---------------
Veff = 0.57640
555.821838 +/- 3.0518 Hz, 0.37225315
1644.937866 +/- 3.0518 Hz, 0.07035561
2740.488037 +/- 3.0518 Hz, 0.02761639
3836.064453 +/- 3.0518 Hz, 0.01446916
---------------
Veff = 0.57692
555.868164 +/- 3.0518 Hz, 0.37360767
1644.942139 +/- 3.0518 Hz, 0.06908622
2740.486084 +/- 3.0518 Hz, 0.02828505
3836.063232 +/- 3.0518 Hz, 0.01491842
---------------
Veff = 0.57693
556.410278 +/- 3.0518 Hz, 0.38141829
1644.937378 +/- 3.0518 Hz, 0.07052008
2740.487793 +/- 3.0518 Hz, 0.02766179
3836.063232 +/- 3.0518 Hz, 0.01489828
Les raies de rang 1,3,5 et 7 sont à présent toujours détectées et la précision en fréquence est évidemment meilleure.
Voici le résultat pour un signal carré de même fréquence :
Veff = 0.99564
547.718567 +/- 3.0518 Hz, 0.92566866
1645.328491 +/- 3.0518 Hz, 0.32004991
2331.545410 +/- 3.0518 Hz, 0.01339120
2740.606934 +/- 3.0518 Hz, 0.21357132
3427.124756 +/- 3.0518 Hz, 0.01451366
3836.109863 +/- 3.0518 Hz, 0.16467927
4522.704590 +/- 3.0518 Hz, 0.01542183
4931.658691 +/- 3.0518 Hz, 0.13511100
6027.226074 +/- 3.0518 Hz, 0.11386438
6713.867188 +/- 3.0518 Hz, 0.01587351
7122.800293 +/- 3.0518 Hz, 0.09661487
7531.739258 +/- 3.0518 Hz, 0.01170165
7809.446777 +/- 3.0518 Hz, 0.01537287
8218.376953 +/- 3.0518 Hz, 0.08158597
8627.318359 +/- 3.0518 Hz, 0.01144123
9313.951172 +/- 3.0518 Hz, 0.06810034
10409.522461 +/- 3.0518 Hz, 0.05586080
11505.095703 +/- 3.0518 Hz, 0.04495265
12603.796875 +/- 3.0518 Hz, 0.03467006
13290.413086 +/- 3.0518 Hz, 0.01514487
13699.366211 +/- 3.0518 Hz, 0.03705170
14385.992188 +/- 3.0518 Hz, 0.01692194
14794.938477 +/- 3.0518 Hz, 0.03820525
15481.572266 +/- 3.0518 Hz, 0.01849142
15890.514648 +/- 3.0518 Hz, 0.03848826
16577.152344 +/- 3.0518 Hz, 0.01987889
16986.091797 +/- 3.0518 Hz, 0.03798583
17672.730469 +/- 3.0518 Hz, 0.02098119
18081.669922 +/- 3.0518 Hz, 0.03690580
18768.308594 +/- 3.0518 Hz, 0.02181497
19863.890625 +/- 3.0518 Hz, 0.02219451
20272.824219 +/- 3.0518 Hz, 0.03339931
20959.468750 +/- 3.0518 Hz, 0.02198614
21368.404297 +/- 3.0518 Hz, 0.03092551
22055.046875 +/- 3.0518 Hz, 0.02114552
22463.982422 +/- 3.0518 Hz, 0.02795272
23559.560547 +/- 3.0518 Hz, 0.02457887
24249.287109 +/- 3.0518 Hz, 0.01696633
Les raies détectées vont jusqu'à une fréquence qui correspondrait à la raie de rang 44 environ. Or il y a 37 raies détectées et en théorie les raies de ce signal sont de rangs impairs donc certaines raies détectées sont en fait des raies de repliement. Pour ce type de signal, il est prudent de monter le seuil de détection. Voici le résultat pour un seuil de 0,05 :
Veff = 0.99585
547.970459 +/- 3.0518 Hz, 0.93633860
1645.322144 +/- 3.0518 Hz, 0.32124394
3836.093506 +/- 3.0518 Hz, 0.16837732
4931.663574 +/- 3.0518 Hz, 0.13383666
6027.221680 +/- 3.0518 Hz, 0.11499963
7122.792969 +/- 3.0518 Hz, 0.09463871
8218.374023 +/- 3.0518 Hz, 0.08086333
9313.951172 +/- 3.0518 Hz, 0.06808086
10409.521484 +/- 3.0518 Hz, 0.05530550
La dernière raie détectée est celle de rang 19 mais la raie de rang 5 n'est pas détectée.
