Convertisseur continu-continu élévateur
1. Introduction
Ce document étudie le fonctionnement d'un convertisseur continu-continu élévateur de tension (ou convertisseur DC-DC boost). L'étude théorique et les simulations numériques sont faites en prenant en compte la résistance interne de la bobine afin de déterminer correctement l'élévation de tension.
La réalisation d'un convertisseur piloté par Arduino est aussi présentée, avec une régulation de la tension par un correcteur proportionnel-intégral.
La simulation Convertisseur DC-DC élévateur met en œuvre les méthodes de calcul présentés dans ce document.
La conversion continu-continu avec élévation est couramment utilisée pour augmenter la tension fournie par un accumulateur, par exemple pour obtenir une tension de 5 V à partir d'un accumulateur Li-Po de 3,7 V. La régénération d'énergie dans une machine synchrone de type BLDC via le pont de transistors fait aussi intervenir une conversion continu-continu avec élévation.
2. Étude théorique
2.a. Schéma du convertisseur
Le convertisseur continu-continu élévateur [1], dans sa version la plus simple (convertisseur non synchrone), comporte un transistor MOSFET (modélisé par une diode en parallèle avec un interrupteur) et une diode :
Figure pleine pageVe est la tension d'entrée, délivrée par la source d'énergie (tension constante). R est la résistance de charge. Vs est la tension de sortie, c'est-à-dire la tension aux bornes de la résistance de charge. Dans cette version, l'énergie ne peut circuler que de la source vers la charge, ce qui est évidemment le but recherché si la charge est purement résistive. Si la charge peut développer une force électromotrice (dans ce cas elle n'est pas équivalente à une simple résistance), l'énergie ne peut pas revenir vers la source. Autrement dit, ce convertisseur est unidirectionnel (non réversible).
Nous considérons le convertisseur suivant (convertisseur synchrone), comportant deux transistors MOSFET :
Figure pleine pageLa diode est remplacée par un transistor, ce qui permet à un courant positif d'aller de la charge vers la source. On reconnaît dans ce circuit un convertisseur abaisseur (DC-DC buck converter) utilisé à l'envers. Ce convertisseur est donc bidirectionnel, une propriété exploitée dans le pilotage des machines synchrones. Il s'agit en conséquence d'un convertisseur permettant la régénération d'énergie dans le cas où la source est un accumulateur électrochimique. Par ailleurs, ce convertisseur a un meilleur rendement énergétique (moins de pertes dans la résistance de la bobine et dans les résistances des transistors) lorsque l'élévation de tension est grande.
Les interrupteurs sont commutés avec une période de découpage T. Le rapport cyclique est : l'état 1 a une durée , l'état 2 a une durée . Remarquons que la définition contraire du rapport cyclique est plus souvent employée. Nous préférons employer cette définition du rapport cyclique car c'est celle qui est utilisée pour le convertisseur abaisseur (obtenu par échange de l'entrée et de la sortie). Dans la version plus simple comportant un seul transistor et une diode, le transistor est passant pendant .
Chacun des deux transistors MOSFET est modélisé par un interrupteur. Lorsque la grille n'est pas polarisée, l'interrupteur est ouvert mais un courant peut circuler de la source vers le drain si le potentiel de la source et supérieur à celui du drain (la caractéristique dans ce sens est à peu près celle d'une diode). Lorsque la grille est polarisée (par rapport à la source), l'interrupteur est fermé : un courant peut circuler du drain vers la source si VD>VS mais aussi de la source vers le drain si VD<VS. On a alors une résistance d'environ 1 ohm entre le drain et la source mais beaucoup plus faible en inverse lorsque la tension de seuil est dépassée. Voici la caractéristique VDS=f(ID) pour les deux états du transistor :
Figure pleine pageLorsque la tension GS est supérieure à 10 V, le transistor est passant : nous avons seulement représenté la zone linéaire à faible tension drain-source, où le courant de drain est proportionnel à la tension drain-source, car c'est cette région qui est effectivement utilisée. La résistance drain-source RDSON dans la zone linéaire est inférieure à 1 ohm. On la négligera dans le modèle, bien qu'elle ne soit pas nécessairement négligeable devant la résistance de la bobine. Lorsque la tension drain-source est en dessous de -0,7 V, la résistance drain-source (en inverse) est encore plus faible.
Même si la réversibilité du convertisseur n'est pas recherchée, il y a un intérêt à remplacer la diode du convertisseur non synchrone par un transistor MOSFET (convertisseur synchrone) : la diode intrinsèque du transistor conduit le courant dès que VD<VS contrairement à une diode qui ne conduit qu'à partir d'un certain seuil de tension. Le convertisseur comportant un transistor MOSFET à la place de la diode est qualifié de synhrone justement parce que le passage du courant dans le commutateur 1 se fait de manière synchrone avec l'ouverture de K2. Expérimentalement, le convertisseur synchrone se comporte comme le convertisseur non synchrone si le transistor 1 est maintenu ouvert en permanence.
Si l'on modélise la diode équivalente par une diode idéale, la résistance drain-source est nulle dès que VD<VS, quel que soit l'état du transistor. On obtient alors le comportement idéalisé suivant :
Figure pleine pageSoit i(t) l'intensité du courant qui traverse la bobine, définie dans le sens sortant par rapport à la source de tension Ve. Considérons l'état 1, dont la durée est . La diode du transistor du bas n'est jamais passante puisque le drain de ce transistor est au potentiel Vs, qui est positif. En conséquence, le courant i(t) traverse le transistor du haut et parvient à la sortie. Voici les équations différentielles dans l'état 1 :
On obtient l'équation différentielle suivante pour la tension en sortie :
On se place dans le cas où la tension d'entrée est constante. On posera donc , où est une tension constante. Il nous faut deux conditions initiales pour l'état 1. La première est fournie par la continuité de la tension aux bornes de la capacité, qui implique la continuité de . La seconde est fournie par la continuité du courant dans L, c'est-à-dire la continuité de i(t). Cette condition est difficile à traduire sur Vs(t) mais elle devient aisé à prendre en compte si on s'en tient au système du premier ordre pour Vs(t) et i(t). Il est donc plus simple de résoudre le système plutôt que l'équation de degré 2. Ce choix étant fait, il y a deux manières de résoudre le système : on obtient les expressions analytiques exactes de Vs(t) et i(t) ou bien on fait une résolution numérique (dans ce cas, le choix du système de degré 1 est impératif). Voici l'écriture explicite du système :
Pour l'état 2, dont la durée est , on obtient les deux équations suivantes :
Dans l'état 2, aucun courant ne traverse le transistor 1 puisque sa diode est polarisée en inverse. Pour mieux comprendre les deux états, voici un schéma dans lequel les diodes sont remplacées par leur schéma équivalent (interrupteurs) :
Figure pleine pageDans l'état 1, le transistor 1 peut faire passer un courant positif dans la diode (flèche rouge) mais aussi négatif à travers la résistance drain source. Le courant i(t) pendant l'état 1 parvient donc au bloc RC quel que soit son signe. Si l'on remplace ce transistor par une simple diode, i(t) ne peut pas être négatif dans l'état 1. Dans l'état 2, le drain du transistor 1 est au potentiel Vs alors que sa source est presque à la masse. En conséquence, aucun courant ne traverse ce transistor via sa diode pendant l'état 2. Le bloc RC reçoit un courant seulement pendant l'état 1 et ce courant peut être négatif.
D'un point de vue énergétique, l'auto-inductance accumule de l'énergie pendant la phase 2 (i(t) augmente) puis cette énergie est transférée vers la sortie pendant l'état 1 (i(t) décroît).
2.b. Résolution numérique
Le système différentiel est résolu entièrement numériquement. L'avantage de cette méthode est qu'elle peut s'adapter sans difficultés au cas où la tension Ve n'est pas constante.
La fonction suivante effectue la résolution numérique sur une période du découpage :
import numpy as np
from matplotlib.pyplot import *
from scipy.integrate import odeint
def periode(L,r,C,R,T,alpha,V0,t0,i0,Vs0,N=100):
def systeme1(Y,t):
dY0 = V0/L-r/L*Y[0]-Y[1]/L
dY1 = -1/(R*C)*Y[1]+Y[0]/C
return [dY0,dY1]
temps1 = np.linspace(t0,t0+T*alpha,N//2)
sol = odeint(systeme1,[i0,Vs0],temps1,rtol=1e-4,atol=1e-4)
i1 = sol[:,0]
Vs1 = sol[:,1]
def systeme2(Y,t):
dY0 = V0/L-r/L*Y[0]
dY1 = -1/(R*C)*Y[1]
return [dY0,dY1]
temps2 = np.linspace(t0+T*alpha,t0+T,N//2)
sol = odeint(systeme2,[i1[-1],Vs1[-1]],temps2,rtol=1e-4,atol=1e-4)
i2 = sol[:,0]
Vs2 = sol[:,1]
temps = np.concatenate((temps1,temps2))
i = np.concatenate((i1,i2))
Vs = np.concatenate((Vs1,Vs2))
return temps,i,Vs
La fonction suivante effectue le calcul pour P périodes :
def simulation(L,r,C,R,T,alpha,V0,t0,i0,Vs0,P,N=100):
tab_temps = np.zeros(N*P)
tab_i = np.zeros(N*P)
tab_Vs = np.zeros(N*P)
k = 0
for p in range(P):
temps,i,Vs = periode(L,r,C,R,T,alpha,V0,t0,i0,Vs0,N)
i0 = i[-1]
Vs0 = Vs[-1]
t0 += T
tab_temps[k:k+N] = temps
tab_i[k:k+N] = i
tab_Vs[k:k+N] = Vs
k += N
return tab_temps,tab_i,tab_Vs
L = 0.5e-3
r = 1
C = 2000e-6
R = 100
V0 = 1
alpha = 0.5
i0 = 0
Vs0 = 0
t0 = 0
T = 1e-4
P = 3000
temps,i,Vs = simulation(L,r,C,R,T,alpha,V0,t0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,Vs)
grid()
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
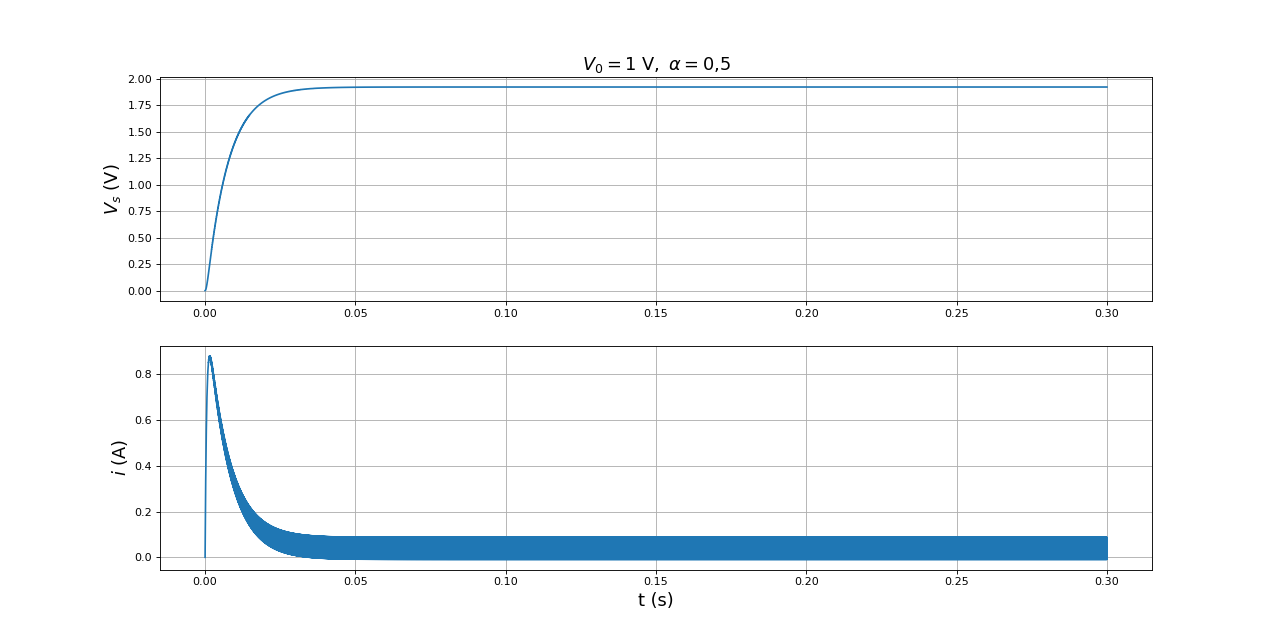 fig1.pdf
fig1.pdf
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\ {\rm V},\ \alpha=0{,}5$",fontsize=16)
plot(temps,Vs)
xlim(0.25,0.251)
ylim(0,2)
grid()
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
xlim(0.25,0.251)
ylim(-0.2,0.2)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
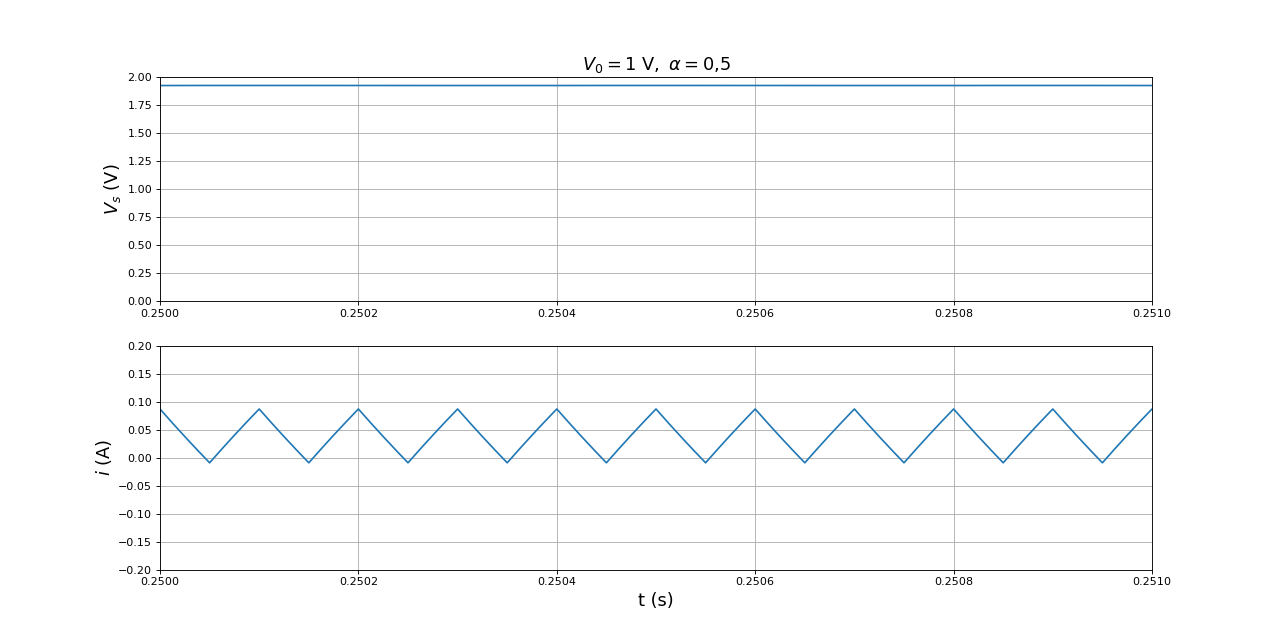 fig2.pdf
fig2.pdf
En régime permanent, la tension Vs est quasi constante (grâce au filtrage RC) et supérieure à la tension d'entrée. Le courant présente de fortes variations. Pour ces valeurs de R et du rapport cyclique, le courant est négatif à certains moments du cycle (à la fin de l'état 1 et au début de l'état 2). Lors du démarrage à partir d'un courant nul dans la bobine, ce courant passe par une valeur maximale relativement grande. Il faut que la source soit capable de fournir ce courant. Dans le cas contraire (par exemple si la source est un accumulateur électrochimique), la courbe de démarrage sera modifiée (le régime permanent arrivera plus tard). Un appel de courant important peut aussi se produire en présence de régulation lorsque la charge est soudainement modifiée.
Voici une simulation avec un rapport cyclique plus petit (rappelons qu'il s'agit du rapport cyclique de fermeture du transistor 1).
alpha = 0.2
i0 = 0
Vs0 = 0
t0 = 0
T = 1e-4
P = 7000
temps,i,Vs = simulation(L,r,C,R,T,alpha,V0,t0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\ {\rm V},\ \alpha=0{,}2$",fontsize=16)
plot(temps,Vs)
grid()
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
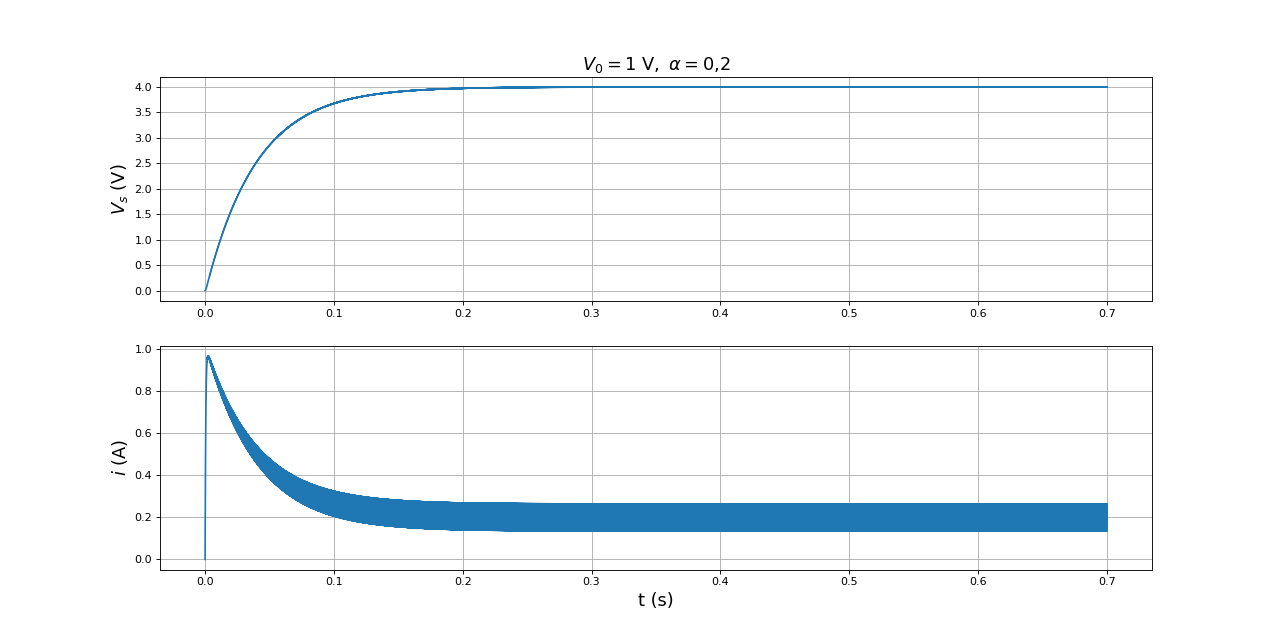 fig3.pdf
fig3.pdf
La tension en sortie est plus élevée lorsque le rapport cyclique est plus bas. Cette fois-ci, le courant est toujours positif. Voici un détail lorsque le régime permanent est atteint :
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\ {\rm V},\ \alpha=0{,}2$",fontsize=16)
plot(temps,Vs)
xlim(0.65,0.651)
ylim(3.8,4.2)
grid()
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
xlim(0.65,0.651)
ylim(0,0.4)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
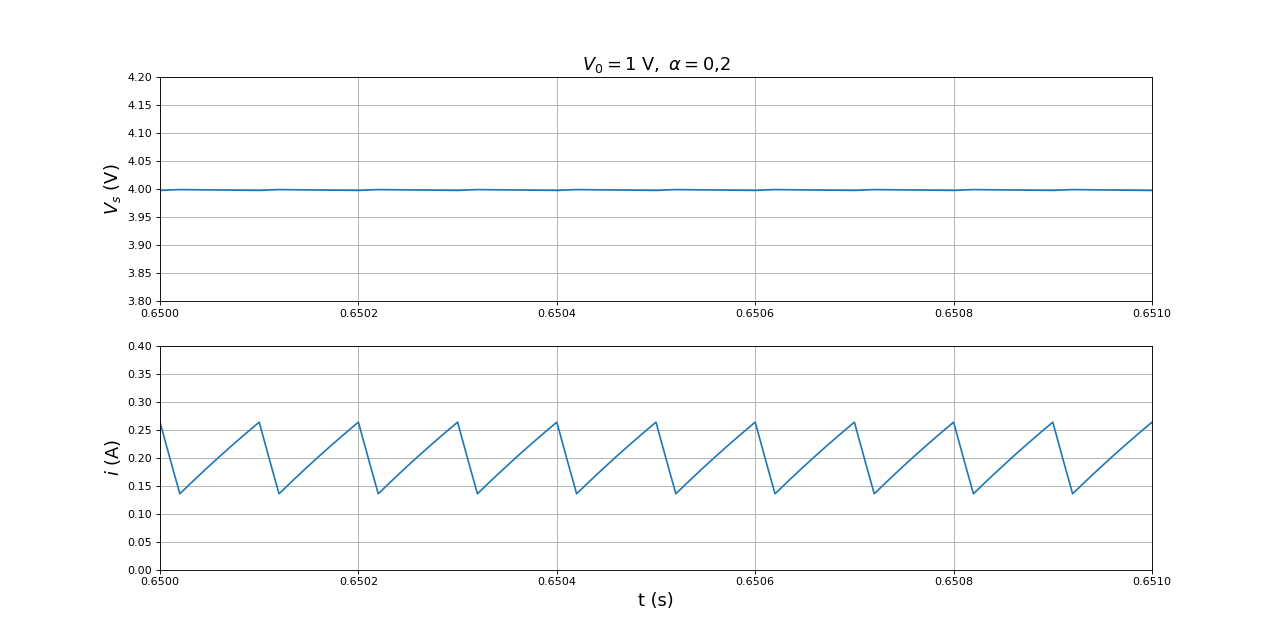 fig4.pdf
fig4.pdf
Pendant l'état 2, le courant augmente (l'énergie stockée dans L augmente). Pendant l'état 1, le courant diminue (l'excédant d'énergie stockée est transférée vers la sortie).
2.c. Résolution semi-analytique
Pour chacun des deux états, le système différentiel peut être résolu analytiquement.
Reprenons le système différentiel pour l'état 1 :
Il s'écrit sous la forme matricielle suivante :
La solution particulière constante Yp est obtenue par résolution du système :
from numpy.linalg import eig,det
def solve(A,B):
detA = det(A)
x1 = det(np.array([[B[0],A[0,1]],[B[1],A[1,1]]]))/detA
x2 = det(np.array([[A[0,0],B[0]],[A[1,0],B[1]]]))/detA
return [x1,x2]
L = 500e-6
r = 51
C = 2000e-6
R = 100
V0 = 5
A = np.array([[-r/L,-1/L],[1/C,-1/(R*C)]])
B = np.array([V0/L,0])
Yp = solve(A,-B)
print(Yp) --> [0.033112582781456956, 3.311258278145697]
La solution générale de l'équation sans second membre, c'est-à-dire , est recherchée sous la forme , ce qui conduit à l'équation . Il s'agit donc de rechercher les valeurs propres et vecteurs propres complexes de la matrice A. Supposons qu'elle soit diagonalisable. La solution générale du système sans second membre s'écrit :
où sont les deux valeurs propres et des vecteurs propres correspondants.
La solution générale du système complet s'obtient en ajoutant la solution particulière constante :
Les constantes c1 et c2 sont obtenues avec la condition de continuité de i(t) et de Vs(t) à l'instant t=t0 :
Pour résoudre ce système, on pose :
Le système linéaire à résoudre est alors : . Afin d'éviter un argument de l'exponentielle trop petit lorsque t devient grand, le calcul de la solution pour chaque période de découpage est fait avec un temps initialisé à zéro au début. Le temps t0 est donc soit égal à 0 (début de l'état 1) soit égal à (début de l'état 2).
Voici la diagonalisation de A :
valProp, vectProp = eig(A)
V1 = vectProp[:,0]
V2 = vectProp[:,1]
lamb1 = valProp[0]
lamb2 = valProp[1]
print((lamb1,lamb2)) --> (-101990.19465518126, -14.805344818736353)
Pour l'état 2, on peut appliquer la même méthode mais les deux équations différentielles du système sont en fait indépendantes :
Dans ce cas, la matrice A est déjà diagonale donc on a immédiatement les valeurs propres et les vecteurs propres.
Bien que la fonction solve de scipy.linalg permette de résoudre un système linéaire (par une méthode d'élimination), voici une implémentation de cette fonction valable pour un système de deux équations, utilisant la règle de Cramer :
def det(A):
return A[0,0]*A[1,1]-A[0,1]*A[1,0]
def solve(A,B):
detA = det(A)
M = A.copy()
M[0,0] = B[0]
M[1,0] = B[1]
x1 = det(M)/detA
M = A.copy()
M[0,1] = B[0]
M[1,1] = B[1]
x2 = det(M)/detA
return np.array([x1,x2])
Voici également une implémentation de la fonction de calcul des valeurs et vecteurs propres pour une matrice réelle 2x2 (les coefficients non diagonaux sont supposés soit tous les deux nuls soit tous les deux non nuls) :
def eig(A):
if A[0,1]==0 and A[1,0]==0:
valProp = np.array([A[0,0],A[1,1]])
vectProp = np.array([[1,0],[0,1]])
return valProp,vectProp
b = -A[0,0]-A[1,1]
c = A[0,0]*A[1,1]-A[0,1]*A[1,0]
delta = b**2-4*c
sq = np.sqrt(delta+1j*0)
lambda1 = (-b+sq)/2
lambda2 = (-b-sq)/2
valProp = np.array([lambda1,lambda2])
vectProp = np.array([[1,1],[(lambda1-A[0,0])/A[0,1],(lambda2-A[0,0])/A[0,1]]])
return valProp,vectProp
Nous pouvons à présent écrire une fonction qui fait le calcul sur une période de découpage. Dans les paramètres de cette fonction, nous devons ajouter les valeurs propres et vecteurs propres pour l'état 1 car ceux-ci doivent être calculés une seule fois, au début de la boucle de calcul. Il en est de même pour les solutions particulières.
La fonction suivante détermine la solution à partir des valeurs et vecteurs propres et de la solution particulière constante, pour une condition initiale donnée :
def solution(valProp,vectProp,Yp,t0,t1,i0,Vs0,N):
V1 = vectProp[:,0]
V2 = vectProp[:,1]
lamb1 = valProp[0]
lamb2 = valProp[1]
e1 = np.exp(lamb1*t0)
e2 = np.exp(lamb2*t0)
D = np.array([[e1*V1[0],e2*V2[0]],[e1*V1[1],e2*V2[1]]])
E = np.array([i0-Yp[0],Vs0-Yp[1]])
C = solve(D,E)
t = np.linspace(t0,t1,N)
a1 = C[0]*np.exp(lamb1*t)
a2 = C[1]*np.exp(lamb2*t)
Y0 = a1*V1[0]+a2*V2[0]+Yp[0]
Y1 = a1*V1[1]+a2*V2[1]+Yp[1]
return t,[Y0,Y1]
La fonction suivante effectue le calcul de i et de Vs sur une période de découpage, en calculant la solution de l'état 1 puis celle de l'état 2 :
def periode(valProp1,vectProp1,valProp2,vectProp2,Yp1,Yp2,T,alpha,V0,t,i0,Vs0,N=100):
temps1,Y1 = solution(valProp1,vectProp1,Yp1,0,alpha*T,i0,Vs0,int(alpha*N))
i1 = Y1[0]
Vs1 = Y1[1]
i0 = i1[-1]
Vs0 = Vs1[-1]
temps2,Y2 = solution(valProp2,vectProp2,Yp2,alpha*T,T,i0,Vs0,N-int(alpha*N))
i2 = Y2[0]
Vs2 = Y2[1]
temps = np.concatenate((t+temps1,t+temps2))
i = np.concatenate((i1,i2))
Vs = np.concatenate((Vs1,Vs2))
return temps,i,Vs
La fonction suivante effectue le calcul complet pour un nombre P de périodes de découpage :
def simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P,N=100):
tab_temps = np.zeros(N*P)
tab_i = np.zeros(N*P)
tab_Vs = np.zeros(N*P)
A1 = np.array([[-r/L,-1/L],[1/C,-1/(R*C)]])
B1 = np.array([V0/L,0])
Yp1 = solve(A1,-B1)
valProp1, vectProp1 = eig(A1)
A2 = np.array([[-r/L,0],[0,-1/(R*C)]])
B2 = np.array([V0/L,0])
Yp2 = solve(A2,-B2)
valProp2, vectProp2 = eig(A2)
k = 0
t = 0
for p in range(P):
temps,i,Vs = periode(valProp1,vectProp1,valProp2,vectProp2,Yp1,Yp2,T,alpha,V0,t,i0,Vs0,N)
i0 = i[-1]
Vs0 = Vs[-1]
t += T
tab_temps[k:k+N] = temps
tab_i[k:k+N] = i
tab_Vs[k:k+N] = Vs
k += N
return tab_temps,tab_i,tab_Vs
L = 0.5e-3
r = 1
C = 2000e-6
R = 100
V0 = 1
alpha = 0.5
i0 = 0
Vs0 = 0
T = 1e-4
P = 3000
temps,i,Vs = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\ {\rm V},\alpha=0{,}5$",fontsize=16)
plot(temps,Vs)
ylim(0,5)
grid()
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
ylim(-1,1)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
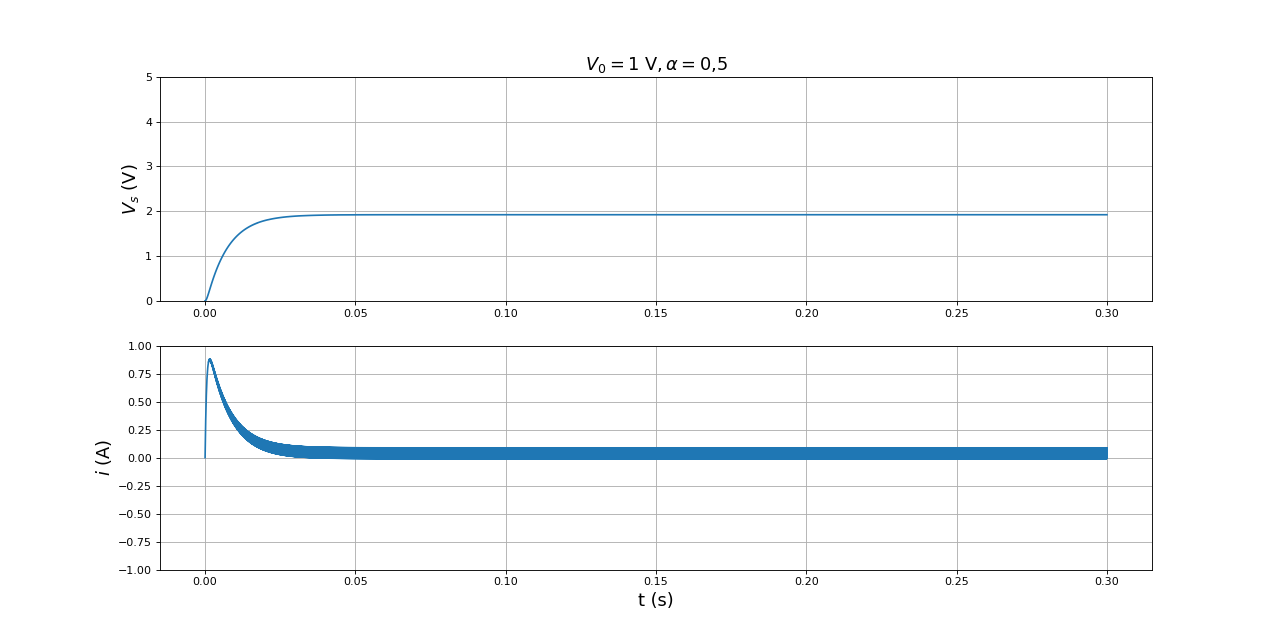 fig5.pdf
fig5.pdf
Voici la simulation pour un rapport cyclique plus bas :
alpha = 0.2
i0 = 0
Vs0 = 0
T = 1e-4
P = 10000
temps,i,Vs = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\ {\rm V},\alpha=0{,}2$",fontsize=16)
plot(temps,Vs)
ylim(0,5)
grid()
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
ylim(-1,1)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
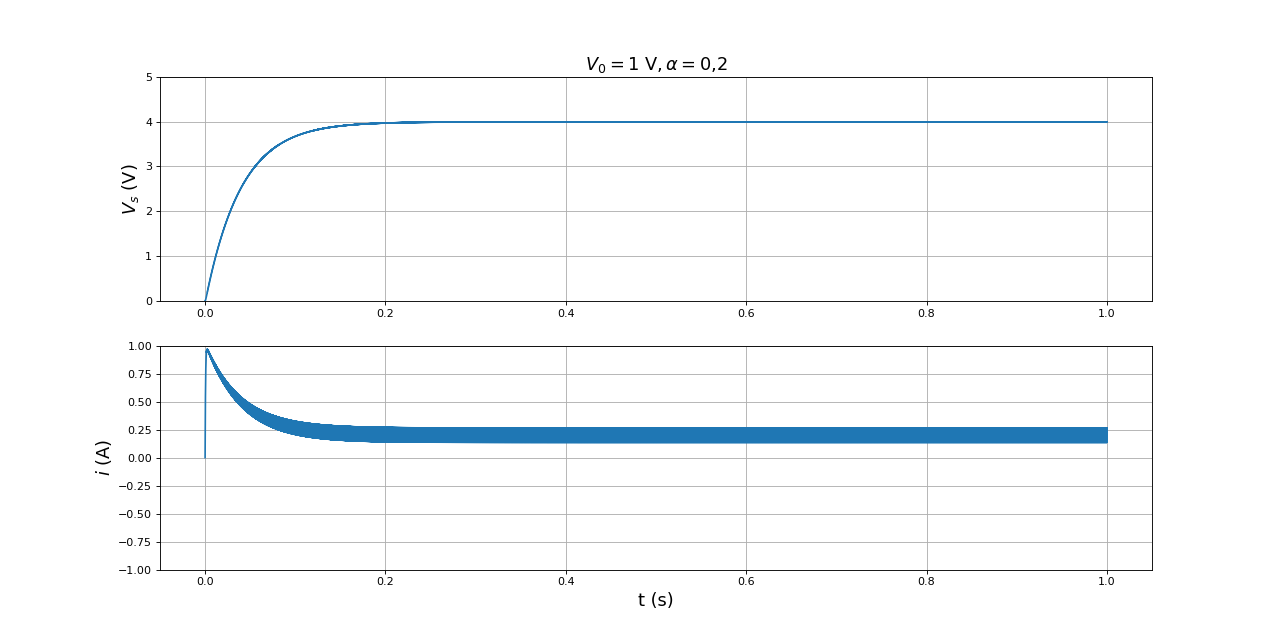 fig6.pdf
fig6.pdf
La tension en sortie est plus grande (la valeur moyenne du courant aussi).
Voici l'effet d'une augmentation soudaine du rapport cyclique :
alpha = 0.7
i0 = i[-1]
Vs0 = Vs[-1]
t0 = temps[-1]
temps1,i1,Vs1 = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
temps = np.concatenate((temps,t0+temps1))
i = np.concatenate((i,i1))
Vs = np.concatenate((Vs,Vs1))
figure(figsize=(16,8))
subplot(211)
title(r"$\alpha=0{,}2\rightarrow 0{,}7$",fontsize=16)
plot(temps,Vs)
ylim(0,5)
grid()
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
ylim(-1,1)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
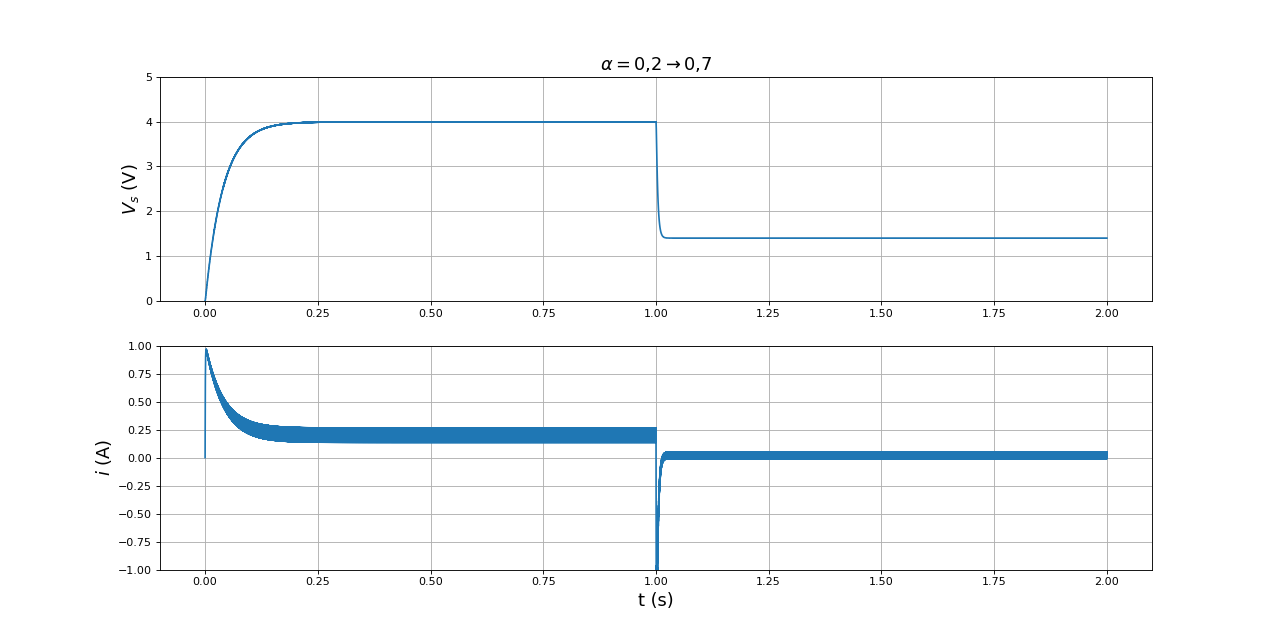 fig7.pdf
fig7.pdf
Il y a un courant i négatif transitoire juste après l'augmentation du rapport cyclique. Une partie de l'énergie stockée dans le condensateur revient vers la source (à condition que celle-ci puisse la recevoir). Si une alimentation de laboratoire est utilisée, celle-ci ne peut pas recevoir un courant positif de manière permanente mais le condensateur placée en sa sortie peut éventuellement absorber ce courant transitoire. Pour éviter ce courant positive vers la source, il suffit de remplacer le transistor 1 par une diode (convertisseur non synchrone) ou bien de laisser le transistor 1 en permanence à l'état ouvert (grille au même potentiel que la source ou plus bas). Si la source est un générateur électrochimique, le fonctionnement réversible du convertisseur permet d'effectuer une régénération : lorsque le rapport cyclique augmente, c'est-à-dire lorsqu'on souhaite abaisser la tension en sortie ou lorsque le demande de courant de la charge diminue, la source peut recevoir de l'énergie. La régénération est en particulier utilisée dans la commande des machines synchrones. Dans le cas présent, l'énergie qui revient vers la source vient du condensateur. Dans le cas d'un moteur, celle-ci provient du moteur lui-même, via la force électromotrice qu'il développe (mais un moteur est plutôt alimenté par un convertisseur abaisseur).
Voici une simulation avec une résistance de charge plus grande :
L = 0.5e-3
r = 1
C = 2000e-6
R = 500
V0 = 1
alpha = 0.5
i0 = 0
Vs0 = 0
T = 1e-4
P = 3000
temps,i,Vs = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\ {\rm V},\alpha=0{,}5$",fontsize=16)
plot(temps,Vs)
ylim(0,5)
grid()
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
ylim(-1,1)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
 fig8.pdf
fig8.pdf
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\ {\rm V},\alpha=0{,}5$",fontsize=16)
plot(temps,Vs)
ylim(0,5)
xlim(0.25,0.251)
grid()
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
ylim(-0.25,0.25)
xlim(0.25,0.251)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
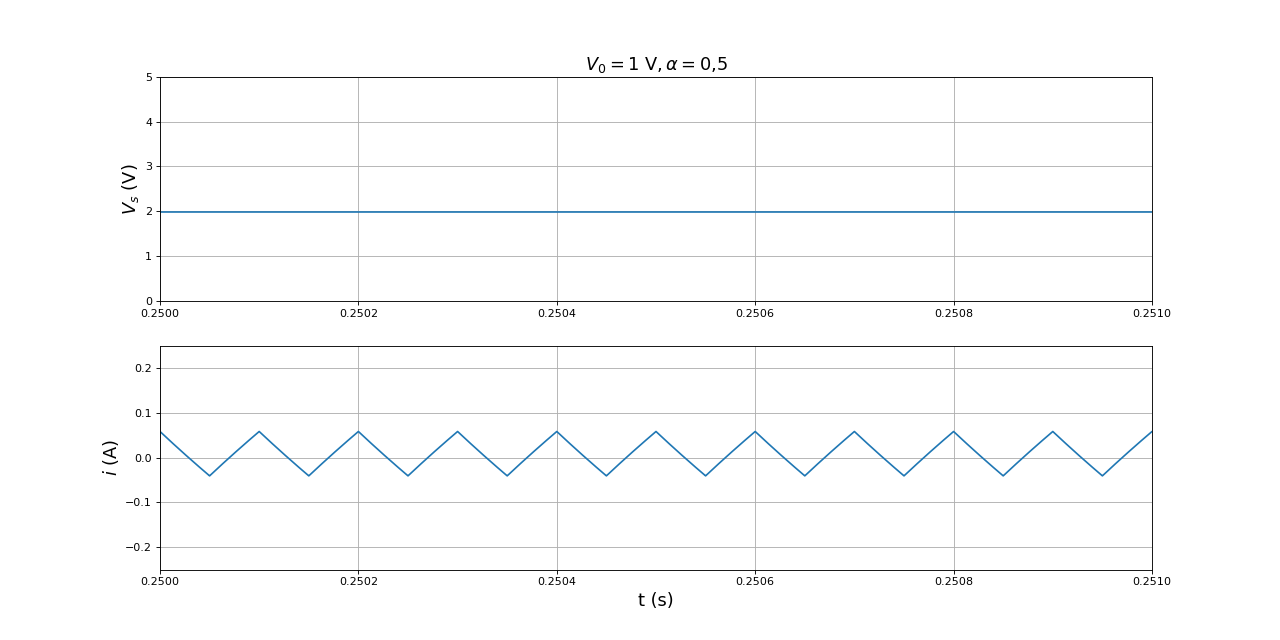 fig9.pdf
fig9.pdf
Dans ce cas, le courant i en régime permanent est négatif pendant une partie du cycle (la fin de l'état 2 et le début de l'état 1). Dans cette situation, le convertisseur synchrone (avec un transistor MOSFET en 1) se comporte différemment du convertisseur non synchrone (avec une diode en 1) puisque pour ce dernier le courant ne peut être négatif.
2.d. Régime permanent
On suppose que le filtrage en sortie est assez efficace pour que la tension Vs soit quasi constante, comme pour la simulation présentée ci-dessus. L'équation différentielle pour l'intensité du courant est :
À la différence du cas général traité par la simulation, la tension Vs est ici constante. La solution est
Les constantes A et B s'obtiennent avec la continuité du courant : et :
Pour simplifier les expressions, posons :
On a :
Remarquons que A>0 et B<0. L'intensité du courant est donc décroissante dans l'état 1 et croissante dans l'état 2. En pratique, la résistance de la bobine est assez faible pour que donc :
Si , les fonctions i1(t) et i2(t) sont affines et on obtient une expression simple de l'amplitude d'ondulation du courant :
L'amplitude de variation du courant est donc pratiquement indépendante de r et elle est maximale pour .
La valeur moyenne de l'intensité du courant s'écrit :
La moyenne de la dérivée par rapport au temps de l'intensité du courant s'écrit :
Après insertion des expressions de A et B, on obtient :
La moyenne de la tension aux bornes de L est donc nulle.
La moyenne de l'équation différentielle s'écrit :
Les deux termes de cette égalité sont formellement égaux, donc l'équation différentielle vérifiée par i(t) ne suffit pas. Voyons l'équation différentielle pour Vs(t) dans l'état 1 :
Bien que Vs soit par hypothèse constante, nous ne pouvons pas annuler la dérivée dans cette équation puisque cela impliquerait que i1(t) soit constant. En toute rigueur, cette équation est donc incompatible avec l'hypothèse Vs constante (en réalité elle n'est pas constante mais ondule faiblement). Nous pouvons cependant considérer le courant moyen dans la charge, qui est égal à Vs/R (constant par hypothèse). Le courant moyen dans C est nul (puisque la tension à ses bornes est constante). Il s'en suit que le courant moyen dans la charge est égal au courant moyen passant dans le transistor du haut en direction du bloc RC. Or ce courant est égal à i1 dans l'état 1 et il est nul dans l'état 2. Écrire l'égalité des courants moyens revient à écrire la conservation de la charge électrique : la quantité de charge reçue par la résistance R pendant un cycle est égale à la quantité de charge apportée par le courant i1(t) pendant l'état 1 (la charge du condensateur ne change pas). On a donc :
ce qui conduit à :
Si on obtient :
Si de plus la résistance de la bobine est nulle, la tension de sortie s'écrit :
def tensionSortie(L,r,C,R,T,alpha,V0):
x = np.exp(-r*T/L)
y = np.exp(-r*alpha*T/L)
return R/r*alpha*V0/(1+R/r*alpha-R/r*L/(r*T)*(1-x/y)*(1-y)/(1-x))
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
Voici la tension de sortie pour les constantes de la simulation précédente :
print(Vsortie) --> 1.9824896584219374
et, pour comparaison, la tension de sortie en régime permanent obtenue avec cette simulation :
print(np.mean(Vs[int(len(Vs)*0.9):-1])) --> 1.9823859697073398
Nous pouvons tracer l'intensité du courant en fonction du temps :
def courant(L,r,C,R,T,alpha,V0,N=100):
x = np.exp(-r*T/L)
y = np.exp(-r*alpha*T/L)
Vs = tensionSortie(L,r,C,R,T,alpha,V0)
A = Vs/r*(1-x/y)/(1-x)
B = Vs/r*(1-1/y)/(1-x)
t1 = np.linspace(0,alpha*T,N)
i1 = A*np.exp(-r*t1/L)+(V0-Vs)/r
t2 = np.linspace(alpha*T,T,N)
i2 = B*np.exp(-r*t2/L)+V0/r
return np.concatenate((t1,t2)),np.concatenate((i1,i2))
L = 0.5e-3
r = 1
C = 2000e-6
R = 100
V0 = 1
alpha = 0.5
T = 1e-4
t,i = courant(L,r,C,R,T,alpha,V0)
figure()
plot(t,i)
grid()
ylim(-1,1)
xlabel("t (s)",fontsize=16)
ylabel("i (A)",fontsize=16)
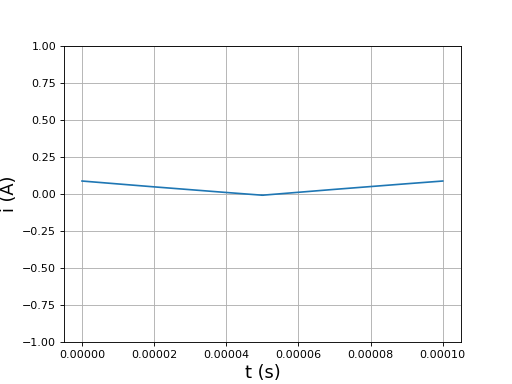 fig10.pdf
fig10.pdf
Dans l'état 1, le courant décroît car Vs>V0. Dans l'état 2, le courant croît car seule la tension V0 est appliquée à la bobine.
La résistance de charge R et la résistance de la bobine r ont une influence sur la tension Vs :
R = np.linspace(1,1000,100)
figure()
r = 10
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(R,Vsortie/V0,label=r"$r=10\,\rm\Omega$")
r = 5
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(R,Vsortie/V0,label=r"$r=5\,\rm\Omega$")
r = 1
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(R,Vsortie/V0,label=r"$r=1\,\rm\Omega$")
grid()
ylim(0,2)
legend(loc="lower right")
xlabel(r"$R\ (\rm\Omega)$",fontsize=16)
ylabel(r"$V_s/V_0$",fontsize=16)
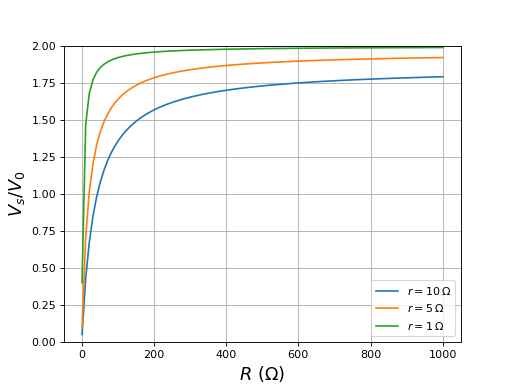 fig11.pdf
fig11.pdf
Voici la tension de sortie en fonction du rapport cyclique :
alpha = np.linspace(0.01,1,500)
figure()
R = 1000
r = 1
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie/V0,label=r"$R=1000\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
R = 100
r = 1
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie/V0,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
R = 10
r = 1
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie/V0,label=r"$R=10\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
grid()
xlim(0,1)
ylim(0,20)
legend(loc="upper right")
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$V_s/V_0$",fontsize=16)
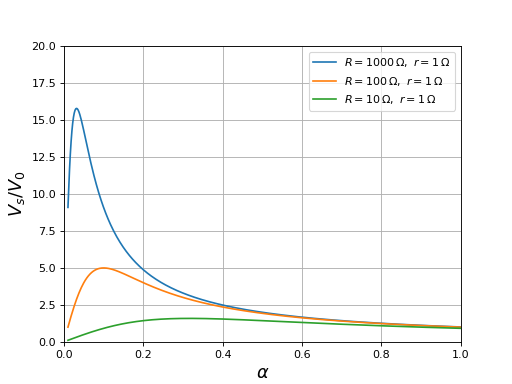 fig12.pdf
fig12.pdf
Ces courbes montrent que l'élévation de tension maximale est d'autant plus grande que la résistance de charge est grande. De plus, le rapport cyclique qui maximise l'élévation de tension dépend de la résistance de charge.
Voici la moyenne de l'intensité du courant en fonction du rapport cyclique :
Imoy1,Imoy2,Imoy3 = [],[],[]
Ic1,Ic2,Ic3 = [],[],[]
for a in alpha:
R = 1000
t,i = courant(L,r,C,R,T,a,V0,N=100)
Vs = tensionSortie(L,r,C,R,T,a,V0)
Imoy1.append(i.mean())
Ic1.append(Vs/R)
R = 100
t,i = courant(L,r,C,R,T,a,V0,N=100)
Vs = tensionSortie(L,r,C,R,T,a,V0)
Imoy2.append(i.mean())
Ic2.append(Vs/R)
R = 10
t,i = courant(L,r,C,R,T,a,V0,N=100)
Vs = tensionSortie(L,r,C,R,T,a,V0)
Imoy3.append(i.mean())
Ic3.append(Vs/R)
figure()
plot(alpha,Imoy1,"r",label=r"$R=1000\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
plot(alpha,Ic1,"r--")
plot(alpha,Imoy2,"b",label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
plot(alpha,Ic2,"b--")
plot(alpha,Imoy3,"g",label=r"$R=10\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
plot(alpha,Ic3,"g--")
grid()
legend(loc="upper right")
xlabel(r"$\alpha$",fontsize=16)
ylabel("I (A)",fontsize=16)
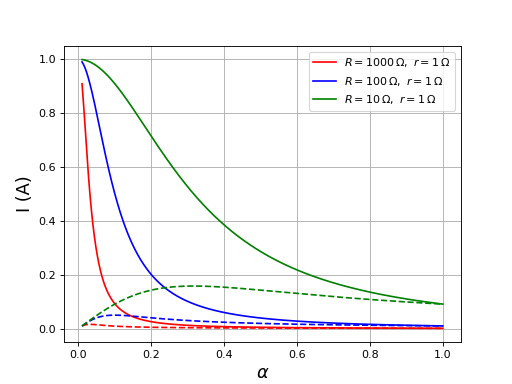 fig13.pdf
fig13.pdf
La moyenne de i est tracée en trait plein, le courant moyen dans la charge est tracé en traits interrompus. Lorsque le rapport cyclique est faible, le courant fourni par la source est très élevé, beaucoup plus que le courant consommé par la charge. Lorsque le rapport cyclique décroît, le courant fourni par la source continu à augmenter alors que celui passant dans la charge diminue. En pratique, on opère dans le domaine de rapports cycliques où la tension en sortie est une fonction décroissante mais, dans la partie inférieure de ce domaine, le courant fourni par la source est grand. Par exemple, pour R=100 Ω, un rapport cyclique de 0,2 conduit à un courant moyen de source de 1 A alors que la tension en sortie vaut :
Vs = tensionSortie(L,r,C,R,T,0.2,V0)
print(Vs) --> 1.4277019752669564
La puissance consommée par la charge est 0,51 W alors que la source fournie 5 W.
Voici le rapport de la puissance reçue par la charge sur la puissance fournie par la source (rendement énergétique) :
rP1,rP2,rP3 = [],[],[]
for a in alpha:
R = 1000
t,i = courant(L,r,C,R,T,a,V0,N=100)
Vs = tensionSortie(L,r,C,R,T,a,V0)
rP1.append(Vs**2/R/(V0*i.mean()))
R = 100
t,i = courant(L,r,C,R,T,a,V0,N=100)
Vs = tensionSortie(L,r,C,R,T,a,V0)
rP2.append(Vs**2/R/(V0*i.mean()))
R = 10
t,i = courant(L,r,C,R,T,a,V0,N=100)
Vs = tensionSortie(L,r,C,R,T,a,V0)
rP3.append(Vs**2/R/(V0*i.mean()))
figure()
plot(alpha,rP1,"r",label=r"$R=1000\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
plot(alpha,rP2,"b",label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
plot(alpha,rP3,"g",label=r"$R=10\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
grid()
legend(loc="lower right")
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$P_c/P_e$",fontsize=16)
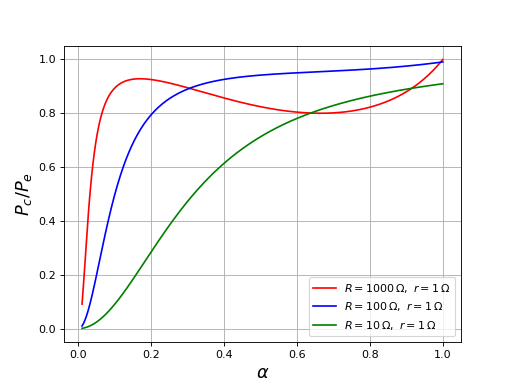 fig14.pdf
fig14.pdf
Le rendement énergétique diminue considérablement lorsque le rapport cyclique diminue, d'autant plus que la résistance de charge est basse. Dans ce modèle, l'énergie perdue est dissipée dans la résistance de la bobine. En réalité, il faudra ajouter la puissance perdue dans la résistance drain-source des transistors.
Voici d'autres courbes pour une résistance de charge donnée mais avec une résistance de bobine variable :
alpha = np.linspace(0.01,1,500)
figure()
R = 100
r = 10
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie/V0,label=r"$R=100\,{\rm\Omega},\ r=10\,{\rm\Omega}$")
R = 100
r = 1
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie/V0,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
R = 100
r = 0.1
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie/V0,label=r"$R=100\,{\rm\Omega},\ r=0.1\,{\rm\Omega}$")
grid()
xlim(0,1)
ylim(0,20)
legend(loc="upper right")
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$V_s/V_0$",fontsize=16)
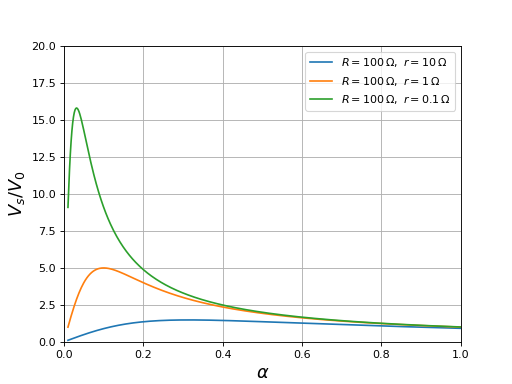 fig15.pdf
fig15.pdf
La résistance interne de la bobine a deux effets importants :
- Elle réduit l'élévation de tension à faible rapport cyclique. Pour une résistance de charge donnée, la valeur maximale de l'élévation de tension est d'autant plus basse que la résistance de la bobine est grande.
- Elle réduit l'efficacité du transfert de puissance entre la source et la charge.
2.e. Influence de L
Voyons l'influence de L (à résistance r constante) :
alpha = np.linspace(0.01,1,500)
R = 100
r = 1
figure()
L = 5e-3
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie/V0,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H$")
L = 1e-3
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie/V0,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=1 \,\rm m H$")
L = 500e-6
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie/V0,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=500\,\rm\mu H$")
grid()
xlim(0,1)
ylim(0,20)
legend(loc="upper right")
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$V_s/V_0$",fontsize=16)
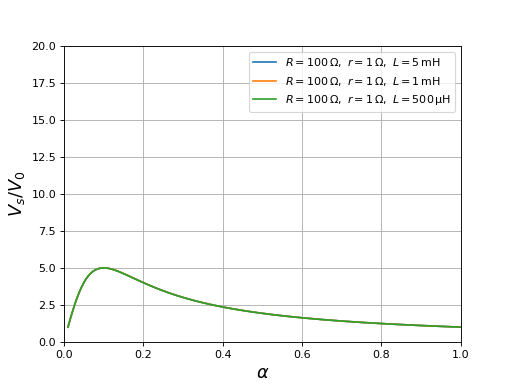 fig16.pdf
fig16.pdf
À résistance constante, l'influence du coefficient d'auto-inductance sur le régime permanent est très faible. Notons cependant que, en pratique, la réduction de la taille de la bobine s'accompagne aussi d'une réduction de sa résistance interne. Voyons l'influence de L sur le régime transitoire et sur les ondulations du courant :
r = 1
C = 2000e-6
R = 100
V0 = 1
alpha = 0.5
i0 = 0
Vs0 = 0
t0 = 0
T = 1e-4
P = 3000
L = 0.5e-3
temps1,i1,Vs1 = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
L = 0.2e-3
temps2,i2,Vs2 = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\,{\rm V},\ \alpha=0{,}5$")
plot(temps2,Vs2,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=1\,\rm m H$")
plot(temps1,Vs1,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm mH$")
grid()
legend(loc="upper right")
ylabel(r"$V_s\ (\rm)$",fontsize=16)
subplot(212)
plot(temps2,i2,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=1\,\rm m H$")
plot(temps1,i1,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H$")
grid()
legend(loc="upper right")
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
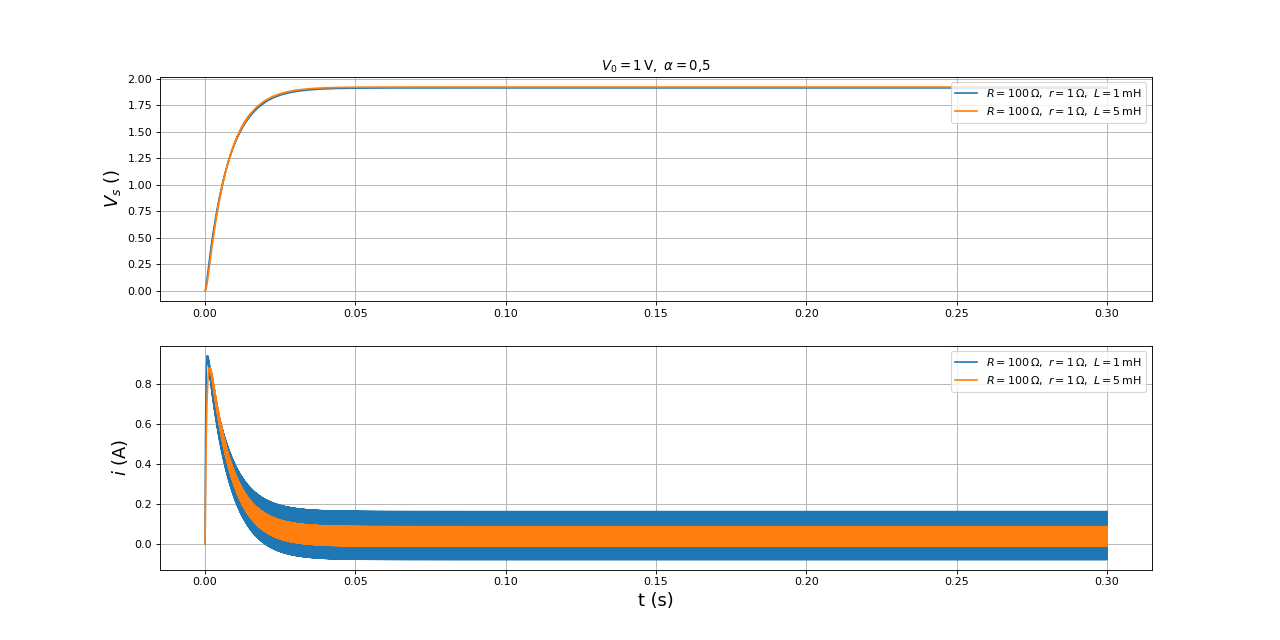 fig17.pdf
fig17.pdf
L'abaissement de la valeur de L a pour effet une augmentation des variations du courant dans la bobine :
L = 0.2e-3
t,i = courant(L,r,C,R,T,alpha,V0)
figure()
plot(t,i)
grid()
ylim(-0.5,0.5)
xlabel("t (s)",fontsize=16)
ylabel("i (A)",fontsize=16)
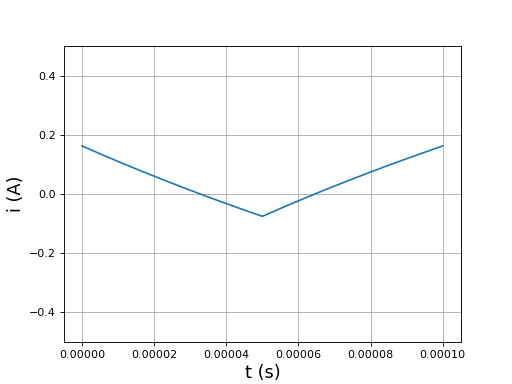 fig18.pdf
fig18.pdf
Ces variations du courant ont pour conséquence une augmentation des pertes dans le noyau (pertes magnétiques et pertes pas courants induits) et des pertes par effet Joule dans le fil, ce qui finalement a une effet négatif sur l'élévation de tension. En pratique, il faudra trouver un compromis pour que la bobine ne soit pas trop volumineuse. Une bobine à noyau semble adapté. Si l'inductance est assez élevée, les variations du courant sont faibles donc on peut utiliser un noyau à poudre de fer. Une bobine sans noyau permettra certainement d'améliorer considérablement le rendement énergétique mais le coefficient L sera beucoup plus petit pour le même encombrement, ce qui obligera à effectuer le découpage à une fréquence beaucoup plus grande.
2.f. Régime transitoire
Voici des courbes obtenues pour différentes valeurs de C :
r = 1
L = 0.5e-3
R = 100
V0 = 1
alpha = 0.5
i0 = 0
Vs0 = 0
t0 = 0
T = 1e-4
P = 3000
C = 2000e-6
temps1,i1,Vs1 = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
C = 500e-6
temps2,i2,Vs2 = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\,{\rm V},\ \alpha=0{,}5$")
plot(temps2,Vs2,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H,\ C=500\,\rm\mu F$")
plot(temps1,Vs1,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm mH,\ C=2000\,\rm\mu F$")
grid()
legend(loc="upper right")
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps2,i2,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H,\ C=500\,\rm\mu F$")
plot(temps1,i1,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H,\ C=2000\,\rm\mu F$")
grid()
legend(loc="upper right")
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
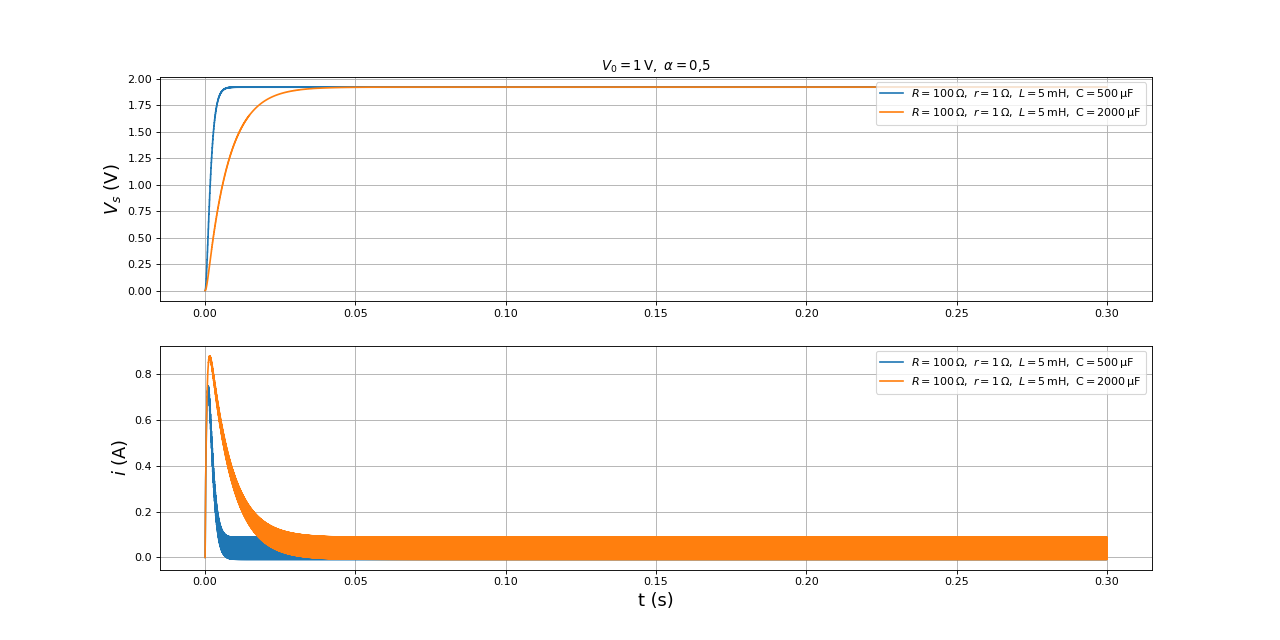 fig19.pdf
fig19.pdf
Comme attendu, le régime transitoire a une durée plus petite lorsque C est plus basse, ce qui est un avantage pour la régulation de tension. Voyons l'effet d'un abaissement encore plus important de C :
Q=0.5
R=100
L=0.5e-3
C=5e-6
r=1
temps,i,Vs = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\,{\rm V},\ \alpha=0{,}5$")
plot(temps,Vs,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H,\ C=%0.2f\,\rm\mu F$"%(C*1e6))
grid()
legend(loc="upper right")
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H,\ C=%0.2f\,\rm\mu F$"%(C*1e6))
grid()
legend(loc="upper right")
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
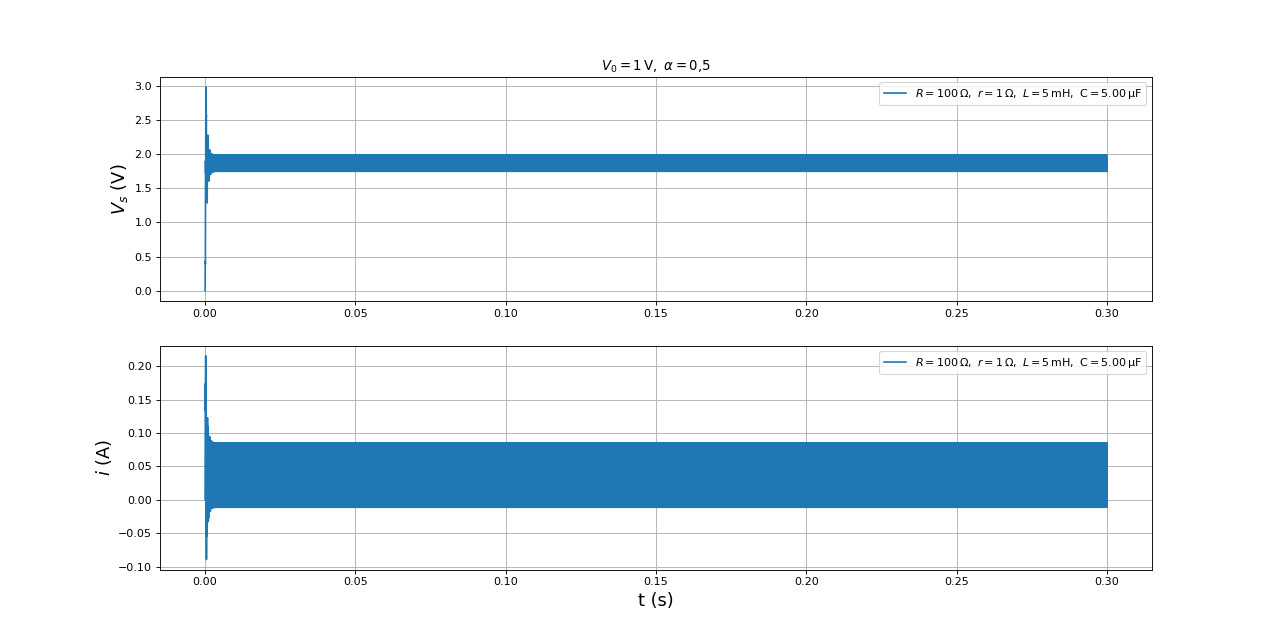 fig20.pdf
fig20.pdf
Dans ce cas, la valeur de C n'est plus assez grande pour obtenir une tension Vs constante en régime permanent. On a en effet , qui est seulement 5 fois plus grand que la période de commutation.
La condition étant satisfaite, la tension Vs est quasi constante mais il est préférable de choisir L et C afin que le régime transitoire soit proche du régime apériodique critique, ce qui assure un temps de réponse court sans oscillations.
Voici des courbes obtenues pour différentes valeurs de R :
r = 1
L = 0.5e-3
V0 = 1
alpha = 0.5
i0 = 0
Vs0 = 0
t0 = 0
T = 1e-4
P = 3000
C = 2000e-6
R = 100
temps1,i1,Vs1 = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
R = 10
temps2,i2,Vs2 = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\,{\rm V},\ \alpha=0{,}5$")
plot(temps2,Vs2,label=r"$R=10\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H,\ C=2000\,\rm\mu F$")
plot(temps1,Vs1,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm mH,\ C=2000\,\rm\mu F$")
grid()
legend(loc="upper right")
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps2,i2,label=r"$R=10\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H,\ C=2000\,\rm\mu F$")
plot(temps1,i1,label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega},\ L=5\,\rm m H,\ C=2000\,\rm\mu F$")
grid()
legend(loc="upper right")
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
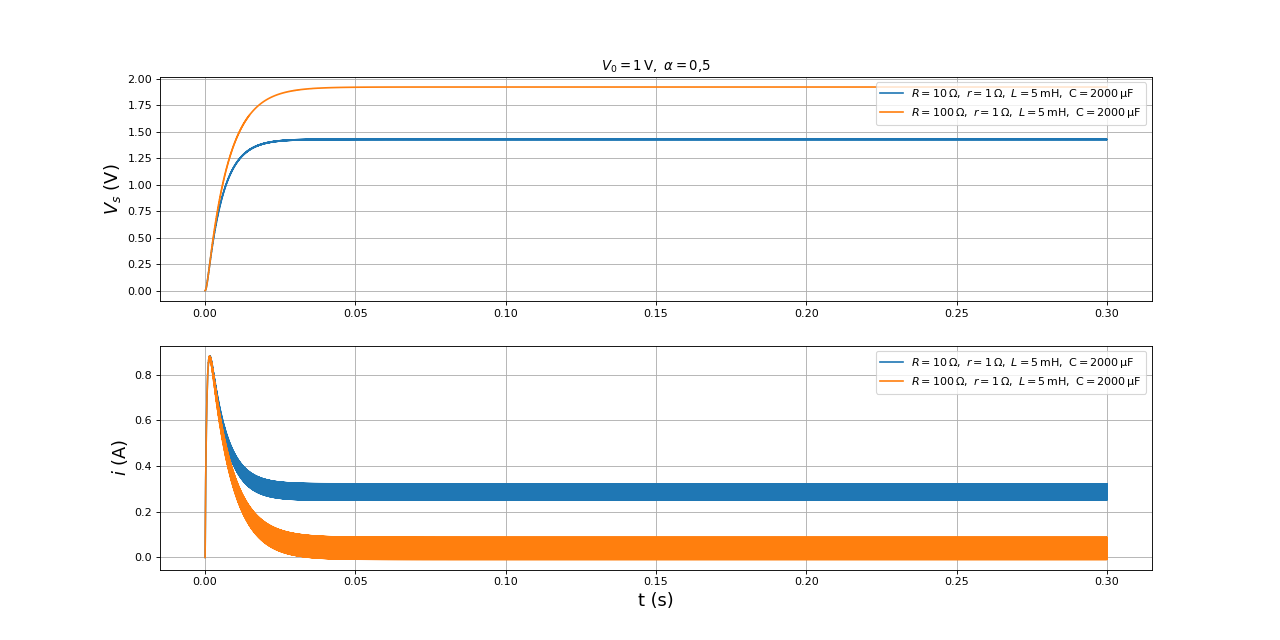 fig21.pdf
fig21.pdf
Comme il a été vu plus haut, l'élévation de tension dépend de la résistance de charge (d'où la nécessité d'une régulation) mais la nature du régime transitoire ne semble pas dépendre de la résistance de charge.
2.g. Simulation SPICE
Une simulation SPICE permet de faire intervenir un modèle plus réaliste des transistors. Lorsque la résistance de la bobine est de l'ordre du ohm, la résistance drain-source du transistor MOSFET lorsqu'il est passant n'est pas négligeable et l'étude précédente suggère une influence importante de cette résistance sur l'élévation de tension à faible rapport cyclique. Par ailleurs, la caractéristique drain-source à tension négative n'est pas celle d'une diode idéale (tension de seuil et résistance non nulle).
Considérons la simulation suivante :
L = 0.5e-3
r = 1
C = 2000e-6
R = 100
V0 = 1
alpha = 0.3
i0 = 0
Vs0 = 0
t0 = 0
T = 1e-4
P = 3000
temps,i,Vs = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\,{\rm V},\ \alpha=0{,}3$")
plot(temps,Vs)
grid()
ylim(0,4)
ylabel(r"$V_s$",fontsize=16)
subplot(212)
plot(temps,i)
ylim(-0.1,1)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
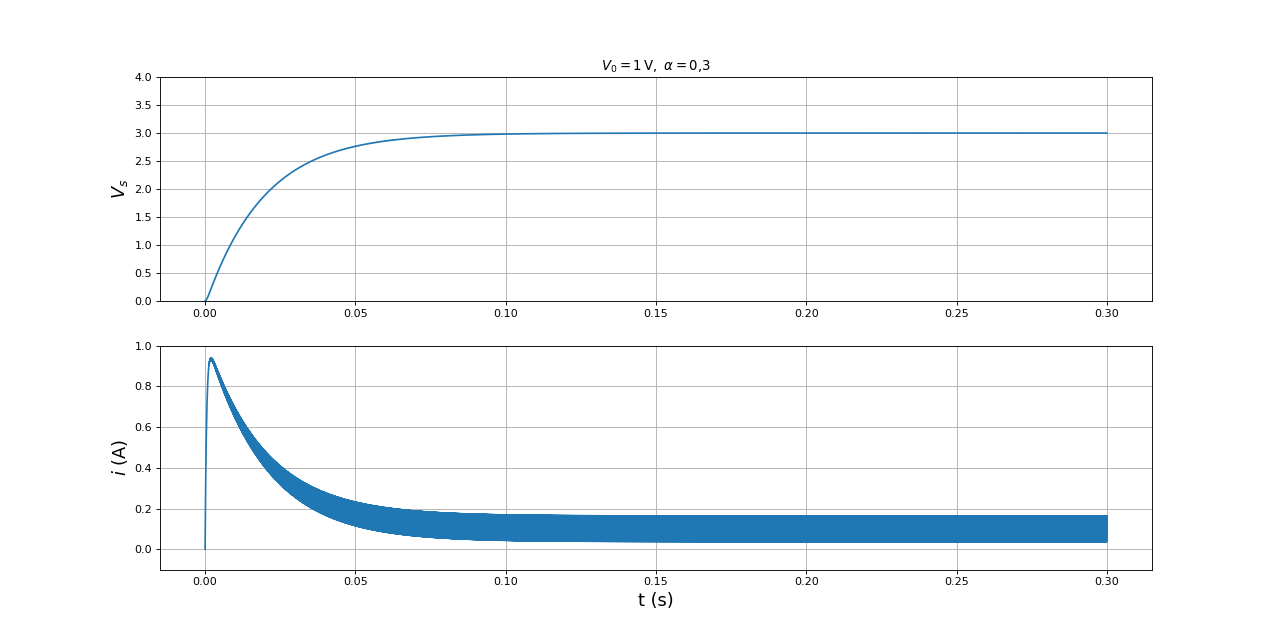 fig22.pdf
fig22.pdf
Voici une simulation effectuée avec LTSpice au moyen du modèle de transitor IPA50R500 (fourni par le fabriquant) :
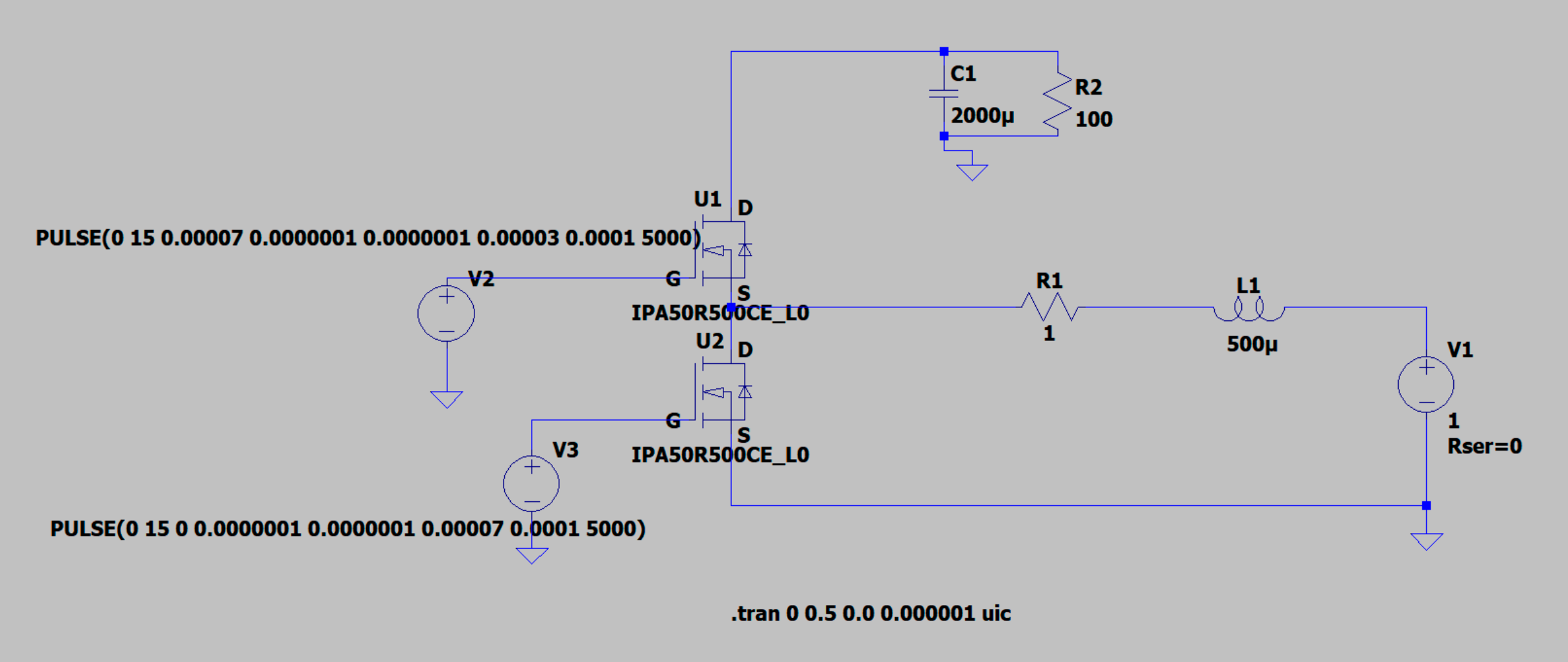
La commande de grille de chaque transistor est effectuée au moyen d'une source de tension qui délivre une tension carrée d'amplitude 15 V et de période 0,1 ms. Le rapport cyclique est 0,3. La directive UIC ajoutée à la commande de simulation TRANS permet d'appliquer la condition initiale choisie par l'utilisateur : ici la tension initiale en sortie est nulle et le courant dans la bobine est nul.
[t,Vs,i] = np.load("convertisseur-boost-1.npy")
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\,{\rm V},\ \alpha=0{,}3$")
plot(t,Vs)
grid()
ylim(0,4)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
ylim(0,1)
plot(t,i)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
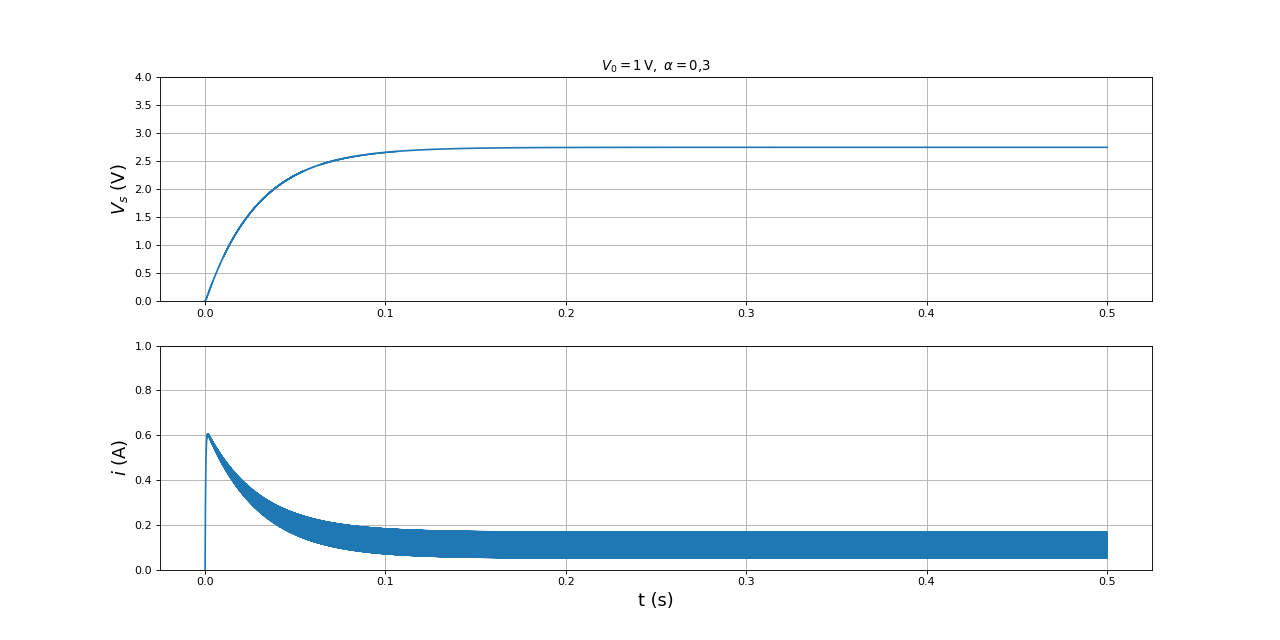 fig23.pdf
fig23.pdf
L'élévation de tension est un peu plus basse que pour la simulation avec les transistors idéaux. Cet effet est attribuable à la résistance RDSON. L'effet de cet résistance devrait être similaire à celui de la résistance série de la bobine. Pour ce transistor, la fiche technique indique RDSON=0,5 Ω. Voici la même simulation que précédemment, avec une résistance r augmentée de 0,5 ohms :
L = 0.5e-3
r = 1.5
C = 2000e-6
R = 100
V0 = 1
alpha = 0.3
i0 = 0
Vs0 = 0
t0 = 0
T = 1e-4
P = 3000
temps,i,Vs = simulation(L,r,C,R,T,alpha,V0,i0,Vs0,P)
figure(figsize=(16,8))
subplot(211)
title(r"$V_0=1\,{\rm V},\ \alpha=0{,}3$")
plot(temps,Vs/V0)
grid()
ylim(0,4)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
subplot(212)
plot(temps,i)
ylim(0,1)
grid()
xlabel("t (s)",fontsize=16)
ylabel(r"$i\ (\rm A)$",fontsize=16)
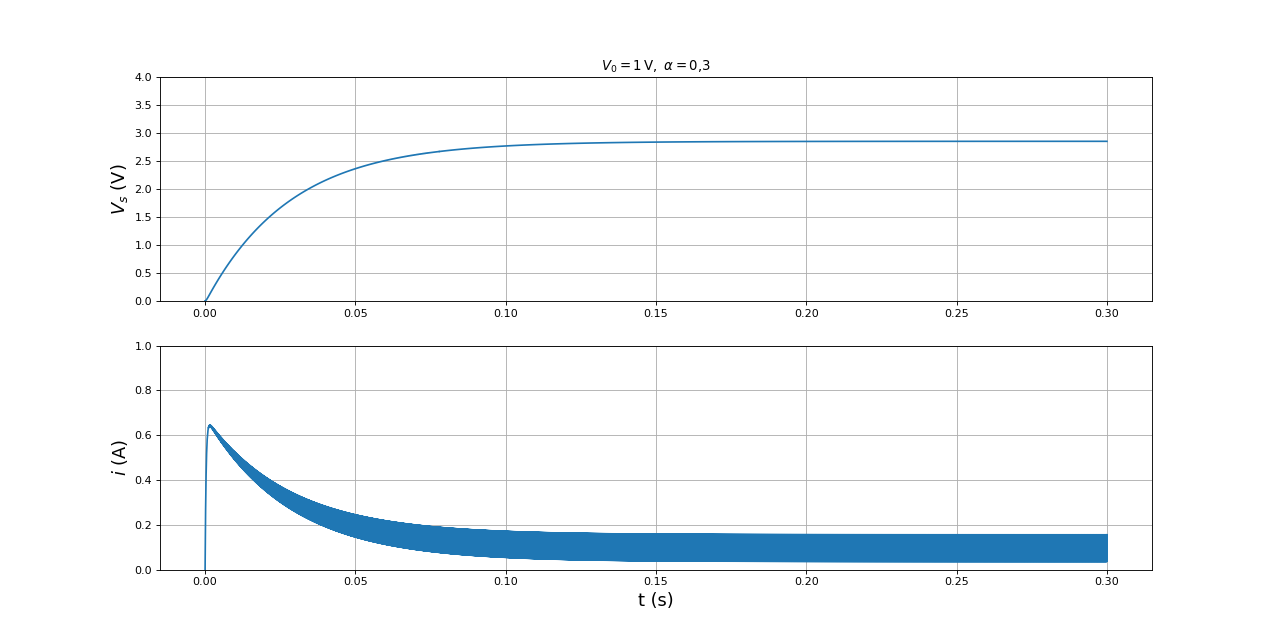 fig24.pdf
fig24.pdf
L'augmentation de la résistance r de 0,5 ohms ne permet pas de rendre compte très précisément de l'abaissement de l'élévation de tension. Il est probable que la caractérique drain-source en inverse joue un rôle non négligeable.
3. Étude expérimentale
3.a. Circuit
La bobine utilisée est un enroulement sur un tore en poude de fer (Wurth Electronik). Les mesures d'impédance sont réalisées avec l'Analog Discovery 2 et le logiciel Waveforms. Un amplificateur linéaire de puissance est utilisé et différentes amplitudes de la tension d'entrée sont choisies. Voici les parties réelle et imaginaire de l'impédance en fonction de la fréquence :
[f1,R1,X1] = np.loadtxt('impedance-bobine-500mV.csv',unpack=True,skiprows=31,delimiter=',')
[f2,R2,X2] = np.loadtxt('impedance-bobine-1V.csv',unpack=True,skiprows=31,delimiter=',')
[f3,R3,X3] = np.loadtxt('impedance-bobine-2V.csv',unpack=True,skiprows=31,delimiter=',')
[f4,R4,X4] = np.loadtxt('impedance-bobine-5V.csv',unpack=True,skiprows=31,delimiter=',')
figure(figsize=(12,8))
subplot(211)
plot(f1,R1,label='0.5 V')
plot(f2,R2,label='1 V')
plot(f3,R3,label='2 V')
plot(f4,R4,label='5 V')
grid()
xscale('log')
yscale('log')
ylabel(r"$R\ (\rm\Omega)$",fontsize=14)
legend(loc='upper left')
subplot(212)
plot(f1,X1,label='0.5 V')
plot(f2,X2,label='1 V')
plot(f3,X3,label='2 V')
plot(f4,X4,label='5 V')
grid()
xscale('log')
yscale('log')
ylabel(r"$X\ (\rm\Omega)$",fontsize=14)
legend(loc='upper left')
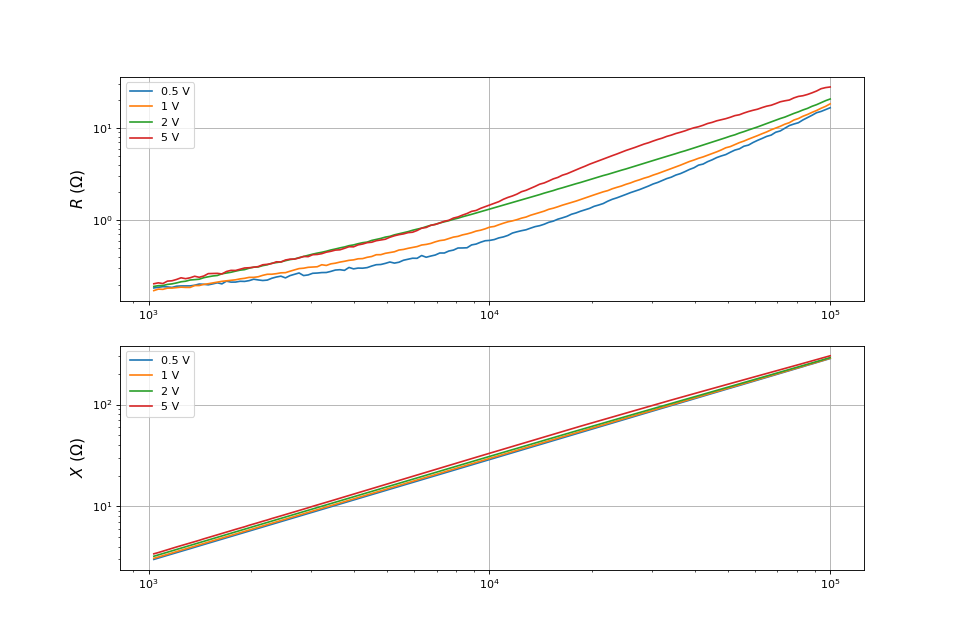 fig25.pdf
fig25.pdf
Voici les valeurs de l'auto-inductance déduites de la pente de la partie imaginaire de l'impédance :
p1 = np.polyfit(f1,X1,deg=1)
L1 = p1[0]/(2*np.pi)
p2 = np.polyfit(f2,X2,deg=1)
L2 = p2[0]/(2*np.pi)
p3 = np.polyfit(f3,X3,deg=1)
L3 = p3[0]/(2*np.pi)
p4 = np.polyfit(f4,X4,deg=1)
L4 = p4[0]/(2*np.pi)
print([L1,L2,L3,L4]) --> [0.0004517477924609051, 0.0004552390667261044, 0.00046315251406330016, 0.0004880015319133239]
L'auto-inductance augmente un peu avec l'intensité du courant (l'intensité est ici de 100 mA maximum). Les valeurs obtenues avec un RLC-mètre sont et à une fréquence de 10 kHz. Il s'agit de valeurs valables pour une intensité du courant faible (quelques dizaines mA). Pour une uitilisation dans un circuit de forte puissance, il faut s'attendre à une valeur nettement plus grande de la résistance.
Comme le montrent les simulations ci-dessus, le courant dans la bobine a une valeur moyenne positive mais présente des ondulations non négligeables à la fréquence de découpage. Pour cette application, le noyau en poudre de fer n'est pas optimal à cause des courants induits dans le fer (un noyau en ferrite serait sans doute plus approprié). Dans les modèles, la résistance est constante alors qu'en réalité elle dépend de la fréquence. La valeur constante la plus pertinente est de l'ordre de 1 ohms car on peut supposer que les ondulations à la fréquence de découpage (10 kHz) imposent la valeur de la résistance, même si leur amplitude est relativement faible.
Voici le schéma du circuit complet, où la bobine est représentée par son auto-inductance et sa résistance en série :
Figure pleine pageLes deux transistors MOSFET sont piloté par le IR2113, qui permet de piloter les deux séparément avec deux signaux de commande. Il existe aussi des pilotes permettant de commander les deux transistors en opposition avec un seul signal de commande (voir Transistors MOSFET de puissance), qui conviendrait très bien pour cette application. Ce circuit peut fonctionner en convertisseur continu-continu abaisseur (DC-DC buck converter) si on échange l'entrée et la sortie. C'est la raison de la présence du condensateur C1 en entrée, qui ne joue évidemment aucun rôle dans les simulations puisqu'une source de tension idéale est placée en entrée. Les expériences décrites plus loin sont réalisées avec une alimentation stabilisée comme source en entrée. Si un accumulateur électrochimique est utilisé, ce condensateur permet de réduire les petites ondulations de tension qui pourraient apparaître à cause des ondulations de courant.
Le potentiomètre permet de réduire la tension de sortie pour la ramener en dessous de 5 V afin d'être envoyée sur l'entrée A0 de l'Arduino pour numérisation.
La commande de grille des deux transistors nécessite une tension de 15 V que nous fournissons avec une alimentation séparée. Ce montage ne pourrait donc pas fonctionner avec seulement la source branchée en entrée (par exemple un accumulateur) car il faut prévoir un moyen de polariser les transistors avec une source de tension faible.
3.b. Programme Arduino
Ce programme tourne sur Arduino MEGA. Les signaux HIN et LIN sont générés par les deux sorties A et B du Timer 1, respectivement câblées sur D11 et D12. La programmation d'un Timer pour la génération de signaux PWM est expliqué dans Pilotage d'un pont L298. Le rapport cyclique est envoyé depuis un script Python selon le protocole de communication décrit dans Échanges de données avec un Arduino.
#define HIN 11 // transistor haut
#define LIN 12 // transistor bas
uint16_t diviseur[6] = {0,1,8,64,256,1024};
uint16_t icr;
uint16_t temps_mort = 0;
uint16_t ocra,ocrb;
float rapport;
// communication série
#define GET_DATA 10
#define SET_DATA 11
#define DATA_0_SIZE 4 // rapport cyclique (float)
#define DATA_1_SIZE 4 // Tension Vs
uint8_t data_0[DATA_0_SIZE];
uint8_t data_1[DATA_1_SIZE];
bool data_1_request = false;
bool data_1_ready = true;
// rapport cyclique du découpage
void set_rapport(float rapport) {
if (icr*rapport>temps_mort) {
ocra = icr*rapport-temps_mort;
ocrb = icr*rapport+temps_mort;
}
else {
ocra = icr*rapport;
ocrb = icr*rapport;
}
OCR1A = ocra;
OCR1B = ocrb;
}
//Timer 1 : OC1A : sortie D11, OC1B : sortie D12
void timer1_init(uint32_t period, float rapport) {
cli();
TCCR1A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR1B = (1 << WGM13);
icr = (F_CPU/1000000*period/2);
int d = 1;
while ((icr>0xFFFF)&&(d<5)) {
d++;
icr = (F_CPU/1000000*period/2/diviseur[d]);
}
TCCR1B |= d;
set_rapport(rapport);
TCNT1 = 0;
ICR1 = icr;
sei();
}
// traitement d'une donnée entrante
void set_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==0) {
while (Serial.available()<DATA_0_SIZE) {};
Serial.readBytes(data_0,DATA_0_SIZE);
memcpy(&rapport,data_0,DATA_0_SIZE);
set_rapport(rapport);
}
}
void get_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==1) data_1_request = true;
}
void send_data() {
if ((data_1_ready)&&(data_1_request)) {
data_1_request = false;
float Vs = analogRead(A0) *5.0/1024*4.0;
Serial.write((uint8_t *)&Vs,DATA_1_SIZE);
}
}
void read_serial() {
char com;
if (Serial.available()>0) {
com = Serial.read();
if (com==GET_DATA) get_data();
else if (com==SET_DATA) set_data();
}
}
void setup() {
Serial.begin(115200);
pinMode(HIN,OUTPUT);
pinMode(LIN,OUTPUT);
rapport = 0.3;
timer1_init(100,rapport); // fréquence 10 kHz
}
void loop() {
read_serial();
send_data();
delay(100);
}
Pour modifier le rapport cyclique, on utilise le script Arduino.py et le script suivant :
from Arduino import Arduino
ard = Arduino('COM3',[4,4])
RAPPORT = 0
TENSION = 1
while True:
r = input('?')
if r=='n': break
elif r=="v":
Vs = ard.read_float(TENSION)
print("Vs = %f"%Vs)
else:
rapport = float(r)
ard.write_float(RAPPORT,rapport)
ard.close()
On entre la valeur du rapport cyclique, ou la lettre v pour obtenir la tension Vs, ou la lettre n pour terminer.
3.c. Résultats
La fréquence de découpage est 10 kHz.
La tension d'entrée est V0=1 V et la résistance de charge R=100 Ω. Voici, pour un rapport cyclique α=0,5, les signaux de commande des deux transistors K1,K2, la tension Vs en sortie du convertisseur (aux bornes de la charge) :
[ta,K1,K2] = np.loadtxt("boost-DC1-PWM-r0,5-R100.txt",unpack=True,skiprows=1)
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r0,5-R100.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Vs,label=r"$V_s$")
#plot(tb,V2,label=r"$V_2$")
xlabel("t (s)",fontsize=16)
ylabel("Volts",fontsize=16)
grid()
ylim(0,5)
legend(loc="upper right")
title(r"$\alpha=0{,}5\ R=100\ {\rm \Omega}$",fontsize=16)
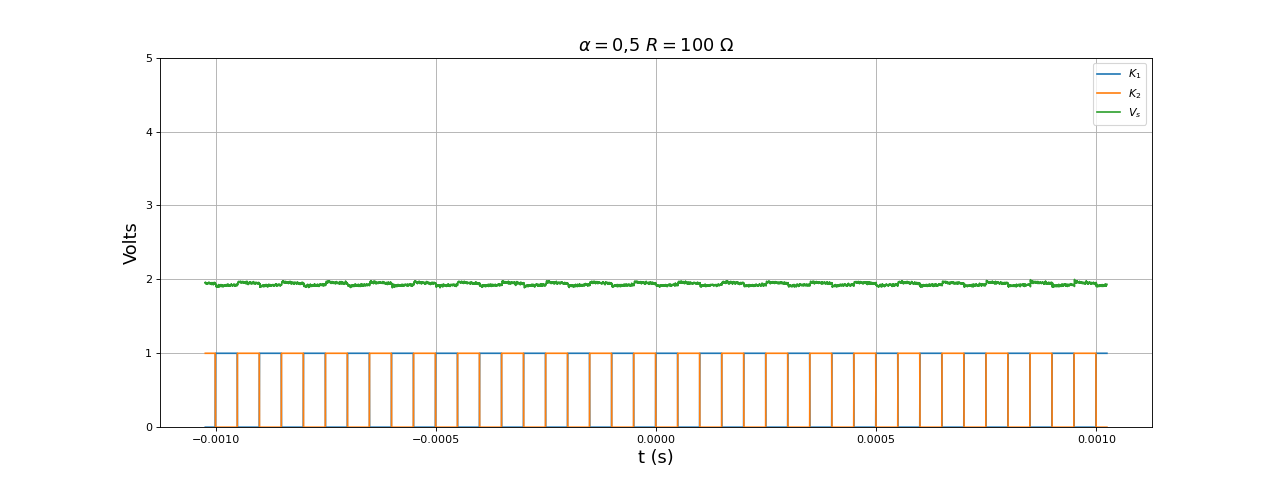 fig26.pdf
fig26.pdf
[ta,K1,K2] = np.loadtxt("boost-DC1-PWM-r0,3-R100.txt",unpack=True,skiprows=1)
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r0,3-R100.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Vs,label=r"$V_s$")
#plot(tb,V2,label=r"$V_2$")
xlabel("t (s)",fontsize=16)
ylabel("Volts",fontsize=16)
grid()
ylim(0,5)
legend(loc="upper right")
title(r"$\alpha=0{,}3\ R=100\ {\rm \Omega}$",fontsize=16)
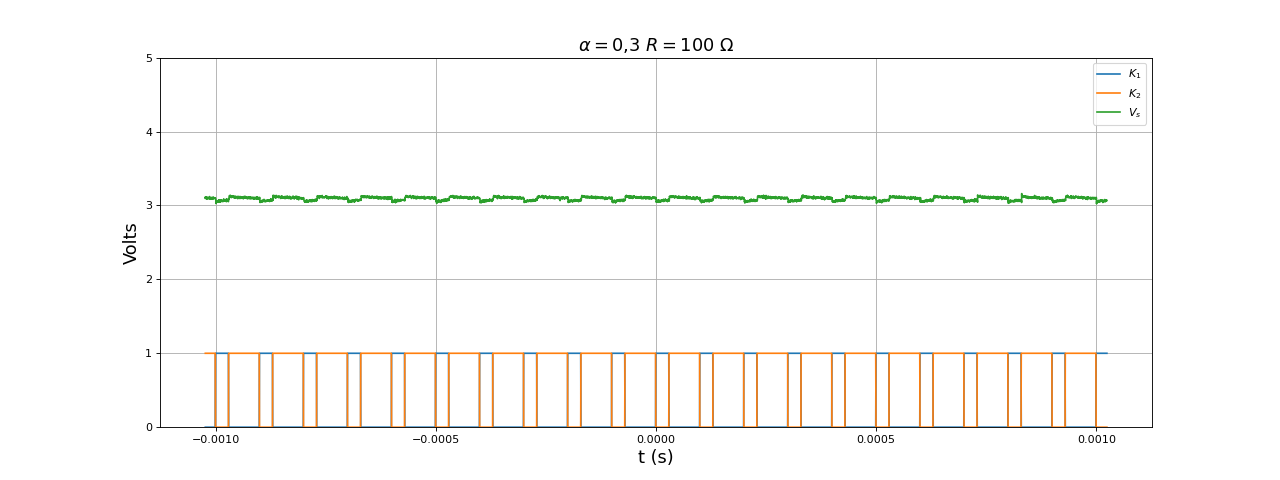 fig27.pdf
fig27.pdf
Voici la tension en sortie en fonction du rapport cyclique, pour deux valeurs différentes de la résistance de charge :
figure()
str = ["0,02","0,03","0,04","0,05","0,07","0,1","0,15","0,2","0,25","0,3","0,4","0,5","0,6","0,7","0,8","0,9"]
alpha = [0.02,0.03,0.04,0.05,0.07,0.1,0.15,0.2,0.25,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
lab = r"$R=100\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R100.txt"%str[i],unpack=True,skiprows=1)
Vs = Vs.mean()
plot(alpha[i],Vs,"ob",label=lab)
lab = ""
str = ["0,01","0,02","0,03","0,06","0,08","0,1","0,15","0,2","0,25","0,3","0,4","0,5","0,6","0,7","0,8","0,9"]
alpha = [0.01,0.02,0.03,0.06,0.08,0.1,0.15,0.2,0.25,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
lab = r"$R=560\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R560.txt"%str[i],unpack=True,skiprows=1)
Vs = Vs.mean()
plot(alpha[i],Vs,"or",label=lab)
lab=""
L = 467e-6
r = 0.7
R = 100
C = 2200e-6
T = 1e-4
V0=1
alpha = np.linspace(0,1,500)
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie,'b--',label=r"$R=100\,\rm\Omega$")
R = 560
Vsortie = tensionSortie(L,r,C,R,T,alpha,V0)
plot(alpha,Vsortie,'r--',label=r"$R=560\,\rm\Omega$")
grid()
xlim(0,1)
ylim(0,15)
legend(loc="upper right")
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$V_0=1{,}0\,{\rm V},\ f=10\,{\rm kHz}$",fontsize=16)
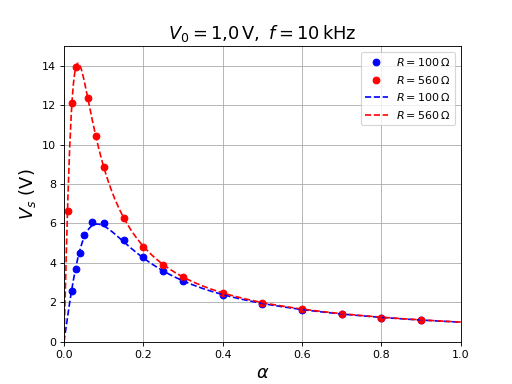 fig28.pdf
fig28.pdf
La courbe en traits interrompus est celle du modèle (MOSFET idéaux) avec la valeur de L déterminée expérimentalement plus haut et une valeur de r choisie pour que la courbe corresponde aux points expérimentaux. La valeur de r est très proche de la résistance à 10 kHz (légèrement plus basse), mais la résistance drain-source des transistors (de l'ordre de 0,5 ohms) contribuent certainement à la résistance totale.
Comme prévu, l'élévation de tension maximale est d'autant plus grande que la résistance de charge est grande. Si l'on veut éviter de mettre en place une stabilisation de la tension de sortie, on doit se limiter au domaine de rapport cyclique où la tension de sortie dépend très peu de la résistance de charge. Par exemple, pour , on obtient une tension en sortie très peu dépendante de la résistance de charge pour la plage de 100 à 500 ohms. Le rapport cyclique qui maximise la tension pour 100 ohms est acceptable si l'on souhaite une tension de 5 V mais il faudra mettre en place une stabilisation.
Afin de mesurer le courant délivré par la source, nous plaçons une résistance de puissance de 1,0 ohms à la sortie positive de l'alimentation. Une mesure différentielle de tension aux bornes de cette résistance avec l'oscilloscope de l'Analog Discovery (et moyennage su 100 ms) donne le courant sortant de cette borne de la source. On en déduit le rendement énergétique, c'est-à-dire le rapport de la puissance dissipée dans la résistance de charge par la puissance fournie par la source :
Ri = 1.0
E = 1.0
alpha = [0.6,0.5,0.4,0.35,0.3,0.25,0.2,0.15,0.1,0.08,0.07,0.06,0.05,0.04,0.03,0.02]
figure(figsize=(12,6))
Vr = np.array([7.6,11.1,17.0,21.4,27.8,37.3,53.7,84.9,156.4,211.5,248.7,294.4,349.1,413,482,548])*1e-3
Vs = np.array([1.56,1.88,2.34,2.67,3.09,3.66,4.47,5.65,7.36,8.12,8.44,8.64,8.60,8.18,7.18,5.43])
R = 563
rapportP = Vs**2/R/(E*Vr/Ri)
plot(alpha,rapportP,"or",label=r"$R=560\,\Omega$")
Vr = np.array([29.4,41.7,62.6,79,102,135.8,187.1,267.7,389.4,448.7,479,509,537,563,584,601])*1e-3
Vs = np.array([1.5,1.78,2.16,2.4,2.69,3.03,3.40,3.69,3.61,3.34,3.12,2.84,2.49,2.07,1.59,1.066])
R = 100
rapportP = Vs**2/R/(E*Vr/Ri)
plot(alpha,rapportP,"ob",label=r"$R=100\,\Omega$")
grid()
xlim(0,1)
ylim(0,1)
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$P_c/P_s$",fontsize=16)
legend(loc="upper right")
title(r"$V_0=1\,{\rm V},\ f=10\,{\rm kHz}$",fontsize=16)
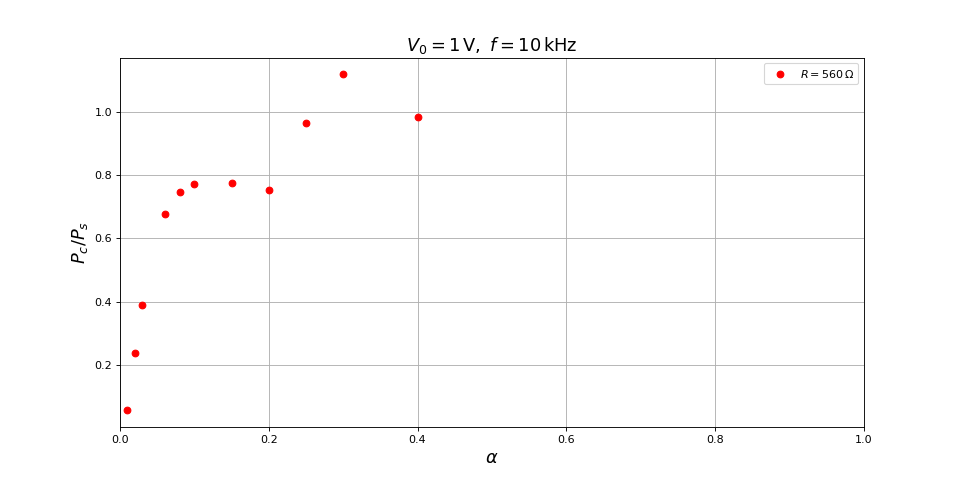 fig29.pdf
fig29.pdf
On constate que pour les faibles rapports cycliques, au voisinage du maximum de tension et dans la partie croissante avant le maximum, le rendement énergétique est très faible, conformément aux résultats de simulation.
Voici les courbes de rendement données par le modèle :
rP1,rP2,rP3 = [],[],[]
alpha = np.linspace(0,1,500)
for a in alpha:
R = 560
t,i = courant(L,r,C,R,T,a,V0,N=100)
Vs = tensionSortie(L,r,C,R,T,a,V0)
rP1.append(Vs**2/R/(V0*i.mean()))
R = 100
t,i = courant(L,r,C,R,T,a,V0,N=100)
Vs = tensionSortie(L,r,C,R,T,a,V0)
rP2.append(Vs**2/R/(V0*i.mean()))
R = 10
t,i = courant(L,r,C,R,T,a,V0,N=100)
Vs = tensionSortie(L,r,C,R,T,a,V0)
rP3.append(Vs**2/R/(V0*i.mean()))
figure()
plot(alpha,rP1,"r--",label=r"$R=560\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
plot(alpha,rP2,"b--",label=r"$R=100\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
plot(alpha,rP3,"g--",label=r"$R=10\,{\rm\Omega},\ r=1\,{\rm\Omega}$")
grid()
legend(loc="lower right")
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$P_c/P_e$",fontsize=16)
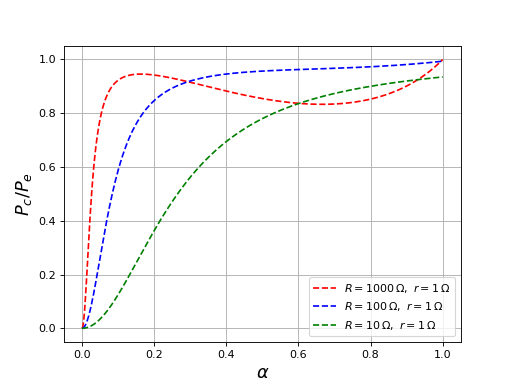 fig30.pdf
fig30.pdf
Voici l'amplitude relative d'ondulation de tension en sortie en fonction du rapport cyclique :
figure(figsize=(12,6))
str = ["0,02","0,03","0,04","0,05","0,07","0,1","0,15","0,2","0,25","0,3","0,4","0,5","0,6","0,7","0,8","0,9"]
alpha = [0.02,0.03,0.04,0.05,0.07,0.1,0.15,0.2,0.25,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
lab = r"$R=100\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R100.txt"%str[i],unpack=True,skiprows=1)
delta = Vs.std()/Vs.mean()
plot(alpha[i],delta,"ob",label=lab)
lab = ""
str = ["0,01","0,02","0,03","0,06","0,08","0,1","0,15","0,2","0,25","0,3","0,4","0,5","0,6","0,7","0,8","0,9"]
alpha = [0.01,0.02,0.03,0.06,0.08,0.1,0.15,0.2,0.25,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
lab = r"$R=560\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R560.txt"%str[i],unpack=True,skiprows=1)
delta = Vs.std()/Vs.mean()
plot(alpha[i],delta,"or",label=lab)
lab=""
ylim(0,0.03)
grid()
xlim(0,1)
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$\frac{\Delta V_s}{V_s}\ (\rm V)$",fontsize=16)
title(r"$V_0=1\,{\rm V},\ f=10\,{\rm kHz}$",fontsize=16)
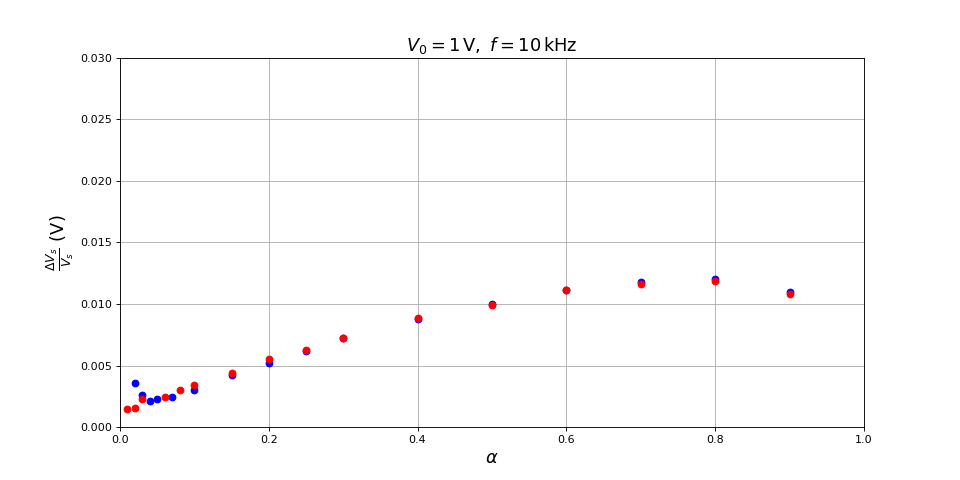 fig31.pdf
fig31.pdf
L'ondulation est faible, d'amplitude relative inférieure à . Voici les résultats pour une fréquence de découpage de 10 kHz, 20 kHz et de 50 kHz avec la résistance de charge de 560 Ω :
figure()
str = ["0,1","0,2","0,3","0,4","0,5","0,6","0,7","0,8","0,9"]
alpha = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
lab = r"$f=50\,{\rm kHz},\ R=560\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R560-f50kHz.txt"%str[i],unpack=True,skiprows=1)
Vs = Vs.mean()
plot(alpha[i],Vs,"or",label=lab)
lab=""
lab = r"$f=20\,{\rm kHz},\ R=560\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R560-f20kHz.txt"%str[i],unpack=True,skiprows=1)
Vs = Vs.mean()
plot(alpha[i],Vs,"ob",label=lab)
lab=""
lab = r"$f=10\,{\rm kHz},\ R=560\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R560.txt"%str[i],unpack=True,skiprows=1)
Vs = Vs.mean()
plot(alpha[i],Vs,"og",label=lab)
lab=""
grid()
xlim(0,1)
ylim(0,20)
legend(loc="upper right")
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$V_0=1\,{\rm V}$",fontsize=16)
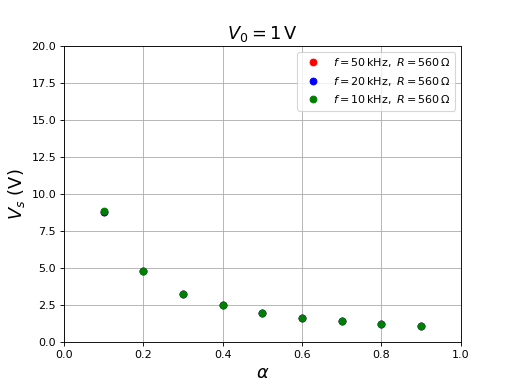 fig32.pdf
fig32.pdf
figure(figsize=(12,6))
str = ["0,1","0,2","0,3","0,4","0,5","0,6","0,7","0,8","0,9"]
alpha = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
lab = r"$f=50\,{\rm kHz},R=560\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R560-f50kHz.txt"%str[i],unpack=True,skiprows=1)
delta = Vs.std()/Vs.mean()
plot(alpha[i],delta,"or",label=lab)
lab=""
lab = r"$f=20\,{\rm kHz},R=560\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R560-f20kHz.txt"%str[i],unpack=True,skiprows=1)
delta = Vs.std()/Vs.mean()
plot(alpha[i],delta,"ob",label=lab)
lab=""
lab = r"$f=10\,{\rm kHz},R=560\,\rm\Omega$"
for i in range(len(str)):
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r%s-R560.txt"%str[i],unpack=True,skiprows=1)
delta = Vs.std()/Vs.mean()
plot(alpha[i],delta,"og",label=lab)
lab=""
grid()
ylim(0,0.03)
xlim(0,1)
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$\frac{\Delta V_s}{V_s}\ (\rm V)$",fontsize=16)
legend(loc="upper right")
title(r"$V_0=1\,{\rm V}$",fontsize=16)
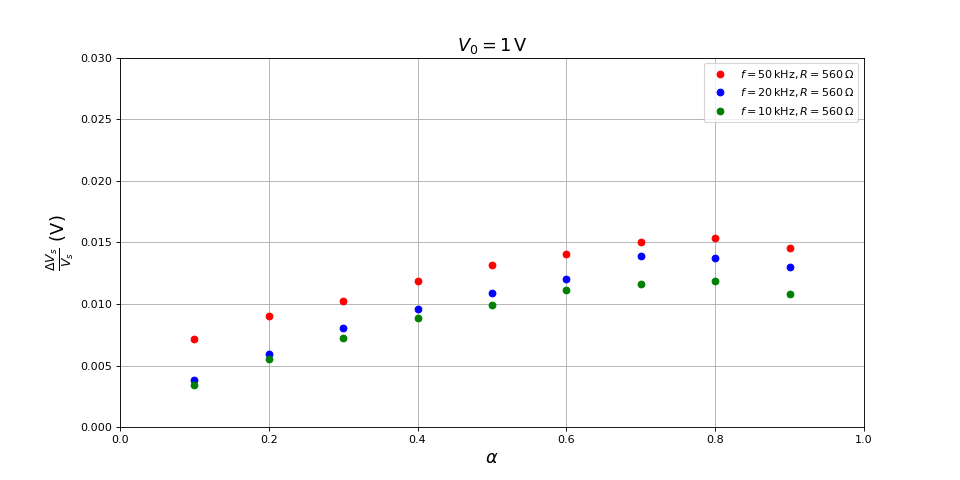 fig33.pdf
fig33.pdf
Le taux d'ondulation augmente un peu lorsque la fréquence de découpage augmente, ce qui est étonnant. Voici la tension en sortie à 50 kHz :
[ta,K1,K2] = np.loadtxt("boost-DC1-PWM-r0,3-R560-f50kHz.txt",unpack=True,skiprows=1)
[tb,Vs,V2] = np.loadtxt("boost-DC1-Vs-r0,3-R560-f50kHz.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
plot(ta,K1,label=r"$K_1$")
plot(ta,K2,label=r"$K_2$")
plot(tb,Vs,label=r"$V_s$")
#plot(tb,V2,label=r"$V_2$")
xlabel("t (s)",fontsize=16)
ylabel("Volts",fontsize=16)
grid()
ylim(0,5)
legend(loc="upper right")
title(r"$\alpha=0{,}3\,\ R=560\ {\rm \Omega}$",fontsize=16)
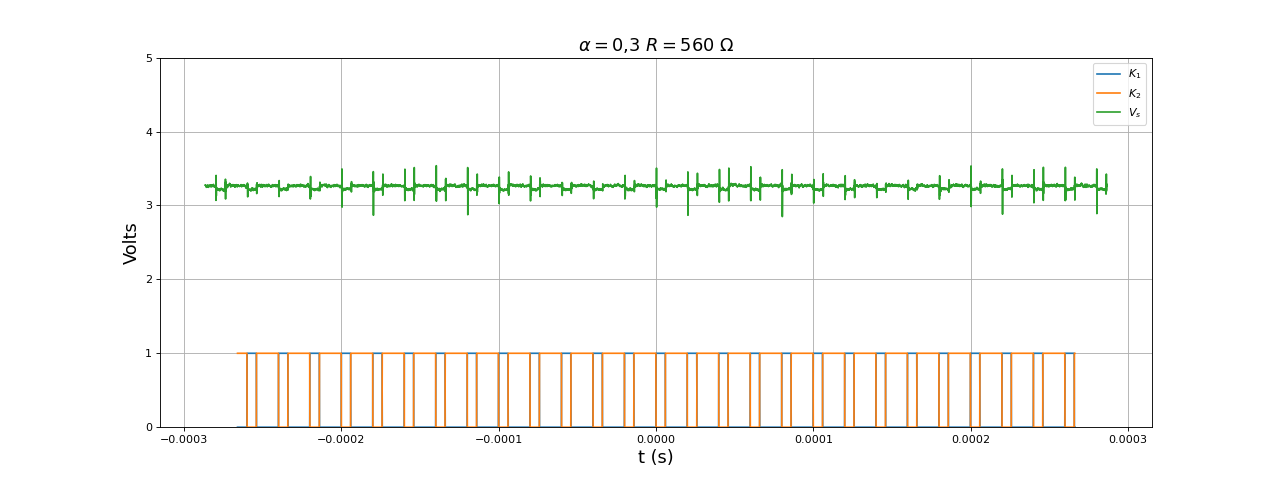 fig34.pdf
fig34.pdf
3.d. Convertisseur non synchrone
Lorsque le transistor 1 est en permanence à l'état ouvert, on obtient l'équivalent du convertisseur non synchrone, comportant une diode à la place de ce transistor. Pour obtenir ce comportement, il suffit de mettre l'entrée de commande de ce transistor (HIN) à la masse.
Ri = 1.0
E = 1.0
alpha = [0.6,0.5,0.4,0.35,0.3,0.25,0.2,0.15,0.1,0.08,0.07,0.06,0.05,0.04,0.03,0.02]
Vr1 = np.array([19.8,27.4,35.17,42.2,45.9,50.2,48.1,80.8,158,217.8,258.3,307.4,365.6,432,500.9,562])*1e-3
Vs1 = np.array([2.47,2.96,3.36,3.68,3.83,4.0,3.93,5.06,6.72,7.39,7.62,7.70,7.50,6.86,5.61,3.697])
R = 563
rapportP1 = Vs1**2/R/(E*Vr1/Ri)
Vr2 = np.array([28.16,37.92,48,63.1,85.2,118.2,169.7,251.8,378.4,440,471,502.8,532,558,581,598])*1e-3
Vs2 = np.array([1.17,1.39,1.58,1.83,2.14,2.51,2.91,3.25,3.21,2.94,2.72,2.44,2.09,1.67,1.21,0.71])
R = 100
rapportP2 = Vs2**2/R/(E*Vr2/Ri)
figure(figsize=(12,6))
plot(alpha,Vs1,"or",label=r"$R=560\,\Omega$")
plot(alpha,Vs2,"ob",label=r"$R=100\,\Omega$")
grid()
xlim(0,1)
ylim(0,15)
legend(loc="upper right")
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$V_0=1{,}0\,{\rm V},\ f=10\,{\rm kHz}$",fontsize=16)
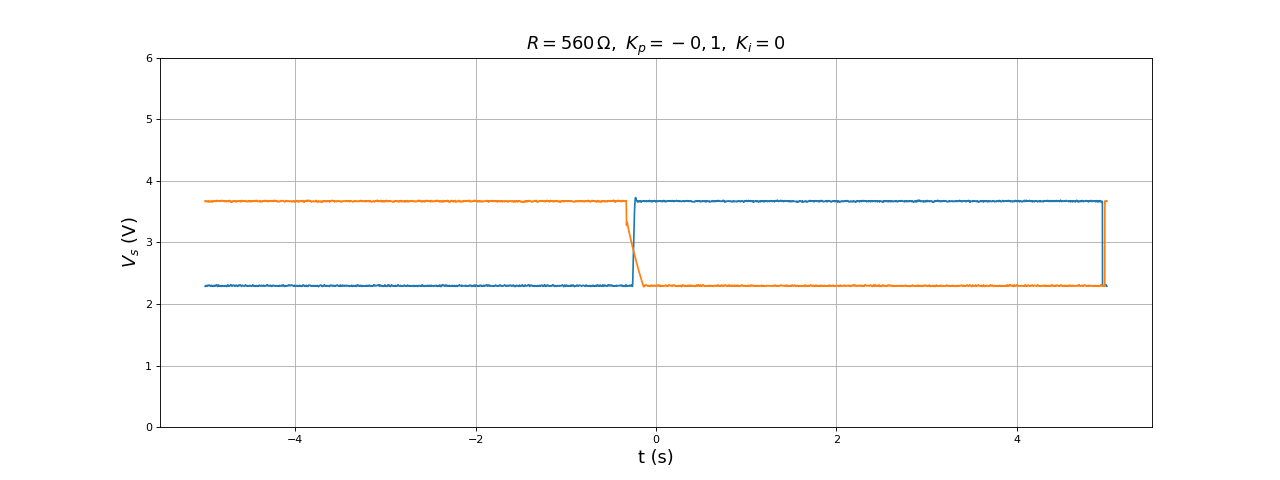 fig35.pdf
fig35.pdf
L'élévation de tension pour le convertisseur non synchrone est plus grande que celle du convertisseur synchrone à grand rapport cyclique mais elle est moins grande à bas rapport cyclique, ce qui fait que ce convertisseur ne permet pas d'atteindre une élévation de tension aussi grande.
figure(figsize=(12,6))
plot(alpha,rapportP1,"or",label=r"$R=560\,\Omega$")
plot(alpha,rapportP2,"ob",label=r"$R=100\,\Omega$")
grid()
xlim(0,1)
ylim(0,1)
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$P_c/P_s$",fontsize=16)
legend(loc="upper right")
title(r"$V_0=1\,{\rm V},\ f=10\,{\rm kHz}$",fontsize=16)
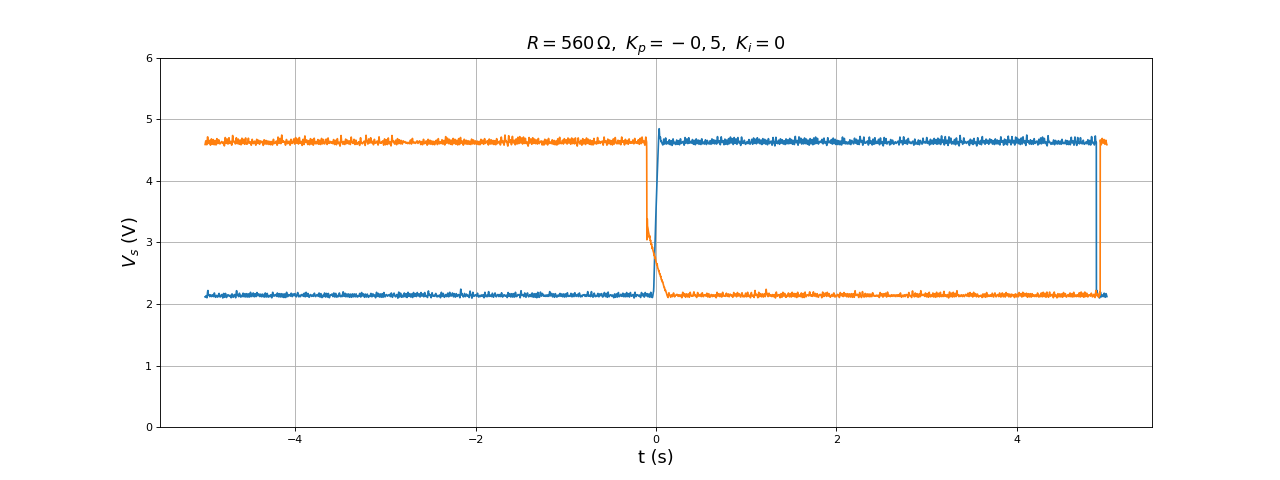 fig36.pdf
fig36.pdf
Le rendement énergétique du convertisseur non synchrone est plus faible : il ne dépasse pas 0,6 alors qu'il atteint 0,8 pour le convertisseur synchrone.
3.e. Régulation de la tension de sortie
La régulation doit se faire au moyen d'une boucle de rétroaction qui permet de maintenir la tension Vs à une valeur proche d'une valeur de consigne. Cette tension peut varier lorsque la demande de courant de la charge varie, autrement dit sa résistance varie. Elle peut aussi varier à cause de variations de la tension de la source. Si la source est un accumulateur, la tension à ses bornes diminue lorsque le courant augmente et diminue lentement au cours de la décharge. Si la source est la sortie d'un convertisseur AC-DC présentant un taux d'ondulation important, il y a des variations importantes de la tension d'entrée à la fréquence du secteur.
Notons Vsc la tension commandée (ou tension consigne). La figure suivante représente le système complet avec la boucle de rétroaction permettant d'obtenir la tension commandée.
Figure pleine pageLe système électronique (convertisseur) a pour entrée le rapport cyclique et pour sortie la tension Vs. D'après ce qui précède, ce système n'est pas linéaire mais nous pouvons considérer en première approche le cas d'un système linéaire, défini par sa fonction de transfert A(s). Le bloc C est généralement nommé correcteur car il corrige le sytème principal (bloc A).
La fonction de transfert du système bouclé est :
Le correcteur proportionnel est défini par :
donc et :
Remarquons que la tension en sortie est une fonction décroissante du rapport cyclique donc Kp<0.
L'erreur étant , l'erreur relative est :
L'erreur en régime stationnaire (à fréquence nulle) est donc :
On conséquence, plus Kp est grand plus l'erreur est petite. Cependant, le système est instable à partir d'une certaine valeur de Kp et on doit donc se contenter d'une erreur plus ou moins grande.
L'ajout d'un intégrateur dans le correcteur permet d'éliminer l'erreur en régime stationnaire. On obtient ainsi un correcteur proportionnel intégral (PI) :
donc :
et :
Dans le cas présent Ki<0. L'erreur relative est :
L'erreur en régime stationnaire (s=0) est donc nulle. Cependant, la présence de l'intégrateur allonge le temps de réponse. Pour voir cela, supposons que le temps de réponse du convertisseur soit négligeable. On a alors et :
L'équation différentielle correspondante est :
Si , la réponse à un échelon se fait avec une exponentielle dont le temps caractéristique est :
alors que si Ki=0 (correcteur proportionnel), la réponse est instantanée. On voit cependant que le temps de réponse diminue lorsqu'on augmente Ki.
La configuration du correcteur PI pour la rétroaction du convertisseur élévateur doit tenir compte de la non-linéarité de la relation entre Vs et . Il faut tout d'abord se limiter à une plage de où Vs est une fonction décroissante de . Si l'on convient que la résistance de charge sera supérieure à 100 Ω, cette plage va de 0,1 à 1. La tension en sortie sera en conséquence inférieure à 6 V (même si on pourra atteindre 14 V pour la résistance la plus grande). Par ailleurs, la relation définit une valeur qui doit pouvoir changer de signe. Il faut donc la modifier pour qu'elle soit à peu près centrée sur l'intervalle de valeurs de :
avec par exemple . Puisque Vs est une fonction décroissante de , Kp et Ki doivent être négatifs.
La tension Vs est échantillonnée avec une période Te. L'intégration numérique (voir Filtres intégrateur et dérivateur) est obtenue par le fitrage récursif suivant :
La tension Vs doit être réduite avec un pont diviseur afin d'être numérisée par l'Arduino (tension maximale de 5 V). Il faut cependant prévoir une protection pour que la tension ne dépasse pas 5 V. La protection par une simple diode permettrait d'empêcher un dépassement de 5,7 V environ, ce qui n'est peut-être pas suffisant (on ne prend pas le risque de détruire l'Arduino). Une autre solution est d'appliquer une division de tension assez grande pour que la tension en sortie ne dépasse jamais 5 V quel soit le rapport cyclique Dans le cas présent, un rapport de 1/3 convient puisque la tension en sortie ne dépasse jamais 15 V (pour une tension d'entrée de 1 V).
Le programme Arduino donné ci-dessous complète le précédent en y ajoutant les fonctions suivantes :
- Transmission de la tension de consigne (tensionVs) et des paramètres Ki,Kp.
- Dans la boucle loop, numérisation de Vs avec une période Te, calcul de la correction PI et changement du rapport cyclique.
La période d'échantillonnage est d'environ 10 ms. Une période aussi grande peut être obtenue par une simple temporisation avec la fonction delay. Nous ajoutons l'émission d'un signal numérique sur la sortie D3 qui change d'état à chaque numérisation, afin de contrôler le bon déroulement et de déterminer précisément la période d'échantillonnage effective. Bien évidemment, le temps de réponse de cet asservissement numérique ne peut être inférieur à la période d'échantillonnage mais, comme nous allons le voir, le temps de réponse du correcteur PI est beaucoup plus grand que cette période (donc il ne sert à rien de réduire celle-ci).
#define HIN 11 // transistor haut
#define LIN 12 // transistor bas
#define CONTROL 3 // PE5
#define AREF 4.93 // tension sur AREF
#define DIVPOT 3.05 // rapport du potentiomètre
uint16_t diviseur[6] = {0,1,8,64,256,1024};
uint16_t icr;
uint16_t temps_mort = 0;
uint16_t ocra,ocrb;
float rapport;
// communication série
#define GET_DATA 10
#define SET_DATA 11
#define DATA_0_SIZE 4 // rapport cyclique (float)
#define DATA_1_SIZE 4 // Tension Vs
#define DATA_2_SIZE 4 // Kp
#define DATA_3_SIZE 4 // Ki
uint8_t data_0[DATA_0_SIZE];
uint8_t data_1[DATA_1_SIZE];
uint8_t data_2[DATA_2_SIZE];
uint8_t data_3[DATA_3_SIZE];
bool data_1_request = false;
bool data_1_ready = true;
float tensionVs, integVs;
float lastVs,Vs;
float Kp = -0.05;
float Ki = -0.02;
uint8_t control = 0;
// rapport cyclique du découpage
void set_rapport(float rapport) {
if (icr*rapport>temps_mort) {
ocra = icr*rapport-temps_mort;
ocrb = icr*rapport+temps_mort;
}
else {
ocra = icr*rapport;
ocrb = icr*rapport;
}
OCR1A = ocra;
OCR1B = ocrb;
}
//Timer 1 : OC1A : sortie D11, OC1B : sortie D12
void timer1_init(uint32_t period, float rapport) {
cli();
TCCR1A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR1B = (1 << WGM13);
icr = (F_CPU/1000000*period/2);
int d = 1;
while ((icr>0xFFFF)&&(d<5)) {
d++;
icr = (F_CPU/1000000*period/2/diviseur[d]);
}
TCCR1B |= d;
set_rapport(rapport);
TCNT1 = 0;
ICR1 = icr;
sei();
}
// traitement d'une donnée entrante
void set_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==0) {
while (Serial.available()<DATA_0_SIZE) {};
Serial.readBytes(data_0,DATA_0_SIZE);
memcpy(&rapport,data_0,DATA_0_SIZE);
set_rapport(rapport);
}
else if (n==1) {
while (Serial.available()<DATA_1_SIZE) {};
Serial.readBytes(data_1,DATA_1_SIZE);
memcpy(&tensionVs,data_1,DATA_1_SIZE);
integVs = 0;
}
else if (n==2) {
while (Serial.available()<DATA_2_SIZE) {};
Serial.readBytes(data_2,DATA_2_SIZE);
memcpy(&Kp,data_2,DATA_2_SIZE);
}
else if (n==3) {
while (Serial.available()<DATA_3_SIZE) {};
Serial.readBytes(data_3,DATA_3_SIZE);
memcpy(&Ki,data_3,DATA_3_SIZE);
}
}
void get_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==1) data_1_request = true;
}
void send_data() {
if ((data_1_ready)&&(data_1_request)) {
data_1_request = false;
float Vs = analogRead(A0) *AREF/1024*DIVPOT;
Serial.write((uint8_t *)&Vs,DATA_1_SIZE);
}
}
void read_serial() {
char com;
if (Serial.available()>0) {
com = Serial.read();
if (com==GET_DATA) get_data();
else if (com==SET_DATA) set_data();
}
}
void setup() {
Serial.begin(115200);
pinMode(HIN,OUTPUT);
pinMode(LIN,OUTPUT);
pinMode(CONTROL,OUTPUT);
digitalWrite(CONTROL,LOW);
rapport = 0.8;
tensionVs = 0.0;
integVs = 0;
lastVs = 0.0;
timer1_init(100,rapport); // fréquence 10 kHz
}
void loop() {
read_serial();
send_data();
delay(10);
float Te = 0.0102;
if (tensionVs!=0.0) {
float Vs = analogRead(A0) *AREF/1024*DIVPOT;
integVs += 0.5*Te*((tensionVs-Vs)+(tensionVs-lastVs));
lastVs = Vs;
rapport = 0.4+(tensionVs-Vs)*Kp+integVs*Ki;
if (rapport > 0.99) rapport = 0.99;
else if (rapport < 0.1) rapport = 0.1;
set_rapport(rapport);
if (control) {
control = 0;
PORTE |= (1<<5); // digitalWrite(CONTROL,HIGH)
}
else {
control=1;
PORTE &= ~(1<<5); // digitalWrite(CONTROL,HIGH)
}
}
}
Le script Python suivant configure le correcteur PI (valeurs de Ki,Kp) puis demande à l'utilisateur une tension de consigne.
from Arduino import Arduino
import time
ard = Arduino('COM3',[4,4])
time.sleep(1)
RAPPORT = 0
TENSION = 1
KP = 2
KI = 3
Kp = -0.05
Ki = -0.1
ard.write_float(KP,Kp)
ard.write_float(KI,Ki)
while True:
r = input('?')
if r=='n': break
elif r=="v":
Vs = ard.read_float(TENSION)
print("Vs = %f"%Vs)
else:
tension = float(r)
ard.write_float(TENSION,tension)
ard.close()
Le choix des paramètres Ki et Kp se fait de manière empirique. On commence par choisir Kp avec Ki=0. Dans ce cas, la réponse est très rapide (limité tout de même par le temps de réponse du convertisseur et par la période d'échantillonnage) mais l'erreur est grande. On diminue l'erreur en augmentant la valeur absolue de Kp mais une valeur trop grande donne des oscillations de la tension Vs. On augmente donc la valeur (absolue) jusqu'à une amplitude d'ondulation de tension jugée acceptable.
Voici la tension Vs pour Kp=-0,1 et Kp=0, lorsque la consigne passe de 2 à 5 V et réciproquement :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0-V2-V5-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0-V5-V2-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
grid()
ylim(0,6)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=560\,{\rm\Omega},\ K_p=-0,1,\ K_i=0$",fontsize=16)
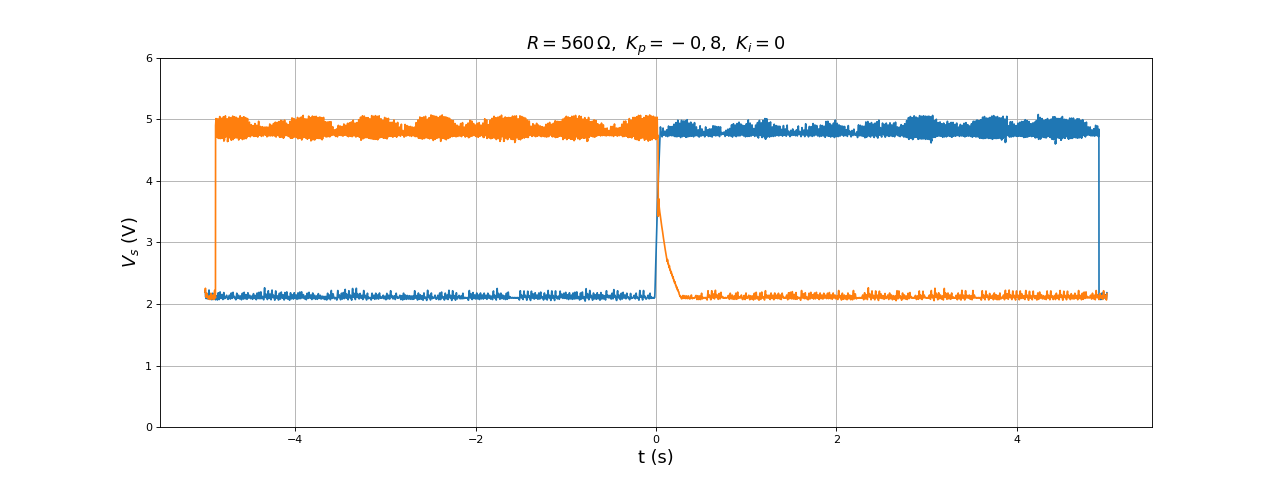 fig37.pdf
fig37.pdf
L'erreur, c'est-à-dire l'écart entre la consigne et la valeur de la tension, est très grande. Le temps de réponse est de l'ordre de 1/10 secondes (beaucoup plus que la période d'échantillonnage, qui est de 10 ms). Voici le résultat pour une valeur de Kp 5 fois plus grande :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("boost-DC1-Kp0,5-Ki0-V2-V5-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
[t,Vs] = np.loadtxt("boost-DC1-Kp0,5-Ki0-V5-V2-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
grid()
ylim(0,6)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=560\,{\rm\Omega},\ K_p=-0,5,\ K_i=0$",fontsize=16)
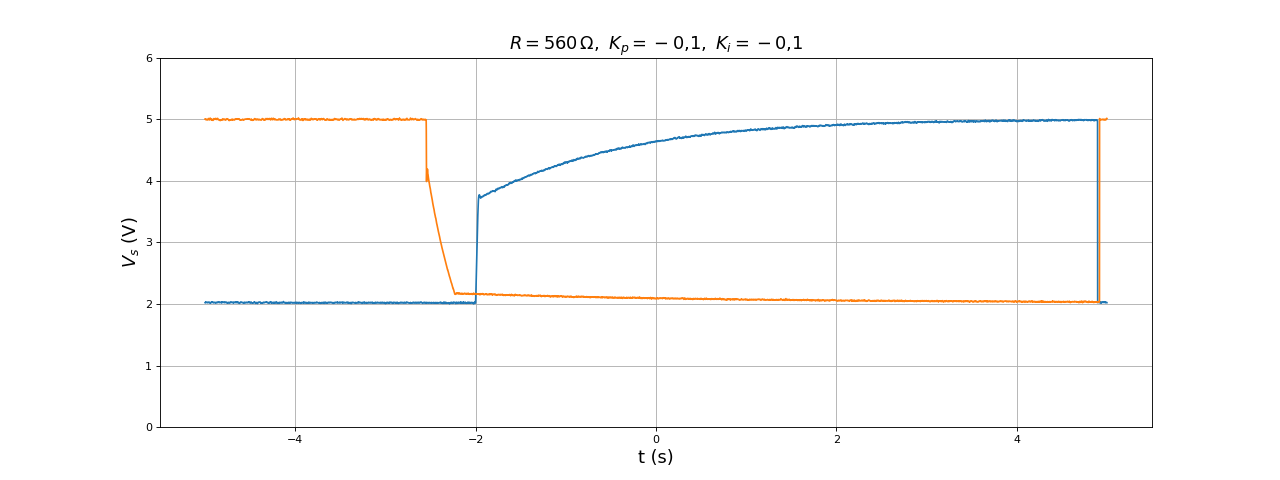 fig38.pdf
fig38.pdf
Comme prévu, l'augmentation de la valeur absolue de Kp permet de réduire l'erreur mais on voit apparaître des oscillations de la tension. Voici le résultat pour une valeur encore plus grande :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("boost-DC1-Kp0,8-Ki0-V2-V5-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
[t,Vs] = np.loadtxt("boost-DC1-Kp0,8-Ki0-V5-V2-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
grid()
ylim(0,6)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=560\,{\rm\Omega},\ K_p=-0,8,\ K_i=0$",fontsize=16)
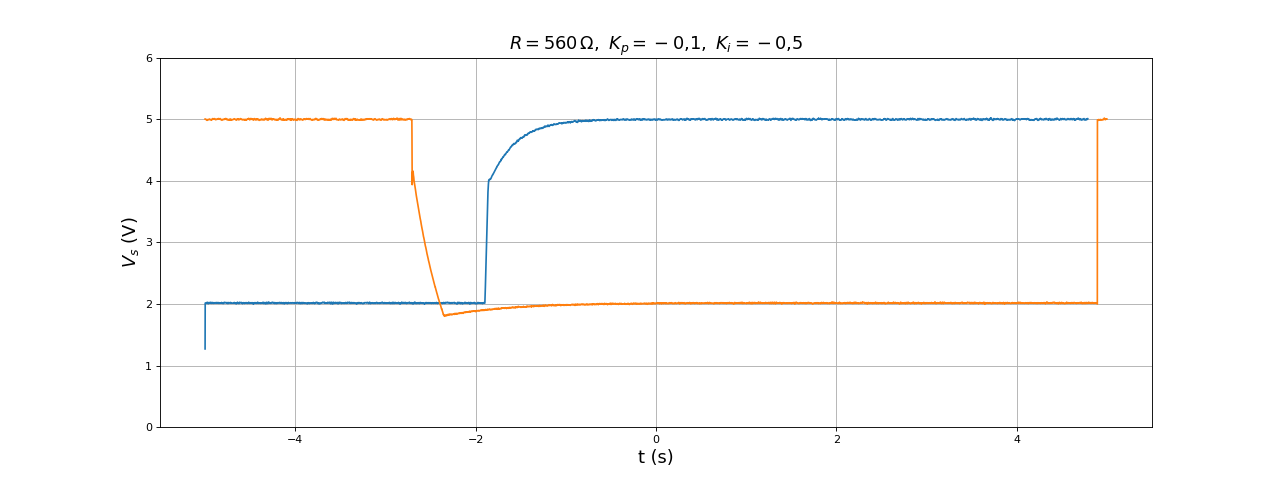 fig39.pdf
fig39.pdf
Nous adoptons la valeur Kp=0,1, qui permet d'avoir une amplitude d'ondulation acceptable. Afin de réduire l'erreur, on ajoute l'intégrateur, avec pour commencer Ki=-0,1 :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0,1-V2-V5-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0,1-V5-V2-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
grid()
ylim(0,6)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=560\,{\rm\Omega},\ K_p=-0{,}1,\ K_i=-0{,}1$",fontsize=16)
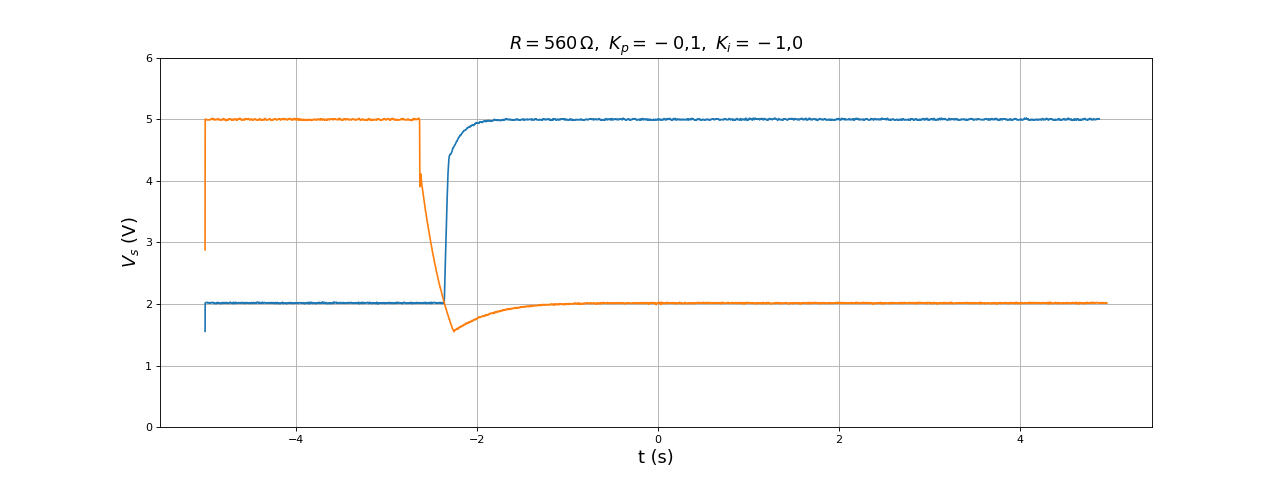 fig40.pdf
fig40.pdf
La précision est considérablement améliorée mais le temps de réponse est beaucoup plus long. On augmente Ki :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0,5-V2-V5-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0,5-V5-V2-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
grid()
ylim(0,6)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=560\,{\rm\Omega},\ K_p=-0{,}1,\ K_i=-0{,}5$",fontsize=16)
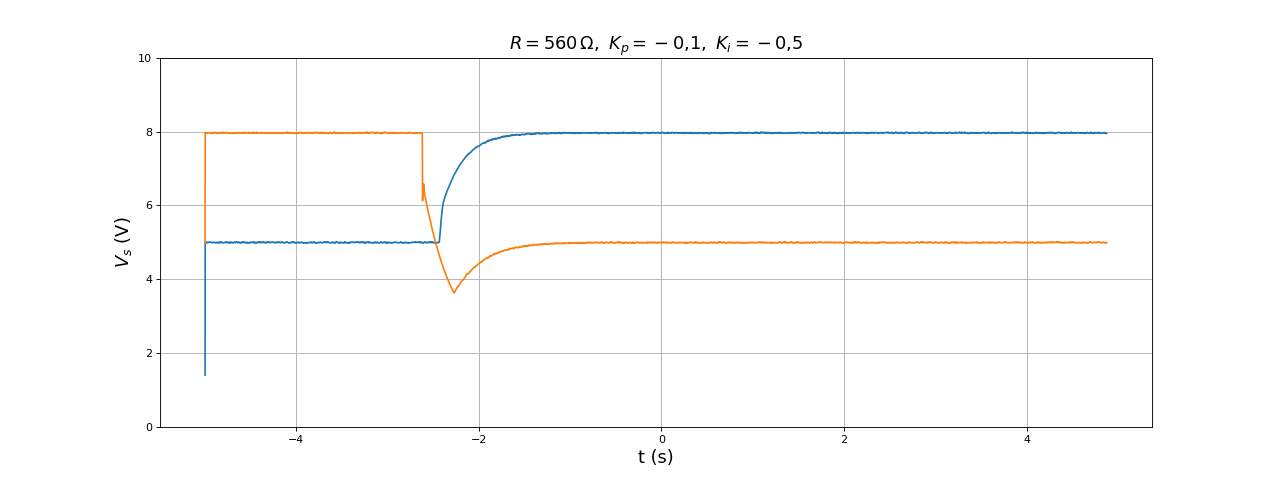 fig41.pdf
fig41.pdf
L'augmentation de Ki (en valeur absolu) permet de réduire le temps de réponse. On constate cependant un léger dépassement dans le cas du passage de 5 à 2 V. Voici le résultat pour une valeur de Ki encore plus grande :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki1,0-V2-V5-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki1,0-V5-V2-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
grid()
ylim(0,6)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=560\,{\rm\Omega},\ K_p=-0{,}1,\ K_i=-1{,}0$",fontsize=16)
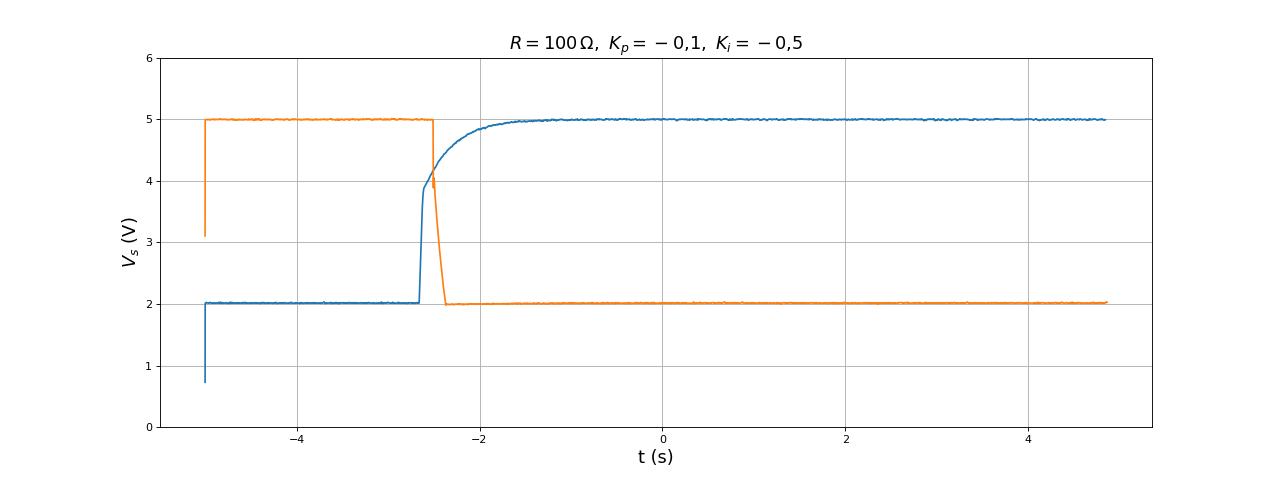 fig42.pdf
fig42.pdf
Le temps de réponse est encore réduit mais le dépassement devient trop grand. On retient finalement les valeurs Kp=-0,1 et Ki=-0,5.
Avec cette résistance de charge, nous pouvons en principe aller jusqu'à une tension de 14 V mais nous constatons que l'erreur devient trop grande à partir de 9 V. Voici le résultat pour un passage de 5 à 8 V :
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0,5-V5-V8-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0,5-V8-V5-R560.txt",skiprows=1,unpack=True)
plot(t,Vs)
grid()
ylim(0,10)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=560\,{\rm\Omega},\ K_p=-0{,}1,\ K_i=-0{,}5$",fontsize=16)
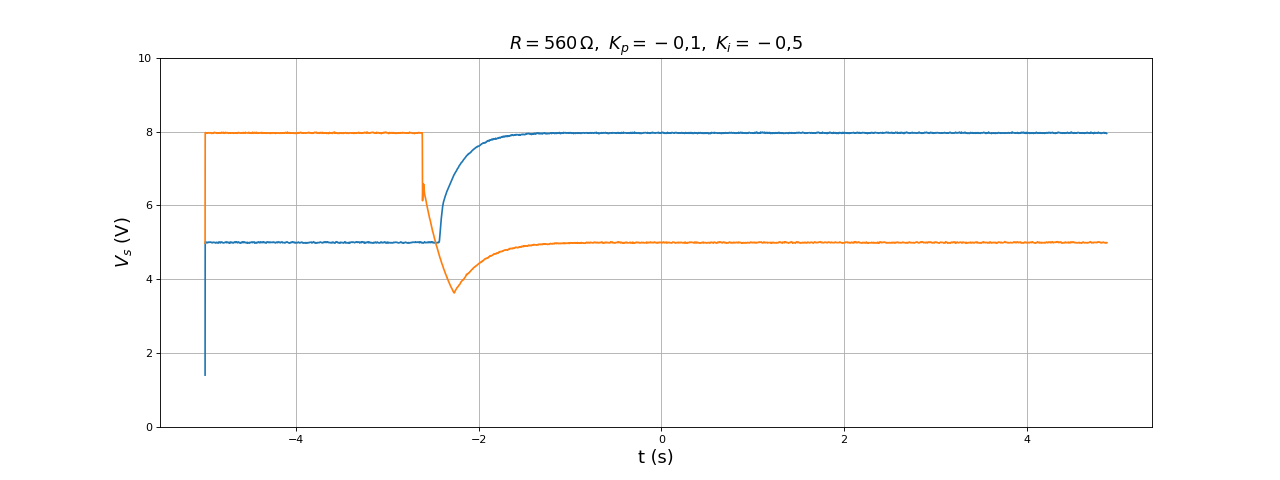 fig43.pdf
fig43.pdf
Le dépassement peut être réduit en ajoutant un terme proportionnel à la dérivée de Vs(t) (correcteur PID). La mise en œuvre d'un correcteur PID est cependant plus difficile car le calcul de la dérivée doit être associé à un filtrage passe-bas.
Nous devons à présent vérifier le fonctionnement du correcteur PI avec la résistance de charge de 100 ohms. Voici un exemple avec une tension de consigne passant de 2 à 5 volts et réciproquement.
figure(figsize=(16,6))
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0,5-V2-V5-R100.txt",skiprows=1,unpack=True)
plot(t,Vs)
[t,Vs] = np.loadtxt("boost-DC1-Kp0,1-Ki0,5-V5-V2-R100.txt",skiprows=1,unpack=True)
plot(t,Vs)
grid()
ylim(0,6)
xlabel("t (s)",fontsize=16)
ylabel(r"$V_s\ (\rm V)$",fontsize=16)
title(r"$R=100\,{\rm\Omega},\ K_p=-0{,}1,\ K_i=-0{,}5$",fontsize=16)
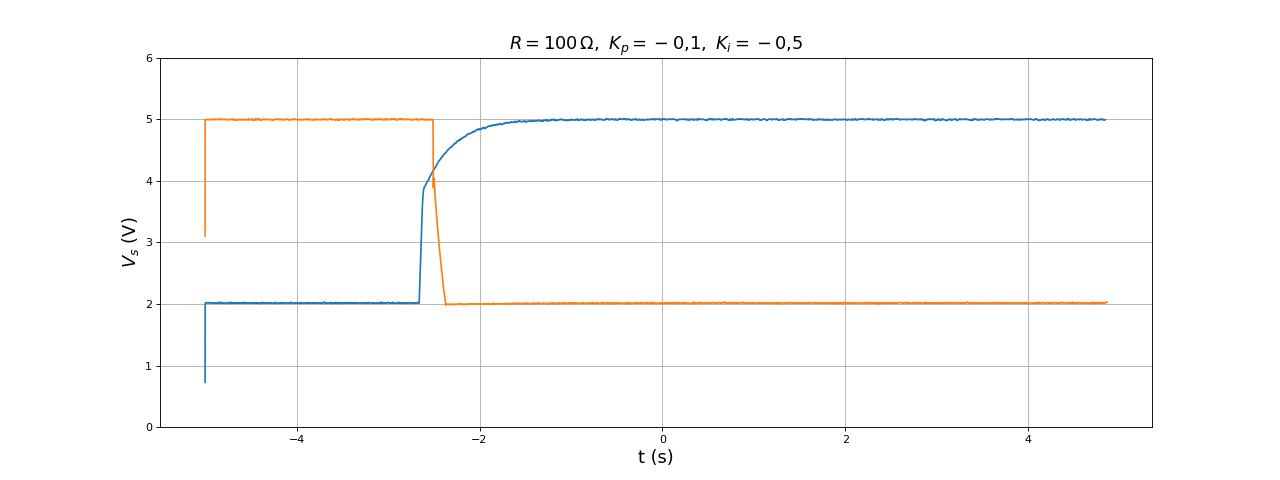 fig44.pdf
fig44.pdf
Pour cette résistance de charge plus petite, il n'y a plus de dépassement. Cela suggère que la constante de temps RC joue un rôle important dans ce dépassement. Le temps de latence due à la période d'échantillonnage de 10 ms est visible sur ces courbes. Il est clairement plus petit que le temps de réponse, ce qui confirme que cette période d'échantillonnage est assez petite.