Machine synchrone à aimants permanents
1. Introduction
Ce document montre comment piloter un moteur synchrone à aimants permanent de type BLDC (brushless direct current motor). Le fonctionnement et le pilotage de ce type de moteur est développé dans Moteur synchrone à aimants permanents, où un prototype de moteur est présenté.
L'objectif est de faire fonctionner un moteur BLDC aussi bien en moteur qu'en générateur. Le convertisseur DC-AC utilisé pour alimenter les trois bobines du stator fonctionne de manière réversible, c'est-à-dire qu'il peut (avec la même séquence de commutation) faire fonctionner la machine en moteur et en générateur. Lorsque le fonctionnement moteur est l'usage principal (par exemple pour propulser un véhicule), le fonctionnement générateur intervient dès qu'on cherche à réduire la vitesse du moteur, en particulier lors du freinage. Dans ce cas, il peut y avoir régénération, c'est-à-dire récupération d'une partie de l'énergie cinétique du véhicule par recharge de l'accumulateur (ou par charge d'un super-condensateur).
La référence du moteur utilisé est 42DMW61-2440 :

Le rotor comporte 8 pôles (c'est-à-dire 8 aimants). La tension nominale est de 24 V et le courant maximal de 3,5 A. La vitesse à vide maximale est de 5000 tours par minute. Il comporte 3 capteurs à effet Hall permettant de déterminer précisément la position du rotor, comme expliqué dans Moteur synchrone à aimants permanents. Voici le schéma de câblage des trois bobinages du stator, montés en étoile (schéma équivalent au repos, sans forces électromotrices) :
Figure pleine pageLe moteur comporte 6 fils :
- Trois fils pour les trois bornes A,B,C des bobines du stator câblées en étoile (rouge,jaune,noir).
- Deux fils d'alimentation pour les capteurs : GND (noir) et +5V (rouge).
- Sorties des trois capteurs (1=bleu, 2=vert, 3=blanc). Il s'agit de sorties en collecteur ouvert, qu'il faut relier avec une résistance de quelques kΩ à la borne +5 V (ou bien à la borne +3,3V si on utilise un microcontrôleur opérant à cette tension).
Remarque : l'ordre de branchement des bobines est sans importance pour le bon fonctionnement du moteur bien que le sens de rotation dépende de l'ordre. En revanche, l'ordre de branchement des capteurs est important : l'auto-pilotage ne peut fonctionner que si les trois capteurs 1,2,3 sont effectivement utilisés dans cet ordre ou bien dans l'ordre inverse 3,2,1.
Voici les valeurs de 2L et 2r mesurées au repos avec un RLC-mètre à différentes fréquences :
- 100 Hz : 2L=140 μH et 2r=1,0 Ω
- 1 kHz : 2L=570 μH et 2r=1,0 Ω
- 10 kHz : 2L=530 μH et 2r=5,5 Ω
Pour le fonctionnement en moteur, pendant un des 6 états de la séquence de commutation, on alimente deux bobines avec une tension constante égale à la tension d'alimentation, ou bien avec la tension d'alimentation découpée pour obtenir une tension effective plus faible contrôlée par le rapport cyclique du découpage. En principe, le courant dans les bobines pendant le découpage doit être quasi constant (après le régime transitoire qui suit le changement d'état). La constante de temps évaluée pour une fréquence de découpage de 10 kHz est . Cette constante de temps est beaucoup plus faible que celle du prototype étudié dans Moteur synchrone à aimants permanents, qui vaut 1 ms. L'obtention d'un courant quasi constant dans une bobine nécessite une fréquence de découpage beaucoup plus grande. Il faut d'ailleurs remarquer que pour une fréquence plus grande que 10 kHz, la résistance augmente donc la constante est encore plus petite. Sachant que la fréquence de découpage d'un pont de transistors MOSFET peut difficilement dépasser 100 kHz, il semble difficile d'obtenir un courant constant dans les bobines de ce moteur. Les ondulations du courant qui en résultent donnent des oscillations du couple mais celles-ci sont sans conséquence étant donné leur fréquence très élevée. Il faudra tout de même que la fréquence de découpage soit en dehors du domaine audible (au dessus de 20 kHz).
2. Étude de la force électromotrice
Pour cette étude, le moteur est relié mécaniquement à un moteur à courant continu qui l'entraîne. Le but est d'analyser la force électromotrice produite par les bobines du stator lorsque le rotor tourne.
Les trois bobines du stator sont câblées en étoile. On dispose donc de trois bornes A,B et C pour le stator. L'expérience suivante consiste à enregistrer la tension U(t) entre deux de ces bornes et, simultanément, les signaux logiques délivrés par les capteurs à effet Hall.
import numpy as np
from matplotlib.pyplot import *
figure(figsize=(16,8))
subplot(211)
[t,U] = np.loadtxt("fem-DC5,6.txt",unpack=True,skiprows=1)
plot(t,U)
grid()
ylabel("U (V)")
subplot(212)
[t,u0,u1,u2] = np.loadtxt("hall-DC5,6.txt",unpack=True,skiprows=1)
plot(t,u0)
plot(t,u1+2)
plot(t,u2+4)
grid()
xlabel("t (s)")
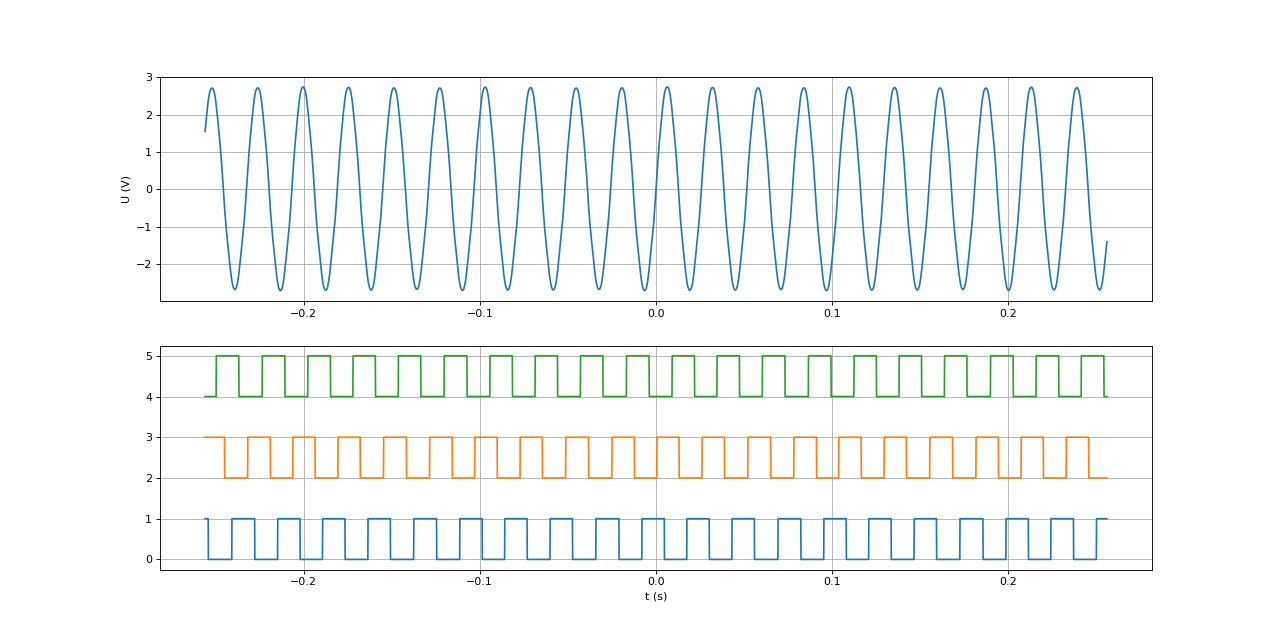 fig1.pdf
fig1.pdf
La tension U(t) est la force électromotrice générée par deux bobines du stator en série. La f.é.m. pour une seule bobine est la moitié de celle-ci.
À tout instant, deux capteurs sont dans le même état (0 ou 1) et le troisième est dans l'état contraire. Il y a donc 6 états pour l'ensemble des capteurs. Un tour complet de rotor correspond à 4 fois le cycle de 6 états. La fonction suivante permet d'obtenir l'état des 3 capteurs sous la forme d'un nombre entre 0 et 5 :
def etatRotor(t,u0,u1,u2):
etat = np.zeros(len(u0))
numEtats = [0,5,3,4,1,0,2]
for i in range(len(u0)):
x = u0[i]*4+u1[i]*2+u2[i]
etat[i] = numEtats[int(x)]
return etat
figure(figsize=(16,8))
subplot(211)
[t,U] = np.loadtxt("fem-DC5,6.txt",unpack=True,skiprows=1)
plot(t,U)
grid()
ylabel("U (V)")
subplot(212)
[t,u0,u1,u2] = np.loadtxt("hall-DC5,6.txt",unpack=True,skiprows=1)
etat = etatRotor(t,u0,u1,u2)
plot(t,etat)
grid()
xlabel("t (s)")
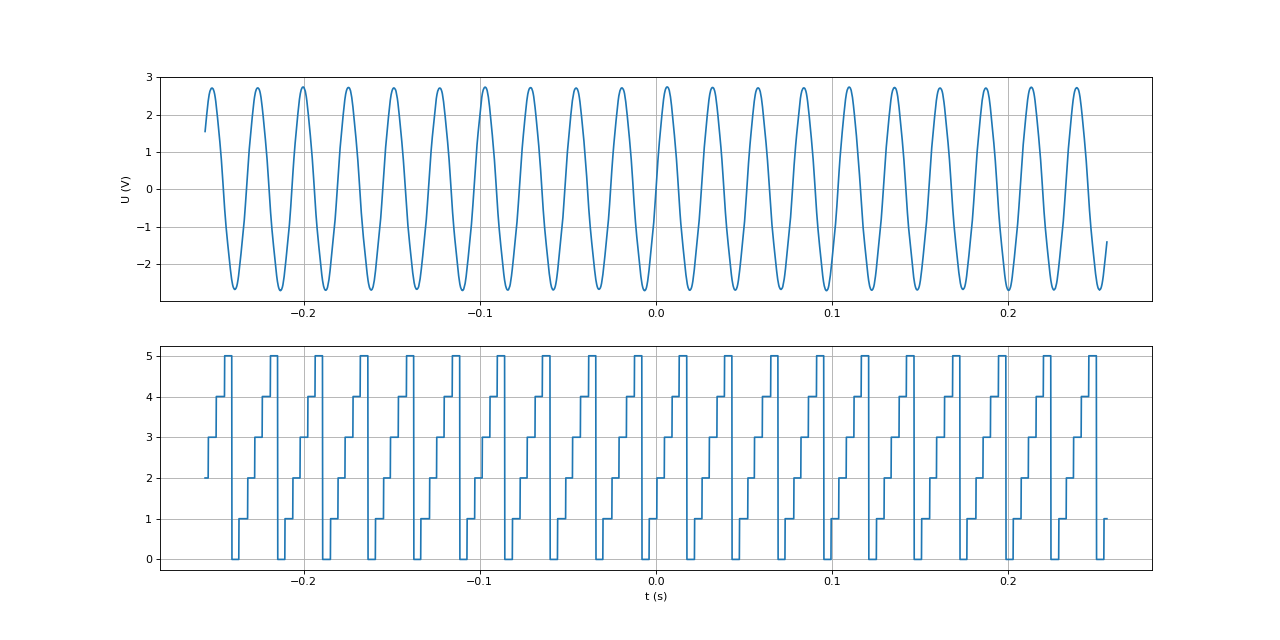 fig2.pdf
fig2.pdf
Un cycle de la tension entre deux bornes de phase correspond exactement à un cycle de 6 états.
Pour obtenir la vitesse de rotation, il suffit de déterminer la période de changement d'état (il y a 24 états par tour de rotor) :
def extractionPeriode(t,u0,u1,u2):
periode = []
temps = []
tchange = t[0]
etat0 = u0[0] > 0.5
etat1 = u1[0] > 0.5
etat2 = u2[0] > 0.5
for i in range(1,len(t)):
if (u0[i] < 0.5 and etat0) or (u0[i] > 0.5 and not(etat0)):
periode.append(t[i]-tchange)
temps.append(t[i])
tchange = t[i]
etat0 = not(etat0)
if (u1[i] < 0.5 and etat1) or (u1[i] > 0.5 and not(etat1)):
periode.append(t[i]-tchange)
temps.append(t[i])
tchange = t[i]
etat1 = not(etat1)
if (u2[i] < 0.5 and etat2) or (u2[i] > 0.5 and not(etat2)):
periode.append(t[i]-tchange)
temps.append(t[i])
tchange = t[i]
etat2 = not(etat2)
periode = np.array(periode)
w = 60/(periode.mean()*24) # pédiode de rotation en tr/min
return periode,w
[t,u0,u1,u2] = np.loadtxt("hall-DC5,6.txt",unpack=True,skiprows=1)
periode,w1 = extractionPeriode(t,u0,u1,u2)
figure()
plot(periode)
grid()
xlabel("etat")
ylabel("Période (s)")
U1 = U.std()
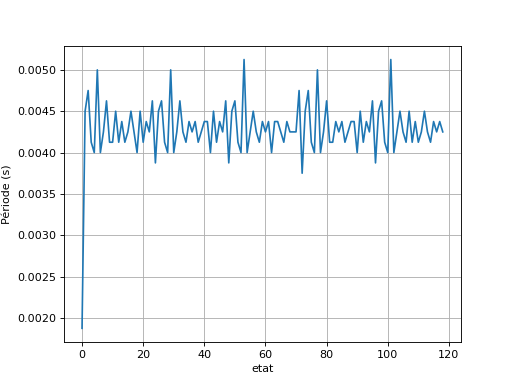 fig3.pdf
fig3.pdf
print(w1) --> 583.0475257226848
print(U1) --> 1.9191095307527348
Pour cette vitesse angulaire (donnée en tours/seconde), la valeur efficace de la f.é.m. mesurée entre deux bornes de phase est 1,9 V.
Voici les signaux pour une vitesse de rotation plus grande :
figure(figsize=(16,8))
subplot(211)
[t,U] = np.loadtxt("fem-DC9.txt",unpack=True,skiprows=1)
plot(t,U)
grid()
ylabel("U (V)")
subplot(212)
[t,u0,u1,u2] = np.loadtxt("hall-DC9.txt",unpack=True,skiprows=1)
plot(t,u0)
plot(t,u1+2)
plot(t,u2+4)
grid()
xlabel("t (s)")
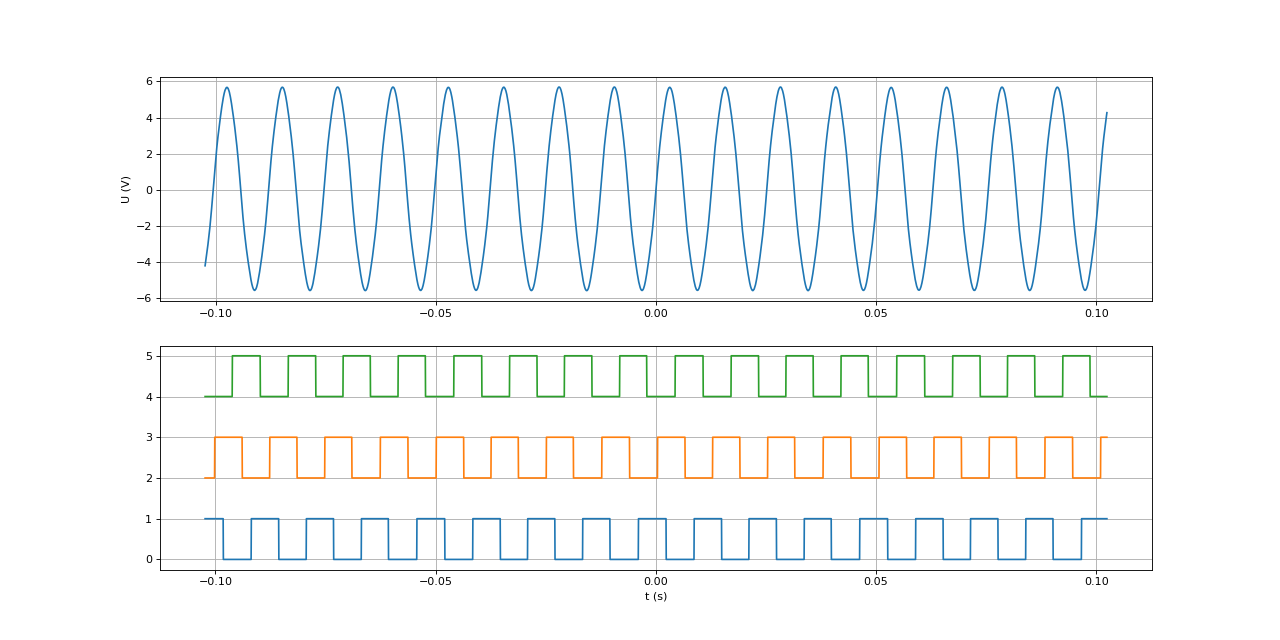 fig4.pdf
fig4.pdf
[t,u0,u1,u2] = np.loadtxt("hall-DC9.txt",unpack=True,skiprows=1)
periode,w2 = extractionPeriode(t,u0,u1,u2)
U2 = U.std()
print(w2) --> 1192.5252028522252
print(U2) --> 3.9052648542074313
Voici les signaux pour une vitesse de rotation plus grande :
figure(figsize=(16,8))
subplot(211)
[t,U] = np.loadtxt("fem-DC12.txt",unpack=True,skiprows=1)
plot(t,U)
grid()
ylabel("U (V)")
subplot(212)
[t,u0,u1,u2] = np.loadtxt("hall-DC12.txt",unpack=True,skiprows=1)
plot(t,u0)
plot(t,u1+2)
plot(t,u2+4)
grid()
xlabel("t (s)")
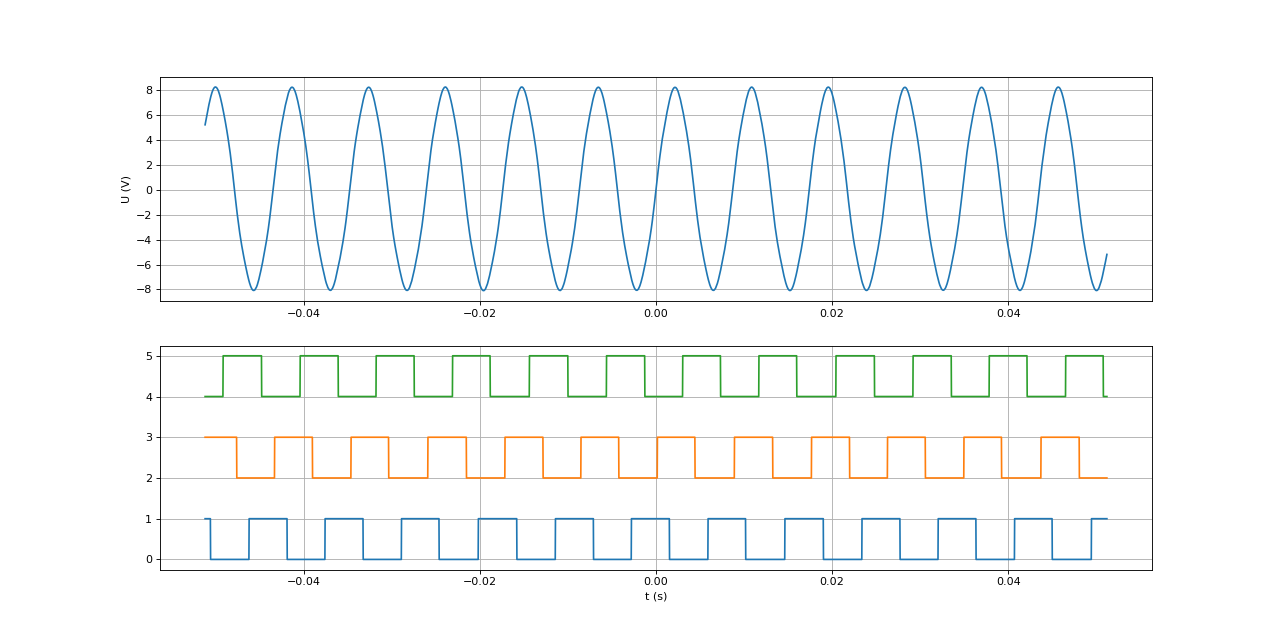 fig5.pdf
fig5.pdf
[t,u0,u1,u2] = np.loadtxt("hall-DC12.txt",unpack=True,skiprows=1)
periode,w3 = extractionPeriode(t,u0,u1,u2)
U3 = U.std()
print(w3) --> 1740.6227016425596
print(U3) --> 5.7039495411165575
Voici la valeur efficace de la f.é.m. (pour deux bobines) en fonction de la vitesse de rotation :
figure()
plot([w1,w2,w3],[U1,U2,U3],"bo")
grid()
xlabel(r"$\omega\ (\rm tr/min)$")
ylabel(r"$U_{\rm eff}\ (\rm V)$")
xlim(0,2000)
ylim(0,6)
coef,cov = np.polyfit([w1,w2,w3],[U1,U2,U3],deg=1,cov='unscaled')
a,b=coef
plot([0,2000],[b,a*2000+b])
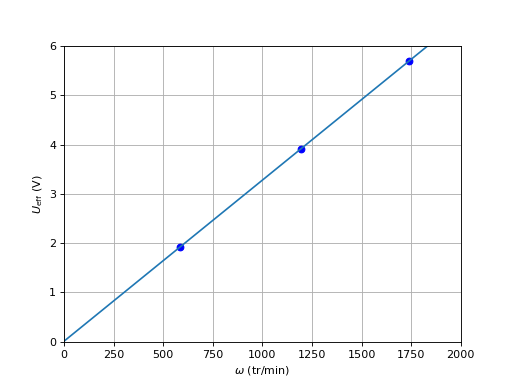 fig6.pdf
fig6.pdf
L'amplitude de crête du flux magnétique dans une bobine est déterminé par la relation :
où la vitesse angulaire est exprimée en radians par seconde.
Phi0 = np.sqrt(2)/2/(2*np.pi/60)*a
print(Phi0) --> 0.022076382927885146
On obtient , soit environ 20 fois plus que pour le prototype étudié dans Moteur synchrone à aimants permanents. À vitesse de rotation égale, la f.é.m. est donc 20 fois plus grande. En conséquence, à tension appliquée égale, la vitesse de rotation (à vide) sera environ 20 fois plus grande.
La forme de la force électromotrice est quasi sinusoïdale et non pas trapézoïdale. La commande optimale de ce type de moteur devrait se faire en appliquant aux bobines du stator des tensions sinusoïdales. Cependant, la commande la plus courante des petits moteurs BLDC se fait en appliquant des tensions constantes par intervalle, ce qui d'ailleurs justifie l'appelation de moteur à courant continu sans balais. Dans le présent document, nous considérons effectivement ce type de commande, qui se fait au moyen d'un Commutateur triphasé à 6 états. Le commutateur est auto-piloté par les capteurs : à chacun des 6 états correspond un état de commutation du pont de transistors. Notons que les trois capteurs à effet Hall ne permettent pas de faire une commande sinusoïdale, qui exige une détermination beaucoup plus précise de la position du rotor (au moyen d'un codeur optique).
3. Fonctionnement en moteur
3.a. Pont de transistors
La commutation à 6 états consiste à alimenter successivement les bobines. À chaque état, deux bobines sont alimentées par une tension constante, ou bien par une tension constante découpée avec un rapport cyclique donné. La troisième bobine est laissée à l'état libre, c'est-à-dire que le potentiel de sa borne n'est pas imposé par le pont. La commutation à 6 états est décrite en détail dans Commutateur triphasé à 6 états.
Voici le schéma électrique de principe du pont, représenté avec la source de tension E et le schéma équivalent des bobines du stator :
Figure pleine pageDans ce schéma, les f.é.m. des bobines du stator sont par convention dans le même sens que l'intensité du courant algébrique (comme il se doit pour l'application de la loi de Faraday). Ces f.é.m. s'opposent (en moyenne) aux variations du courant imposées par la source, d'où l'appelation courante de force contre électromotrice (qui désigne plutôt l'opposée de celle définie sur ce schéma). Nous préférons employer l'expression force électromotrice dans les bobines du stator plutôt que force contre-électromotrice car dans le cas du fonctionnement en générateur (par exemple en freinage régénératif), la notion de force contre-électromotrice perd son sens. Par ailleurs, il ne faut pas oublier que les forces électromotrices du stator sont alternatives donc de valeur moyenne nulle. Cependant, si le moteur est représenté par un moteur à courant continu équivalent, la force électromotrice est constante et négative.
La simulation Moteur synchrone montre le fonctionnement du pont.
La figure suivante représente l'état 0 de la commutation à 6 états (en l'absence de MLI) :
Figure pleine pageLe trait rouge représente le sens du courant positif lorsque le régime permanent de l'état.
Voici l'état 1 :
Figure pleine pageVoici l'état 2 :
Figure pleine pageVoici l'état 3 :
Figure pleine pageVoici l'état 4 :
Figure pleine pageVoici l'état 5 :
Figure pleine pageRemarque : à chaque état, une des trois bobines est à l'état libre, c'est-à-dire que le potentiel de sa borne n'est pas imposé par le pont. Cependant, un courant transitoire peut circuler dans cette bobine via la diode du transistor du bas. Lorsque la vitesse de rotation du moteur est assez grande, le courant dans les bobines ne s'annule jamais. La description courante consistant à affirmer que le courant ne passe que dans deux bobines à la fois est donc inexacte.
La régulation de la vitesse par modulation de largeur d'impulsion unipolaire (MLI ou PWM) consite a découper la tension E en commutant, pour chaque état, le transistor du haut K du bras de pont qui impose le potentiel positif avec un rapport cyclique alors que le transistor du bas K' est commuté en opposition. Par exemple pour l'état 0, le transistor K'2 est fermé en permanence mais le transitor K1 est fermé seulement pendant la durée , où T est la période de découpage (fréquence de découpage de l'ordre de 10 kHz à 100 kHz). Lorsque K1 est ouvert, K'1 est fermé et inversement. La figure suivante schématise l'état 0 en mode MLI :
Figure pleine pageNotons qu'il est possible de faire une MLI bipolaire : dans ce cas, les deux bras de pont sont commutés en opposition à la fréquence de découpage, par exemple le bras 1 et le bras 2 pour l'état 0.
Ce schéma de commutation permet de faire fonctionner la machine en moteur mais aussi, comme nous allons le montrer, en générateur.
Voici le schéma du pont de transistors MOSFET, comportant 6 transistors MOSFET et trois pilotes de pont (IR2113) :
Figure pleine pageCe circuit comporte aussi trois comparateurs permettant de faire un pilotage sans capteurs (non utilisé ici).
3.b. Programme Arduino
La génération des signaux de commande du pont au moyen de Timers est décrite dans Commutateur triphasé à six états et dans Moteur synchrone à aimants permanents. Le protocole de communication décrit dans Échanges de données avec un Arduino permet de configurer et de piloter la commande depuis un script Python.
Les données échangées sont :
- Le rapport cyclique de découpage (float 32 bits).
- Le sens de rotation (int 8 bits).
- Période de découpage en microsecondes (float 32 bits).
- Mode de fonctionnement (int 8 bits) : 0 pour le mode où le rapport cyclique est imposé, 1 pour le mode où une vitesse de consigne est donnée.
- Tampon de float 32 bits contenant les dernières périodes mesurées (taille BUFSIZE).
- Vitesse de rotation (float 32 bits). Cette valeur peut être envoyée vers l'Arduino dans le mode 1 ou bien fournie par l'Arduino dans le mode 0.
- Commande de l'alimentation (int 8 bits), utilisée avec le circuit d'interface entre l'alimentation et le pont (voir 5.a) : 1 pour le fonctionnement moteur, 2 pour la roue libre, 3 pour le frein moteur.
- Kp (float 32 bits) : coefficient pour le correcteur PI de la régulation de vitesse.
- Ki (float 32 bits) : coefficient pour le correcteur PI.
Les sorties des trois capteurs à effet Hall doivent être branchés sur les entrées IN1,IN2 et IN3 (dans cet ordre).
La commande des 6 transistors du pont (schéma ci-dessus) est effectée sur les sorties indiquées dans le code (HINA,LINA,HINB,LINB,HINC,LINC).
Pour le frein moteur et la roue libre, la commande des deux transistors du circuit d'interface de l'alimentation (voir 5.a) se fait avec ALLIN et ALHIN.
#include "Arduino.h"
// bras de pont phase A
#define INA_1 11 // transistor haut du bras A : HINA
#define INA_2 12 // transistor bas du bras A : LINA
// bras de pont phase B
#define INB_1 5 // HINB
#define INB_2 2 // LINB
// bras de pont phase C
#define INC_1 6 // HINC
#define INC_2 7 //LINC
#define PWM // activation du découpage
// sans PWM la vitesse du moteur est déterminée par la tension de la source
#define TRIGGER 3 // PE5 sortie de déclenchement pour l'oscilloscope
#define CONTROL 4 // PG5 signal de contrôle, change d'état à chaque tour du rotor
// commande de l'alimentation
#define ALIN_EN 14 // enable
#define ALLIN 15 // transistor du bas (connecté à la masse)
#define ALHIN 16 // transistor du haut (connecté à l'alimentation)
// états d'un bras de pont
#define HIGH_0_LOW_1 0 // sortie à la masse (état 01)
#define HIGH_1_LOW_0 1 // sortie en PWM (état 10)
#define HIGH_0_LOW_0 2 // sortie non connectée (état 00)
uint8_t sequence_A[6] = {1,1,2,0,0,2};
uint8_t sequence_B[6] = {0,2,1,1,2,0};
uint8_t sequence_C[6] = {2,0,0,2,1,1};
uint8_t sensRot = 0;
uint8_t etat_capteurs_anterieur;
// capteurs HALL
#define IN1 18 // PD3
#define IN2 19 // PD2
#define IN3 20 // PD1
uint8_t tableEtats[8];
uint32_t compteur;
uint32_t temps;
float period;
float omega;
float omegaDemand = 1.0;
float Kp=0.02;
float Ki=0.02;
float integOmega;
#define BUFSIZE 10
float bufPeriod[BUFSIZE];
uint8_t ibuf;
uint8_t etatControl;
bool commut = true;
uint32_t updateTime;
bool rotation;
uint16_t icr;
uint16_t ocra,ocrb;
uint16_t temps_mort = 10;
uint16_t diviseur[6] = {0,1,8,64,256,1024};
float periodPWM = 50;
float rapport = 0.0;
uint8_t mode = 0; // mode de fonctionnement : 0 : contrôle du rapport cyclique, 1 : contrôle de la vitesse
uint8_t alim = 0; // alimentation 1 : moteur, 2 : roue libre, 3 : freinage
#define RAPPORT_MIN 0.05
#define RAPPORT_MAX 0.7
// communication Série
#define GET_DATA 10
#define SET_DATA 11
#define DATA_0_SIZE 4 // rapport cyclique (float)
#define DATA_1_SIZE 1 // sens de rotation (int8)
#define DATA_2_SIZE 4 // période en us (float)
#define DATA_3_SIZE 1 // mode de fonctionnement (int8)
#define DATA_4_SIZE 4*BUFSIZE // tampon des périodes
#define DATA_5_SIZE 4 // vitesse en tours/s (float)
#define DATA_6_SIZE 1 // alimentation 1 : moteur, 2 : roue libre, 3 : freinage
#define DATA_7_SIZE 4 // Kp
#define DATA_8_SIZE 4 // Ki
uint8_t data_0[DATA_0_SIZE];
uint8_t data_1[DATA_1_SIZE];
uint8_t data_2[DATA_2_SIZE];
uint8_t data_3[DATA_3_SIZE];
uint8_t data_5[DATA_5_SIZE];
uint8_t data_6[DATA_6_SIZE];
uint8_t data_7[DATA_7_SIZE];
uint8_t data_8[DATA_8_SIZE];
bool data_2_ready = true;
bool data_2_request = false;
bool data_4_ready = false;
bool data_4_request = false;
void config_timers(float period, float rapport) {
// period : période du PWM en microsecondes
cli();
TCCR1A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR1B = (1 << WGM13);
TCCR3A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR3B = (1 << WGM13);
TCCR4A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR4B = (1 << WGM13);
icr = (F_CPU/1000000*period/2);
int d = 1;
while ((icr>0xFFFF)&&(d<5)) {
d++;
icr = (F_CPU/1000000*period/2/diviseur[d]);
}
TCCR1B |= d;
TCCR3B |= d;
TCCR4B |= d;
if (icr*rapport>temps_mort) {
ocra = icr*rapport-temps_mort;
ocrb = icr*rapport+temps_mort;
}
else {
ocra = icr*rapport;
ocrb = icr*rapport;
}
TCNT1 = 0;
TCNT3 = 0;
TCNT4 = 0;
ICR1 = icr;
ICR3 = icr;
ICR4 = icr;
OCR1A = ocra;
OCR1B = ocrb;
OCR3A = ocra;
OCR3B = ocrb;
OCR4A = ocra;
OCR4B = ocrb;
sei();
}
void stop_pwm() {
TCCR1A &= ~((1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0));
TCCR3A &= ~((1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0));
TCCR4A &= ~((1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0));
}
void start_pwm() {
TCCR1A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR3A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
TCCR4A = (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
}
void open_all() {
digitalWrite(INA_1,LOW);
digitalWrite(INA_2,LOW);
digitalWrite(INB_1,LOW);
digitalWrite(INC_2,LOW);
digitalWrite(INC_1,LOW);
digitalWrite(INC_2,LOW);
}
void changer_rapport_pwm(float rapport) {
if (icr*rapport>temps_mort) {
ocra = icr*rapport-temps_mort;
ocrb = icr*rapport+temps_mort;
}
else {
ocra = icr*rapport;
ocrb = icr*rapport;
}
}
void etat_bras_A(uint8_t etat) {
#ifdef PWM
switch (etat) {
case HIGH_0_LOW_1:
OCR1A = 0;
OCR1B = 0;
break;
case HIGH_1_LOW_0:
OCR1A = ocra;
OCR1B = ocrb;
break;
case HIGH_0_LOW_0:
OCR1A = 0;
OCR1B = icr+1;
break;
}
#else
switch (etat) {
case HIGH_0_LOW_1:
digitalWrite(INA_1,LOW);
digitalWrite(INA_2,HIGH);
break;
case HIGH_1_LOW_0:
digitalWrite(INA_1,HIGH);
digitalWrite(INA_2,LOW);
break;
case HIGH_0_LOW_0:
digitalWrite(INA_1,LOW);
digitalWrite(INA_2,LOW);
break;
}
#endif
}
void etat_bras_B(uint8_t etat) {
#ifdef PWM
switch (etat) {
case HIGH_0_LOW_1:
OCR3A = 0;
OCR3B = 0;
break;
case HIGH_1_LOW_0:
OCR3A = ocra;
OCR3B = ocrb;
break;
case HIGH_0_LOW_0:
OCR3A = 0;
OCR3B = icr+1;
break;
}
#else
switch (etat) {
case HIGH_0_LOW_1:
digitalWrite(INB_1,LOW);
digitalWrite(INB_2,HIGH);
break;
case HIGH_1_LOW_0:
digitalWrite(INB_1,HIGH);
digitalWrite(INB_2,LOW);
break;
case HIGH_0_LOW_0:
digitalWrite(INB_1,LOW);
digitalWrite(INB_2,LOW);
break;
}
#endif
}
void etat_bras_C(uint8_t etat) {
#ifdef PWM
switch (etat) {
case HIGH_0_LOW_1:
OCR4A = 0;
OCR4B = 0;
break;
case HIGH_1_LOW_0:
OCR4A = ocra;
OCR4B = ocrb;
break;
case HIGH_0_LOW_0:
OCR4A = 0;
OCR4B = icr+1;
break;
}
#else
switch (etat) {
case HIGH_0_LOW_1:
digitalWrite(INC_1,LOW);
digitalWrite(INC_2,HIGH);
break;
case HIGH_1_LOW_0:
digitalWrite(INC_1,HIGH);
digitalWrite(INC_2,LOW);
break;
case HIGH_0_LOW_0:
digitalWrite(INC_1,LOW);
digitalWrite(INC_2,LOW);
break;
}
#endif
}
void change_rapport() { // régulation PI
if (omega!=0) integOmega += (omegaDemand-omega)/omega;
else integOmega += omegaDemand*0.2;
rapport = Kp*(omegaDemand-omega)+Ki*integOmega;
if (rapport>RAPPORT_MAX) rapport = RAPPORT_MAX;
if (rapport<0) rapport = RAPPORT_MIN;
changer_rapport_pwm(rapport);
}
void change_etat() {
if (commut==false) return;
uint32_t t;
uint8_t etat_capteurs = (PIND >> 1)&0b111;
if (omega!=0) {
if (etat_capteurs==etat_capteurs_anterieur) return;
etat_capteurs_anterieur = etat_capteurs;
}
if ((etat_capteurs==0)||(etat_capteurs==0xb111)) return;
uint8_t is = tableEtats[etat_capteurs];
etat_bras_A(sequence_A[is]);
etat_bras_B(sequence_B[is]);
etat_bras_C(sequence_C[is]);
compteur += 1;
if (compteur>=2) rotation =true;
if (compteur==24) { // 1 tour
if (etatControl==0) {
PORTG |= (1<<5); //digitalWrite(CONTROL,HIGH);
etatControl = 1;
}
else {
PORTG &= ~(1<<5); //digitalWrite(CONTROL,LOW);
etatControl = 0;
}
compteur = 0;
t = micros();
period = t-temps;
temps = t;
bufPeriod[ibuf] = period;
PORTE &= ~(1<<5); //digitalWrite(TRIGGER,LOW);
if (mode==1) {
omega = 1/(period*1e-6);
change_rapport();
}
ibuf++;
if (ibuf==BUFSIZE) {
ibuf = 0;
data_4_ready = true;
}
memcpy(data_2,&period,DATA_2_SIZE);
data_2_ready = true;
}
}
void remplir_table_etats(uint8_t sensRot) {
if (sensRot==0) {
tableEtats[B010] = 3;
tableEtats[B011] = 4;
tableEtats[B001] = 5;
tableEtats[B101] = 0;
tableEtats[B100] = 1;
tableEtats[B110] = 2;
}
else {
tableEtats[B010] = 0;
tableEtats[B011] = 1;
tableEtats[B001] = 2;
tableEtats[B101] = 3;
tableEtats[B100] = 4;
tableEtats[B110] = 5;
}
}
void get_data() {
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==2) data_2_request = true;
if (n==4) data_4_request = true;
}
void send_data() {
if ((data_2_ready)&&(data_2_request)) {
//data_2_ready = false;
data_2_request = false;
Serial.write(data_2,DATA_2_SIZE);
}
if ((data_4_ready)&&(data_4_request)) {
//data_4_ready = false;
data_4_request = false;
Serial.write((uint8_t *)bufPeriod,DATA_4_SIZE);
}
}
void set_data() { // données reçues
char n;
while (Serial.available()<1) {};
n = Serial.read();
if (n==0) { // rapport cyclique de découpage
while (Serial.available()<DATA_0_SIZE) {};
Serial.readBytes(data_0,DATA_0_SIZE);
memcpy(&rapport,data_0,DATA_0_SIZE);
//digitalWrite(TRIGGER,HIGH)
changer_rapport_pwm(rapport);
period = 0.0;
change_etat();
}
else if (n==1) { // sens de rotation
while (Serial.available()<DATA_1_SIZE) {};
Serial.readBytes(data_1,DATA_1_SIZE);
memcpy(&sensRot,data_1,DATA_1_SIZE);
remplir_table_etats(sensRot);
}
else if (n==3) { // mode de fonctionnement
while (Serial.available()<DATA_3_SIZE) {};
Serial.readBytes(data_3,DATA_3_SIZE);
memcpy(&mode,data_3,DATA_3_SIZE);
}
else if (n==5) { // vitesse angulaire consigne
while (Serial.available()<DATA_5_SIZE) {};
Serial.readBytes(data_5,DATA_5_SIZE);
memcpy(&omegaDemand,data_5,DATA_5_SIZE);
digitalWrite(TRIGGER,HIGH);
change_rapport();
change_etat();
}
else if (n==6) { // état du pont d'alimentation
while (Serial.available()<DATA_6_SIZE) {};
Serial.readBytes(data_6,DATA_6_SIZE);
memcpy(&alim,data_6,DATA_6_SIZE);
digitalWrite(ALIN_EN,LOW);
if (alim==1) { // alimentation connectée
commut = true;
start_pwm();
// transistor du haut passant
digitalWrite(ALLIN,LOW);
digitalWrite(ALHIN,HIGH);
}
else if (alim==2) { // alimentation déconnectée, roue libre
digitalWrite(TRIGGER,LOW);
digitalWrite(TRIGGER,HIGH);
//commut = false; // à décommenter pour obtenir une roue libre sans commutation
stop_pwm();
open_all(); // permet d'ouvrir tout les transistors du pont
// deux transistors ouverts
digitalWrite(ALHIN,LOW);
digitalWrite(ALLIN,LOW);
}
else if (alim==3) { // alimentation déconnectée, frein moteur
commut = true;
start_pwm();
// transistor du bas passant
digitalWrite(ALLIN,HIGH);
digitalWrite(ALHIN,LOW);
digitalWrite(TRIGGER,LOW);
digitalWrite(TRIGGER,HIGH);
}
digitalWrite(ALIN_EN,HIGH);
}
else if (n==7) {
while (Serial.available()<DATA_7_SIZE) {};
Serial.readBytes(data_7,DATA_7_SIZE);
memcpy(&Kp,data_7,DATA_7_SIZE);
}
else if (n==8) {
while (Serial.available()<DATA_8_SIZE) {};
Serial.readBytes(data_8,DATA_8_SIZE);
memcpy(&Ki,data_8,DATA_8_SIZE);
}
}
void read_serial() {
char com;
if (Serial.available()>0) {
com = Serial.read();
if (com==GET_DATA) get_data();
else if (com==SET_DATA) set_data();
}
}
void setup() {
Serial.begin(115200);
while(!Serial);
remplir_table_etats(sensRot);
pinMode(INA_1,OUTPUT);
digitalWrite(INA_1,LOW);
pinMode(INA_2,OUTPUT);
digitalWrite(INA_2,LOW);
pinMode(INB_1,OUTPUT);
digitalWrite(INB_1,LOW);
pinMode(INB_2,OUTPUT);
digitalWrite(INB_2,LOW);
pinMode(INC_1,OUTPUT);
digitalWrite(INC_1,LOW);
pinMode(INC_2,OUTPUT);
digitalWrite(INC_2,LOW);
pinMode(IN1,INPUT);
pinMode(IN2,INPUT);
pinMode(IN3,INPUT);
pinMode(TRIGGER,OUTPUT);
digitalWrite(TRIGGER,LOW);
pinMode(CONTROL,OUTPUT);
digitalWrite(CONTROL,LOW);
pinMode(ALIN_EN,OUTPUT);
pinMode(ALHIN,OUTPUT);
pinMode(ALLIN,OUTPUT);
digitalWrite(ALHIN,LOW);
digitalWrite(HIN_IN2,HIGH);
digitalWrite(ALLIN,HIGH);
attachInterrupt(digitalPinToInterrupt(IN1),change_etat,CHANGE);
attachInterrupt(digitalPinToInterrupt(IN2),change_etat,CHANGE);
attachInterrupt(digitalPinToInterrupt(IN3),change_etat,CHANGE);
updateTime = millis();
#ifdef PWM
config_timers(periodPWM,rapport);
#endif
ibuf = 0;
compteur = 0;
temps = micros();
omega = 0;
integOmega = 0;
etatControl = 0;
etat_capteurs_anterieur = 0;
commut = true;
rotation = false;
change_etat();
}
void loop() {
read_serial();
send_data();
delay(100);
if ((mode==1)&&(omega==0)) {
change_rapport();
change_etat();
}
}
3.c. Fonctionnement à tension imposée
La source de tension est une alimentation de laboratoire stabilisée en tension.
Dans ce mode de fonctionnement (mode 0), on choisit le rapport cyclique de découpage, ce qui a pour effet d'imposer une tension effective aux bobines, égale à la tension d'alimentation multipliée par le rapport cyclique. La vitesse de rotation est évidemment d'autant plus grande que cette tension effective est grande.
Pour contrôler le bon fonctionnement du programme de pilotage, un signal est émis sur la sortie CONTROL (D4), qui change d'état à chaque tour de moteur, c'est-à-dire à chaque fois que 24 changements d'état des capteurs se sont produits. La moitié de la période de ce signal est égale à la période de rotation. Autrement dit, le double de sa fréquence est égal à la fréquence de rotation en tours par seconde.
Voici un test fait avec une tension d'alimentation E=12 V. L'arbre du moteur est relié à celui d'un moteur à courant continu mais les bornes de celui-ci ne sont pas branchées. On a donc un couple mécanique modéré mais plus grand que si le moteur tourne à vide. Pour un rapport cyclique donné, on enregistre les signaux des trois capteurs et le signal CONTROL. On récupère aussi une liste de périodes de rotation calculées par le programme lui-même.
Voici les signaux pour un rapport cyclique . La période du signal CONTROL est 666 ms, ce qui fait une période de rotation de 333 ms.
[t,u0,u1,u2,uc] = np.loadtxt("hall-Vs12-R0,1.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
title(r"$E = 12\ {\rm V}, \alpha = 0,1$")
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
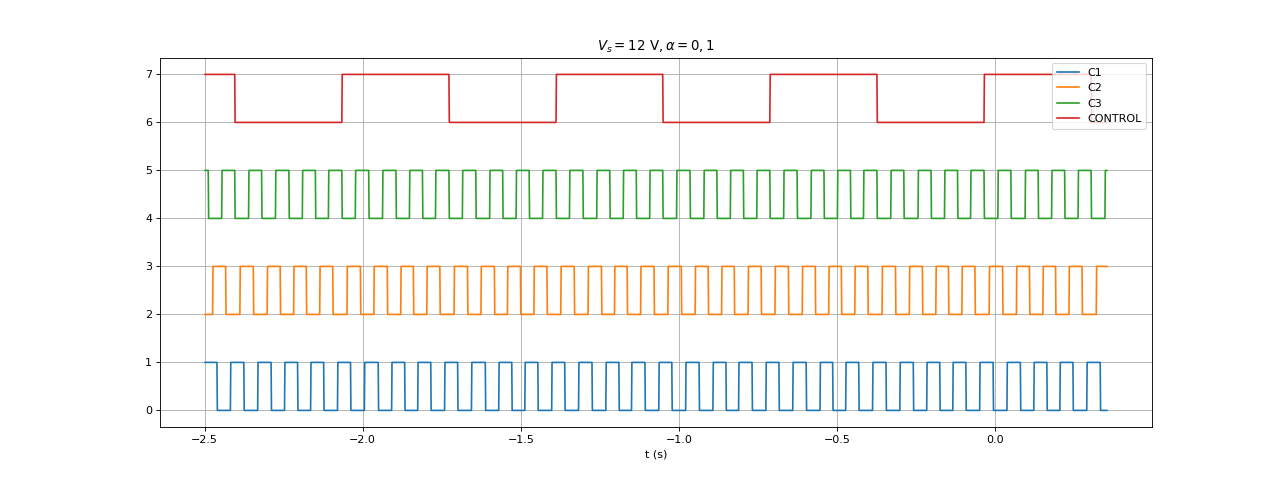 fig7.pdf
fig7.pdf
Voici la liste des 10 périodes fournie par le programme (en microsecondes) :
338308. 338556. 338336. 338680. 338460. 338380. 338632. 338264. 338424. 338168.
Cette période est un peu plus grande que la période fournie par le signal CONTROL, de 5 ms environ.
Un tour de rotor, correspondant à un état du signal CONTROL, se fait en 24 états des capteurs, soit 4 cycles de 6 états. Sachant que chaque capteur change 2 fois d'état par cycle de 6 états, chaque capteur doit changer 8 fois d'état pendant un tour de rotor. C'est bien ce qu'on observe sur les signaux ci-dessus.
Voici les résultats pour . La période de CONTROL est 270 ms, soit une période de rotation de 135 ms.
[t,u0,u1,u2,uc] = np.loadtxt("hall-Vs12-R0,2.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
title(r"$E = 12\ {\rm V}, \alpha = 0,2$")
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
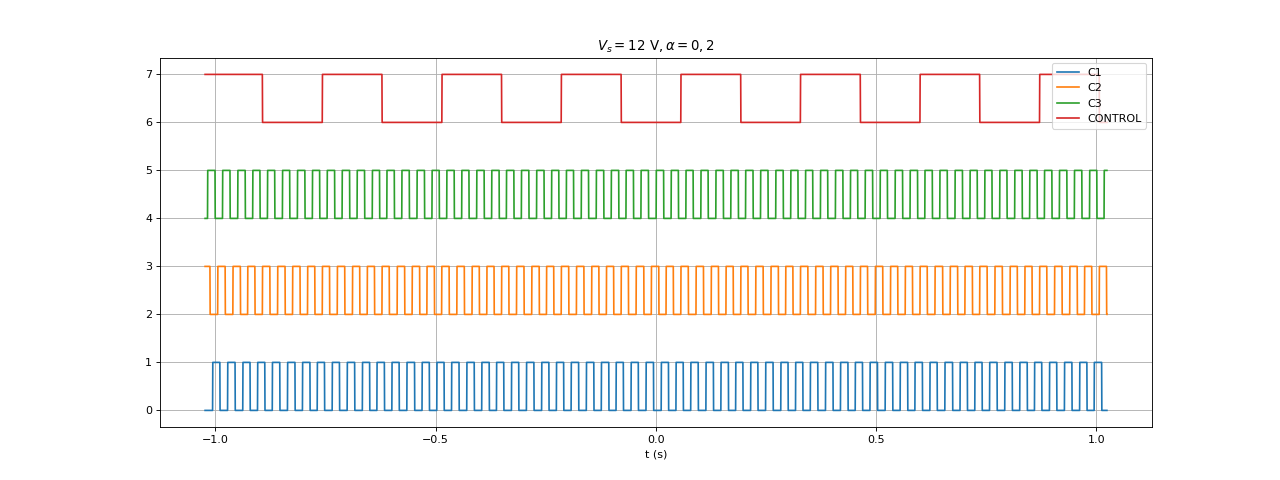 fig8.pdf
fig8.pdf
Voici la liste des 10 périodes fournie par le programme (en microsecondes) :
135992. 135904. 135944. 136000. 135892. 135996. 135996. 136092. 136016. 135920.
Voici les résultats pour . La période de CONTROL est 122 ms, soit une période de rotation de 61 ms.
[t,u0,u1,u2,uc] = np.loadtxt("hall-Vs12-R0,4.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
title(r"$E = 12\ {\rm V}, \alpha = 0,4$")
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
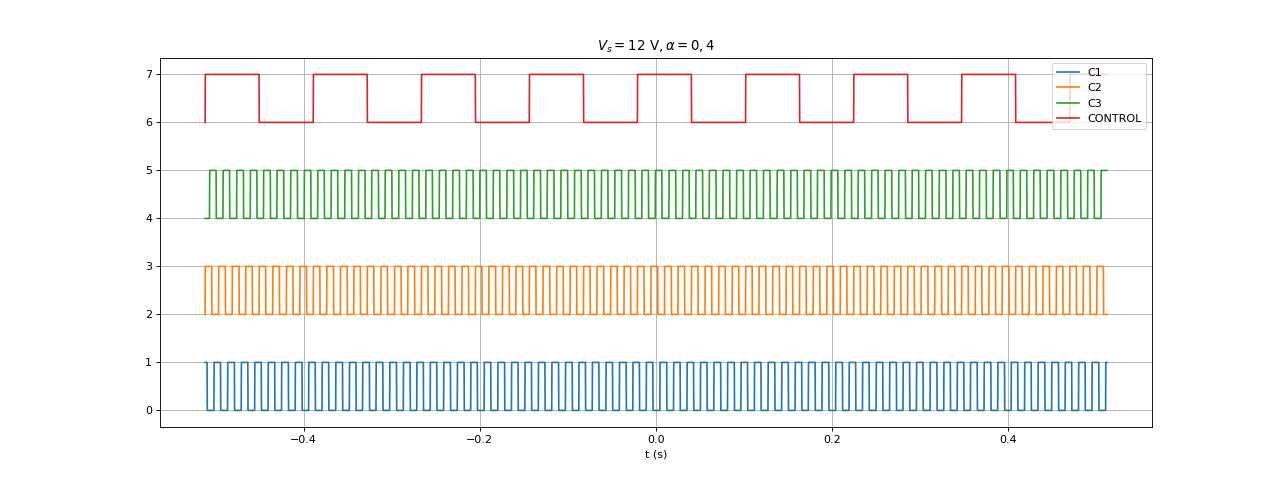 fig9.pdf
fig9.pdf
Voici la liste des 10 périodes fournie par le programme (en microsecondes) :
61360. 61364. 61364. 61376. 61308. 61348. 61392. 61380. 61392. 61412.
Voici les résultats pour . La période de CONTROL est 79 ms, soit une période de rotation de 38 ms.
[t,u0,u1,u2,uc] = np.loadtxt("hall-Vs12-R0,6.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
title(r"$E = 12\ {\rm V}, \alpha = 0,6$")
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
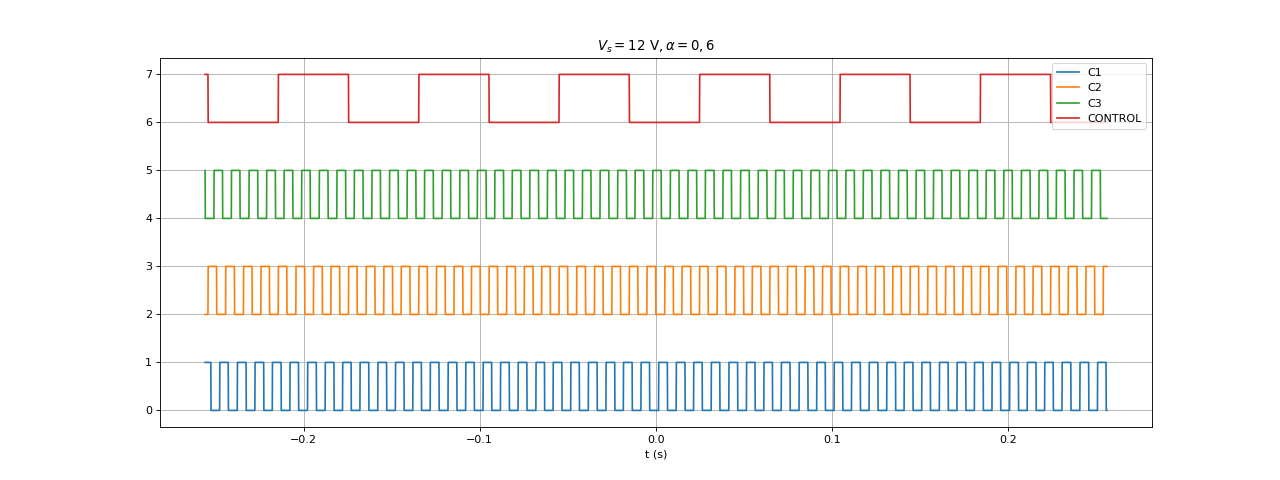 fig10.pdf
fig10.pdf
39884. 39892. 39892. 39884. 39900. 39924. 39892. 39904. 39896. 39888.
Voici les résultats pour . La période de CONTROL est 59 ms, soit une période de rotation de 29,5 ms.
[t,u0,u1,u2,uc] = np.loadtxt("hall-Vs12-R0,8.txt",unpack=True,skiprows=1)
figure(figsize=(16,6))
title(r"$E = 12\ {\rm V}, \alpha = 0,8$")
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
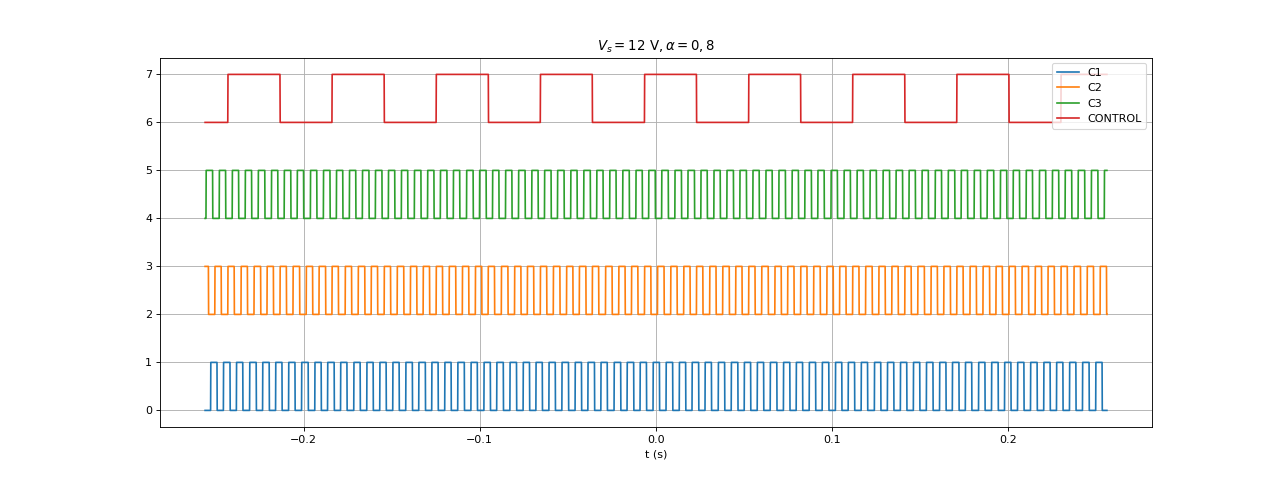 fig11.pdf
fig11.pdf
29592. 29572. 29592. 29580. 29588. 29596. 29556. 29592. 29588. 29604.
Voici la vitesse de rotation en fonction du rapport cyclique (rappelons que le moteur est sous charge légère) :
T = np.array([333,135,61,38,29.5])
alpha = [0.1,0.2,0.4,0.6,0.8]
w = 60/(T*1e-3)
figure()
title("E = 10 V")
plot(alpha,w,"o")
grid()
xlabel(r"$\alpha$",fontsize=16)
xlim(0,1)
ylim(0,3000)
ylabel(r"$\omega\ (\rm tours/min)$",fontsize=16)
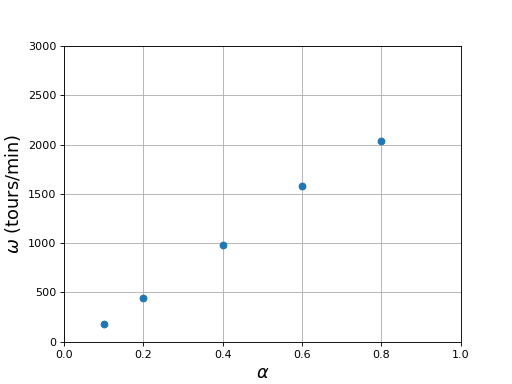 fig12.pdf
fig12.pdf
La vitesse augmente proportionnellement au rapport cyclique, c'est-à-dire à la tension effective appliquée aux bobine. Il s'agit du comportement d'un moteur à courant continu à couple nul (moteur tournant à vide, sans couple mécanique). Remarquons toutefois que, en réalité, la manière dont la charge mécanique évolue avec la vitesse de rotation a un effet sur cette dépendance. La dépendance linéaire vient du fait que le couple mécanique dépend linéairement de la vitesse. C'est à peu près le cas lorsque le moteur tourne à vide et c'est aussi le cas ici puisque le moteur ne fait qu'entraîner un moteur à courant continu (dont les bornes sont déconnectées).
4. Fonctionnement en générateur
4.a. Étude sans charge électrique
Le moteur est entraîné par un moteur à courant continu. On enregistre la tension aux bornes d'entrée du pont (tension Vout).
Figure pleine pageOn a placé sur ce schéma le condensateur de capacité C=2200 uF qui se trouve à l'entrée du pont car il joue un rôle important dans le fonctionnement en générateur.
Voici les signaux pour un rapport cyclique :
figure(figsize=(16,8))
subplot(211)
title(r"$\alpha=0{,}8$")
[t,Vout] = np.loadtxt("generateur-Vout-DC10-r0,8.txt",unpack=True,skiprows=1)
V1 = Vout.mean()
plot(t,Vout)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
grid()
ylim(0,20)
subplot(212)
[t,u0,u1,u2,uc] = np.loadtxt("generateur-hall-DC10-r0,8.txt",unpack=True,skiprows=1)
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
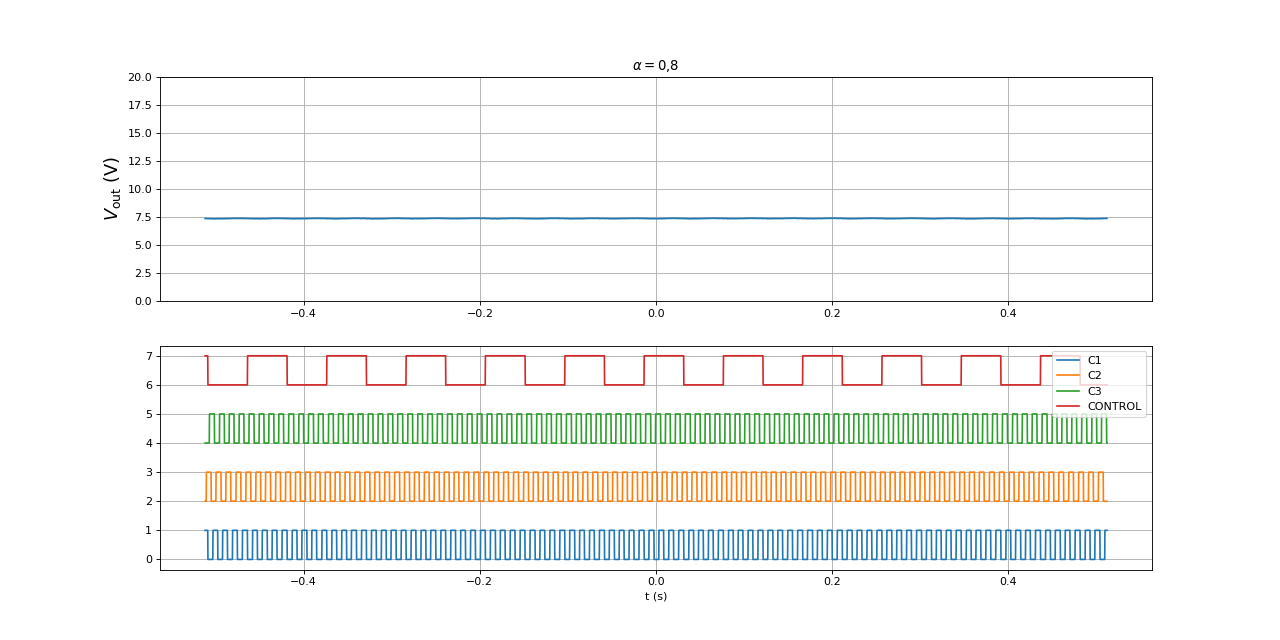 fig13.pdf
fig13.pdf
et la période de rotation (en microsecondes) :
45232. 45284. 45224. 45220. 45224. 45244. 45256. 45216. 45236. 45212.
La tension Vout est quasi constante. Voici les ondulations de cette tension :
figure(figsize=(16,8))
subplot(211)
title(r"$\alpha=0{,}8$")
[t,Vout] = np.loadtxt("generateur-Vout-DC10-r0,8.txt",unpack=True,skiprows=1)
plot(t,Vout)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
grid()
ylim(7,7.6)
subplot(212)
[t,u0,u1,u2,uc] = np.loadtxt("generateur-hall-DC10-r0,8.txt",unpack=True,skiprows=1)
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
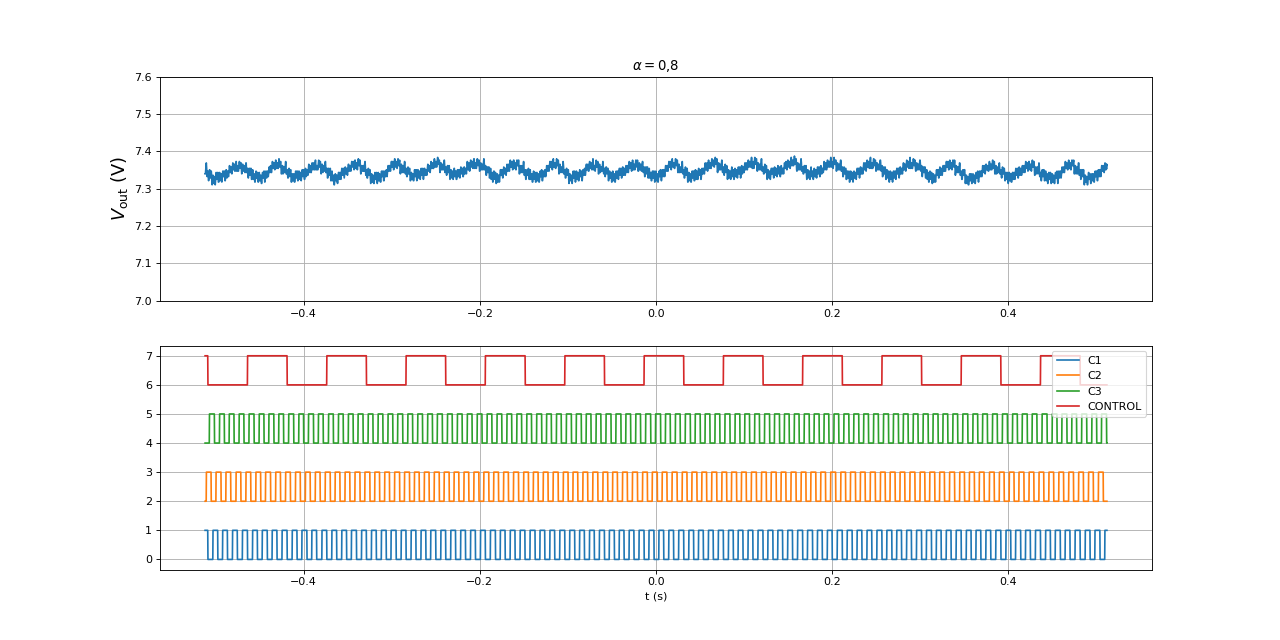 fig14.pdf
fig14.pdf
L'amplitude relative de crête à crête de l'ondulation est d'environ .
Voici les signaux pour un rapport cyclique :
figure(figsize=(16,8))
subplot(211)
title(r"$\alpha=0{,}5$")
[t,Vout] = np.loadtxt("generateur-Vout-DC10-r0,5.txt",unpack=True,skiprows=1)
V2 = Vout.mean()
plot(t,Vout)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
grid()
ylim(0,20)
subplot(212)
[t,u0,u1,u2,uc] = np.loadtxt("generateur-hall-DC10-r0,5.txt",unpack=True,skiprows=1)
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
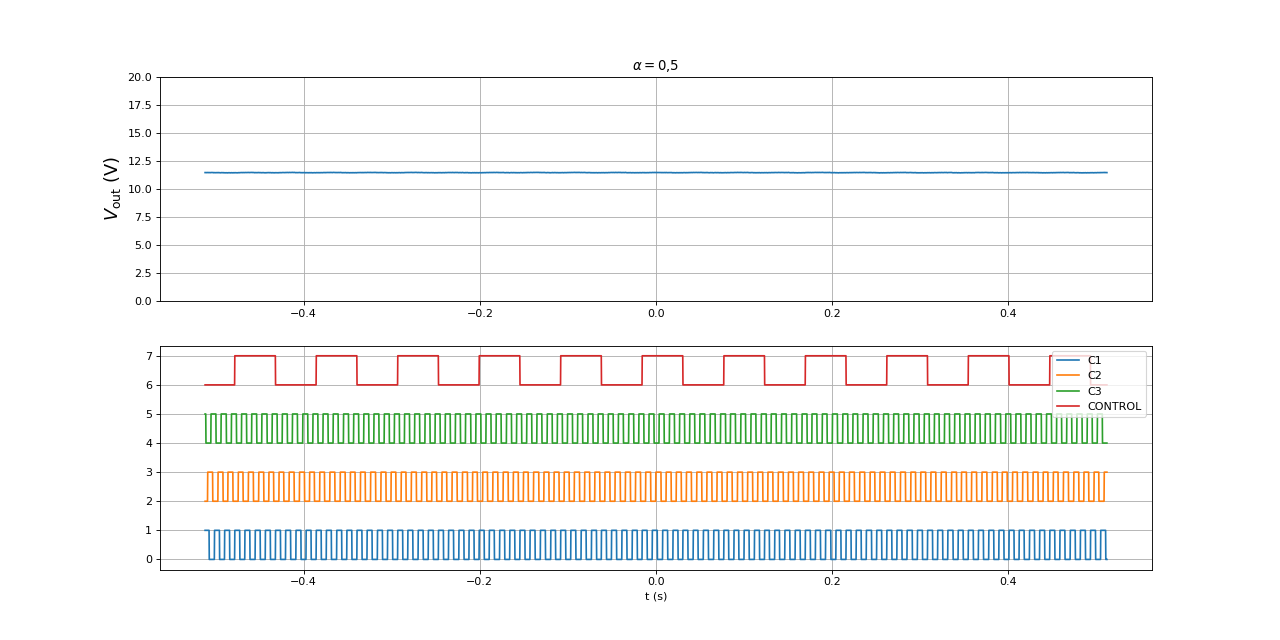 fig15.pdf
fig15.pdf
45892. 45884. 45904. 45896. 45856. 45868. 45876. 45896. 45860. 45884.
Voici les signaux pour un rapport cyclique :
figure(figsize=(16,8))
subplot(211)
title(r"$\alpha=0{,}3$")
[t,Vout] = np.loadtxt("generateur-Vout-DC10-r0,3.txt",unpack=True,skiprows=1)
V3 = Vout.mean()
plot(t,Vout)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
grid()
ylim(0,20)
subplot(212)
[t,u0,u1,u2,uc] = np.loadtxt("generateur-hall-DC10-r0,3.txt",unpack=True,skiprows=1)
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
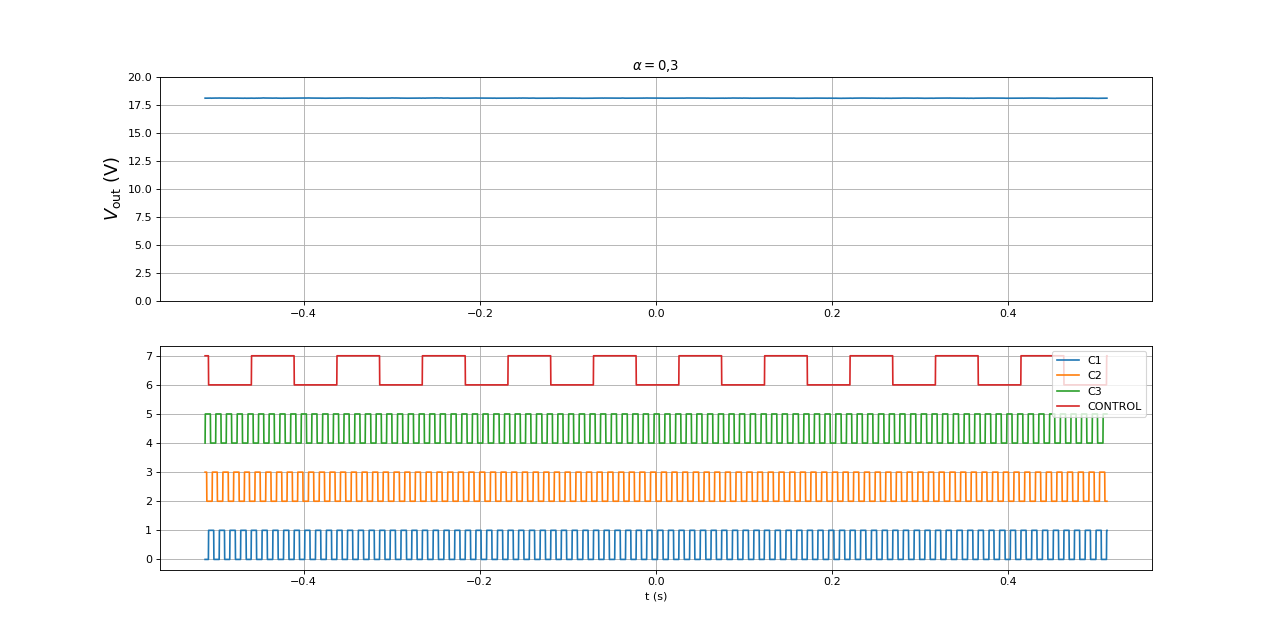 fig16.pdf
fig16.pdf
48764. 48764. 48736. 48748. 48788. 48784. 48776. 48784. 48808. 48800.
Voici la tension Vout en fonction du rapport cyclique :
rapport = [0.3,0.5,0.8]
Vout = [V3,V2,V1]
figure()
plot(rapport,Vout,"o")
grid()
xlabel(r"$\alpha$",fontsize=16)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
xlim(0,1)
ylim(0,20)
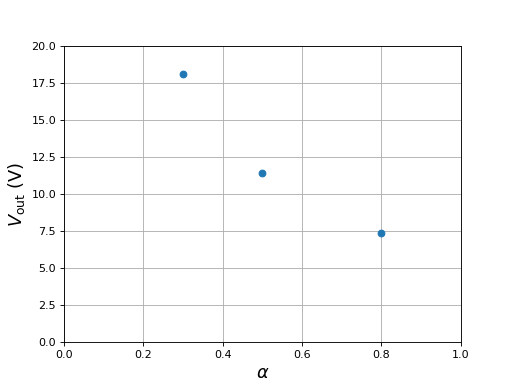 fig17.pdf
fig17.pdf
La tension en entrée du pont est d'autant plus grande que le rapport cyclique est bas. Dans les trois cas, la vitesse de rotation est à peu près la même (environ 1300 tours pas minute), ce qui est logique puisqu'aucune charge n'est branchée sur Vout. La petite différence de vitesse observée provient sans doute des pertes dans les transistors du pont.
Il est possible d'éliminer complètement le découpage en enlevant la définition de la macro PWM. Voici le résultat (la période de rotation est de 44 ms) :
figure(figsize=(16,8))
subplot(211)
title(r"$\alpha = 1$"+" (pas de PWM)")
[t,Vout] = np.loadtxt("generateur-Vout-DC10-r1.txt",unpack=True,skiprows=1)
V4 = Vout.mean()
plot(t,Vout)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
grid()
ylim(0,20)
subplot(212)
[t,u0,u1,u2,uc] = np.loadtxt("generateur-hall-DC10-r1.txt",unpack=True,skiprows=1)
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
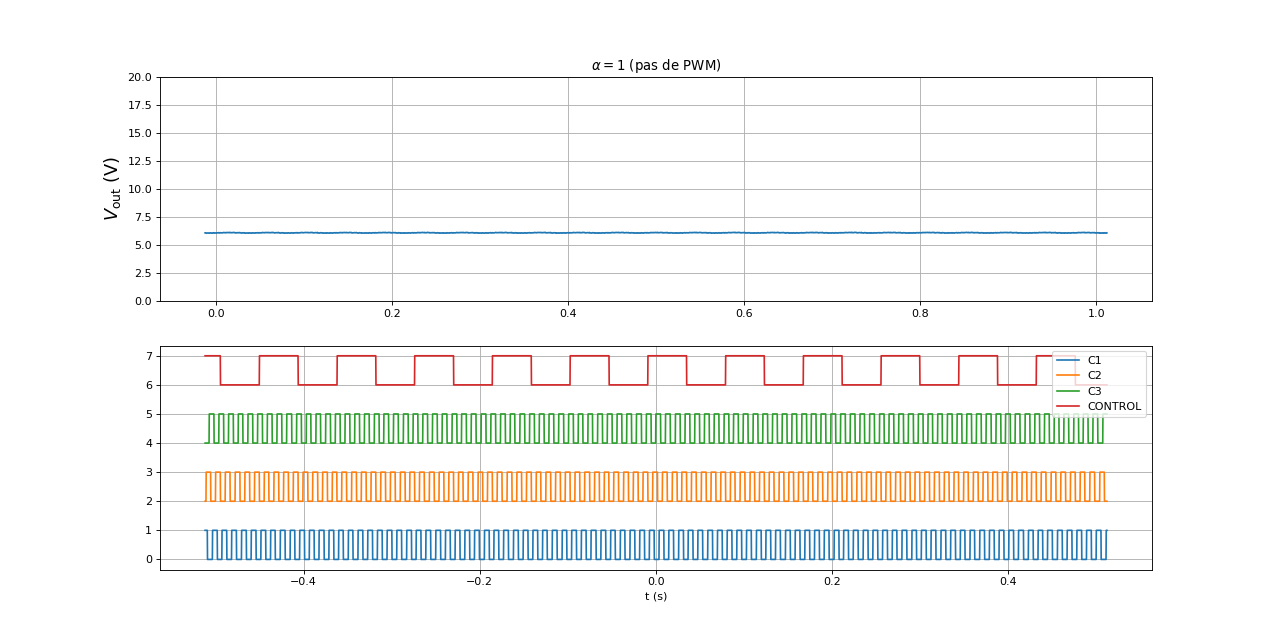 fig18.pdf
fig18.pdf
Ce résultat confirme que la tension en sortie est minimale (environ 6 V lorsque le moteur DC est alimenté en 10 V) lorsque le rapport cyclique vaut 1. La vitesse de rotation est à peine plus élevée dans ce cas que lorsque le rapport cyclique vaut 0,3 (44 ms pour un rapport de 1, 48 ms pour un rapport de 0,3).
Lorsque le rapport cyclique est inférieur à 1, il semble que le système se comporte comme un convertisseur boost. Le rôle de la commutation à 6 états et de fournir en sortie une tension quasi constante V0, égale environ à la force électromotrice maximale développée par une paire de bobine. Pour comprendre l'effet du découpage, nous pouvons considérer le schéma simplifié suivant :
Figure pleine pageLes deux transistors commutent en opposition, celui du haut étant fermé avec un rapport cyclique . On reconnaît effectivement un convertisseur DC-DC élévateur de tension (ou boost) [1], dont une étude complète est présentée dans Convertisseur continu-continu élévateur. Dans le cas idéal où r=0, la tension en sortie est donnée par :
où est le rapport cyclique, défini comme la fraction de période où le transistor K1 est passant (on garde évidemment la même définition que pour le fonctionnement en moteur). La tension en sortie est donc d'autant plus grande que le rapport cyclique est faible. En réalité, la tension en entrée n'est pas tout à fait constante à cause de la forme sinusoïdale de la f.é.m. mais la structure boost a tendance à lisser les ondulations de la f.é.m. à cause du condensateur en sortie (le taux d'ondulation en sortie est en effet très faible). Par ailleurs, la résistance r a pour effet de réduire la tension en sortie à faible rapport cyclique, ce qui fait que la relation précédente n'est valable qu'au dessus d'un certain rapport cyclique, d'autant pus grand que la résistance est grande.
Dans l'expérience ci-dessus, la vitesse de rotation pour est de 1360 tr/min. La f.é.m. maximale pour cette vitesse de rotation est (on suppose que le forme est sinusoïdale) :
Vmax = a*1360*np.sqrt(2)
print(Vmax) --> 6.288186886449838
Cette valeur doit être comparée à la tension en sortie :
print(V4) --> 6.073083600032742
La tension en sortie lorsque le rapport cyclique vaut 1 est donc un peu inférieure à la f.é.m. maximale (aux bornes d'une paire de bobines), ce qui est bien le résultat attendu.
Pour conclure, le pont de 6 transistors réalise à la fois une conversion AC-DC (commandée par la phase) et une conversion DC-DC avec élévation (Convertisseur continu-continu élévateur).
4.b. Étude avec charge électrique
Une résistance R est placée en sortie (en parallèle du condensateur). Le moteur à courant continu qui entraîne le moteur BLDC est alimenté avec une tension de 10 V. Voici tout d'abord les signaux sans la résistance :
figure(figsize=(16,8))
subplot(211)
title("DC = 10V, "+ r"$\alpha = 1$"+", sans résistance")
[t,Vout] = np.loadtxt("generateur-Vout-DC10-r1-2.txt",unpack=True,skiprows=1)
V1 = Vout.mean()
plot(t,Vout)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
grid()
ylim(0,10)
subplot(212)
[t,u0,u1,u2,uc] = np.loadtxt("generateur-hall-DC10-r1-2.txt",unpack=True,skiprows=1)
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
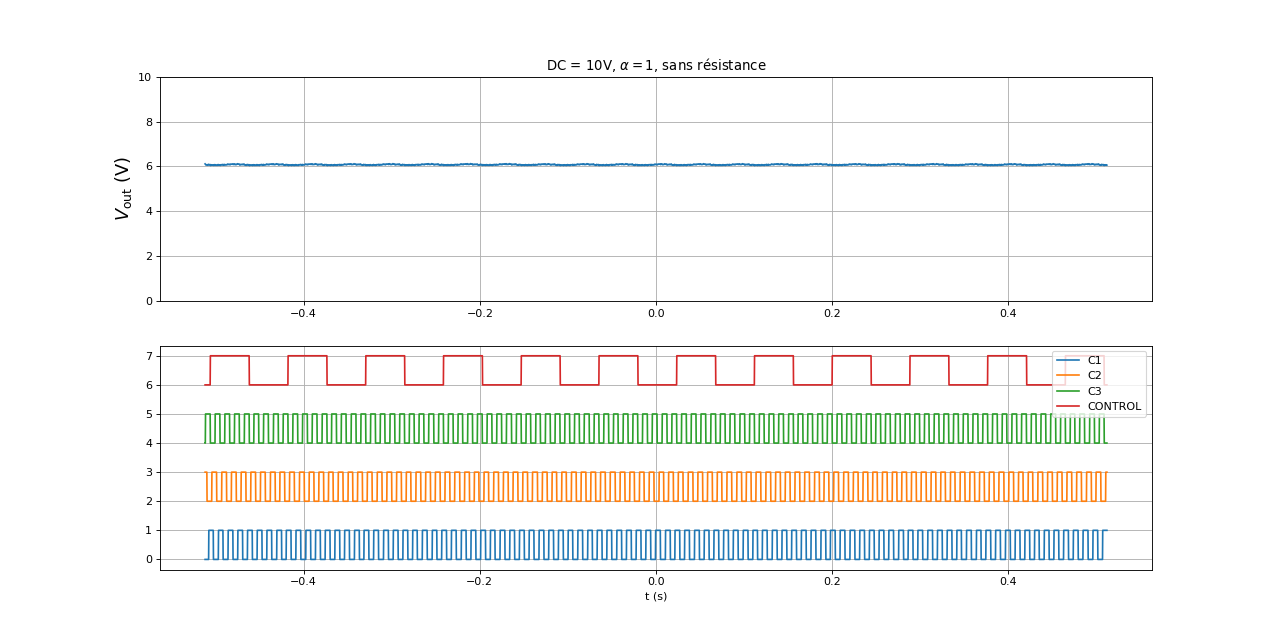 fig19.pdf
fig19.pdf
print(Vout)
--> array([6.11292709, 6.10926406, 6.10560103, ..., 6.06897074, 6.06530771,
6.05798165])
La période de rotation est 44 ms.
Voici les signaux avec une résistance de R=15 Ω :
figure(figsize=(16,8))
subplot(211)
title("DC = 10V, "+ r"$\alpha = 1,\ R=15\,{\rm\Omega}$")
[t,Vout] = np.loadtxt("generateur-Vout-DC10-r1-R15.txt",unpack=True,skiprows=1)
V2 = Vout.mean()
plot(t,Vout)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
grid()
ylim(0,10)
subplot(212)
[t,u0,u1,u2,uc] = np.loadtxt("generateur-hall-DC10-r1-R15.txt",unpack=True,skiprows=1)
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
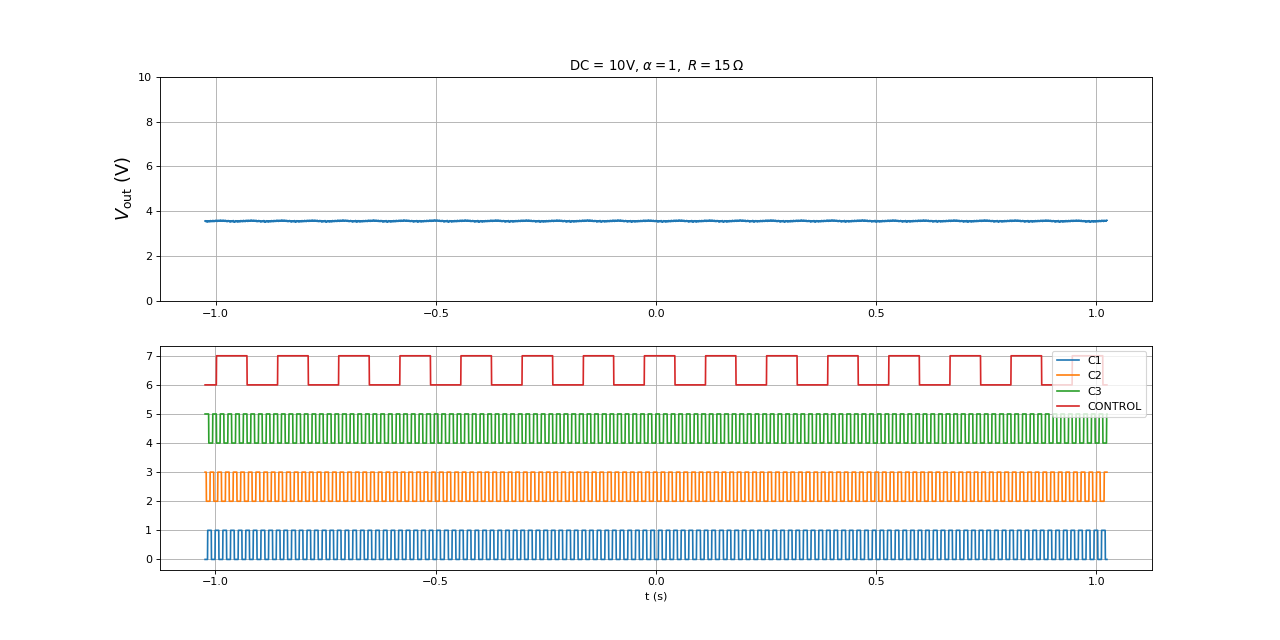 fig20.pdf
fig20.pdf
print(V2) --> 3.5608040158961614
La période de rotation est 66,5 ms. Elle est nettement plus grande que sans la résistance (pour la même tension d'alimentation du moteur DC), ce qui montre l'effet de freinage. Voici le courant dans la résistance et la puissance qu'elle reçoit :
R2 = 15
I2 = V2/R2
P2 = V2**2/R2
print(I2) --> 0.23738693439307743
print(P2) --> 0.8452883493081487
Voici les signaux avec une résistance de R=5 Ω :
figure(figsize=(16,8))
subplot(211)
title("DC = 10V, "+ r"$\alpha = 1,\ R=5\,{\rm\Omega}$")
[t,Vout] = np.loadtxt("generateur-Vout-DC10-r1-R5.txt",unpack=True,skiprows=1)
V3 = Vout.mean()
plot(t,Vout)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
grid()
ylim(0,10)
subplot(212)
[t,u0,u1,u2,uc] = np.loadtxt("generateur-hall-DC10-r1-R5.txt",unpack=True,skiprows=1)
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
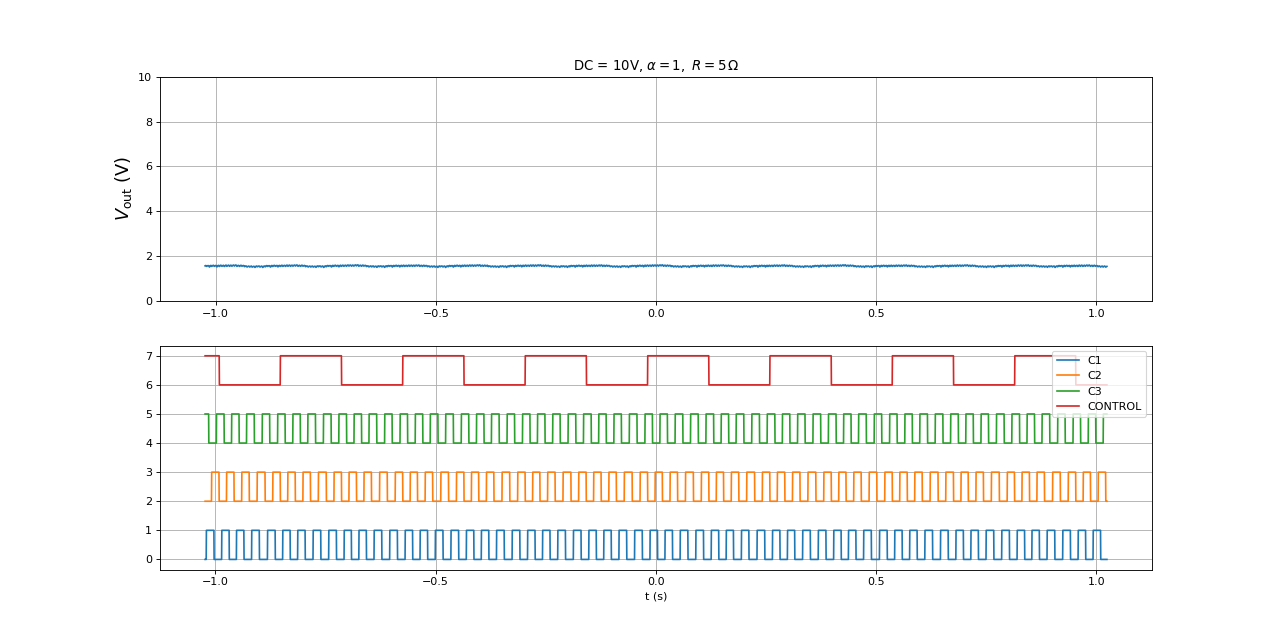 fig21.pdf
fig21.pdf
print(V3) --> 1.55419417384178
La période de rotation est 138 ms. Voici la puissance reçue par la résistance :
R3 = 5
I3 = V3/R3
P3 = V3**2/R3
print(I3) --> 0.310838834768356
print(P3) --> 0.48310390600074654
Voici les signaux avec une résistance de R=1 Ω :
figure(figsize=(16,8))
subplot(211)
title("DC = 10V, "+ r"$\alpha = 1,\ R=1\,{\rm\Omega}$")
[t,Vout] = np.loadtxt("generateur-Vout-DC10-r1-R1.txt",unpack=True,skiprows=1)
V4 = Vout.mean()
plot(t,Vout)
ylabel(r"$V_{\rm out}\ (\rm V)$",fontsize=16)
grid()
ylim(0,10)
subplot(212)
[t,u0,u1,u2,uc] = np.loadtxt("generateur-hall-DC10-r1-R1.txt",unpack=True,skiprows=1)
plot(t,u0,label="C1")
plot(t,u1+2,label="C2")
plot(t,u2+4,label="C3")
plot(t,uc+6,label="CONTROL")
grid()
legend(loc="upper right")
xlabel("t (s)")
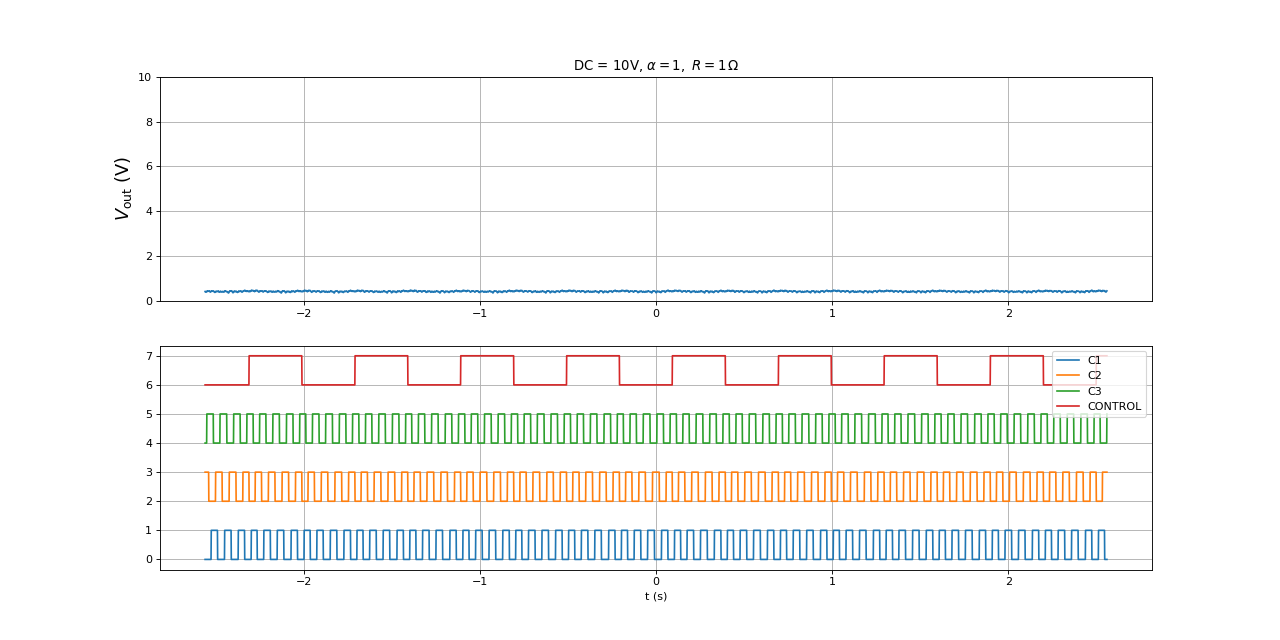 fig22.pdf
fig22.pdf
print(V4) --> 0.41973138703558177
La période de rotation est 310 ms (7 fois plus que sans résistance). Voici la puissance reçue par la résistance :
R4 = 1
I4 = V4/R4
P4 = V4**2/R4
print(I4) --> 0.41973138703558177
print(P4) --> 0.17617443726281334
D'après les valeurs de U et I données par l'alimentation, la puissance électrique reçue par le moteur DC est 5,9 W.
L'amplitude de crête de la f.é.m. développée par une paire de bobine peut être calculée au moyen de la vitesse de rotation et du coefficient déterminé plus haut.
R = [R2,R3,R4]
I = [I2,I3,I4]
P = [P2,P3,P4]
V = [V2,V3,V4]
T = np.array([66.5,138,310])
w = 1/(T*1e-3)*60
e = a*w*np.sqrt(2)
figure(figsize=(8,10))
subplot(411)
plot(R,e,"bo")
plot(R,e,label="f.e.m.")
plot(R,V,"bo")
plot(R,V,label="Vout")
grid()
ylim(0,6)
ylabel("V",fontsize=16)
legend(loc="lower right")
subplot(412)
plot(R,I,"bo")
plot(R,I)
ylim(0,0.5)
grid()
ylabel("I (A)",fontsize=16)
subplot(413)
plot(R,w,"bo")
plot(R,w)
ylim(0,1000)
ylabel(r"$\omega\ (\rm tr/min)$",fontsize=16)
grid()
subplot(414)
plot(R,P,"bo")
plot(R,P)
ylim(0,1)
grid()
ylabel("P (W)",fontsize=16)
xlabel(r"$R\ (\rm\Omega)$",fontsize=16)
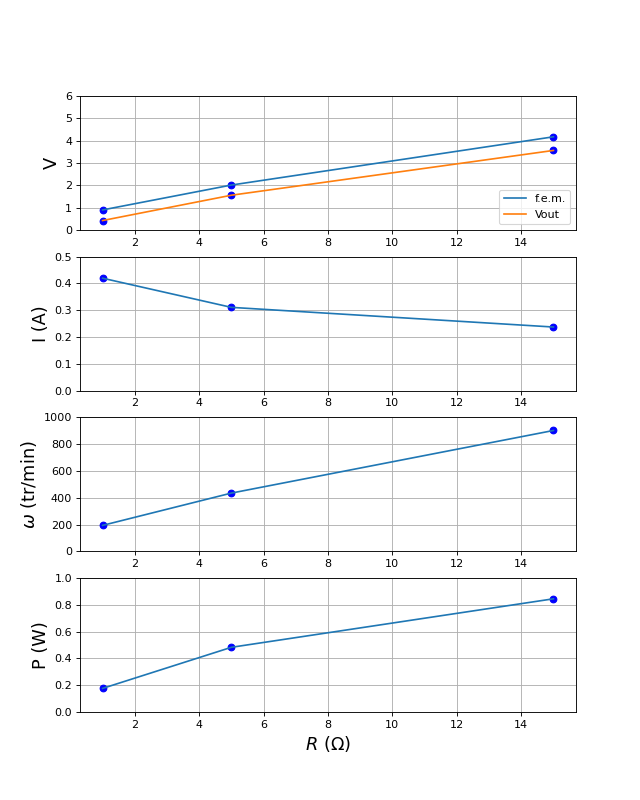 fig23.pdf
fig23.pdf
Lorsque R diminue, la vitesse de rotation diminue, ce qui montre que le couple de freinage par induction augmente, conformément à l'augmentation du courant. Cependant, la puissance reçue par la résistance diminue car l'amplitude de la f.é.m. diminue (à cause de la diminution de la vitesse).
5. Frein moteur - Freinage régénératif
5.a. Principe
On suppose que le moteur entraîne une roue ou un véhicule possèdant une grande énergie cinétique (c'est-à-dire une grande masse). Pour notre expérience, nous ajoutons un volant d'inertie directement sur l'arbre du moteur. Supposons que le moteur tourne en régime permanent avec un rapport cyclique . Plus ce rapport est élevé, plus la vitesse de rotation est grande. Pour réduire la vitesse du moteur (à charge mécanique constante), il y a quatre possibilités :
- (1) Laisser la source d'énergie connectée et abaisser le rapport cyclique. Ce rapport cyclique peut être contrôlé au moyen d'une commande de vitesse (par une boucle de rétroaction).
- (2) Déconnecter la source d'énergie et laisser l'entrée du pont en circuit ouvert (roue libre).
- (3) Déconnecter la source d'énergie et court-circuiter l'entrée du pont (frein moteur).
- (4) Si la source est un accumulateur, la laisser connectée et mettre en place un schéma de commutation qui permet au courant induit de circuler vers l'accumulateur pour le recharger (freinage régénératif). La recharge se fait si la tension aux bornes de l'accumulateur est supérieure à sa f.é.m..
Voici le schéma de principe d'un circuit permettant de réaliser les trois premières possibilités. Le schéma simplifié du moteur comporte une seule phase et, en conséquence, le pont de commutation ne porte qu'un seul bras de deux transistors. La f.é.m. délivrée par ce moteur simplifié est constante pour une vitesse de rotation donnée (il s'agit d'un moteur à courant continu).
Figure pleine pageLa source d'énergie (modélisée par une source de tension E en série avec une résistance rs) est connectée si Ka est fermé et K'a ouvert. Le comportement du système dans le cas (1) dépend du type de source :
- La source est une alimentation stabilisée, qui ne peut fournir qu'un courant positif : Is>0.
- La source est un accumulateur électrochimique, qui peut fournir un courant négatif (Is<0) en situation de recharge. Pour cela, il faut que la tension qu'on lui applique, c'est-à-dire VOUT, soit supérieure à sa force électromotrice. La recharge de l'accumulateur lorsque la tension VOUT est supérieure à la f.é.m. de l'accumulateur est la régénération. Juste après l'abaissement du rapport cyclique (tant que la vitesse stationnaire n'est pas atteinte), on s'attend effectivement à avoir une tension VOUT supérieure à E.
Remarquons que si l'accumulateur est relié au circuit de commande via un régulateur (par exemple un régulateur élévateur), le comportement de ce régulateur joue un rôle dans le fonctionnement.
Dans le cas où une alimentation de laboratoire est utilisée, un courant Is transitoire négatif est possible par charge du condensateur Ce mais il s'accompagne inévitablement d'une augmentation de la tension en sortie de l'alimentation (aux bornes du condensateur). En situation de régénération, ce condensateur (ainsi que C) joue donc le rôle d'un super condensateur de stockage.
La situation (2), c'est-à-dire la roue libre, est obtenue lorsque Ka et K'a sont tous les deux ouverts. Les transistors du pont de commande doivent être aussi tous ouverts. Il faut cependant remarquer que le courant peut tout de même circuler dans les diodes drain-source des transistors du haut, comme indiqué sur la figure suivante :
Figure pleine pageCe retour du courant vers la source ne se fait que si la tension aux bornes des diodes dépasse la tension de seuil d'environ 0,8 V. Il faut pour cela que la force électromotrice développé par le moteur excède la tension de la source. Dans l'expérience que nous réalisons, cela ne se produit jamais car la vitesse diminue toujours après déclenchement de la roue libre (cela pourrait être différent pour un véhicule dans une descente).
La situation (3) est réalisée lorsque Ka est ouvert et K'a fermé. Le courant passe dans la résistance drain-source du transistor du bas. Cette résistance très faible (environ 0,5 ohms) doit conduire à un freinage moteur très efficace. Bien sûr, il n'y a pas dans ce cas de régénération puisque toute l'énergie cinétique est dissipée dans la résistance drain-source.
5.b. Roue libre
En fonctionnement roue libre, il n'y a pas de freinage élecromagnétique. La source doit être déconnectée et aucun courant ne doit circuler dans les bobines du stator. L'ouverture de l'interrupteur Ka nous permet de déconnecter la source mais notre circuit ne permet pas de déconnecter le condensateur C qui se trouve à l'entrée du pont. En conséquence, ce condensateur peut fournir de l'énergie au moteur lorsque la source est déconnectée. Pour obtenir une roue libre parfaite, il faut ouvrir tous les transistors du pont (les interrupteurs K1,K'1,K2,K'2,K3,K'3). Dans ce cas, il n'est pas nécessaire de déconnecter la source (on peut laisser Ka fermé). Si la source est un accumulateur branché directement sur le pont, on peut obtenir ainsi la roue libre.
Les deux fonctions suivantes permettent d'obtenir la vitesse angulaire en fonction du temps à partir des signaux délivrés par les capteurs à effet Hall :
from scipy.signal import firwin,convolve
def analyseCapteurs(t,u0,u1,u2):
periode = []
temps = []
tchange = t[0]
etat0 = u0[0] > 0.5
etat1 = u1[0] > 0.5
etat2 = u2[0] > 0.5
for i in range(1,len(t)):
if (u0[i] < 0.5 and etat0) or (u0[i] > 0.5 and not(etat0)):
periode.append(t[i]-tchange)
temps.append(t[i])
tchange = t[i]
etat0 = not(etat0)
if (u1[i] < 0.5 and etat1) or (u1[i] > 0.5 and not(etat1)):
periode.append(t[i]-tchange)
temps.append(t[i])
tchange = t[i]
etat1 = not(etat1)
if (u2[i] < 0.5 and etat2) or (u2[i] > 0.5 and not(etat2)):
periode.append(t[i]-tchange)
temps.append(t[i])
tchange = t[i]
etat2 = not(etat2)
j = 0
periode = periode[j:len(periode)-j]
temps = temps[j:len(temps)-j]
P = 20
b = firwin(2*P+1,cutoff=[0.01],window='hann',fs=0.5)
periode = convolve(periode,b,mode='valid')
temps = temps[P:len(temps)-P]
return np.array(temps),np.array(periode)
def plotOmega(filename,label):
[t,u0,u1,u2,uc] = np.loadtxt(filename,skiprows=1,unpack=True)
temps,periode = analyseCapteurs(t,u0,u1,u2)
plot(temps,1/(periode*24),label=label)
Voici la vitesse angulaire pour une tension d'alimentation de 10 V et pour différents rapports cyclique (avant le déclenchement de la roue libre), donc pour différentes vitesses initiales.
figure()
title("E = 10 V, roue libre sans commutation")
plotOmega("rouelibre-complet-hall-DC10-r0,2.txt",r"$\alpha=0,2$")
plotOmega("rouelibre-complet-hall-DC10-r0,3.txt",r"$\alpha=0,3$")
plotOmega("rouelibre-complet-hall-DC10-r0,4.txt",r"$\alpha=0,4$")
plotOmega("rouelibre-complet-hall-DC10-r0,6.txt",r"$\alpha=0,6$")
plotOmega("rouelibre-complet-hall-DC10-r0,7.txt",r"$\alpha=0,7$")
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
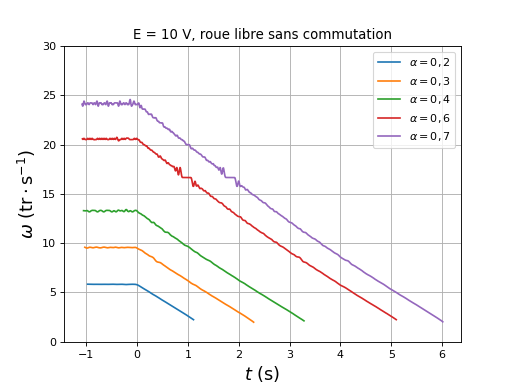 fig24.pdf
fig24.pdf
Voici la vitesse angulaire et la tension aux bornes du condensateur :
figure()
title("E = 10 V, quasi roue libre sans commutation")
plotOmega("rouelibre-complet-hall-DC10-r0,4-1.txt",r"$\alpha=0,4$")
[t,Vout] = np.loadtxt("rouelibre-complet-Vout-DC10-r0,4-1.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
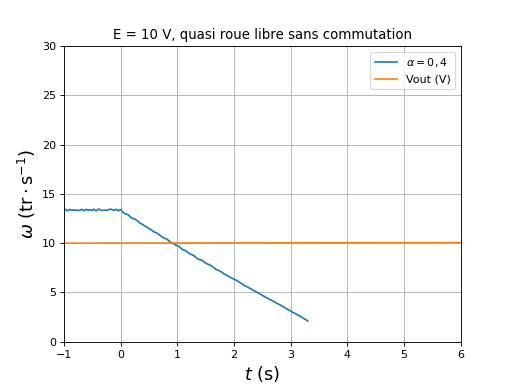 fig25.pdf
fig25.pdf
Nous constatons que, pendant la roue libre, la vitesse angulaire décroît proportionnellement au temps. Le couple de frottement est donc constant (indépendant de la vitesse). Par ailleurs, la tension aux bornes du condensateur reste constante, ce qui montre qu'aucun courant ne traverse les diodes des transistors du haut du pont (ce courant aurait pour effet d'augmenter la charge du condensateur). Ces courbes serviront de référence pour l'étude du freinage électromagnétique.
Une quasi roue libre peut être obtenue en maintenant le fonctionnement du pont après avoir ouvert Ka (K'a restant ouvert). En effet, nous avons vu que le pont se comporte comme un convertisseur AC-DC élévateur qui permet de faire fonctionner la machine en générateur. En conséquence, il devrait suffire de laisser la sortie de ce convertisseur ouverte (c'est-à-dire K'a ouvert) pour obtenir une roue libre.
Dans l'expérience suivante, la roue libre est obtenue par ouverture de Ka, la commutation du pont est maintenue et le rapport cyclique de MLI est maintenu à sa valeur initiale.
figure()
title("E = 10 V, quasi roue libre avec commutation")
plotOmega("rouelibre-hall-DC10-r0,2.txt",r"$\alpha=0,2$")
plotOmega("rouelibre-hall-DC10-r0,3.txt",r"$\alpha=0,3$")
plotOmega("rouelibre-hall-DC10-r0,4.txt",r"$\alpha=0,4$")
plotOmega("rouelibre-hall-DC10-r0,6.txt",r"$\alpha=0,6$")
plotOmega("rouelibre-hall-DC10-r0,7.txt",r"$\alpha=0,7$")
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
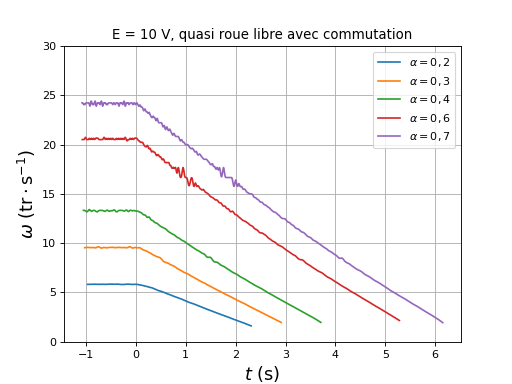 fig26.pdf
fig26.pdf
Le temps d'arrêt est un peu plus grand que précédemment, ce qui signifie qu'il y a moins de courant de freinage dans le pont que lorsque tous les transistors du pont restent en permanence ouvert. Ce résultat se comprend car dans le cas présent, le condensateur C continue à fournir de l'énergie au moteur (en se déchargeant) après que Ka soit ouvert.
Dans l'expérience suivante, la roue libre est obtenue en ouvrant Ka puis, juste après, le rapport cyclique est fixé à 0,2 :
figure()
title("E = 10 V, quasi roue libre avec commutation")
plotOmega("rouelibre-r0,2-hall-DC10-r0,2.txt",r"$\alpha=0,2$")
plotOmega("rouelibre-r0,2-hall-DC10-r0,3.txt",r"$\alpha=0,3$")
plotOmega("rouelibre-r0,2-hall-DC10-r0,4.txt",r"$\alpha=0,4$")
plotOmega("rouelibre-r0,2-hall-DC10-r0,6.txt",r"$\alpha=0,6$")
plotOmega("rouelibre-r0,2-hall-DC10-r0,7.txt",r"$\alpha=0,7$")
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
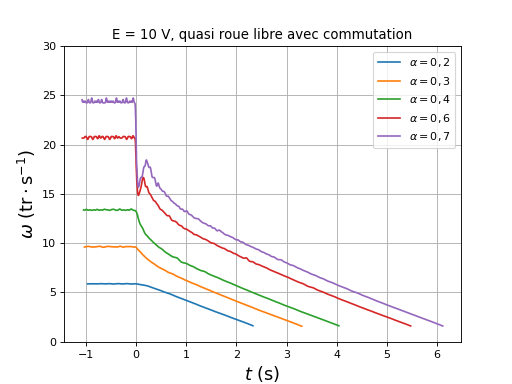 fig27.pdf
fig27.pdf
Pour les grands rapports cycliques, la vitesse diminue très rapidement juste après l'ouverture de Ka. Cependant, le temps d'arrêt ne change pas, seule la forme de la courbe change.
Voici la vitesse angulaire et la tension aux bornes du condensateur :
figure()
title("E = 10 V, quasi roue libre avec commutation")
plotOmega("rouelibre-r0,2-hall-DC10-r0,4-1.txt",r"$\alpha=0,4$")
[t,Vout] = np.loadtxt("rouelibre-r0,2-Vout-DC10-r0,4-1.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
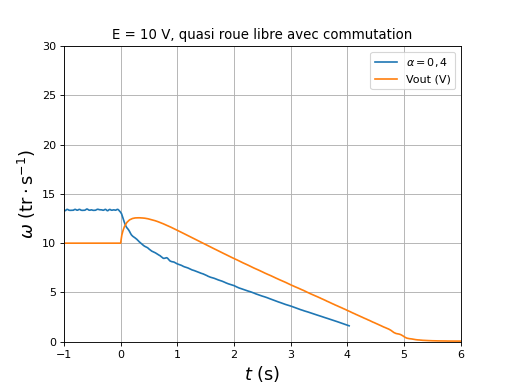 fig28.pdf
fig28.pdf
figure()
title("E = 10 V, quasi roue libre avec commutation")
plotOmega("rouelibre-r0,2-hall-DC10-r0,6-1.txt",r"$\alpha=0,4$")
[t,Vout] = np.loadtxt("rouelibre-r0,2-Vout-DC10-r0,6-1.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
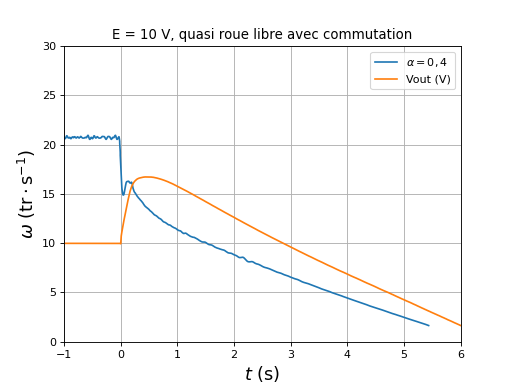 fig29.pdf
fig29.pdf
On constate que la tension aux bornes du condensateur augmente juste après la déconnection de la source et l'abaissement du rapport cyclique. Ce résultat est logique puisque le convertisseur fonctionne dans ce sens en élévateur avec un rapport de tension élevé (puisque le rapport cyclique est faible). Cette charge du condensateur s'accompage d'un courant important fourni par le moteur, ce qui explique la diminution très rapide de la vitesse. Cette expérience est intéressante pour comprendre ce qui se passera si le rapport cyclique est abaissé alors que Ka reste fermé lorsque la source sera un accumulateur : juste après l'abaissement du rapport cyclique, un courant positif retourne vers l'accumulateur et permet de le recharger brièvement (régénération). L'augmentation de la charge du condensateur correspond à ce qui serait observé dans le cas d'une régénération par charge d'un super-condensateur (mais la capacité serait au moins 1000 fois plus grande).
Dans l'expérience suivante, la roue libre est obtenue en ouvrant Ka puis, juste après, le rapport cyclique est fixé à 0,7 :
figure()
title("E = 10 V, quasi roue libre avec commutation")
plotOmega("rouelibre-r0,7-hall-DC10-r0,2.txt",r"$\alpha=0,2$")
plotOmega("rouelibre-r0,7-hall-DC10-r0,3.txt",r"$\alpha=0,3$")
plotOmega("rouelibre-r0,7-hall-DC10-r0,4.txt",r"$\alpha=0,4$")
plotOmega("rouelibre-r0,7-hall-DC10-r0,6.txt",r"$\alpha=0,6$")
plotOmega("rouelibre-r0,7-hall-DC10-r0,7.txt",r"$\alpha=0,7$")
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
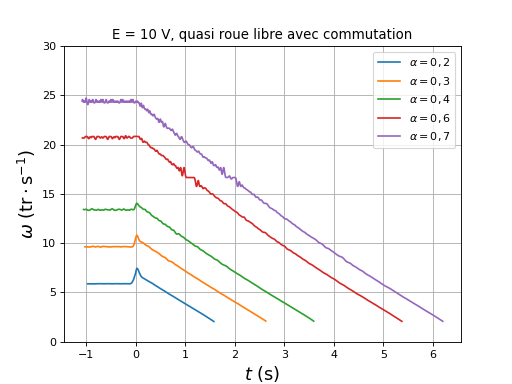 fig30.pdf
fig30.pdf
Voici la vitesse angulaire avec la tension aux bornes du condensateur :
figure()
title("E = 10 V, quasi roue libre avec commutation")
plotOmega("rouelibre-r0,7-hall-DC10-r0,3-1.txt",r"$\alpha=0,3$")
[t,Vout] = np.loadtxt("rouelibre-r0,7-Vout-DC10-r0,3-1.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
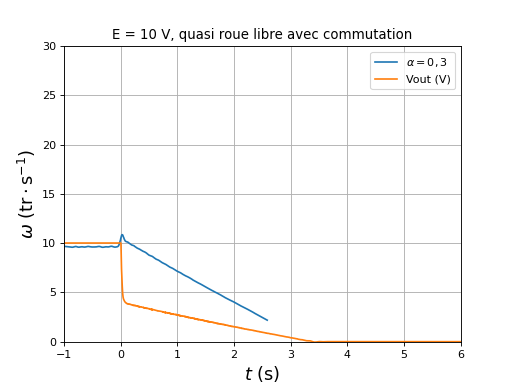 fig31.pdf
fig31.pdf
Pour les faibles rapport cycliques, l'augmentation du rapport cyclique juste après l'ouverture de Ka fait augmenter légèrement la vitesse. En même temps, le condensateur se décharge partiellement.
Nous constatons que la roue libre avec commutation du pont (Ka ouvert) fonctionne et donne à peu près le même temps d'arrêt quel que soit le rapport cyclique. On peut donc laisser le rapport cyclique à sa valeur initiale (avant déclenchement de la roue libre). On constate aussi que la roue libre obtenue par ouverture de tous les transistors du pont conduit à un temps d'arrêt un peu plus court que lorsque la commutation est maintenue. L'explication semble être que, dans le cas où le condensateur C rete connecté, celui-ci continue brièvement à fournir de l'énergie au moteur, d'où un temps d'arrêt un peu plus long (mais dans ce cas il ne s'agit pas d'une roue libre parfaite).
En pratique dans un véhicule électrique, le fonctionnement en roue libre a peu d'intérêt. Si l'on souhaite réduire lentement la vitesse, il suffit de réduire le rapport cyclique progressivement.
5.c. Regénération
La régénération peut être définie comme l'état de fonctionnement où un courant positif provient du moteur. Comme nous avons vu ci-dessus, l'abaissement du rapport cyclique sans changement du schéma de commutation s'accompagne d'un courant positif vers la source, qui dans notre expérience ne fait que charger le condensateur mais qui pourrait recharger un accumulateur.
Voici la vitesse, la tension aux bornes du condensateur et la tension en sortie de l'alimentation lorsque le rapport cyclique passe soudainement de 0,6 à 0,3 :
figure()
title("E = 10 V, réduction du rapport cyclique")
plotOmega("reduction-hall-DC10-r0,6-r0,3-1.txt",r"$\alpha=0,6\ {\rm à\ }\alpha=0,3$")
[t,Vout,Vs] = np.loadtxt("reduction-Vs-Vout-DC10-r0,6-r0,3-1.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
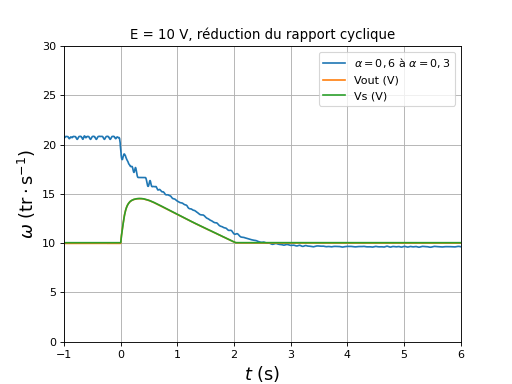 fig32.pdf
fig32.pdf
La charge du condensateur augmente (puis diminue) alors qu'il reste connecté à l'alimentation stabilisée (en tension) puisque Ka reste fermé. La tension en sortie de l'alimentation stabilisée augmente exactement comme celle aux bornes de C (ce qui est logique puisque Ka reste fermé). L'augmentation de tension est d'ailleurs visible sur l'afficheur de tension de l'alimentation. On observe donc le phénomène de régénération lorsque le rapport cyclique est abaissé, sans aucun changement de la séquence de commutation. Dans le cas présent, cette régénération se fait vers le condensateur. L'énergie supplémentaire reçue par celui-ci est tout de suite restituée au moteur. Si la source était un accumulateur, on pourrait obtenir un courant de recharge à condition que la tension dépasse la f.é.m. de l'accumulateur. Cela devrait se produire spontanément : si l'accumulateur a une f.é.m. de 10 V, la réduction du rapport cyclique fait passer la tension à presque 15 V, ce qui permet de faire la recharge. Cependant, il sera sans doute nécessaire de réguler cette tension par ajustement du rapport cyclique. Il est intéressant de remarquer que la stabilisation de tension ne fonctionne pas lorsqu'un courant positif revient vers l'entrée du pont. Ce courant recharge le condensateur et le circuit de l'alimentation ne peut empêcher cette recharge. Un condensateur de plus grande capacité permettrait de stocker la même énergie avec une augmentation de tension plus faible. Si une grande quantité d'énergie peut être récupérée par régénération (par exemple dans un véhicule), un super-condensateur doit être utilisé. L'utilisation d'un super-condensateur pose toutefois une difficulté supplémentaire car ce type de condensateur a une tension maximale très basse (de l'ordre du volt), ce qui impose une régulation de la tension au moment de la régénération, donc l'ajout d'un convertisseur DC-DC abaisseur. Ce convertisseur doit être réversible : il doit effectuer un abaissement de tension pour charger le condensateur et, dans l'autre sens, effectuer une élévation de tension lors de la décharge.
Voici une expérience où le rapport cyclique est augmenté :
figure()
title("E = 10 V, réduction du rapport cyclique")
plotOmega("reduction-hall-DC10-r0,3-r0,6.txt",r"$\alpha=0,3\ {\rm à\ }\alpha=0,6$")
[t,Vout,Vs] = np.loadtxt("reduction-Vs-Vout-DC10-r0,3-r0,6.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
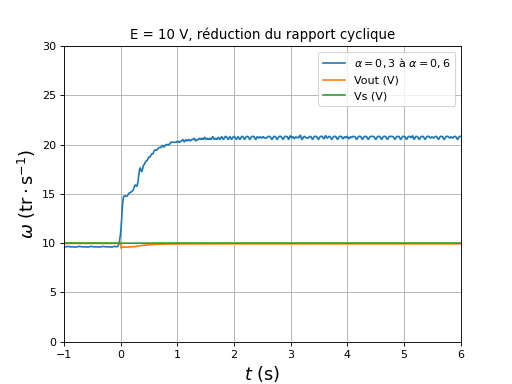 fig33.pdf
fig33.pdf
Dans ce cas, la tension en sortie de l'alimentation est constante. Celle aux bornes de C subit une toute petite baisse et, en même temps que cette baisse, la vitesse du rotor augmente subitement, avant d'augmenter plus lentement alors que la tension revient à sa valeur normale. Pendant une durée très courte, le condensateur fournit un supplément d'énergie au moteur qui lui permet d'augmenter très vite sa vitesse (de 10 à 15 tours/s).
5.d. Frein moteur
Le but est d'étudier le freinage moteur mais sans régénération. La source est une alimentation stabilisée, dont le courant sortant est toujours positif. Nous obtenons cette situation avec Ka ouvert et K'a fermé.
La première solution consiste à maintenir la commutation dans le pont sans changer le rapport cyclique de la MLI, à ouvrir Ka et à fermer K'a. La machine se comporte alors comme un générateur dont la sortie est court-circuitée.
figure()
title("E = 10 V, frein moteur")
plotOmega("freinmoteur-hall-DC10-r0,6.txt",r"$\alpha=0,6$")
[t,Vout,Vs] = np.loadtxt("freinmoteur-Vout-Vs-DC10-r0,6.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
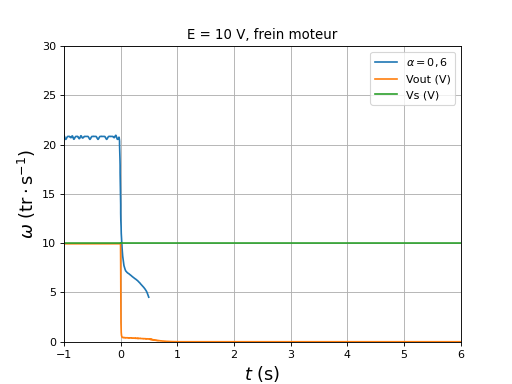 fig34.pdf
fig34.pdf
figure()
title("E = 10 V, frein moteur")
plotOmega("freinmoteur-hall-DC10-r0,2.txt",r"$\alpha=0,2$")
plotOmega("freinmoteur-hall-DC10-r0,3.txt",r"$\alpha=0,3$")
plotOmega("freinmoteur-hall-DC10-r0,4.txt",r"$\alpha=0,4$")
plotOmega("freinmoteur-hall-DC10-r0,6.txt",r"$\alpha=0,6$")
plotOmega("freinmoteur-hall-DC10-r0,7.txt",r"$\alpha=0,7$")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
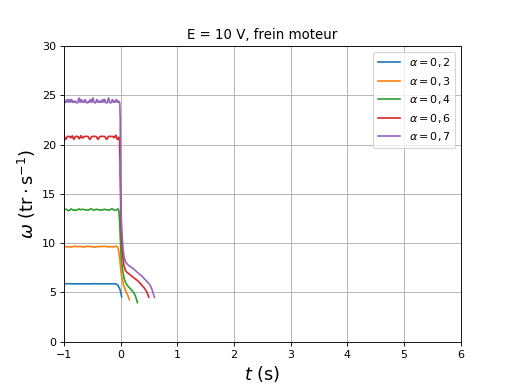 fig35.pdf
fig35.pdf
Le freinage moteur conduit à un arrêt beaucoup plus rapide que la roue libre. Voici une comparaison des deux pour un rapport cyclique de 0,6 :
figure()
title(r"$E = 10 {\rm V}, \alpha=0.6$")
plotOmega("rouelibre-complet-hall-DC10-r0,6.txt","roue libre")
plotOmega("freinmoteur-hall-DC10-r0,6.txt","frein moteur")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
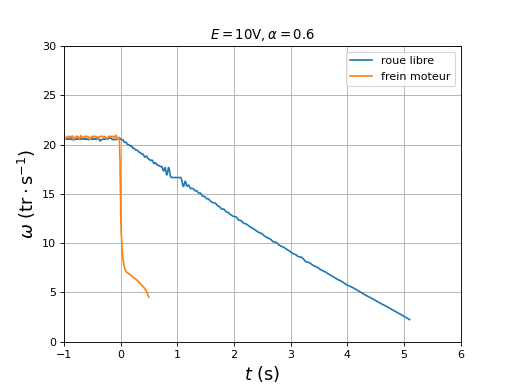 fig36.pdf
fig36.pdf
Voici la vitesse et les tensions lorsqu'un rapport cyclique de 0,2 est appliqué pendant le freinage (avec un rapport initial de 0,6) :
figure()
title("E = 10 V, frein moteur")
plotOmega("freinmoteur-hall-DC10-r0,6-r0,2.txt",r"$\alpha=0,6$")
[t,Vout,Vs] = np.loadtxt("freinmoteur-Vout-Vs-DC10-r0,6-r0,2.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-1,6)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
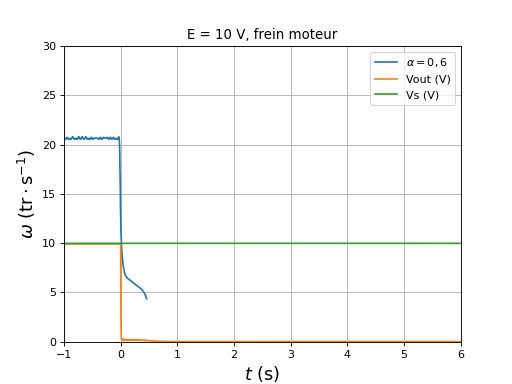 fig37.pdf
fig37.pdf
Le freinage moteur (avec passage du courant dans K'a fermé) ne semble pas affecté par le rapport cyclique pendant la phase de freinage. Bien évidemment, il en sera autrement en cas de régénération puisque la tension Vout dans ce cas dépendra du rapport cyclique (elle augmente lorsque le rapport diminue).
5.e. Freinage régénératif
Le freinage régénératif consiste à réaliser un freinage moteur avec retour de l'énergie vers l'accumulateur. Comme nous l'avons vu plus haut, le simple fait d'abaisser le rapport cyclique sans changer le schéma de commutation réalise un freinage moteur avec régénération, c'est-à-dire avec un courant positif vers l'alimentation (vers le condensateur dans le cas d'une alimentation stabilisée).
Il est possible de modifier le schéma de commutation afin d'obtenir un freinage très efficace (aussi efficace que celui obtenu ci-dessus en fermant K'a) tout en ayant la possibilité de réguler la tension Vout (c'est-à-dire la tension aux bornes de l'accumulateur) par modification du rapport cyclique.
6. Régulation de la vitesse
6.a. Principe
Dans le mode de fonctionnement 1, on choisit la vitesse de rotation et le programme effectue un ajustement du rapport cyclique (à chaque tour) de manière à obtenir la vitesse demandée. Ce mode fait appel à l'asservissement représenté ci-dessous :
Figure pleine pageLa vitesse angulaire est évaluée à chaque tour complet. Soit la vitesse angulaire demandée (ou vitesse angulaire consigne). L'erreur est . Nous optons pour un correcteur proportionnel-intégral (PI), pour lequel rapport cyclique du découpage est défini par la relation :
Le terme proportionnel permet d'obtenir une réponse instantanée mais conduit à une erreur non nulle en régime stationnaire. Le terme intégral permet d'annuler l'erreur en régime stationnaire mais introduit un temps de retard. La mise à jour du rapport cyclique est faite après chaque tour de rotor, en fonction de la vitesse angulaire mesurée sur ce tour. Si l'on note la valeur de l'intégrale précédente, le nouveau rapport cyclique se calcule par :
On a en principe mais le facteur est omis car la constante Ki est suffisante pour contrôler le terme intégrale. Pour le démarrage du moteur, la vitesse angulaire est nulle donc la relation ci-dessus n'est pas valide. On la remplace par :
où est une constante petite (par exemple 0,1).
Le correcteur PI est étudié avec un exemple dans Convertisseur continu-continu élévateur. Un correcteur proportionnel permet d'obtenir une réponse instantanée mais avec une erreur importante. Cette erreur diminue lorsque Kp augmente mais une valeur trop grande de ce dernier conduit à des oscillations de la vitesse angulaire. L'ajout de l'intégrateur permet d'éliminer l'erreur en régime stationnaire mais introduit un temps de réponse. Celui-ci diminue lorsqu'on augmente Ki mais une valeur trop grande de ce dernier conduit à un dépassement lorsque la consigne de vitesse est changée par échelon.
Les valeurs de Ki et Kp sont obtenues de manière empirique. La vitesse du moteur est une fonction croissante du rapport cyclique donc ces deux coefficients sont positifs.
6.b. Expériences
Nous effectuons des tests de changement de vitesses pour différentes valeurs des paramètres Kp et Ki.
Les paramètres sont Ki=0,01 et Kp=0,01. La vitesse est 1 tr/s et on la fait passer à 5 tr/s :
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.01")
plotOmega("vitesse-hall-DC10-1-5-Ki0,01-Kp0,01.txt",r"$\omega=1\rightarrow 5$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-1-5-Ki0,01-Kp0,01.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-3,7)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
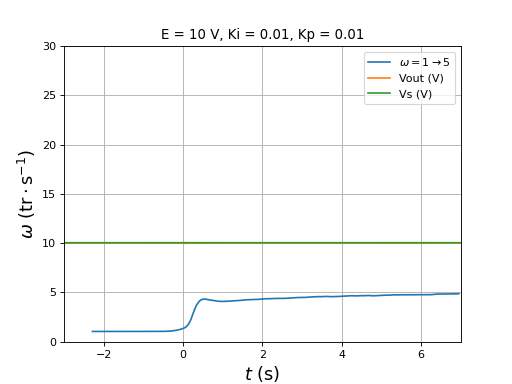 fig38.pdf
fig38.pdf
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.01")
plotOmega("vitesse-hall-DC10-1-10-Ki0,01-Kp0,01.txt",r"$\omega=1\rightarrow 10$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-1-10-Ki0,01-Kp0,01.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-3,7)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
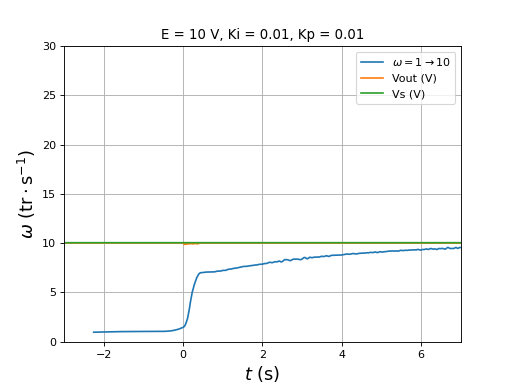 fig39.pdf
fig39.pdf
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.01")
plotOmega("vitesse-hall-DC10-10-1-Ki0,01-Kp0,01.txt",r"$\omega=10\rightarrow 1$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-10-1-Ki0,01-Kp0,01.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-3,7)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
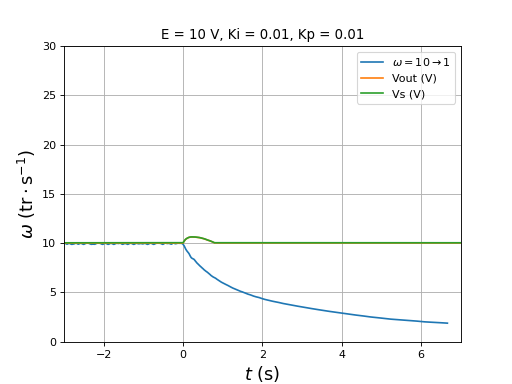 fig40.pdf
fig40.pdf
On remarque qu'une diminution importante de la vitesse déclenche une augmentation transitoire de la tension d'entrée du pont. Cela montre que la régénération se fera aussi (avec une accumulateur électrochimique comme source) lorsqu'on commande une baisse de la vitesse, donc indirectement une baisse du rapport cyclique.
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.01")
plotOmega("vitesse-hall-DC10-10-5-Ki0,01-Kp0,01.txt",r"$\omega=10\rightarrow 5$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-10-5-Ki0,01-Kp0,01.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
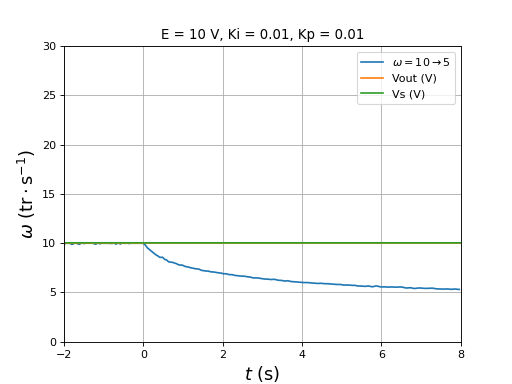 fig41.pdf
fig41.pdf
Les paramètres sont Ki=0,01 et Kp=0,02.
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.02")
plotOmega("vitesse-hall-DC10-1-5-Ki0,01-Kp0,02.txt",r"$\omega=1\rightarrow 5$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-1-5-Ki0,01-Kp0,02.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
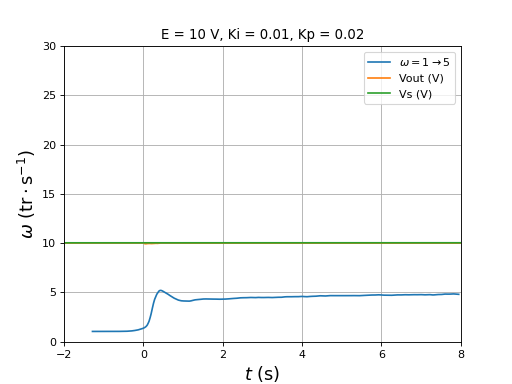 fig42.pdf
fig42.pdf
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.02")
plotOmega("vitesse-hall-DC10-1-10-Ki0,01-Kp0,02.txt",r"$\omega=1\rightarrow 10$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-1-10-Ki0,01-Kp0,02.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
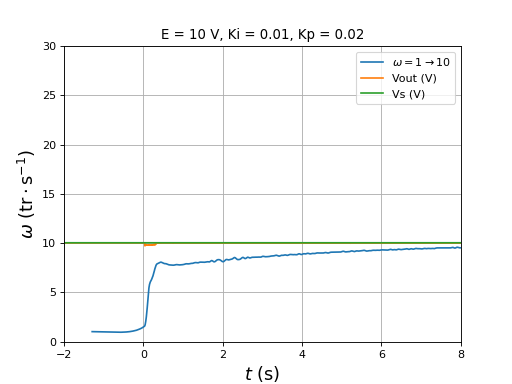 fig43.pdf
fig43.pdf
Les paramètres sont Ki=0,01 et Kp=0,03.
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.03")
plotOmega("vitesse-hall-DC10-1-5-Ki0,01-Kp0,03.txt",r"$\omega=1\rightarrow 5$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-1-5-Ki0,01-Kp0,03.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
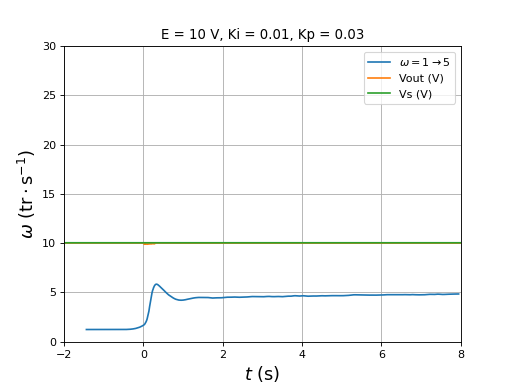 fig44.pdf
fig44.pdf
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.03")
plotOmega("vitesse-hall-DC10-1-10-Ki0,01-Kp0,03.txt",r"$\omega=1\rightarrow 10$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-1-10-Ki0,01-Kp0,03.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
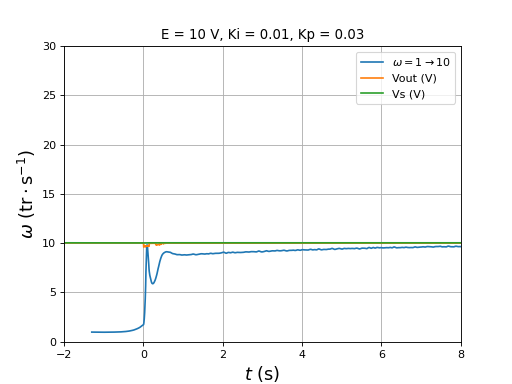 fig45.pdf
fig45.pdf
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.03")
plotOmega("vitesse-hall-DC10-10-1-Ki0,01-Kp0,03.txt",r"$\omega=10\rightarrow 1$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-1-10-Ki0,01-Kp0,03.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
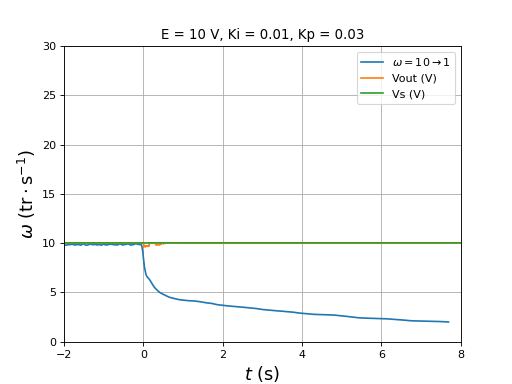 fig46.pdf
fig46.pdf
figure()
title("E = 10 V, Ki = 0.01, Kp = 0.03")
plotOmega("vitesse-hall-DC10-10-5-Ki0,01-Kp0,03.txt",r"$\omega=10\rightarrow 5$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-10-5-Ki0,01-Kp0,03.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
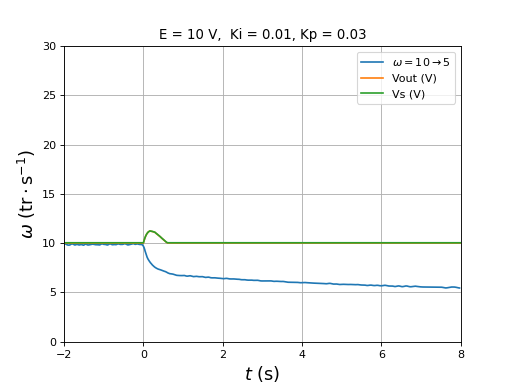 fig47.pdf
fig47.pdf
Les paramètres sont Ki=0,02 et Kp=0,02.
figure()
title("E = 10 V, Ki = 0.02, Kp = 0.02")
plotOmega("vitesse-hall-DC10-1-5-Ki0,02-Kp0,02.txt",r"$\omega=1\rightarrow 5$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-1-5-Ki0,02-Kp0,02.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
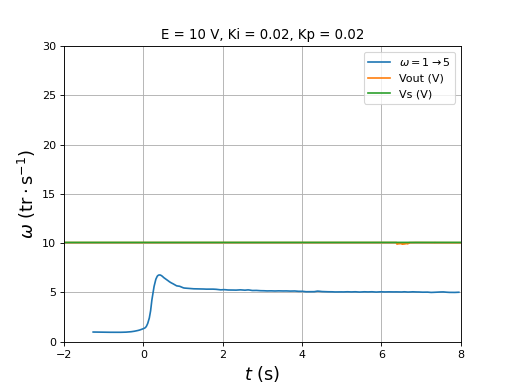 fig48.pdf
fig48.pdf
figure()
title("E = 10 V, Ki = 0.02, Kp = 0.02")
plotOmega("vitesse-hall-DC10-1-10-Ki0,02-Kp0,02.txt",r"$\omega=1\rightarrow 10$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-1-10-Ki0,02-Kp0,02.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
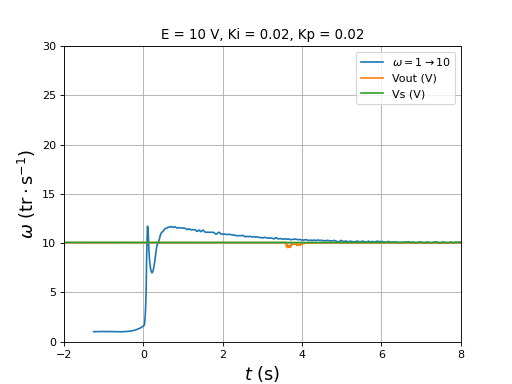 fig49.pdf
fig49.pdf
figure()
title("E = 10 V, Ki = 0.02, Kp = 0.02")
plotOmega("vitesse-hall-DC10-10-1-Ki0,02-Kp0,02.txt",r"$\omega=10\rightarrow 1$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-10-1-Ki0,02-Kp0,02.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
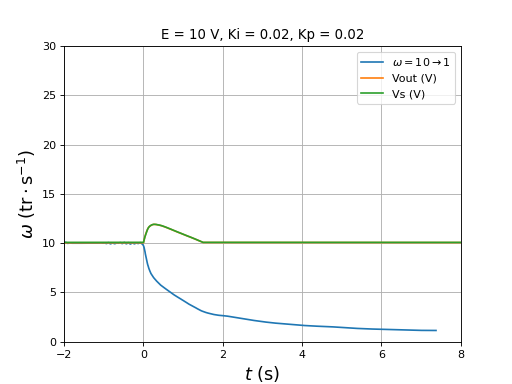 fig50.pdf
fig50.pdf
figure()
title("E = 10 V, Ki = 0.02, Kp = 0.02")
plotOmega("vitesse-hall-DC10-10-5-Ki0,02-Kp0,02.txt",r"$\omega=10\rightarrow 5$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-10-5-Ki0,02-Kp0,02.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
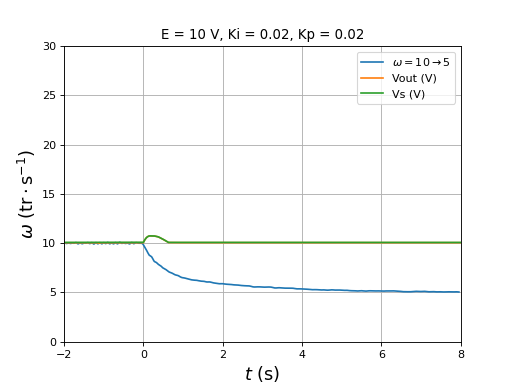 fig51.pdf
fig51.pdf
figure()
title("E = 10 V, Ki = 0.02, Kp = 0.02")
plotOmega("vitesse-hall-DC10-5-10-Ki0,02-Kp0,02.txt",r"$\omega=5\rightarrow 10$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-5-10-Ki0,02-Kp0,02.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
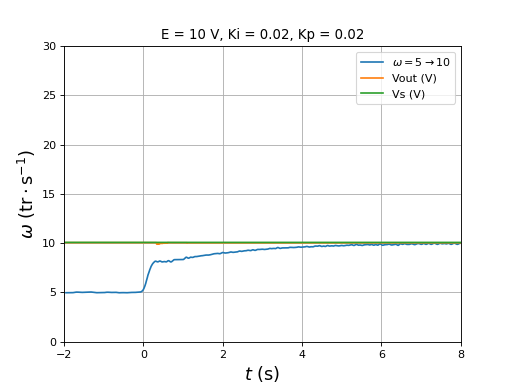 fig52.pdf
fig52.pdf
figure()
title("E = 10 V, Ki = 0.02, Kp = 0.02")
plotOmega("vitesse-hall-DC10-5-20-Ki0,02-Kp0,02.txt",r"$\omega=5\rightarrow 20$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-5-20-Ki0,02-Kp0,02.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
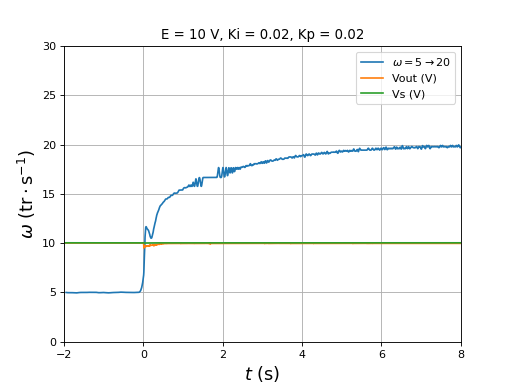 fig53.pdf
fig53.pdf
figure()
title("E = 10 V, Ki = 0.02, Kp = 0.02")
plotOmega("vitesse-hall-DC10-20-5-Ki0,02-Kp0,02.txt",r"$\omega=20\rightarrow 5$")
[t,Vout,Vs] = np.loadtxt("vitesse-Vout-Vs-DC10-20-5-Ki0,02-Kp0,02.txt",unpack=True,skiprows=1)
plot(t,Vout,label="Vout (V)")
plot(t,Vs,label="Vs (V)")
xlim(-2,8)
ylim(0,30)
legend(loc="upper right")
xlabel(r"$t\ (\rm s)$",fontsize=16)
ylabel(r"$\omega\ (\rm tr\cdot s^{-1})$",fontsize=16)
grid()
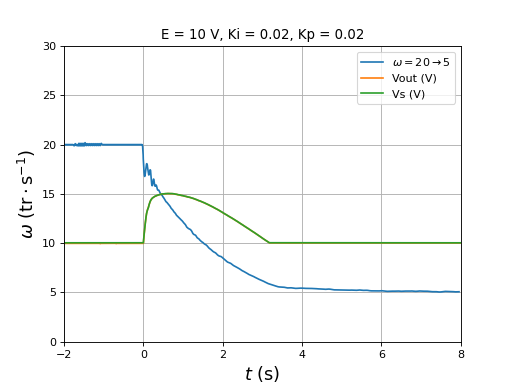 fig54.pdf
fig54.pdf