Filtres passe-bas de Bessel

2.a. Fonction de transfert

Posons $s=j\omega$. Une fonction de transfert d'ordre 2 (sans zéros) s'écrit :

$$H\left(s\right)=\frac{b_0}{a_0{s}^2+a_{1}s+a_2}\text{(1)}$$

Le gain à fréquence nulle est $G_0=b_0/a_2$. Si ${\omega }_c$ est la pulsation de coupure à -3 dB, on a :

$$\frac{b_0^2}{{(a_2-a_0{\omega }_c^2)}^2+a_1^2{\omega }_c^2}=\frac{1}{2}\text{(2)}$$

La fonction scipy.signal.bessel permet de calculer les coefficients pour un gain unité à fréquence nulle et une pulsation de coupure quelconque. Nous pouvons obtenir une expression de la fonction de transfert indépendante de la pulsation de coupure en posant $s=j\frac{\omega }{{\omega }_c}$. Les coefficients correspondants sont obtenus avec une pulsation de coupure égale à 1 :

from scipy.signal import bessel,butter,residue
import numpy as np
from matplotlib.pyplot import *

N=2
Wn = 1 # pulsation de coupure
b_bessel,a_bessel = bessel(N,Wn,btype='low',analog=True,output='ba',norm='mag')
                  

print(b_bessel)
--> array([1.61803399])

print(a_bessel)
--> array([1.        , 2.20320266, 1.61803399])

Il est bien sûr aisé d'obtenir un gain à fréquence nulle différent de 1 en multipliant cette fonction de transfert par le gain souhaité.

Voici le gain en décibel en fonction de la fréquence :

def transfert(a,b,f,fc):
    s = 1j*f/fc
    return b[0]/(a[0]*s**2+a[1]*s+a[2])

f = np.logspace(-2,2,1000) # fréquence réduite
H = transfert(a_bessel,b_bessel,f,1)
G_bessel = np.absolute(H)
GdB_bessel = 20*np.log10(G_bessel)
phi_bessel = np.angle(H)

figure(figsize=(8,6))
plot(f,GdB_bessel)
grid()
xscale('log')
xlabel(r"$f/f_c$",fontsize=16)
ylabel(r"$G_{dB}$",fontsize=16)              
                  

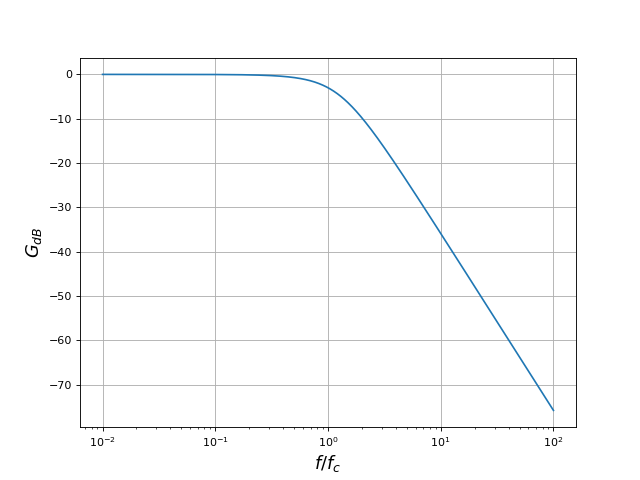fig1.pdf

et le déphasage en fonction de la fréquence (en échelle linéaire) :

figure(figsize=(8,6))
plot(f,phi_bessel)
grid()
xlabel(r"$f/f_c$",fontsize=16)
ylabel(r"$\phi\ (\rm rad)$")
xlim(0,2)
                  

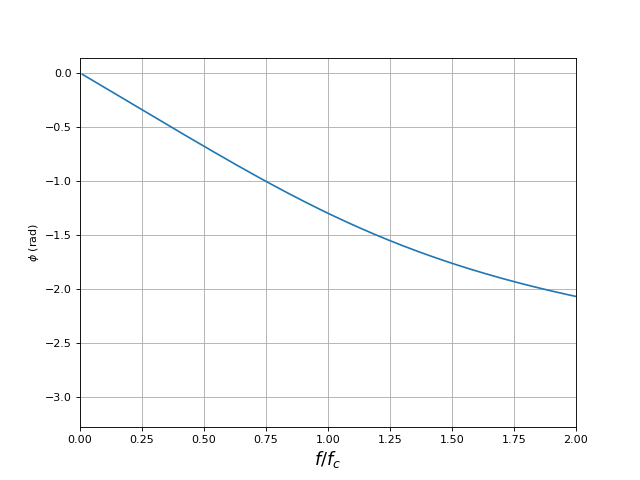fig2.pdf

Voici la comparaison avec un filtre de Butterworth :

b_butter,a_butter = butter(N,Wn,btype='low',analog=True,output='ba')
H = transfert(a_butter,b_butter,f,1)
G_butter = np.absolute(H)
GdB_butter = 20*np.log10(G_butter)
phi_butter = np.angle(H)

figure(figsize=(8,6))
plot(f,G_bessel,label="Bessel")
plot(f,G_butter,label="Butterworth")
grid()
xlabel(r"$f/f_c$",fontsize=16)
ylabel(r"$G$",fontsize=16)
legend(loc="upper right")
xlim(0,2)
                  

print(b_butter)
--> array([1.])

print(a_butter)
--> array([1.        , 1.41421356, 1.        ])

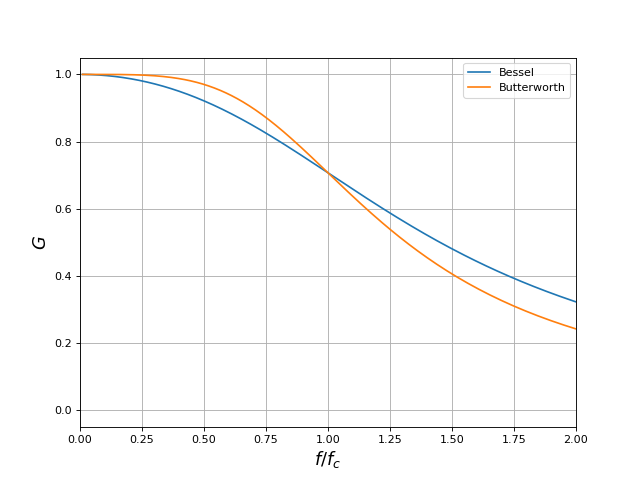fig3.pdf

figure(figsize=(8,6))
plot(f,GdB_bessel,label="Bessel")
plot(f,GdB_butter,label="Butterworth")
grid()
xlabel(r"$f/f_c$",fontsize=16)
ylabel(r"$G$",fontsize=16)
legend(loc="upper right")
xscale('log')
                  

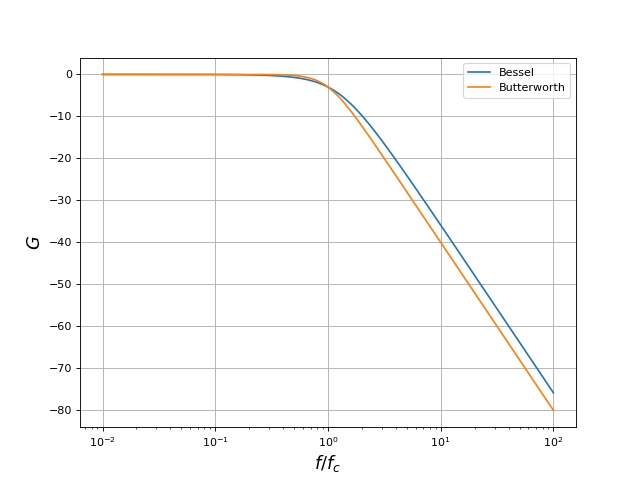fig4.pdf

figure(figsize=(8,6))
plot(f,phi_bessel,label="Bessel")
plot(f,phi_butter,label="Butterworth")
grid()
xlabel(r"$f/f_c$",fontsize=16)
ylabel(r"$\phi\ (\rm rad)$")
legend(loc="upper right")
xlim(0,2)
                  

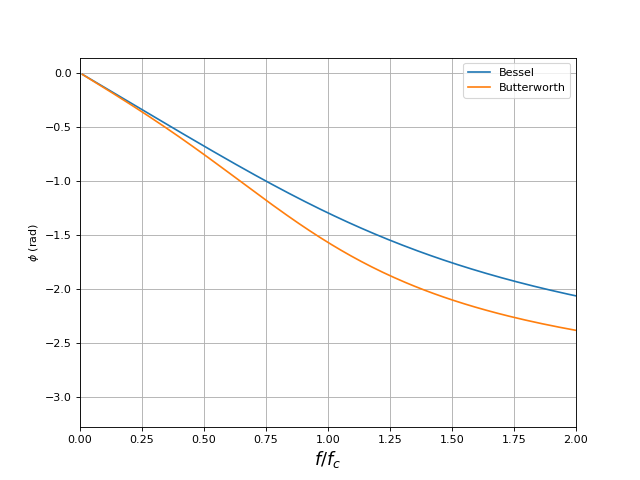fig5.pdf

Dans la bande passante, le filtre de Bessel présente un déphasage dont la linéarité avec la fréquence est bien meilleure que le filtre de Butterworth (remarquer que les pentes sont identiques à fréquence nulle). En revanche, son gain a une décroissance répartie sur une plus large bande de fréquence. Dans la bande de transition, la pente asymptotique est la même que celle du filtre de Butterworth mais elle est atteinte à une fréquence plus élevée, ce qui fait que le gain est plus élevé d'environ 2 dB pour une fréquence donnée.

Il est intéressant de comparer la réponse à un échelon (ou réponse indicielle). La transformée de Laplace d'un échelon étant 1/s, celle de la réponse indicielle est :

$$F\left(s\right)=\frac{1}{s}H\left(s\right)=\frac{b_0}{a_0{s}^3+a_1{s}^2+a_{2}s}\text{(3)}$$

Cette fraction rationnelle doit être décomposée en éléments simples. La fonction scipy.signal.residue permet de le faire :

a = a_bessel
b = b_bessel
r,p,k = residue(b,[a[0],a[1],a[2],0],tol=0.001)
                    

Voici les pôles :

print(p)
--> array([ 0.        +0.j        , -1.10160133+0.63600982j,
       -1.10160133-0.63600982j])

et les résidus correspondants :

print(r)
--> array([ 1. +0.j       , -0.5+0.8660254j, -0.5-0.8660254j])

La décomposition en éléments simples est :

$$F\left(p\right)=\frac{r_0}{s-p_0}+\frac{r_1}{s-p_1}+\frac{r_2}{s-p_2}\text{(4)}$$

La réponse indicielle est la transformée de Laplace inverse de F(p) :

$$f\left(t\right)=r_0{e}^{p_{0}t}+r_1{e}^{p_{1}t}+r_2{e}^{p_{2}t}=r_0+2Re\left[r_1{e}^{p_{1}t}\right]\text{(5)}$$

t = np.linspace(0,50,1000)
f_bessel = r[0]+2*np.real(r[1]*np.exp(p[1]*t))
a = a_butter
b = b_butter
r,p,k = residue(b,[a[0],a[1],a[2],0],tol=0.001)
f_butter = r[0]+2*np.real(r[1]*np.exp(p[1]*t))


figure()
plot(t,f_bessel,label="Bessel")
plot(t,f_butter,label="Butterworth")
grid()
xlabel(r"$f_ct$",fontsize=16)
ylabel(r"$f(t)$",fontsize=16)
legend(loc="lower right")
                    

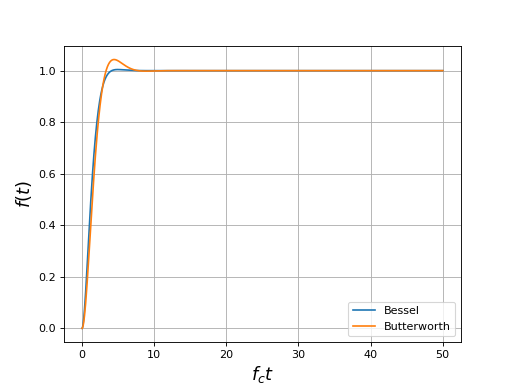fig6.pdf

La réponse indicielle du filtre de Bessel présente un dépassement très faible, contrairement à celle du filtre de Butterworth.

2.b. Filtre de Sallen et Key

Le filtre de Sallen et Key est un filtre actif d'ordre 2 réalisé au moyen d'un amplificateur de tension de gain K :

Figure pleine page

Si l'amplificateur est réalisé au moyen d'un amplificateur linéaire intégré (ALI) en montage non-inverseur, on obtient le circuit suivant :

Figure pleine page

Pour un ALI idéal de gain infini, la fonction de transfert est de la forme suivante :

$$H\left(\omega \right)=\frac{K}{1+mj\frac{\omega }{{\omega }_0}+(j\frac{\omega }{{\omega }_0}{)}^2}\text{(6)}$$

avec :

$$\begin{array}{ccc}\hfill & {\omega }_0=\frac{1}{R\sqrt{C_1{C}_2}}\hfill & \hfill \text{(7)}\\ \hfill & m=2\sqrt{\frac{C_1}{C_2}}+\sqrt{\frac{C_2}{C_1}}(1-K)\hfill & \hfill \text{(8)}\end{array}$$

Le gain à fréquence nulle est K. On pourrait opter pour un gain à fréquence nulle égal à 1 (amplificateur suiveur) mais cela obligerait à satisfaire une valeur bien précise pour C₁/C₂. En pratique, il n'est pas nécessaire d'avoir un gain unité à fréquence nulle. On adopte plutôt C₁=C₂=C (qui sera plus facile à satisfaire qu'un rapport donné), ce qui conduit à :

$$m=3-K\text{(9)}$$

Si ${\omega }_c$ désigne la pulsation de coupure à -3 dB, posons : $\alpha =\frac{{\omega }_0}{{\omega }_c}$ et $s=j\frac{\omega }{{\omega }_c}$. On obtient :

$$H\left(s\right)=\frac{K{\alpha }^2}{s^2+m\alpha s+{\alpha }^2}\text{(10)}$$

Le gain à fréquence nulle est K (proche de 1). Par identification avec la fonction de transfert obtenue plus haut, on a :

$$\begin{array}{ccc}\hfill & m\alpha =\frac{a_1}{a_0}\hfill & \hfill \text{(11)}\\ \hfill & {\alpha }^2=\frac{a_2}{a_0}\hfill & \hfill \text{(12)}\end{array}$$

Voici les valeurs :

a = a_bessel
alpha = np.sqrt(a[2]/a[0])
m = a[1]/a[0]/alpha
K = 3-m
                

print(alpha)
--> 1.272019649514069

print(m)
--> 1.7320508075688772

print(K)
--> 1.2679491924311228

Dans [1] ces valeurs sont données dans un tableau (table 6.2) où la constante $\alpha$ est notée c_n.

Pour une fréquence de coupure f_c on a

$$RC=\frac{1}{2\pi \alpha f_c}\text{(13)}$$

Voici un exemple où la valeur de C est choisie en premier :

fc = 1000
RC = 1/(2*np.pi*alpha*fc)
C = 100e-9
R = RC/C
                

print(R)
--> 1251.1987778859782

Les résistances (K-1)R₀ et R₀ sont réalisées avec un potentiomètre dont le curseur est branché sur l'entrée inverseuse de l'ALI : c'est en effet le rapport de ces résistances qui détermine le gain K. La valeur de K est facile à ajuster avec le potentiomètre puisqu'il s'agit du gain à fréquence nulle.

Pour finir, nous écrivons une fonction qui permet de calculer les paramètres du filtre de Sallen et Key d'ordre 2 à partir des coefficients du dénominateur de la fonction de transfert :

def SK2(a):
    alpha = np.sqrt(a[2]/a[0])
    m = a[1]/a[0]/alpha
    K = 3-m
    return (alpha,m,K)
                

3.a. Fonction de transfert

Calculons la fonction de transfert d'un filtre de Bessel d'ordre 4 (de gain unitaire à fréquence nulle) :

N=4
Wn = 1 # pulsation de coupure
b_bessel_4,a_bessel_4 = bessel(N,Wn,btype='low',analog=True,output='ba',norm='mag')            
                

print(b_bessel)
--> array([1.61803399])

print(a_bessel)
--> array([1.        , 2.20320266, 1.61803399])

def transfert_4(a,b,f,fc):
    s = 1j*f/fc
    return b[0]/(a[0]*s**4+a[1]*s**3+a[2]*s**2+a[3]*s+a[4])
H = transfert_4(a_bessel_4,b_bessel_4,f,1)
G_bessel_4 = np.absolute(H)
GdB_bessel_4 = 20*np.log10(G_bessel_4)
phi_bessel_4 = np.unwrap(np.angle(H))

figure()
plot(f,GdB_bessel,label="Bessel d'ordre 2")
plot(f,GdB_bessel_4,label="Bessel d'ordre 4")
grid()
xscale('log')
xlabel(r"$f/f_c$",fontsize=16)
ylabel(r"$G_{dB}$",fontsize=16) 
legend(loc="lower left")  
                  

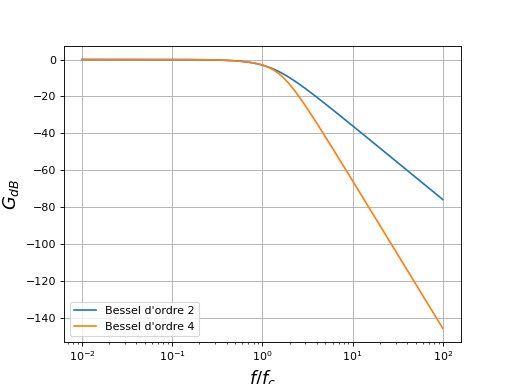fig7.pdf

figure()
plot(f,phi_bessel,label="Bessel d'ordre 2")
plot(f,phi_bessel_4,label="Bessel d'ordre 4")
grid()
xlabel(r"$f/f_c$",fontsize=16)
ylabel(r"$\phi\ (\rm rad)$")
xlim(0,2)
legend(loc="lower left")  
                  

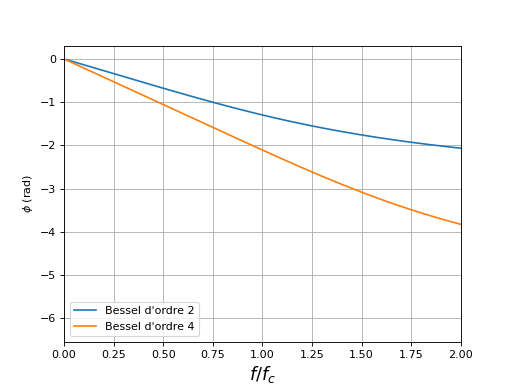fig8.pdf

Par rapport à l'ordre 2, la linéarité de la phase est améliorée mais le retard est bien évidemment plus grand.

Pour implémenter ce filtre sous la forme de deux filtres d'ordre 2 en cascade, nous devons rechercher ses pôles :

r,p,k = residue(b_bessel_4,a_bessel_4,tol=0.001)

                  

print(p)
--> array([-1.37006783+0.41024972j, -1.37006783-0.41024972j,
       -0.99520876+1.25710574j, -0.99520876-1.25710574j])

print(r)
--> array([ 0.78687616-3.97191452j,  0.78687616+3.97191452j,
       -0.78687616+1.06157271j, -0.78687616-1.06157271j])

On a ainsi :

$$H\left(s\right)=b_0\frac{1}{(s-p_0)(s-p_1)}\frac{1}{(s-p_2)(s-p_3)}\text{(14)}$$

que l'on écrit comme le produit de deux fonctions de transfert de gain unitaire à fréquence nulle :

$$H\left(s\right)=b_0\frac{1}{s^2-2Re\left[p_0\right]s+|p_0{|}^2}\frac{1}{s^2-2Re\left[p_2\right]s+|p_2{|}^2}=\frac{|p_0{|}^2}{s^2-2Re\left[p_0\right]s+|p_0{|}^2}\frac{|p_2{|}^2}{s^2-2Re\left[p_2\right]s+|p_2{|}^2}\text{(15)}$$

3.b. Filtre de Sallen et Key

Le décomposition précédente permet de réaliser le filtre d'ordre 4 au moyen de deux filtres de Sallen et Key en cascade.

(alpha1,m1,K1) = SK2([1,-2*np.real(p[0]),np.absolute(p[0])**2])
(alpha2,m2,K2) = SK2([1,-2*np.real(p[2]),np.absolute(p[2])**2])
                

print((alpha1,K1))
--> (1.4301715599939886, 1.084051076281786)

print((alpha2,K2))
--> (1.6033575162169704, 1.7585940699010034)

Les valeurs de $\alpha$ sont différentes pour les deux étages. La fréquence de coupure doit être la même donc ces deux filtres d'ordre 2 n'ont pas la même valeur de RC.

Supposons que les deux filtres aient la même valeur de C et calculons les résistances pour une fréquence de coupure choisie :

fc = 1000
RCa = 1/(2*np.pi*alpha1*fc)
RCb = 1/(2*np.pi*alpha2*fc)
C = 15e-9
Ra = RCa/C
Rb = RCb/C
                

print((Ra,Rb))
--> (7418.920803812017, 6617.569339428521)

Chaque filtre devra bien sûr être réglé séparément en ajustant le potentiomètre afin que son gain pour une tension d'entrée constante soit égal à K.

Remarquons que si l'on souhaite utiliser le premier filtre seul comme filtre de Bessel, sa valeur de $\alpha$ est plus grande (1,47) que la valeur correcte pour un filtre d'ordre 2 (1,27) : en conséquence, sa fréquence de coupure sera un peu en dessous de 1000 Hz.

5.a. Filtre d'ordre 2

Voici les paramètres pour un filtre de Bessel d'ordre 2 réalisé avec une structure de Sallen et Key :

alpha,m,K = filtreBessel(1)
                

print((alpha[0],K[0]))
--> (1.2720196495140692, 1.267949192431123)

On souhaite une fréquence de coupure de 1000 Hz. La valeur nominale de C est 100 nF. Voici la valeur de R nécessaire :

fc = 1000
RC = 1/(2*np.pi*alpha[0]*fc)
C = 100e-9
R = RC/C            
                

print(R)
--> 1251.1987778859782

On opte pour deux résistances de valeur nominale 1,2 kΩ. L'ALI est un TL081. Voici le circuit réalisé, avec les valeurs mesurées des résistances et capacités :

Figure pleine page

L'étude expérimentale est faite avec l'Analog Discovery 2 et le logiciel Waveforms. L'outil Network permet d'acquérir la réponse fréquentielle.

Voici tout d'abord l'étude sur une large plage de fréquence :

[f,GdBe,GdB,phi] = np.loadtxt("filtre1-GdB-phase.txt",unpack=True,skiprows=1)
phi = np.unwrap(phi)
figure(figsize=(10,10))
title("Bessel")
subplot(211)
plot(f,GdB)
xscale('log')
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$G_{dB}$",fontsize=16)
subplot(212)
plot(f,phi)
grid()
xscale('log')
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\phi\ (\rm deg)$",fontsize=16)
                 

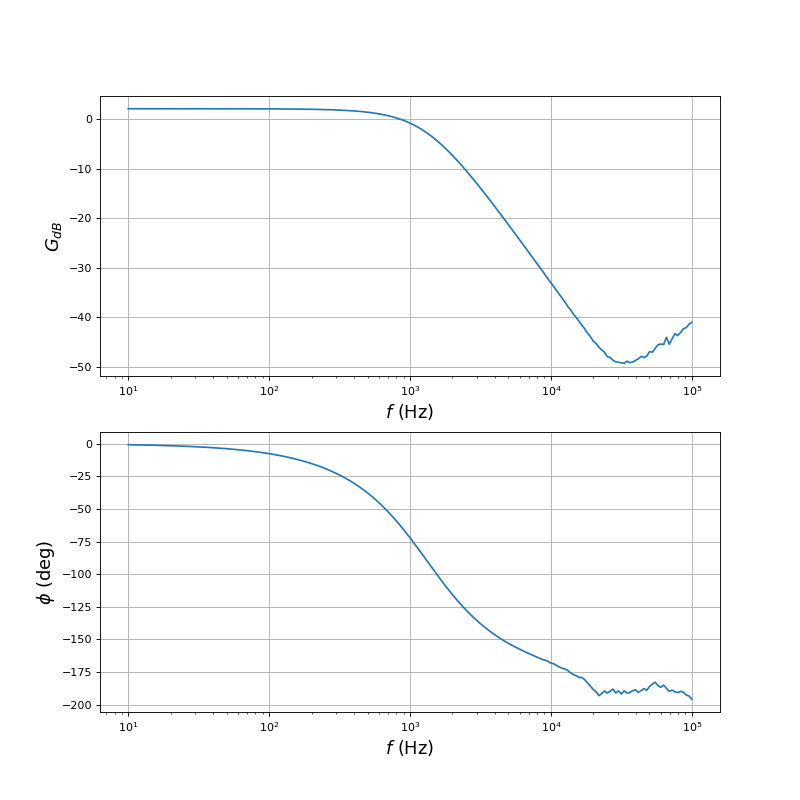fig9.pdf

On observe vers 20 kHz une remontée du gain, qui s'explique par la réponse fréquentielle de l'ALI (pas prise en compte dans le calcul avec l'ALI idéal). Ce comportement est typique des filtres de Salle et Key et limite l'atténuation à haute fréquence.

Voici les courbes de gain et de déphasage de 0 à 5 kHz :

[f,Ge,G,phi] = np.loadtxt("filtre1-gain-phase.txt",unpack=True,skiprows=1)
phi = np.unwrap(phi)
figure(figsize=(10,10))
title("Bessel")
subplot(211)
plot(f,G)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$G$",fontsize=16)
subplot(212)
plot(f,phi)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\phi\ (\rm deg)$",fontsize=16)
                 

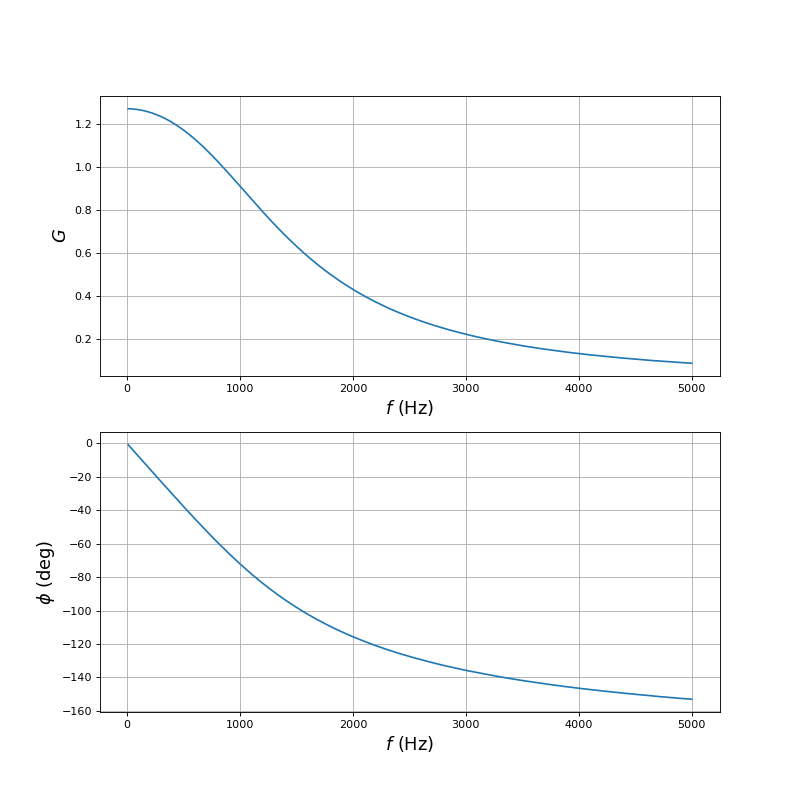fig10.pdf

Le gain à fréquence nulle est G₀=1,27 (valeur réglée avec le potentiomètre). Le gain à 1000 Hz vaut 0,91, ce qui confirme que 1000 Hz est la fréquence de coupure. Dans la bande passante, la linéarité du déphasage (par rapport à la fréquence) semble bien vérifiée. On peut aussi tracer le décalage temporel :

tau = phi/(360*f)
figure(figsize=(10,6))
title("Bessel")
plot(f,tau*1e3)
xlim(0,1000)
ylim(-0.3,0)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\tau\ (\rm ms)$",fontsize=16)
                  

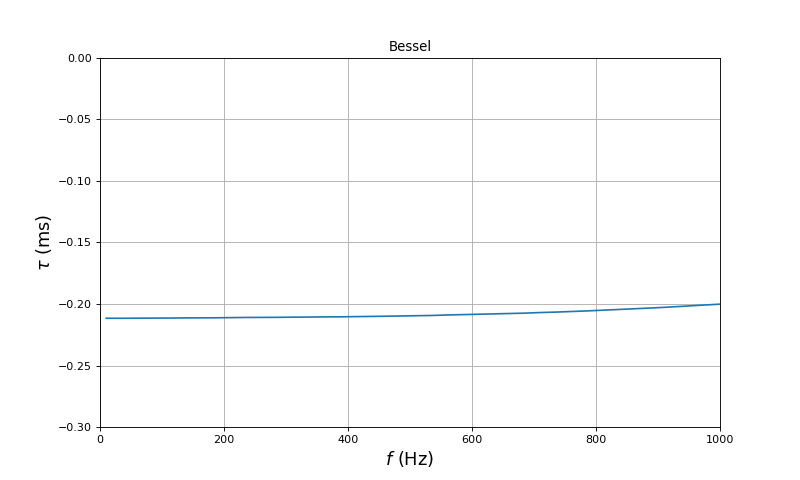fig11.pdf

Voici la variation relative du retard dans la bande passante :

figure(figsize=(10,6))
title("Bessel")
plot(f,np.abs((tau-tau[0])/tau[0]))
xlim(0,1000)
ylim(0,0.15)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\Delta\tau\/\tau (\rm ms)$",fontsize=16)
                  

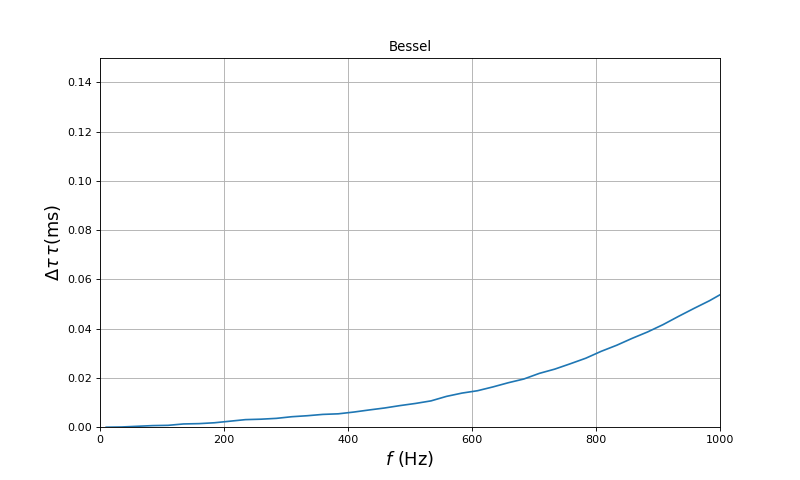fig12.pdf

Le retard varie de $5,5\%$.

Voici la réponse à un échelon (de hauteur 2 V) :

[t,e,s] = np.loadtxt("filtre1-echelon.txt",unpack=True,skiprows=1)
figure(figsize=(12,6))
title("Bessel")
plot(t*1e3,e,label="e(t)")
plot(t*1e3,s,label="s(t)")
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts",fontsize=16)
legend(loc="upper left")
                  

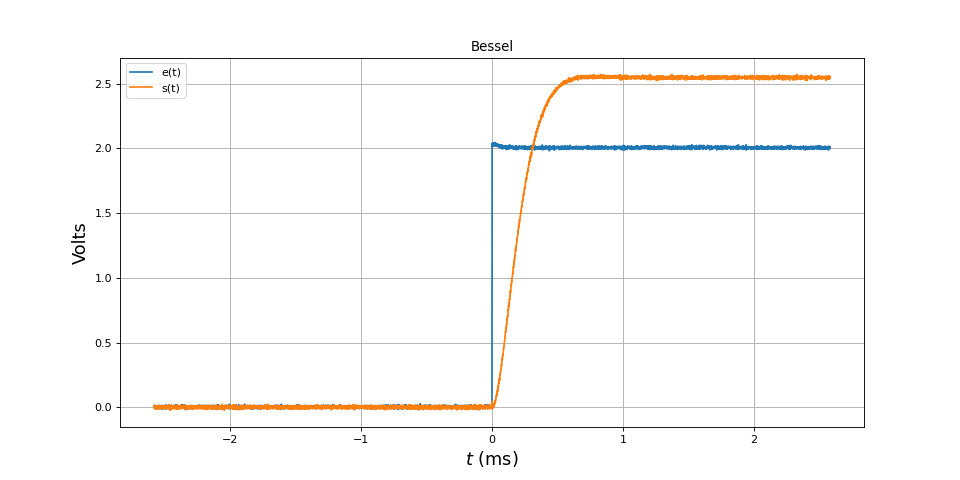fig13.pdf

Voici le filtrage d'un signal triangulaire de fréquence 100 Hz :

[t,e,s] = np.loadtxt("filtre1-triangle.txt",unpack=True,skiprows=1)
figure(figsize=(12,6))
title("Bessel")
plot(t*1e3,e,label="e(t)")
plot(t*1e3,s,label="s(t)")
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts",fontsize=16)
legend(loc="upper left")
                  

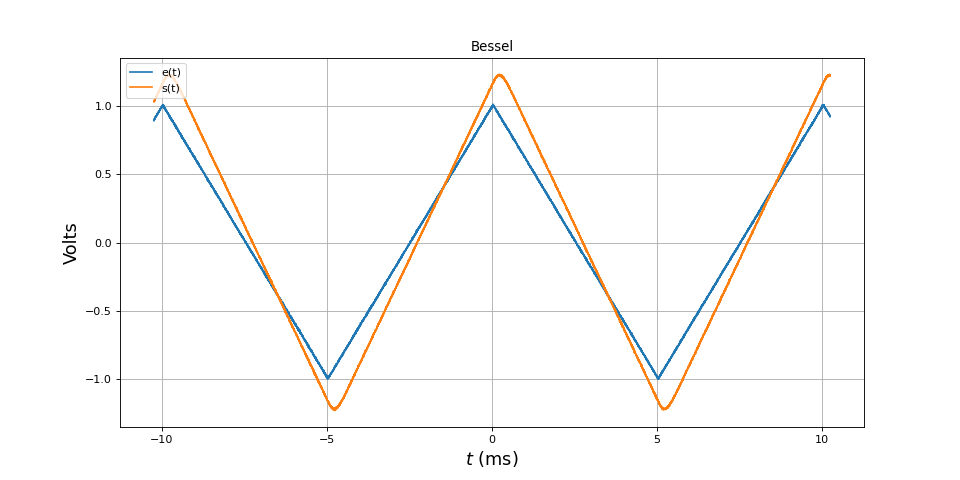fig14.pdf

Il est possible de transformer ce filtre de Bessel en filtre de Butterworth (sans changer R et C) :

alpha,m,K = filtreButter(1)
                

print((alpha[0],K[0]))
--> (1.0000000000000002, 1.5857864376269049)

Il suffit de régler le gain à fréquence nulle à cette nouvelle valeur de K (plus grande que pour le filtre de Bessel). La fréquence de coupure est modifiée :

fc = 1/(2*np.pi*RC)
                

print(fc)
--> 1272.019649514069

Voici le diagramme de Bode tracé avec celui du filtre de Bessel:

[fa,GdBe,GdBa,phia] = np.loadtxt("filtre1-GdB-phase.txt",unpack=True,skiprows=1)
[fb,GdBe,GdBb,phib] = np.loadtxt("filtre2-GdB-phase.txt",unpack=True,skiprows=1)
phia = np.unwrap(phia,period=360)
phib = np.unwrap(phib,period=360)
figure(figsize=(10,10))
subplot(211)
plot(fa,GdBa,label="Bessel")
plot(fb,GdBb,label="Butterworth")
xscale('log')
grid()
legend(loc="upper right")
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$G_{dB}$",fontsize=16)
subplot(212)
plot(fa,phia,label="Bessel")
plot(fb,phib,label="Butterworth")
legend(loc="upper right")
grid()
xscale('log')
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\phi\ (\rm deg)$",fontsize=16)
                 

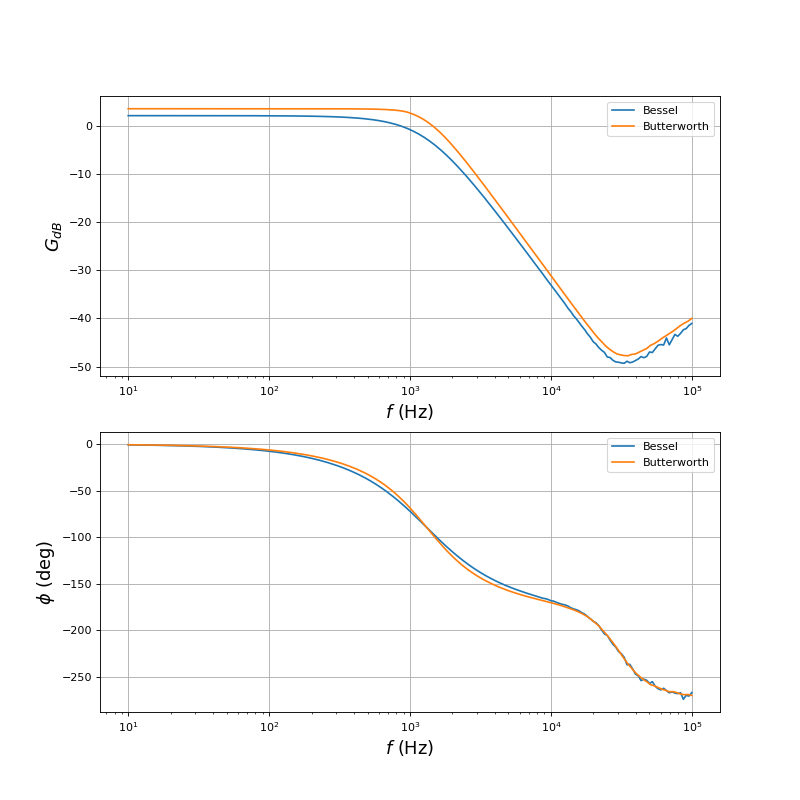fig15.pdf

Voici les courbes de gain et de déphasage. Pour comparer le gain, on le normalise par le gain à fréquence nulle :

[fa,Ge,Ga,phia] = np.loadtxt("filtre1-gain-phase.txt",unpack=True,skiprows=1)
[fb,Ge,Gb,phib] = np.loadtxt("filtre2-gain-phase.txt",unpack=True,skiprows=1)
phia = np.unwrap(phia,period=360)
phib = np.unwrap(phib,period=360)
figure(figsize=(10,10))
subplot(211)
plot(fa,Ga/Ga[0],label="Bessel")
plot(fb,Gb/Gb[0],label="Butterworth")
grid()
legend(loc="upper right")
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$G/G(0)$",fontsize=16)
subplot(212)
plot(fa,phia)
plot(fb,phib)
grid()
legend(loc="upper right")
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\phi\ (\rm deg)$",fontsize=16)
                 

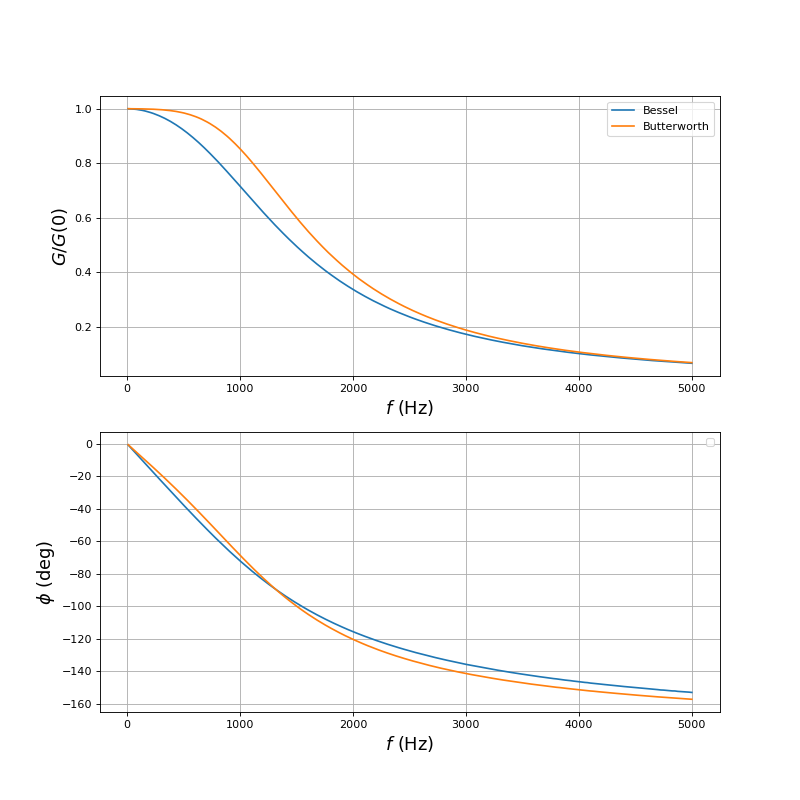fig16.pdf

Voici le décalage temporel :

tau = phib/(360*fb)
figure(figsize=(10,6))
title("Butterworth")
plot(fb,tau*1e3)
xlim(0,1200)
ylim(-0.3,0)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\tau\ (\rm ms)$",fontsize=16)
                  

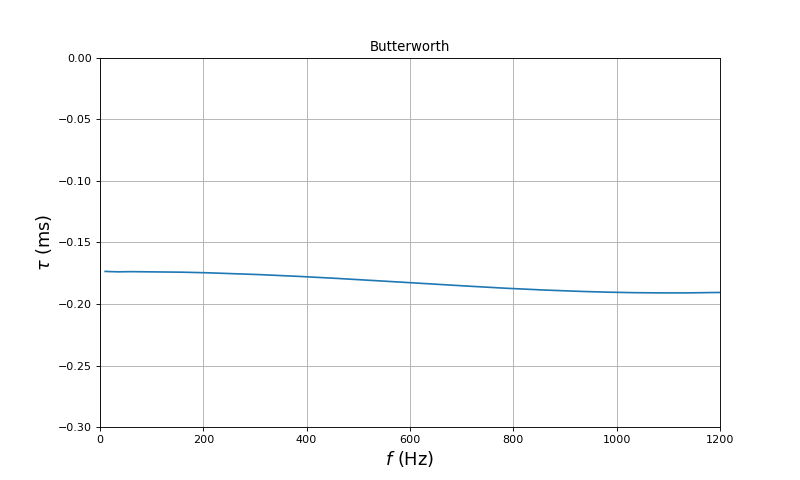fig17.pdf

Voici la variation relative du retard dans la bande passante :

figure(figsize=(10,6))
title("Butterworth")
plot(fb,np.abs((tau-tau[0])/tau[0]))
xlim(0,1200)
ylim(0,0.15)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\Delta\tau/\tau\ (\rm ms)$",fontsize=16)
                  

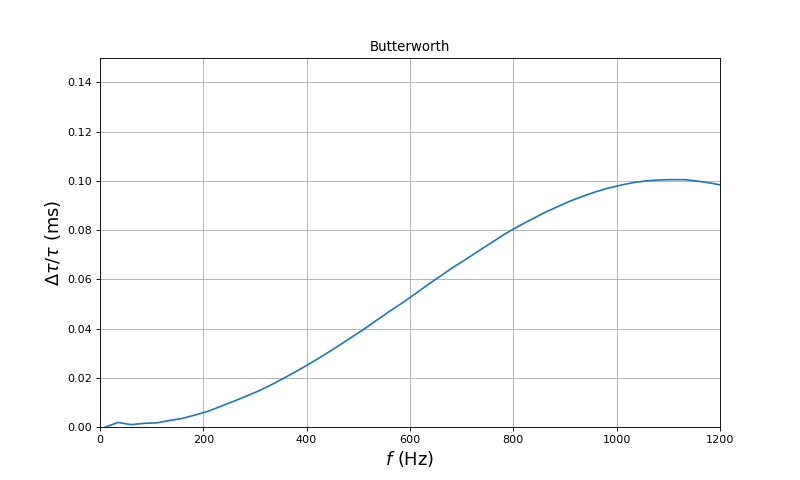fig18.pdf

Le retard varie de $10\%$, soit presque deux fois plus que pour le filtre de Bessel.

Voici la réponse à un échelon (de hauteur 2 V) :

[t,e,s] = np.loadtxt("filtre2-echelon.txt",unpack=True,skiprows=1)
figure(figsize=(12,6))
title("Butterworth")
plot(t*1e3,e,label="e(t)")
plot(t*1e3,s,label="s(t)")
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16) 
ylabel("Volts",fontsize=16)
legend(loc="upper left")
                  

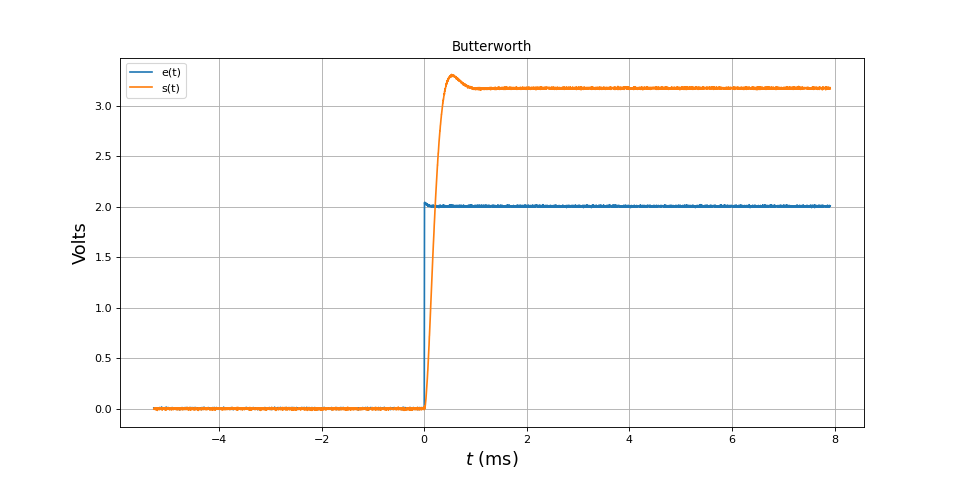fig19.pdf

La réponse à un échelon présente un dépassement important, contrairement à celle du filtre de Bessel.

Voici le filtrage d'un signal triangulaire de fréquence 100 Hz :

[t,e,s] = np.loadtxt("filtre2-triangle.txt",unpack=True,skiprows=1)
figure(figsize=(12,6))
title("Butterworth")
plot(t*1e3,e,label="e(t)")
plot(t*1e3,s,label="s(t)")
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts",fontsize=16)
legend(loc="upper left")
                  

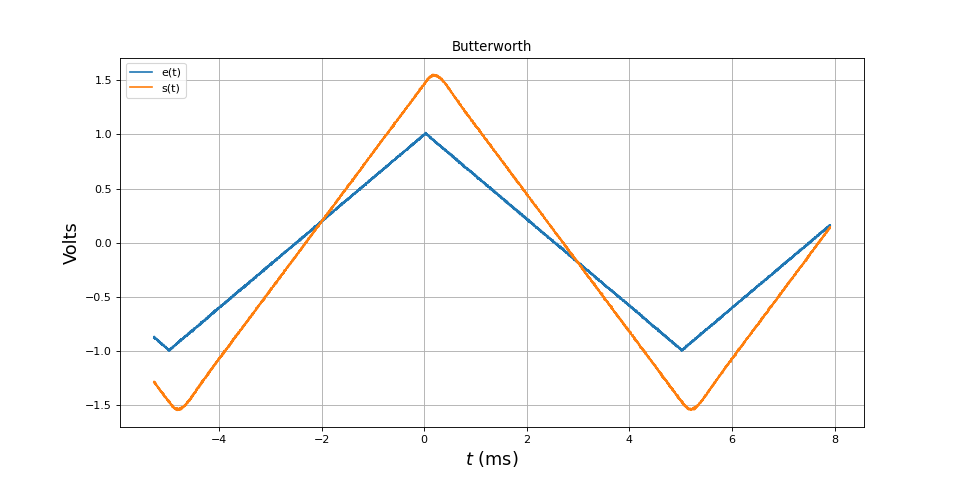fig20.pdf

Sur ce signal et à cette fréquence, l'avantage du filtre de Bessel sur le filtre de Butterworth n'est pas visible. Il l'est évidemment sur un signal carré.

Le même circuit peut réaliser un filtre de Chebyshev, avec une variation maximale de 2 dB dans la bande passante :

alpha,m,K = filtreCheby(1,2)
                

print((alpha[0],K[0]))
--> (0.9072267779732325, 2.113985114148045)

Voici la nouvelle fréquence de coupure :

fc = 1/(2*np.pi*RC*alpha[0])
                

print(fc)
--> 1402.0966757129822

Voici le diagramme de Bode tracé avec celui du filtre de Bessel et de Butterworth :

[fa,GdBe,GdBa,phia] = np.loadtxt("filtre1-GdB-phase.txt",unpack=True,skiprows=1)
[fb,GdBe,GdBb,phib] = np.loadtxt("filtre2-GdB-phase.txt",unpack=True,skiprows=1)
[fc,GdBe,GdBc,phic] = np.loadtxt("filtre3-GdB-phase.txt",unpack=True,skiprows=1)
phia = np.unwrap(phia,period=360)
phib = np.unwrap(phib,period=360)
phic = np.unwrap(phic,period=360)
figure(figsize=(10,10))
subplot(211)
plot(fa,GdBa,label="Bessel")
plot(fb,GdBb,label="Butterworth")
plot(fb,GdBc,label="Chebyshev 2 dB")
xscale('log')
grid()
legend(loc="upper right")
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$G_{dB}$",fontsize=16)
subplot(212)
plot(fa,phia,label="Bessel")
plot(fb,phib,label="Butterworth")
plot(fc,phic,label="Chebyshev 2 dB")
legend(loc="upper right")
grid()
xscale('log')
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\phi\ (\rm deg)$",fontsize=16)
                 

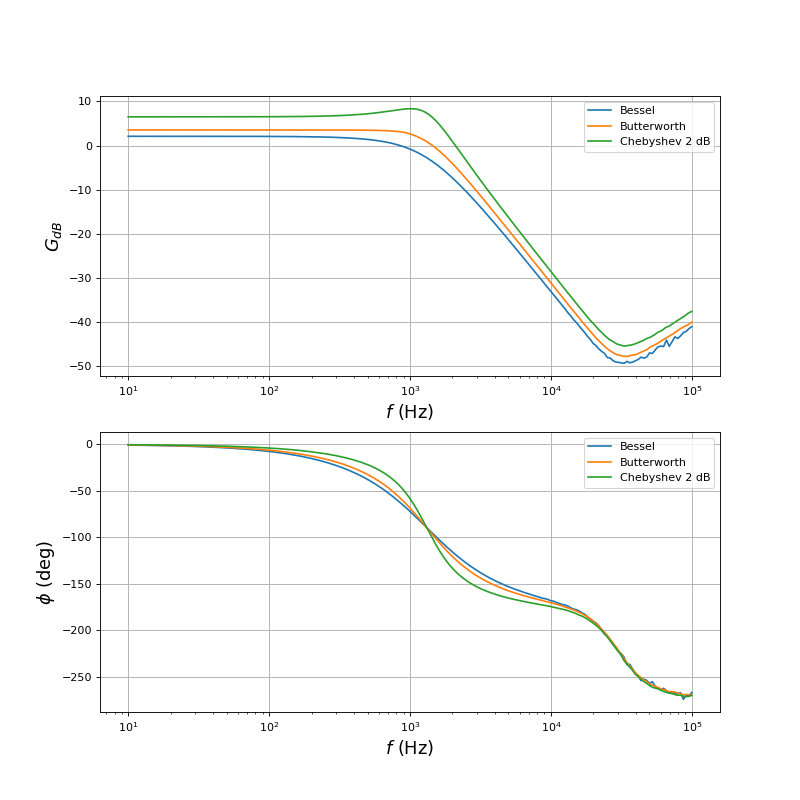fig21.pdf

Voici les courbes de gain et de déphasage. Pour comparer le gain, on le normalise par le gain à fréquence nulle :

[fa,Ge,Ga,phia] = np.loadtxt("filtre1-gain-phase.txt",unpack=True,skiprows=1)
[fb,Ge,Gb,phib] = np.loadtxt("filtre2-gain-phase.txt",unpack=True,skiprows=1)
[fc,Ge,Gc,phic] = np.loadtxt("filtre3-gain-phase.txt",unpack=True,skiprows=1)
phia = np.unwrap(phia,period=360)
phib = np.unwrap(phib,period=360)
phic = np.unwrap(phic,period=360)
figure(figsize=(10,10))
subplot(211)
plot(fa,Ga/Ga[0],label="Bessel")
plot(fb,Gb/Gb[0],label="Butterworth")
plot(fc,Gc/Gc[0],label="Chebyshev 2 dB")
grid()
legend(loc="upper right")
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$G/G(0)$",fontsize=16)
subplot(212)
plot(fa,phia,label="Bessel")
plot(fb,phib,label="Butterworth")
plot(fc,phic,label="Chebyshev 2 dB")
grid()
legend(loc="upper right")
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\phi\ (\rm deg)$",fontsize=16)
                 

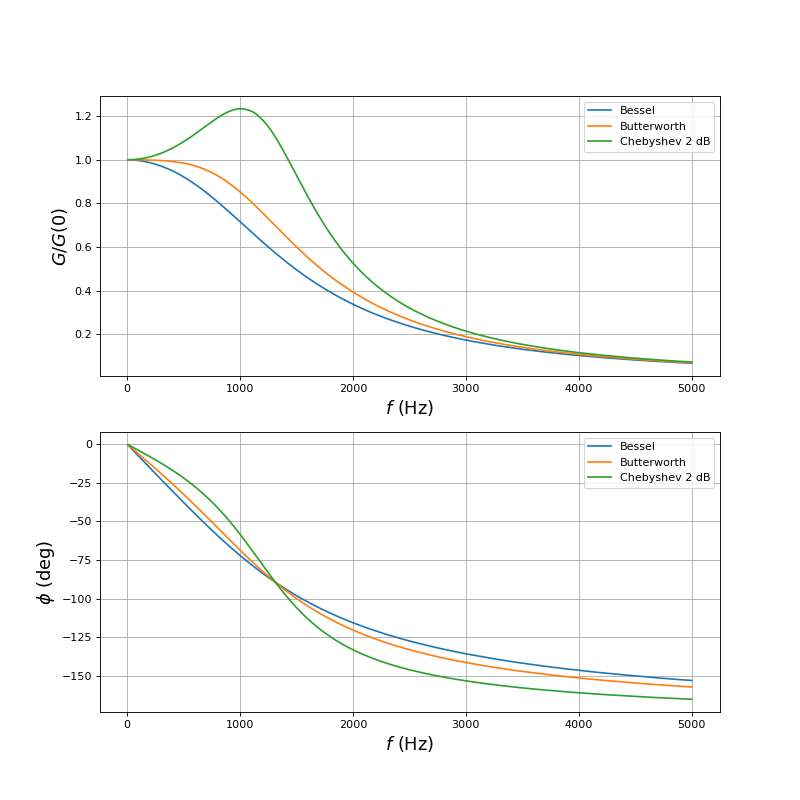fig22.pdf

Le filtre de Chebyshev donne une décroissance du gain dans la bande de transition très rapide en contrepartie d'un variation plus grande dans la bande passante (ici 2 dB). Le déphasage n'est pas du tout linéaire par rapport à la fréquence.

Voici le décalage temporel :

tau = phic/(360*fc)
figure(figsize=(10,6))
title("Chebyshev")
plot(fc,tau*1e3)
xlim(0,1200)
ylim(-0.3,0)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\tau\ (\rm ms)$",fontsize=16)
                  

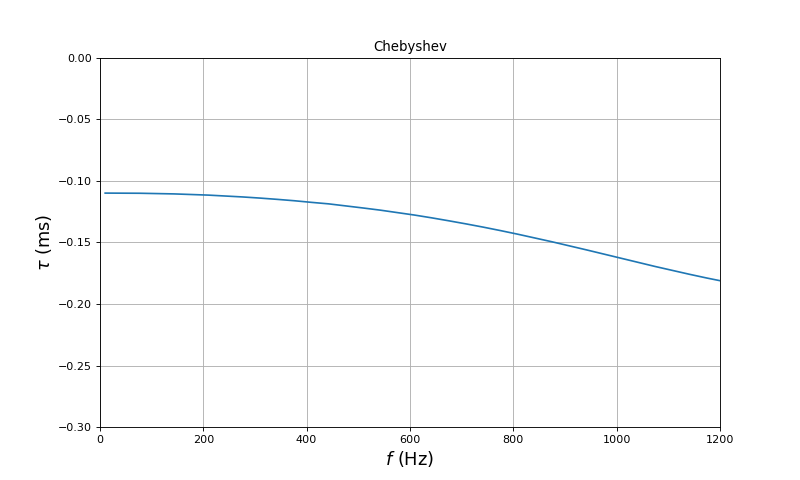fig23.pdf

Avec un filtre de Chebyschev 2dB, le retard varie beaucoup dans la bande passante. Voici la variation relative du retard dans la bande passante :

figure(figsize=(10,6))
title("Chebyshev")
plot(fc,np.abs((tau-tau[0])/tau[0]))
xlim(0,1400)
ylim(0,1)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\Delta\tau/\tau\ (\rm ms)$",fontsize=16)
                  

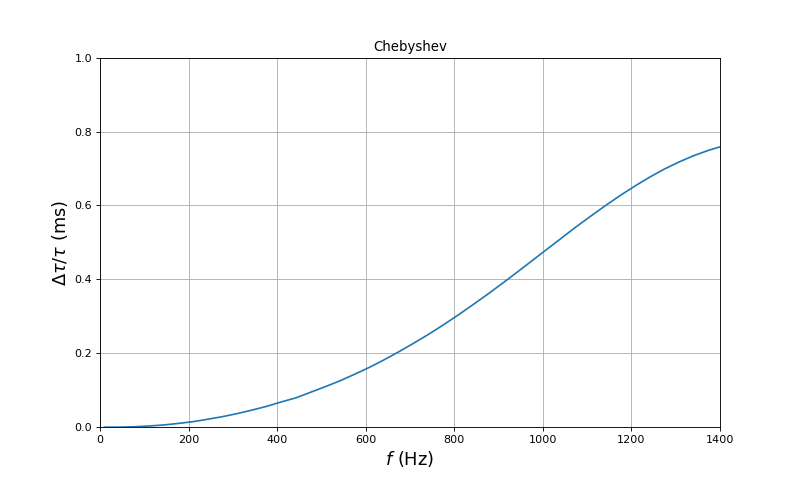fig24.pdf

Voici la réponse à un échelon (de hauteur 2 V) :

[t,e,s] = np.loadtxt("filtre3-echelon.txt",unpack=True,skiprows=1)
figure(figsize=(12,6))
title("Chebyshev")
plot(t*1e3,e,label="e(t)")
plot(t*1e3,s,label="s(t)")
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16) 
ylabel("Volts",fontsize=16)
legend(loc="upper left")
                  

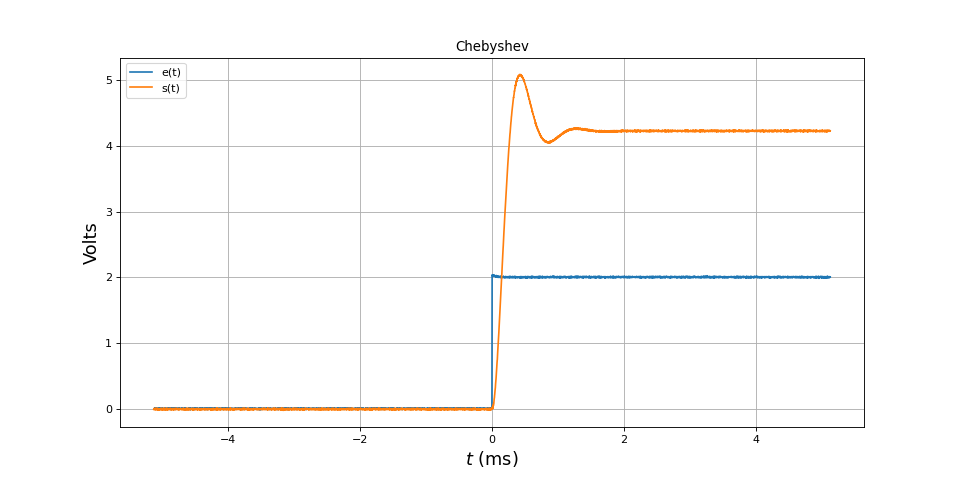fig25.pdf

La réponse à un échelon présente un dépassement très grand, plus grand qu'avec le filtre de Butterworth.

Voici le filtrage d'un signal triangulaire de fréquence 100 Hz :

[t,e,s] = np.loadtxt("filtre3-triangle.txt",unpack=True,skiprows=1)
figure(figsize=(12,6))
title("Chebyshev")
plot(t*1e3,e,label="e(t)")
plot(t*1e3,s,label="s(t)")
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts",fontsize=16)
legend(loc="upper left")
                  

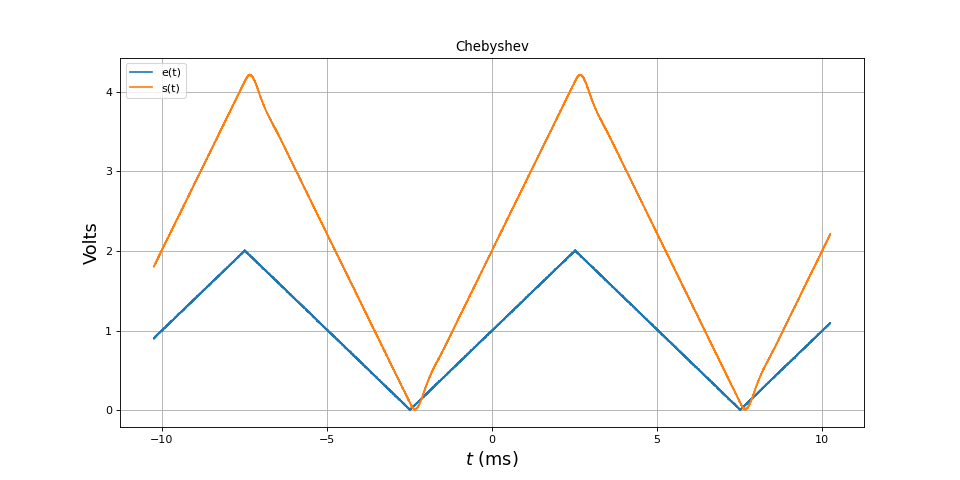fig26.pdf

Sur ce signal, la distorsion de la forme est bien visible. Ce type de filtre est intéressant lorsque le signal utile est sinusoïdal car il offre une très bonne réduction au dessus de la fréquence de coupure mais il ne convient pas si le signal utile comporte des harmoniques.

5.b. Filtre d'ordre 4

Voici les paramètres pour réaliser un filtre de Bessel avec deux filtres de Sallen et Key en cascade :

alpha,m,K = filtreBessel(2)
            

print((alpha[0],K[0]))
--> (1.4301715599939886, 1.084051076281786)

print((alpha[1],K[1]))
--> (1.6033575162169704, 1.7585940699010034)

On souhaite une fréquence de coupure de 1000 Hz. La valeur nominale de C est 15 nF pour les deux circuits. Voici la valeur de R nécessaire :

fc = 1000
RCa = 1/(2*np.pi*alpha[0]*fc)
RCb = 1/(2*np.pi*alpha[1]*fc)
C = 15e-9
Ra = RCa/C
Rb = RCb/C          
                

print((Ra,Rb))
--> (7418.920803812017, 6617.569339428521)

Il n'est pas aisé d'obtenir précisément ces valeurs avec un stock disponible de résistances. Nous optons pour l'association de deux résistances en série. R_a est réalisée avec deux résistances de valeurs nominales 8,8 k et 560. R_b est réalisée avec deux résistances de valeurs nominales 5,6 k et 1,0 k. Voici le schéma du circuit réalisé avec les valeurs mesurées de R et C :

Figure pleine page

Pour le premier filtre on règle le potentiomètre afin d'avoir un gain à fréquence nulle égal à 1,08. Pour le second le gain à fréquence nulle est 1,76.

Voici le diagramme de Bode, jusqu'à 10 kHz :

[fa,GdBe,GdBa,phia] = np.loadtxt("filtre4-GdB-phase-10Hz-10kHz.txt",unpack=True,skiprows=1)
phia = np.unwrap(phia,period=360)
figure(figsize=(10,10))
subplot(211)
plot(fa,GdBa,label="Bessel")
xscale('log')
grid()
legend(loc="upper right")
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$G_{dB}$",fontsize=16)
subplot(212)
plot(fa,phia,label="Bessel")
legend(loc="upper right")
grid()
xscale('log')
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\phi\ (\rm deg)$",fontsize=16)
                 

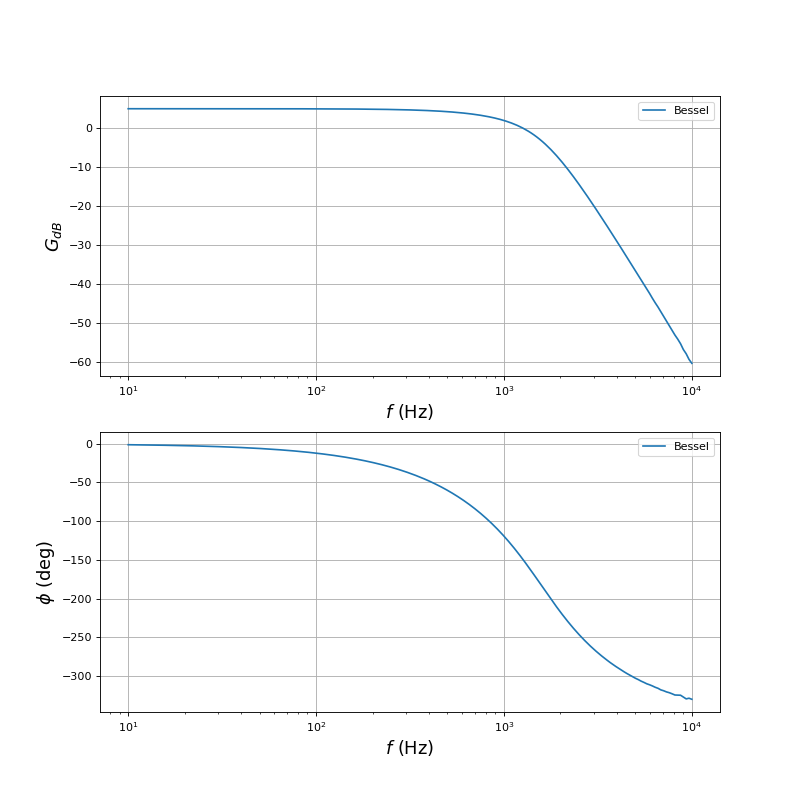fig27.pdf

Voici les courbes de gain et de déphasage :

[fa,Ge,Ga,phia] = np.loadtxt("filtre4-gain-phase.txt",unpack=True,skiprows=1)
phia = np.unwrap(phia,period=360)
figure(figsize=(10,10))
subplot(211)
plot(fa,Ga,label="Bessel")
grid()
legend(loc="upper right")
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$G$",fontsize=16)
subplot(212)
plot(fa,phia,label="Bessel")
grid()
legend(loc="upper right")
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\phi\ (\rm deg)$",fontsize=16)
                 

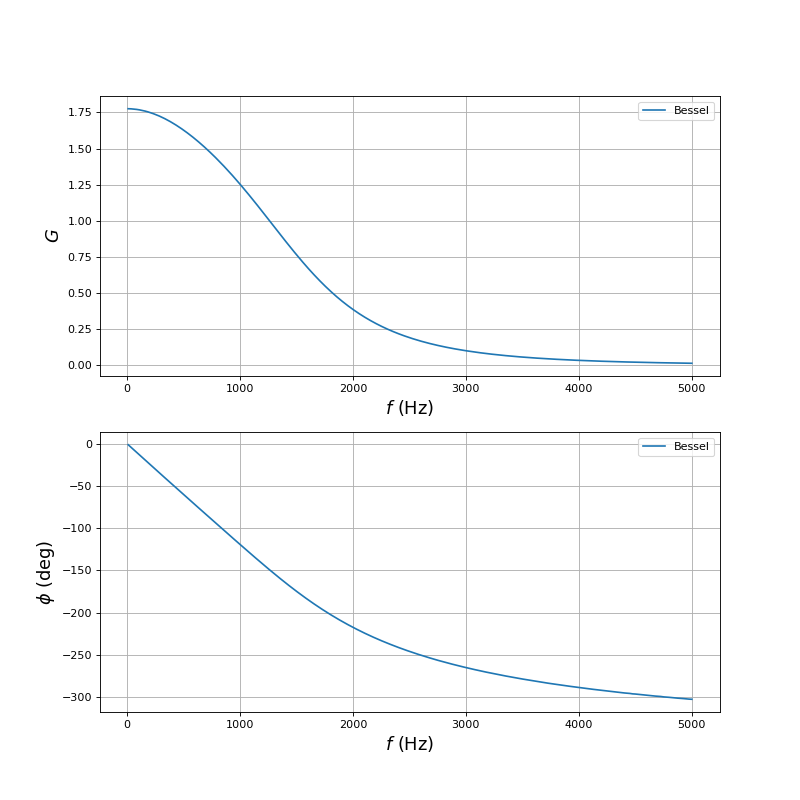fig28.pdf

La linéarité du déphasage par rapport à la fréquence semble très bonne et s'étend largement en dehors de la bande passante.

Voici le décalage temporel dans la bande passante :

tau = phia/(360*fa)
figure(figsize=(10,6))
title("Bessel")
plot(fa,tau*1e3)
xlim(0,1000)
ylim(-0.4,0)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\tau\ (\rm ms)$",fontsize=16)
                  

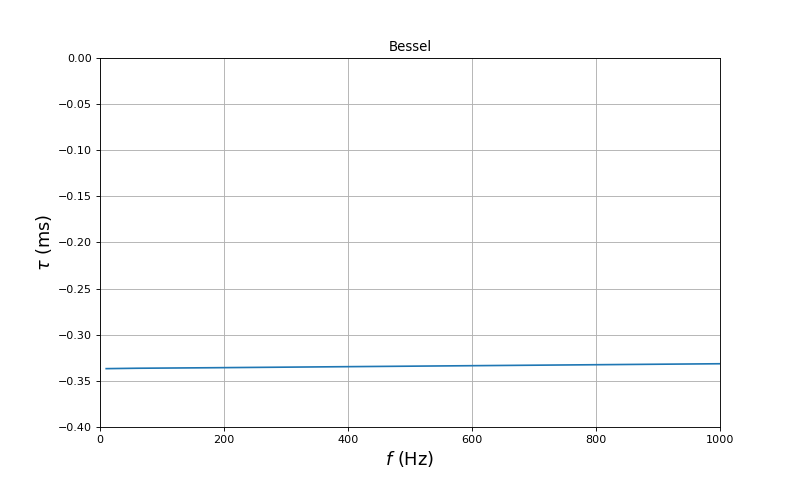fig29.pdf

Voici la variation relative du retard dans la bande passante :

figure(figsize=(10,6))
title("Bessel")
plot(fa,np.abs((tau-tau[0])/tau[0]))
xlim(0,1000)
ylim(0,0.15)
grid()
xlabel(r"$f\ (\rm Hz)$",fontsize=16)
ylabel(r"$\Delta\tau/\tau\ (\rm ms)$",fontsize=16)
                  

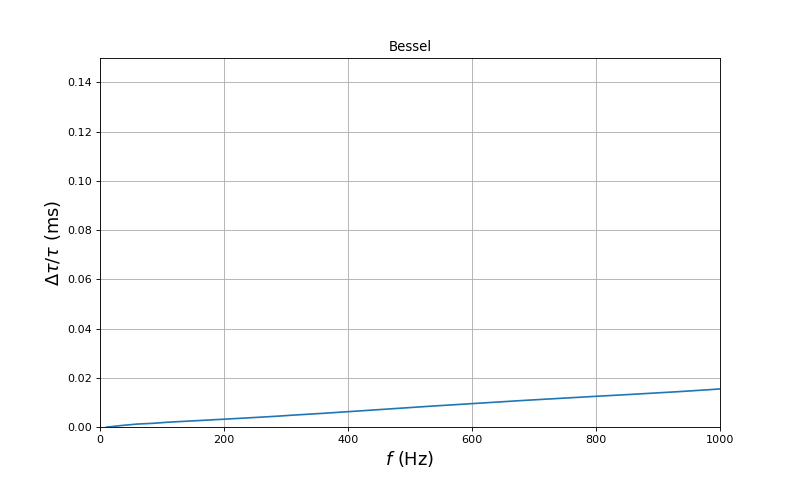fig30.pdf

La variation relative du retard est beaucoup plus petite qu'avec le filtre d'ordre 2.

Le filtre de Bessel d'ordre 4 présente une linéarité du déphasage (donc un retard constant) dans la bande passante bien meilleure que le filtre d'ordre 2. Les filtres de Bessel ont en effet une linéarité du déphasage qui s'améliore lorsque l'ordre augmente, à l'inverse des filtres de Butterworth ([1].

Voici la réponse à un échelon (de hauteur 2 V) :

[t,e,s] = np.loadtxt("filtre4-echelon.txt",unpack=True,skiprows=1)
figure(figsize=(12,6))
title("Bessel")
plot(t*1e3,e,label="e(t)")
plot(t*1e3,s,label="s(t)")
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16) 
ylabel("Volts",fontsize=16)
legend(loc="upper left")
                  

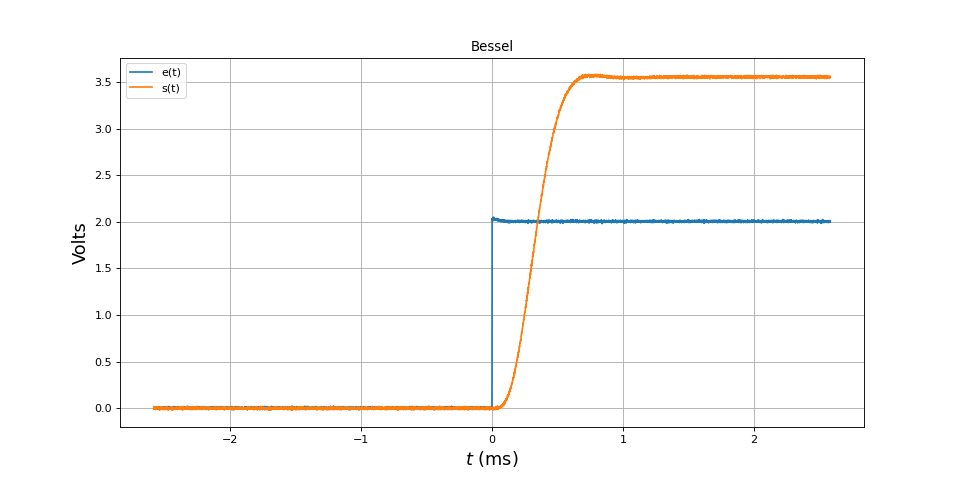fig31.pdf

Voici le filtrage d'un signal triangulaire de fréquence 100 Hz :

[t,e,s] = np.loadtxt("filtre4-triangle.txt",unpack=True,skiprows=1)
figure(figsize=(12,6))
title("Bessel")
plot(t*1e3,e,label="e(t)")
plot(t*1e3,s,label="s(t)")
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts",fontsize=16)
legend(loc="upper left")
                  

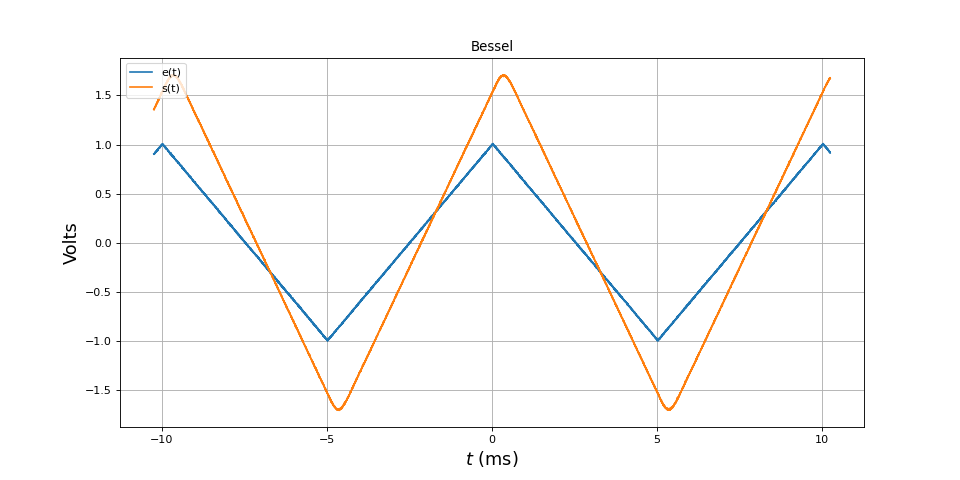fig32.pdf

et de fréquence 200 Hz :

[t,e,s] = np.loadtxt("filtre4-triangle-200Hz.txt",unpack=True,skiprows=1)
figure(figsize=(12,6))
title("Bessel")
plot(t*1e3,e,label="e(t)")
plot(t*1e3,s,label="s(t)")
grid()
xlabel(r"$t\ (\rm ms)$",fontsize=16)
ylabel("Volts",fontsize=16)
legend(loc="upper left")
                  

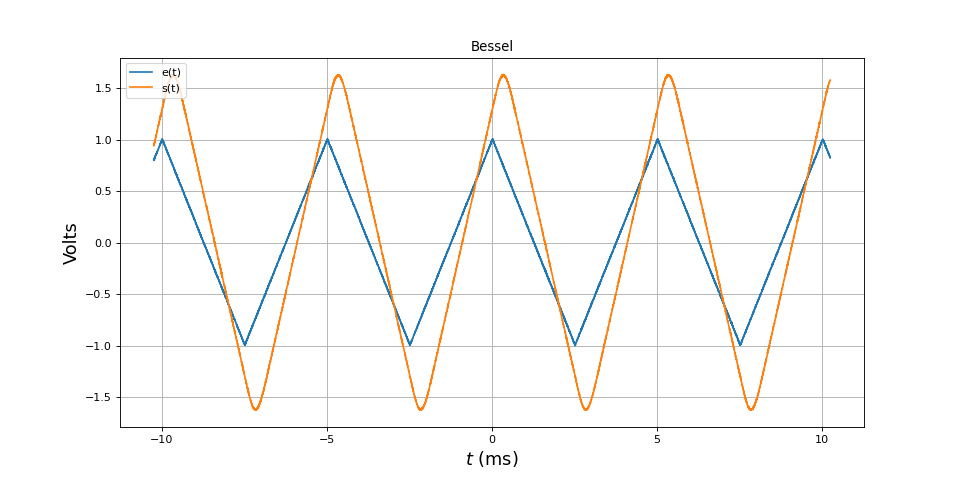fig33.pdf