Filtrage numérique

1. Introduction

Nous avons vu dans les TP précédents comment un convertisseur analogique/numérique permet d'obtenir un signal numérique, c'est-à-dire une suite de nombres correspondant aux échantillons du signal prélevés à la fréquence d'échantillonnage.

Le filtrage numérique consiste à modifier le signal numérique de manière à obtenir différents effets, comme le filtrage passe-bas, passe-bande, la dérivation, etc. Il existe des microprocesseurs spécialisés dans le filtrage numérique (DSP : Digital Signal Processor), capables de traiter des signaux numériques en temps réel avec une cadence très élevée (plusieurs millions d'échantillons par seconde).

Le schéma suivant montre le principe d'une chaîne complète de traitement numérique, comportant un convertisseur analogique/numérique (CAN), un processeur de signal numérique, et un convertisseur numérique/analogique (CNA).

Figure pleine page

Les filtres numériques sont utilisés dans les appareils électroniques (téléphones, téléviseurs, audio, etc.). Les capteurs à sortie numérique (par ex. les accéléromètres) contiennent un filtre numérique intégré. Les filtres numériques permettent d'obtenir des filtrages très efficaces beaucoup plus facilement que les filtres analogiques. Par ailleurs, un filtre numérique est défini par une suite de coefficients, qu'il est très facile de modifier pour changer le filtrage (par exemple la fréquence de coupure). Une telle souplesse est impossible à obtenir avec un filtre analogique.

Dans certains cas, il n'y a pas de conversion numérique/analogique à l'issu du traitement, mais stockage ou transmission numérique (par exemple en prise de son ou d'image numérique). Le filtrage numérique peut alors intervenir de manière différée, au moment de la lecture ou de la réception du signal.

L'objectif de ce TP est de découvrir le filtrage numérique par convolution. Nous allons faire la conversion analogique/numérique d'un signal périodique puis appliquer au signal échantillonné un filtrage numérique passe-bas. Le filtrage sera fait sur l'ordinateur après l'acquisition (sur un signal stocké en mémoire) et non pas en temps réel comme dans un processeur de signal. Cependant, nous simulerons le fonctionnement d'un filtre temps réel.

2. Filtrage par convolution

2.a. Principe

La figure suivante montre le fonctionnement d'un filtrage numérique par convolution.

Figure pleine page

Seuls les 6 derniers échantillons de l'entrée x_n sont représentés. La convolution se fait avec un noyau, qui dans cet exemple comporte trois coefficients b[0],b[1],b[2]. Le signal filtré est noté y_n. Pour obtenir le dernier échantillon du signal filtré, on effectue une combinaison linéaire des trois derniers échantillons du signal d'entrée :

y_{n} = b_{0} x_{n} + b_{1} x_{n - 1} + b_{2} x_{n - 2}

Plus généralement, si N est le nombre d'élements du noyau, l'échantillon n de la sortie se calcule en faisant une combinaison linéaire des N derniers échantillons de l'entrée :

y_{n} = \sum_{k = 0}^{N - 1} b_{k} x_{n - k} (1)

Cette relation définit la convolution discrète, et permet donc de réaliser un filtrage par convolution. L'effet du filtre dépend évidemment des coefficients choisis pour le noyau.

Dans le schéma ci-dessus, y_n et x_n sont considérés comme simultanés. Dans un filtre fonctionnant en temps réel, y_n est calculé dès que x_n est disponible et le temps de calcul doit être inférieur à la période d'échantillonnage. Si le temps de calcul est faible par rapport à T_e, y_n et x_n sont pratiquement simultanés. Pour la simulation d'un filtre fonctionnant en temps réel, on considérera que y_n et x_n sont simultanés.

Le filtre de convolution le plus simple est un filtre moyenneur à deux coefficients, qui réalise la moyenne arithmétique des deux derniers échantillons :

y_{n} = \frac{1}{2} (x_{n} + x_{n - 1})

Le filtre suivant définit y_n comme la moyenne arithmétique des N derniers échantillons :

y_{n} = \frac{1}{N} \sum_{k = 0}^{N - 1} x_{n - k}

2.b. Réponse impulsionnelle

Une impulsion est un signal numérique défini par :

\begin{matrix} x_{0} = 1 \\ x_{n} = 0 (n \neq 0) \end{matrix}

La sortie est alors :

\begin{matrix} y_{n} = 0 (n < 0) \\ y_{0} = b_{0} x_{0} = b_{0} \\ y_{1} = b_{1} x_{0} = b_{1} \\ \dots \\ y_{N - 1} = b_{N - 1} x_{0} = b_{N - 1} \\ y_{n} = 0 (n \geq M) \end{matrix}

Les coefficients b₀,b₁... b_N-1 (le noyau du filtre) constituent donc la réponse impulsionnelle du filtre.

Un filtre de convolution est dit à réponse impulsionnelle finie (RIF) car le nombre de termes de la réponse impulsionnelle est fini.

Les filtres numériques RIF sont toujours stables : si l'entrée reste bornée, la sortie l'est aussi.

2.c. Réponse fréquentielle

Pour obtenir la réponse fréquentielle théorique du filtre, on considère un signal d'entrée sinusoïdal, de fréquence f et d'amplitude unité. L'échantillonnage à la période T_e donne le signal numérique suivant :

x_{n} = exp (i 2 π f n T_{e})

Le signal en sortie s'écrit :

\begin{matrix} y_{n} = & \sum_{k = 0}^{N - 1} b_{k} x_{n - k} \\ = & exp (i 2 π n f T_{e}) \sum_{k = 0}^{N - 1} b_{k} exp (- i 2 π f k T_{e}) \\ = & x_{n} H (Z) \end{matrix}

avec :

\begin{matrix} H (Z) = \sum_{k = 0}^{N - 1} b_{k} Z^{- k} & (2) \\ Z = exp (i 2 π f T_{e}) & (3) \end{matrix}

On voit donc que la sortie (écrite sous forme complexe) est proportionnelle à l'entrée. H(Z) est la fonction de transfert en Z, analogue à la fonction de transfert des signaux continus. La réponse fréquentielle est finalement :

H_{f} (f) = \sum_{k = 0}^{N - 1} b_{k} exp (- i 2 π k f T_{e}) (4)

On remarque que cette réponse fréquentielle est en fait une fonction de fT_e, qui est le rapport de la fréquence du signal sinusoïdal sur la fréquence d'échantillonnage f_e=1/T_e. D'après le théorème de Shannon, ce rapport doit être inférieur à 1/2.

La représentation graphique de la réponse fréquentielle consiste à tracer le module de H_f et son argument en fonction de la fréquence sur l'intervalle [0,f_e/2].

2.d. Exemple : filtre moyenneur

Considérons le filtre suivant, qui définit y_n comme la moyenne des 19 derniers échantillons de l'entrée :

y_{n} = \frac{1}{19} \sum_{k = 0}^{18} x_{n - k}

La suite de ces coefficients (qui est aussi sa réponse impulsionnelle) est placée dans un tableau :

import numpy as np
b = np.ones(19)*1/19

La réponse fréquentielle peut être obtenue avec la fonction scipy.signal.freqz :

import scipy.signal
w,H=scipy.signal.freqz(b)

Le tableau w contient les pulsations (500 points par défaut) et le tableau H contient les valeurs complexes de la réponse fréquentielle. Voici comment tracer le gain et le déphasage en fonction de la fréquence :

from matplotlib.pyplot import *               
figure()
subplot(211)
plot(w/(2*np.pi),np.absolute(H))
ylabel("G")
grid()
subplot(212)
plot(w/(2*np.pi),np.unwrap(np.angle(H)))
xlabel("f/fe")
ylabel("déphasage")
grid()

figA0.pdf

Le filtre moyenneur est donc un filtre passe-bas. Pour les filtres numériques, il est d'usage de définir la fréquence de coupure comme la fréquence pour laquelle le gain vaut 1/2 (c'est donc une fréquence de coupure à -6 dB). Le déphasage dans la bande passante varie parfaitement linéairement avec la fréquence, ce qui est la propriété recherchée pour le filtrage des signaux périodiques, car elle implique que le retard est constant.

3. Réalisation d'un filtre moyenneur

L'objectif de cette partie est de faire la numérisation d'un signal périodique délivré par le générateur de signaux et de réaliser un filtrage par convolution du signal échantillonné.

Le filtrage n'est pas réalisé en temps réel mais il doit simuler le résultat d'un filtre numérique fonctionnant en temps réel. En conséquence, l'échantillon de la sortie y_n doit être considéré comme simultané avec l'échantillon de l'entrée x_n. Dans un filtre fonctionnant en temps réel, ces deux échantillons sont en effet quasi simultanés (décalés d'au plus une durée égale à la période d'échantillonnage).

Le signal échantillonné, comportant N_e échantillons, est stocké dans un tableau x. Le noyau du filtre de convolution, comportant N coefficients, est stocké dans un tableau b. Il faut écrire une fonction qui calcule le signal de sortie et renvoie le tableau correspondant y. Voici la signature de cette fonction :

def filtrage_convolution(x,b):
    # à compléter
    return y

Il faut remarquer que le calcul de y_n par la relation $(1)$ nécessite de diposer au minimum des N premières valeurs du signal d'entrée : $x_{0}, x_{1}, \dots x_{N - 1}$ . En conséquence, le calcul de y_n ne peut commencer qu'à l'indice n=N-1. Les N premières valeurs du tableau y sont donc nulles.

Le traitement complet est fait dans le script filtrageNumeriqueConvolution.py, à télécharger et à exécuter en local avec IDLE.

Ce script comporte :

La numérisation du signal avec la carte Sysam SP5 (sur la voie EA0).
La définition d'un filtre.
Le tracé de la réponse fréquentielle du filtre (gain et déphasage en fonction de la fréquence).
La fonction filtrage_convolution à compléter.
La réalisation du filtrage.
Le tracé des signaux échantillonnés x_n et y_n.
Le calcul du gain au moyen des valeurs efficaces CA (écart-type des échantillons).

On dispose aussi du script filtrageNumeriqueConvolutionAnimation.py, qui comporte une boucle permettant de répéter la numérisation et le filtrage en boucle et de tracer les signaux, comme le fait un oscilloscope.

Le premier filtre étudié est un filtre moyenneur à N=2P+1 coefficients, défini par :

b_{k} = \frac{1}{N} p o u r k = 0, 1, \dots N - 1

[1] Écrire la fonction filtrage_convolution.

[2] Le générateur de signaux envoie sur la voie EA0 de la carte d'acquisition un signal sinusoïdal, d'amplitude inférieure à 5 V et de fréquence environ 100 Hz. Réaliser la numérisation et le filtrage de ce signal.

Le gain G est calculé dans le script (rapport des valeurs efficaces CA). Pour déterminer le retard τ de la sortie par rapport à l'entrée, il faudra faire un relevé direct sur la fenêtre graphique (utiliser le zoom).

[3] Relever le gain et le retard pour les fréquences suivantes : 50, 100, 200, 450, 520, 750 Hz. Vérifier que ces mesures sont bien en accord avec les courbes théoriques de gain et de déphasage.

[4] La courbe de déphasage montre des discontinuités du déphasage. Sont-elles confirmées par l'expérience ?

[5] Le retard entre la sortie est l'entrée est exactement τ=PT_e. Vérifier cette propriété en changeant la fréquence d'échantillonnage à f_e=20000 Hz et en modifiant la valeur de P.

[6] Réaliser le filtrage d'un signal triangulaire de fréquence environ 100 Hz. Interpréter la forme observée ? Peut-on définir un retard de la sortie par rapport à l'entrée ? Quelle est sa valeur ?

[7] Réaliser le filtrage d'un signal créneau de fréquence environ 10 Hz. Interpréter la forme observée ? Peut-on définir un retard de la sortie par rapport à l'entrée ?

[8] Quel est le principal défaut de ce filtre passe-bas ?

4. Amélioration du filtre passe-bas

Les caractéristiques du filtre moyenneur sont très mauvaises dans la bande atténuante. Pour améliorer le filtrage, il faut faire une moyenne pondérée en choisissant des coefficients b_k avec un maximum en k=P. On peut par exemple utiliser une fonction gaussienne pour définir ces coefficients. On obtient ainsi un filtre gaussien, un type de filtre très utilisé en traitement d'image (moins en traitement du signal). Voici comment définir un filtre gaussien à N coefficients en spécifiant l'écart-type de la gaussienne :

from scipy.signal.windows import gaussian
P = 9
N = 2*P+1
ecart_type = P/3
b = gaussian(N,std=ecart_type)*1/N
b = b/b.sum()

La dernière ligne sert à normaliser le filtre gaussien, afin que son gain à très basse fréquence soit égal à 1.

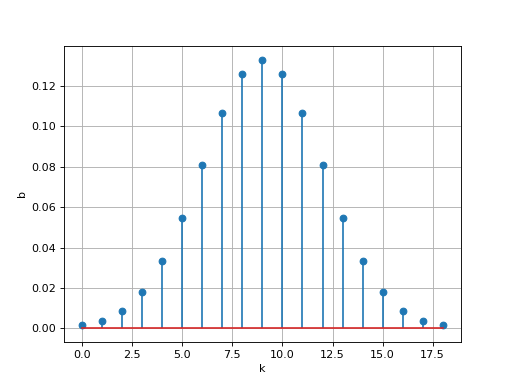
Voici la représentation de la réponse impulsionnelle de ce filtre, qui est simplement la suite de ses coefficients :

figure()
stem(b)
xlabel('k')
ylabel('b')
grid()

figB.pdf

L'écart-type doit être choisi afin que les coefficients b₀ et b_N-1 soient très faibles.

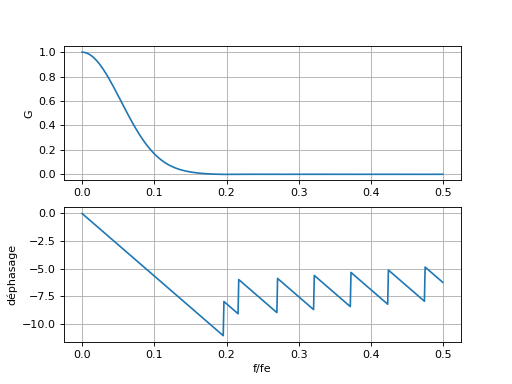
Voici sa réponse fréquentielle :

w,H=scipy.signal.freqz(b)             
figure()
subplot(211)
plot(w/(2*np.pi),np.absolute(H))
ylabel("G")
grid()
subplot(212)
plot(w/(2*np.pi),np.unwrap(np.angle(H)))
xlabel("f/fe")
ylabel("déphasage")
grid()

figC.pdf

[9] Comparer ces courbes à celles du filtre moyenneur. En quoi ce filtre est-il une amélioration importante ? A-t-on toujours la linéarité du déphasage dans la bande passante ?

[10] Réaliser ce filtrage sur un signal sinusoïdal, avec une fréquence d'échantillonnage f_e=10000 Hz.

[11] Vérifier que le gain diminue de manière monotone et qu'il est très faible à partir de 2000 Hz. On pourra utiliser pour cela le script filtrageNumeriqueConvolutionAnimation.py.

[12] Réaliser le filtrage d'un signal triangulaire de fréquence environ 100 Hz. Vérifier que le retard est PT_e.

[13] Tester le filtre avec un signal créneau d'environ 10 Hz.

5. Filtre passe-bas très sélectif

Un filtre passe-bas est d'autant plus sélectif que son gain décroît rapidement dans la bande atténuante. Un filtre gaussien ne permet pas d'obtenir une très grande sélectivité, car sa courbe de gain est une gaussienne.

Il est possible de réaliser un filtre de convolution très sélectif au moyen de la fonction scipy.signal.firwin, qui permet d'obtenir les coefficients d'un filtre FIR (Finite Impulse Response) par la méthode du fenêtrage. Cette fonction permet d'obtenir des filtres passe-bas, passe-haut, passe-bande et coupe-bande.

Voici comment définir un filtre passe-bas de fréquence de coupure f_c et comportant N=2P+1 coefficients :

P=29
N=2*P+1
fe = 10000
fc = 500.0
b = scipy.signal.firwin(N,cutoff=[fc/fe],fs=1,window='hamming')

La fréquence de coupure qu'il faut fournir est en fait le rapport de la fréquence de coupure par la fréquence d'échantillonnage. L'argument fs=1 permet de préciser que c'est bien ce rapport qui est fourni (fréquence d'échantillonnage égale à 1).

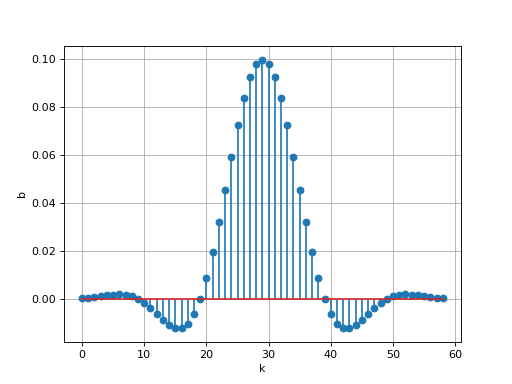
Voici la représentation de la réponse impulsionnelle de ce filtre, qui est simplement la suite de ses coefficients :

figure()
stem(b)
xlabel('k')
ylabel('b')
grid()

figD.pdf

On remarque que certains coefficients sont négatifs.

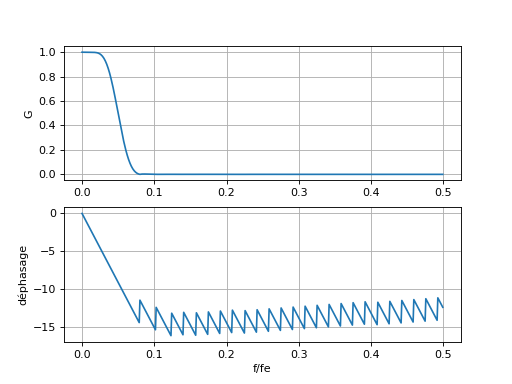
Voici la réponse fréquentielle de ce filtre :

w,H=scipy.signal.freqz(b)            
figure()
subplot(211)
plot(w/(2*np.pi),np.absolute(H))
ylabel("G")
grid()
subplot(212)
plot(w/(2*np.pi),np.unwrap(np.angle(H)))
xlabel("f/fe")
ylabel("déphasage")
grid()

figE.pdf

Le filtre est d'autant plus sélectif que N est grand. Par définition, l'ordre d'un filtre de convolution est N, le rang du dernier coefficient. Plus l'ordre est élevé, plus le filtre est sélectif. Le retard entre la sortie et l'entrée est toujours :

τ = P T_{e} (5)

En conséquence, un filtre très sélectif donne un grand retard et le déphasage peut atteindre des valeurs grandes (voir la courbe de déphasage ci-dessus). Le grand retard de la sortie par rapport à l'entrée est le prix à payer pour la grande sélectivité.

Par ailleurs, il faut remarquer que ce retard n'existe que dans un filtrage en temps réel (que nous simulons ici). Dans le cas où on filtre un signal numérique entièrement en mémoire (dans un tableau), il est possible d'éliminer ce retard en avançant la sortie de P échantillons.

[14] Tester ce filtre avec un signal sinusoïdal. Vérifier la valeur du gain et du déphasage pour la fréquence f=f_c.

[15] Au moyen du script faisant l'acquisition et le filtrage en boucle, augmenter progressivement la fréquence en partant de 100 Hz. Que se passe-t-il lorsque le retard atteint une période ?

[16] Tester le filtre avec un signal triangulaire d'environ 100 Hz. Vérifier la valeur du retard.

[17] Tester le filtre avec un signal créneau d'environ 10 Hz.

6. Application : réduction du bruit

Le bruit est une perturbation du signal qui a la forme d'un signal stochastique, c'est-à-dire dont la valeur à tout instant est une variable aléatoire. On parle de bruit blanc lorsque le spectre du bruit a une amplitude indépendante de la fréquence. Le bruit blanc contient donc aussi bien des faibles fréquences que des très hautes fréquences. Pour générer un signal périodique avec du bruit ajouté, nous utilisons Pure Data, un logiciel libre de synthèse et de traitement du son à programmation graphique. Pure Data est en fait un langage de programmation visuel permettant de créer un système de traitement du signal au moyen de blocs de traitement reliés entre eux. Il peut traiter des signaux du domaine audio en temps réel.

[18] Au moyen du câble prévu pour cela, relier la sortie audio du PC (prise jack) à l'entrée EA0 de la carte et à la voie 1 de l'oscilloscope.

[19] Au moyen du fichier PureData syntheseHarmonique.pd, générer un signal périodique comportant 3 harmoniques, tous dans la bande passante du filtre. Ajouter du bruit.

[20] Au moyen de la fonction FFT de l'oscilloscope, analyser le spectre du signal bruité (en échelle décibel). Modifier en temps réel le niveau de bruit et observer comment le spectre est modifié.

[21] Réaliser le filtrage passe-bas du signal bruité (avec le filtre précédent). Observer la réduction du bruit.

[22] Comment expliquer que le filtre passe-bas réduit le bruit sans altérer la forme du signal ?

[23] En reprenant la méthode développée dans le TP Analyse spectrale des signaux périodiques, compléter le script de filtrage pour obtenir le spectre de l'entrée et le spectre de la sortie.

[24] Modifier l'ordre du filtre (le nombre N=2P+1) afin de voir la plus ou moins grande efficacité du filtrage du bruit.

TP5 - Filtrage numérique