Equations algébriques

Localisation des racines d’une fonction

Soit une fonction \(f:\mathbb{R}\rightarrow\mathbb{R}\) dont on cherche les racines, c’est-à-dire les valeurs de \(x\) telles que \(f(x)=0\). Lorsqu’il n’existe pas d’expression analytique de ces racines, il est possible de déterminer leur valeur approchée par une méthode numérique itérative.

Il faut tout d’abord faire une localisation approximative des racines de manière à définir un ou plusieurs intervalles sur lesquels la fonction ne possède qu’une seule racine.

Considérons l’équation algébrique suivante (pour \(x>0\)) :

\[\cos(x)=\alpha x\]

La fonction dont on cherche les racines dans l’intervalle \([0,+\infty[\) est définie par :

\[f(x)=\cos(x)-\alpha x\]

Il n’existe pas d’algorithme permettant de déterminer de manière certaine toutes les racines d’une fonction ni même de les localiser approximativement. La localisation des racines ne peut être faite que par une intelligence humaine, soit sur la base d’une démonstration mathématique, soit sur la base d’une étude graphique.

La méthode graphique ne possède pas la rigueur d’une démonstration mathématique mais elle permet de localiser de manière quasi certaine les racines. Pour l’exemple ci-dessus, nous pouvons tracer séparément \(cos(x)\) et \(\alpha x\) afin de localiser les intersections, ou bien tracer \(f(x)\) :

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0,8*np.pi,1000)
alpha=0.1
y1 = np.cos(x)
y2 = alpha*x
plt.figure()
plt.plot(x,y1,label='cos(x)')
plt.plot(x,y2,label='ax')
plt.grid()
plt.xlabel('x',fontsize=16)
plt.legend(loc='upper right')
plt.savefig('intersections.png')
plt.figure()
plt.plot(x,y1-y2)
plt.grid()
plt.xlabel('x',fontsize=16)
plt.ylabel('f(x)',fontsize=16)
plt.savefig('racines.png')
plt.show()

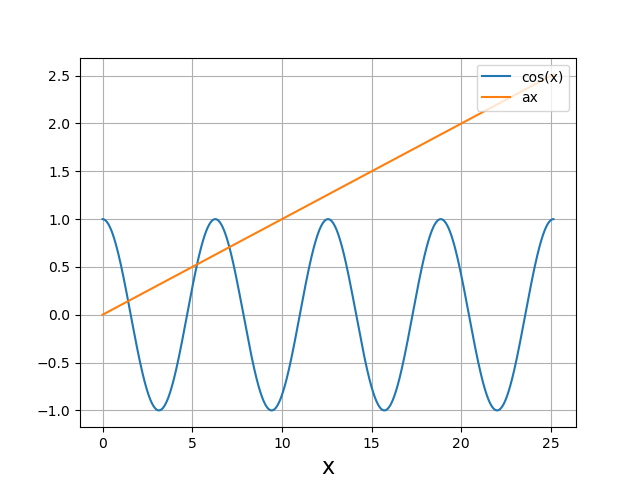
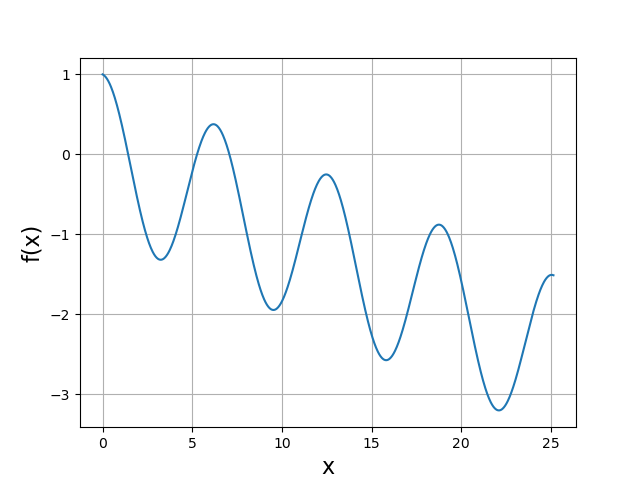
On repère trois intervalles contenant une et une seule racine :

a1,b1 = 0,3
a2,b2 = 4,6
a3,b3 = 6,8

Méthode de dichotomie

La méthode de dichotomie, aussi nommée méthode de la bissection, permet de déterminer numériquement la racine d’une fonction continue dans un intervalle \([a,b]\) où la fonction n’admet qu’une seule racine, notée \(x_1\). La figure suivente montre le principe de la méthode :

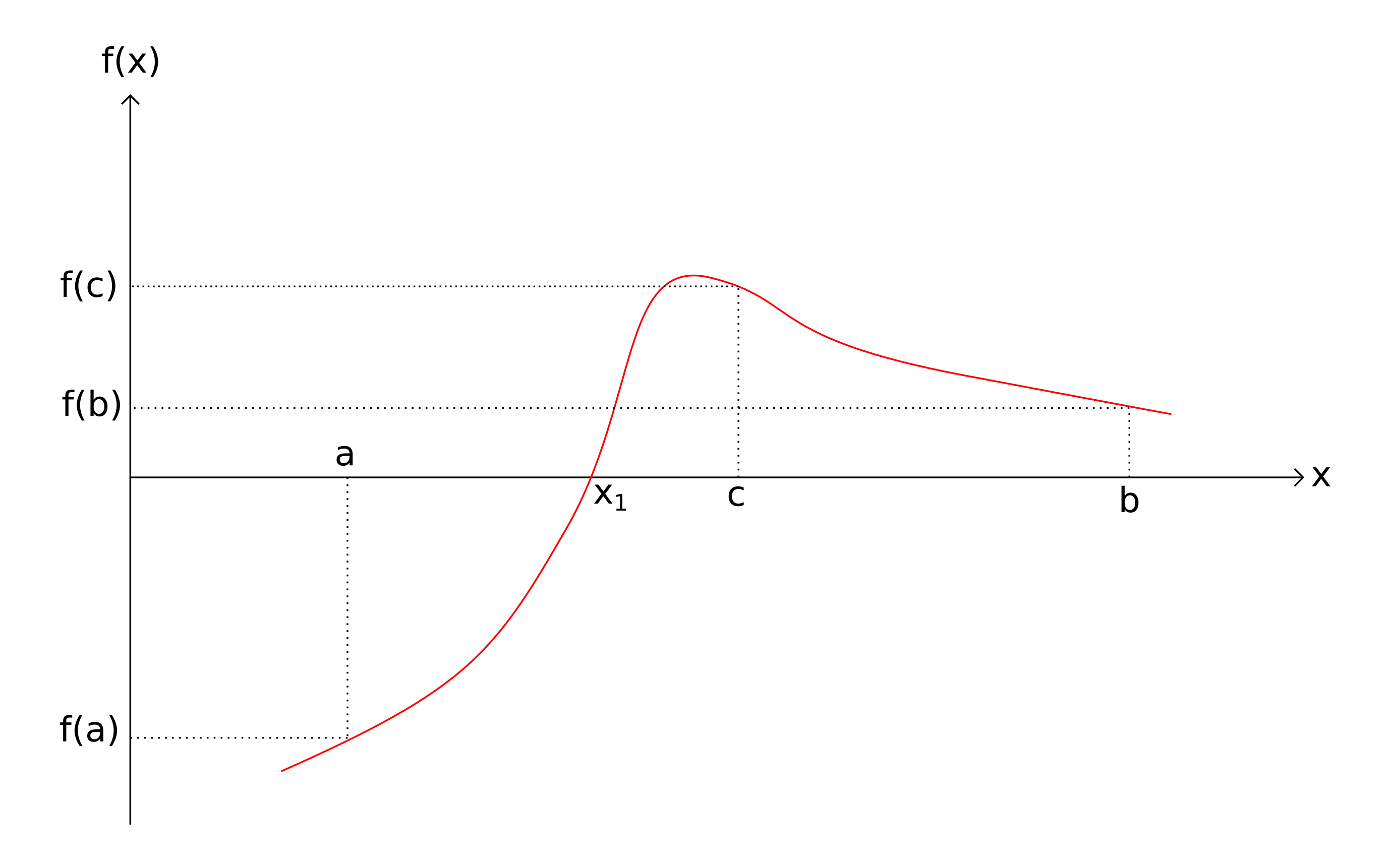
La fonction étant continue, \(f(a)\) et \(f(b)\) sont de signes opposés. Considérons le milieu de l’intervalle :

\[c=\frac{a+b}{2}\]

Si \(f(a)\) et \(f(c)\) sont de signes opposés alors la racine \(x_1\) se trouve dans l’intervalle \([a,c]\), sinon elle se trouve dans l’intervalle \([c,b]\). Nous obtenons ainsi un nouvel intervalle contenant la racine, deux fois plus petit que l’intervalle initial, l’intervalle \([a,c]\) sur la figure ci-dessus.

La procédure est répétée de manière itérative, ce qui permet d’obtenir un intervalle de plus en plus petit contenant la racine. Soit \(\epsilon\) la précision absolue de l’approximation que l’on souhaite obtenir. Cette précision doit être compatible avec la précision des nombres à virgule flottante 64 bits : si la racine est proche de 1, \(\epsilon\) doit être supérieure à \(10^{-15}\). La procédure de division de l’intervalle est stoppée lorsque la largeur de l’intervalle est inférieure à \(\epsilon\).

Nous devons écrire une fonction Python qui effectue la recherche de racine par dichotomie. Les arguments de cette fonction sont la fonction \(f\), les bornes de l’intervalle \([a,b]\) et la précision \(\epsilon\). La fonction Python qui définit la fonction \(f\) a besoin du paramètre \(\alpha\). Ce paramètre peut être défini dans une variable globale :

alpha = 0.1

def f(x):
    return np.cos(x)-alpha*x # alpha est une variable globale

Voici un exemple de fonction Python réalisant la recherche par dichotomie :

def dichotomie(f,a,b,epsilon):
    fa = f(a)
    fb = f(b)
    if fa*fb>0:
        raise Exception("f(a) et f(ab) doivent être de signes contraires")
    largeur = b-a
    while largeur > epsilon:
        c = (a+b)/2
        fc = f(c)
        if fa*fc<0:
            b = c
            fb = fc
        else:
            a = c
            fa = fc
        largeur = b-a
    return c

Rappelons que les paramètres d’une fonction Python sont, à l’intérieur de celle-ci, des variables locales. Le paramètre f contient la fonction dont on recherche la racine. Les paramètres a et b, qui contiennent à l’appel de la fonction les bornes de l’intervalle initial, sont utilisés en tant que variables locales pour contenir les bornes des intervalles successifs contenant la racine.

Dans cette implémentation de la dichotomie, nous comparons les signes de \(f(a)\) et \(f(c)\) en testant le signe du produit \(f(a)f(c)\). La boucle while permet d’accomplir itérativement la division de l’intervalle tant que sa largeur est strictement supérieure à la précision souhaitée.

Voici comment obtenir les approximations des trois racines de l’exemple considéré, avec une précision \(\epsilon=10^{-4}\), largement suffisante dans la plupart des cas.

alpha = 0.1
epsilon = 1e-4
x1 = dichotomie(f,a1,b1,epsilon)
x2 = dichotomie(f,a2,b2,epsilon)
x3 = dichotomie(f,a3,b3,epsilon)
print(x1,x2,x3)

1.427581787109375 5.26715087890625 7.06890869140625

Etant donné la précision de ces approximations, un affichage avec 4 décimales est plus pertinent :

print("%0.4f"%x1,"%0.4f"%x2,"%0.4f"%x3)

1.4276 5.2672 7.0689

Le fait d’utiliser une variable globale alpha dans la fonction Python f nécessite de définir la valeur de alpha avant d’appeler la fonction dichotomie. L’utilisation de variables globales pour définir des paramètres ne pose pas de problème lorsque ces paramètres sont constants, mais peut être la source d’erreurs lorsqu’on veut faire varier ces paramètres. Il est donc préférable (mais pas obligatoire) de faire apparaître explicitement alpha dans les paramètres de la fonction f, de la manière suivante :

def f(x,alpha):
    return np.cos(x)-alpha*x

Nous devons alors légèrement modifier la fonction dichotomie car la valeur de alpha doit être précisée lors de son appel. Pour ce faire, nous ajoutons un paramètre args qui contient les arguments supplémentaires à fournir à la fonction f (arguments en plus de x). Dans le cas présent, il n’y a qu’un seul argument supplémentaire, mais il peut y en avoir plusieurs. Nous utilisons donc un n-uplet (type tuple) pour préciser ces arguments. Voici la fonction modifiée :

def dichotomie(f,a,b,epsilon,args):
    fa = f(a,*args)
    fb = f(b,*args)
    if fa*fb>0:
        raise Exception("f(a) et f(ab) doivent être de signes contraires")
    largeur = b-a
    while largeur > epsilon:
        c = (a+b)/2
        fc = f(c,*args)
        if fa*fc<0:
            b = c
            fb = fc
        else:
            a = c
            fa = fc
        largeur = b-a
    return c

epsilon = 1e-4
alpha = 0.1
x1 = dichotomie(f,a1,b1,epsilon,(alpha,))
x2 = dichotomie(f,a2,b2,epsilon,(alpha,))
x3 = dichotomie(f,a3,b3,epsilon,(alpha,))

L’opérateur * placé devant args permet de convertir le contenu du n-uplet en arguments pour la fonction f. Dans cet exemple, le n-uplet ne contient qu’une seule valeur. La syntaxe (alpha,) permet de définir un n-uplet ne contenant qu’un seul élément (noter la virgule).

Dans ce cas, il est impossible d’oublier d’affecter la valeur souhaitée à alpha car l’appel de la fonction dichotomie exige de fournir les arguments supplémentaires de la fonction f (une erreur est déclenchée si on ne le fait pas).

Tolérances absolue et relative

Nous avons utilisé une tolérance absolue (ou précision absolue) pour décider à quel moment stopper la dichotomie. Cette méthode convient lorsque la racine est de l’ordre de grandeur de 1 mais pose problème lorsqu’elle est petite. Dans ce cas, l’utilisation d’une tolérance relative est préférable. Il est d’usage d’utiliser à la fois une tolérance absolue \(\epsilon_a\) et une tolérance relative \(\epsilon_r\). La condition d’arrêt de la recherche est alors

\[|b-a| < \epsilon_a+|a|\epsilon_r\]

Voici la nouvelle fonction :

def dichotomie(f,a,b,tolA,tolR,args):
    fa = f(a,*args)
    fb = f(b,*args)
    if fa*fb>0:
        raise Exception("f(a) et f(ab) doivent être de signes contraires")
    largeur = b-a
    while largeur > tolA+abs(a)*tolR:
        c = (a+b)/2
        fc = f(c,*args)
        if fa*fc<0:
            b = c
            fb = fc
        else:
            a = c
            fa = fc
        largeur = b-a
    return c

Si l’on souhaite utiliser seulement la tolérance relative, il suffit d’attribuer une valeur nulle à la tolérance absolue (et réciproquement) :

alpha = 0.1
tolA = 0
tolR = 1e-4
x1 = dichotomie(f,a1,b1,tolA,tolR,(alpha,))
x2 = dichotomie(f,a2,b2,tolA,tolR,(alpha,))
x3 = dichotomie(f,a3,b3,tolA,tolR,(alpha,))
print("%0.4f"%x1,"%0.4f"%x2,"%0.4f"%x3)

1.4276 5.2671 7.0688

Fonction bisect

Le module scipy.optimize de la bibliothèque Scipy comporte une fonction nommée bisect qui effectue la recherche de racine par dichotomie, ce qui dispense d’écrire la fonction dichotomie. Nous pouvons importer cette fonction de la manière suivante :

from scipy.optimize import bisect

Les paramètres obligatoires de la fonction bisect sont f,a,b (fonction et bornes de l’intervalle de recherche, à passer en argument dans cet ordre). Les paramètres optionnels sont xtol (la tolérance absolue), rtol (la tolérance relative) et args (les arguments supplémentaires à transmettre à la fonction f). Pour fournir un argument correspondant à un paramètre optionnel, il n’est pas nécessaire de connaître l’ordre de ces paramètres car on utilise leur nom dans l’appel :

alpha = 0.1
tolA = 1e-10 # la valeur 0 n'est pas permise
tolR = 1e-4
x1 = bisect(f,a1,b1,xtol=tolA,rtol=tolR,args=(alpha,))
x2 = bisect(f,a2,b2,xtol=tolA,rtol=tolR,args=(alpha,))
x3 = bisect(f,a3,b3,xtol=tolA,rtol=tolR,args=(alpha,))
print("%0.4f"%x1,"%0.4f"%x2,"%0.4f"%x3)

1.4276 5.2671 7.0688

Les paramètres optionnels d’une fonction (ici xtol,rtol,args) ont toujours une valeur par défaut, qui est affectée automatiquement à la variable locale correspondante lorsque la valeur n’est pas transmise en argument. Voir la documentation de bisect pour les valeurs par défaut des tolérances, qui sont très petites.