Dérivation¶
Soit une fonction \(f:\mathbb{R}\rightarrow\mathbb{R}\) et \(f'\) sa dérivée. Si les expressions de \(f(x)\) et de \(f'(x)\) sont connues, le calcul numérique de \(f'(x)\) consiste simplement à évaluer une expression. Nous nous intéressons aux cas où l’expression de la dérivée n’est pas connue, ce qui se présente dans les situations suivantes :
L’expression de \(f(x)\) est connue mais celle de \(f'(x)\) est trop complexe à déterminer.
Le calcul de \(f(x)\) se fait par une simulation et \(f'(x)\) n’est pas connue.
Seules les valeurs de \(f\) pour un échantillonnage d’un intervalle \([a,b]\) sont connues, par exemple des valeurs expérimentales.
Différence finie¶
Considérons la définition de la dérivée, pour une fonction dérivable en \(x\) :
Si \(h\) est un nombre réel assez petit, on peut obtenir une approximation de la dérivée par la relation suivante :
Cette relation est nommée différence finie, car elle consiste à calculer la différence entre deux points séparés d’une distance finie. La question se pose de savoir ce que signifie \(h\) assez petit et de la précision de la différence finie. Pour répondre à cette question, considérons le développement de Taylor suivant :
où \(O(h^4)\) désigne un terme dont la valeur absolue est inférieure à une constante multipliée par \(h^4\) lorsque \(h\) est assez petit (terme d’ordre 4). On en déduit l’expression suivante de la dérivée :
Cette relation montre que l’erreur de troncature, c’est-à-dire l’erreur commise en utilisant la différence finie (1), est \(O(h)\) (grand O de h). Cela signifie qu’il existe une constante \(K_1\) telle que, pour \(h\) assez petit, la valeur absolue de l’erreur est inférieure ou égale à \(K_1|h|\). La relation (1) constitue donc un schéma numérique d’ordre 1.
Un résultat plus précis peut être obtenu en utilisant les développements de Taylor de \(f(x+h)\) et \(f(x-h)\), qui conduisent à :
Nous obtenons alors la différence finie suivante comme approximation de la dérivée :
Cette différence finie est qualifiée de différence centrée car elle utilise la valeur de la fonction de part et d’autre du point où l’on cherche la dérivée. Pour la différence finie (2), l’erreur de troncature est \(O(h^2)\), soit une erreur d’ordre 2 alors qu’elle est d’ordre 1 pour la différence finie (1).
Les erreurs de troncature des différences finies (1) et (2) vérifient, pour \(h\) assez petit, les inégalités suivantes :
Cela implique qu’une réduction de \(h\) d’un facteur 10 réduit l’erreur d’un facteur 10 pour la première, d’un facteur 100 pour la seconde. Pour cette raison, la seconde méthode est qualifiée de plus précise. Il faut cependant noter que les constantes \(K_1\) et \(K_2\) peuvent être très différentes.
Dérivation d’une fonction¶
Supposons que le calcul de la fonction à dériver soit fait par une fonction Python dont la signature est :
def f(x):
# calcul et renvoie de f(x)
Voici deux fonctions qui renvoient la valeur de la dérivée, respectivement pour le schéma (1) et le schéma (2) :
def deriv1(f,x,h):
return (f(x+h)-f(x))/h
def deriv2(f,x,h):
return (f(x+h)-f(x-h))/(2*h)
Afin de tester ces fonctions, considérons le cas d’une fonction dont la dérivée est connue : \(f:x\rightarrow \sin(x)\):
import numpy as np
def f(x):
return np.sin(x)
Voici un exemple de calcul de la dérivée et de l’erreur correspondante :
x = 0.2
deriv = np.cos(x)
h=1e-3
e1 = deriv1(f,x,h)-deriv
e2 = deriv2(f,x,h)-deriv
print(e1,e2,e1/e2)
-9.949800152520005e-05 -1.633444142168372e-07 609.1301132165927
Pour cette valeur de \(h\), le schéma (2) donne une erreur environ 600 fois plus faible que le schéma (1). Divisons \(h\) par 10 :
h=1e-4
e1 = deriv1(f,x,h)-deriv
e2 = deriv2(f,x,h)-deriv
print(e1,e2,e1/e2)
-9.935100041102984e-06 -1.633630564157329e-09 6081.607591755471
L’erreur du schéma (2) est environ 6000 fois plus faible que celle du schéma (1). On observe bien une réduction de l’erreur d’un facteur 10 pour la première, d’un facteur 100 pour la seconde.
Il faut remarquer que la différence fondamentale entre les formules (1) et (2) réside dans le fait que la seconde est centrée alors que la première ne l’est pas. La seconde utilise un espacement deux fois plus grand que la première (\(2h\) au lieu de \(h\)), ce qui ne l’empêche pas d’être beaucoup plus précise, du moins dans cet exemple.
Dérivation d’une fonction échantillonnée¶
Si l’on veut calculer et tracer la dérivée d’une fonction sur un intervalle \([a,b]\), il faut tout d’abord l’échantillonner sur cet intervalle, c’est-à-dire calculer les valeurs suivantes, pour \(n=0,1,\ldots N-1\) :
Pour reprendre l’exemple précédent, l’échantillonnage sur l’intervalle \([0,2\pi]\) se fait de la manière suivante :
N=1000
X = np.linspace(0,2*np.pi,N)
Y = f(X)
La valeur de \(h\) qui est utilisée pour le calcul des valeurs de la dérivée est la période d’échantillonnage :
Si nous optons pour la différence finie (2), la valeur approchée de la dérivée en \(x=x_n\) est donnée par :
Nous devons tenir compte du fait que la dérivée ne pourra pas être calculée en \(x_0\) et en \(x_{N-1}\) (le premier et le dernier point de l’échantillonnage). Les valeurs \(x_n\) correspondantes sont obtenues en sélectionnant une tranche du tableau X :
X2 = X[1:N-1] # éléments d'indice 1 à N-2
DY2 = np.zeros(N-2) # tableau pour la dérivée
Le remplissage du tableau contenant les échantillons de la dérivée se fait dans une boucle, après avoir obtenu la valeur de \(h\) à partir du tableau des valeurs de \(x_n\) :
h = X2[1]-X2[0]
for n in range(1,N-1):
DY2[n-1] = (Y[n+1]-Y[n-1])/(2*h)
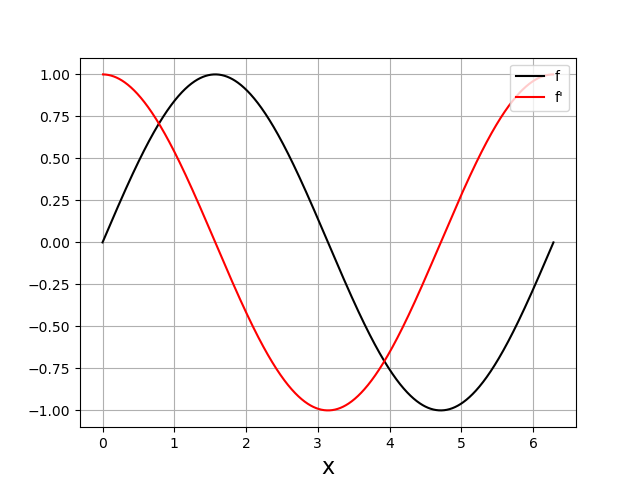
Pour finir, voici le tracé de la fonction et de sa dérivée obtenu avec les tableaux :
plt.figure()
plt.plot(X,Y,"k-",label='f')
plt.plot(X2,DY2,"r-",label="f'")
plt.xlabel('x',fontsize=16)
plt.legend(loc='upper right')
plt.grid()
plt.show()
Dérivation d’une grandeur expérimentale échantillonnée¶
On considère le cas d’une grandeur dont la valeur expérimentale est échantillonnée à une période constante. L’exemple traité est le mouvement d’un pendule pesant obtenu à partir d’un enregistrement vidéo. La position de la masselotte est enregistrée dans un fichier texte sous forme tabulaire. La première colonne donne l’abscisse en unité pixel, la seconde donne l’ordonnée. La période d’échantillonnage ne figure pas dans le fichier mais nous savons qu’elle est de 1/120 secondes.
On commence par obtenir deux tableaux contenant respectivement les abscisses et les ordonnées :
X,Y = np.loadtxt('pendule-120fps-13-objet.txt',unpack=True)
N = len(X) # nombre d'échantillons
Connaissant la période d’échantillonnage, nous pouvons générer un tableau contenant les instants :
h = 1/120.0
T = np.arange(N)*h
Le calcul de la dérivée \(\frac{dx}{dt}\) au moyen de la différence finie (2) se fait comme précédemment :
T2 = T[1:N-1]
DX2 = np.zeros(N-2)
for n in range(1,N-1):
DX2[n-1] = (X[n+1]-X[n-1])/(2*h)
Pour finir, on trace l’abscisse et sa dérivée, c’est-à-dire la vitesse \(V_x\), sur la même figure mais sur deux subplots différents :
plt.figure(figsize=(12,6))
plt.subplot(211)
plt.plot(T,X,"k-")
plt.ylabel('x (pixel)',fontsize=16)
plt.xlim(0,15)
plt.grid()
plt.subplot(212)
plt.plot(T2,DX2,"r")
plt.xlabel('t (s)',fontsize=16)
plt.ylabel(r'$V_x$ (pixel/s)',fontsize=16)
plt.xlim(0,15)
plt.grid()
plt.show()
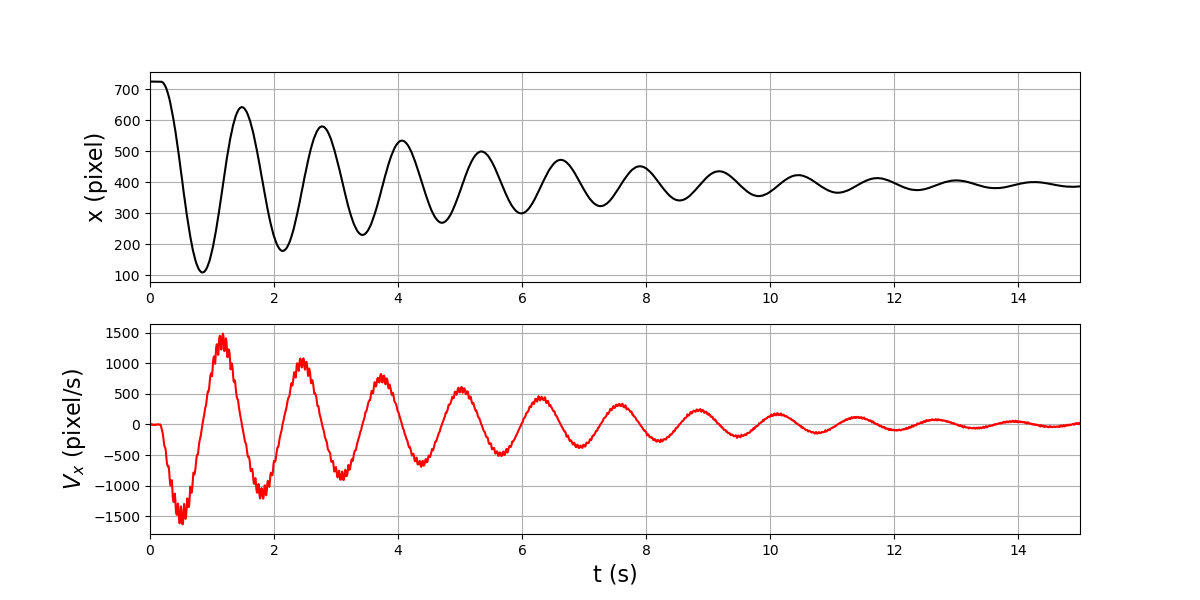
Le signal obtenu par dérivation comporte un bruit très important, alors que celui-ci est invisible dans \(x\). La dérivation constitue en effet un filtrage passe-haut, qui amplifie les fluctuations aléatoires présentes dans le signal expérimental.