Probabilités et statistiques

Nombres aléatoires

La génération de nombres pseudo-aléatoires peut se faire avec le module random, qui fait partie de la bibliothèque standard, ou bien avec le module numpy.random de la bibliothèque NumPy. Ce dernier est plus intéressant pour les simulations de variables aléatoires car il permet de générer très rapidement des tableaux de nombres aléatoires.

Nous importons le module numpy.random en créant un alias :

import numpy.random as random

La fonction numpy.random.randint permet de tirer un ou plusieurs nombres entiers dans un intervalle donné \([a,b[\) (intervalle ouvert à droite), avec une distribution de probabilités uniforme. Voici par exemple 10 tirages d’un dé :

a,b = 1,7 # bornes de l'intervalle (ouvert en b)
for k in range(10):
    print(random.randint(a,b))

2
5
6
6
4
1
6
5
5
4

La fonction randint du module random est similaire mais l’intervalle spécifié est \([a,b]\) (intervalle fermé à droite).

La fonction randint peut être utilisée pour faire des choix aléatoires, par exemple pour réaliser une première action avec une probabilité de 2/3 ou une seconde avec une probabilité de 1/3 :

if random.randint(1,4) < 3:
    # action 1
else:
    # action 2

Les simulations faisant intervenir des variables aléatoires (simulations de Monte-Carlo) demandent la génération d’un très grand nombre d’échantillons aléatoires. La fonction randint du module numpy.random, comme toutes les fonctions de génération du même module, permet d’obtenir directement un tableau numpy.ndarray contenant un nombre N de tirages :

N = 10000 # nombre de tirages
x = random.randint(1,7,N)
print(x[0:10]) # 10 premiers éléments du tableau

[4 5 4 4 6 1 2 2 4 1]

Comme toujours, l’utilisation d’une fonction générant un tableau est beaucoup plus efficace que l’écriture d’une boucle pour remplir une liste ou un tableau, car la boucle de génération est exécutée par un code compilé.

Intéressons-nous à la génération d’échantillons d’une variable réelle à densité. Soit une variable aléatoire réelle \(x\in[a,b]\) et la densité de probabilité \(p:[a,b]\rightarrow\mathbb{R}\). Par définition, la probabilité d’obtenir \(x\) dans l’intervalle \([x_1,x_2]\) est :

\[\mathcal{P}(x_1\le x\le x_2)=\int_{x_1}^{x_2}p(x){\rm d}x\]

La fonction numpy.random.uniform permet de tirer des nombres à virgule flottante qui représentent les valeurs d’une variable aléatoire réelle de densité uniforme sur l’intervalle \([a,b]\), c.a.d. \(p=1/(b-a)\) :

a,b = 0,10
N = 5
print(random.uniform(a,b,N))

[6.49872461 3.43255267 5.91171323 5.32139159 0.36943068]

Il faut remarquer que le générateur de nombres pseudo-aléatoires génère en réalité des nombres entiers, qui sont convertis en nombres à virgule flottante sur l’intervalle demandé. En conséquence, la probabilité d’obtenir un nombre particulier, par ex. 6.49872461, n’est pas nulle alors qu’elle l’est en théorie. En pratique, cette limitation est peu gênante compte tenu de la précision des flottants 64 bits.

Il existe aussi une fonction numpy.random.random, qui fournit des nombres dans l’intervalle \([0,1[\) (ouvert à droite). Cette fonction est similaire à la fonction du même nom du module random de la bibliothèque standard.

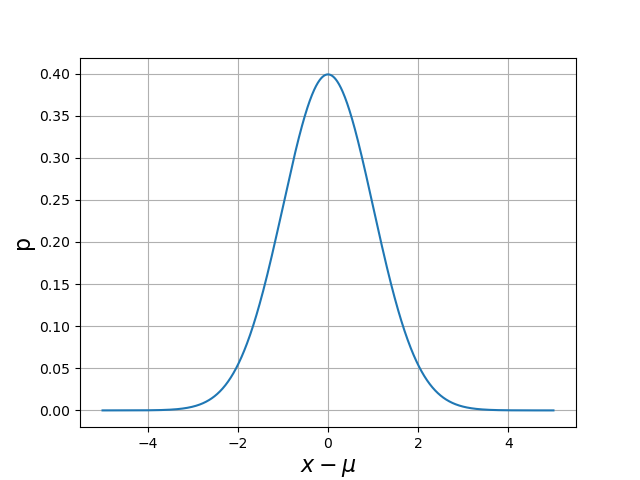
La loi normale (ou loi de Gauss) pour une variable aléatoire d’espérance \(\mu\) et d’écart-type \(\sigma\) est définie par la densité de probabilité suivante :

\[p(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]

Pour cette distribution, la variable peut prendre en principe toute valeur réelle (intervalle non borné) mais la probabilité d’obtenir une valeur en dehors de l’intervalle \([\mu-5\sigma,\mu+5\sigma]\) est extrêmement faible. Voici une représentation graphique de la densité sur cet intervalle :

sigma = 1
mu = 0
x = np.linspace(mu-5*sigma,mu+5*sigma,1000)
p = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-(x-mu)**2/(2*sigma**2))
plt.figure()
plt.plot(x,p)
plt.grid()
plt.xlabel(r'$x-\mu$',fontsize=16)
plt.ylabel('p',fontsize=16)
plt.show()

La fonction numpy.random.normal permet de générer des nombres aléatoires suivant la loi normale :

mu=10.0
sigma=0.1
print(random.normal(mu,sigma,5))

[10.02154228  9.98851472 10.01492233 10.02490359  9.99917556]

Une des utilisations de la loi normale est la simulation des mesures physiques. En effet, les multiples mesures d’une grandeur physique sont très souvent distribuées suivant une loi normale. L’écart-type \(\sigma\) est, par définition, l’incertitude-type de la mesure.

Notons que l’intervalle \([\mu-\sigma,\mu+\sigma]\) correspond à une probabilité de 68 % (intervalle de confiance de 68 %). L’intervalle \([\mu-2\sigma,\mu+2\sigma]\) correspond à une probabilité de 95 %.

Moyenne et écart-type

La moyenne d’un ensemble de \(N\) tirages \(x_i\) d’une variable aléatoire est la moyenne arithmétique :

\[m = \frac{1}{n}\sum_{i=0}^{N-1}x_i\]

Cette moyenne constitue une estimation de l’espérance de la variable aléatoire (moyenne d’un nombre infini de tirages). La variance d’un ensemble de tirages est la moyenne du carré de l’écart entre \(x\) et sa moyenne :

\[v = \frac{1}{N}\sum_{i=0}^{N-1}(x_i-m)^2\]

Après développement du carré et simplification, on obtient l’expression suivante :

\[v = \frac{1}{N}\sum_{i=0}^{N-1}x_i^2-m^2\]

L’écart-type de l’ensemble des tirages est la racine carrée de la variance :

\[\sigma = \sqrt{v}\]

La moyenne est elle-même une variable aléatoire, puisque des séries de N tirages donnent des valeurs différentes de la moyenne. La variance de la moyenne est égale à la variance de la variable \(x\) divisée par \(N\). On peut donc estimer la variance de la moyenne par :

\[var(m)=\frac{v}{N}\]

L’écart-type de la moyenne (racine carrée de \(var(m)\)) constitue l’incertitude-type de l’estimation de l’espérance.

La fonction numpy.mean calcule la moyenne des valeurs placées dans un tableau. La fonction numpy.var calcule la variance et numpy.std calcule l’écart-type.

Voyons comme exemple un ensemble de tirages d’une variable aléatoire obéissant à la loi normale. On effectue \(N\) tirages dont on calcule la moyenne et l’écart-type. L’écart-type de la moyenne constitue l’incertitude de l’évaluation de l’espérance, ce qui permet de présenter le résultat avec son incertitude.

mu=10.0
sigma=1.0
N = 100
x = random.normal(mu,sigma,N)
m=x.mean()
s=x.std()
incertitude = s/np.sqrt(N)
print("espérance = %0.2e +/- %0.1e"%(m,incertitude))
print("écart-type = %0.2e"%s)

espérance = 9.85e+00 +/- 1.1e-01
écart-type = 1.06e+00

Si l’on veut gagner un facteur 10 sur la précision de l’estimation de l’espérance, il faut augmenter le nombre de tirages d’un facteur 100 :

mu=10.0
sigma=1.0
N = 10000
x = random.normal(mu,sigma,N)
m=x.mean()
s=x.std()
incertitude = s/np.sqrt(N)
print("espérance = %0.2e +/- %0.1e"%(m,incertitude))
print("écart-type = %0.2e"%s)

espérance = 1.00e+01 +/- 1.0e-02
écart-type = 1.01e+00

Histogramme

Un ensemble de tirages d’une variable aléatoire peut être représenté graphiquement sous la forme d’un histogramme, qui permet de visualiser la distribution des tirages. Soit \([a,b]\) l’intervalle de définition de la variable. Si l’intervalle est non borné (comme pour la loi normale), on doit choisir un intervalle borné tel que la probabilité d’occurence d’une valeur en dehors de cet intervalle soit négligeable.

L’intervalle \([a,b]\) est divisé en \(Q\) sous-intervalles de largeur \(\delta=(b-a)/Q\), chacun correspondant à une classe de valeurs de la variable aléatoire. La classe d’indice \(q=0,1,\ldots Q-1\) regroupe les tirages dont la valeur est dans l’intervalle \([q\delta,(q+1)\delta]\). Le tracé de l’histogramme consiste à représenter, pour chaque classe, un rectangle dont la hauteur est égale au nombres de tirages de cette classe.

La fonction matplotlib.pyplot.hist permet d’obtenir un histogramme d’un ensemble de valeurs placées dans un tableau. Le paramètre bins précise le nombre de classes (\(Q\)), le paramètre range précise l’intervalle \([a,b]\). Si celui-ci n’est pas précisé, les valeurs minimale et maximale de l’ensemble sont pris comme bornes de l’intervalle.

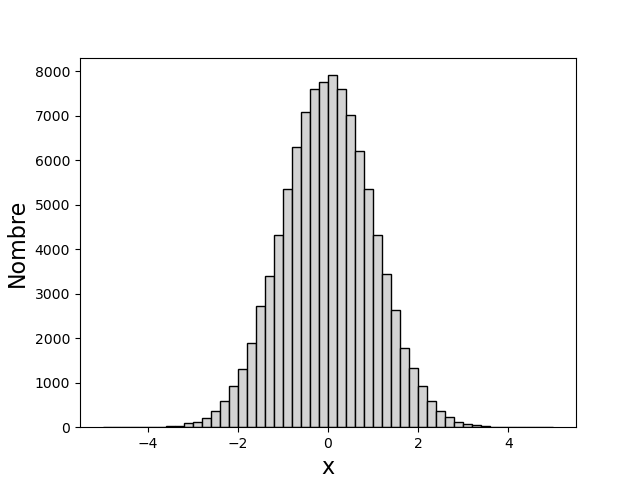
Voici comment obtenir un histogramme de 100000 tirages d’une variable aléatoire suivant la loi normale :

N = 100000
mu = 0
sigma = 1
x = random.normal(mu,sigma,N)
plt.figure()
plt.hist(x,bins=50,range=(-5,5),color='lightgrey',edgecolor='k')
plt.xlabel('x',fontsize=16)
plt.ylabel('Nombre',fontsize=16,rotation=90)
plt.show()

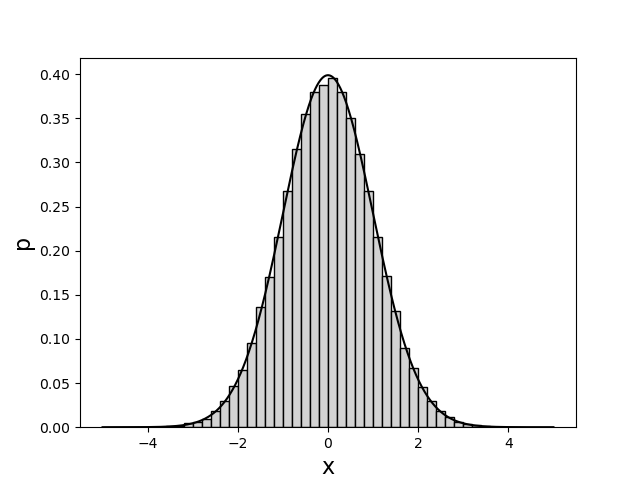
La propabilité d’avoir une valeur dans une classe peut être estimée en divisant le nombre de tirages dans cette classe par le nombre de tirages total. La densité de probabilité est estimée en divisant la probabilité par la largeur des classes. Pour obtenir la densité de probabilité, il suffit d’attribuer la valeur True au paramètre optionnel density :

plt.figure()
plt.hist(x,bins=50,range=(-5,5),density=True,color='grey',edgecolor='k')
x = np.linspace(mu-5*sigma,mu+5*sigma,1000)
p = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-(x-mu)**2/(2*sigma**2))
plt.plot(x,p,'k-') # tracé de la loi normale
plt.xlabel('x',fontsize=16)
plt.ylabel('p',fontsize=16,rotation=90)
plt.show()

Régression linéaire

La régression linéaire est une méthode de moindres carrés appliquée à une fonction affine à deux paramètres. Soit un ensemble de \(N\) échantillons \((x_i,y_i)\in\mathbb{R}^2\), par exemple des données expérimentales. On cherche les paramètres \(a,b\) qui permettent de représenter au mieux ces échantillons sous la forme d’une relation affine :

\[y = ax+b\]

La méthode des moindres carrés consiste à déterminer les paramètres \(a,b\) qui minimisent la somme suivante :

\[e = \sum_{i=0}^{N-1}(y_i-ax_i-b)^2\]

La condition d’annulation des dérivées partielles de \(e\) par rapport aux deux paramètres conduit à un système de deux équations linéaires pour ceux-ci. D’une manière générale, la méthode des moindres carrés conduit à un système linéaire pour les paramètres lorsque la relation \(y=f(x)\) recherchée dépend linéairement des paramètres. C’est le cas notamment lorsqu’on recherche une fonction polynomiale dont les paramètres sont les coefficients.

La fonction numpy.polyfit permet de réaliser un ajustement d’une fonction polynomiale sur des données par la méthode des moindres carrés.

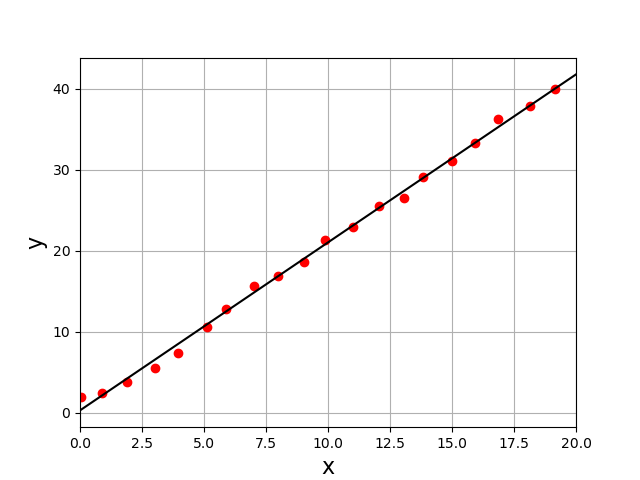
Afin de montrer l’utilisation de cette fonction pour faire une régression linéaire (polynôme de degré 1), nous simulons des données aléatoires au moyen de la loi normale. La fonction polyfit est appelée avec l’argument optionnel cov égal à True, ce qui fait qu’elle renvoie, outre les coefficients du polynôme, la matrice de covariance.

N = 20
x = []
y = []
a,b = 2.0,1.0
for k in range(N):
    x.append(random.normal(k,0.1))
    y.append(random.normal(a*k+b,0.8))
deg = 1 # degré du polynôme
coef,cov = np.polyfit(x,y,deg,cov=True)
[A,B] = coef
plt.figure()
plt.plot(x,y,"ro")
plt.plot([0,N],[B,A*N+B],'k-')
plt.xlim(0,20)
plt.xlabel('x',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.grid()
print('a = %f, b = %f'%(a,b))
print(cov) # matrice de covariance
plt.show()

a = 2.073992, b = 0.299763
[[ 0.00067866 -0.00644   ]
[-0.00644     0.08380021]]