Equations différentielles¶
Intégration numérique d’une équation différentielle du premier ordre¶
Comme exemple d’une équation différentielle du premier ordre, considérons le cas d’une fonction \(y:\mathbb{R}\rightarrow\mathbb{R}\) vérifiant l’équation différentielle du premier ordre à coefficients constants suivante :
La variable est notée \(t\) car il s’agit souvent du temps. \(\tau\) est une constante et \(g\) une fonction de \(t\). Si la valeur de \(y\) est donnée pour \(t=t_0\), il existe une et une seule fonction \(y\) vérifiant cette équation différentielle. \(y(t_0)\) constitue la condition initiale. L’intégration numérique de l’équation différentielle consiste à rechercher des valeurs approchées de \(y\) pour des valeurs de \(t\) réparties sur l’intervalle \([t_0,t_0+T]\). Nous considérons le cas d’un échantillonnage régulier :
Le pas de temps est l’intervalle de temps entre deux instants successifs :
Soit \(y_0=y(t_0)\) la valeur initiale de la fonction. Une méthode numérique d’intégration consiste à obtenir une approximation de \(y(t_1)\), notée \(y_1\), puis une approximation de \(y(t_2)\), notée \(y_2\), et ainsi de suite jusqu’à une approximation de \(y(t_{N-1})\), notée \(y_{N-1}\). Les approximations successives \(y_1,y_2,\ldots y_{N-1}\) sont calculées itérativement au moyen d’une relation de récurrence.

L’erreur à l’instant \(t_n\) est, par définition, l’écart entre la approchée et la valeur exacte de la fonction :
Cette erreur est aussi nommée erreur de troncature globale, ou plus rarement erreur de consistance.
Méthode d’Euler – Définition¶
La méthode d’Euler (1770) repose sur l’idée suivante. Supposons que \(y(t_n)\) soit connue. La dérivée de \(y\) à cet instant peut être approximée par la différence finie suivante :
ce qui conduit à l’approximation :
Plus précisément, le développement de Taylor :
montre que l’erreur commise par l’approximation (3) est \(O(h^2)\) (grand O de \(h^2\)). Cette erreur est appelée erreur de troncature locale ou simplement erreur locale.
La méthode d’Euler consiste à utiliser la relation (3) pour définir la relation de récurrence suivante permettant de calculer les approximations successives :
Si l’on reprend l’exemple (1), cette relation de récurrence s’écrit :
Elle permet bien de calculer les approximations \(y_1,y_2,\ldots y_{N-1}\) de manière itérative.
L’erreur de troncature globale \(e_n\) résulte de l’erreur \(e_{n-1}\) et de l’erreur de troncature locale commise par application du schéma d’Euler (4). L’erreur globale résulte donc d’un effet cumulatif des erreurs de troncature locales, mais d’une manière en général complexe (l’erreur globale n’est pas nécessairement croissante avec \(n\)).
La méthode d’Euler est une méthode d’ordre 1 au moins, ce qui signifie que l’erreur globale est \(O(h)\), autrement dit qu’il existe une constante \(C\) telle que sa valeur absolue vérifie l’inégalité suivante (pour \(h\) assez petit) :
Il existe donc en général un majorant de l’erreur proportionnel à \(h\). Cette propriété garantit la convergence de la méthode d’Euler : plus \(h\) est petit, c’est-à-dire plus \(N\) est grand, plus l’erreur est petite. On a donc :
Dans certains cas, il est possible que l’erreur soit proportionnelle à \(h^2\) mais un exposant supérieur à 2 est très peu probable car l’erreur locale est \(O(h^2)\). La méthode d’Euler est considérée comme une méthode d’ordre 1 car seul l’ordre 1 est garanti dans le cas général. La proportionnalité de l’erreur avec \(h\) est d’ailleurs souvent vérifiée en pratique (on peut mesurer l’erreur lorsqu’on connaît la solution exacte).
La constante \(C\) dépend de l’équation différentielle considérée et augmente avec l’intervalle de \(t\) sur lequel on fait le calcul (la durée \(T\)). Tout ce qu’on peut dire en général est que, pour une durée \(T\) donnée, la réduction de \(h\) d’un facteur 10 a pour effet la réduction de l’erreur d’un facteur 10 (au moins) pour tout \(n=0,1,\ldots N-1\). Une méthode d’ordre 1 comme la méthode d’Euler est qualifiée de méthode peu précise car il existe des méthodes d’ordre plus élevé. Même une méthode d’ordre 2 offrira une précision beaucoup plus grande que la méthode d’Euler. Malgré ses piètres performances, la méthode d’Euler est intéressante car elle est très simple à mettre en oeuvre. Par ailleurs, son étude met en évidence des problèmes de précision et de stabilité, que l’on retrouve dans toutes les méthodes numériques à des degrés divers.
La question de l’évolution de l’erreur lorsqu’on augmente \(T\) constitue le problème de la statibilité. La méthode numérique est dite stable si l’erreur reste bornée lorsque \(T\) augmente, ce qui revient à dire que la constante \(C\) est bornée. Dans le cas contraire, la méthode est dite instable. En pratique, une méthode instable se reconnaît par le fait qu’elle conduit à une solution non bornée lorsque la solution exacte est bornée.
L’étude générale de la stabilité n’est possible que pour les équations différentielles linéaires et la méthode d’Euler est instable pour ces équations. Elle partage cet inconvénient avec d’autres méthodes beaucoup plus précises, ce qui montre que stabilité et précision sont deux notions différentes. De manière générale, on parvient à définir une méthode stable en faisant appel à un schéma numérique implicite. Par exemple, la méthode d’Euler implicite est définie par la relation suivante :
La méthode d’Euler implicite, comme toute méthode implicite, est beaucoup plus difficile à mettre en oeuvre car elle nécessite la résolution d’une équation algébrique à chaque itération et cette équation est en générale résolue par une méthode itérative.
Méthode d’Euler – Implémentation¶
Pour réaliser la méthode d’Euler, il est judicieux d’écrire une fonction Python qui permettra de le faire dans le cas général d’une équation différentielle du premier ordre. En effet, cela permettra de réutiliser le code pour différents problèmes et l’écriture du cas général est plus simple et plus claire que l’implémentation d’un cas particulier. Cela nous permettra en outre d’introduire les conventions utilisées dans la fonction scipy.integrate.odint que nous étudierons plus loin.
La forme générale d’une équation du premier ordre est :
où \(F:\mathbb{R}^2\rightarrow\mathbb{R}\). Par exemple, dans le cas de l’équation (1) on a :
La variable (ici le temps) apparaît explicitement via la fonction \(g\) et implicitement via \(y(t)\). Dans d’autres cas, l’équation différentielle ne fait pas intervenir explicitement le temps mais on garde quand même la forme générale (5).
Il faut donc définir une fonction Python permettant d’évaluer \(F\). Voici le prototype de cette fonction :
def derive(y,t):
deriv_y = # calcul de y'
return deriv_y
Reprenons l’exemple et supposons que la fonction \(g\) soit définie par :
L’instant initial sera \(t=0\). La fonction derive a besoin des valeurs de \(\tau,t_1,G\). Il y a deux manières de procéder : attribuer ces valeurs à trois variables globales ou bien les transmettre en arguments de la fonction. Voyons d’abord la première méthode, plus simple à mettre en oeuvre.
1 2 3 4 5 6 7 8 9 | def derive(y,t):
# calcule la dérivée de y
# utilise les variables globales G,t1,tau
if t<t1:
g = G
else:
g = 0
deriv_y = g-y/tau
return deriv_y
|
Le premier inconvénient de faire appel à des variables globales est qu’il est nécessaire d’examiner le code de la fonction pour savoir quelles variables elle utilise. Nous avons donc ajouté un commentaire pour le préciser.
La fonction euler ci-dessous implémente la méthode d’Euler. La signification des différents paramètres de la fonction est ajoutée dans le corps de la fonction sous la forme d’une chaîne de caractères occupant plusieurs lignes (plus commode que les commentaires).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def euler(derive,t0,y0,T,N):
'''
Paramètres :
derive : fonction F(y,t)
t0 : instant initial
y0 : valeur initiale de y
T : durée
N : nombre de points
Objets renvoyés :
t : tableau des instants
Y : tableau des valeurs de y
'''
t = np.linspace(t0,t0+T,N)
h = t[1]-t[0]
Y = np.zeros(N)
Y[0] = y0
for n in range(0,N-1):
Y[n+1] = Y[n] + h*derive(Y[n],t[n])
return (t,Y)
|
Voyons comment utiliser les deux fonctions précédentes. Nous devons tout d’abord définir les variables globales tau,t1,G. Pour définir y0,T,N, qui sont des valeurs à transmettre en argument à la fonction euler, nous définissons aussi des variables globales.
tau = 1
t1 = 10
G = 1
t0 = 0
y0 = 0
T = 20
plt.figure()
N = 100
(t,Y) = euler(derive,t0,y0,T,N)
plt.plot(t,Y,'r--',label='N=100')
plt.xlabel('t',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.ylim(0,1.2)
plt.grid()
N = 1000
(t,Y) = euler(derive,t0,y0,T,N)
plt.plot(t,Y,'b-',label='N=1000')
N = 5000
(t,Y) = euler(derive,t0,y0,T,N)
plt.plot(t,Y,'k:',label='N=5000')
plt.legend(loc='upper right')
plt.show()
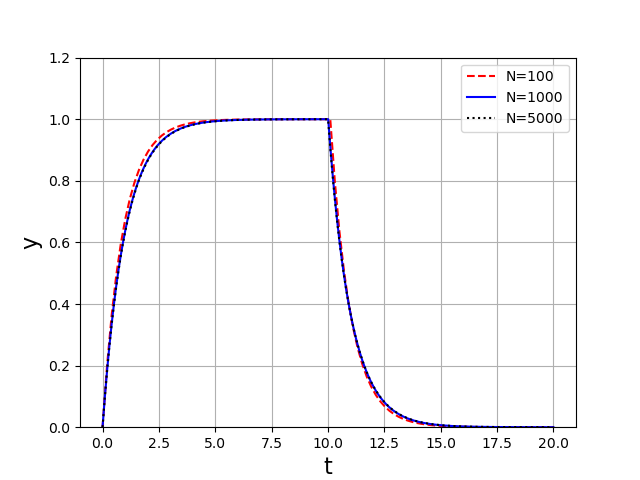
Si l’on souhaite refaire le calcul avec une valeur différente de T, il suffit de changer la valeur attribuée à la variable correspondante (idem pour la condition initiale). Il est donc judicieux de toujours définir des variables globales pour préciser les valeurs des arguments transmis aux fonctions, en utilisant les mêmes noms que les noms des paramètres de la fonction. Cette pratique a en outre l’avantage de rendre le code bien compréhensible. En effet, si on avait écrit :
(t,Y) = euler(derive,0,0,20,N)
à chaque appel de la fonction, il aurait été laborieux de changer les valeurs des paramètres t0,y0,T et le code aurait été moins clair.
Nous avons effectué le calcul pour trois valeurs de \(N\). Nous constatons qu’il y a une différence significative entre les courbes pour \(N=100\) et pour \(N=1000\), ce qui montre que la seconde valeur apporte un gain de précision par rapport à la première. En revanche, la valeur \(N=5000\) n’apporte pas de gain notable par rapport à \(N=1000\) (du moins graphiquement), ce qui montre qu’il n’est pas nécessaire d’augmenter encore \(N\) (donc de réduire le pas \(h\)). Cette manière de procéder empirique pour déterminer la valeur de \(N\) nécessaire peut sembler rudimentaire et peu rigoureuse mais c’est en fait la seule méthode permettant de vérifier que le pas de temps est assez petit : il n’existe pas de moyen général de connaître l’erreur globale en fonction de \(h\).
La valeur de \(N\) étant choisie, sous souhaitons refaire le calcul pour différentes valeurs de \(t_1\) :
N = 1000
tau = 1
G = 1
t0 = 0
y0 = 0
T = 20
plt.figure()
t1 = 10
(t,Y) = euler(derive,t0,y0,T,N)
plt.plot(t,Y,'r-',label='t1=10')
t1 = 5
(t,Y) = euler(derive,t0,y0,T,N)
plt.plot(t,Y,'b-',label='t1=5')
t1 = 1
(t,Y) = euler(derive,t0,y0,T,N)
plt.plot(t,Y,'g-',label='t1=1')
plt.xlabel('t',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.ylim(0,1.2)
plt.grid()
plt.legend(loc='upper right')
plt.savefig('euler-eq1-fig2.png')
plt.show()
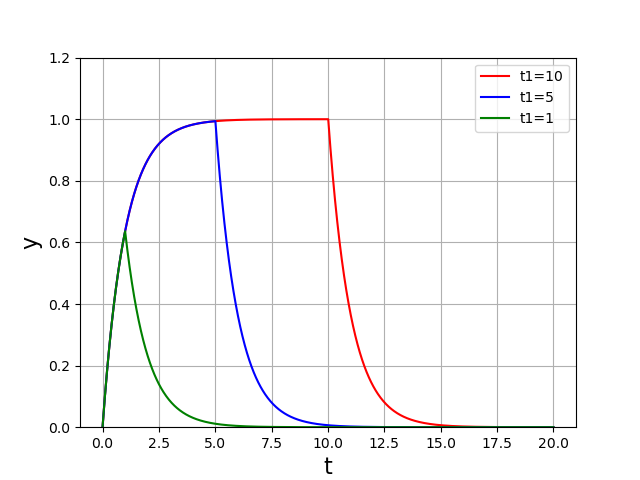
Il faut modifier le contenu de la variable globale t1 avant chaque nouvel appel de la fonction euler. On voit ici un deuxième inconvénient du fait que la fonction derive fait appel à des variables globales : la nécessité de préciser la valeur de \(t_1\) n’apparaît pas dans la ligne :
(t,Y) = euler(derive,t0,y0,T,N)
Pour les scripts simples et de petite taille, ce n’est pas un gros inconvénient. Cela peut en revanche le devenir pour des projets plus grands ou lorsqu’on utilise des fonctions écrites par une autre personne. Pour éviter cet inconvénient, il faudrait définir la fonction derive de la manière suivante :
1 2 3 4 5 6 7 | def derive(y,t,tau,t1,G):
if t<t1:
g = G
else:
g = 0
deriv_y = g-y/tau
return deriv_y
|
Dans cette nouvelle version, toutes les données nécessaires à la fonction apparaissent en paramètre. Si l’on oublie de préciser la valeur d’un paramètre, l’interpréteur le signale par une erreur. Il faut toujours se rappeler que les bugs les plus difficiles à détecter sont justement ceux qui ne déclenchent pas d’erreur. Cependant, une difficulté supplémentaire surgit : il faut transmettre les valeurs des paramètres à la fonction euler puisque c’est elle qui appelle la fonction derive. Il suffit de transmettre à euler la liste de ces valeurs sous la forme d’un n-uplet, via un paramètre nommé args (un nom souvent utilisé pour cet usage). La nouvelle fonction serait :
1 2 3 4 5 6 7 8 | def euler(derive,t0,y0,T,N,args=()):
t = np.linspace(t0,t0+T,N)
h = t[1]-t[0]
Y = np.zeros(N)
Y[0] = 0
for n in range(0,N-1):
Y[n+1] = Y[n] + h*derive(Y[n],t[n],*args)
return (t,Y)
|
Une valeur par défaut est attribuée au paramètre args, ce qui implique qu’il n’est pas nécessaire de fournir l’argument correspondant lors de l’appel de la fonction. Lors de l’appel de la fonction euler, il suffit d’ajouter *args comme troisième argument. L’opérateur * placé en préfixe a pour effet de convertir le contenu du n-uplet en liste d’arguments. Voici comment se ferait l’appel :
(t,Y) = euler(derive,t0,y0,T,N,args=(tau,t1,G))
Le code est ainsi plus clair et surtout, oublier un des paramètres déclencherait une erreur de la part de l’interpréteur.
Système d’équations différentielles du premier ordre¶
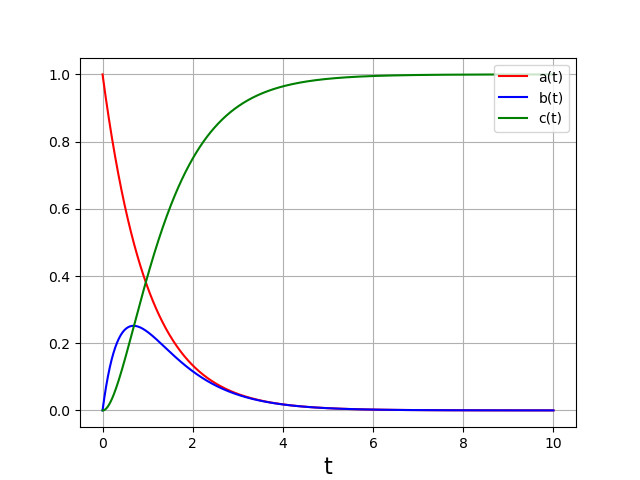
Considérons le système d’équations différentielles suivant, pour trois fonctions \(a(t),b(t),c(t)\) :
Il s’agit d’un système d’équations linéaires dont on peut déterminer la solution exacte, mais il nous permet de voir comment traiter en général les systèmes d’équations différentielles couplées. Même dans le cas d’un système linéaire, il est parfois plus rapide de réaliser une intégration numérique, surtout si l’objectif et de tracer des courbes.
Un système d’équations du premier ordre se prête au schéma numérique d’Euler. Il suffit pour cela de placer les trois fonctions inconnues dans une matrice ligne de trois colonnes :
Pour généraliser, nous aurons une matrice ligne à P colonnes, autant que d’équations dans le système. Le système s’écrit de manière générale :
ce qui est similaire à la forme (5). La fonction \(F:\mathbb{R}^P\times\mathbb{R}\rightarrow\mathbb{R}^P\) renvoie une matrice ligne qui contient les P dérivées des P fonctions inconnues.
Le schéma d’Euler défini par la relation (4) se généralise aisément :
D’un point de vue informatique, la transcription de cette relation est immédiate si \(Y_n\) et \(Y'\) sont des tableaux numpy.ndarray à une dimension et à P éléments.
Voici la définition d’une fonction qui évalue \(F\) pour le système donné en exemple :
def derive(Y,t,k1,k2):
return np.array([-k1*Y[0],k1*Y[0]-k2*Y[1],k2*Y[1]])
Le tableau renvoyé, contenant les trois dérivées, est de type numpy.ndarray.
Afin de mémoriser les valeurs de la matrice ligne Y aux différents instants, nous utilisons un tableau à deux dimensions comportant N lignes et P colonnes. La fonction euler est similaire à la précédente :
def euler(derive,t0,y0,T,N,args=()):
'''
Paramètres :
derive : fonction F(Y,t)
t0 : instant initial
y0 : valeurs initiales
T : durée
N : nombre de points
args : arguments supplémentaire pour derive
Objets renvoyés :
t : tableau des instants
Y : tableau des valeurs de y (N lignes et P colonnes)
'''
P = len(y0)
t = np.linspace(t0,t0+T,N)
h = t[1]-t[0]
Y = np.zeros((N,P)) # tableau à N lignes et P colonnes
Y[0] = y0
for n in range(0,N-1):
Y[n+1] = Y[n] + h*derive(Y[n],t[n],*args)
return (t,Y)
La condition initiale est donnée sous la forme d’un tableau (ou d’une liste) à P éléments. Le nombre d’équations est d’ailleurs déduit de la taille de ce tableau. À chaque itération de la boucle on remplit une ligne du tableau Y. À la fin du calcul, chaque colonne de ce tableau contient les valeurs d’une des fonctions du système.
Voici un exemple d’utilisation :
k1=1
k2=2
t0=0
T=10
N=1000
y0 = [1,0,0]
(t,Y) = euler(derive,t0,y0,T,N,(k1,k2))
plt.figure()
plt.plot(t,Y[:,0],"r-",label='a(t)') # première colonne de Y : a(t)
plt.plot(t,Y[:,1],"b-",label='b(t)')
plt.plot(t,Y[:,2],"g-",label='c(t)')
plt.xlabel('t',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.savefig('euler-systeme.png')
plt.show()
Equations différentielles du second ordre¶
Une équation différentielle du second ordre (ou un système d’équations) doit être mise sous la forme d’un système du premier ordre pour être traitée par la méthode d’Euler. Prenons l’exemple de l’équation différentielle du pendule :
L’introduction de la vitesse angulaire permet d’écrire un système du premier ordre :
On posera donc :
Voici la définition de la fonction correspondante :
a = (2*np.pi)**2 # constante en nom global
def derive(y,t):
return np.array([y[1],-a*np.sin(y[0])])
Le nombre \((2\pi)^2\) est défini comme constante dans une variable globale pour éviter le calcul du carré à chaque itération. D’une manière générale, l’efficacité exige de ne pas répéter les calculs qui peuvent être fait en amont.
y0=(1,0)
T=5
N=10000
(t,Y)=euler(derive,0,y0,T,N)
plt.figure()
plt.plot(t,Y[:,0],"b-")
plt.xlabel('t',fontsize=16)
plt.ylabel(r'$\theta$',fontsize=16)
plt.grid()
plt.show()
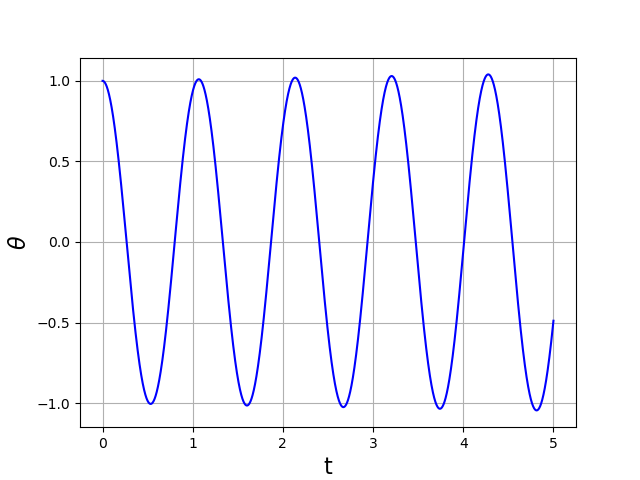
Sur cet exemple avec un pas de temps \(h=5\cdot 10^{-4}\), on remarque que l’amplitude d’oscillation ne reste pas constante. Si on augmente la durée de calcul sans changer ce pas :
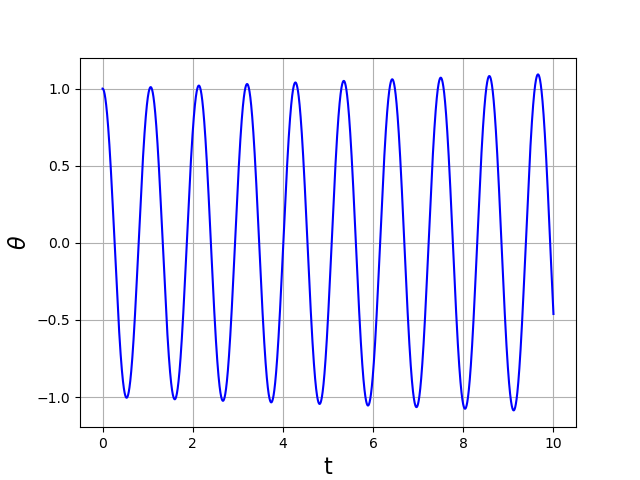
Cet exemple met en évidence le caractère instable de la méthode d’Euler appliquée à cette équation. On peut en effet montrer que la méthode d’Euler explicite est instable pour les équations linéaires. On constate ici qu’elle est aussi instable pour l’équation différentielle du pendule, ce qui n’est pas étonnant car celle-ci est proche de l’équation de l’oscillateur harmonique.
La caractéristique d’une méthode instable est qu’elle conduit à une solution approchée non bornée alors que la solution exacte l’est. Dans le cas présent, l’instabilité se traduit par une amplitude d’oscillation qui augmente avec la durée \(T\) (à pas de temps constant). Pour une durée fixée, il est bien sûr possible de réduire ce phénomène en réduisant le pas :
y0=(1,0)
T=10
N=20000*10
(t,Y)=euler(derive,0,y0,T,N)
plt.figure()
plt.plot(t,Y[:,0],"b-")
plt.xlabel('t',fontsize=16)
plt.ylabel(r'$\theta$',fontsize=16)
plt.grid()
plt.show()
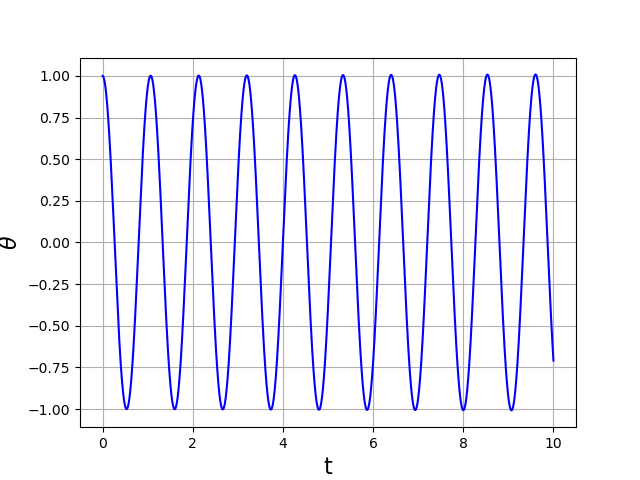
Le temps de calcul est allongé d’un facteur 10. Pour résoudre cette équation, il est préférable de se tourner vers des méthodes d’ordre supérieur, plus précises. Même si elles sont aussi instables, elles conduiront à une erreur plus faible pour le même pas de temps. L’intérêt d’utiliser la méthode d’Euler sur cet exemple est justement de montrer la notion de méthode numérique instable. Pour une méthode instable, quelle que soit le choix fait pour le pas de temps, l’augmentation de la durée \(T\) conduit à un écart croissant entre la solution approchée et la solution exacte. Bien entendu, cela pose problème surtout lorsqu’on ne connaît pas la nature de la solution. Le phénomène d’instabilité du schéma numérique peut être éliminé en faisant appel à une méthode implicite. Pour les systèmes mécaniques conservatifs, il existe une variante de la méthode d’Euler permettant de la rendre stable (voir paragraphe suivant).
Il ne faut pas confondre l’instabilité de la méthode numérique avec l’instabilité de l’équation différentielle, qui se définie comme une extrême sensibilité à la condition initiale (l’équation du pendule n’est pas instable). Lorsque l’équation elle-même est instable, comme c’est le cas pour les systèmes chaotiques, les choses se compliquent car il peut être difficile de savoir si le comportement observé est due à l’équation elle-même ou au schéma numérique.
Systèmes mécaniques conservatifs¶
Pour les système mécaniques conservatifs, une variante de la méthode d’Euler (nommée méthode d’Euler symplectique, ou encore méthode d’Euler semi-implicite) permet d’obtenir un comportement stable. Cette méthode est très importante car les méthodes utilisées pour traiter le problème des N corps (par ex. en dynamique moléculaire) sont similaires.
Considérons un système dynamique conservatif à un degré de liberté. Son mouvement est décrit par une variable \(x(t)\) et par la vitesse associée \(v(t)=\frac{dx}{dt}\).
Pour un système conservatif, la dérivée de la vitesse par rapport au temps (l’accélération) s’exprime en fonction de la variable de position seulement (pas de la vitesse) :
La fonction \(F\) représente la force par unité de masse. La méthode d’Euler semi-implicite est définie par :
La différence avec la méthode d’Euler explicite est subtile : la vitesse à l’instant \(t_{n+1}\) est calculée après évaluée la force avec la nouvelle valeur de la position. La comparaison avec le schéma implicite (\(y_{n+1}=y_n+hy'(t_{n+1})\)) permet de comprendre le sens de l’appelation méthode semi-implicite : l’évaluation de la vitesse \(v_{n+1}\) se fait en suivant le schéma implicite. Cependant, il n’y pas dans ce cas d’équation algébrique à résoudre car la force ne dépend que de la position, qui est évaluée par un schéma explicite. Bien qu’elle ne soit pas complètement implicite, cette méthode est stable pour les systèmes linéaires, contrairement à la méthode explicite.
Pour implémenter cette méthode, il faut définir une fonction qui calcule les forces en fonction des variables de positions, par exemple pour l’équation du pendule :
a = (2*np.pi)**2
def force(x):
return np.array([-a*np.sin(x[0])])
Voici la fonction qui réaliser la méthode d’Euler. Les variables de position et les vitesses sont traitées séparément :
def euler_s(force,t0,x0,v0,T,N,args=()):
P = len(x0)
t = np.linspace(t0,t0+T,N)
h = t[1]-t[0]
X = np.zeros((N,P))
V = np.zeros((N,P))
X[0] = x0
V[0] = v0
for n in range(0,N-1):
X[n+1] = X[n] + h*V[n]
V[n+1] = V[n] + h*force(X[n+1])
return (t,X,V)
Voici un exemple
x0=(1,)
v0=(0,)
T=100
N=10000
(t,X,V)=euler_s(force,0,x0,v0,T,N)
plt.figure(figsize=(12,5))
plt.plot(t,X[:,0],"b-")
plt.xlabel('t',fontsize=16)
plt.ylabel(r'$\theta$',fontsize=16)
plt.grid()
plt.show()
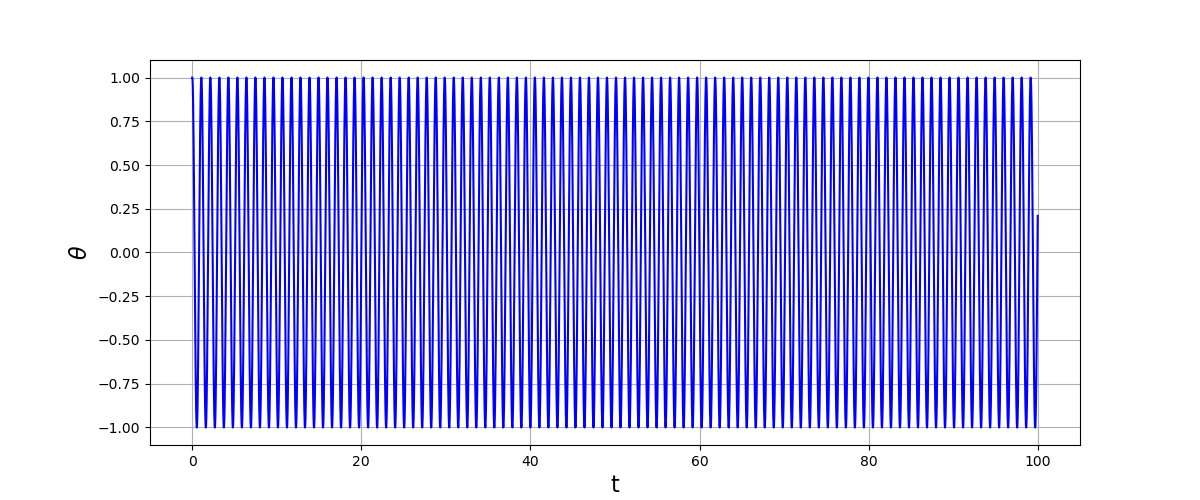
Bien que le pas de temps soit beaucoup plus grand que précédemment (\(h=10^{-2}\)), la méthode ne montre aucun signe d’instabilité sur cette durée de calcul (elle est stable en effet). Pour les équations de systèmes dynamiques conservatifs, la stabilité de la méthode numérique est le critère le plus important, bien plus que la précision.
Utilisation de la fonction odeint¶
Le module scipy.integrate comporte des fonctions permettant d’intégrer numériquement des équations différentielles ordinaires (ODE) à condition initiale. La fonction odeint est la plus simple à utiliser et son usage figure explicitement dans les programmes officiels, bien qu’elle ait été remplacée par des fonctions plus évoluées (mais plus difficiles à utiliser).
La fonction odint fait appel à la bibliothèque odepack, écrite en langage FORTRAN. Il s’agit donc d’une fonction dont la qualité est éprouvée par une utilisation intensive dans le domaine du calcul scientifique. La méthode numérique mise en oeuvre permet d’atteindre une précision très supérieure à la méthode d’Euler (pour le même pas de temps) et offre une offre une très bonne stabilité dans la plupart des cas. Il y a en fait deux méthodes numériques : la méthode d’Adams et la méthode BDF (backward differentiation formula). La première est une méthode explicite très efficace pour résoudre précisement et rapidement un grand nombre d’équations, la seconde est une méthode implicite qui présente la stabilité nécessaire pour résoudre les équations différentielles raides (qui répondent mal aux méthodes explicites) . L’algorithme choisit lui-même la méthode en fonction du comportement de l’équation différentielle.
L’algorithme utilisé effectue un contrôle automatique du pas. À chaque instant \(t_n\), une estimation de l’erreur de troncature locale est faite. Notons \(\tilde e_n\) cette estimation de l’erreur locale, qui repose sur la comparaison de \(y_{n+1}\) obtenu avec le pas \(h\) et de \(y_{n+1}\) obtenu avec un pas deux fois plus petit. Le contrôle du pas se fait au moyen de deux tolérances : la tolérance absolue \(\epsilon_a\) et la tolérance relative \(\epsilon_r\). Si
alors le pas \(h\) est diminué. Dans le cas contraire, il est augmenté. Cela permet de réduire le pas lorsque l’erreur de troncature estimée est trop grande ou au contraire de l’augmenter lorsque c’est possible. Lorsque la réduction du pas devient trop forte, l’algorithme bascule automatique à la méthode BDF, plus lourde mais pouvant traiter les équations raides. Les tolérances permettent à l’utilisateur de contrôler la précision du calcul dans le sens ou faire varier ces tolérances permet de faire varier l’erreur globale. Cependant, l’erreur globale ne peut en aucun cas être déduite directement de ces valeurs de tolérance.
Pour utiliser odeint, il faut écrire une fonction Python pour définir le système différentiel du premier ordre, dont la signature est la même que celle que nous avons déjà utilisée. Par exemple pour l’équation du pendule :
a = (2*np.pi)**2
def derive(y,t):
return np.array([y[1],-a*np.sin(y[0])])
Un appel de cette fonction se présente comme suit :
Y = odeint(derive,Y0,t,atol,rtol,args)
Y0 est une liste (ou un tableau à une dimension) contenant les conditions initiales. t est un tableau (ou une liste) contenant les instants auquels on souhaite mémoriser les différentes approximations \(Y_n\). La période d’échantillonnage doit être choisie assez petite pour obtenir une bonne représentation graphique des fonctions. Il ne faut pas confondre cette période avec le pas de temps de la méthode numérique, qui est plus petit que la période d’échantillonnage et dont la valeur n’est pas fixée puisqu’elle change automatiquement en fonction de l’estimation de l’erreur locale et des tolérances. L’utilisateur ne choisit pas le pas \(h\) mais les tolérances absolue et relative. Les deux paramètres correspondant sont atol et rtol (arguments optionnels). Voici un exemple :
Y0 = [1,0]
T = 10
t = np.linspace(0,T,1000)
Y = odeint(derive,Y0,t,rtol=1e-4,atol=1e-12)
plt.figure()
plt.plot(t,Y[:,0],"b-")
plt.xlabel('t',fontsize=16)
plt.ylabel(r'$\theta$',fontsize=16)
plt.grid()
plt.show()
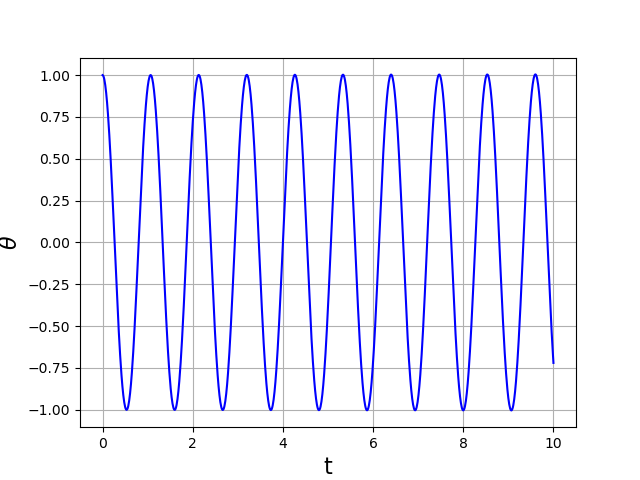
Le fait de choisir une tolérance absolue très faible permet de faire intervenir principalement la tolérance relative.
Voyons, pour cette même valeur de tolérance, le comportement sur une durée beaucoup plus grande :
T = 1000
t = np.linspace(0,T,100000)
Y = odeint(derive,Y0,t,rtol=1e-4,atol=1e-12)
plt.figure()
plt.plot(Y[:,0],Y[:,1],"b-")
plt.xlabel(r'$\theta$',fontsize=16)
plt.ylabel(r'$\omega$',fontsize=16)
plt.grid()
plt.show()
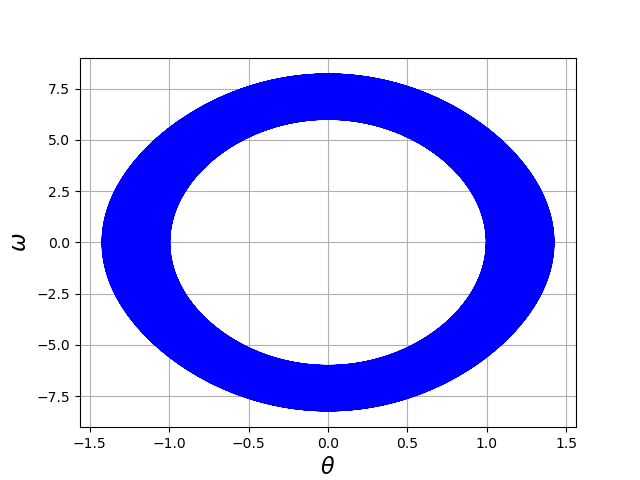
Cette représentation de la trajectoire dans l’espace des phases montre que la solution approchée est très mauvaise sur une temps aussi long, ce qui semble indiquer un comportement instable. Réduisons la tolérance :
T = 1000
t = np.linspace(0,T,100000)
Y = odeint(derive,Y0,t,rtol=1e-5,atol=1e-12)
plt.figure()
plt.plot(Y[:,0],Y[:,1],"b-")
plt.xlabel(r'$\theta$',fontsize=16)
plt.ylabel(r'$\omega$',fontsize=16)
plt.grid()
plt.show()
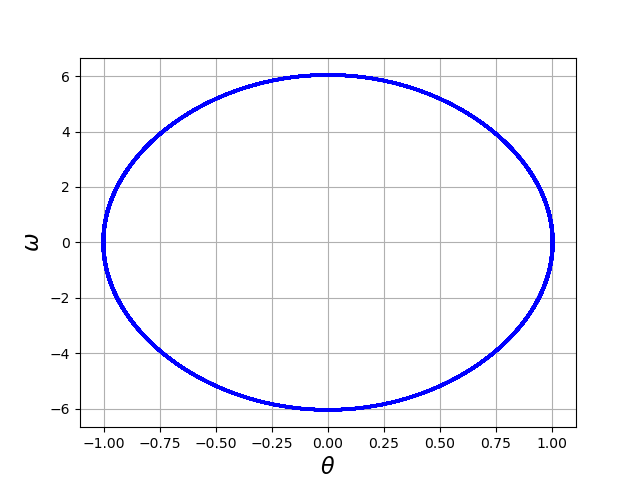
Avec cette tolérance, le résultat est conforme à ce qu’on attend d’un pendule. Lorsqu’on résout numériquement une équation différentielle dont on ne connaît pas la solution, il faut essayer des valeurs de plus en plus petites de la tolérance. Lorsque la diminution de la tolérance ne donne plus de variation visible de la solution, la bonne tolérance est atteinte. L’obtention d’une tolérance asse petite ne peut être faite que de maière empirique, car il n’existe pas de relation générale permettant de calculer a priori la bonne tolérance pour une erreur globale souhaitée.
Il est possible d’utiliser odeint sans préciser les tolérances. Cela donne dans la plupart des cas un très bon résultat car les valeurs par défaut sont très faibles (\(10^{-8}\)) mais on se prive alors de vérifier que ce résultat est correct. Par ailleurs, il peut être intéressant d’augmenter la tolérance jusqu’à une valeur acceptable lorsque le système à résoudre comporte beaucoup d’équations (pour réduire le temps de calcul).