Graphiques

La bibliothèque de fonctions Matplotlib permet d’obtenir des représentations graphiques de toutes sortes, statiques ou animées. Le module racine de cette bibliothèque est matplotlib.

Le sous-module le plus utilisé est matplotlib.pyplot, que nous importerons au moyen d’un alias :

import matplotlib.pyplot as plt

Le module pyplot apporte des fonctions qui permettent d’obtenir très simplement des représentations graphiques de fonctions mathématiques ou de données tabulaires.

Dans cette page, nous décrivons seulement l’utilisation de la fonction matplotlib.pyplot.plot, qui permet de tracer des nuages de points et des courbes.

Création d’une figure

La fonction pyplot.figure crée une figure dans laquelle les fonctions suivantes opèrent. Pour afficher toutes les figures, on utilise la fonction pyplot.show.

Par exemple, voici comment créer et afficher deux figures :

plt.figure() # création de la figure 1
# fonctions graphiques opérant sur la figure 1
plt.figure() # création de la figure 2
# fonction graphiques opérant sur la figure 2
plt.show() # affichage des figures 1 et 2

La fonction plt.show a pour effet d’ouvrir une fenêtre pour chaque figure. Sur certains IDE (par ex. IDLE) cette fonction est bloquante (à moins d’ajouter l’argument optionnel block=False), c’est-à-dire qu’il faut fermer toute les fenêtres pour que l’exécution du script se poursuive. Avec les IDE Pyzo et Spyder, la fonction show n’est pas bloquante. Si les calculs effectués entre deux figures sont très longs à exécuter, on a intérêt à demander l’affichage de chaque figure dès qu’elle est terminée :

plt.figure() # création de la figure 1
# fonctions graphiques opérant sur la figure 1
plt.show() # affichage de la figure 1
plt.figure() # création de la figure 2
# fonction graphiques opérant sur la figure 2
plt.show() # affichage de la figure 2

Avec l’IDE Pyzo, l’exécution du script par F5 n’initialise pas la mémoire de l’interpréteur et ne ferme pas les fenêtres graphiques déjà ouvertes. Ce comportement est plutôt agaçant et nous préférons donc utiliser la fonction Run file a script pour exécuter le script.

Représentation graphique d’un nuage de points

La fonction pyplot.plot permet de tracer des points dans un plan muni de deux axes. Pour l’utiliser, il faut tout d’abord placer les coordonnées de ces points dans deux tableaux numpy.ndarray (Tableaux à une dimension). Il est aussi possible d’utiliser des listes, mais les calculs numériques et les lectures de fichiers conduisent en général à des tableaux.

La fonction prend au minimum deux arguments, selon la syntaxe suivante :

plt.plot(X,Y)

où X est un tableau à une dimension (ou une liste) contenant les abscisses des points et Y un tableau à une dimension (ou une liste) contenant les ordonnées de ces points. Ces deux tableaux doivent avoir la même longueur (N). Il est cependant possible d’omettre le tableau des abscisses, auquel cas il est remplacé par un tableau contenant les nombres entiers de 0 à N-1, qui correspondent aux indices du tableau Y.

Ces deux tableaux peuvent provenir d’un calcul numérique ou bien de données expérimentales. Considérons ce dernier cas et supposons que les données soient sous forme tabulaire dans un fichier texte. L’expérience est un dosage potentiométrique d’une solution de sulfate de fer par une solution de sulfate de cérium. Les données ont été saisies dans un fichier CSV dont voici les premières lignes :

v (mL)      U (mV)
0   318
0.5 343
1   357
1.5 366

La première colonne contient le volume versé, la seconde contient la tension mesurée. Le fichier est nommé titrageFeSO4-Ce4.csv.

La lecture du fichier se fait comme expliqué dans Enregistrement dans un fichier :

v,U = np.loadtxt('titrageFeSO4-Ce4.csv',skiprows=1,unpack=True)

La structure des deux tableaux est obtenue avec l’attribut shape :

>>> v.shape,U.shape
((54,), (54,))

Il s’agit donc de deux tableaux de longueur 54. Il est souvent nécessaire de faire des calculs sur les données avant de tracer les points. Dans le cas présent, on veut calculer le potentiel d’oxydoréduction et le convertir en volts :

E = (U+244)*1e-3

Voici comment obtenir la représentation graphique du potentiel en fonction du volume, sous forme de points :

plt.figure()
plt.plot(v,E,'ro')
plt.xlabel('v (mL)',fontsize=18)
plt.ylabel('E (V)',fontsize=18)
plt.grid()
plt.savefig('dosage-potentiometrique.png')
plt.show()

Le troisième argument fourni à la fonction plot correspond au paramètre optionnel fmt, qui précise le format des points sous la forme d’une chaîne de caractères. Le caractère “r” signifie que les points sont coloriés en rouge, le caractère “o” que les marqueurs sont des ronds. Les différents marqueurs et couleurs sont listés dans la documentation de plot.

Les fonctions pyplot.xlabel et pyplot.ylabel permettent de légender les axes. La fonction pyplot.grid permet d’ajouter une grille. La figure peut être enregistrée sous différents formats d’image (PNG, JPG, PDF). Il est possible de le faire à la main depuis la fenêtre graphique, ou bien directement dans le script au moyen de la fonction pyplot.savefig.

Voici la figure obtenue :

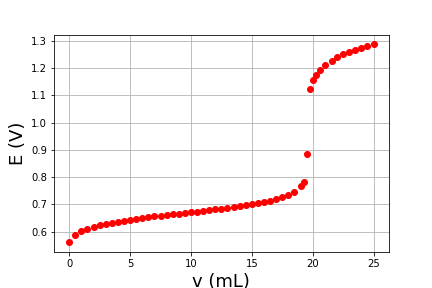
La fonction plot calcule les intervalles d’abscisses et d’ordonnées qui permettent de représenter tous les points demandés, mais il est fréquent qu’on souhaite ajuster soi-même ces intervalles. Cela se fait au moyen des fonctions pyplot.xlim et pyplot.ylim.

Voici par exemple comment refaire le graphique précédent avec une échelle de potentiel s’étendant de 0 à 2 V. On ajoute aussi un titre au moyen de la fonction pyplot.title.

plt.figure()
plt.plot(v,E,"ro")
plt.ylim(0,2)
plt.xlabel('v (mL)',fontsize=18)
plt.ylabel('E (V)',fontsize=18)
plt.title('Dosage de FeSO4 par CeSO4')
plt.grid()
plt.show()

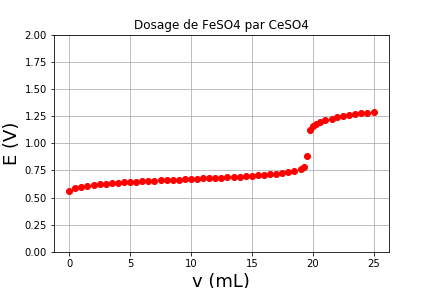
Représentation graphique d’une fonction

La représentation graphique d’une fonction (d’une variable réelle et à valeurs réelles) s’obtient aussi avec la fonction plot. Il faut pour cela échantillonner la fonction sur l’intervalle choisi et tracer les points correspondants.

Prenons comme exemple le tracé de la courbe de gain et de déphasage d’un système linéaire dont la fonction de transfert en régime harmonique est définie par :

\[\underline{H}(f)=\frac{1}{1+j\frac{f}{f_c}}\]

Il s’agit d’un filtre passe-bas du premier ordre dont la fréquence de coupure est \(f_c\). Un tracé général est obtenu au moyen de la variable sans dimensions \(x=f/f_c\). On commence par échantillonner l’intervalle de x choisi puis on génère un tableau contenant les valeurs correspondantes de \(\underline{H}\) :

x = np.linspace(0,10,100)
H = 1/(1+1j*x)

Le tableau H contient des nombres complexes (type numpy.complex128). Voici comment calculer le module pour obtenir le gain :

G = np.absolute(H)

Le tracé de la courbe représentant le gain en fonction de x se fait comme celui d’un nuage de points, avec la fonction plot, mais il ne faut pas marquer les points et les relier par des segments rectilignes :

plt.figure()
plt.plot(x,G,'b-') # points reliés par des segments rectilignes de couleur bleue
plt.grid()
plt.xlabel('f/fc',fontsize=18)
plt.ylabel('G',fontsize=18)
plt.savefig('gain-filtre.png')
plt.show()

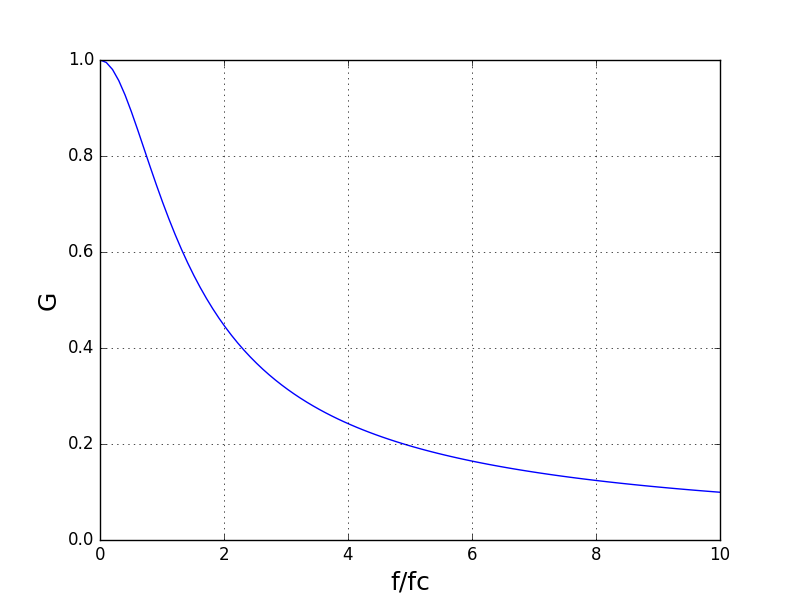
Les autres types de traits sont listés dans la documentation de plot. Le fait de relier les points de l’échantillonnage par des segments rectilignes revient à faire une interpolation linéaire entre ces points.

La ligne obtenue est une bonne représentation de la fonction si le nombre de points de l’échantillonnage est assez grand. Celui-ci doit être adapté aux variations de la fonction sur l’intervalle considéré et il est parfois nécessaire de faire quelques essais avant de trouver le nombre d’échantillons suffisants. Voici ce qu’on obtient avec seulement 10 échantillons :

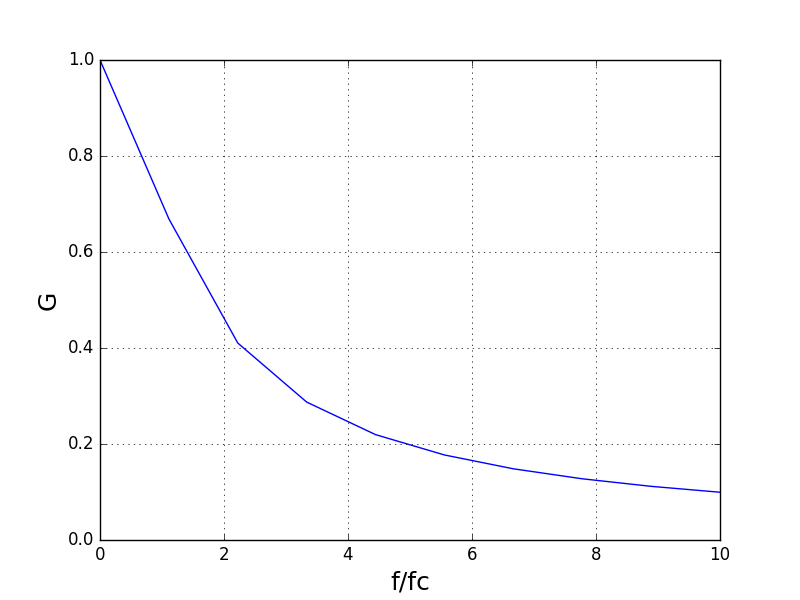
Si l’on souhaite faire varier x sur plusieurs décades et faire un tracé en échelle logarithmique, l’échantillonnage peut être fait avec la fonction numpy.logspace, qui répartit les points uniformément sur une échelle logarithmique :

x = np.logspace(-2,2,100)
H=1/(1+1j*x)
GdB = 20*np.log10(np.absolute(H))
plt.figure()
plt.plot(x,GdB,"b-")
plt.xlabel('f/fc',fontsize=18)
plt.ylabel('G dB',fontsize=18)
plt.grid()
plt.xscale('log')
plt.ylim(-40,10)
plt.savefig('gaindB-filtre.png')
plt.show()

La fonction pyplot.xscale permet d’obtenir une échelle d’abscisse logarithmique.

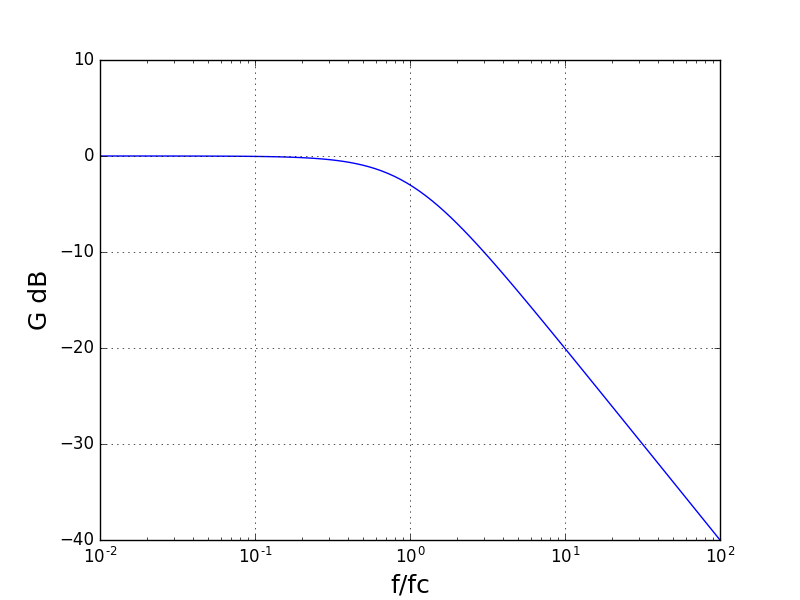
Tracé de plusieurs courbes

Il est fréquent qu’on ait besoin de tracer plusieurs courbes sur la même figure afin de les comparer. Considérons par exemple la fonction de transfert suivante :

\[\underline{H}(f)=\frac{1}{1+j\frac{1}{Q}\frac{f}{f_c}-\left(\frac{f}{f_c}\right)^2}\]

Nous souhaitons tracer la représentation graphique du gain pour différentes valeurs de Q. Lorsqu’une expression doit être évaluée plusieurs fois, il est judicieux de définir une fonction (Définition d’une fonction) :

def gain_db(x,Q):
    H =  1/(1+1j*x/Q-x**2)
    return 20*np.log10(np.absolute(H))

Pour tracer plusieurs courbes, il suffit d’appeler la fonction plot autant de fois que nécessaire. Le paramètre optionnel label permet de donner un nom à chaque courbe et les noms sont affichés grace à la fonction pyplot.legend.

x = np.logspace(-1,1,500)
plt.figure()
Q = 0.5
GdB = gain_db(x,Q)
plt.plot(x,GdB,"k-",label='Q=%0.1f'%Q)
Q = 1
GdB = gain_db(x,Q)
plt.plot(x,GdB,"r-",label='Q=%0.1f'%Q)
Q = 10
GdB = gain_db(x,Q)
plt.plot(x,GdB,"b-",label='Q=%0.1f'%Q)
plt.xlabel('f/fc',fontsize=18)
plt.ylabel('G dB',fontsize=18)
plt.grid()
plt.xscale('log')
plt.ylim(-40,20)
plt.legend(loc='upper right')
plt.savefig('gaindB-filtre2.png')
plt.show()

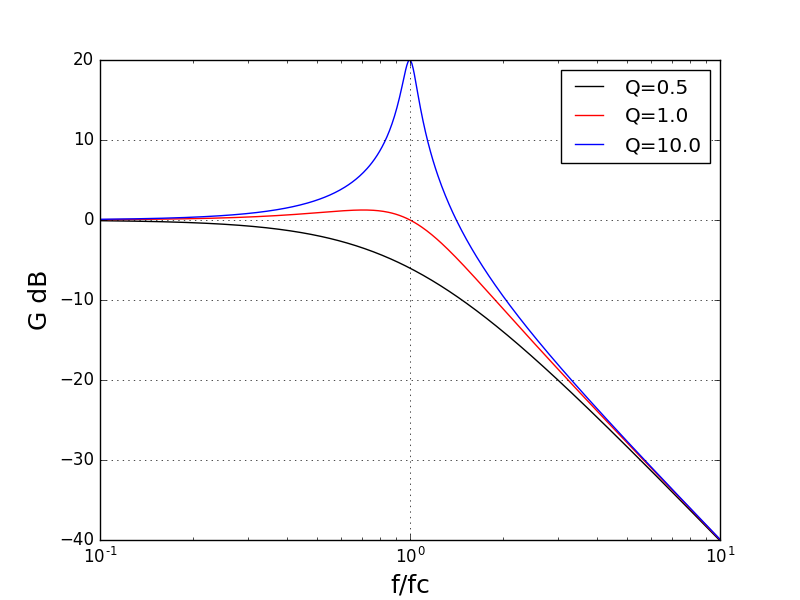
Courbe plane paramétrée

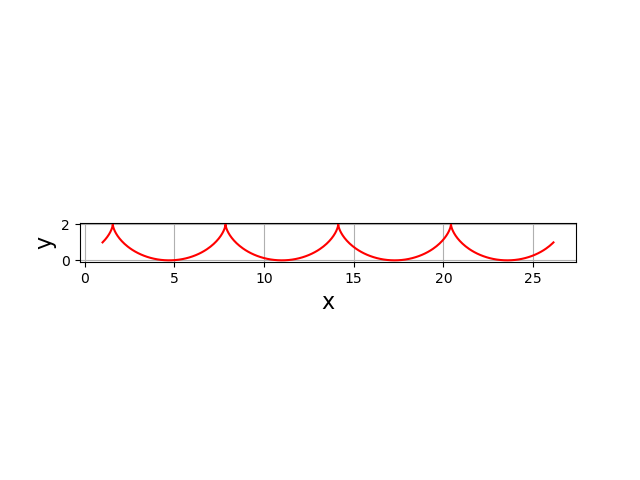
Considérons le mouvement d’un point situé sur un cercle de rayon \(R\) qui roule sur un plan en tournant à la vitesse angulaire \(\omega\) et dont le centre se déplace à la vitesse \(V\). On cherche à tracer la trajectoire de ce point. Si le roulement se fait sans glissement (\(V=R\omega\)), il s’agit d’une cycloïde.

\[\begin{split}&x=Vt+R\cos(\omega t)\\ &y=R(1+\sin(\omega t))\end{split}\]

Après avoir échantillonné le paramètre sur l’intervalle choisi, on calcule deux tableaux contenant respectivement x et y :

R = 1
omega = 2*np.pi
V = R*omega
t = np.linspace(0,4,500)
x = V*t+R*np.cos(omega*t)
y = R*(1+np.sin(omega*t))

Le tracé de la courbe paramétrée se fait avec la fonction plot. Afin d’obtenir une représentation correcte de la forme de la courbe, il faut que l’échelle soit identique sur les deux axes.

Pour obtenir cela, il faut créer la figure avec la fonction subplots, ce qui permet de récupérer un objet de la classe matplotlib.axes.Axes, qui contient les informations de configuration de la figure. La fonction set_aspect de cet objet permet de choisir le rapport d’échelle entre les deux axes.

fig,ax = plt.subplots()
plt.plot(x,y,"r-")
ax.set_aspect('equal')
plt.xlabel('x',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.grid()
plt.savefig('trajectoire.png')
plt.show()