Tableaux

Listes

Les représentations graphiques et les calculs numériques nécessitent de disposer de tableaux de nombres, le plus souvent des nombres à virgule flottante. Un tableau de nombres peut être construit au moyen d’une liste (type List).

Considérons par exemple l’échantillonnage de la fonction sinus sur l’intervalle \([0,2\pi]\). L’échantillonnage d’une fonction est une opération courante en calcul numérique. Elle est notamment nécessaire pour obtenir une représentation graphique de la fonction.

Pour faire un échantillonnage à N points, il faut générer deux listes contenant les valeurs suivantes, pour \(i=0,1,\ldots N-1\) :

\[\begin{split}&x_i = \frac{2\pi}{N-1}i\\ &y_i = sin(x_i)\end{split}\]

La figure suivante montre ces échantillons pour \(N=30\) :

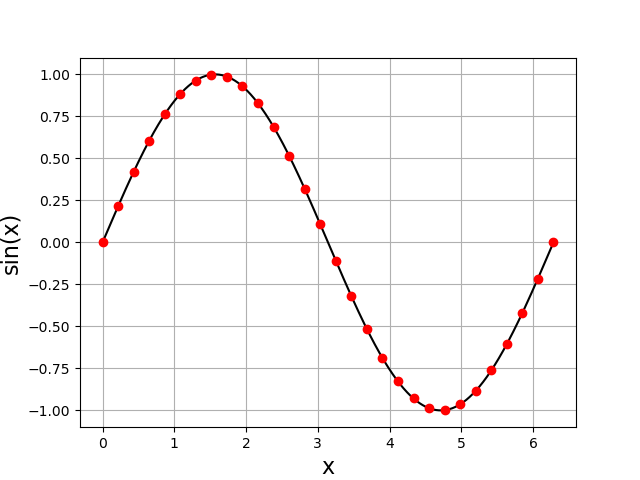
On commence par créer deux listes contenant N nombres nuls puis on remplit les deux listes au moyen d’une boucle :

import math
N=30
X = [0]*N
Y = [0]*N
delta_x = 2*math.pi/(N-1)
for i in range(N):
    X[i] = delta_x * i
    Y[i] = math.sin(x[i])

Il est aussi possible de créer des listes vides et d’ajouter les éléments dans la boucle au fur et à mesure:

X = []
Y = []
delta_x = 2*math.pi/(N-1)
for i in range(N):
    xx = delta_x * i
    X.append(xx)
    Y.append(math.sin(x))

Tableaux à une dimension

Le module numpy (module racine de la bibliothèque NumPy), apporte une structure de données permettant de stocker des nombres sous forme de tableaux. Ces tableaux sont des objets de type numpy.ndarray. Un tableau ndarray, appelé aussi tableau NumPy, peut avoir un nombre quelconque de dimensions (ndarray signifie N-dimensional array).

Un tableau à une dimension ressemble beaucoup à une liste mais il ne peut contenir qu’un seul type de nombres, c’est-à-dire que les éléments d’un tableau sont des objets d’un type bien déterminé.

Il y a différentes manières de créer un tableau. On peut créer un tableau dont les éléments sont tous nuls, en précisant sa longueur et le type de ses éléments :

>>> import numpy as np
>>> A = np.zeros(10,np.float32)
>>> A
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)

La précision du type n’est pas nécessaire et dans ce cas le type est float64.

Il est aussi possible de créer un tableau à partir d’une liste :

>>> A = np.array([1.0,2.0,3.0])
>>> type(A[0])
<class 'numpy.float64'>

Si les éléments de la liste sont des entiers (type int) alors un tableau d’entiers est créé :

>>> A = np.array([1,2,3])
>>> type(A[0])
<class 'numpy.int32'>

La fonction numpy.arange, qui s’utilise comme la fonction range, permet de créer un tableau contenant des nombres entiers en progression arithmétique :

>>> A = np.arange(10)
>>> A
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

>>> A = np.arange(1,10,2)
>>> A
array([1, 3, 5, 7, 9])

La fonction linspace, probablement la plus utile pour le calcul numérique, permet de créer un tableau contenant un échantillonnage régulier d’un intervalle :

>>> X = np.linspace(0,2*np.pi,20)
>>> X
array([0.        , 0.33069396, 0.66138793, 0.99208189, 1.32277585,
       1.65346982, 1.98416378, 2.31485774, 2.64555171, 2.97624567,
       3.30693964, 3.6376336 , 3.96832756, 4.29902153, 4.62971549,
       4.96040945, 5.29110342, 5.62179738, 5.95249134, 6.28318531])

La longueur d’un tableau peut être obtenue avec la fonction len (qui fonctionne aussi avec une liste) :

>>> len(X)
20

Il est aussi possible d’utilise l’attribut size de l’objet :

>>> X.size
20

L’attribut shape fournit la structure du tableau :

>>> X.shape
(20,)

Pour un tableau à une dimension, il sagit d’un n-uplet à un élément.

L’accès à un élément d’un tableau à une dimension se fait au moyen d’un indice, qui est un nombre entier compris entre 0 et N-1, où N est la longueur du tableau. Voici par exemple comment accéder au troisième élément d’un tableau :

>>> X[2]
0.6613879270715354

Les tableaux ndarray sont des objets mutables (tout comme les listes), c’est-à-dire que leurs éléments sont modifiables :

>>> A=np.arange(10)
>>> A[1] = 0
>>> A
array([0, 0, 2, 3, 4, 5, 6, 7, 8, 9])

Mais, contrairement aux listes, il n’est pas possible de modifier le type d’un élément, car le type est défini au moment de la création du tableau :

>>> A[1] = 2.5
>>> A[1]
2

Alors que les listes contiennent en réalité des références à d’autres objets, les tableaux ndarray sont des zones de la mémoire qui contiennent effectivement les nombres contenus dans le tableau. Par exemple, un tableau contenant 10 nombres de type float64 est en fait une zone de mémoire de 640 octets (5120 bits). Lorsqu’on modifie l’élément d’un tableau, on change le contenu de la zone mémoire correspondante, sans créer de nouvel objet. Pour cette raison, les tableaux sont beaucoup plus efficaces que les listes lors des calculs numériques intensifs.

L’accès à une partie d’un tableau peut se faire en utilisant des tranches, identiques aux tranches utilisées pour les listes. Par exemple pour obtenir les éléments d’indices 0 à 3 :

>>> X[0:4]
array([0.        , 0.33069396, 0.66138793, 0.99208189])

et pour obtenir tous les éléments d’indice pair :

>>> x[0::2]
array([0.        , 0.66138793, 1.32277585, 1.98416378, 2.64555171,
       3.30693964, 3.96832756, 4.62971549, 5.29110342, 5.95249134])

Opérations sur les tableaux

Le principal avantage des tableaux ndarray sur les listes est la possibilité d’effectuer des opérations mathématiques.

La multiplication d’un tableau par un nombre a pour effet de multiplier tous les éléments du tableau par ce nombre :

>>> N=20
>>> A=np.arange(N)
>>> x=A*2*np.pi/N
>>> x
array([0.        , 0.31415927, 0.62831853, 0.9424778 , 1.25663706,
       1.57079633, 1.88495559, 2.19911486, 2.51327412, 2.82743339,
       3.14159265, 3.45575192, 3.76991118, 4.08407045, 4.39822972,
       4.71238898, 5.02654825, 5.34070751, 5.65486678, 5.96902604])

>>> A = np.arange(10)
>>> 2*A
array([ 0,  2,  4,  6,  8, 10, 12, 14, 16, 18])

Il est possible d’appliquer l’opérateur d’addition (+) à deux tableaux, à condition qu’ils aient la même longueur :

>>> A=np.arange(10)
>>> B=np.ones(10)*2
>>> A+B
array([  2.,   3.,   4.,   5.,   6.,   7.,   8.,   9.,  10.,  11.])

L’addition est effectuée élément par élément. De même pour la multiplication :

>>> A*B
array([  0.,   2.,   4.,   6.,   8.,  10.,  12.,  14.,  16.,  18.])

Fonctions universelles

Les fonctions universelles de NumPy (type numpy.ufunc) sont des fonctions qui permettent d’appliquer la même fonction à tous les éléments d’un tableau. Lorsqu’on leur fournit en argument un tableau, elles renvoient un tableau. Elles sont qualifiées d’universelles car elles s’appliquent aussi bien aux types élémentaires de nombres qu’aux tableaux.

Les fonctions mathématiques les plus courantes existent dans le module numpy sous la forme de fonctions universelles.

Nous pouvons par exemple utiliser la fonction universelle numpy.sin pour effectuer l’échantillonnage de la fonction sinus présenté plus haut :

>>> N = 30
>>> X = np.linspace(0,2*np.pi,N)
>>> Y = np.sin(X)

Le tableau Y est obtenu en appliquant la fonction sinus à chaque élément du tableau X, ce qui correspond précisément à l’opération d’échantillonnage. Alors que l’utilisation des listes nécessitait l’écriture d’une boucle sur l’indice, l’utilisation d’une fonction universelle dispense d’écrire cette boucle. Bien sûr, la boucle est bien exécutée en arrière plan mais de manière beaucoup plus efficace car elle est accomplie par un code écrit en langage C et déjà transformé par un compilateur en code exécutable (les tableaux eux-mêmes sont des structures de données du langage C). L’utilisation de fonctions universelles est donc un bon moyen de faire des calculs numériques sur de très grands tableaux de manière rapide.

Le code suivant permet de comparer les temps d’exécution d’un échantillonnage réalisé avec une boucle à celui du même échantillonnage réalisé avec une fonction universelle :

import numpy as np
import time

N=1000000
t1 = time.clock()
X = [0]*N
Y = [0]*N
for i in range(N):
    X[i] = i*np.pi*2/(N-1)
    Y[i] = np.sin(X[i])
print((time.clock()-t1)/N)
t1 = time.clock()
X = np.linspace(0,2*np.pi,N)
Y = np.sin(X)
print((time.clock()-t1)/N)

Ce programme affiche les durées par élément. On obtient :

1.37528589e-06
5.541590999999997e-08

ce qui montre que la seconde méthode est environ 25 fois plus rapide que la première. Lorsqu’on fait des calculs numériques dans lesquels les mêmes opérations sont appliquées à des tableaux de grande taille, à de multiples reprises, cet avantage des tableaux numpy et des fonctions universelles est très important.

Une fonction que l’on définit soi-même peut être automatiquement convertie en fonction universelle. Supposons que l’on souhaite échantillonner une fonction comportant une somme de fonctions cosinus :

def serie(x,A):
    S = 0.0
    for k in range(len(A))
        S += A[k]*np.cos(k*x)
    return S

On pourra écrire :

X = np.linspace(0,2*np.pi,N)
A = [2,1,0.2]
Y = serie(X,A)

Cette fonction peut être convertie en fonction universelle car elle agit sur le tableau qui est donné en argument seulement via des fonctions universelles.

Si l’on doit effectuer des tests sur les éléments d’un tableau, la conversion en fonction universelle ne peut se faire automatiquement. Supposons que l’on souhaite écrire une fonction qui rend nul tous les éléments négatifs d’un tableau :

def positif(u):
    if u > 0 :
        return u
    else:
        return 0

On obtient l’erreur suivante :

>>> X=np.linspace(0,10*np.pi,1000)
>>> Y=np.sin(X)
>>> positif(Y)
Traceback (most recent call last):
  File "<pyshell#11>", line 1, in <module>
    positif(Y)
  File "D:/Personnel/web/pynum/source/outils/tableaux-3.py", line 7, in positif
    if u >0 :
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

En effet, un opérateur de comparaison n’est pas une fonction universelle et l’interpréteur déclenche une erreur car comparer un tableau à un nombre n’a pas de sens. Il faut alors convertir explicitement la fonction de la manière suivante :

 positif_ufunc = np.frompyfunc(positif,1,1)
 positif(Y) # fonctionne

Tableaux à deux dimensions

Un tableau à deux dimensions comporte des lignes et des colonnes. La structure d’un tel tableau est donnée par un n-uplet de la forme (nl,nc) où nl est le nombre de lignes et nc est le nombre de colonnes.

Les tableaux à deux dimensions sont utiles pour stocker dans un même objet des données qui ont une relation entre elles, par exemple un tableau de données expérimentales. Il sont aussi utilisés pour représenter les images (en niveaux de gris).

Voici comment créer un tableau à 2 lignes et 3 colonnes contenant les nombres (flottants) 0 :

>>> A = np.zeros((2,3))

>>> A
array([[0., 0., 0.],
       [0., 0., 0.]])

Ce tableau peut être vu comme une liste de listes. Il est donc possible d’accéder à la ligne d’indice i par la syntaxe :

>>> i = 0 # indice de ligne
>>> A[i]

On pourra donc accéder à l’élément dont l’indice de ligne est i et l’indice de colonne j par :

>>> i=0 # indice de ligne
>>> j=0 # indice de colonne
>>> A[i][j] = 1.0

Une autre syntaxe permet d’accéder à cet élément :

>>> A[i,j]
1.0

Un tableau à deux dimensions peut être créé à partir de tableaux à une dimension. Supposons que l’on souhaite créer un tableau contenant en première ligne l’échantillonnage d’une variable réelle sur un intervalle, en deuxième ligne l’échantillonnage d’une fonction de cette variable et en troisième ligne l’échantillonnage d’une autre fonction.

X = np.linspace(0,2*np.pi,100)
Y1 = np.sin(X)
Y2 = np.cos(X)
A = np.array([X,Y1,Y2])

>>> A.shape
(3, 100)

Comme prévu, le tableau A comporte 3 lignes et 100 colonnes. On préfère parfois disposer chacun des tableaux à une dimension en colonne, ce qui correspond à la représentation utilisée dans un tableur. Il suffit pour cela d’utiliser l’opérateur de transposition :

>>> B = A.T
>>> B.shape
(100,3)

ce qui donne un tableau de 100 lignes et 3 colonnes. Pour obtenir la colonne d’indice j de ce tableau, on utilise la syntaxe suivante :

>>> j = 1 # indice de colonne
>>> colonne = B[:,j]
>>> colonne.shape
(100,)

La notation : donne une tranche dont les indices de départ et d’arrivée ont la valeur par défaut, ce qui sélectionne tous les indices de ligne. Si l’on veut obtenir seulement les 10 premières lignes de la même colonne :

>>> colonne = B[:10,j]
>>> colonne.shape
(10,)

Enregistrement dans un fichier

La fonction numpy.savetxt permet d’enregistrer le contenu d’un tableau sous forme de fichier texte. Par exemple, le tableau précédent (comportant 3 colonnes) peut être enregistré par :

>>> np.savetxt("tableau.txt",B,header="x sin cos")

Voici les 4 premières lignes du fichier obtenu

# x sin cos
0.000000000000000000e+00 0.000000000000000000e+00 1.000000000000000000e+00
6.346651825433925753e-02 6.342391965656450636e-02 9.979866764718844374e-01
1.269330365086785151e-01 1.265924535737492640e-01 9.919548128307953405e-01

La première ligne, introduite par le paramètre optionel header, donne une information sur la signification des colonnes. À chaque ligne du tableau correspond une ligne dans le fichier. Par défaut, les nombres sont séparés par des espaces. On parle aussi de fichier CSV (comma separated values) même si le séparateur n’est pas une virgule. On peut d’ailleurs donner l’extension .csv au fichier, ce qui permet aux logiciels tableurs de le reconnaître automatiquement comme un fichier contenant un tableau.

La fonction numpy.loadtxt permet de lire un fichier texte contenant des données tabulaires. Elle crée un tableau ndarray contenant ces données.

Par exemple, le tableau enregistré dans le fichier créé ci-dessus pourra être récupéré par :

>>> B = np.loadtxt("tableau.txt",skiprows=1)

Le paramètre skiprows indique le nombre de lignes à sauter avant de lire le tableau (ici une ligne contenant la légende des colonnes). Le tableau obtenu est identique au tableau d’origine.

Il peut être intéressant de récupérer directement les colonnes du fichier sous la formes de tableaux à une dimension :

>>> X,Y1,Y2 = np.loadtxt("tableau.txt",skiprows=1,unpack=True)

Bien sûr, cette fonction peut être utilisée pour lire les fichiers CSV produits par un autre logiciel, par exemple un logiciel d’acquisition de données.