Cinétique chimique

Deux actes élémentaires successifs

Capacité numérique (PCSI) : Etablir un système d’équations différentielles et le résoudre numériquement afin de visualiser l’évolution temporelle des concentrations et de leurs dérivées dans le cas d’un mécanisme à deux actes élémentaires successifs. Mettre en évidence l’étape cinétiquement déterminante ou l’approximation de l’état quasi stationnaire d’un intermédiaire réactionnel.

Capacité numérique (BCPST1) : Tracer, dans le cas de deux actes élémentaires successifs, l’évolution des concentrations par résolution numérique du système d’équations différentielles et mettre en évidence les conditions d’application de l’approximation de l’état quasistationnaire

On considère deux actes élémentaires successifs :

\[{\rm A}\xrightarrow[]{k_1}{\rm B}\xrightarrow[]{k_2}{\rm C}\]

Si les concentrations de \(A,B,C\) sont notées \(a(t),b(t),c(t)\), elles obéissent au système d’équations différentielles suivant :

\[\begin{split}&\frac{da(t)}{dt}=-k_1a(t)\\ &\frac{db(t)}{dt}=k_1a(t)-k_2b(t)\\ &\frac{dc(t)}{dt}=k_2b(t)\end{split}\]

Les trois concentrations sont placées dans un tableau :

\[Y(t) = (a(t),b(t),c(t))\]

ce qui permet d’écrire la fonction Python qui définit le système :

1
2
def derive(Y,t,k1,k2):
    return np.array([-k1*Y[0],k1*Y[0]-k2*Y[1],k2*Y[1]])

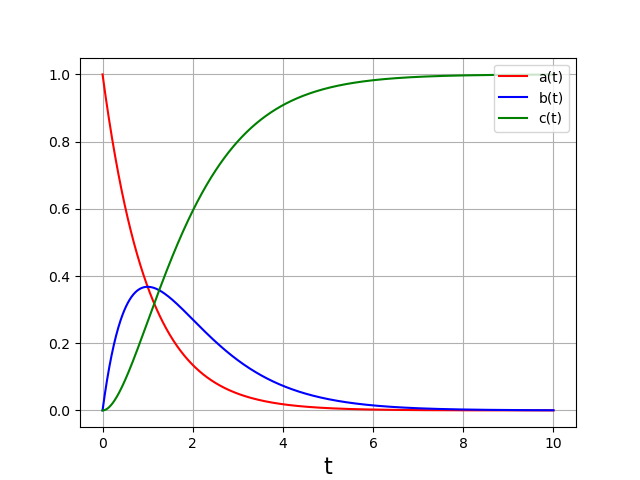
Voici la résolution numérique avec la fonction scipy.integrate.odeint, dans le cas où les deux étapes ont la même vitesse :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
k1=1
k2=1
t0=0
T=10
N=1000
t = np.linspace(0,T,N)
y0 = [1,0,0]
Y = odeint(derive,y0,t,args=(k1,k2))
plt.figure()
plt.plot(t,Y[:,0],"r-",label='a(t)')
plt.plot(t,Y[:,1],"b-",label='b(t)')
plt.plot(t,Y[:,2],"g-",label='c(t)')
plt.xlabel('t',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.show()
../_images/DeuxActesSuccessifs-fig1.png

Voici les courbes dans le cas où la seconde étape est beaucoup plus rapide que la première :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
k1=1
k2=100
t0=0
T=10
N=1000
t = np.linspace(0,T,N)
y0 = [1,0,0]
Y = odeint(derive,y0,t,args=(k1,k2))
plt.figure()
plt.plot(t,Y[:,0],"r-",label='a(t)')
plt.plot(t,Y[:,1],"b-",label='b(t)')
plt.plot(t,Y[:,2],"g-",label='c(t)')
plt.xlabel('t',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.show()
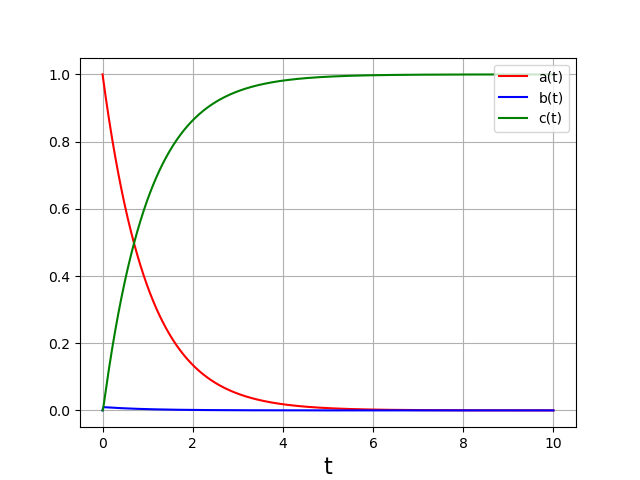
../_images/DeuxActesSuccessifs-fig2.png

La concentration de l’intermédiaire réactionnel (\(B\)) est très faible. Pendant la phase d’évolution (\(t<6\)), la dérivée de sa concentration est très faible par rapport aux dérivées de \(a(t)\). Pour confirmer cette propriété, il est judicieux de tracer les dérivées :

1
2
3
4
5
6
7
plt.figure()
plt.plot(t,-k1*Y[:,0],"r-",label=r'$\frac{a(t)}{dt}$')
plt.plot(t,k1*Y[:,0]-k2*Y[:,1],"b-",label=r'$\frac{b(t)}{dt}$')
plt.plot(t,k2*Y[:,1],"g-",label=r'$\frac{c(t)}{dt}$')
plt.xlabel('t',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
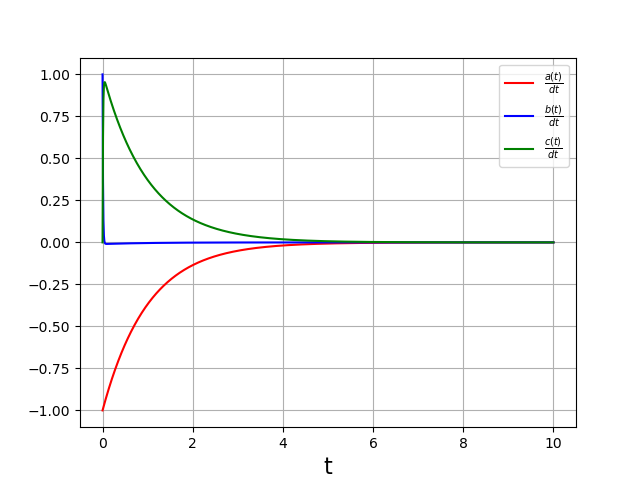
../_images/DeuxActesSuccessifs-fig3.png

et voici un détail du début de l’évolution :

1
plt.xlim(0,0.5)
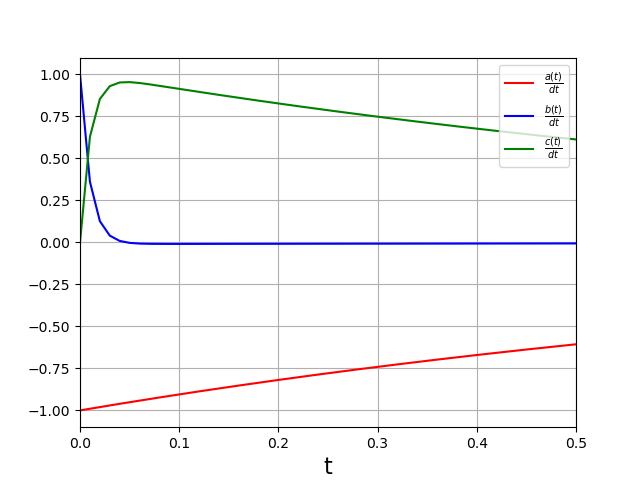
../_images/DeuxActesSuccessifs-fig4.png

Ces courbes confirment que pendant la phase d’évolution des concentrations et à l’exception du début (\(t<0{,}05\)), il est possible de négliger la dérivée \(\frac{db}{dt}\) devant les deux autres dérivées. Autrement dit, on peut poser cette dérivée égale à zéro dans les équations (approximation de l’état quasi stationnaire).

Deux actes élémentaires opposés

Capacité numérique : Modélisation d’une transformation par deux actes élémentaires opposés. Tracer l’évolution des concentrations par résolution numérique de l’équation différentielle.

On considère les deux actes élémentaires suivants :

\[\begin{split}&{\rm A}\xrightarrow[]{k_1}{\rm B}\\ &{\rm A}\xleftarrow[k_2]{}{\rm B}\end{split}\]

Si les concentrations de \(A,B\) sont notées \(a(t),b(t)\), elles obéissent au système d’équations différentielles suivant :

\[\begin{split}&\frac{da(t)}{dt}=k_2b(t)-k_1a(t)\\ &\frac{db(t)}{dt}=k_1a(t)-k_2b(t)\end{split}\]

Les deux concentrations sont placées dans un tableau :

\[Y(t) = (a(t),b(t))\]

ce qui permet d’écrire la fonction Python qui définit le système :

1
2
def derive(Y,t,k1,k2):
    return [k2*Y[1]-k1*Y[0],k1*Y[0]-k2*Y[1]]

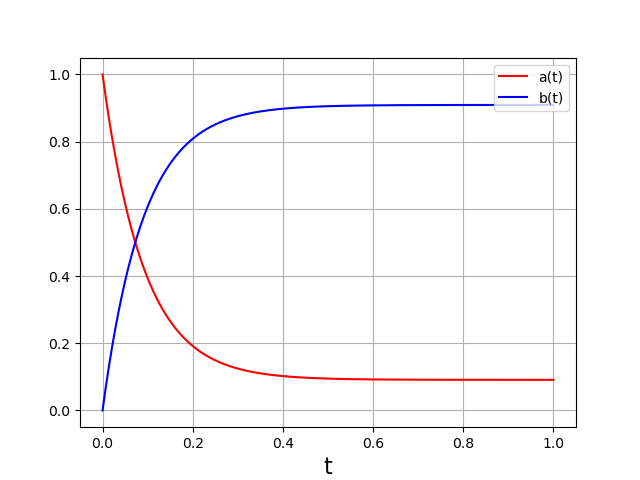
Voici un exemple, avec une réaction inverse 10 fois plus lente que la réaction directe :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
k1=10
k2=1
t0=0
T=1
N=1000
t = np.linspace(0,T,N)
y0 = [1,0]
Y = odeint(derive,y0,t,args=(k1,k2))
plt.figure()
plt.plot(t,Y[:,0],"r-",label='a(t)')
plt.plot(t,Y[:,1],"b-",label='b(t)')
plt.xlabel('t',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.show()
../_images/DeuxActesOpposes-fig1.png

Contrôle cinétique ou thermodynamique

Capacité numérique : Etablir un système d’équations différentielles et le résoudre numériquement afin de visualiser l’évolution temporelle des concentrations pour mettre en évidence les situations de contrôle cinétique ou thermodynamique.

On considère les quatre réactions élémentaires suivantes :

\[\begin{split}&{\rm A}\xrightarrow[]{k_1}{\rm B}\\ &{\rm A}\xleftarrow[k_{-1}]{}{\rm B}\\ &{\rm A}\xrightarrow[]{k_2}{\rm C}\\ &{\rm A}\xleftarrow[k_{-2}]{}{\rm C}\end{split}\]

Si les concentrations de \(A,B,C\) sont notées \(a(t),b(t),c(t)\), elles obéissent au système d’équations différentielles suivant :

\[\begin{split}&\frac{da(t)}{dt} = -(k_1+k_2)a(t)+k_{-1}b(t)+k_{-2}c(t)\\ &\frac{db(t)}{dt} = k_1a(t)-k_{-1}b(t)\\ &\frac{dc(t)}{dt} = k_2a(t)-k_{-2}c(t)\end{split}\]

Les trois concentrations sont placées dans un tableau :

\[Y(t) = (a(t),b(t),c(t))\]

ce qui permet d’écrire la fonction Python qui définit le système :

1
2
def derive(Y,t,k1,km1,k2,km2):
    return np.array([-k1*Y[0]+km1*Y[1]-k2*Y[0]+km2*Y[2],k1*Y[0]-km1*Y[1],k2*Y[0]-km2*Y[2]])

On étudie le cas où la formation de A a la même constante d’équilibre que la formation de B (100) mais la première est 10 fois plus rapide :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
k1=1
km1=0.01
k2=0.1
km2=1e-3
T=10
N=1000
t = np.linspace(0,T,N)
y0 = [1,0,0]
Y = odeint(derive,y0,t,args=(k1,km1,k2,km2))
plt.figure()
plt.plot(t,Y[:,0],"r-",label='a(t)')
plt.plot(t,Y[:,1],"b-",label='b(t)')
plt.plot(t,Y[:,2],"g-",label='c(t)')
plt.xlabel('t',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.show()
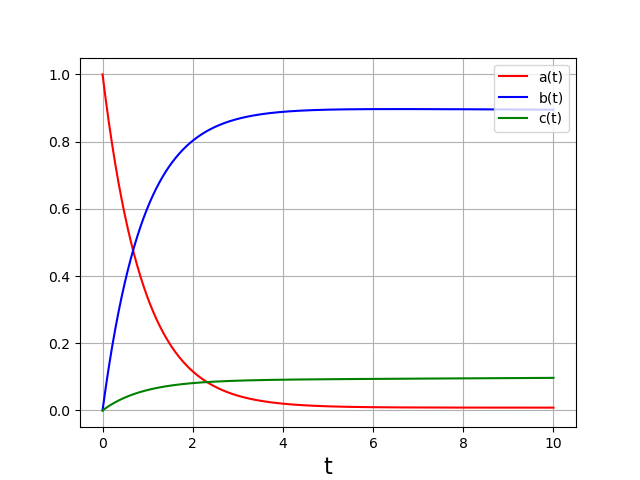
../_images/ControleCinetiqueThermo-fig1.png

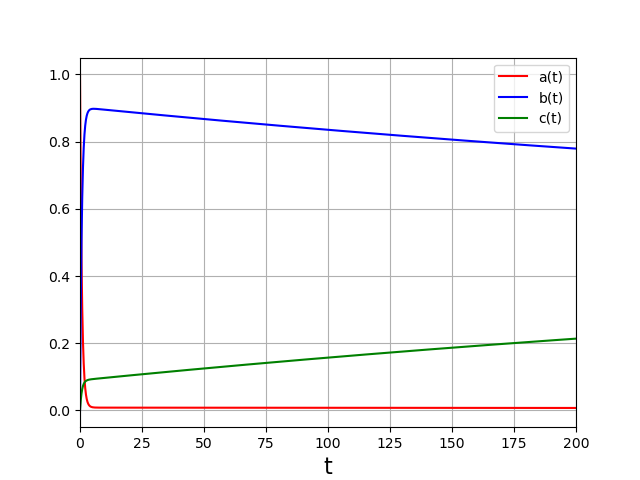
Cette simulation est faite sur une durée relativement courte, qui correspond à une situation de contrôle cinétique. Les concentrations de B et C semblent atteindre un plateau, mais la concentration de B est beaucoup plus grande car sa vitesse de formation est plus grande. Voici un calcul fait sur une durée 10 fois plus grande :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
T=100
N=1000
t = np.linspace(0,T,N)
y0 = [1,0,0]
Y = odeint(derive,y0,t,args=(k1,km1,k2,km2))
plt.figure()
plt.plot(t,Y[:,0],"r-",label='a(t)')
plt.plot(t,Y[:,1],"b-",label='b(t)')
plt.plot(t,Y[:,2],"g-",label='c(t)')
plt.xlabel('t',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.show()
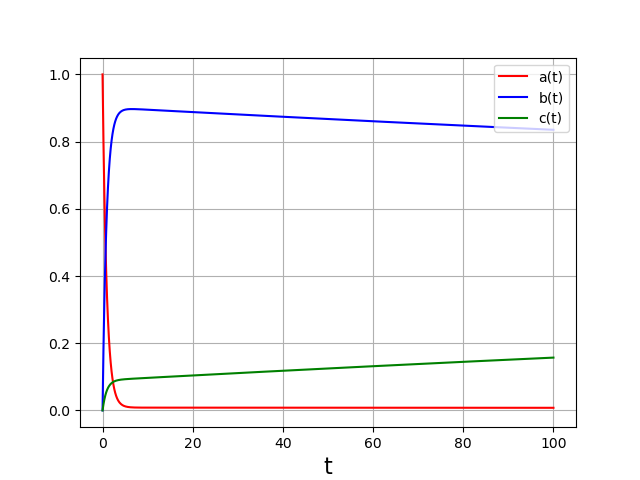
../_images/ControleCinetiqueThermo-fig2.png

La concentration de C, qui semblait avoir atteint un plateau à courte échelle de temps, commence à augmenter alors que celle de B diminue. Voyons sur une durée plus longue :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
T=3000
N=1000
t = np.linspace(0,T,N)
y0 = [1,0,0]
Y = odeint(derive,y0,t,args=(k1,km1,k2,km2))
plt.figure()
plt.plot(t,Y[:,0],"r-",label='a(t)')
plt.plot(t,Y[:,1],"b-",label='b(t)')
plt.plot(t,Y[:,2],"g-",label='c(t)')
plt.xlabel('t',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.show()
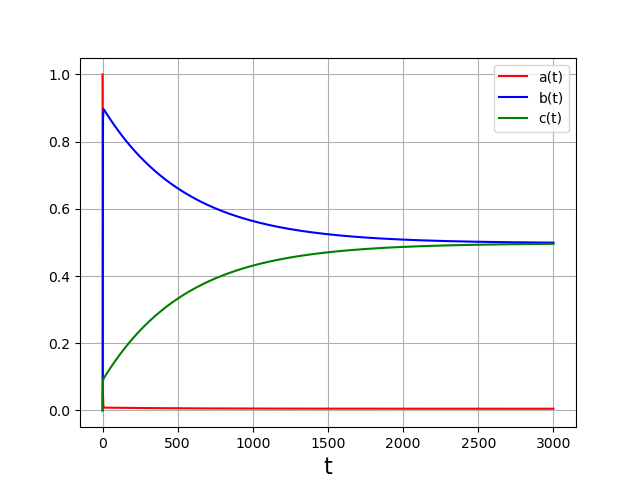
../_images/ControleCinetiqueThermo-fig3.png

Sur cette durée, le système est sous contrôle thermodynamique. Les concentrations atteignent leur valeur d’équilibre. Ici \(b=c\) puisque les deux réactions ont la même constante d’équilibre.

Pour ce système d’équations différentielles, les variations des grandeurs se font sur deux échelles de temps très différente, la première correspondant au contrôle cinétique, la seconde correspondant au contrôle thermodynamique. Si la seconde réaction est 100 fois plus lente que la première, l’écart entre ces deux échelles de temps est encore plus important.

Un système différentiel de ce type est qualifié de système raide. Son intégration numérique par la méthode d’Euler (ou par les méthodes similaires) peut poser problème. En effet, il faut que le pas de temps soit assez petit pour donner un résultat satisfaisant lorsque les concentrations varient rapidement (au début) mais ce pas de temps conduit à un calcul beaucoup trop long lorsque les concentrations varient lentement.

La fonction introduite dans Système d’équations différentielles du premier ordre permet de résoudre ce système avec la méthode d’Euler :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
def euler(derive,t0,y0,T,N,args=()):
    '''
    Paramètres :
        derive : fonction F(Y,t)
        t0 : instant initial
        y0 : valeurs initiales
        T : durée
        N : nombre de points
        args : arguments supplémentaire pour derive
    Objets renvoyés :
        t : tableau des instants
        Y : tableau des valeurs de y (N lignes et P colonnes)
    '''
    P = len(y0)
    t = np.linspace(t0,t0+T,N)
    h = t[1]-t[0]
    Y = np.zeros((N,P))
    Y[0] = y0
    for n in range(0,N-1):
        Y[n+1] = Y[n] + h*derive(Y[n],t[n],*args)
    return (t,Y)

Voici ce qu’il arrive si le pas de temps n’est pas assez petit :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
t0=0
T=3000
N=2000
y0 = [1,0,0]
(t,Y) = euler(derive,t0,y0,T,N,(k1,km1,k2,km2))
plt.figure()
plt.plot(t,Y[:,0],"r-",label='a(t)')
plt.plot(t,Y[:,1],"b-",label='b(t)')
plt.plot(t,Y[:,2],"g-",label='c(t)')
plt.xlabel('t',fontsize=16)
plt.xlim(0,200) # tracé du début
plt.grid()
plt.legend(loc='upper right')
plt.show()
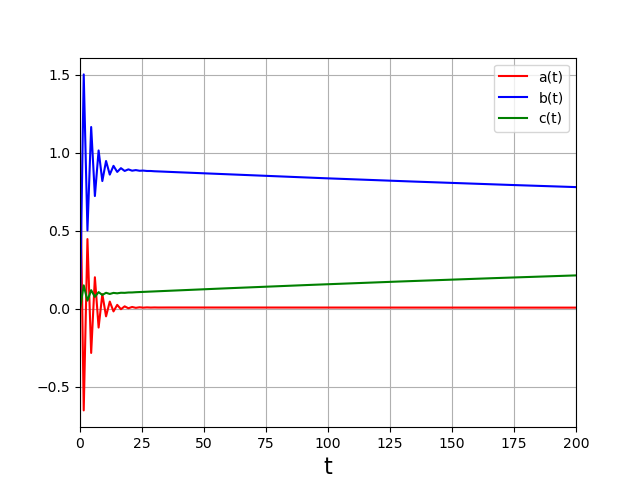
../_images/ControleCinetiqueThermo-fig4.png

Bien que l’évolution à long terme soit correcte, les variations à court terme sont fausses. Ce système peut cependant être traité par la méthode d’Euler. Il suffit pour cela de réduire le pas de temps :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
t0=0
T=3000
N=10000
y0 = [1,0,0]
(t,Y) = euler(derive,t0,y0,T,N,(k1,km1,k2,km2))
plt.figure()
plt.plot(t,Y[:,0],"r-",label='a(t)')
plt.plot(t,Y[:,1],"b-",label='b(t)')
plt.plot(t,Y[:,2],"g-",label='c(t)')
plt.xlabel('t',fontsize=16)
plt.grid()
plt.xlim(0,200) # tracé du début
plt.legend(loc='upper right')
plt.show()
../_images/ControleCinetiqueThermo-fig5.png