Equilibre chimique

Avancement d’une réaction à l’équilibre

Capacité numérique : Déterminer l’état final d’un système, siège d’une transformation, modélisée par une ou deux réactions à partir des conditions initiales et valeurs des constantes d’équilibre.

Considérons la réaction en phase gazeuse suivante (production de dihydrogène à partir du méthane) :

\[\rm CH_4(g)+H_2O(g)=CO(g)+3H_2(g)\]

On suppose que la réaction est réalisée à une température \(T\) et à une pression \(P\) fixées. La constante d’équilibre à cette température est \(K^{\circ}(T)\).

Initialement, on met en présence 1 mole de méthane pour n moles d’eau. Le quotient de réaction s’écrit :

\[Q_r(x) = \frac{27x^4}{(1-x)(n-x)(n+1+2x)^2}P^2\]

où \(x\) désigne l’avancement de la réaction. La pression est exprimée en bars. L’équation algébrique à résoudre pour déterminer l’avancement à l’équilibre est \(Q_r(x)=K^{\circ}\), qui peut s’écrire sous la forme d’une équation polynomiale.

Il peut être intéressant de considérer l’enthalpie libre de la réaction :

\[\begin{split}\Delta_rG(x)&=\Delta_rG^{\circ}(T)+RT\ln Q_r(x)\\ &=\Delta_rH^{\circ}-T\Delta_rS^{\circ}+RT\ln(27x^4P^2)-RT\ln((1-x)(n-x)(n+1+2x)^2)\end{split}\]

L’équation algébrique est alors \(\Delta_rG^{\circ}(x)=0\). L’avancement maximal est déterminé par le réactif en défaut donc la solution est à rechercher dans l’intervalle \([0,\min(1,n)]\).

Les constantes sont définies dans des variables globales. Une fonction permet de calculer \(\Delta_rG\) :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import bisect

R = 8.31 # J/K/mol
DrH0 = 206 # kJ/mol
DrS0 = 216 # J/K/mol

def DrG(x,n,T,P):
    return DrH0*1e3-T*DrS0+R*T*(np.log(27*x**4*P**2)-np.log((1-x)*(n-x)*(n+1+2*x)**2))

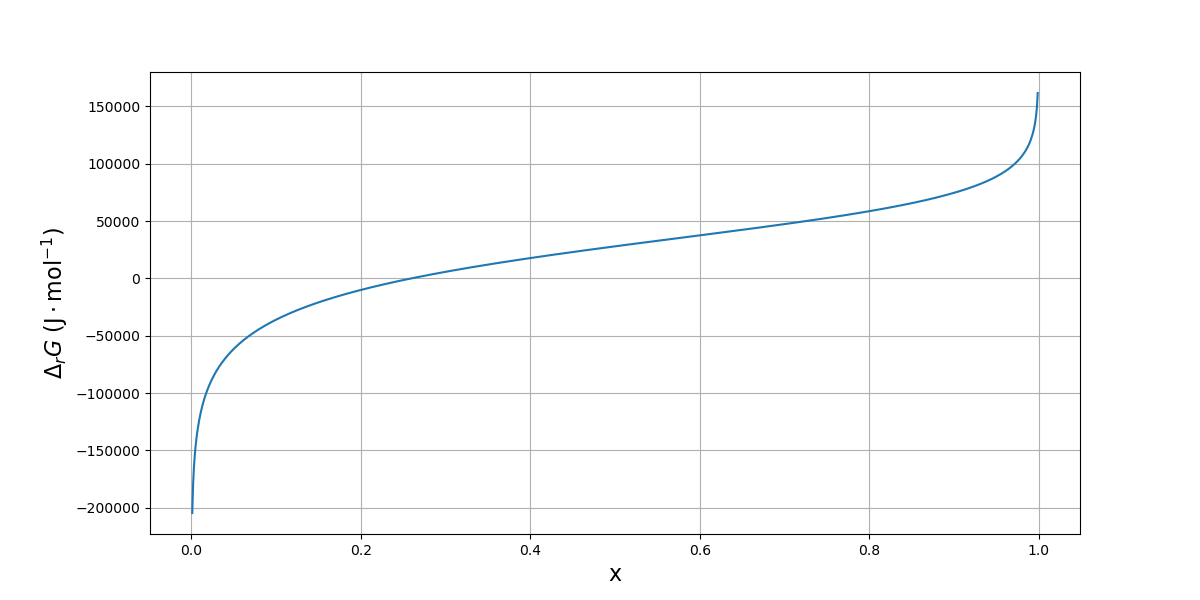
Voici une représentation graphique de \(\Delta_rG\) en fonction de l’avancement, pour \(T,P,n\) donnés :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
T = 1100
P = 30
n = 1
xmax = min(1,n)
x = np.linspace(1e-3,xmax-1e-3,1000)
G = DrG(x,n,T,P)
plt.figure(figsize=(12,6))
plt.plot(x,G)
plt.grid()
plt.xlabel('x',fontsize=16)
plt.ylabel(r'$\Delta_rG\ (\rm J\cdot mol^{-1})$',rotation=90,fontsize=16)
plt.show()
../_images/AvancementReaction-fig1.png

L’avancement à l’équilibre peut être déterminé graphiquement avec une précision suffisante mais, pour automatiser la détermination de la racine, nous allons utiliser la méthode de dichotomie, au moyen de la fonction scipy.optimize.bisect :

1
2
3
4
x = bisect(DrG,0,xmax,args=(n,T,P))
print(x)

0.259595589226592

Voici un tracé de l’avancement en fonction de la température, pour deux valeurs différentes de \(n\) :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
N=100
T = np.linspace(300,1500,N)
P = 30
n1 = 1
n2 = 5
X1 = np.zeros(N)
X2 = np.zeros(N)
for i in range(N):
    X1[i] = bisect(DrG,0,min(1,n1),args=(n1,T[i],P))
    X2[i] = bisect(DrG,0,min(1,n2),args=(n2,T[i],P))
plt.figure(figsize=(12,6))
plt.plot(T,X1,label='n=1')
plt.plot(T,X2,label='n=5')
plt.xlabel('T (K)',fontsize=16)
plt.ylabel('x',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.show()
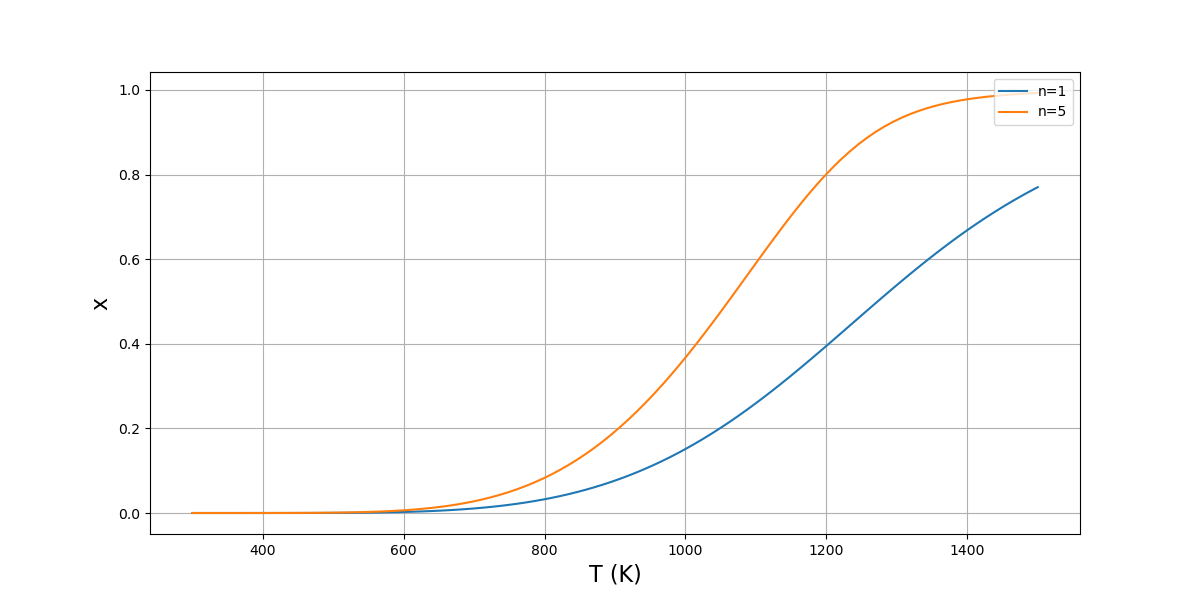
../_images/AvancementReaction-fig2.png

Diagramme de distribution d’un diacide

Capacité numérique : Tracer le diagramme de distribution des espèces d’un ou plusieurs couple(s) acide-base, et déterminer la valeur du point isoélectrique d’un acide aminé.

Soit un diacide, noté \(\rm AH_2\). Le couple \(\rm AH_2/AH^-\) a un pK égal à \({\rm p}K_1\). Le couple \(\rm AH^-/A^{2-}\) a un pK égal à \({\rm p}K_2\).

Le diagramme de distribution représente les concentrations de \(\rm AH_2,AH^-,A^{2-}\) en fonction du pH, pour une concentration apportée d’acide donnée \(C_a\). On a les trois équations suivantes :

\[\begin{split}&{\rm \frac{[AH^-][H_2O^+]}{[AH_2]}}=K_1\\ &{\rm \frac{[A^{2-}][H_3O^+]}{[AH^-]}}=K_2\\ &C_a=\rm [AH_2]+[AH^-]+[A^{2-}]\\\end{split}\]

Posons \(h=[{\rm H_3O^+}]\). Après avoir exprimé les concentrations \(\rm[A^{2-}]\) et \(\rm[AH^-]\) en fonction de \(\rm[AH_2]\), on obtient :

\[\begin{split}&{\rm [AH_2]}=\frac{C_a}{1+\frac{K_1}{h}+\frac{K_1K_2}{h^2}}\\ &{\rm [AH^-]} = \frac{K_1}{h}{\rm [AH_2]}\\ &{\rm [A^{2-}]} = \frac{K_2}{h}{\rm [AH^-]}\end{split}\]

Ces trois relations permettent de calculer les trois concentrations en fonction du pH.

Les constantes sont définies dans des variables globales :

1
2
3
4
5
6
7
8
import numpy as np
import matplotlib.pyplot as plt

Ca = 0.01
pK1 = 6.35
pK2 = 10.33
K1 = 10**(-pK1)
K2 = 10**(-pK2)

On peut définir une fonction pour chaque concentration :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
def AH2(pH):
    h = 10**(-pH)
    return Ca/(1+K1*K2/h**2+K1/h)

def AH(pH):
    h = 10**(-pH)
    return K1/h*AH2(pH)

def A(pH):
    h = 10**(-pH)
    return K2/h*AH(pH)

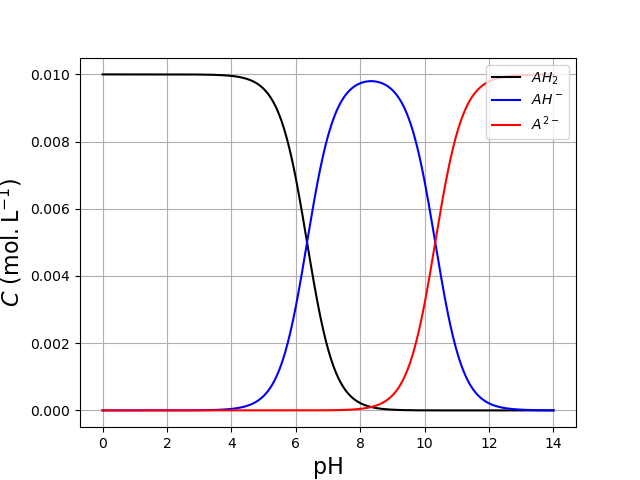
et voici le tracé du diagramme de distribution :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
plt.figure()
pH = np.linspace(0,14,500)
plt.plot(pH,AH2(pH),'k',label='$AH_2$')
plt.plot(pH,AH(pH),'b',label='$AH^-$')
plt.plot(pH,A(pH),'r',label='$A^{2-}$')
plt.grid()
plt.xlabel('pH',fontsize=16)
plt.ylabel(r'$C\ (\rm mol.L^{-1})$',rotation=90,fontsize=16)
plt.legend(loc='upper right')
plt.show()
../_images/DistributionDiacide-fig1.png

Précipitation sélective d’hydoxydes métalliques

Capacité numérique : Déterminer les conditions optimales pour séparer deux ions par précipitation sélective.

On considère la précipitation d’un ion métallique sous la forme d’un hydroxyde :

\[\rm M^{n+}+n\,OH^-\rightarrow M(OH)_n\]

Soit \(K_s\) le produit de solubilité de l’hydroxyde et \(pK_s=-\log(K_s)\). La concentration maximale de l’ion est \(C_0\). Le pH d’apparition du précipité est :

\[pH_0=pK_e+\frac{1}{n}(pC_0-pK_s)\]

et pour \(pH>pH_0\), la concentration en ion est donnée par :

\[pC = pK_s+n(pH-pK_e)\]

On définit une fonction qui calcule pC pour un pH donné :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
import numpy as np
import matplotlib.pyplot as plt

pKe = 14

def pC_MOHn(n,pKs,pC0,pH):
    if pH < pKe+(pC0-pKs)/n:
        return pC0
    else:
        return pKs+n*(pH-pKe)

Afin de tracer les concentrations en fonction du pH, on la convertit en fonction universelle :

1
pC_MOHn = np.frompyfunc(pC_MOHn,4,1)

Considérons le cas du cobalt (\(\rm Co^{2+}\)) et du magnésium (\(\rm Mg^{2+}\)).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
pC0 = 2
pK1 = 14.2 #Co(OH)2
pK2 = 10.8 #Mg(OH)2

pH = np.linspace(0,14,1000)
pC1 = pC_MOHn(2,pK1,pC0,pH)
pC2 = pC_MOHn(2,pK2,pC0,pH)

plt.figure(figsize=(10,6))
plt.plot(pH,pC1,label='$Co^{2+}$')
plt.plot(pH,pC2,label='$Mg^{2+}$')
plt.grid()
plt.xticks(np.arange(15))
plt.xlabel('pH',fontsize=16)
plt.ylabel('pC',fontsize=16)
plt.legend(loc='upper left')
plt.show()
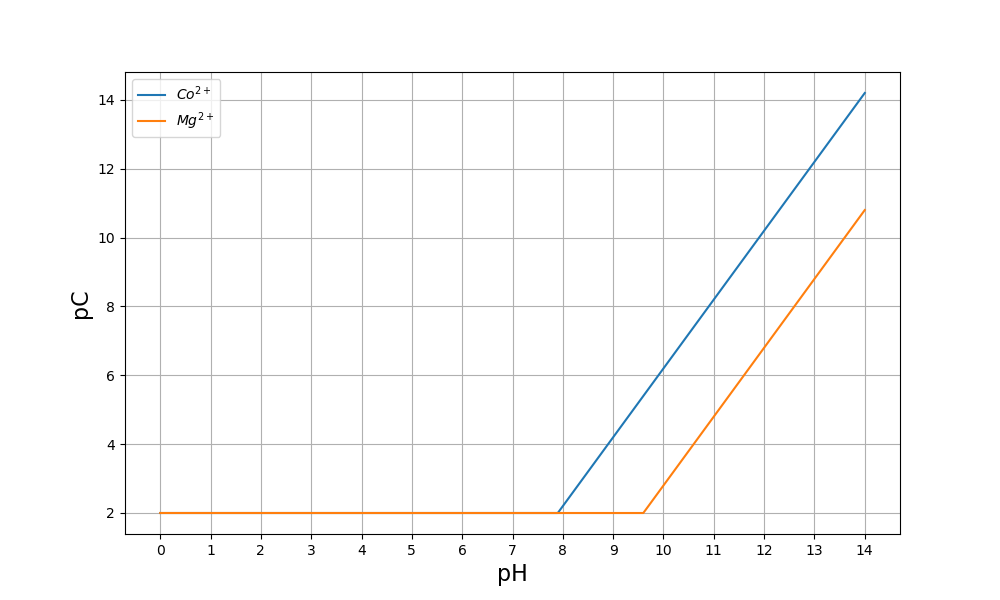
../_images/PrecipitationHydroxyde-fig1.png

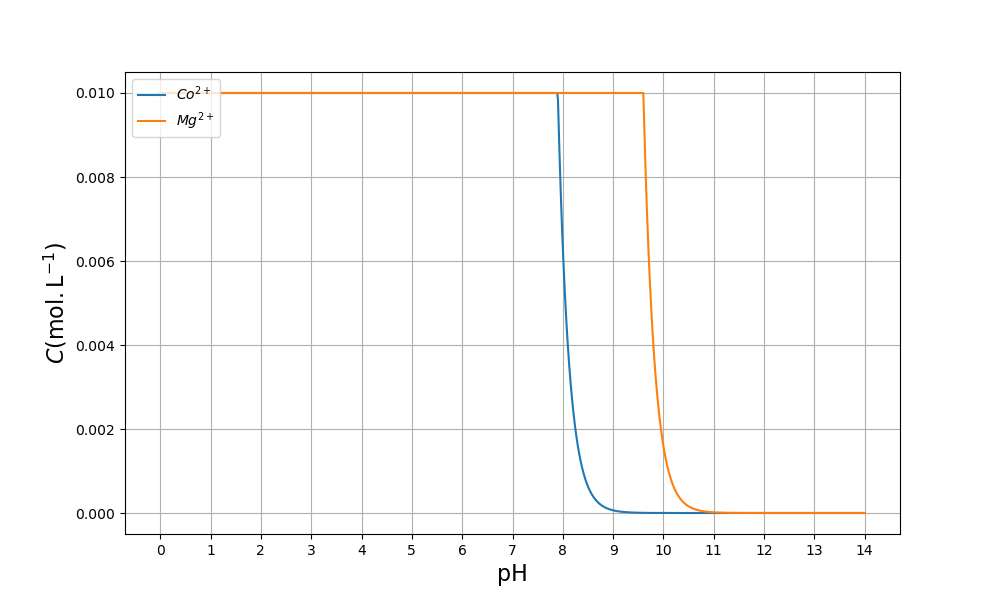
L’analyse de cette figure permet de déterminer la plage de pH qui permet de précipiter plus de 99 % du cobalt (\(pC>4\)) sans précipier le magnésium : \(8{,}9<pH<9{,}6\).

On peut aussi tracer les concentrations en échelle linéaire :

1
2
3
4
5
6
7
8
9
plt.figure(figsize=(10,6))
plt.plot(pH,10**(-pC1),label='$Co^{2+}$')
plt.plot(pH,10**(-pC2),label='$Mg^{2+}$')
plt.grid()
plt.xticks(np.arange(15))
plt.xlabel('pH',fontsize=16)
plt.ylabel(r'$C (\rm mol.L^{-1})$',fontsize=16,rotation=90)
plt.legend(loc='upper left')
plt.show()
../_images/PrecipitationHydroxyde-fig2.png