Mécanique

Oscillateurs linéaires et non linéaires

Capacité numérique : Résoudre numériquement une équation différentielle du deuxième ordre non linéaire et faire apparaître l’effet des termes non linéaires.

On considère l’oscillateur défini par l’équation différentielle suivante :

\[\frac{d^2y(t)}{dt^2}+a\omega_0\frac{dy(t)}{dt}+\omega_0^2(y(t)+by(t)^3)=0\]

où \(\omega_0\) est la pulsation propre de l’oscillateur, \(a\) une constante sans dimensions qui détermine l’intensité de la dissipation et \(b\) une constante sans dimensions qui introduit un terme non linéaire.

On se propose de faire une résolution numérique de cette équation au moyen de la fonction scipy.integrate.odeint. Il faut tout d’abord mettre cette équation sous la forme d’un système différentiel du premier ordre. On pose \(y_0(t)=y(t)\) et \(y_1(t)=y'(t)\), ce qui donne le système :

\[\begin{split}&\frac{dy_0(t)}{dt}=y_1(t)\\ &\frac{dy_1(t)}{dt}=-a\omega_0y_1(t)-\omega_0^2(y_0(t)+by_0(t)^3)\end{split}\]

Voici la fonction Python qui définit ce système :

1
2
3
4
def derive(y,t,w0,a,b):
    dy0 = y[1]
    dy1 = -w0*a*y[1]-w0**2*(y[0]+b*y[0]**3)
    return [dy0,dy1]

Comme premier exemple, considérons le cas d’un oscillateur sans dissipation (\(a=0\)) et voyons l’effet du terme non linéaire :

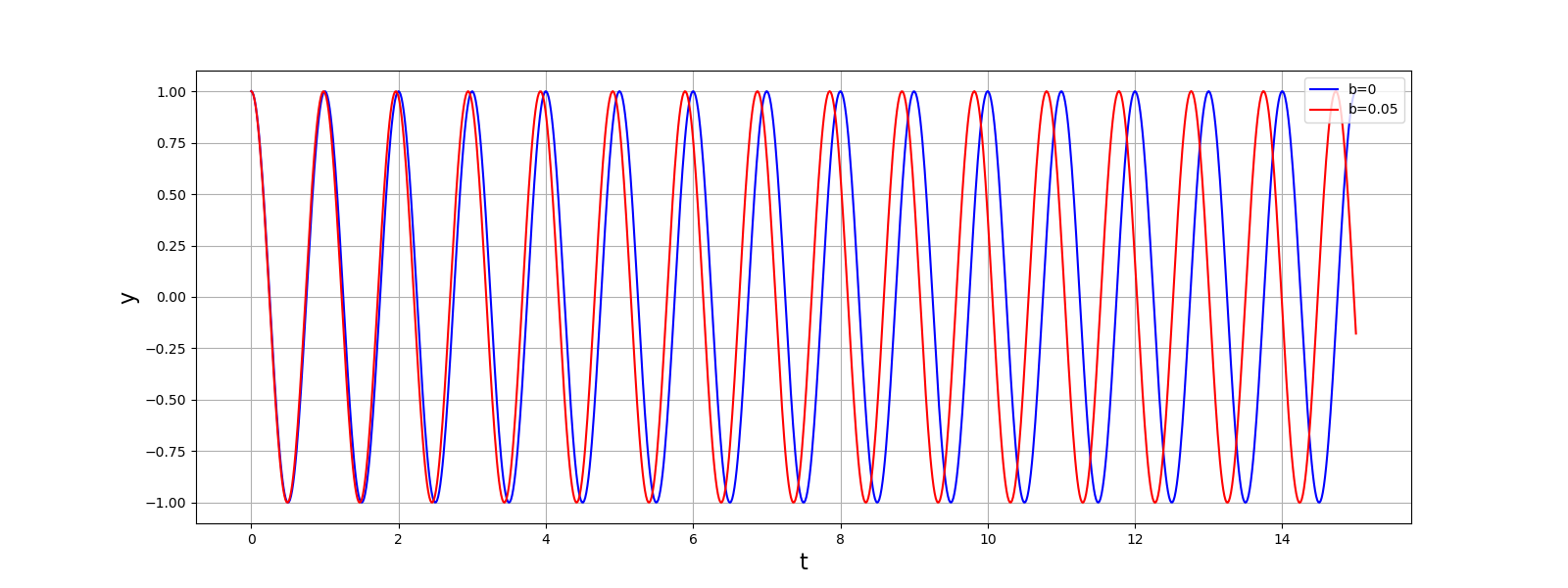
../_images/OscillateurNonLineaire-fig1.png

La présence du terme non linéaire (\(b>0\)) a pour effet de réduire la période d’oscillations. Voici la même comparaison mais avec un amortissement très intense :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
Yi = [1,0]
T = 15
t = np.linspace(0,T,1000)
w0 = 2*np.pi
a = 0.1
b = 0
Y1 = odeint(derive,Yi,t,rtol=1e-4,atol=1e-12,args=(w0,a,b))
b = 0.05
Y2 = odeint(derive,Yi,t,rtol=1e-4,atol=1e-12,args=(w0,a,b))
plt.figure(figsize=(16,6))
plt.plot(t,Y1[:,0],"b-",label='b=0')
plt.plot(t,Y2[:,0],"r-",label='b=0.05')
plt.xlabel('t',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.show()
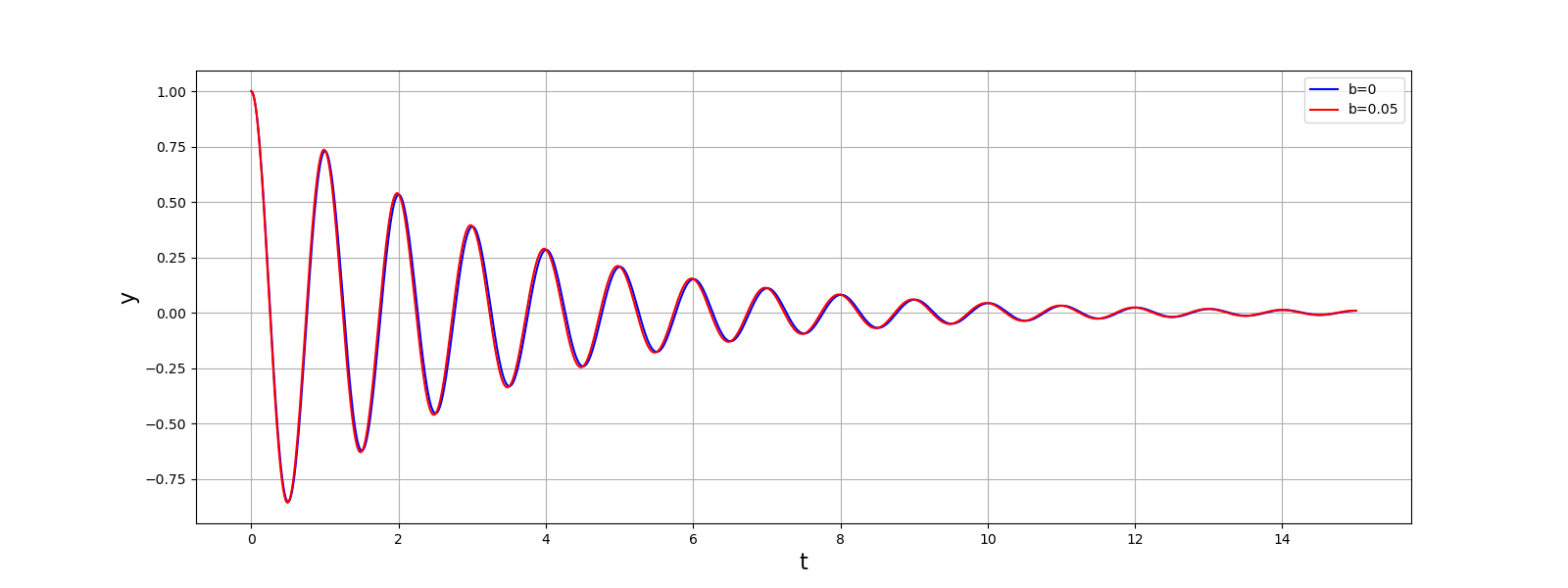
../_images/OscillateurNonLineaire-fig2.png

On constate que l’effet du terme non linéaire est beaucoup plus faible en présence d’amortissement.

L’effet du terme non linéaire est d’autant plus important que l’amplitude des oscillations est grande, comme on le voit sur l’exemple ci-dessous avec \(b<0\) :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
Yi = [2,0]
T = 15
t = np.linspace(0,T,1000)
w0 = 2*np.pi
a = 0
b = 0
Y1 = odeint(derive,Yi,t,rtol=1e-4,atol=1e-12,args=(w0,a,b))
b = 0.05
Y2 = odeint(derive,Yi,t,rtol=1e-4,atol=1e-12,args=(w0,a,b))
plt.figure(figsize=(16,6))
plt.plot(t,Y1[:,0],"b-",label='b=0')
plt.plot(t,Y2[:,0],"r-",label='b=0.05')
plt.xlabel('t',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.grid()
plt.legend(loc='upper right')
plt.show()
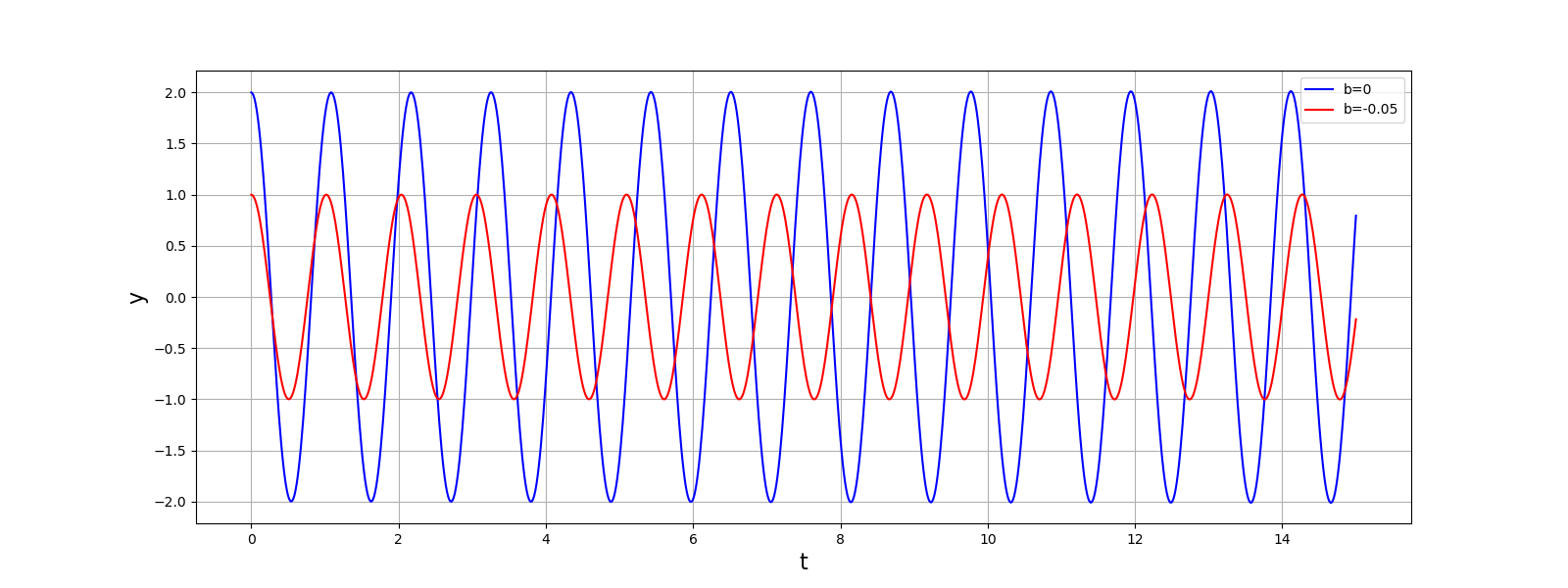
../_images/OscillateurNonLineaire-fig3.png

Cet exemple met en évidence le non-isochronisme des oscillations pour un oscillateur non linéaire.

Pendule pesant

Capacité numérique : mettre en évidence le non isochronisme des oscillations.

On considère l’équation différentielle du pendule pesant (conservatif) :

\[\frac{d^2y(t)}{dt^2}+\omega_0^2\sin(y(t))=0\]

et le système différentiel du premier ordre équivalent :

\[\begin{split}&\frac{dy_0(t)}{dt}=y_1(t)\\ &\frac{dy_1(t)}{dt}=-\omega_0^2\sin(y_0(t))\end{split}\]

La résolution numérique de ce système se fait comme précédemment. Voici la fonction Python qui définit ce système :

1
2
3
4
def derive(y,t,w0):
    dy0 = y[1]
    dy1 = -w0**2*np.sin(y[0])
    return [dy0,dy1]

Voici une comparaison des oscillations obtenues avec deux valeurs initiales de \(y_0\) différentes :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
T = 15
t = np.linspace(0,T,1000)
w0 = 2*np.pi
Yi = [1,0]
Y1 = odeint(derive,Yi,t,rtol=1e-4,atol=1e-12,args=(w0,))
Yi = [2,0]
Y2 = odeint(derive,Yi,t,rtol=1e-4,atol=1e-12,args=(w0,))
plt.figure(figsize=(16,6))
plt.plot(t,Y1[:,0],"b-")
plt.plot(t,Y2[:,0],"r-")
plt.xlabel('t',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.grid()
plt.show()
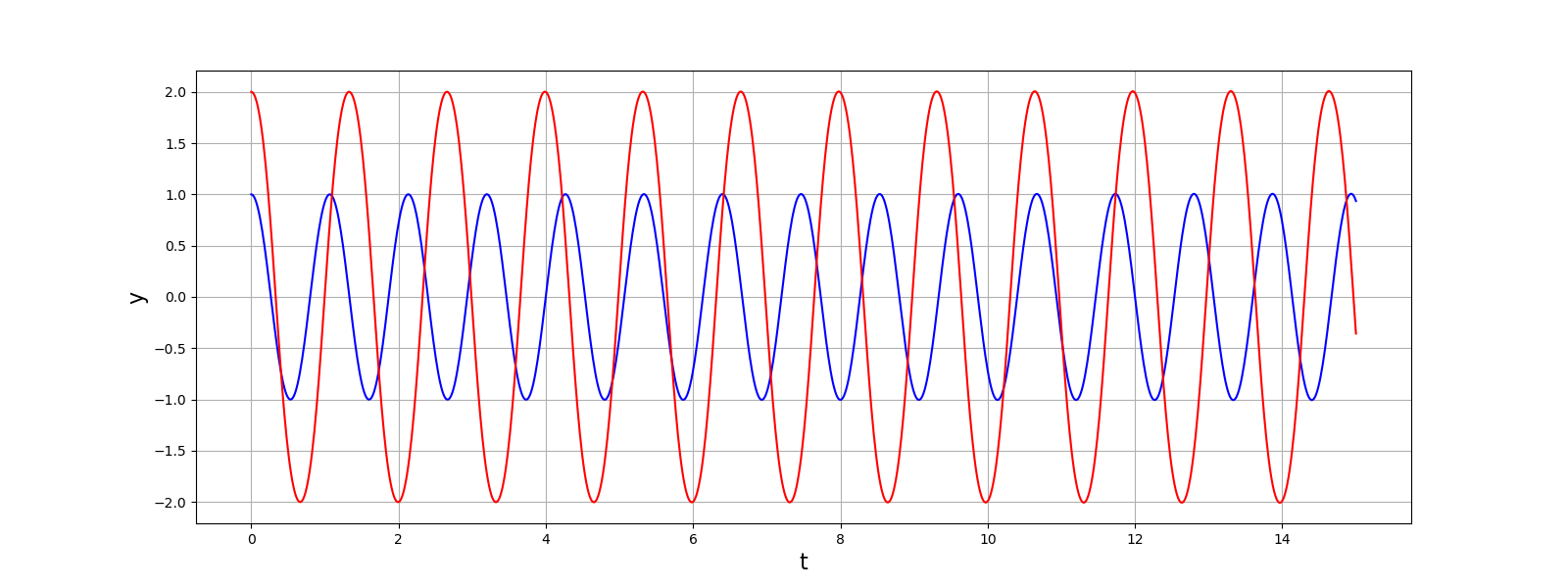
../_images/PendulePesant-fig1.png

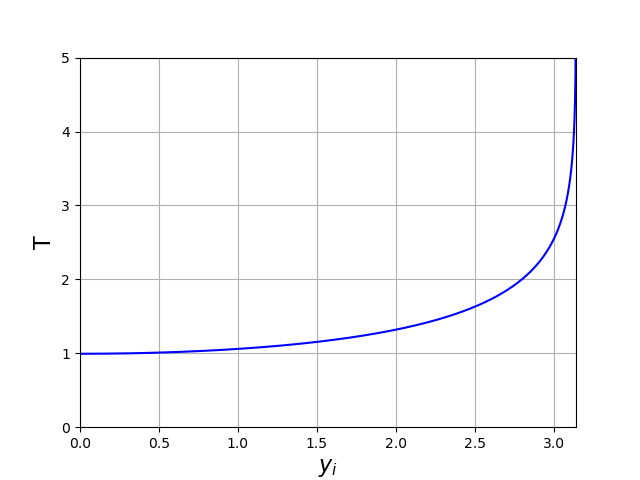
La période est d’autant plus grande que l’amplitude des oscillations est grande. L’oscillateur précédent avec \(b<0\) donne le même comportement.

La période d’oscillation s’exprime en fonction de la valeur initiale \(y_i\in[0,\pi]\) par l’intégrale suivante :

\[T(y_i)=\frac{4}{\omega_0\sqrt{2}}\int_0^{y_i}\frac{dy}{\sqrt{\cos(y)-\cos(y_i)}}\]

On cherche à calculer cette intégrale par la méthode des rectangles, dans le but de tracer la période en fonction de \(y_i\). La méthode est expliquée dans Intégration d’une fonction.

La fonction à intégrer n’est pas définie en \(y=y_i\) mais la méthode des rectangles à gauche ne nécessite pas de calculer la valeur de la fonction pour la borne supérieure de l’intervalle d’intégration. La fonction suivante calcule la période, en appliquant la méthode des rectangles avec 10000 rectangles :

1
2
3
4
5
6
7
def periode(w0,yi):
    N=10000
    h = yi/(N-1)
    y = np.arange(N-1)*h
    f = 1/np.sqrt(np.cos(y)-np.cos(yi))
    I = h*np.sum(f)
    return I*4/(np.sqrt(2)*w0)

Voici le tracé de la période en fonction de la valeur initiale :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
N = 1000
yi = np.linspace(0.01,np.pi,N)
T = np.zeros(N)
w0 = 2*np.pi
for k in range(N):
    T[k] = periode(w0,yi[k])
plt.figure()
plt.plot(yi,T,"b-")
plt.xlim(0,np.pi)
plt.ylim(0,5)
plt.xlabel(r'$y_i$',fontsize=16)
plt.ylabel('T',fontsize=16)
plt.grid()
plt.show()
../_images/PendulePesant-fig2.png

Mouvement à force centrale

Capacité numérique : obtenir des trajectoires d’un point matériel soumis à un champ de force centrale conservatif.

On considère un point matériel M soumis à une force centrale de centre O. Le mouvement se fait dans un plan muni d’un repère \((Oxy)\). On s’intéresse au cas d’une force centrale proportionnelle à l’inverse de \(r^n\), où \(n\) est un nombre réel. L’équation du mouvement est :

\[\frac{d^2\overrightarrow{OM}}{dt^2}=-\frac{K}{r^{n+1}}\overrightarrow{OM}\]

On pose \(v_x(t)=x'(t)\) et \(v_y(t)=y'(t)\). Le système différentiel du premier ordre s’écrit :

\[\begin{split}&\frac{dx(t)}{dt}=v_x(t)\\ &\frac{dy(t)}{dt}=v_y(t)\\ &\frac{dv_x(t)}{dt}=\dfrac{-K}{(x^2+y^2)^{(n+1)/2}}x(t)\\ &\frac{dv_y(t)}{dt}=\dfrac{-K}{(x^2+y^2)^{(n+1)/2}}y(t)\end{split}\]

On pose \(Y(t)=(x(t),y(t),v_x(t),v_y(t))\). Voici la fonction qui calcule la dérivée de \(Y\) :

1
2
3
4
5
6
7
8
9
def centrale(Y,t,K,n):
    x = Y[0]
    y = Y[1]
    vx = Y[2]
    vy = Y[3]
    r = np.sqrt(x*x+y*y)
    ax = -K*np.power(r,-(n+1))*x
    ay = -K*np.power(r,-(n+1))*y
    return([vx,vy,ax,ay])

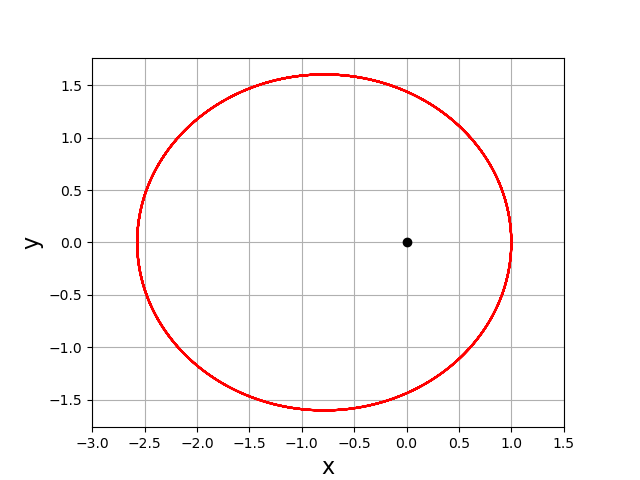
Considérons d’abord le cas d’une force centrale newtonienne (\(n=2\)). Si on pose \(K=1\) et \(r(0)=1\) (distance initiale) alors la vitesse de libération est \(\sqrt{2}\). Voici un exemple de trajectoire fermée :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
K=1
n=2
Y0 = [1,0,0,1.2]
N = 10000
t = np.linspace(0,100,N)
Y = odeint(centrale,Y0,t,args=(K,n),rtol=1e-5,atol=1e-12)
fig,ax = plt.subplots()
plt.plot(Y[:,0],Y[:,1],'r-')
ax.set_aspect('equal')
plt.xlabel('x',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.xlim(-3,1.5)
plt.grid()
plt.show()
../_images/ForceCentrale-fig1.png

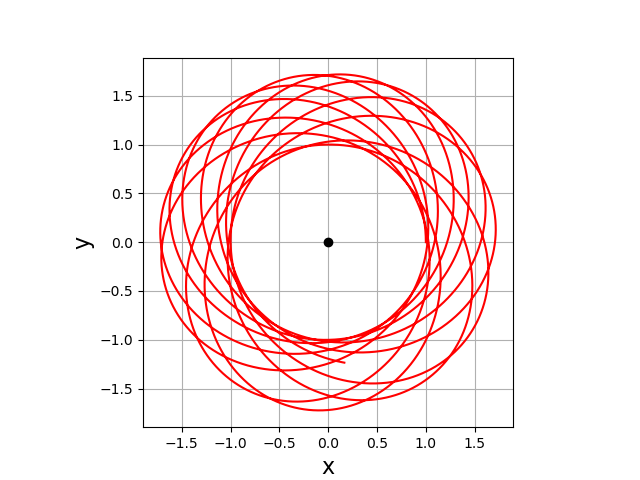
Voici un autre exemple, avec un exposant \(n=1{,}5\) :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
K=1
n=1.5
Y0 = [1,0,0,1.2]
N = 10000
t = np.linspace(0,100,N)
Y = odeint(centrale,Y0,t,args=(K,n),rtol=1e-5,atol=1e-12)
fig,ax = plt.subplots()
plt.plot(Y[:,0],Y[:,1],'r-')
ax.set_aspect('equal')
plt.xlabel('x',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.grid()
plt.show()
../_images/ForceCentrale-fig2.png

Chute d’une bille dans un fluide

Capacité numérique : Résoudre l’équation différentielle vérifiée par la vitesse, en utilisant une modélisation fournie du coefficient de traînée Cx en fonction du nombre de Reynolds, dans le cas de la chute d’une bille sphérique dans un fluide newtonien.

Soit une bille sphérique de masse \(m\) et de rayon \(R\), en mouvement dans le champ de pesanteur \(\overrightarrow{g}\) uniforme et soumis à une force de traînée caractérisée par le coefficient \(C_x\). La vitesse initiale étant nulle, la bille chute verticalement. Si le point \(O\) est sa position initiale et si l’axe \((Oz)\) est vertical descendant, l’équation du mouvement s’écrit :

\[m\frac{d^2z(t)}{dt^2}=\left(m-\frac{4}{3}\pi R^3\rho\right)g-\frac{1}{2}C_x\rho S\left(\frac{dz(t)}{dt}\right)^2\]

où \(\rho\) est la masse volumique du fluide et \(S=\pi R^2\).

Cette équation n’est valable que si le coefficient \(C_x\) est constant. Plus généralement, ce coefficient est fonction du nombre de Reynolds, qui lui même dépend de la vitesse :

\[Re = \frac{2\rho R}{\eta}\left(\frac{dz}{dt}\right)\]

où \(\eta\) est la viscosité dynamique du fluide. Posons \(v_z=\frac{dz}{dt}\) et écrivons le système différentiel du premier ordre :

\[\begin{split}&\frac{dz}{dt}=v_z(t)\\ &\frac{dv_z(t)}{dt}=\left(1-\frac{4}{3}\frac{\pi R^3\rho}{m}\right)g-\frac{1}{2}C_x(v_z(t))\frac{\rho\pi R^2}{m} v_z(t)^2\end{split}\]

où \(C_x(v_x)\) désigne le coefficient de traîné en fonction de la vitesse.