Intégration¶
Soit une fonction \(f:\mathbb{R}\rightarrow\mathbb{R}\) dont on cherche à calculer l’intégrale suivante :
Le calcul numérique de cette intégrale est nécessaire dans les cas suivants :
L’expression de \(f\) est connue mais sa primitive ne l’est pas.
Le calcul de \(f(x)\) se fait par une simulation et la primivive n’est pas connue.
Seules les valeurs de \(f\) pour un échantillonnage d’un intervalle \([a,b]\) sont connues, par exemple des valeurs expérimentales.
Méthode des rectangles¶
Considérons l’échantillonnage suivant de la fonction sur l’intervalle \([a,b]\), pour \(n=0,1,\ldots N-1\) :
La méthode des rectangles consiste à utiliser l’approximation suivante :
La figure suivante en montre le principe graphiquement : l’intégrale sur chaque sous-intervalle est assimilée à l’aire d’un rectangle, c’est-à-dire que la fonction est assimilée à une constante égale à sa valeur à gauche.
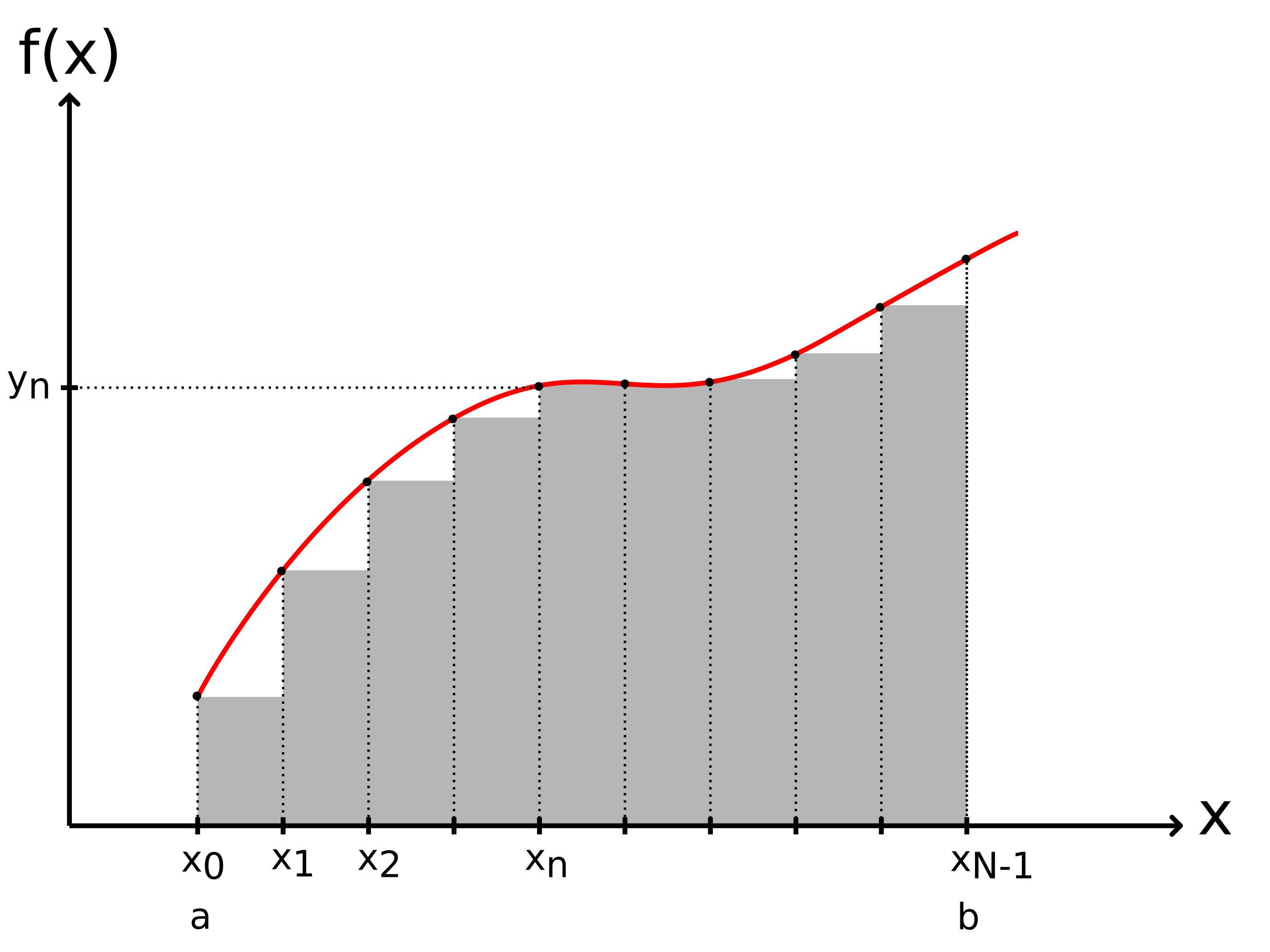
Cette méthode est nommée méthode des rectangles à gauche car, pour chaque sous-intervalle, on utilise la valeur à gauche du sous-intervalle. L’approximation de l’intégrale s’écrit :
La limite de cette expression lorsque \(N\rightarrow\infty\) est précisément la définition de l’intégrale de Riemann, ce qui garantit la convergence vers l’intégrale lorsque \(N\) augmente, c’est-à-dire lorsque le pas
est de plus en plus petit. L’expression (1) montre que le calcul de l’intégrale par la méthode des rectangles revient en fait à calculer la somme suivante :
Pour la méthode des rectangles à droite, on aurait à calculer la somme
Lorsque \(N\) est grand, ces deux sommes sont très proches et les deux méthodes sont donc équivalentes.
Intégration d’une fonction¶
Supposons qu’on dispose d’une expression de la fonction \(f\) et qu’une fonction Python évalue cette expression. La signature d’une telle fonction est :
def f(x):
# calcul et renvoie de f(x)
La fonction suivante réalise le calcul approché par la méthode des rectangles (à gauche) :
1 2 3 4 5 6 | import numpy as np
def integrale(f,a,b,N):
X = np.linspace(a,b,N)
Y = f(X)
return (b-a)/(N-1)*np.sum(Y[0:N-1])
|
Pour calculer la somme, nous sélectionnons les éléments d’indice 0 à N-2 au moyen d’une tranche puis nous appelons la fonction np.sum avec le tableau comme argument. Il est bien sûr possible d’écrire explicitement la boucle de calcul de la somme :
1 2 3 4 5 6 7 | def integrale_moins_rapide(f,a,b,N):
X = np.linspace(a,b,N)
Y = f(X)
S = 0
for n in range(N-1):
S += Y[n]
return (b-a)/(N-1)*S
|
Pour tester une méthode numérique, il est judicieux de le faire sur un cas où la solution exacte est connue. Considérons l’intégrale de la fonction sinus sur l’intervalle \([0,\pi/2]\), qui vaut exactement 1 :
def f(x):
return np.sin(x)
print(integrale(f,0,np.pi/2,100))
print(integrale(f,0,np.pi/2,1000))
print(integrale(f,0,np.pi/2,10000))
0.9920457059690396
0.9992136096236359
0.9999214502723134
Ces résultats suggèrent que l’erreur est divisée par 10 lorsque \(N\) est augmenté d’un facteur 10. La méthode des rectangles est en effet d’ordre 1, c’est-à-dire que la valeur absolue de l’erreur est majorée par \(K|h|\), où \(K\) est une constante.
Fonction intégrale¶
Il arrive fréquemment qu’on ait besoin de représenter graphiquement une fonction qui s’exprime sous la forme d’une intégrale :
Il serait bien sûr extrêmement inefficace d’appeler la fonction integrale (définie plus haut) pour chaque valeur de \(x\) de l’intervalle sur lequel on veut représenter la fonction. La bonne méthode consiste à échantillonner l’intervalle sur lequel on veut calculer \(g(x)\) puis calculer l’intégrale de proche en proche au moyen de la relation :
Ce schéma de calcul consitue en fait la méthode d’Euler apliquée à l’équation différentielle suivante :
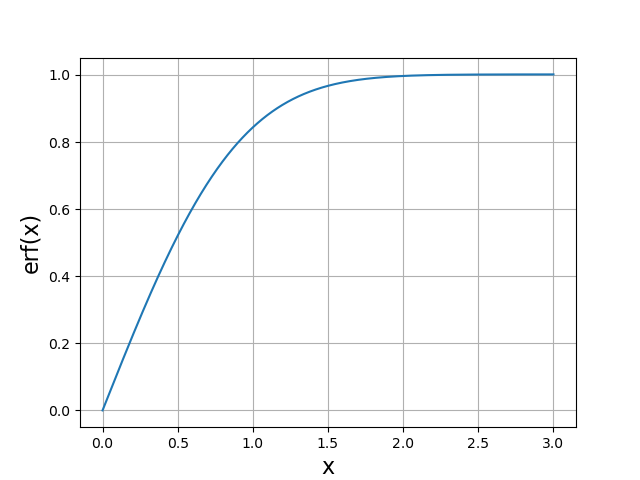
Voyons par exemple la fonction erreur, définie par :
Cette fonction existe dans le module scipy.special, qui permet d’évaluer un grand nombre de fonctions spéciales, mais nous souhaitons, à titre d’exemple, obtenir sa représentation graphique par la méthode des rectangles.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | import numpy as np
import matplotlib.pyplot as plt
N = 1000
x = np.linspace(0,3,N)
h = x[1]-x[0]
erf = np.zeros(N)
I = 0
for n in range(N):
erf[n] = I
I += np.exp(-x[n]**2)
erf *= 2*h/np.sqrt(np.pi)
plt.figure()
plt.plot(x,erf)
plt.xlabel('x',fontsize=16)
plt.ylabel('erf(x)',fontsize=16)
plt.grid()
plt.show()
|