Systèmes linéaires et filtrage

Réponse d’un système linéaire

Capacité numérique : mettre en oeuvre la méthode d’Euler pour simuler la réponse d’un système linéaire du premier ordre à une excitation de forme quelconque.

Un système linéaire du premier ordre est défini par l’équation différentielle suivante :

\[y'(t)+\frac{1}{\tau}y(t)=g(t)\]

où la fonction \(g\) définie l’excitation. La méthode d’Euler permet d’intégrer numériquement cette équation pour une fonction d’excitation quelconque. Considérons la fonction suivante :

\[\begin{split}&g(t)=G\ {\rm si\ }t\in[0,t_1]\\ &g(t)=0\ {\rm si\ }t>t_1\end{split}\]

Il peut s’agit, par exemple, d’un filtre RC passe-bas (\(\tau=RC\)) auquel on soumet une tension de valeur \(\tau G\) pendant une durée \(t_1\). Pour cet exemple simple, la solution analytique petu être obtenue, mais l’utilisation de la méthode d’Euler permettra de résoudre des cas plus complexes.

L’équation différentielle est définie par la fonction suivante, qui renvoie la valeur de \(y'\) :

def derive(y,t,tau,t1,G):
    if t<t1:
        g = G
    else:
        g = 0
    deriv_y = g-y/tau
    return deriv_y

Voici la fonction qui permet de mettre en oeuvre la méthode d’Euler, décrite dans Méthode d’Euler – Implémentation :

def euler(derive,t0,y0,T,N,args=()):
    '''
    Paramètres :
        derive : fonction F(y,t)
        t0 : instant initial
        y0 : valeur initiale de y
        T : durée
        N : nombre de points
        args : arguments supplémentaires de la fonction derive
    Objets renvoyés :
        t : tableau des instants
        Y : tableau des valeurs de y
    '''
    t = np.linspace(t0,t0+T,N)
    h = t[1]-t[0]
    Y = np.zeros(N)
    Y[0] = 0
    for n in range(0,N-1):
        Y[n+1] = Y[n] + h*derive(Y[n],t[n],*args)
    return (t,Y)

L’exemple ci-dessous montre la réponse du système à un échelon, que l’on obtient en posant \(T=t_1\) :

tau = 1
t1 = 10
G = 1
t0 = 0
y0 = 0
T = t1
N = 10000
(t,Y) = euler(derive,t0,y0,T,N,args=(tau,t1,E))
plt.figure()
plt.plot(t,Y,'r-')
plt.xlabel('t',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.ylim(0,1.2)
plt.grid()
plt.show()

La réponse impulsionnelle est obtenue avec \(t_1\ll T\) et \(G=1/t_1\) :

tau = 1
t1 = 0.01
G = 1/t1
t0 = 0
y0 = 0
T = 10
N = 10000
(t,Y) = euler(derive,t0,y0,T,N,args=(tau,t1,G))
plt.figure()
plt.plot(t,Y,'r-')
plt.xlabel('t',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.ylim(0,1.2)
plt.grid()
plt.show()

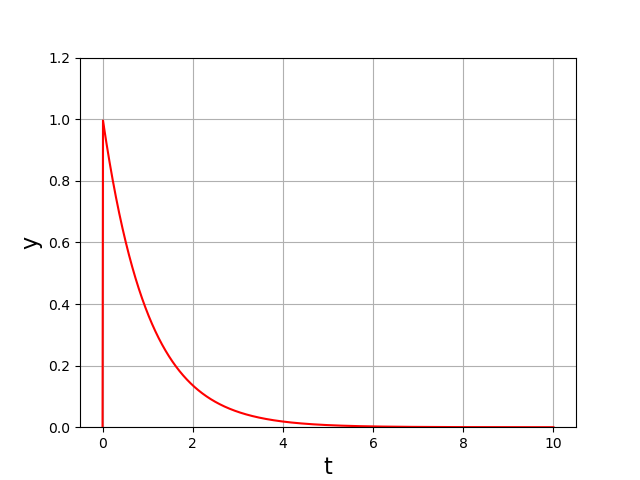
Considérons l’excitation suivante :

\[\begin{split}&g(t)=G\sin\left(2\pi\frac{t}{t_2}\right)\ {\rm si\ }t\in[0,t_1]\\ &g(t)=0\ {\rm si\ }t>t_1\end{split}\]

Pour traiter ce cas, nous définissons une fonction pour \(g\) car nous allons aussi tracer sa courbe :

def g(t,t1,t2,G):
    if t<t1:
        return G*np.sin(2*np.pi/t2*t)
    else:
        return 0

Voici la fonction qui définit l’équation différentielle :

def derive(y,t,tau,t1,t2,G):
    return g(t,t1,t2,G)-y/tau

Voici par exemple la réponse à une excitation comportant 5 cycles sinusoïdaux :

tau = 1
t1 = 1
t2 = 0.2
G = 1
t0 = 0
y0 = 0
T = 5
N = 10000
(t,Y) = euler(derive,t0,y0,T,N,args=(tau,t1,t2,G))
plt.figure()
plt.subplot(211)
gg = np.zeros(len(t))
for i in range(len(gg)):
    gg[i] = g(t[i],t1,t2,E)
plt.plot(t,gg,'b-')
plt.xlabel('t',fontsize=16)
plt.ylabel('g',fontsize=16)
plt.grid()
plt.subplot(212)
plt.plot(t,Y,'r-')
plt.xlabel('t',fontsize=16)
plt.ylabel('y',fontsize=16)
plt.grid()
plt.show()

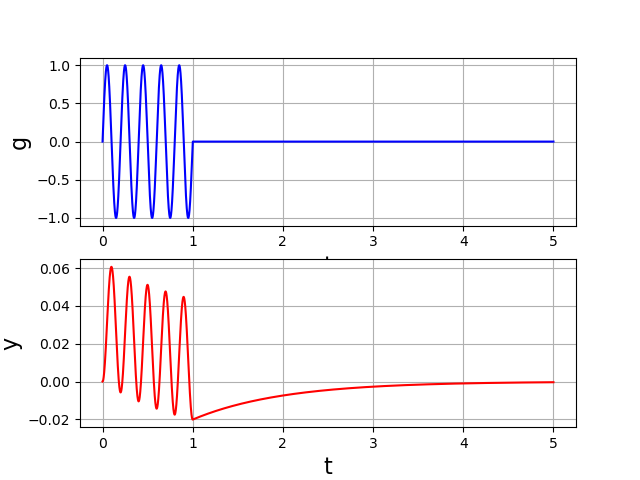
Filtrage d’un signal périodique

Capacité numérique : simuler l’action d’un filtre sur un signal périodique dont le spectre est fourni. Mettre en évidence l’influence des caractéristiques du filtre sur l’opération de filtrage.

Le signal périodique, de fréquence fondamentale \(f\), est défini par les amplitudes de ses harmoniques (\(A_k\) pour \(k=0,1,\ldots P\)) et par leur phase à l’origine (\(\phi_k\)) :

\[e(t)=\sum_{k=0}^PA_k\cos(2\pi kft+\phi_k)\]

où \(P\) est le rang de l’harmonique de plus haute fréquence, s’il existe, ou bien le rang auquel on décide de stopper la somme pour en donner une approximation.

La fonction signal définie ci-dessous effectue le calcul de cette somme et renvoie sa valeur :

def signal(t,f,A,phi):
    '''
        Paramètres :
            t : temps
            f : fréquence
            A : liste des amplitudes des harmoniques
            phi : liste des phases à l'origine des harmoniques
        Objets renvoyés :
            y : somme des harmoniques
    '''
    y = 0.0
    for k in range(len(A)):
        y += A[k]*np.cos(2*np.pi*k*f*t+phi[k])
    return y

Voici un exemple de signal, comportant 5 harmoniques :

A = [0,1,0.0,0.4,0.0,0.1]
phi = [0,0,0,-0.7,0,0.4]
P = len(A)+1
f=1.0 # fréquence
(a,b)=(0,4/f) # intervalle du tracé
N = 100*P # 100 échantillons par période pour l'harmonique de rang P
t = np.linspace(a,b,N)
plt.figure()
plt.plot(t,signal(t,f,A,phi),'b',label='e(t)')
plt.grid()
plt.xlabel('t',fontsize=16)
plt.ylabel('u',fontsize=16)
plt.legend(loc='upper right')

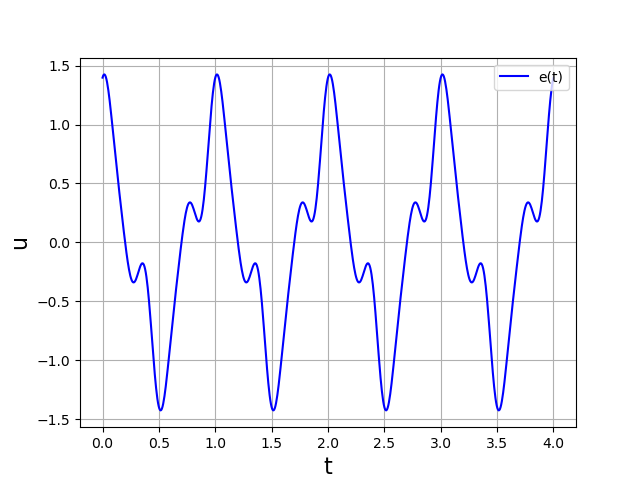
L’action du filtre sur un signal périodique est déterminée par la fonction de transfert harmonique. Par exemple, pour un filtre passe-bas du premier ordre, on définit la fonction suivante :

def H(f,fc):
    return 1/(1+1j*(f/fc))

On suppose, par convention, que le premier paramètre de la fonction est la fréquence. Les autres paramètres (ici fc) permettent de définir les paramètres du filtre.

La fonction suivante applique une fonction de transfert à un signal défini par la liste des amplitudes et des phases de ses harmoniques :

def filtrage(H,A,phi,args):
    '''
        Paramètres :
            H : fonction de transfert (premier paramètre = fréquence)
            A : liste des amplitudes des harmoniques
            phi : liste des phases à l'origine des harmoniques
            args : arguments supplémentaires pour la fonction H (n-uplet)
        Objets renvoyés :
            A_f : liste des amplitudes du signal filtré
            phi_f : liste des phases à l'origine du signal filtré
    '''
    A_f = A.copy() # on doit faire une copie des listes pour ne pas les modifier
    phi_f = phi.copy()
    for k in range(len(A)):
        h = H(k*f,*args) # harmonique de fréquence k*f
        A_f[k] *= np.absolute(h)
        phi_f[k] += np.angle(h)
    return (A_f,phi_f)

Voici par exemple le filtrage passe-bas du signal défini plus haut, avec une fréquence de coupure égale à sa fréquence. La courbe du signal filtré est tracée sur la même figure que la courbe du signal d’entrée.

(A_f,phi_f) = filtrage(H,A,phi,(1,))
t = np.linspace(a,b,N)
plt.plot(t,signal(t,f,A_f,phi),'r',label='s(t)')
plt.legend(loc='upper right')
plt.show()

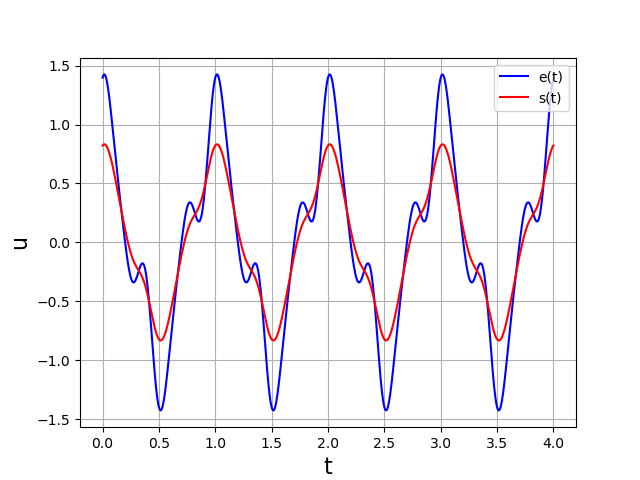
Lorsque le signal périodique comporte une infinité d’harmoniques, on doit choisir \(P\) assez grand pour obtenir une représentation satisfaisante du signal. Considérons l’exemple du signal créneau :

P=100
A = [0]*(P+1)
phi = [0]*(P+1)
for k in range(1,P+1):
    A[k] = 2*(1-(-1)**k)/(np.pi*(k))
    phi[k] = np.pi/2
f=1.0 # fréquence
(a,b)=(0,4/f) # intervalle du tracé
N = 100*P
t = np.linspace(a,b,N)
plt.figure()
plt.plot(t,signal(t,f,A,phi),'b',label='e(t)')
plt.grid()
plt.xlabel('t',fontsize=16)
plt.ylabel('u',fontsize=16)
(A_f,phi_f) = filtrage(H,A,phi,(5,))
t = np.linspace(a,b,N)
plt.plot(t,signal(t,f,A_f,phi),'r',label='s(t)')
plt.legend(loc='upper right')
plt.show()

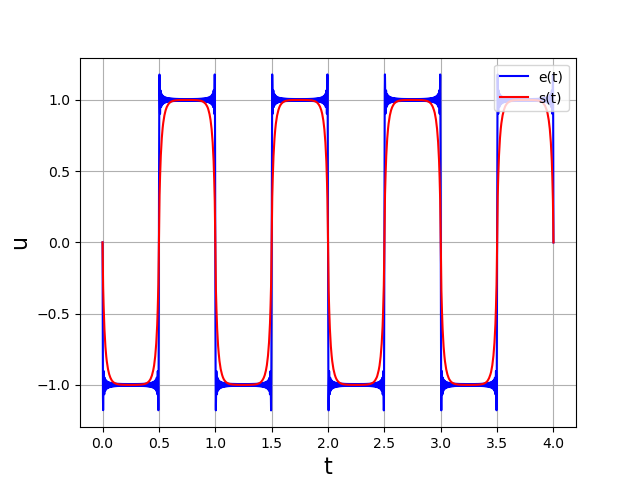
Pour le signal créneau, l’obtention d’une forme correcte nécessite un \(P\) très grand, en raison du phénomène de Gibbs. Dans le cas d’un filtrage passe-bas, le signal de sortie ne présente pas ce problème.