Mesures et incertitudes

Composition des incertitudes

Capacité numérique : simuler un processus aléatoire permettant de caractériser la variabilité de la valeur d’une grandeur composée.

La distribution normale est utilisée pour simuler un ensemble de mesures dont l’espérance est \(\mu\) et l’incertitude-type \(\sigma\).

On simule des mesures d’une grandeur \(x_1\) dont l’espérance est \(\mu_1=2\) et l’incertitude-type \(\sigma_1=0{,}1\), et des mesures d’une grandeur \(x_2\) dont l’espérance est \(\mu_2=5\) et l’incertitude-type \(\sigma_2=0{,}1\)

import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random

mu1 = 2
sigma1 = 0.1
mu2 = 5
sigma2 = 0.1
N = 100000
x1 = random.normal(mu1,sigma1,N)
x2 = random.normal(mu2,sigma2,N)

Si l’on dispose seulement d’une valeur expérimentale de \(x_1\), l’espérance est inconnue mais on utilise cette valeur comme estimation de l’espérance pour faire la simulation.

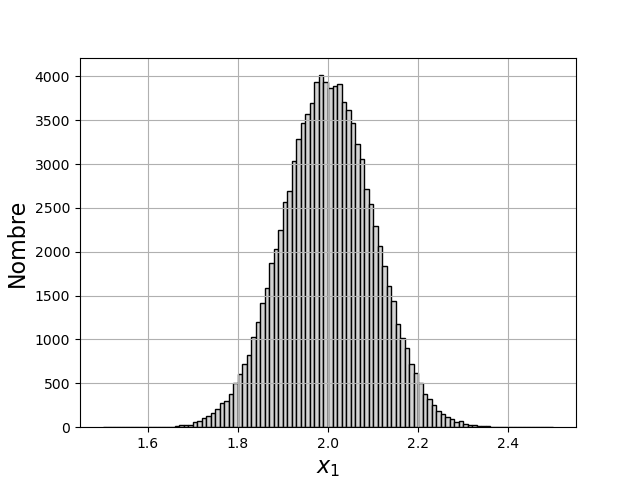
Voici un histogramme de \(x_1\), qui désigne la variable aléatoire correspondant aux différentes valeurs mesurées :

plt.figure()
plt.hist(x1,bins=100,range=(mu1-5*sigma1,mu1+5*sigma1),color='lightgrey',edgecolor='k')
plt.xlabel('$x_1$',fontsize=16)
plt.ylabel('Nombre',fontsize=16,rotation=90)
plt.grid()
plt.show()

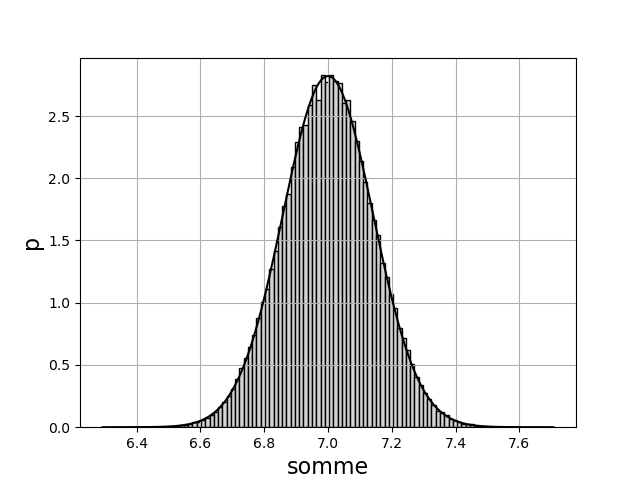
On considère la somme \(s=x_1+x_2\) :

somme = x1+x2

L’espérance de la somme est \(\mu=\mu_1+\mu_2\). Pour calculer l’écart-type, on peut utiliser la formule de composition des incertitudes pour une somme :

\[\sigma^2=\sigma_1^2+\sigma_2^2\]

ou bien obtenir une estimation à partir des échantillons de la simulation (méthode plus générale) :

mu = mu1+mu2
sigma = np.sqrt(sigma1**2+sigma2**2)
print(sigma,somme.std())

0.14142135623730953 0.14139559017545333

On peut tracer un histogramme avec une conversion en densité et tracer la loi normale avec l’espérance et l’écart-type calculés :

plt.figure()
plt.hist(somme,bins=100,density=True,color='lightgrey',edgecolor='k')
plt.xlabel('somme',fontsize=16)
plt.ylabel('p',fontsize=16)
plt.grid()
som = np.linspace(mu-5*sigma,mu+5*sigma,1000)
p = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-(som-mu)**2/(2*sigma**2))
plt.plot(som,p,'k-') # tracé de la loi normale
plt.show()

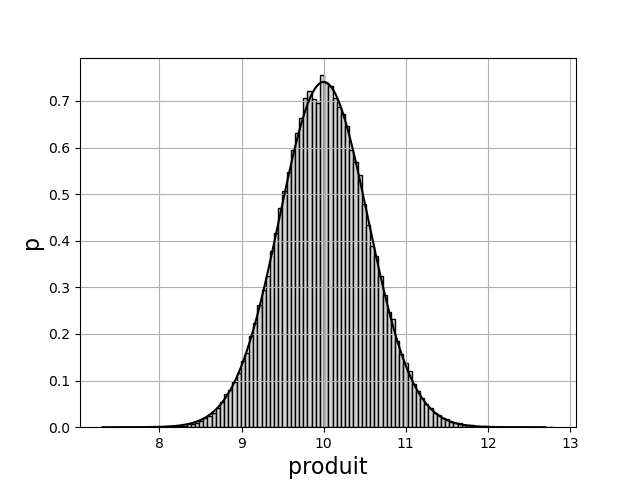
Voici la même simulation pour le produit \(p=x_1x_2\). Dans ce cas, la formule de composition des incertitudes s’écrit :

\[\left(\frac{\sigma}{\mu}\right)^2=\left(\frac{\sigma_1}{\mu_1}\right)^2+\left(\frac{\sigma_2}{\mu_2}\right)^2\]

produit = x1*x2
mu = mu1*mu2
sigma = mu*np.sqrt((sigma1/mu1)**2+(sigma2/mu2)**2)
plt.figure()
plt.hist(produit,bins=100,density=True,color='lightgrey',edgecolor='k')
plt.xlabel('produit',fontsize=16)
plt.ylabel('p',fontsize=16)
plt.grid()
prod = np.linspace(mu-5*sigma,mu+5*sigma,1000)
p = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-(prod-mu)**2/(2*sigma**2))
plt.plot(prod,p,'k-') # tracé de la loi normale
plt.show()

Ce type de simulation a surtout un intérêt lorsque la fonction de composition est plus complexe, par exemple :

def f(x1,x2):
    return x1*np.log(np.abs(x2))

y = f(x1,x2)
mu = f(mu1,mu2)
sigma = y.std()
print(sigma)

0.16638197039186856

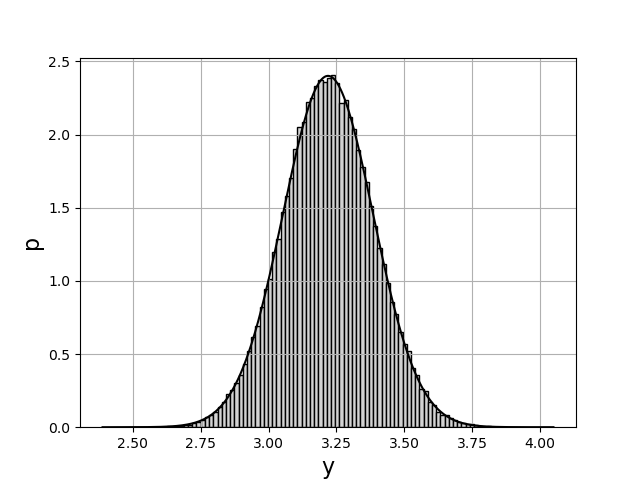
On obtient ainsi l’incertitude de la grandeur composée. Remarquons à nouveau que, dans un contexte expérimental, \(\mu_1\) et \(\mu_2\) sont les valeurs mesurées (estimations des espérances) et \(\sigma_1\) et \(\sigma_2\) sont les incertitudes-types expérimentales. Les quelques lignes de code ci-dessus constituent une estimation de l’incertitude par une méthode de Monte-Carlo, et remplacerons avantageusement un calcul laborieux de composition des incertitudes.

Le tracé de l’histogramme permet de vérifier que la répartition des valeurs suit bien la loi normale :

plt.figure()
plt.hist(y,bins=100,density=True,color='lightgrey',edgecolor='k')
plt.xlabel('y',fontsize=16)
plt.ylabel('p',fontsize=16)
plt.grid()
yy = np.linspace(mu-5*sigma,mu+5*sigma,1000)
p = 1/(np.sqrt(2*np.pi)*sigma)*np.exp(-(yy-mu)**2/(2*sigma**2))
plt.plot(yy,p,'k-')

Régression linéaire : incertitude des paramètres

Capacité numérique : simuler un processus aléatoire de variation des valeurs expérimentales de l’une des grandeurs pour évaluer l’incertitude sur les paramètres du modèle.

La méthode des moindres carrés permet de déterminer les paramètres d’une fonction modèle qui permettent de l’ajuster au mieux à des données expérimentales. Or ces données expérimentales sont sujettes à des incertitudes. On se propose d’utiliser une simulation de Monte-Carlo pour déterminer l’incertitude qui en découle sur les paramètres du modèle.

Supposons qu’on ait une série de \(N\) valeurs \(x_n\) dont l’incertitude-type est \(\sigma_x\) et une série de valeurs mesurées correspondantes \(y_n\) dont l’incertitude-type est \(\sigma_y\). Les variations aléatoires des valeurs mesurées de \(x\) et de \(y\) peuvent être simulées par une distribution normale d’espérance nulle et d’écart-type \(\sigma_x\) et \(\sigma_y\).

Si nous faisons l’hypothèse que la relation entre les grandeurs \(x\) et \(y\) est \(y=ax+b\), une régression linéaire permet de déterminer les paramètres \(a\) et \(b\) optimaux (au sens des moindres carrés).

Une simulation de Monte-Carlo permet de déterminer les paramètres \(a\) et \(b\) moyens et leur incertitude. Pour cela, on effectue un grand nombre \(N_t\) de tirages. Pour chacun de ces tirages, on ajoute à chaque valeur \(x_n\) une valeur aléatoire obéissant à la loi de distribution normale avec une espérance nulle et un écart-type \(\sigma_x\) (de même pour les valeurs \(y_n\)) ce qui permet de simuler l’effet des incertitudes. Une régression linéaire effectuée sur les \(x_n\) et les \(y_n\) modifiés donne un couple de paramètres \((a,b)\). Il s’agit alors de calculer la moyenne et l’écart-type de la série des \(N_t\) valeurs de \(a\) obtenue, et de la série des valeurs de \(b\). On obtient ainsi les valeurs des paramètres \(a\) et \(b\) et leur incertitude.

Il faut remarquer que l’espérance de la loi normale utilisée pour simuler le processus aléatoire de la mesure est la valeur expérimentale (obtenue par une mesure unique ou par plusieurs mesures), qui constitue en effet une estimation de l’espérance, même si elle est d’autant plus grossière que l’incertitude est grande.

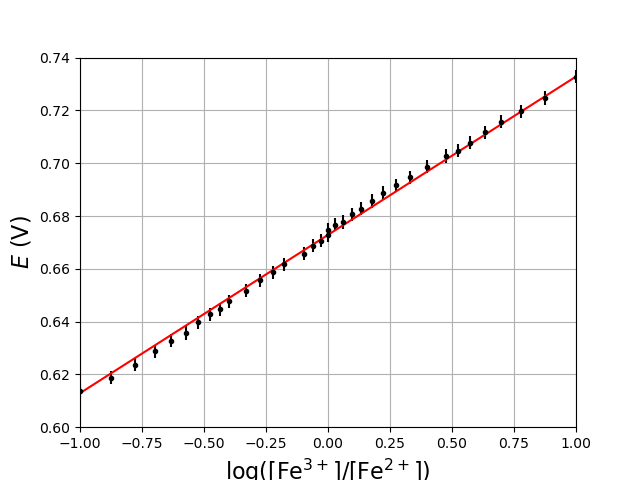
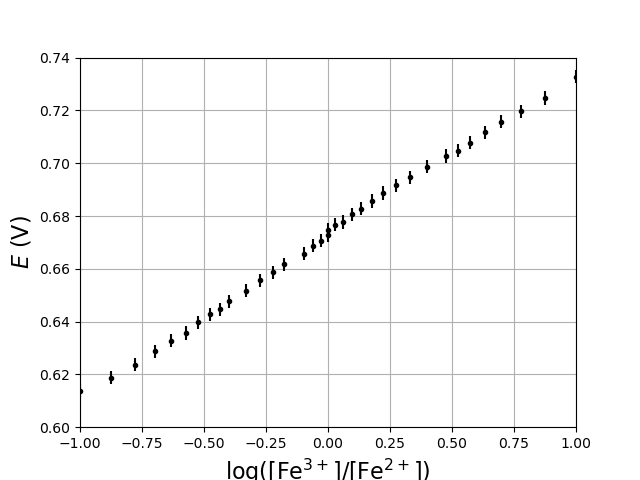
Appliquons cette méthode à des résultats expérimentaux. Il s’agit d’une vérification expérimentale de la relation de Nernst pour le couple \(\rm Fe^{3+}/Fe^{2+}\). On trace le nuage de points dont l’abscisse et le logarithme du rapport des concentrations, l’ordonnée le potentiel d’oxydoréduction. Les données sont extraites d’un fichier CSV. Afin de tracer les points avec des barres d’incertitudes, on utilise la fonction pyplot.errorbar :

import numpy as np
import matplotlib.pyplot as plt
import numpy.random as random

[v1,U1]=np.loadtxt("Fe2-Fe3(v).csv",skiprows=1,unpack=True)
[v2,U2]=np.loadtxt("Fe3-Fe2(v).csv",skiprows=1,unpack=True)
E1=U1+247.7
E2=U2+247.7
E1*=1e-3
E2*=1e-3
c=0.01
v0=30
log1=np.log10(v1/v0)
log2=np.log10(v0/v2)
log=np.concatenate((log1,log2))
E=np.concatenate((E1,E2))

# incertitudes
sigma_y = 0.0025
sigma_x = 6e-3

plt.figure()
plt.errorbar(log,E,yerr=sigma_y,xerr=sigma_x,ecolor='k',fmt='k.')
plt.xlim(-1.0,1.0)
plt.ylim(0.600,0.740)
plt.grid()
plt.ylabel(r"$E\ (\rm V)$",fontsize=16)
plt.xlabel(r"${\rm log}([\rm Fe^{3+}]/[\rm Fe^{2+}])$",fontsize=16)
plt.show()

Un régression linéaire par la méthode des moindres carrés permet les coefficients \(a,b\) de la relation \(y=ax+b\) qui minimise la somme des écarts au carré entre les points expérimentaux et la droite :

coef,cov = np.polyfit(log,E,deg=1,cov=True)
a = coef[0]
b = coef[1]
print('a = %f, b = %f'%(a,b))

a = 0.059990, b = 0.672865

Une simulation de Monte-Carlo permet de déterminer l’incertitude de chacun de ces paramètres. La fonction parametres définie ci-dessous ajoute à chaque point expérimental une variation aléatoire obéissant à la loi normale, puis effectue la régression linéaire pour ces nouveaux points :

def parametres(X,Y,sigma_x,sigma_y):
    N = len(X)
    Ya = Y + random.normal(0,sigma_x,N)
    Xa = X + random.normal(0,sigma_y,N)
    [A,B] = np.polyfit(Xa,Ya,deg=1)
    return (A,B)

Voici un exemple :

print(parametres(log,E,sigma_x,sigma_y))

(0.059297596395972436, 0.6723097734244442)

La réalisation de \(N_t\) calculs de paramètres permet d’obtenir les valeurs moyennes de ces paramètres et les incertitudes-types :

print(parametres(log,E,sigma_x,sigma_y))

def statistique_parametres(X,Y,sigma_x,sigma_y,Nt):
    tab_A = np.zeros(Nt)
    tab_B = np.zeros(Nt)
    for k in range(Nt):
        (A,B) = parametres(X,Y,sigma_x,sigma_y)
        tab_A[k] = A
        tab_B[k] = B
    mA,eA = tab_A.mean(),tab_A.std() # moyenne et écart-type du paramètre a
    mB,eB = tab_B.mean(),tab_B.std() # moyenne et écart-type du paramètre b
    return (mA,eA,mB,eB)

(mA,eA,mB,eB) = statistique_parametres(log,E,sigma_x,sigma_y,10000)
print("a = %f +/- %f"%(mA,eA))
print("b = %f +/- %f"%(mB,eB))

a = 0.059953 +/- 0.001589
b = 0.672867 +/- 0.000955

Pour finir, on tracer la droite d’équation \(y=ax+b\) avec les points expérimentaux :

plt.figure()
plt.errorbar(log,E,yerr=sigma_y,xerr=sigma_x,ecolor='k',fmt='k.')
plt.plot([-1,1],[-mA+mB,mA+mB],'r-')
plt.xlim(-1.0,1.0)
plt.ylim(0.600,0.740)
plt.grid()
plt.ylabel(r"$E\ (\rm V)$",fontsize=16)
plt.xlabel(r"${\rm log}([\rm Fe^{3+}]/[\rm Fe^{2+}])$",fontsize=16)